Archivo de la etiqueta: media geométrica

Geometría Moderna I: Desigualdades geométricas

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada, con la ayuda de varias fórmulas y resultados que hemos visto hasta ahora, mostraremos algunas desigualdades geométricas básicas e importantes, entre ellas la desigualdad entre las medias geométrica y aritmética, y la desigualdad de Erdos Mordell.

Medias armónica, geométrica, aritmética y cuadrática

Teorema 1. Dados dos segmentos de longitudes $a$ y $b$ tenemos las siguientes desigualdades:
$\dfrac{2ab}{a + b} \leq \sqrt{ab} \leq \dfrac{a + b}{2} \leq \sqrt{\dfrac{a^2 + b^2}{2}}$.

De izquierda a derecha estas cantidades se conocen como media armónica, media geométrica, media aritmética y media cuadrática de $a$ y $b$.

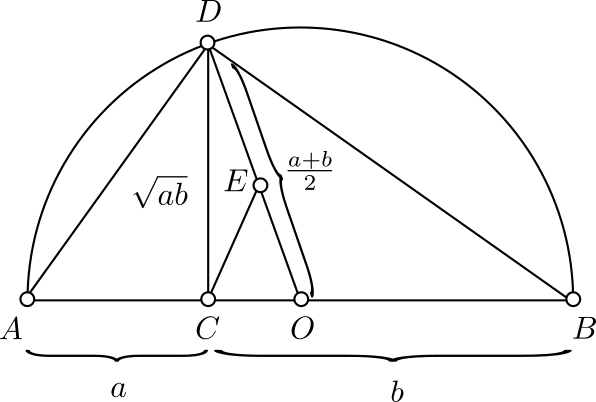
Demostración. Tracemos un semicírculo tomando como diámetro un segmento $BC$  de longitud $a + b$ y sea $D \in BC$ tal que $BD = a$ y $DC = b$, en $D$ levantamos una perpendicular a $BC$ que corta al arco $\overset{\LARGE{\frown}}{CB}$ en $A$, entonces $\triangle ABC$ es un triángulo rectángulo con $\angle A = \dfrac{\pi}{2}$.

Por criterio de semejanza AA $\triangle ADB \sim \triangle CDA$ y tenemos que $\dfrac{AD}{CD} = \dfrac{BD}{AD}$.

Por lo tanto $AD$ es la media geométrica de $BD$ y $DC$, esto es $AD^2 = BD \times CD$.

Figura 1

Consideremos $O$ el punto medio de $BC$, sea $E \in AO$ tal que $DE  \perp AO$, como $\triangle ADO \sim \triangle AED$ entonces
$\dfrac{AD}{AE} = \dfrac{AO}{AD}$
$\Rightarrow AE = \dfrac{2AD^2}{2AO} = \dfrac{2BD \times DC}{BC} = \dfrac{2ab}{a + b}$.

Por el teorema de Pitágoras en $\triangle AED$
$AD^2 = AE^2 + DE^2 \Rightarrow AE \leq AD \Rightarrow \dfrac{2ab}{a + b} \leq \sqrt{ab}$.

Por el teorema de Pitágoras en $\triangle ADO$
$AO^2 = AD^2 + DO^2 \Rightarrow AD \leq AO \Rightarrow \sqrt{ab} \leq \dfrac{a + b}{2}$.

Ahora tracemos $OF$ el radio perpendicular a $BC$, entonces
$OD = \dfrac{a + b}{2} – a = \dfrac{b – a}{2}$.

Aplicando el teorema de Pitágoras a $\triangle ODF$ obtenemos,
$DF^2 = OF^2 + OD^2 = (\dfrac{b – a}{2})^2 + (\dfrac{a + b}{2})^2 =\dfrac{a^2 + b^2}{2}$.

Como $OF \leq DF \Rightarrow \dfrac{a + b}{2} \leq \sqrt{\dfrac{a^2 + b^2}{2}}$.

$\blacksquare$

Corolario. Sean $w$, $x$, $y$, $z$ números reales positivos entonces:
$wxyz \leq (\dfrac{w + x + y + z}{4})^4$, y la igualdad se da si y solo si $w = x = y = z$.

Demostración. Aplicamos la desigualdad entre las medias geométrica y aritmética a los pares de números $w$, $x$; $y$, $z$.
$\sqrt{wx} \leq \dfrac{w + x}{2}$, $\sqrt{yz} \leq \dfrac{y + z}{2}$.

Por lo tanto, $\sqrt{wxyz} \leq (\dfrac{w + x}{2}) (\dfrac{y + z}{2})$.

Ahora volvemos a usar la desigualdad entre las medias geométrica y aritmética
$\sqrt{\dfrac{(w + x)}{2} \dfrac{(y + z)}{2}} \leq \dfrac{\dfrac{w + x}{2} + \dfrac{y + z}{2}}{2} = \dfrac{w + x + y + z}{4}$

Por lo tanto, $\sqrt[4]{wxyz} \leq \sqrt{\dfrac{(w + x)}{2} \dfrac{(y + z)}{2}} \leq \dfrac{w + x + y + z}{4}$.

En consecuencia, $wxyz \leq (\dfrac{w + x + y + z}{4})^4$.

$\blacksquare$

Desigualdad de Erdos Mordell

Lema de Mordell. Sea $\triangle ABC$ y $P$ un punto en su interior, considera $D$, $E$ y $F$ las proyecciones de $P$ a los lados $BC$, $AC$ y $AB$ respectivamente, entonces $PA \sin A \geq PF \sin B + PE \sin C$.

Demostración. Notemos que la circunferencia con diámetro $PA$ pasa por $F$ y por $E$, pues $AP$ subtiende ángulos rectos en $F$ y $E$.

Figura 2

Por la ley extendida de los senos,
$\sin BAC = \sin (\pi – BAC) = \sin EPF = \dfrac{EF}{PA}$, esto implica que $PA \sin A = EF$.

Sean $G$ y $H$ las proyecciones de $E$ y $F$ respectivamente en la recta que pasa por $P$ y $D$.

$\square FBDP$ es cíclico, pues $PB$ subtiende ángulos rectos en $F$ y $D$, entonces $\angle DBA$ y $\angle FPD$ son y suplementarios por lo tanto $\sin DBA = \sin HPF = \dfrac{FH}{FP}$.

Como resultado $FP \sin B = FH$, igualmente podemos ver que $PE \sin C = EG$.

Sea $I = EF \cap HP$, por el teorema de Pitágoras podemos ver que $IE \geq GE$ y $FI \geq FH$,

Por lo tanto, $PA \sin A \geq PF \sin B + PE \sin C$.

$\blacksquare$

Teorema 2, desigualdad de Erdos Mordell. Sea $\triangle ABC$ y $P$ un punto en su interior, considera $D$, $E$ y $F$ las proyecciones de $P$ a los lados $BC$, $AC$ y $AB$ respectivamente, entonces $PA + PB + PC \geq 2(PD + PE + PF)$.

Demostración. Debido al lema anterior tenemos lo siguiente:
$PA \geq PF\dfrac{\sin B}{\sin A} + PE\dfrac{\sin C}{\sin A}$,
$PB \geq PF\dfrac{\sin A}{\sin B} + PD\dfrac{\sin C}{\sin B}$,
$PC \geq PE\dfrac{\sin A}{\sin C} + PD\dfrac{\sin B}{\sin C}$.

Sumamos estas tres desigualdades
$PA + PB + PC \geq$

$PF(\dfrac{\sin B}{\sin A} + \dfrac{\sin A}{\sin B}) + PE(\dfrac{\sin C}{\sin A} + \dfrac{\sin A}{\sin C}) + PD(\dfrac{\sin B}{\sin C} + \dfrac{\sin C}{\sin B})$

$= PF(\dfrac{\sin^2A + \sin^2 B}{\sin A \sin B}) + PE(\dfrac{\sin^2 A + \sin^2 C}{\sin A \sin C}) + PD(\dfrac{\sin^2 B + \sin^2 C}{\sin B \sin C})$.

Sustituimos $a$ y $b$ por $a^2$ y $b^2$ en la desigualdad entre las medias geométrica y aritmética
$\dfrac{a^2 + b^2}{2} \geq \sqrt{a^2b^2}$, por lo tanto, $\dfrac{a^2 + b^2}{ab} \geq 2$.

Aplicamos esto a nuestra suma y como resultado obtenemos
$PA + PB + PC \geq 2(PD + PE + PF)$.

$\blacksquare$

Problema 1. Sea $\triangle ABC$ e $I$ su incentro, considera $P$, $Q$ y $R$ los puntos medios de los arcos $\overset{\LARGE{\frown}}{BC}$, $\overset{\LARGE{\frown}}{CA}$ y $\overset{\LARGE{\frown}}{AB}$ que no contienen a los vértices de $\triangle ABC$, entonces $IP + IQ + IR \geq IA + IB + IC$.

Solución. Sean $D = PQ \cap CR$, $E = QR \cap AP$ y $F = RP \cap BQ$.

Figura 3

Por la entrada anterior sabemos que $Q$ es el centro de una circunferencia que pasa por $I$, $A$ y $C$, y que $R$ es el centro de una circunferencia que pasa por $I$, $A$ y $B$, entonces $QA = QI$ y $RA = RI$.

Por lo tanto, $\square ARIQ$ es un rombo, de esto se sigue que $QR \perp AI$ y $AE = IE$.

Igualmente vemos que $RP \perp BI$, $BF = IF$ y $PQ \perp CI$, $CD = ID$.

Aplicamos la desigualdad de Erdos Mordell a $\triangle PQR$ y al punto $I$
$IP + IQ + IR \geq 2(ID + IE + IF) = 2(\dfrac{IC}{2} + \dfrac{IA}{2} + \dfrac{IB}{2})$.

En conclusión, $IP + IQ + IR \geq IA + IB + IC$.

$\blacksquare$

Desigualdades de Euler y de Padoa

Proposición 1, desigualdad de Euler. El circunradio $R$ y el inradio $r$ de todo triangulo cumplen $R \geq 2r$ y la igualdad se cumple si y solo si el triángulo es equilátero.

Demostración. La fórmula de Euler nos asegura que $0 \leq OI^2 = R(R – 2r) = R^2 – 2Rr$, donde $I$ es el incentro y $O$ el circuncentro del triángulo.

Como resultado, $R \geq 2r$.

$\blacksquare$

Proposición 2, desigualdad de Padoa. Sea $\triangle ABC$ con lados $c = AB$, $a = BC$ y $b = AC$ entonces $abc \geq (a + b – c)(a + c – b)(b + c – a)$.

Demostración. Sean $s = \dfrac{a + b + c}{2}$, $R$ el circunradio y $r$ el inradio de $\triangle ABC$, entonces tenemos las siguientes fórmulas para el área de $\triangle ABC$:
$(\triangle ABC) = \sqrt{s(s – a)(s – b)(s – c)} = \dfrac{abc}{4R} = rs$.

Notemos lo siguiente
$(a + b – c)(a + c – b)(b + c – a) = (2s – 2)(2s – 2b)(2s – 2a) = 8(s – c)(s – b)(s – a) $
$= \dfrac{8(\triangle ABC)^2 }{s} = \dfrac{8r^2s^2}{s} = 8r^2s$.

Por otro lado, $abc = 4Rrs$.

Por lo tanto, la desigualdad que queremos mostrar es equivalente a $8r^2s \leq 4Rrs$ que a su vez es equivalente a $2r \leq R$, lo cual es cierto por la proposición anterior.

$\blacksquare$

Transformación de Ravi

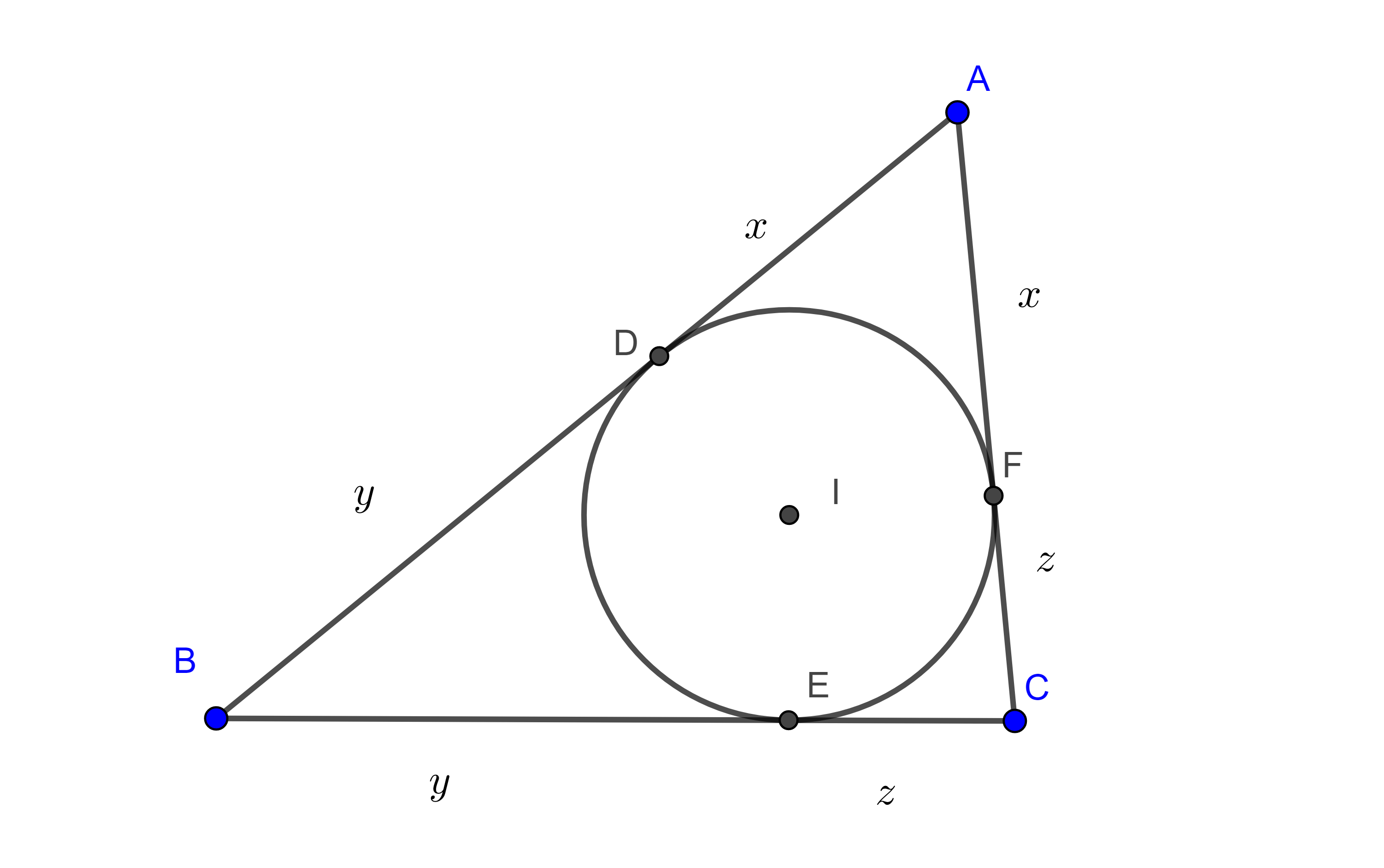
Recordemos que las tangentes desde un punto a una circunferencia son iguales, por lo que los puntos de tangencia del incírculo de un triángulo, divide al perímetro del triángulo en tres pares de segmentos iguales, así que podemos expresar a los lados de un triángulo de esta manera para resolver algunas desigualdades geométricas.

$a = BC = y + z$, $b = AC = x + z$, $c = AB = x + y$.

Figura 4

Problema 2. Para los ángulos internos de un triángulo $\triangle ABC$ tenemos la siguiente desigualdad.
$\sin \dfrac{A}{2} \sin \dfrac{B}{2} \sin \dfrac{C}{2} \leq \dfrac{1}{8}$.

Solución. Usando la identidad para el seno del ángulo medio y la ley de los cosenos tenemos:
$\sin^2 \dfrac{A}{2} = \dfrac{1}{2}(1 – \cos A) = \dfrac{1}{2}(1 + \dfrac{a^2 – (b^2 + c^2)}{2bc})$
$= \dfrac{a^2 – (b – c)^2}{4bc} = \dfrac{y^2 + 2yz + z^2 – (z – y)^2}{4bc} = \dfrac{yz}{bc}$.

Igualmente tenemos
$\sin^2 \dfrac{B}{2} = \dfrac{xz}{ac}$ y $\sin^2 \dfrac{C}{2} = \dfrac{xy}{ab}$.

A continuación despejamos y hacemos el producto
$\sin \dfrac{A}{2} \sin \dfrac{B}{2} \sin \dfrac{C}{2} = \dfrac{\sqrt{yz}\sqrt{xz}\sqrt{xy}}{abc}$.

Ahora aplicamos la desigualdad entre las medias geométrica y aritmética
$\dfrac{\sqrt{yz}\sqrt{xz}\sqrt{xy}}{abc} \leq \dfrac{1}{abc}(\dfrac{y + z}{2})(\dfrac{x + z}{2})(\dfrac{x + y}{2}) = \dfrac{abc}{8abc} = \dfrac{1}{8}$.

Por lo tanto, $\sin \dfrac{A}{2} \sin \dfrac{B}{2} \sin \dfrac{C}{2} \leq \dfrac{1}{8}$.

$\blacksquare$

Desigualdad de Nesbitt

Proposición 3. Sean $a$, $b$ y $c$ tres números positivos entonces la siguiente desigualdad es cierta
$(a +b + c)(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}) \geq 9$.

Demostración. La desigualdad entre las medias geométrica y aritmética puede ser vista como
$\dfrac{a}{b} + \dfrac{b}{a} \geq 2\sqrt{\dfrac{a}{b} \dfrac{b}{a}} = 2$.

Por lo tanto,
$(a +b + c)(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}) = \dfrac{a}{b} + \dfrac{b}{a} + \dfrac{a}{c} + \dfrac{c}{a} + \dfrac{b}{c} + \dfrac{c}{b} + 3 \geq 6 +3 = 9$.

$\blacksquare$

Proposición 4. Desigualdad de Nesbitt. Para cualesquiera números positivos $a$, $b$, $c$ ocurre que $\dfrac{a}{b + c} + \dfrac{b}{a + c} + \dfrac{c}{a + b} \geq \dfrac{3}{2}$.

Demostración.
$\dfrac{a}{b + c} + \dfrac{b}{a + c} + \dfrac{c}{a + b}$
$= \dfrac{a}{b + c} + \dfrac{b + c}{b + c} + \dfrac{b}{a + c} + \dfrac{a + c}{a + c} + \dfrac{c}{a + b} + \dfrac{a + b}{a + b} – 3$
$ = \dfrac{a + b + c}{b + c} + \dfrac{ a + b + c}{a + c} + \dfrac{ a + b + c }{a + b} – 3$
$= (a + b + c)( \dfrac{1}{b + c} + \dfrac{1}{a + c} + \dfrac{1}{a + b}) – 3$
$=\dfrac{1}{2}((a + b) + (a + c) + (b + c))( \dfrac{1}{b + c} + \dfrac{1}{a + c} + \dfrac{1}{a + b}) – 3$
$\geq \dfrac{9}{2} – 3 = \dfrac{3}{2}$.

Donde la última desigualdad se obtiene al aplicar la proposición anterior.

Por lo tanto, $\dfrac{a}{b + c} + \dfrac{b}{a + c} + \dfrac{c}{a + b} \geq \dfrac{3}{2}$.

$\blacksquare$

Desigualdad de Weitzenböck

Proposición 5. Desigualdad de Weitzenböck. Si $a$, $b$, $c$ son las longitudes de los lados de $\triangle ABC$ entonces $a^2 + b^2 + c^2 \geq 4\sqrt{3} (\triangle ABC)$.

Demostración. De acuerdo a la fórmula de Herón
$(\triangle ABC) = \sqrt{s(s – a)(s – b)(s – c)}$
$= \sqrt{(\dfrac{a + b + c}{2})(\dfrac{b + c – a}{2})(\dfrac{a + c – b}{2})(\dfrac{a + b – c}{2})}$
$= \dfrac{1}{4} \sqrt{2(a^2b^2 + a^2c^2 + b^2c^2) – (a^4 + b^4 + c^4)}$.

Por otro lado
$\begin{equation} (a^2 – b^2)^2 + (b^2 – c^2)^2 + (c^2 – a^2)^2 \geq 0 \end{equation}$

$\Leftrightarrow$ $2(a^4 + b^4 + c^4) – 2(a^2b^2 + a^2c^2 + b^2c^2) \geq 0$
$\Leftrightarrow$ $\dfrac{4}{3} (a^4 + b^4 + c^4) \geq \dfrac{4}{3} (a^2b^2 + a^2c^2 + b^2c^2)$
$ \Leftrightarrow$ $\dfrac{4}{3} (a^4 + b^4 + c^4) + \dfrac{- 3(a^4 + b^4 + c^4) + 2(a^2b^2 + a^2c^2 + b^2c^2)}{3}$
$\geq \dfrac{4}{3} (a^2b^2 + a^2c^2 + b^2c^2) + \dfrac{- 3(a^4 + b^4 + c^4) + 2(a^2b^2 + a^2c^2 + b^2c^2)}{3}$
$\Leftrightarrow$ $\dfrac{a^4 + b^4 + c^4 + 2(a^2b^2 + a^2c^2 + b^2c^2)}{3} \geq 2(a^2b^2 + a^2c^2 + b^2c^2) – (a^4 + b^4 + c^4)$
$\Leftrightarrow$ $\dfrac{(a^2 + b^2 + c^2)^2}{3} \geq 2(a^2b^2 + a^2c^2 + b^2c^2) – (a^4 + b^4 + c^4) = (4(\triangle ABC))^2$.
$ \Leftrightarrow$ $a^2 + b^2 + c^2 \geq 4\sqrt{3} (\triangle ABC)$.

De la desigualdad $(1)$ podemos notar que la igualdad ocurre si y solo si $a = b = c$, es decir el triángulo es equilátero.

$\blacksquare$

Más adelante…

En la próxima entrada estudiaremos algunas propiedades de las medianas y el centroide de un triángulo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea $P$ un punto en el interior de un triangulo $\triangle ABC$, muestra que al menos uno de los ángulos $\angle BAP$, $\angle CBP$ y $\angle ACP$ es igual a $\dfrac{\pi}{6}$.
  2. Considera $P$ un punto en el interior de $\triangle ABC$ cuyo circunradio es $R$, demuestra que $\dfrac{PA}{BC^2} + \dfrac{PB}{AC^2} + \dfrac{PC}{AB^2} \geq \dfrac{1}{R}$.
  3. Sea $P$ un punto en el interior de $\triangle ABC$, denota por $R_a$, $R_b$, $R_c$ los circunradios de los triángulos $\triangle PBC$, $\triangle PAC$ y $\triangle PAB$ respectivamente, prueba que $\dfrac{PB \times PC}{R_a} + \dfrac{PA \times PC}{R_b} + \dfrac{PA \times PB}{R_c} \leq PA + PB + PC$.
  4. Si $a$, $b$ y $c$ son los lados de un triangulo prueba que $(a + b)(b + c)(a + c) \geq 8(a + b – c)(b + c – a)(a + c -b)$.
  5.  Sean $\triangle ABC$, $\alpha = \angle BAC$, $\beta = \angle CBA$, $\gamma = \angle ACB$, muestra que $\cos \alpha + \cos \beta + \cos \gamma \leq \dfrac{3}{2}$.
  6. Sean $\triangle ABC$, $AD$, $BE$, $CF$, sus alturas y $H$ el ortocentro muestra que:
    $i)$ $\dfrac{AD}{HD} + \dfrac{BE}{HE} + \dfrac{CF}{HF} \geq 9$,
    $ii)$ $\dfrac{HD}{HA} + \dfrac{HE}{HB} + \dfrac{HF}{HC} \geq \dfrac{3}{2}$.
Figura 5
  1. Sea $\triangle ABC$ un triángulo rectángulo con catetos $a$ y $b$ e hipotenusa $c$, muestra que se cumple la siguiente desigualdad $a + b \leq \sqrt{2}c$.
  2. Considera $A’$ y $B’$ los puntos medios de $BC$ y $AC$ en $\triangle ABC$, muestra que $3(BC + AC) > 2(AA’ + BB’)$.

Entradas relacionadas

Fuentes

  • Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 287-297.
  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 27-29, 98-103.
  • Art of Problem Solving
  • Wikipedia
  • Cut the Knot

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Seminario de Resolución de Problemas: Desigualdades básicas

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

En las entradas correspondientes a esta parte del curso aprenderemos varias técnicas que nos permitirán resolver problemas que involucren desigualdades. El área es enorme y hay libros enteros dedicados a ello. Nosotros sólo veremos algunas técnicas. Comenzaremos con desigualdades básicas y nos enfocaremos en los siguientes temas:

  • Desigualdad $x^2\geq 0$ y desigualdad del triángulo
  • Desigualdades de medias
  • La desigualdad de Cauchy-Schwarz
  • Técnicas de cálculo en desigualdades

En esta entrada veremos el primer inciso, que consiste de dos ideas muy sencillas:

Desigualdad $x^2\geq 0$. El cuadrado de cualquier número real es mayor o igual a cero. Es cero si y sólo si el número es cero.

Desigualdad del triángulo. Si $V$ es un espacio vectorial con norma $\norm{\cdot}$, entonces para cualesquiera vectores $u$ y $v$ se tiene que $$\norm{u}+\norm{v}\geq \norm{u+v}.$$

La desigualdad $x^2\geq 0$ parece muy inocente. Sin embargo, es una herramienta muy versátil cuando se combina con manipulaciones algebraicas creativas. La desigualdad del triángulo la estamos enunciando para espacios vectoriales con norma en general. Dos casos particulares que a lo mejor te son más familiares son los siguientes:

Desigualdad del triángulo para $\mathbb{R}$. Si $a$ y $b$ son números reales, entonces $|a|+|b| \geq |a+b|$.

Desigualdad del triángulo en $\mathbb{R}^n$. Si $ABC$ es un triángulo en el plano (o dimensiones más altas) , de lados de longitudes $\overline{AB}=c$, $\overline{BC}=a$ y $\overline{CA}=b$, entonces
\begin{align*}
a+b&\geq c\\
b+c &\geq a\\
c+a &\geq b.
\end{align*}

Si una de las igualdades se da, $ABC$ es un triángulo degenerado, es decir, con sus tres vértices alineados. En otro caso, todas las desigualdades son estrictas.

Veamos aplicaciones de estas desigualdades básicas.

La desigualdad $\frac{a^2+b^2}{2}\geq \sqrt{ab}$

Comenzaremos probando de dos formas distintas una desigualdad que también resulta útil en otras ocasiones.

Problema. Sean $a$ y $b$ números reales mayores o iguales a cero. Muestra que $$\frac{a+b}{2}\geq \sqrt{ab},$$ y que la igualdad se da si y sólo si $a$ y $b$ son iguales.

A esta desigualdad se le conoce como la desigualdad MA-MG para dos números reales. También forma parte de las desigualdades básicas que te ayudará conocer. Se llama así pues en el lado izquierdo tenemos a la media aritmética de los números $a$ y $b$, y al lado derecho tenemos la media geométrica de los números $a$ y $b$. En realidad la desigualdad se vale para más reales no negativos, pero esto lo veremos en otra entrada.

Sugerencia pre-solución. El problema se puede resolver tanto de manera algebraica, (usando $x^2\geq 0$) como de manera geométrica (usando la desigualdad del triángulo).

Para resolverlo de la primera forma, trabaja hacia atrás. Haz manipulaciones algebraicas para formular problemas equivalentes hasta que llegues a una desigualdad obvia.

Para resolverlo de la segunda forma, haz una figura en la que puedas representar tanto a la media geométrica como a la aritmética. Una forma de hacerlo es comenzar con una semicircunferencia de diámetro $a+b$.

Para identificar el caso de igualdad, haz un análisis de casos.

Solución algebraica. Queremos mostrar que $$\frac{a+b}{2}\geq \sqrt{ab}.$$ Pasando el dos multiplicando, y luego $2\sqrt{ab}$ restando al lado izquierdo, esta desigualdad igualdad ocurre si y sólo si $$a+b-2\sqrt{ab}\geq 0.$$ En el lado izquierdo identificamos un binomio al cuadrado, que se puede factorizar para dar la desigualdad equivalente $$\left(\sqrt{a}-\sqrt{b}\right)^2\geq 0.$$

Esta desigualdad es de la forma $x^2\geq 0$, así que es claramente cierta. La igualdad ocurre si y sólo si $\sqrt{a}-\sqrt{b}=0$, lo cual sucede si y sólo si $a=b$. Todos los pasos que hicimos son reversibles. Esto termina la solución.

$\square$

Solución geométrica. Consideremos la siguiente figura, en donde tenemos una semicircunferencia de diámetro $\overline{AB}=a+b$ y centro $O$. Aquí $C$ es un punto en $AB$ tal que $\overline{AC}=a$ y entonces $\overline{CB}=b$. Además, $D$ es un punto sobre la circunferencia tal que $DC$ es perpendicular a $AB$. Llamemos $d=\overline{CD}$.

Prueba visual de la desigualdad entre la media aritmética y media geométrica usando desigualdades básicas
Prueba visual de MA-MG

Como $\triangle AOD$ y $\triangle BOD$ son isósceles por tener dos lados iguales al radio de la circunferencia, tenemos que $\angle ADO = \angle DAO$ y $\angle BDO = \angle DBO$. Usando estas igualdades y que la suma de los ángulos internos de $\triangle ABD$ es $180^\circ$, se puede mostrar que el ángulo $ADB$ es de $90^\circ$.

De este modo, $\triangle ACD$ y $\triangle DCB$ son semejantes (por ser ambos semejantes a $\triangle ABD$ por criterio AA). Por la semejanza, tenemos que $$\frac{a}{d}=\frac{d}{b},$$ de donde $d=\sqrt{ab}$.

Para terminar la demostración, tomamos un punto $E$ sobre $DO$ tal que $\angle EOC = \angle ECO$. Por la desigualdad del triángulo en $\triangle DEC$, tenemos que

\begin{align*}
\sqrt{ab}&=\overline{DC}\\
&\leq \overline{DE} + \overline{EC}\\
&= \overline{DE} + \overline {EO}\\
&= \overline{DO}\\
&=\frac{a+b}{2}.
\end{align*}

Con esto demostramos la desigualdad. Para terminar el problema, necesitamos ver cuándo se dan los casos de igualdad. Se tiene la igualdad si y sólo si $\triangle DEC$ es un triángulo degenerado, lo cual sucede si y sólo si $E$ está en el segmento $DC$. Esto sólo es posible cuando $DO$ es perpendicular a $AB$, lo cual sucede si y sólo si $C=O$, si y sólo si $AC=CB$, si y sólo si $a=b$.

$\square$

Desigualdades básicas aplicadas a un problema de la Olimpiada Mexicana de Matemáticas

El siguiente problema apareció como parte de los exámenes selectivos que el Comité Nacional de la Olimpiada Mexicana de Matemáticas envía a los estados para seleccionar a sus estudiantes en distintas etapas. Tiene muchas formas de resolverse, pero veamos cómo se puede resolver con desigualdades básicas.

Problema. Sean $a,b,c,d$ reales positivos con $a^2+b^2+c^2+d^2=4$. Muestra que $$a^5+b^5+c^5+d^5 \geq a+b+c+d$$

Sugerencia pre-solución. Modifica el problema a mostrar como desigualdad auxiliar que para un real no negativo $x$ se tiene que $$x^5-2x^2-x+2\geq 0.$$ Esta desigualdad se puede demostrar usando que los cuadrados son no negativos.

Solución. Vamos a probar primero la desigualdad $$x^5-2x^2-x+2\geq 0.$$ Para que sea un poco más fácil, factorizaremos la expresión del lado izquierdo.

Notemos que $1$ es una raíz de $x^5-2x^2-x+2$, de modo que por el teorema del factor podemos factorizar $x-1$ del polinomio. Obtenemos que $$x^5-2x^2-x+2=(x-1)(x^4+x^3+x^2-x-2).$$

Notemos que, nuevamente, $1$ es una raíz de $(x^4+x^3+x^2-x-2)$. Al factorizar $x-1$ de nuevo, obtenemos que $$x^5-2x^2-x+2=(x-1)^2(x^3+2x^2+3x+2).$$

Ya estamos listos para probar la desigualdad que queremos. Notemos que $(x-1)^2\geq 0$ y que $x^3+2x^2+3x+2$ es mayor o igual que cero para $x\geq 0$ pues es un polinomio con puros coeficientes positivos. Esto prueba la desigualdad auxiliar. Reescribiéndola, tenemos que $$x^5\geq 2x^2+x-2.$$ Aplicándola en esta forma a los cuatro reales positivos $a,b,c,d$ del problema, y usando que la suma de cuadardos es $4$, obtenemos que
\begin{align*}
a^5 & + b^5+c^5+d^5\\
&\geq 2(a^2+b^2+c^2+d^2)+a+b+c+d-8\\
&=2\cdot 4 + a+b+c+d-8\\
&=a+b+c+d.
\end{align*}

Esto termina el problema.

$\square$

El primer paso parece un poco artificial. ¿Por qué queremos probar esa desigualdad auxiliar? En otra entrada de blog escribí cómo se puede llegar a las ideas de esta solución.

Desigualdad del triángulo aplicada a la construcción de tetraedros

Si pegamos cuatro triángulos equiláteros en el espacio se hace un tetraedro regular. De manera similar, si pegamos cuatro triángulos como el siguiente, también se hace un tetraedro en el espacio:

Pegar cuatro triángulos congruentes para hacer un tetraedro

La intuición nos dice que debería poderse con cualquier triángulo. Pero esta intuición está mal.

Problema. Sea $ABC$ un triángulo con un ángulo mayor a $90^\circ$. Muestra que no existe ningún tetraedro en el espacio tal que sus cuatro caras sean congruentes a $ABC$.

Sugerencia pre-solución. Procede por contradicción. Por simetría, puedes asumir que el ángulo mayor a $90^\circ$ es el ángulo en $A$. Usa como punto auxiliar al punto medio de $BC$ y usa desigualdades.

Solución. Una observación inicial es que si $ABC$ es un triángulo, $M$ es el punto medio de $BC$ y su ángulo interno en $A$ es mayor a $90^\circ$, entonces $2\overline{AM}<\overline{BC}$. Esto se muestra trazando una circunferencia de diámetro $BC$.

Desigualdad para la mediana en términos del ángulo que hace.

De hecho,

  • Un punto $X$ está sobre la circunfencia si y sólo si $\angle BXC = 90 ^\circ$, si y sólo si $\overline{OX}=\overline{OA}$.
  • $X$ está dentro de la circunferencia si y sólo si $\angle BXC > 90^\circ$, si y sólo si $\overline{OX}<\overline{OA}$ y
  • $X$ está fuera de la circunferencia si y sólo si $\angle BXC < 90^\circ$, si y sólo si $\overline{OX}>\overline{OA}$.

Resolvamos el problema. Sin pérdida de generalidad, el ángulo en $A$ es mayor a $90^\circ$. Entonces $\overline{AM}<\frac{\overline{BC}}{2}$, de donde $2\overline{AM}<\overline{BC}$.

Supongamos que se pudiera hacer en el espacio un tetraedro $WXYZ$ tal que cada una de las caras es congruente al triángulo $ABC$. Sin pérdida de generalidad, tenemos que
\begin{align*}
\overline{WX}&=\overline{YZ}=\overline{AB}\\
\overline{XY}&=\overline{ZW}=\overline{BC}\\
\overline{WY}&=\overline{XZ}=\overline{CA}.
\end{align*}

Tomemos el punto medio $M$ de $XY$. En $\triangle ZMW$, tenemos que
\begin{align*}
\overline{ZM}&=\overline{AM}\\
\overline{WM}&=\overline{AM}.
\end{align*}

Así, usando la desigualdad del triángulo en $\triangle ZMW$ tenemos que \begin{align*}
2\overline{AM}&=\overline{ZM}+\overline{WM}\\
&\geq \overline{ZW}\\
&=\overline{BC}.
\end{align*}

Esto es una contradicción con la desigualdad $2\overline{AM}<\overline{BC}$ que ya habíamos mostrado.

$\square$

Más problemas

Puedes encontrar más problemas de desigualdades básicas en la sección 7.1 del libro Problem Solving through Problems de Loren Larson. También puedes consultar más técnicas y problemas en el libro Desigualdades de la Olimpiada Mexicana de Matemáticas.

Un problema de probabilidad y escuchar música

Por Leonardo Ignacio Martínez Sandoval

4 respuestas

El problema

Les comparto un problema que se me ocurrió en las (muchas) horas que he pasado en el carro escuchando música, cuando vivía en la Ciudad de México. El estéreo del carro ordena las canciones alfabéticamente. Tiene un botón que permite «avanzar una canción». Pero a veces tarda mucho: si estoy escuchando «Adele – Hello», hay que apretar el botón muchas veces para llegar a «Shakira – Dónde están los ladrones».

En esas épocas descubrí una estrategia «intuitiva» para llegar más rápido a la canción. La idea es la siguiente: pasar temporalmente al modo de «canción aleatoria», apretar el botón unas cuantas veces para acercarme a la canción que quiero (en el ejemplo anterior, digamos que después de dos o tres veces el botón me lleva a «Paquita la del Barrio – Rata de dos Patas»), y de ahí quitar el aleatorio y avanzar normal. Eso, intuitivamente, siempre me ahorró muchos pasos. El problema consiste en encontrar la estrategia óptima, en donde se permiten mezclar pasos normales y aleatorios.

Para eso, voy a plantear un problema muy concreto. De aquí en adelante supondré que el lector sabe un poco de probabilidad. Pensemos que hay $2n$ canciones, numeradas de $1$ a $2n$. Estoy en la canción $n$ y quiero llegar a la canción $2n$. Pensemos que el estéreo tiene exactamente dos botones, el $A$ que avanza $1$ (y de $2n$ lleva a $1$), y el $B$ que lleva a una canción aleatoria (cualquiera de las canciones, incluida la actual, tiene probabilidad $1/2n$ de ser elegida). En cada paso se permite ver en qué canción estoy, y de ahí decidir apretar $A$ o $B$. ¿Cuál es la estrategia que en valor esperado tiene menos pasos? ¿Cuál es ese valor esperado?

En la imagen de aquí abajo se muestra un ejemplo de una forma de apretar los botones para $n=5$, con $2n=10$ canciones. Las flechas rojas corresponden a avanzar $1$ apretando el botón $A$. Las flechas azules corresponden a ir a un lugar aleatorio apretando el botón $B$. Se apretaron los botones en el orden $ABBAA$, de modo que se hicieron $5$ pasos.

Ejemplo de estrategia ABBAA
Un ejemplo en el que se usa la estrategia ABBAA. La canción 1 es de ABBA. Es Dancing Queen. «Feel the beat form the tambourine… Oh yeah…».

Ese es el enunciado del problema. De aquí en adelante empiezo a hablar de ideas para resolverlo, así que si quieres intentarlo, este es el momento correcto.

Primeras ideas

Notemos que la estrategia «siempre $A$, hasta llegar a $2n$» toma exactamente $n$ pasos siempre. La estrategia «siempre $B$» es para intentar atinarle, y en cada paso tiene probabilidad de éxito $1/2n$. Entonces, en esta segunda estrategia la cantidad de pasos requeridos es una variable aleatoria con distribución geométrica de parámetro $p=1/2n$, de modo que el número esperado de pasos es $1/p=2n$.

Sin embargo, suena a que la estrategia esbozada al inicio de esta entrada es intuitivamente mejor: usar el $B$ para acercarse y luego el $A$ para llegar.

La solución

Vamos a mostrar que la mejor estrategia en valor esperado es la siguiente: «apretar el botón $B$ hasta llegar aproximadamente al intervalo $[n-2\sqrt{n}, n]$, y de ahí apretar el botón $A$» hasta llegar a $n$.

El primer argumento es que en cada paso, lo que hace la estrategia sólo depende de en qué canción estamos. En efecto, el paso $A$ es determinista y el $B$ es una variable uniforme independiente de todo lo demás.

El segundo argumento es que, si en algún momento de la estrategia usamos el botón $A$, entonces después de ello nunca nos conviene usar el botón $B$. Lo probamos por contradicción: supongamos que por cualquier razón en la estrategia óptima tenemos que hacer un $AB$. El paso $A$ es determinista, y sabíamos exactamente a qué canción nos iba a llevar (a la siguiente). Pero hacer el paso $B$ en cualquier lugar que estemos es simétrico, pues nos lleva a una canción aleatoria. Si a priori sabíamos que íbamos a hacer un paso $B$, lo mejor es hacerlo lo antes posible. Así, la estrategia que substituye esos pasos $AB$ por $B$ se ahorra un paso, y no es óptima. Contradicción.

Ahora, afirmo lo siguiente. Si la estrategia óptima es apretar $A$ cuando estamos en la canción $j$, entonces también va a ser apretar $A$ cuando estemos en cualquier canción $k$ con $j\leq k < 2n$. Esto es debido al argumento anterior: al apretar $A$ llegamos a $j+1$, que por el párrafo de arriba, no le puede tocar $B$. Entonces le toca $A$. De ahí llegamos a $j+2$, que de nuevo no le puede tocar $B$. Y así sucesivamente (inductivamente), hasta llegar a $2n-1$.

Lo que acabamos de probar es que la estrategia óptima se ve de la siguiente manera para algún entero $k$: «Apretar $B$ hasta que lleguemos a alguno de los últimos $k$ elementos. De ahí, apretar $A$ hasta llegar a $2n$.» Nos falta determinar cuál es la mejor $k$ que podemos usar.

A estas alturas ya podemos calcular explícitamente el valor esperado de pasos en esta estrategia. El evento «llegar a alguno de los últimos $k$ elementos» tiene probabilidad $k/2n$ de ocurrir cada que se aprieta el botón $B$, así que la cantidad de veces que hay que apretar $B$ para ello es una variable aleatoria geométrica de valor esperado $2n/k$. Una vez que llegamos a los últimos $k$ elementos, caemos a cualquier elemento del intervalo $\{2n-k+1, 2n-k+2,\ldots,2n\}$ con la misma probabilidad, y respectivamente nos tomará $\{k-1, k-2,\ldots, 0\}$ pasos en llegar a $2n$, es decir, la cantidad de pasos que hacemos es una variable aleatoria uniforme discreta de media $(k-1)/2$.

Así, en total usamos $(2n/k) + (k-1)/2$ pasos para llegar. Queremos lograr que esta expresión sea lo más pequeña posible. Usando la desigualdad entre la media geométrica y la aritmética, notamos que $$\frac{2n}{k}+\frac{k-1}{2}=\frac{2n}{k}+\frac{k}{2}-\frac{1}{2} \geq 2\sqrt{n} – \frac{1}{2},$$ y que la igualdad se da si y sólo si $\frac{2n}{k}=\frac{k}{2}$, es decir, si y sólo si $k=2\sqrt{n}$. En este caso, la cantidad media de pasos que usamos es $2\sqrt{n}-\frac{1}{2}$.

Aquí arriba hicimos un poquito de trampa. En realidad $k=2\sqrt{n}$ tiene sentido para la estrategia sólo cuando $\sqrt{n}$ es un número entero. Sin embargo, por la convexidad de la función $
\frac{2n}{k}+\frac{k}{2}$ tenemos la garantía de que o bien $\lfloor
2\sqrt{n} \rfloor$ o bien $\lceil 2\sqrt{n} \rceil$ dan el máximo.

Conclusión y otros problemas

Está cool que hayamos bajado la cantidad de pasos que se necesitan de valor esperado de algo que era $n$ a algo que es del tamaño $2\sqrt{n}$. Para hacerse una idea de los pasos que se pueden ahorrar, toma una colección de $800$ canciones. Originalmente se necesitaban $400$ pasos $+1$ para ir de la mitad al final. Con la nueva estrategia se requieren como $40$.

Hacer esta estrategia en la vida real es un poco complicado pues los estéreos no muestran el número exacto de la canción en la que se está, además de que es difícil memorizar a qué canción le toca qué número. Pero a veces sí muestran el nombre de la canción y más o menos «se le puede aproximar».

Hay un par de variantes interesantes. Una es ¿qué sucede si además de tener botón $+1$ y aleatorio, también tenemos botón $-1$?. En esta variante la solución no cambia mucho, pero es bueno intentarla para repasar las ideas de la prueba.

La otra variante es la siguiente. La estrategia óptima, como está descrita arriba, tiene un problema: es posible que nunca termine, o que tome muchísimos pasos en terminar (esto será muy improbable y por eso el valor medio se compensa). Así, imaginemos que queremos la restricción adicional de que la estrategia que usemos nunca use más de, digamos, 4n pasos. En esta variante: ¿cuál es la estrategia óptima? ¿cuántos pasos toma?

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario:

Modificar el problema

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

HeuristicasOtra técnica de resolucion de problemas es proponer un problema que ayude, pero que no necesariamente sea equivalente. Esto puede ser a través de problemas más particulares o de problemas más difíciles.

En esta serie de videos veremos esta técnica en acción en cuatro problemas.

Ir a los videos…