Archivo de la etiqueta: desigualdad del triángulo

Cálculo Diferencial e Integral I: Valor absoluto. Desigualdad del triángulo

Por Karen González Cárdenas

Deja un comentario

Introducción

En esta entrada veremos una función muy particular: el valor absoluto. Ésta nos permitirá «medir la distancia» entre un par de números reales. Finalizaremos con la demostración de la Desigualdad del triángulo y algunas de sus consecuencias. Esta desigualdad es usada en las demostraciones de Límite y Continuidad que veremos más adelante.

Definición formal

Definición (Valor absoluto): Para todo $x\in \r$ definimos la función valor absoluto como sigue:
\begin{equation*}
|x|=
\begin{cases}
x &\text{si $x \geq 0$}\\
-x & \text{si $x< 0$}
\end{cases}
\end{equation*}

Recordando las propiedades de orden, la definición quedaría de la siguiente manera:
\begin{equation*}
|x|=
\begin{cases}
x &\text{si $x =0 \quad\text{o}\quad x\in P$}\\
-x & \text{si $-x\in P$}
\end{cases}
\end{equation*}
Esta última nos será de utilidad para la demostración de la desigualdad del triángulo que veremos más adelante.


Observación: De la definición anterior notamos que para toda $x \in \r$, su valor absoluto $|x|$ es mayor o igual a cero.

Midiendo distancias

Si observamos la definición del valor absoluto, notamos que asocia a cualquier número real con su distancia respecto al cero. Veámoslo en los ejemplos siguientes:

  • $|-3|=3$
  • $|14|= 14$

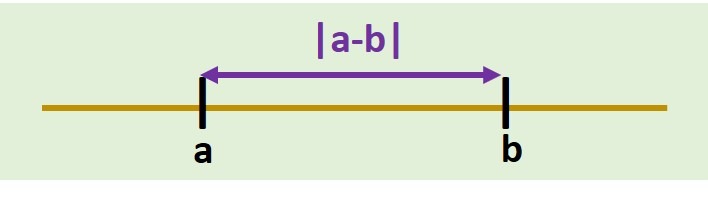
En consecuencia, si consideramos la distancia entre cualquier par de números reales tendríamos la siguiente definición.

Definición: Para cualesquiera $a,b \in \r$ tenemos que están a distancia $|a-b|$.
Observemos que la distancia siempre será positiva o cero.

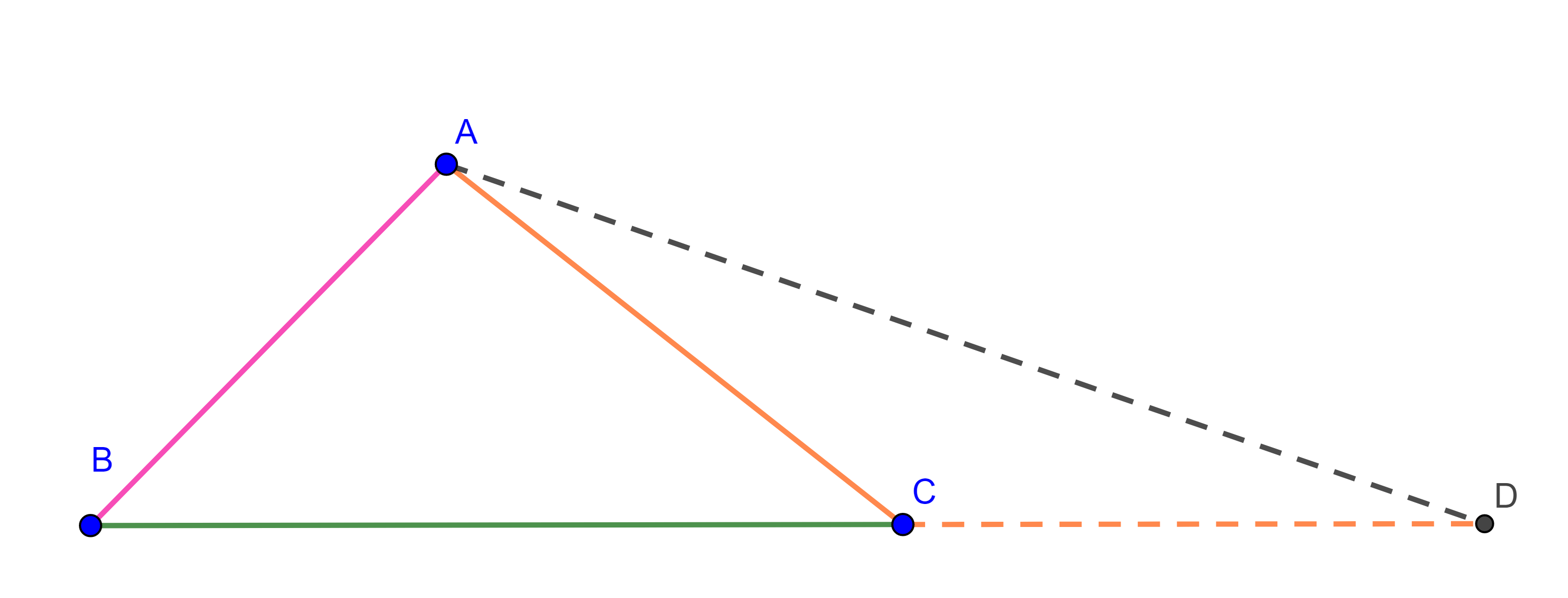
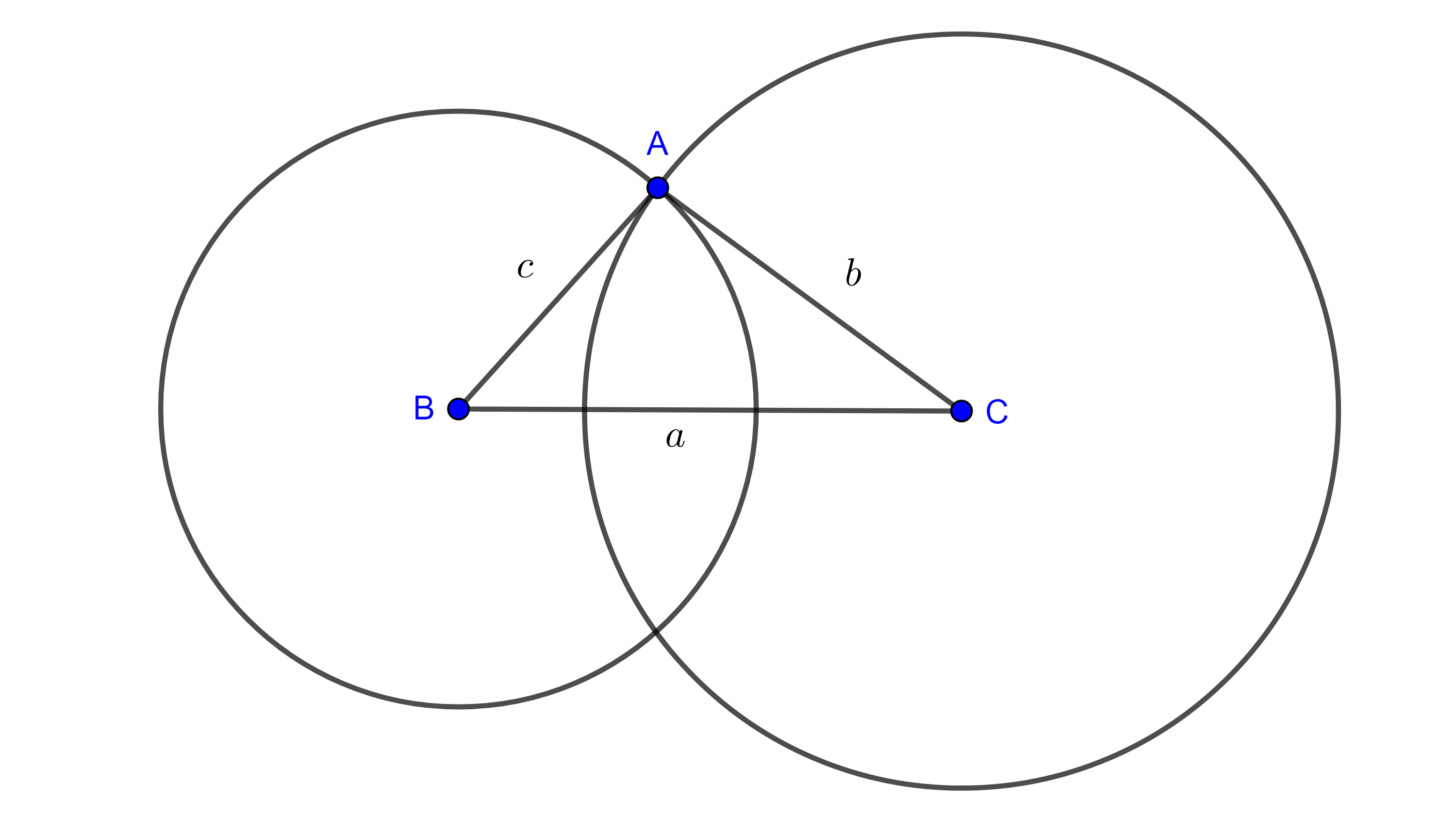
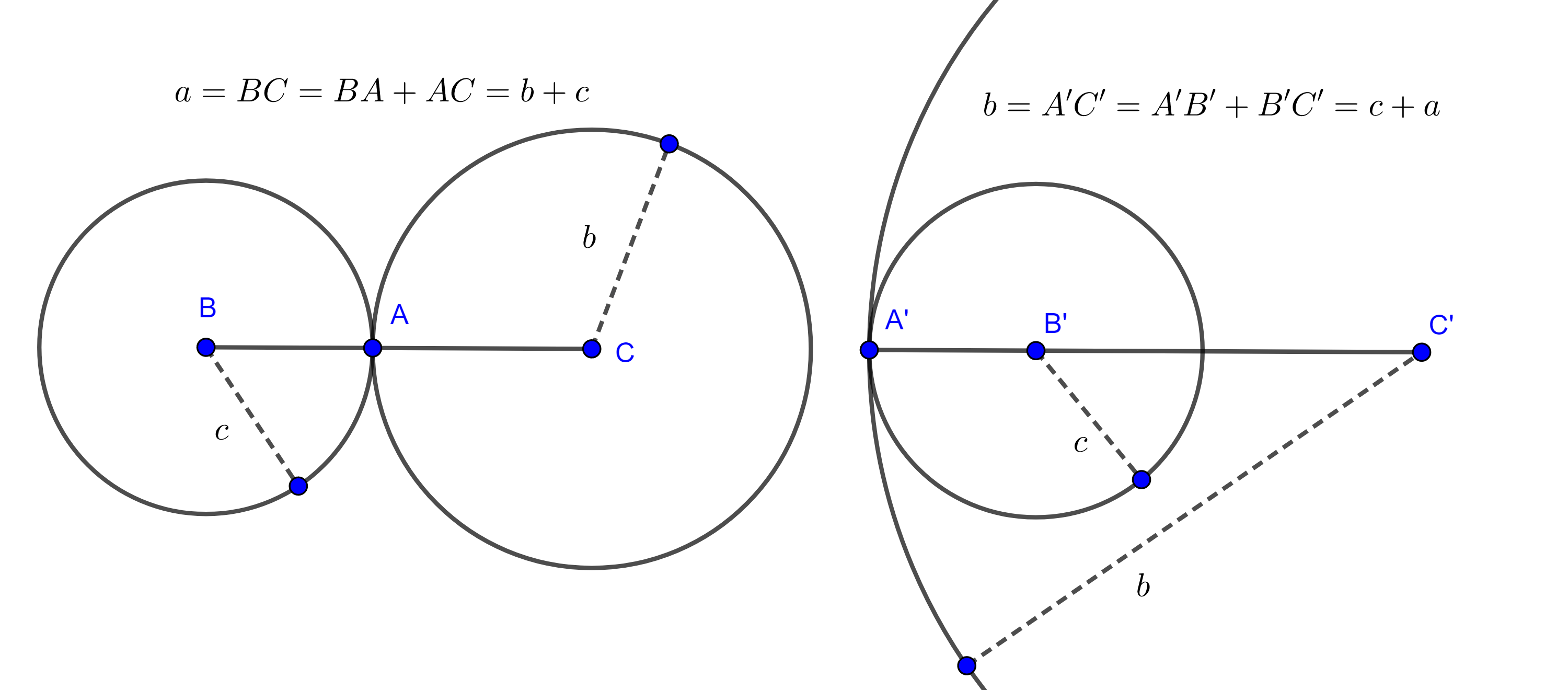
Desigualdad del triángulo

Teorema (Desigualdad del triángulo): Para todo $a,b \in \r$ se cumple la siguiente desigualdad:
$$|a+b| \leq |a|+|b|\text{.}$$

Demostración: Dada la definición del valor absoluto, debemos considerar casos sobre los signos de $a$ y $b$.
CASO 1: $a \geq 0$ y $b \geq 0$.
Recordemos que $P$ es cerrado bajo la suma, por lo que tenemos lo siguiente:
\begin{align*}
|a+b|&= a + b\\
&= |a|+|b|.
\end{align*}
La última igualdad se sigue de $a = |a|$ y $b = |b|$.

Para los siguientes casos haremos uso de los siguientes resultados que serán demostrados posteriormente:

Resultados: Para cualesquiera $a,b,c \in \r$ se cumplen:

  1. $-a-b=-(a+b)$.
  2. Si $b<0 \Rightarrow b<-b$.
  3. Si $a<b \Rightarrow a+c < b+c$.

CASO 2: $a < 0$ y $b < 0$.
Notemos que $-a \in P$ y $-b \in P$ por lo que $-a-b \in P$. Así se sigue que:
\begin{align*}
|a+b|&= -(a+b)\tag{por ser $a+b$ negativo}\\
&= -a – b\tag{por el resultado 1}\\
&= (-a)+(-b)\\
&= |a|+|b|,
\end{align*}
porque $|a|=-a$ y $|b|=-b$.

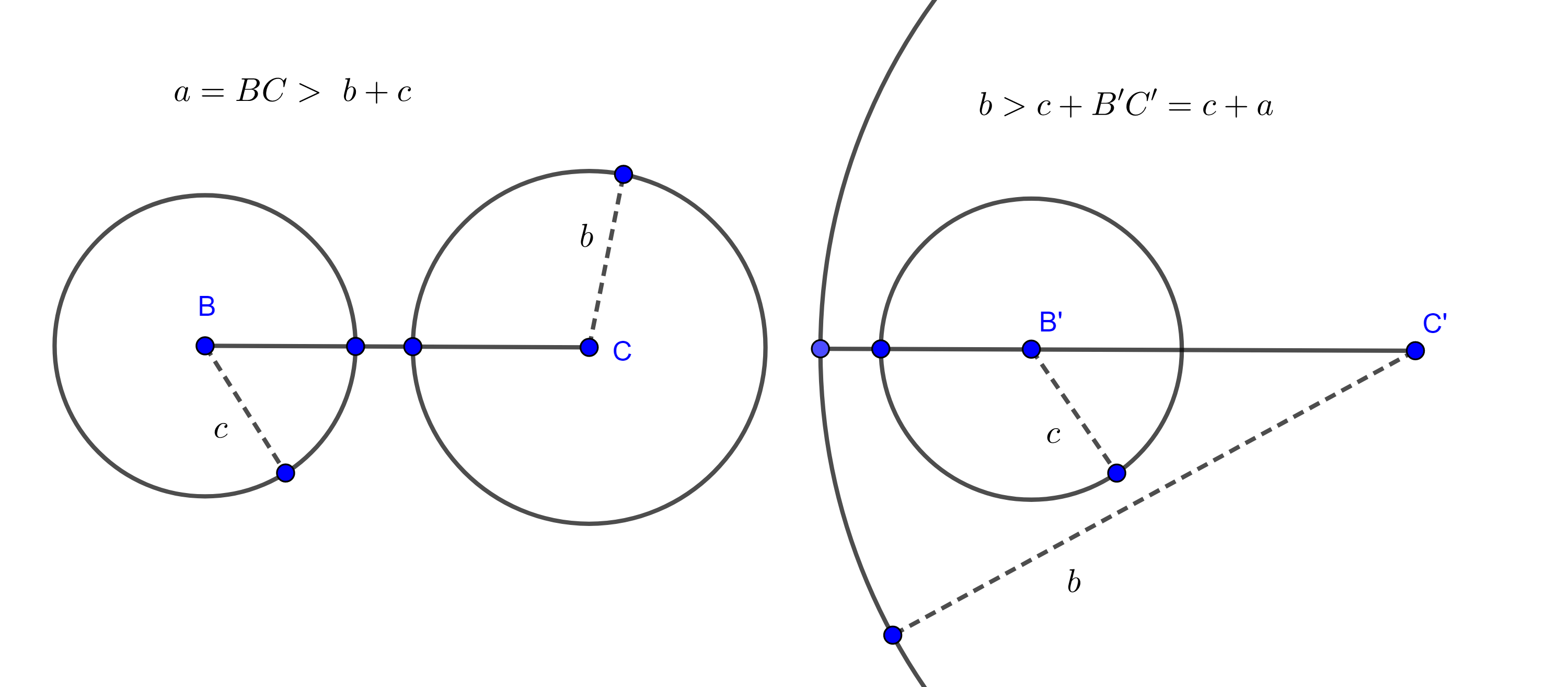
CASO 3: $a \geq 0$ y $b < 0$.
Para esta demostración debemos considerar dos subcasos.
SUBCASO 1: $a+b \geq 0$.
Dado lo anterior aplicando la definición de valor absoluto ocurre que:
\begin{align*}
|a+b|&=a+b\\
&< a-b. \tag{por los resultados 2 y3}\\
\end{align*}
Como tenemos que $a-b = |a|+|b|$, concluimos:
$$|a+b|<|a|+|b|.$$
SUBCASO 2: $a+b < 0$.
Procederemos análogamente al subcaso anterior:
\begin{align*}
|a+b|&=-(a+b)\\
&= -a-b\\
&< a-b. \tag{por resultados 2 y3}\\
\end{align*}
Ya que $a-b = |a|+|b|$, tenemos:
$$|a+b|<|a|+|b|.$$

CASO 4: $a < 0$ y $b \geq 0$.
Al igual que en el caso 3, para verificar la desigualdad se deberán considerar dos subcasos. La demostración de este caso se deja como parte de la Tarea moral.

$\square$

Para poder dar por terminada la prueba, debemos demostrar los siguientes resultados auxiliares que utilizamos:

Resultados: Para cualesquiera $a,b,c \in \r$ se cumplen:

  1. $-a-b=-(a+b)$.
  2. Si $b<0 \Rightarrow b<-b$.
  3. Si $a<b \Rightarrow a+c < b+c$.

Demostración:
1. Debemos verificar que $-a-b =(-a)+(-b)$ es inverso aditivo de $a+b$.
\begin{align*}
(a+b)+((-a)+(-b))&= (b+a)+((-a)+(-b))\\
&= ((b+a)+(-a))+(-b)\\
&= (b+(a+(-a))+(-b)\\
&= (b+0)+(-b)\\
&= b + (-b)\\
&=0.
\end{align*}
Concluimos que $(-a)+(-b) = -(a+b)$.

2. Ya que $b<0$ sabemos que $-b \in P$. Queremos probar que $-b-b > 0$.
Observemos que: $-b-b=(-b)+(-b)\in P$.
Por lo que concluimos que $b<-b$.

3. Bastaría ver que $(b+c)-(a+c) \in P$. Debido a que $b-a \in P$. Observamos lo siguiente.
\begin{align*}
b-a &= (b-a)+0\\
&= (b-a) + (c-c)\\
&= (b+c)-(a+c).
\end{align*}
$$\therefore\quad (b+c)-(a+c) \in P.$$
$$\therefore \quad b+c > a+c.$$

$\square$

Observemos que las demostraciones de estos resultados no utilizan la desigualdad del triángulo, más bien hacen uso de las propiedades vistas en las entradas anteriores.

Consecuencias de la desigualdad del triángulo

Proposición (Consecuencias de la desigualdad del triángulo): Sean $a,b \in \r$. Se cumplen las siguientes desigualdades:

  1. $|a-b| \leq |a|+|b|$
  2. $|a|-|b|\leq |a-b|$
  3. $|b|-|a|\leq |a-b|$

En esta ocasión sólo probaremos el punto 2.

Demostración:
2. Como $|a|= |a+0|$, al desarrollar esta igualdad obtenemos:
\begin{align*}
|a|&= |a+0|\\
&= |a+ (b+ (-b))|\\
&= |(a-b)+b|\\
&\leq |a-b| + |b| \tag{por la desigualdad del triángulo}\\
\end{align*}
$$\therefore |a| \leq |a-b| + |b|$$
$$\therefore |a|-|b| \leq |a-b|$$

$\square$

Más adelante

En la próxima entrada comenzaremos a resolver desigualdades donde el valor absoluto se encuentra involucrado.

Tarea moral

  • Propiedades del valor absoluto.
    Prueba los siguientes resultados:
    • $|a|=|-a|.$
    • $|ab|=|a||b|$.
    • $|\frac{1}{a}|=\frac{1}{|a|}$ con $a\neq 0$.
    • $\frac{|a|}{|b|}=|\frac{a}{b}|$ con $b \neq 0$.
  • Desigualdad del triángulo.
    • Realiza la prueba del CASO 4 .
    • Demuestra que para cualesquiera $a,b \in \r$:
      • $|a-b| \leq |a|+|b|$.
      • $|b|-|a|\leq |a-b|$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Desigualdad del triángulo y lugar geométrico

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta ocasión estudiaremos una propiedad muy importante de los triángulos, la desigualdad del triángulo que básicamente nos dice que la distancia mas corta entre dos puntos es el segmento de recta que los une, también veremos lo que es un lugar geométrico y mostraremos un par de ejemplos importantes.

Desigualdad del triángulo

Proposición 1. En todo triángulo al mayor de los lados se opone el mayor de los ángulos.

Demostración. Sea $\triangle ABC$ tal que $AB > AC$, debemos mostrar que $\angle C > \angle B$.

Figura 1

Como $AB > AC$, podemos construir un punto $D \in AB$ tal que $AD = AC$, ya que $\triangle ADC$ es isósceles, por la proposición de la entrada anterior, se cumple $\angle CDA = \angle ACD$, de aquí se sigue que:

$\begin{equation} \angle C = \angle ACB > \angle ACD = \angle DCA. \end{equation}$

Como $\angle ADC$ es un ángulo exterior de $\triangle DBC$, entonces $\angle ADC$ es mayor que los ángulos internos de $\triangle DBC$, no adyacentes a él, en particular

$\begin{equation} \angle ADC > CBD = \angle B. \end{equation}$

De $(1)$ y $(2)$ se sigue que $\angle C > \angle B$.

$\blacksquare$

Corolario. En todo triángulo el ángulo mayor es opuesto al lado mayor.

Demostración. Sea $\triangle ABC$ tal que $\angle A > \angle B$, por demostrar que $BC > AC$. Supongamos lo contrario.

Figura 2

Caso 1. Si $BC = AC$, entonces $\triangle ABC$ es isósceles por lo que $\angle A = \angle B$, lo que es una contradicción a nuestra hipótesis.

Caso2. Si $BC < AC$, entonces por la proposición anterior $\angle B > \angle A$, esto nuevamente contradice la hipótesis.

Por lo tanto, no queda otra opción más que $\angle A > \angle B$.

$\blacksquare$

Proposición 2. Si dos lados de un triángulo son iguales a dos lados de un segundo triángulo, pero el ángulo comprendido entre el primer par de lados es mayor que el ángulo formado por los lados del segundo triangulo, entonces el lado restante del primer triángulo será mayor al tercer lado del segundo triangulo.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB = A’B’$, $AC = A’C’$ y $\angle A > \angle A’$, por demostrar que $BC > B’C’$.

Figura 3

Sobre $A’B’$ y tomando como vértice $A’$ construimos un ángulo igual a $\angle A$, y construimos $D$ tal que $A’D = AC$, entonces por criterio LAL, $\triangle ABC \cong \triangle A’B’D$ por lo que $B’D = BC$.

Notemos que $\triangle C’A’D$ es isósceles, entonces $\angle DC’A = \angle A’DC’$.

Ahora en $\triangle DC’B’$ tenemos $\angle DC’B’ = \angle A’C’B’ + \angle DC’A$,
$\Rightarrow \angle DC’B’ > \angle DC’A = \angle A’DC’$.

Pero $\angle A’DC’ = \angle A’DB’ + \angle B’DC’$,
$\Rightarrow \angle A’DC’ > \angle B’DC’$.

Por transitividad, $\angle DC’B’ > \angle B’DC’$.

Aplicando el corolario obtenemos $B’D > B’C’$, pero $B’D = BC$,
$\Rightarrow BC > B’C’$.

$\blacksquare$

Teorema 1, desigualdad del triángulo. Para todo triangulo se cumple que la suma de cualesquiera dos de sus lados es mayor al lado restante.

Demostración. Sea $\triangle ABC$, sobre la recta que pasa por $B$ y $C$, construimos un punto $D$ tal que $CD = AC$.

Figura 4

Como $\triangle ACD$ es isósceles, $\angle CAD = \angle ADC$, entonces en $\triangle ABD$ tenemos $\angle BAD > \angle CAD = \angle ADC = \angle ADB$, por el corolario anterior $BD > AB$.

Pero $BD = BC + CD = BC + AC$, por lo tanto, $AC + BC > AB$.

Las otras desigualdades, $AB + BC > AC$ y $AB + AC > BC$, se muestran de manera similar.

$\blacksquare$

El reciproco de este teorema también es cierto y lo mostramos a continuación.

Construcción de un triángulo y un ángulo

Teorema 2. Si $a$, $b$ y $c$ son tres números positivos tales que $a + b > c$, $a + c > b$ y $b + c > a$, entonces es posible construir un triángulo de lados $a$, $b$ y $c$.

Demostración. Construyamos un segmento $BC$ de longitud $a$, trazamos una circunferencia con centro en $B$ y radio $c$ $(B, c)$, trazamos otra circunferencia con centro en $C$ y radio $b$ $(C, b)$.

$(B, c)$ y $(C, b)$ se intersecan en dos puntos, sea $A$ uno de estos puntos. $AB = c$ por ser radio de $(B, c)$, $AC = b$ por ser radio de $(C, b)$ y $BC = a$ por construcción.

Figura 5

Notemos que si $(B, c)$ y $(C, b)$ se intersecaran en un solo punto entonces la intersección estaría sobre $BC$ o su extensión, y en tal caso se tendría alguna de las siguientes igualdades
$a = b + c$, $b = a + c$ o $c = a + b$, figura 6.

Figura 6

Y si $(B, c) \cap (C, b) = \varnothing$, entonces alguna de las cantidades seria mayor que la suma de las otras dos, $a > b + c$, $b > a + c$ o $c > a + b$, figura 7, lo que sería una contradicción a nuestras hipótesis.

Figura 7

Por lo tanto, $\triangle ABC$ es el triángulo buscado.

$\blacksquare$

Problema. Sobre una recta dada construir un ángulo igual a un ángulo dado.

Solución. Sea $\angle AOB$ el ángulo dado y $l$ la recta dada.

Con centro en $O$ y radio arbitrario $r > 0$ trazamos una circunferencia $(O, r)$ que corte a $OA$ en $C$ y a $OB$ en $D$.

Figura 8

Tomamos $O’ \in l$ y construimos una circunferencia con centro en $O’$ y radio $r$, $(O’, r)$, tomamos una de las intersecciones de $l$ con $(O’, r)$, digamos $D’$, trazamos otra circunferencia con centro en $D’$ y radio $CD$, $(D’, CD)$, sea $C’$ una de las intersecciones de $(O’, r)$ con $(D´, CD)$, entonces por criterio LLL $\triangle COD \cong \triangle C’O’D’$

Por lo tanto, $\angle AOB = \angle C’O’D’$.

$\blacksquare$

Lugar geométrico

Un lugar geométrico es un conjunto de puntos que cumplen un conjunto de condiciones dadas. Para probar que una figura geométrica es un lugar geométrico por lo general la prueba se divide en dos partes.

  • Probar que todos los puntos que satisfacen las condiciones pertenecen a la figura.
  • Probar que todos los puntos que pertenecen a la figura satisfacen las condiciones.

Teorema 3. El lugar geométrico de los puntos que equidistan a dos puntos dados, es la mediatriz del segmento que une los puntos dados.

Demostración. Sean $AB$ un segmento dado, $M$ el punto medio y $m$ la mediatriz de $AB$ respectivamente.

Figura 9

Primero vemos que los puntos en la mediatriz de $AB$  equidistan de $A$ y $B$.

Sea $P \in m$, por definición de mediatriz, $m \cap AB = M$ y $l \perp AB$.

Entonces por criterio LAL (lado, ángulo, lado), $\triangle PMA \cong \triangle PMB$, en consecuencia, $PA = PB$.

$\blacksquare$

Ahora veamos que todos los puntos que equidistan de $A$ y $B$, son los puntos en la mediatriz $m$ de $AB$.

Sea $P$ un punto que satisface las condiciones dadas, entonces $PA = PB$ y así $\triangle APB$ es isósceles, en la entrada anterior vimos que la mediatriz de un triángulo isósceles, pasa por el vértice que comparten los lados iguales, por lo tanto, $P \in m$.

$\blacksquare$

Definición. Definimos la distancia de un punto $P$ a una recta $l$ como la distancia entre $P$ y el pie de la perpendicular trazada desde $P$ a $l$.

Teorema 4. El lugar geométrico de los puntos que equidistan a dos rectas que se intersecan son las bisectrices de los ángulos formados por las rectas.

Demostración. Sean $l_{1}$ y $l_{2}$, dos rectas que se intersecan en $O$, consideremos $b_{1}$ la bisectriz de uno de los ángulos formados por $l_{1}$ y $l_{2}$, digamos $\alpha$, y sea $b_{2}$ la bisectriz del ángulo suplementario a $\alpha$.

Primero veamos que todos los puntos en la bisectriz de $\alpha$ equidistan a $l_{1}$ y $l_{2}$.

Figura 10

Sea $P \in b_{1}$, y sean $A$ y $B$ las intersecciones de las perpendiculares trazadas desde $P$ a $l_{1}$ y $l_{2}$ respectivamente.

Como $b_{1}$ es bisectriz, $\angle AOP = \angle POB$, además $\angle PAO = \angle OBP = \dfrac{\pi}{2}$, como la suma de los ángulos internos de todo triángulo es constante entonces $\angle OPA = \angle BPO$.

Entonces en los triángulos $\triangle PAO$ y $\triangle PBO$, $\angle AOP = \angle POB$, $\angle OPA = \angle BPO$ y $OP$ es un lado común.

Por criterio LAL, $\triangle PAO \cong \triangle PBO$, por lo tanto $PA = PB$, así la distancia de $P$ a $l_{1}$ y a $l_{2}$ es la misma.

De manera análoga podemos ver que los puntos en $b_{2}$ son equidistantes a $l_{1}$ y $l_{2}$.

$\blacksquare$

Ahora mostremos que todos los puntos que son equidistantes a $l_{1}$ y $l_{2}$ pertenecen a $b_{1}$ o $b_{2}$.

Sea $P$ un punto que satisface que $PA = PB$, donde $A$ y $B$ son los pies de las perpendiculares trazadas desde $P$ a $l_{1}$ y $l_{2}$ respectivamente.

Figura 11

Entonces $\triangle PAO$ y $\triangle PBO$ son triángulos rectángulos donde la hipotenusa es la misma, y por hipótesis tienen un cateto igual, $PA = PB$, por criterio hipotenusa – cateto $\triangle PAO \cong \triangle PBO$, en particular $\angle AOP =\angle POB$.

Notemos que las dos rectas dividen al plano en cuatro regiones distintas y en cada región podemos hacer el mismo procedimiento, pero dos rectas que se intersecan solo tienen dos bisectrices distintas.

Por lo tanto si $PA = PB$, entonces $P \in b_{1}$ o $P \in b_{2}$.

$\blacksquare$

Más adelante…

En al siguiente entrada estudiaremos a los paralelogramos y sus propiedades.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB = A’B’$, $AC = A’C’$ y $BC > B’C’$, muestra que $\angle A > \angle A’$.
  2. Sea $\square ABCD$ un cuadrado y $O$ un punto en el plano muestra que $OA < OB + OC + OD$.
  3. Sean $\triangle ABC$ y $A’$ un punto en el interior del triángulo, muestra que $AB + AC > A’B + A’C$ y que $\angle BA’C > \angle BAC$.
  4. En un poblado situado junto a un rio, cuyo borde es totalmente recto, hay un incendio en un punto $A$, la estación de bomberos se encuentra en un punto $B$ del mismo lado del río donde se dio el incendio, los bomberos necesitan pasar primero por el río para abastecerse de agua. ¿Qué punto $P$ en el borde del río hace que el trayecto $BP + PA$ sea mínimo?
  5. Muestra que si dos circunferencias se intersecan en un solo punto entonces el punto pertenece al segmento que une los centros o a su extensión.
  6. $i)$ Dados una recta y un punto en ella construye la perpendicular a la recta por el punto dado.
    $ii)$ Dados una recta y un punto fuera de ella construye la paralela a la recta por el punto dado.
    $iii)$ Dados una recta y un punto fuera de ella construye la perpendicular a la recta por el punto dado.
  7. $i)$ Dados una recta y un numero $a > 0$ encuentra el el lugar geométrico de los puntos cuya distancia a la recta es $a$.
    $ii)$ ¿Cuál es el lugar geométrico de los puntos cuya distancia a una circunferencia dada $(O, r)$ es una constante dada $b > 0$?

Entradas relacionadas

Fuentes

  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 9-12, 44-54.
  • Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 16-18.
  • Geometría interactiva
  • Geometry Help

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Seminario de Resolución de Problemas: Desigualdades básicas

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

En las entradas correspondientes a esta parte del curso aprenderemos varias técnicas que nos permitirán resolver problemas que involucren desigualdades. El área es enorme y hay libros enteros dedicados a ello. Nosotros sólo veremos algunas técnicas. Comenzaremos con desigualdades básicas y nos enfocaremos en los siguientes temas:

  • Desigualdad $x^2\geq 0$ y desigualdad del triángulo
  • Desigualdades de medias
  • La desigualdad de Cauchy-Schwarz
  • Técnicas de cálculo en desigualdades

En esta entrada veremos el primer inciso, que consiste de dos ideas muy sencillas:

Desigualdad $x^2\geq 0$. El cuadrado de cualquier número real es mayor o igual a cero. Es cero si y sólo si el número es cero.

Desigualdad del triángulo. Si $V$ es un espacio vectorial con norma $\norm{\cdot}$, entonces para cualesquiera vectores $u$ y $v$ se tiene que $$\norm{u}+\norm{v}\geq \norm{u+v}.$$

La desigualdad $x^2\geq 0$ parece muy inocente. Sin embargo, es una herramienta muy versátil cuando se combina con manipulaciones algebraicas creativas. La desigualdad del triángulo la estamos enunciando para espacios vectoriales con norma en general. Dos casos particulares que a lo mejor te son más familiares son los siguientes:

Desigualdad del triángulo para $\mathbb{R}$. Si $a$ y $b$ son números reales, entonces $|a|+|b| \geq |a+b|$.

Desigualdad del triángulo en $\mathbb{R}^n$. Si $ABC$ es un triángulo en el plano (o dimensiones más altas) , de lados de longitudes $\overline{AB}=c$, $\overline{BC}=a$ y $\overline{CA}=b$, entonces
\begin{align*}
a+b&\geq c\\
b+c &\geq a\\
c+a &\geq b.
\end{align*}

Si una de las igualdades se da, $ABC$ es un triángulo degenerado, es decir, con sus tres vértices alineados. En otro caso, todas las desigualdades son estrictas.

Veamos aplicaciones de estas desigualdades básicas.

La desigualdad $\frac{a^2+b^2}{2}\geq \sqrt{ab}$

Comenzaremos probando de dos formas distintas una desigualdad que también resulta útil en otras ocasiones.

Problema. Sean $a$ y $b$ números reales mayores o iguales a cero. Muestra que $$\frac{a+b}{2}\geq \sqrt{ab},$$ y que la igualdad se da si y sólo si $a$ y $b$ son iguales.

A esta desigualdad se le conoce como la desigualdad MA-MG para dos números reales. También forma parte de las desigualdades básicas que te ayudará conocer. Se llama así pues en el lado izquierdo tenemos a la media aritmética de los números $a$ y $b$, y al lado derecho tenemos la media geométrica de los números $a$ y $b$. En realidad la desigualdad se vale para más reales no negativos, pero esto lo veremos en otra entrada.

Sugerencia pre-solución. El problema se puede resolver tanto de manera algebraica, (usando $x^2\geq 0$) como de manera geométrica (usando la desigualdad del triángulo).

Para resolverlo de la primera forma, trabaja hacia atrás. Haz manipulaciones algebraicas para formular problemas equivalentes hasta que llegues a una desigualdad obvia.

Para resolverlo de la segunda forma, haz una figura en la que puedas representar tanto a la media geométrica como a la aritmética. Una forma de hacerlo es comenzar con una semicircunferencia de diámetro $a+b$.

Para identificar el caso de igualdad, haz un análisis de casos.

Solución algebraica. Queremos mostrar que $$\frac{a+b}{2}\geq \sqrt{ab}.$$ Pasando el dos multiplicando, y luego $2\sqrt{ab}$ restando al lado izquierdo, esta desigualdad igualdad ocurre si y sólo si $$a+b-2\sqrt{ab}\geq 0.$$ En el lado izquierdo identificamos un binomio al cuadrado, que se puede factorizar para dar la desigualdad equivalente $$\left(\sqrt{a}-\sqrt{b}\right)^2\geq 0.$$

Esta desigualdad es de la forma $x^2\geq 0$, así que es claramente cierta. La igualdad ocurre si y sólo si $\sqrt{a}-\sqrt{b}=0$, lo cual sucede si y sólo si $a=b$. Todos los pasos que hicimos son reversibles. Esto termina la solución.

$\square$

Solución geométrica. Consideremos la siguiente figura, en donde tenemos una semicircunferencia de diámetro $\overline{AB}=a+b$ y centro $O$. Aquí $C$ es un punto en $AB$ tal que $\overline{AC}=a$ y entonces $\overline{CB}=b$. Además, $D$ es un punto sobre la circunferencia tal que $DC$ es perpendicular a $AB$. Llamemos $d=\overline{CD}$.

Prueba visual de la desigualdad entre la media aritmética y media geométrica usando desigualdades básicas
Prueba visual de MA-MG

Como $\triangle AOD$ y $\triangle BOD$ son isósceles por tener dos lados iguales al radio de la circunferencia, tenemos que $\angle ADO = \angle DAO$ y $\angle BDO = \angle DBO$. Usando estas igualdades y que la suma de los ángulos internos de $\triangle ABD$ es $180^\circ$, se puede mostrar que el ángulo $ADB$ es de $90^\circ$.

De este modo, $\triangle ACD$ y $\triangle DCB$ son semejantes (por ser ambos semejantes a $\triangle ABD$ por criterio AA). Por la semejanza, tenemos que $$\frac{a}{d}=\frac{d}{b},$$ de donde $d=\sqrt{ab}$.

Para terminar la demostración, tomamos un punto $E$ sobre $DO$ tal que $\angle EOC = \angle ECO$. Por la desigualdad del triángulo en $\triangle DEC$, tenemos que

\begin{align*}
\sqrt{ab}&=\overline{DC}\\
&\leq \overline{DE} + \overline{EC}\\
&= \overline{DE} + \overline {EO}\\
&= \overline{DO}\\
&=\frac{a+b}{2}.
\end{align*}

Con esto demostramos la desigualdad. Para terminar el problema, necesitamos ver cuándo se dan los casos de igualdad. Se tiene la igualdad si y sólo si $\triangle DEC$ es un triángulo degenerado, lo cual sucede si y sólo si $E$ está en el segmento $DC$. Esto sólo es posible cuando $DO$ es perpendicular a $AB$, lo cual sucede si y sólo si $C=O$, si y sólo si $AC=CB$, si y sólo si $a=b$.

$\square$

Desigualdades básicas aplicadas a un problema de la Olimpiada Mexicana de Matemáticas

El siguiente problema apareció como parte de los exámenes selectivos que el Comité Nacional de la Olimpiada Mexicana de Matemáticas envía a los estados para seleccionar a sus estudiantes en distintas etapas. Tiene muchas formas de resolverse, pero veamos cómo se puede resolver con desigualdades básicas.

Problema. Sean $a,b,c,d$ reales positivos con $a^2+b^2+c^2+d^2=4$. Muestra que $$a^5+b^5+c^5+d^5 \geq a+b+c+d$$

Sugerencia pre-solución. Modifica el problema a mostrar como desigualdad auxiliar que para un real no negativo $x$ se tiene que $$x^5-2x^2-x+2\geq 0.$$ Esta desigualdad se puede demostrar usando que los cuadrados son no negativos.

Solución. Vamos a probar primero la desigualdad $$x^5-2x^2-x+2\geq 0.$$ Para que sea un poco más fácil, factorizaremos la expresión del lado izquierdo.

Notemos que $1$ es una raíz de $x^5-2x^2-x+2$, de modo que por el teorema del factor podemos factorizar $x-1$ del polinomio. Obtenemos que $$x^5-2x^2-x+2=(x-1)(x^4+x^3+x^2-x-2).$$

Notemos que, nuevamente, $1$ es una raíz de $(x^4+x^3+x^2-x-2)$. Al factorizar $x-1$ de nuevo, obtenemos que $$x^5-2x^2-x+2=(x-1)^2(x^3+2x^2+3x+2).$$

Ya estamos listos para probar la desigualdad que queremos. Notemos que $(x-1)^2\geq 0$ y que $x^3+2x^2+3x+2$ es mayor o igual que cero para $x\geq 0$ pues es un polinomio con puros coeficientes positivos. Esto prueba la desigualdad auxiliar. Reescribiéndola, tenemos que $$x^5\geq 2x^2+x-2.$$ Aplicándola en esta forma a los cuatro reales positivos $a,b,c,d$ del problema, y usando que la suma de cuadardos es $4$, obtenemos que
\begin{align*}
a^5 & + b^5+c^5+d^5\\
&\geq 2(a^2+b^2+c^2+d^2)+a+b+c+d-8\\
&=2\cdot 4 + a+b+c+d-8\\
&=a+b+c+d.
\end{align*}

Esto termina el problema.

$\square$

El primer paso parece un poco artificial. ¿Por qué queremos probar esa desigualdad auxiliar? En otra entrada de blog escribí cómo se puede llegar a las ideas de esta solución.

Desigualdad del triángulo aplicada a la construcción de tetraedros

Si pegamos cuatro triángulos equiláteros en el espacio se hace un tetraedro regular. De manera similar, si pegamos cuatro triángulos como el siguiente, también se hace un tetraedro en el espacio:

Pegar cuatro triángulos congruentes para hacer un tetraedro

La intuición nos dice que debería poderse con cualquier triángulo. Pero esta intuición está mal.

Problema. Sea $ABC$ un triángulo con un ángulo mayor a $90^\circ$. Muestra que no existe ningún tetraedro en el espacio tal que sus cuatro caras sean congruentes a $ABC$.

Sugerencia pre-solución. Procede por contradicción. Por simetría, puedes asumir que el ángulo mayor a $90^\circ$ es el ángulo en $A$. Usa como punto auxiliar al punto medio de $BC$ y usa desigualdades.

Solución. Una observación inicial es que si $ABC$ es un triángulo, $M$ es el punto medio de $BC$ y su ángulo interno en $A$ es mayor a $90^\circ$, entonces $2\overline{AM}<\overline{BC}$. Esto se muestra trazando una circunferencia de diámetro $BC$.

Desigualdad para la mediana en términos del ángulo que hace.

De hecho,

  • Un punto $X$ está sobre la circunfencia si y sólo si $\angle BXC = 90 ^\circ$, si y sólo si $\overline{OX}=\overline{OA}$.
  • $X$ está dentro de la circunferencia si y sólo si $\angle BXC > 90^\circ$, si y sólo si $\overline{OX}<\overline{OA}$ y
  • $X$ está fuera de la circunferencia si y sólo si $\angle BXC < 90^\circ$, si y sólo si $\overline{OX}>\overline{OA}$.

Resolvamos el problema. Sin pérdida de generalidad, el ángulo en $A$ es mayor a $90^\circ$. Entonces $\overline{AM}<\frac{\overline{BC}}{2}$, de donde $2\overline{AM}<\overline{BC}$.

Supongamos que se pudiera hacer en el espacio un tetraedro $WXYZ$ tal que cada una de las caras es congruente al triángulo $ABC$. Sin pérdida de generalidad, tenemos que
\begin{align*}
\overline{WX}&=\overline{YZ}=\overline{AB}\\
\overline{XY}&=\overline{ZW}=\overline{BC}\\
\overline{WY}&=\overline{XZ}=\overline{CA}.
\end{align*}

Tomemos el punto medio $M$ de $XY$. En $\triangle ZMW$, tenemos que
\begin{align*}
\overline{ZM}&=\overline{AM}\\
\overline{WM}&=\overline{AM}.
\end{align*}

Así, usando la desigualdad del triángulo en $\triangle ZMW$ tenemos que \begin{align*}
2\overline{AM}&=\overline{ZM}+\overline{WM}\\
&\geq \overline{ZW}\\
&=\overline{BC}.
\end{align*}

Esto es una contradicción con la desigualdad $2\overline{AM}<\overline{BC}$ que ya habíamos mostrado.

$\square$

Más problemas

Puedes encontrar más problemas de desigualdades básicas en la sección 7.1 del libro Problem Solving through Problems de Loren Larson. También puedes consultar más técnicas y problemas en el libro Desigualdades de la Olimpiada Mexicana de Matemáticas.

Álgebra Superior II: Norma y distancia en los complejos

Por Leonardo Ignacio Martínez Sandoval

3 respuestas

Introducción

Ya definimos a $\mathbb{C}$ y sus operaciones. También definimos y dimos las propiedades de la conjugación compleja. Ahora hablaremos de la norma en los números complejos.

Definición. Dado el número complejo $w=a+bi$, su norma es $\sqrt{a^2+b^2}$. Denotamos a la norma de $w$ por $\Vert w \Vert$.

Ejemplo. La norma del complejo $\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i$ es $$\sqrt{\left(\frac{1}{\sqrt 2}\right)^2+ \left(\frac{1}{\sqrt 2}\right)^2}=\sqrt{\left(\frac{1}{2}+\frac{1}{2}\right)}=\sqrt{1}=1.$$ La norma del complejo $-3i$ es $$\sqrt{0^2+(-3)^2}=\sqrt{9}=3.$$

$\triangle$

Cuando pensamos a los números complejos como elementos del plano, identificando al complejo $a+bi$ con el punto $(a,b)$, la norma es una forma de medir qué tan alejado está del origen.

A partir de la noción de norma podemos definir la noción de distancia, que dice qué tan lejos están dos complejos entre sí.

Definición. Para dos números complejos $w$ y $z$ definimos la distancia entre $w$ y $z$ como la norma de $w-z$, es decir, $\Vert w-z\Vert$. La denotamos por $d(w, z)$

Propiedades básicas de la norma en los complejos

La norma en los complejos está relacionada con otras operaciones definidas como sigue:

Teorema 1. Sean $w$ y $z$ números complejos. Entonces:

  1. La norma es la raíz del producto de un complejo por su conjugado, es decir, $\Vert z \Vert = \sqrt{z\overline{z}}.$
  2. $\Vert z \Vert$ es un número real no negativo.
  3. $\Vert z \Vert = 0$ si y sólo si $z=0$.
  4. La norma es multiplicativa, es decir, $\Vert zw \Vert = \Vert z \Vert \Vert w \Vert$.

Demostración. Si $z=a+ib$, entonces $\overline{z}=a-ib$, y por lo tanto

\begin{align*}
\sqrt{z\overline{z}}&=\sqrt{a^2-(ib)^2}\\
&=\sqrt{a^2+b^2}\\
&=\Vert z \Vert.
\end{align*}

La norma de $z=a+ib$ es la suma del cuadrado de dos reales. Cada uno de ellos es no negativo, así que esa suma es no negativa. De este modo, al sacar raíz cuadrada obtenemos un número real y no negativo. Para que este número sea cero, necesitamos que $a^2=b^2=0$, es decir, que $a=b=0$, lo cual sucede justo cuando $z=0$.

Para mostrar la última propiedad, se pueden tomar dos números complejos explícitos y hacer las cuentas. Sin embargo, también podemos probarla usando la primer propiedad y la conmutatividad del producto, de números complejos, como sigue:

$$\Vert zw \Vert ^2= zw\overline{zw} = z\overline{z} w\overline{w}= \Vert z \Vert^2 \Vert w \Vert ^2.$$

Sacando raíz cuadrada de ambos lados obtenemos el resultado deseado.

$\square$

Ejercicios que usan las propiedades básicas

Veamos algunas formas en las que podemos usar las propiedades anteriores, de la norma, en los complejos.

Ejercicio 1. Muestra que $z$ y $\overline{z}$ tienen la misma norma.

Solución. Usando que $\overline{\overline{z}}=z$, la propiedad 1 del Teorema 1 y la conmutatividad del producto en $\mathbb{C}$ tenemos que $$\Vert \overline{z}\Vert = \sqrt{\overline{z}z}=\sqrt{z\overline{z}} = \Vert z \Vert.$$

$\triangle$

El siguiente es un corolario de la propiedad 4 del Teorema 1, que se puede mostrar usando inducción. La prueba de este corolario se deja como tarea moral.

Corolario. Para $z$ un complejo y $n$ un natural, se tiene que $$\Vert z^n \Vert = \Vert z \Vert ^n.$$

Ejercicio 2. Determina la norma del complejo $$\left(3+4i\right)^{20}.$$

Solución. Tomemos $u=3+4i$. El problema nos pide determinar $\Vert u^{20} \Vert$. Una forma de hacerlo es realizar primero la operación $u^{20}$, pero esto parece ser complicado. En vez de eso, usamos el Corolario anterior. Para ello, notamos que $$\Vert u \Vert = \sqrt{3^2+4^2}= \sqrt{25}=5.$$

De este forma, por el corolario, la norma que buscamos es $$\Vert u^{20} \Vert = \Vert u \Vert ^{20}= 5^{20}.$$

$\triangle$

Ejercicio 3. Sea $z$ un número complejo. Muestra que los siguientes números complejos tienen la misma norma: $$z, -z, iz, -iz.$$

Solución. Se sigue de la propiedad $4$ del Teorema 1 y de que $$\Vert -1 \Vert = \Vert i \Vert = \Vert -i \Vert = 1.$$

$\square$

Ejercicio 4. Muestra que para un número real, $r$, su norma compleja coincide con su valor absoluto.

Solución. Usando la propiedad 1 del Teorema 1 y que $\overline{r}=r$, tenemos que $$\Vert r \Vert = \sqrt{\overline{r}r}=\sqrt{r^2}=|r|.$$

$\square$

La desigualdad del triángulo

¿Cómo se comporta la norma con la suma de los complejos? Lo responderemos en esta sección. Pero antes, de pasar al teorema 2 que contiene la respuesta, veamos un pequeño resultado auxiliar.

Lema. Si $z$ es un número complejo, entonces $|\text{Re}(z)| \leq \Vert z \Vert$ y $|\text{Im}(z)|\leq \Vert z \Vert$. La primer igualdad se da si y sólo si $z$ es un número real y la segunda si y sólo si $z$ es un número imaginario puro, es decir, si su parte real es $0$.

Demostración. Tomemos $z=a+ib$. Tenemos que $a^2\leq a^2+b^2$, de modo que sacando raíces cuadradas tenemos que $$|\text{Re}(z)| = |a| = \sqrt{a^2}\leq \sqrt{a^2+b^2}=\Vert z \Vert.$$ La igualdad se da si y sólo si $b=0$, lo cual sucede si y sólo si $z$ es real.

$\square$

La demostración de la segunda parte es análoga, y queda como tarea moral.

Teorema 2 (desigualdad del triángulo). Para dos números complejos $w$ y $z$ se tiene que $$\Vert w+z \Vert \leq \Vert w \Vert + \Vert z \Vert.$$ La igualdad se da si y sólo si $w$ es un múltiplo real de $z$, es decir, si y sólo si existe un real $r$ tal que $w=rz$.

Demostración. Tenemos que:
\begin{align*}
\Vert w+z \Vert^2 &= (w+z)\overline{(w+z)}\\
&=(w\overline{w}+w\overline{z}+\overline{w}z+z\overline{z})\\
&=\Vert w \Vert^2 + 2\text{Re}(w\overline{z}) + \Vert z \Vert^2.
\end{align*}

Podemos continuar usando la desigualdad del Lema anterior (notemos que se obtiene la igualdad si y sólo si $w\overline{z}$ es real)

\begin{align*}
&\leq \Vert w \Vert^2 + 2\Vert w\overline{z}\Vert + \Vert z \Vert^2\\
&=\Vert w \Vert ^2 + 2 \Vert w \Vert \Vert z \Vert + \vert z \Vert^2\\
&=\left(\Vert w \Vert + \Vert z \Vert \right)^2.
\end{align*}

Esta cadena de desigualdades se resume a $$ \Vert w+z \Vert^2 \leq \left(\Vert w \Vert + \Vert z \Vert \right)^2, $$ de donde sacando raíz cuadrada en ambos lados, obtenemos lo deseado.

Como observamos durante la demostración, la igualdad se da si y sólo si $w\overline{z}$ es un número real, es decir, si y sólo si existe un real $s$ tal que $w\overline{z}=s$. Multiplicando por $z$ de ambos lados, obtenemos que $$w\Vert z \Vert^2 = sz.$$ Si $z=0$, entonces $w=0$ y por lo tanto $w$ es trivialmente un múltiplo real de $z$. Si $z\neq 0$, entonces $w=\frac{s}{\Vert z \Vert ^2}\cdot z$ también es un múltiplo real de $z$, con $r=\frac{s}{\Vert z \Vert ^2}$. Esto termina el análisis, de los casos, de la igualdad.

$\square$

Propiedades de la distancia

En la introducción definimos la distancia entre dos números complejos $w$ y $z$ como la norma de $w-z$, en símbolos, $d(w,z)=\Vert w-z \Vert$. Para formalizar ideas veamos la siguiente definición.

Definición. Sea $X$ un conjunto y $e: X\times X\rightarrow \mathbb{R}^{+}\cup \lbrace 0\rbrace$ una función, $e$ es una métrica en $X$ si, para todo $x$, $y$ y $z\in X$, satisface que:

  1. $e(x, y)\geq 0$.
  2. $e(x, y)=0$ si, y sólo si, $x=y$.
  3. $e(x, y)=e(y, x)$.
  4. $e(x, y)\leq e(x, z) + e(y, z)$.

Observa que a partir de los teoremas 1 y 2, la distancia $d$ cumple las propiedades de esta definición, por lo que decimos que $d$ es una métrica en $\mathbb{C}$. Así tenemos el siguiente teorema.

Teorema 3. Sean $w$ y $z$ dos números complejos cualesquiera y $d(w, z)=\vert\vert w- z\vert\vert$. Entonces $d$ es una métrica en $\mathbb{C}$.

Demostrar este teorema es sencillo a partir de lo que ya vimos, así que su demostración queda como tarea moral.

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra la propiedad 4 del Teorema 1 usando de manera explícita las partes reales e imaginarias de los complejos $z$ y $w$.
  2. Demuestra el corolario de normas de potencias de complejos.
  3. Determina la norma del complejo $(12-5i)^{10}$.
  4. Determina la norma del complejo $(1+2i)(-3+4i)(5-6i)(-7-8i)$.
  5. Demuestra la segunda parte del Lema.
  6. Demuestra el Teorema 3.
  7. Sean $w=(3+4i)(5-i)$ y $z=(5-i)(4+2i)$. Determina $d(w,z)$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»