Introducción
En esta entrada, con la ayuda de varias fórmulas y resultados que hemos visto hasta ahora, mostraremos algunas desigualdades geométricas básicas e importantes, entre ellas la desigualdad entre las medias geométrica y aritmética, y la desigualdad de Erdos Mordell.
Medias armónica, geométrica, aritmética y cuadrática
Teorema 1. Dados dos segmentos de longitudes $a$ y $b$ tenemos las siguientes desigualdades:
$\dfrac{2ab}{a + b} \leq \sqrt{ab} \leq \dfrac{a + b}{2} \leq \sqrt{\dfrac{a^2 + b^2}{2}}$.
De izquierda a derecha estas cantidades se conocen como media armónica, media geométrica, media aritmética y media cuadrática de $a$ y $b$.
Demostración. Tracemos un semicírculo tomando como diámetro un segmento $BC$ de longitud $a + b$ y sea $D \in BC$ tal que $BD = a$ y $DC = b$, en $D$ levantamos una perpendicular a $BC$ que corta al arco $\overset{\LARGE{\frown}}{CB}$ en $A$, entonces $\triangle ABC$ es un triángulo rectángulo con $\angle A = \dfrac{\pi}{2}$.
Por criterio de semejanza AA $\triangle ADB \sim \triangle CDA$ y tenemos que $\dfrac{AD}{CD} = \dfrac{BD}{AD}$.
Por lo tanto $AD$ es la media geométrica de $BD$ y $DC$, esto es $AD^2 = BD \times CD$.
Consideremos $O$ el punto medio de $BC$, sea $E \in AO$ tal que $DE \perp AO$, como $\triangle ADO \sim \triangle AED$ entonces
$\dfrac{AD}{AE} = \dfrac{AO}{AD}$
$\Rightarrow AE = \dfrac{2AD^2}{2AO} = \dfrac{2BD \times DC}{BC} = \dfrac{2ab}{a + b}$.
Por el teorema de Pitágoras en $\triangle AED$
$AD^2 = AE^2 + DE^2 \Rightarrow AE \leq AD \Rightarrow \dfrac{2ab}{a + b} \leq \sqrt{ab}$.
Por el teorema de Pitágoras en $\triangle ADO$
$AO^2 = AD^2 + DO^2 \Rightarrow AD \leq AO \Rightarrow \sqrt{ab} \leq \dfrac{a + b}{2}$.
Ahora tracemos $OF$ el radio perpendicular a $BC$, entonces
$OD = \dfrac{a + b}{2} – a = \dfrac{b – a}{2}$.
Aplicando el teorema de Pitágoras a $\triangle ODF$ obtenemos,
$DF^2 = OF^2 + OD^2 = (\dfrac{b – a}{2})^2 + (\dfrac{a + b}{2})^2 =\dfrac{a^2 + b^2}{2}$.
Como $OF \leq DF \Rightarrow \dfrac{a + b}{2} \leq \sqrt{\dfrac{a^2 + b^2}{2}}$.
$\blacksquare$
Corolario. Sean $w$, $x$, $y$, $z$ números reales positivos entonces:
$wxyz \leq (\dfrac{w + x + y + z}{4})^4$, y la igualdad se da si y solo si $w = x = y = z$.
Demostración. Aplicamos la desigualdad entre las medias geométrica y aritmética a los pares de números $w$, $x$; $y$, $z$.
$\sqrt{wx} \leq \dfrac{w + x}{2}$, $\sqrt{yz} \leq \dfrac{y + z}{2}$.
Por lo tanto, $\sqrt{wxyz} \leq (\dfrac{w + x}{2}) (\dfrac{y + z}{2})$.
Ahora volvemos a usar la desigualdad entre las medias geométrica y aritmética
$\sqrt{\dfrac{(w + x)}{2} \dfrac{(y + z)}{2}} \leq \dfrac{\dfrac{w + x}{2} + \dfrac{y + z}{2}}{2} = \dfrac{w + x + y + z}{4}$
Por lo tanto, $\sqrt[4]{wxyz} \leq \sqrt{\dfrac{(w + x)}{2} \dfrac{(y + z)}{2}} \leq \dfrac{w + x + y + z}{4}$.
En consecuencia, $wxyz \leq (\dfrac{w + x + y + z}{4})^4$.
$\blacksquare$
Desigualdad de Erdos Mordell
Lema de Mordell. Sea $\triangle ABC$ y $P$ un punto en su interior, considera $D$, $E$ y $F$ las proyecciones de $P$ a los lados $BC$, $AC$ y $AB$ respectivamente, entonces $PA \sin A \geq PF \sin B + PE \sin C$.
Demostración. Notemos que la circunferencia con diámetro $PA$ pasa por $F$ y por $E$, pues $AP$ subtiende ángulos rectos en $F$ y $E$.
Por la ley extendida de los senos,
$\sin BAC = \sin (\pi – BAC) = \sin EPF = \dfrac{EF}{PA}$, esto implica que $PA \sin A = EF$.
Sean $G$ y $H$ las proyecciones de $E$ y $F$ respectivamente en la recta que pasa por $P$ y $D$.
$\square FBDP$ es cíclico, pues $PB$ subtiende ángulos rectos en $F$ y $D$, entonces $\angle DBA$ y $\angle FPD$ son y suplementarios por lo tanto $\sin DBA = \sin HPF = \dfrac{FH}{FP}$.
Como resultado $FP \sin B = FH$, igualmente podemos ver que $PE \sin C = EG$.
Sea $I = EF \cap HP$, por el teorema de Pitágoras podemos ver que $IE \geq GE$ y $FI \geq FH$,
Por lo tanto, $PA \sin A \geq PF \sin B + PE \sin C$.
$\blacksquare$
Teorema 2, desigualdad de Erdos Mordell. Sea $\triangle ABC$ y $P$ un punto en su interior, considera $D$, $E$ y $F$ las proyecciones de $P$ a los lados $BC$, $AC$ y $AB$ respectivamente, entonces $PA + PB + PC \geq 2(PD + PE + PF)$.
Demostración. Debido al lema anterior tenemos lo siguiente:
$PA \geq PF\dfrac{\sin B}{\sin A} + PE\dfrac{\sin C}{\sin A}$,
$PB \geq PF\dfrac{\sin A}{\sin B} + PD\dfrac{\sin C}{\sin B}$,
$PC \geq PE\dfrac{\sin A}{\sin C} + PD\dfrac{\sin B}{\sin C}$.
Sumamos estas tres desigualdades
$PA + PB + PC \geq$
$PF(\dfrac{\sin B}{\sin A} + \dfrac{\sin A}{\sin B}) + PE(\dfrac{\sin C}{\sin A} + \dfrac{\sin A}{\sin C}) + PD(\dfrac{\sin B}{\sin C} + \dfrac{\sin C}{\sin B})$
$= PF(\dfrac{\sin^2A + \sin^2 B}{\sin A \sin B}) + PE(\dfrac{\sin^2 A + \sin^2 C}{\sin A \sin C}) + PD(\dfrac{\sin^2 B + \sin^2 C}{\sin B \sin C})$.
Sustituimos $a$ y $b$ por $a^2$ y $b^2$ en la desigualdad entre las medias geométrica y aritmética
$\dfrac{a^2 + b^2}{2} \geq \sqrt{a^2b^2}$, por lo tanto, $\dfrac{a^2 + b^2}{ab} \geq 2$.
Aplicamos esto a nuestra suma y como resultado obtenemos
$PA + PB + PC \geq 2(PD + PE + PF)$.
$\blacksquare$
Problema 1. Sea $\triangle ABC$ e $I$ su incentro, considera $P$, $Q$ y $R$ los puntos medios de los arcos $\overset{\LARGE{\frown}}{BC}$, $\overset{\LARGE{\frown}}{CA}$ y $\overset{\LARGE{\frown}}{AB}$ que no contienen a los vértices de $\triangle ABC$, entonces $IP + IQ + IR \geq IA + IB + IC$.
Solución. Sean $D = PQ \cap CR$, $E = QR \cap AP$ y $F = RP \cap BQ$.
Por la entrada anterior sabemos que $Q$ es el centro de una circunferencia que pasa por $I$, $A$ y $C$, y que $R$ es el centro de una circunferencia que pasa por $I$, $A$ y $B$, entonces $QA = QI$ y $RA = RI$.
Por lo tanto, $\square ARIQ$ es un rombo, de esto se sigue que $QR \perp AI$ y $AE = IE$.
Igualmente vemos que $RP \perp BI$, $BF = IF$ y $PQ \perp CI$, $CD = ID$.
Aplicamos la desigualdad de Erdos Mordell a $\triangle PQR$ y al punto $I$
$IP + IQ + IR \geq 2(ID + IE + IF) = 2(\dfrac{IC}{2} + \dfrac{IA}{2} + \dfrac{IB}{2})$.
En conclusión, $IP + IQ + IR \geq IA + IB + IC$.
$\blacksquare$
Desigualdades de Euler y de Padoa
Proposición 1, desigualdad de Euler. El circunradio $R$ y el inradio $r$ de todo triangulo cumplen $R \geq 2r$ y la igualdad se cumple si y solo si el triángulo es equilátero.
Demostración. La fórmula de Euler nos asegura que $0 \leq OI^2 = R(R – 2r) = R^2 – 2Rr$, donde $I$ es el incentro y $O$ el circuncentro del triángulo.
Como resultado, $R \geq 2r$.
$\blacksquare$
Proposición 2, desigualdad de Padoa. Sea $\triangle ABC$ con lados $c = AB$, $a = BC$ y $b = AC$ entonces $abc \geq (a + b – c)(a + c – b)(b + c – a)$.
Demostración. Sean $s = \dfrac{a + b + c}{2}$, $R$ el circunradio y $r$ el inradio de $\triangle ABC$, entonces tenemos las siguientes fórmulas para el área de $\triangle ABC$:
$(\triangle ABC) = \sqrt{s(s – a)(s – b)(s – c)} = \dfrac{abc}{4R} = rs$.
Notemos lo siguiente
$(a + b – c)(a + c – b)(b + c – a) = (2s – 2)(2s – 2b)(2s – 2a) = 8(s – c)(s – b)(s – a) $
$= \dfrac{8(\triangle ABC)^2 }{s} = \dfrac{8r^2s^2}{s} = 8r^2s$.
Por otro lado, $abc = 4Rrs$.
Por lo tanto, la desigualdad que queremos mostrar es equivalente a $8r^2s \leq 4Rrs$ que a su vez es equivalente a $2r \leq R$, lo cual es cierto por la proposición anterior.
$\blacksquare$
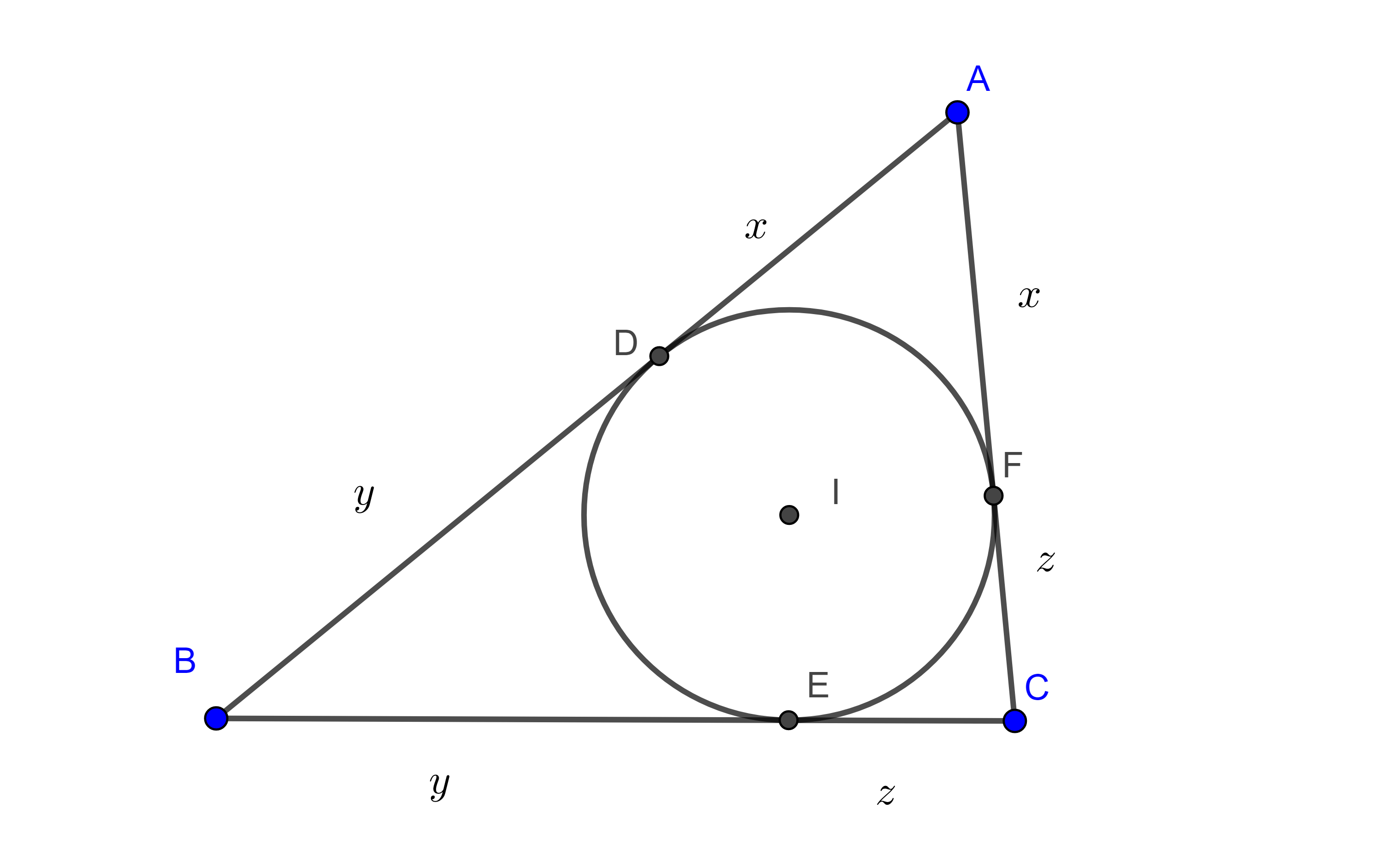
Transformación de Ravi
Recordemos que las tangentes desde un punto a una circunferencia son iguales, por lo que los puntos de tangencia del incírculo de un triángulo, divide al perímetro del triángulo en tres pares de segmentos iguales, así que podemos expresar a los lados de un triángulo de esta manera para resolver algunas desigualdades geométricas.
$a = BC = y + z$, $b = AC = x + z$, $c = AB = x + y$.
Problema 2. Para los ángulos internos de un triángulo $\triangle ABC$ tenemos la siguiente desigualdad.
$\sin \dfrac{A}{2} \sin \dfrac{B}{2} \sin \dfrac{C}{2} \leq \dfrac{1}{8}$.
Solución. Usando la identidad para el seno del ángulo medio y la ley de los cosenos tenemos:
$\sin^2 \dfrac{A}{2} = \dfrac{1}{2}(1 – \cos A) = \dfrac{1}{2}(1 + \dfrac{a^2 – (b^2 + c^2)}{2bc})$
$= \dfrac{a^2 – (b – c)^2}{4bc} = \dfrac{y^2 + 2yz + z^2 – (z – y)^2}{4bc} = \dfrac{yz}{bc}$.
Igualmente tenemos
$\sin^2 \dfrac{B}{2} = \dfrac{xz}{ac}$ y $\sin^2 \dfrac{C}{2} = \dfrac{xy}{ab}$.
A continuación despejamos y hacemos el producto
$\sin \dfrac{A}{2} \sin \dfrac{B}{2} \sin \dfrac{C}{2} = \dfrac{\sqrt{yz}\sqrt{xz}\sqrt{xy}}{abc}$.
Ahora aplicamos la desigualdad entre las medias geométrica y aritmética
$\dfrac{\sqrt{yz}\sqrt{xz}\sqrt{xy}}{abc} \leq \dfrac{1}{abc}(\dfrac{y + z}{2})(\dfrac{x + z}{2})(\dfrac{x + y}{2}) = \dfrac{abc}{8abc} = \dfrac{1}{8}$.
Por lo tanto, $\sin \dfrac{A}{2} \sin \dfrac{B}{2} \sin \dfrac{C}{2} \leq \dfrac{1}{8}$.
$\blacksquare$
Desigualdad de Nesbitt
Proposición 3. Sean $a$, $b$ y $c$ tres números positivos entonces la siguiente desigualdad es cierta
$(a +b + c)(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}) \geq 9$.
Demostración. La desigualdad entre las medias geométrica y aritmética puede ser vista como
$\dfrac{a}{b} + \dfrac{b}{a} \geq 2\sqrt{\dfrac{a}{b} \dfrac{b}{a}} = 2$.
Por lo tanto,
$(a +b + c)(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}) = \dfrac{a}{b} + \dfrac{b}{a} + \dfrac{a}{c} + \dfrac{c}{a} + \dfrac{b}{c} + \dfrac{c}{b} + 3 \geq 6 +3 = 9$.
$\blacksquare$
Proposición 4. Desigualdad de Nesbitt. Para cualesquiera números positivos $a$, $b$, $c$ ocurre que $\dfrac{a}{b + c} + \dfrac{b}{a + c} + \dfrac{c}{a + b} \geq \dfrac{3}{2}$.
Demostración.
$\dfrac{a}{b + c} + \dfrac{b}{a + c} + \dfrac{c}{a + b}$
$= \dfrac{a}{b + c} + \dfrac{b + c}{b + c} + \dfrac{b}{a + c} + \dfrac{a + c}{a + c} + \dfrac{c}{a + b} + \dfrac{a + b}{a + b} – 3$
$ = \dfrac{a + b + c}{b + c} + \dfrac{ a + b + c}{a + c} + \dfrac{ a + b + c }{a + b} – 3$
$= (a + b + c)( \dfrac{1}{b + c} + \dfrac{1}{a + c} + \dfrac{1}{a + b}) – 3$
$=\dfrac{1}{2}((a + b) + (a + c) + (b + c))( \dfrac{1}{b + c} + \dfrac{1}{a + c} + \dfrac{1}{a + b}) – 3$
$\geq \dfrac{9}{2} – 3 = \dfrac{3}{2}$.
Donde la última desigualdad se obtiene al aplicar la proposición anterior.
Por lo tanto, $\dfrac{a}{b + c} + \dfrac{b}{a + c} + \dfrac{c}{a + b} \geq \dfrac{3}{2}$.
$\blacksquare$
Desigualdad de Weitzenböck
Proposición 5. Desigualdad de Weitzenböck. Si $a$, $b$, $c$ son las longitudes de los lados de $\triangle ABC$ entonces $a^2 + b^2 + c^2 \geq 4\sqrt{3} (\triangle ABC)$.
Demostración. De acuerdo a la fórmula de Herón
$(\triangle ABC) = \sqrt{s(s – a)(s – b)(s – c)}$
$= \sqrt{(\dfrac{a + b + c}{2})(\dfrac{b + c – a}{2})(\dfrac{a + c – b}{2})(\dfrac{a + b – c}{2})}$
$= \dfrac{1}{4} \sqrt{2(a^2b^2 + a^2c^2 + b^2c^2) – (a^4 + b^4 + c^4)}$.
Por otro lado
$\begin{equation} (a^2 – b^2)^2 + (b^2 – c^2)^2 + (c^2 – a^2)^2 \geq 0 \end{equation}$
$\Leftrightarrow$ $2(a^4 + b^4 + c^4) – 2(a^2b^2 + a^2c^2 + b^2c^2) \geq 0$
$\Leftrightarrow$ $\dfrac{4}{3} (a^4 + b^4 + c^4) \geq \dfrac{4}{3} (a^2b^2 + a^2c^2 + b^2c^2)$
$ \Leftrightarrow$ $\dfrac{4}{3} (a^4 + b^4 + c^4) + \dfrac{- 3(a^4 + b^4 + c^4) + 2(a^2b^2 + a^2c^2 + b^2c^2)}{3}$
$\geq \dfrac{4}{3} (a^2b^2 + a^2c^2 + b^2c^2) + \dfrac{- 3(a^4 + b^4 + c^4) + 2(a^2b^2 + a^2c^2 + b^2c^2)}{3}$
$\Leftrightarrow$ $\dfrac{a^4 + b^4 + c^4 + 2(a^2b^2 + a^2c^2 + b^2c^2)}{3} \geq 2(a^2b^2 + a^2c^2 + b^2c^2) – (a^4 + b^4 + c^4)$
$\Leftrightarrow$ $\dfrac{(a^2 + b^2 + c^2)^2}{3} \geq 2(a^2b^2 + a^2c^2 + b^2c^2) – (a^4 + b^4 + c^4) = (4(\triangle ABC))^2$.
$ \Leftrightarrow$ $a^2 + b^2 + c^2 \geq 4\sqrt{3} (\triangle ABC)$.
De la desigualdad $(1)$ podemos notar que la igualdad ocurre si y solo si $a = b = c$, es decir el triángulo es equilátero.
$\blacksquare$
Más adelante…
En la próxima entrada estudiaremos algunas propiedades de las medianas y el centroide de un triángulo.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Sea $P$ un punto en el interior de un triangulo $\triangle ABC$, muestra que al menos uno de los ángulos $\angle BAP$, $\angle CBP$ y $\angle ACP$ es igual a $\dfrac{\pi}{6}$.
- Considera $P$ un punto en el interior de $\triangle ABC$ cuyo circunradio es $R$, demuestra que $\dfrac{PA}{BC^2} + \dfrac{PB}{AC^2} + \dfrac{PC}{AB^2} \geq \dfrac{1}{R}$.
- Sea $P$ un punto en el interior de $\triangle ABC$, denota por $R_a$, $R_b$, $R_c$ los circunradios de los triángulos $\triangle PBC$, $\triangle PAC$ y $\triangle PAB$ respectivamente, prueba que $\dfrac{PB \times PC}{R_a} + \dfrac{PA \times PC}{R_b} + \dfrac{PA \times PB}{R_c} \leq PA + PB + PC$.
- Si $a$, $b$ y $c$ son los lados de un triangulo prueba que $(a + b)(b + c)(a + c) \geq 8(a + b – c)(b + c – a)(a + c -b)$.
- Sean $\triangle ABC$, $\alpha = \angle BAC$, $\beta = \angle CBA$, $\gamma = \angle ACB$, muestra que $\cos \alpha + \cos \beta + \cos \gamma \leq \dfrac{3}{2}$.
- Sean $\triangle ABC$, $AD$, $BE$, $CF$, sus alturas y $H$ el ortocentro muestra que:
$i)$ $\dfrac{AD}{HD} + \dfrac{BE}{HE} + \dfrac{CF}{HF} \geq 9$,
$ii)$ $\dfrac{HD}{HA} + \dfrac{HE}{HB} + \dfrac{HF}{HC} \geq \dfrac{3}{2}$.
- Sea $\triangle ABC$ un triángulo rectángulo con catetos $a$ y $b$ e hipotenusa $c$, muestra que se cumple la siguiente desigualdad $a + b \leq \sqrt{2}c$.
- Considera $A’$ y $B’$ los puntos medios de $BC$ y $AC$ en $\triangle ABC$, muestra que $3(BC + AC) > 2(AA’ + BB’)$.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Circunferencias tritangentes.
- Siguiente entrada del curco: Medianas y centroide.
- Otros cursos.
Fuentes
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 287-297.
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 27-29, 98-103.
- Art of Problem Solving
- Wikipedia
- Cut the Knot
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»