Introducción
En esta entrada veremos dos lugares geométricos importantes, uno es la caracterización de arco de circunferencia y el otro la circunferencia de Apolonio.
Arco de circunferencia
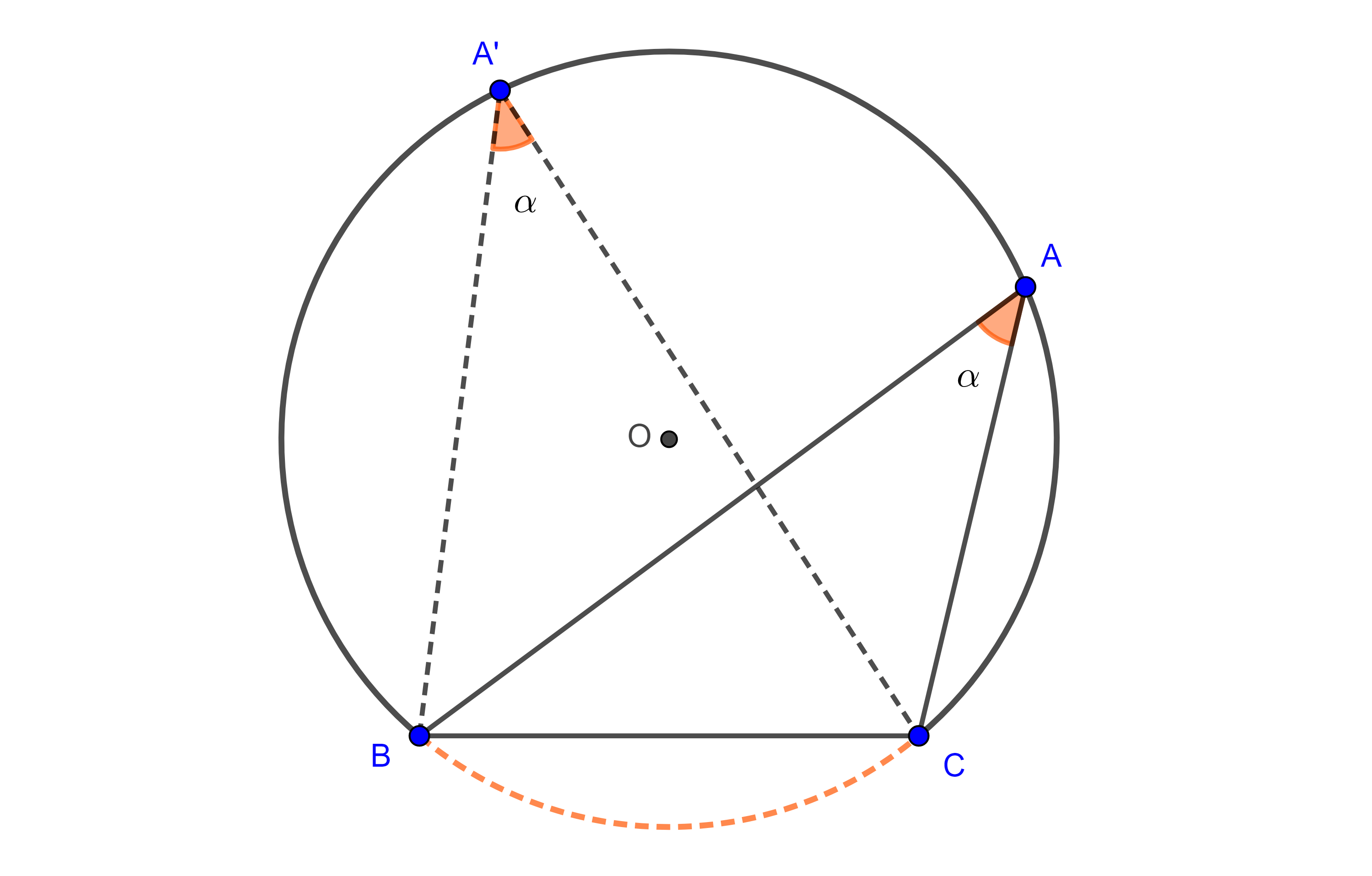
Teorema 1. Dados un segmento $BC$ y un ángulo $\alpha < \pi$ el lugar geométrico de los puntos $A$ que están sobre un mismo lado de la recta $BC$ y tal que el ángulo $\angle BAC = \alpha$, es un arco de circunferencia que pasa por $B$ y $C$.
Demostración. Sea $A$ un punto tal que $\angle BAC = \alpha$, consideremos el circuncírculo $\Gamma (O)$ de $\triangle ABC$.
Todos los puntos $A’$ en el arco $\overset{\LARGE{\frown}}{CB}$ cumplen que $\angle BA’C =\alpha$ pues $\angle BAC$ y $\angle BA’C$ abarcan el mismo arco $\overset{\LARGE{\frown}}{BC}$.
Por lo tanto, el arco $\overset{\LARGE{\frown}}{CB}$ es parte del lugar geométrico.
$\blacksquare$
Ahora tomemos $A’$ del mismo lado que $A$ respecto de $BC$ pero $A’ \notin \overset{\LARGE{\frown}}{CB}$ y consideremos $B’ = A’B \cap \overset{\LARGE{\frown}}{CB}$ y $C’ = A’C \cap \overset{\LARGE{\frown}}{CB}$.
Si $A’$ está dentro del circuncírculo de $\triangle ABC$ (izquierda figura 2), entonces los teoremas de la medida del ángulo interior y el ángulo inscrito nos dicen que
$\angle BA’C = \dfrac{\angle BOC + \angle B’OC’}{2} > \dfrac{\angle BOC}{2} = \angle BAC$.
Por tanto, $A’$ no está en el lugar geométrico.
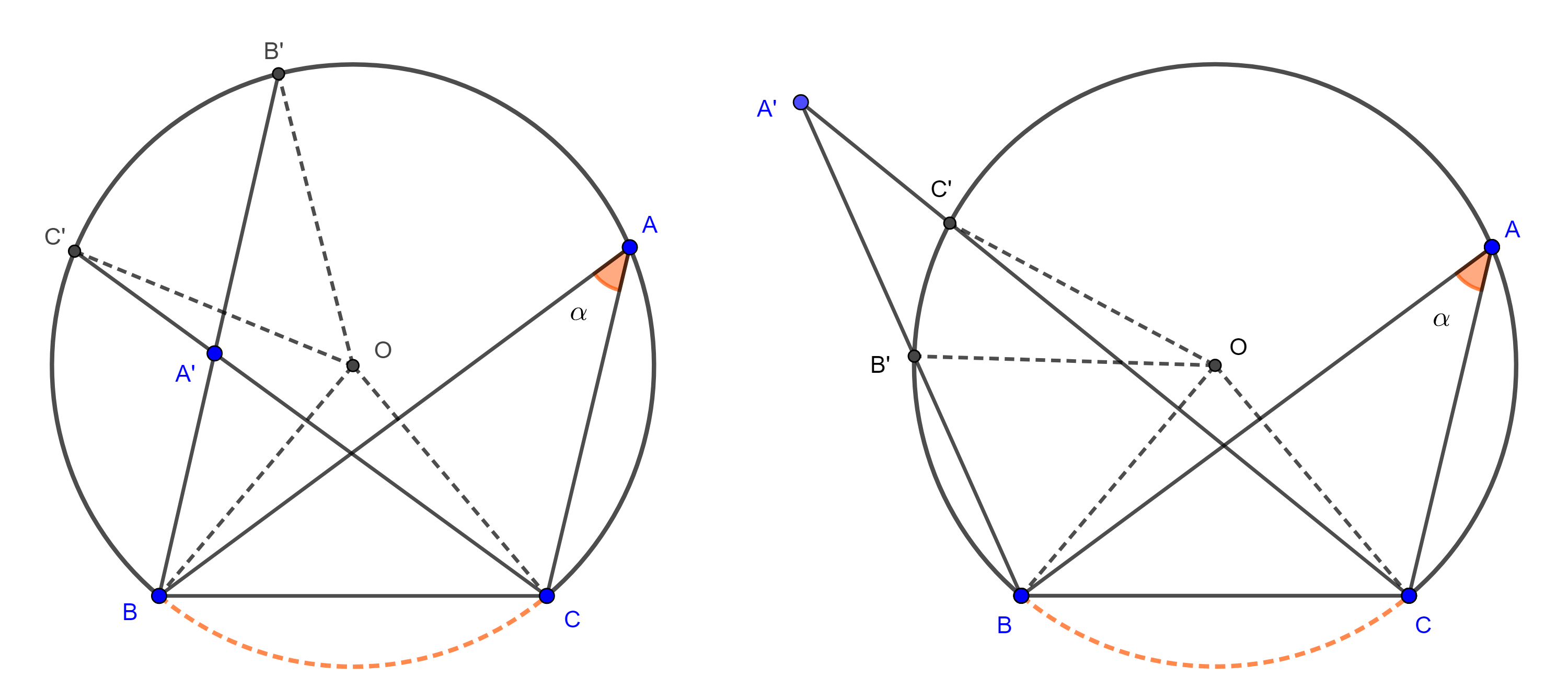
Si $A’$ esta fuera del circuncírculo de $\triangle ABC$ (derecha figura 2) , entonces la medida del ángulo exterior es
$\angle BA’C = \dfrac{\angle BOC – \angle C’OB’}{2} < \dfrac{\angle BOC}{2} = \angle BAC$.
En consecuencia no existe $A’$ en el lugar geométrico fuera del arco $\overset{\LARGE{\frown}}{CB}$ y así queda demostrado el teorema.
$\blacksquare$
Observación. Si quitamos la condición de que los puntos $A$ estén de un mismo lado respecto de $BC$ entonces obtendremos dos arcos de circunferencia que son simétricos respecto de $BC$.
Corolario. Dados un segmento $BC$ el lugar geométrico de los puntos $A$ tal que el ángulo $\angle BAC = \dfrac{\pi}{2}$, es una circunferencia de diámetro $BC$.
Demostración. Por el teorema 1 y la observación, el lugar geométrico son dos arcos de circunferencia simétricos respecto de $BC$, además, por el teorema de Tales, $BC$ es diámetro de cada uno de estos arcos, por tanto los dos arcos forman una misma circunferencia.
$\blacksquare$
Circunferencia de Apolonio
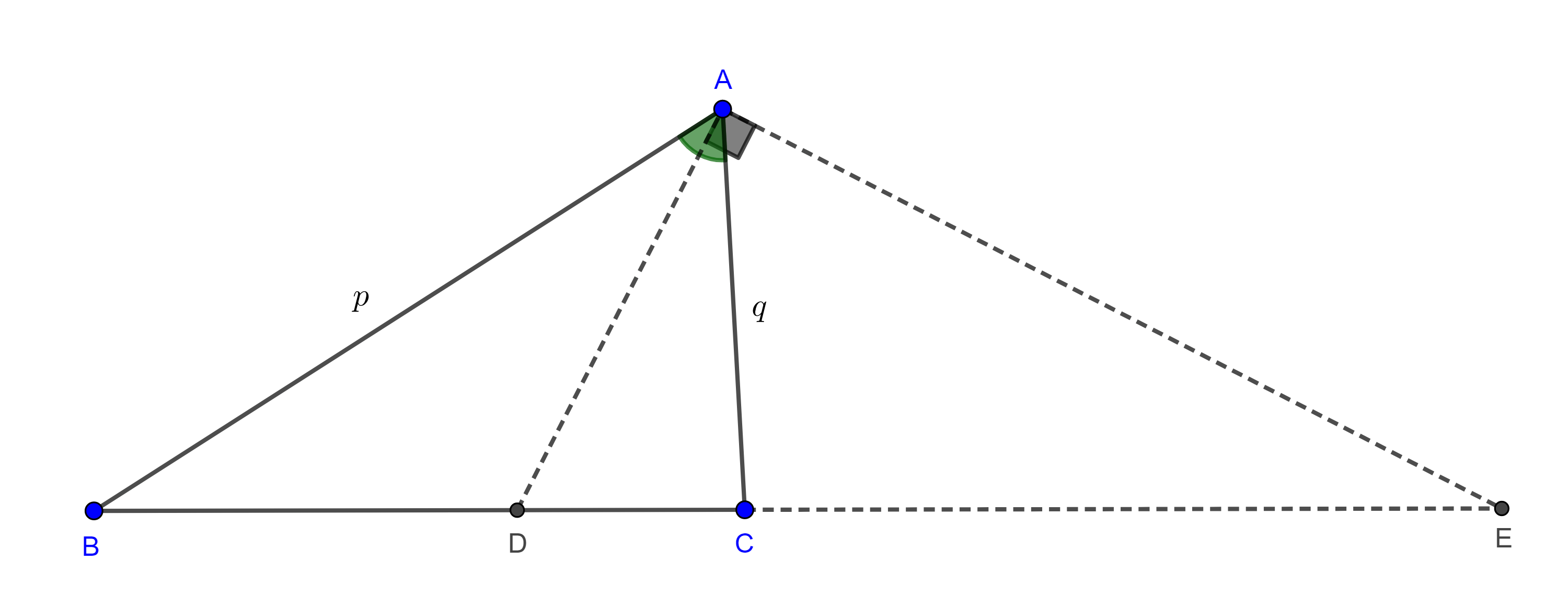
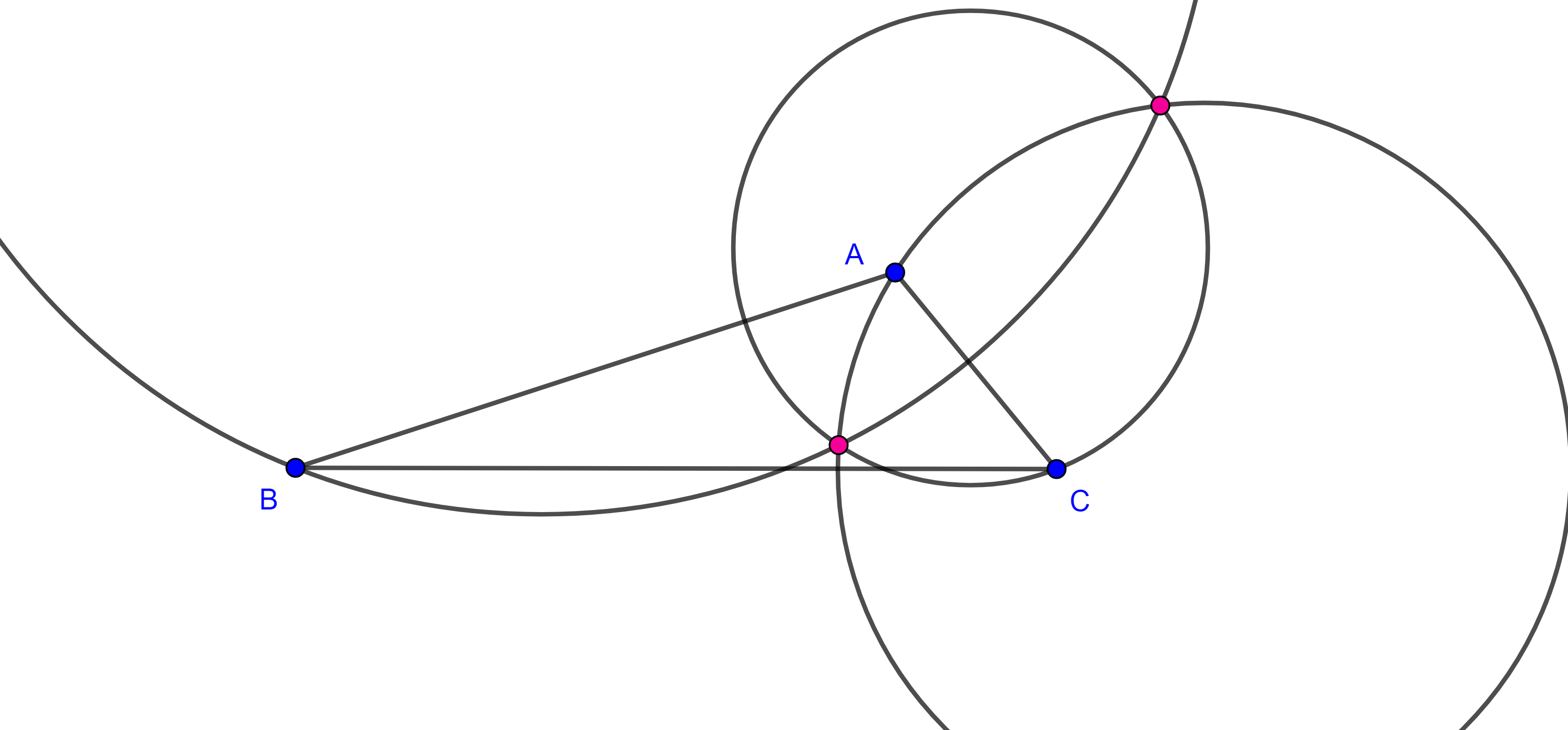
Teorema 2. El lugar geométrico de los puntos $A$ tales que la razón de las distancias a dos puntos fijos $B$ y $C$ es igual a una razón dada $\dfrac{p}{q}$, es una circunferencia llamada circunferencia de Apolonio.
Demostración. Sea $BC = a$, construimos un triángulo de lados $p$, $q$ y $a$, si $p + q < a$ entonces tomamos un múltiplo $mp$ y $mq$ tal que $m(p + q) > a$.
Sea $A$ el vértice construido tal que $AB = p$ y $AC = q$, por el teorema de la bisectriz, las bisectrices interna $AD$ y externa $AE$ de $\angle A$ dividen al segmento $CB$ en la razón dada
$\dfrac{p}{q} = \dfrac{AB}{AC} = \dfrac{BD}{DC} = \dfrac{BE}{CE}$.
De esta manera, hemos encontrado dos putos $D$ y $E$ en la recta $BC$ del lugar geométrico.
Sea $A’$ cualquier punto en el lugar geométrico, entonces $\dfrac{A’B}{A’C} = \dfrac{p}{q} = \dfrac{BD}{DC} = \dfrac{BE}{CE}$.
Por el reciproco del teorema de la bisectriz esto implica que las cevianas $AD$ y $AE$ son las bisectrices interna y externa del ángulo $\angle BA’C$.
Como las bisectrices interna y externa de todo ángulo son perpendiculares entre si tenemos que $\angle DA’C = \dfrac{\pi}{2}$.
Por el corolario anterior, $A’ \in \Gamma$, la circunferencia cuyo diámetro es $DE$.
$\blacksquare$
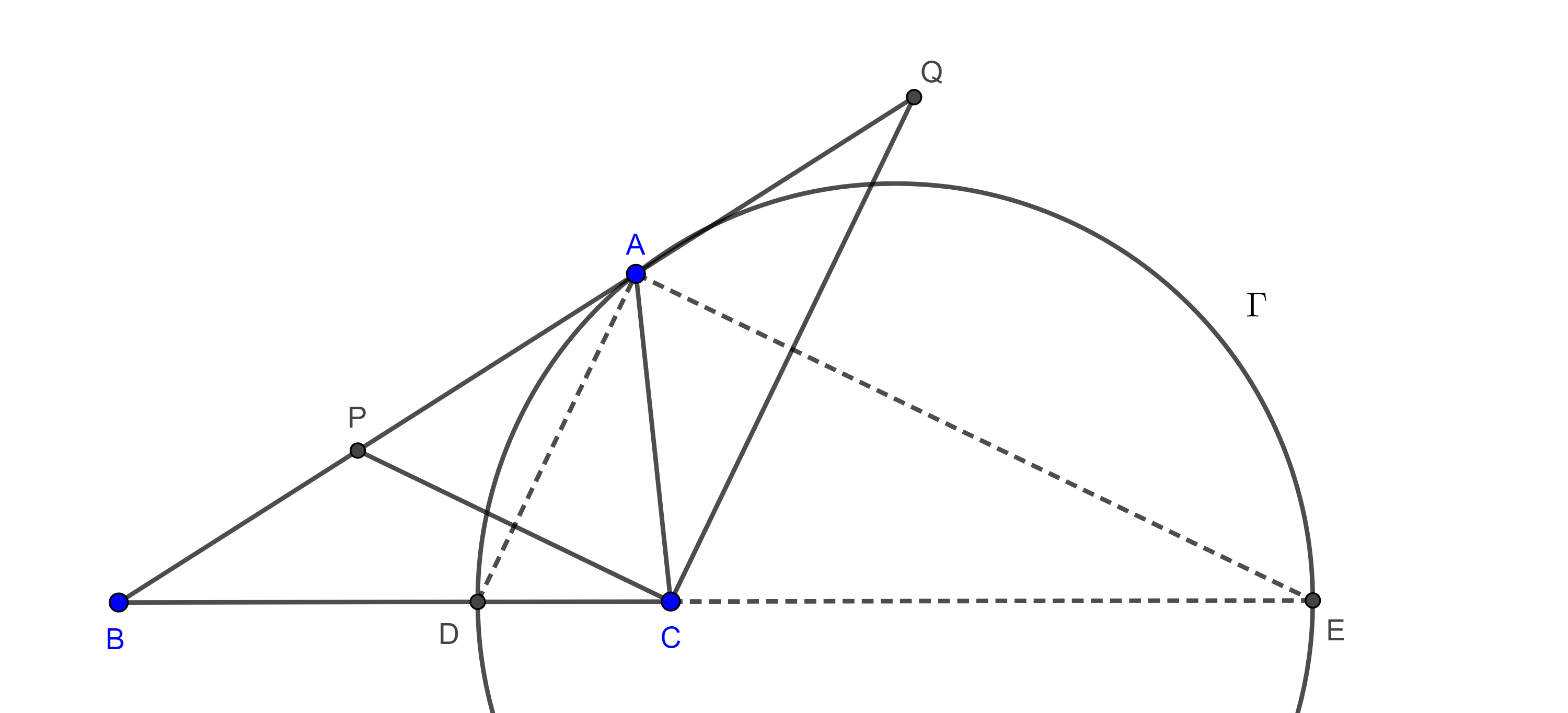
Ahora, sea $A \in \Gamma$, entonces $AD \perp AE$ ya que $DE$ es diámetro.
Por $C$ trazamos las paralelas a $AE$ y $AD$ las cuales intersecan a $AB$ en $P$ y en $Q$ respectivamente, como $AD \perp AE$ entonces $PC \perp CQ$.
Aplicando el teorema de Tales a $\triangle BQC$ y $\triangle BAE$ tenemos
$\begin{equation} \dfrac{AB}{AQ} = \dfrac{BD}{DC} \end{equation}$
$\begin{equation} \dfrac{AB}{AP} = \dfrac{BE}{CE}. \end{equation}$
Por construcción $\dfrac{BD}{DC} = \dfrac{BE}{CE}$
$\Rightarrow \dfrac{AB}{AQ} = \dfrac{AB}{AP} \Rightarrow AP = AQ$.
Es decir, $A$ es el punto medio de la hipotenusa en el triángulo rectángulo $\triangle CPQ$, por tanto, equidista a los tres vértices del triangulo
$\Rightarrow AP = AQ = AC$
Reemplazando en las ecuaciones $(1)$ y $(2)$ obtenemos
$\dfrac{AB}{AC} = \dfrac{BD}{DC} = \dfrac{BE}{CE} = \dfrac{p}{q}$.
Por tanto, $A$ está en el lugar geométrico.
$\blacksquare$
Observación 1. Notemos que, si la razón dada es $1$, el lugar geométrico son los puntos que equidistan a los puntos dados, esto es la mediatriz del segmento que une los puntos dados.
Observación 2. Si $B$, $C$ son los puntos fijos y $\dfrac{p}{q}$ es la razón dada, los puntos $A$ tales que $\dfrac{AB}{AC} = \dfrac{p}{q}$, describen una circunferencia de Apolonio, pero los puntos $A’$ tales que $\dfrac{A’C}{A’B} = \dfrac{p}{q}$ también describen una circunferencia de Apolonio, estos dos lugares no coinciden a menos que $\dfrac{p}{q} = 1$.
En consecuencia, para un segmento dado y una razón dada tenemos dos circunferencias de Apolonio.
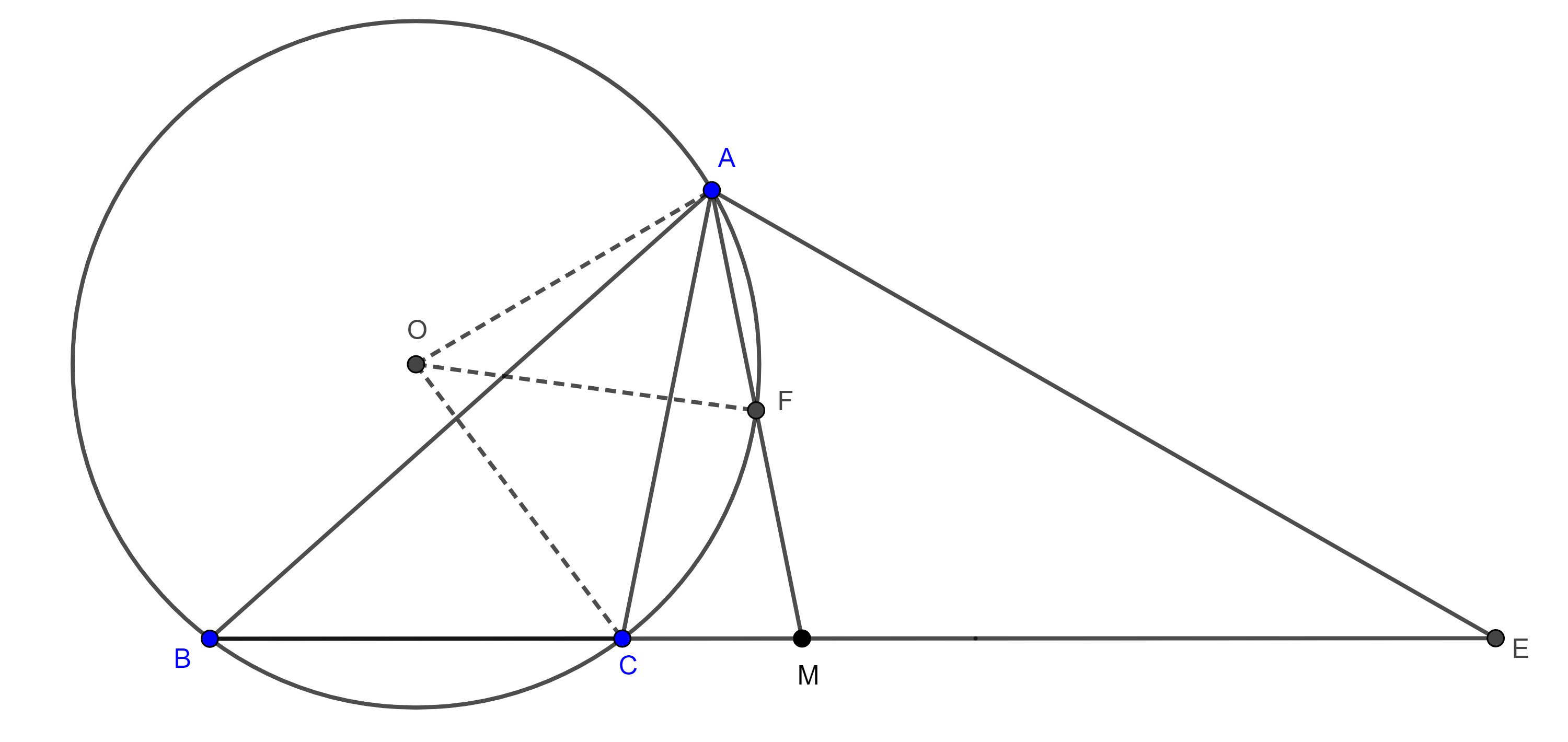
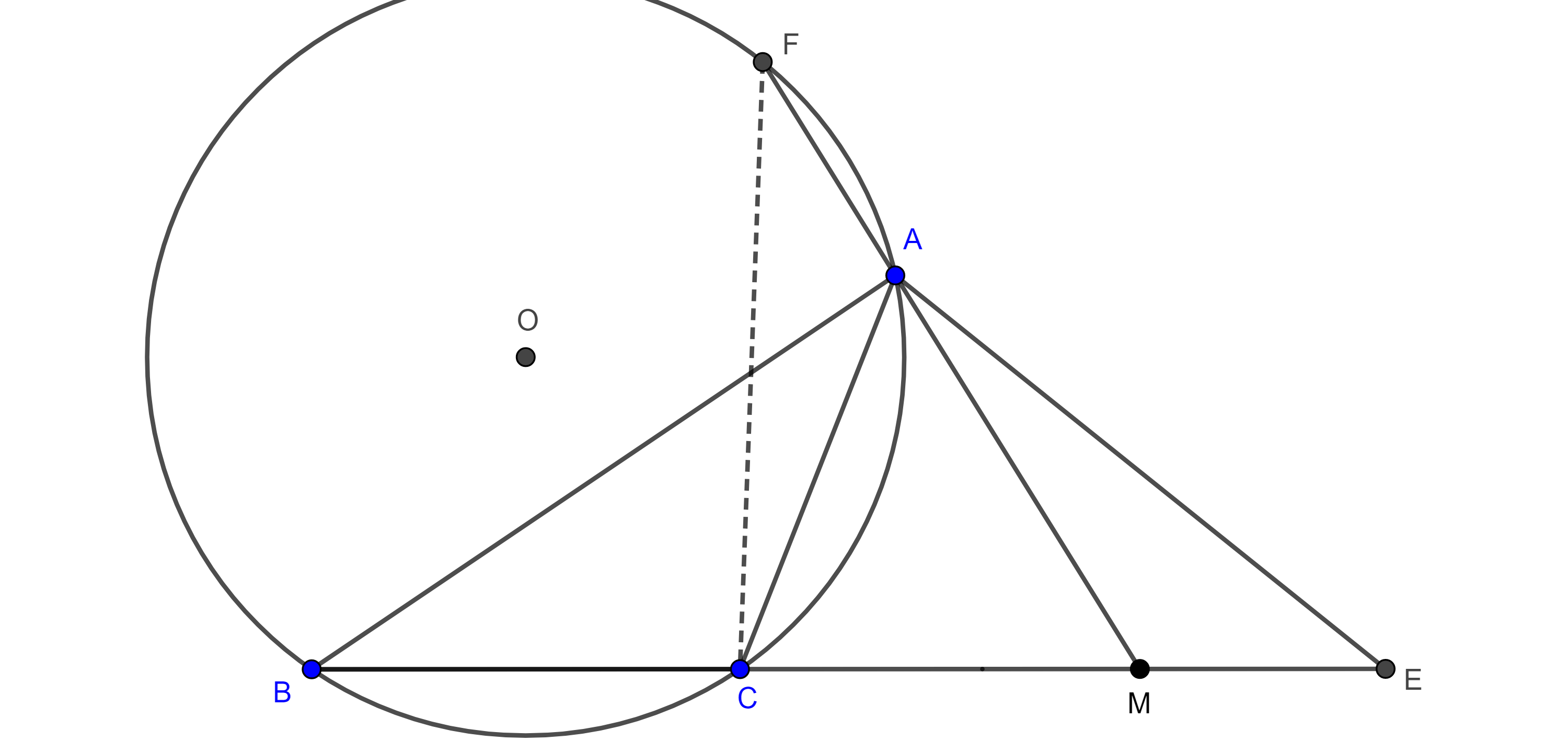
Construcción de un triangulo ($a$, $h_a$, $\dfrac{c}{b}$)
Problema. Construye un triángulo $\triangle ABC$ dados la base, la altura trazada por el vértice opuesto y la razón entre los lados restantes ($BC = a$, $AD = h_a$, $\dfrac{AB}{AC} = \dfrac{c}{b}$).
Solución. Construimos un segmento $BC$ de longitud $a$ y trazamos la circunferencia de Apolonio $\Gamma$ de los puntos $P$ tales que la razón de las distancias a $B$ y a $C$ es la razón dada, $\dfrac{PB}{PC} = \dfrac{c}{b}$.
Luego trazamos una recta $l$ paralela a $BC$ y a una distancia $h_a$. Una de las intersecciones de $l$ con $\Gamma$ es el tercer vértice del triángulo $\triangle ABC$.
Sea $D$ el pie de la perpendicular a $BC$ trazado desde $A$, entonces por construcción $BC = a$, $AD = h_a$ y $\dfrac{AB}{AC} =\dfrac{c}{b}$.
$\blacksquare$
Círculos de Apolonio de un triángulo
Definición 1. Consideremos un triángulo $\triangle ABC$, el lugar geométrico de los puntos $P$ tales que $\dfrac{PB}{PC} = \dfrac{AB}{AC}$, es la $A$-circunferencia de Apolonio de $\triangle ABC$. De esta manera todo triangulo tiene tres circunferencias de Apolonio asociadas a él, una que pasa por cada vértice.
Definición 2. Decimos que dos circunferencias son ortogonales si se intersecan y los radios trazados desde el punto de intersección son perpendiculares.
Proposición. Cada circunferencia de Apolonio asociada a un triángulo es ortogonal con el circuncírculo del triángulo.
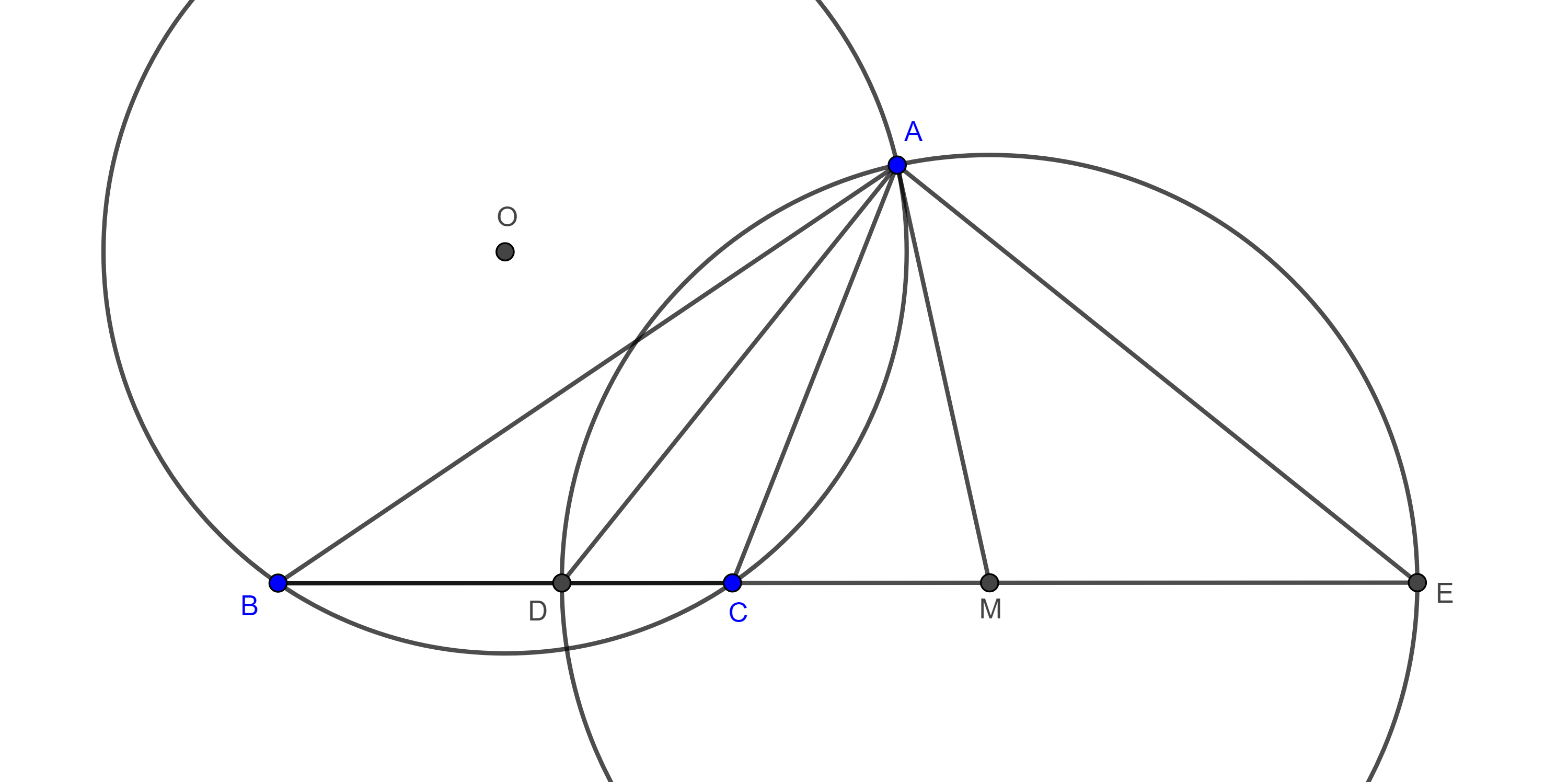
Demostración. Sean $\triangle ABC$, $D$ y $E$ los pies de la bisectriz interior y exterior respectivamente de $\angle A$, consideremos $M$ el punto medio de $DE$.
La circunferencia con centro $M$ y radio $AM$, $(M, AM)$ es la $A$-circunferencia de Apolonio de $\triangle ABC$.
Tenemos lo siguiente
$\dfrac{\pi}{2} = \angle DAE = \angle DAC + \angle CAM + \angle MAE = \dfrac{\angle BAC}{2} + \angle CAM + \dfrac{\angle AMB}{2}$.
$\Rightarrow \pi = \angle BAC + 2\angle CAM + \angle AMB = \angle BAM + \angle AMB + \angle CAM$
$\Rightarrow \angle CBA = \pi – (\angle BAM + \angle AMB)$
$\begin{equation} = \angle CAM. \end{equation}$
Ahora consideremos el circuncírculo $(O, AO)$ de $\triangle ABC$, y supongamos que $AM$ es secante a $(O, AO)$ en $A$ y $F$, tenemos dos casos:
- $F$ esta entre $A$ y $M$,
$\Rightarrow \angle CBA = \dfrac{\angle COA}{2} > \dfrac{\angle COF}{2} = \angle CAF = \angle CAM$.
- $A$ esta entre $F$ y $M$,
$\Rightarrow \angle CAM > \angle CFA = \angle CBA$.
Ninguno de los dos casos anteriores es posible, puesto que por la ecuación $(3)$, $\angle CBA = \angle CAM$, por lo tanto, $A$ es tangente a $(O, AO)$ y así $(O, AO)$ y $(M, AM)$ son ortogonales.
La prueba para las otras dos circunferencias de Apolonio de $\triangle ABC$ es análoga.
$\blacksquare$
Más adelante…
En la siguiente entrada estudiaremos un par de métodos generales que nos pueden ayudar a resolver problemas de construcciones geométricas.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Dada una circunferencia, muestra que el lugar geométrico de los puntos medios de las cuerdas que pasan por un punto dado es una circunferencia, si el punto esta dentro o en la circunferencia. Analiza el caso cuando el punto se encuentra fuera de la circunferencia.
- Dados dos segmentos consecutivos $AB$ y $BC$ sobre una misma recta encuentra el lugar geométrico de los puntos $P$ tales que $\angle APB = \angle BPC$.
- Dados tres puntos $A$, $B$, $C$ y un ángulo $\alpha$, construye una circunferencia que pase por $A$ y $B$ y tal que el ángulo entre las tangentes trazadas desde $C$ a la circunferencia sea igual a $\alpha$.
- Construye un triangulo, dados:
$i)$ la base, la mediana trazada desde el vértice opuesto y la razón entre los lados restantes,
$ii)$ la base, la bisectriz del ángulo opuesto y la razón entre los lados restantes. - Muestra que las tres circunferencias de Apolonio de un triangulo concurren en dos puntos.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Ángulos en la circunferencia.
- Siguiente entrada del curso: Construcciones geométricas.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 11-16.
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 275-276.
- Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 135-137.
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 38-39.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»