Introducción

En esta ocasión estudiaremos algunas propiedades de las circunferencias tritangentes de un triángulo, esto nos permitirá entre otras cosas, derivar formulas para el área del triángulo.

Definición 1. El incírculo $(I,r)$ y los tres excírculos $(I_a,r_a)$, $(I_b,r_b)$ y $(I_c,r_c)$ de un triángulo a veces son referidos como las circunferencias tritangentes del triángulo, sus centros como centros tritangentes y sus radios, radios tritangentes.

Centros tritangentes

Teorema 1. El segmento que une dos centros tritangentes de un triángulo es el diámetro de una circunferencia que contiene dos de los vértices del triángulo, los cuales no son colineales con los centros tritangentes considerados.

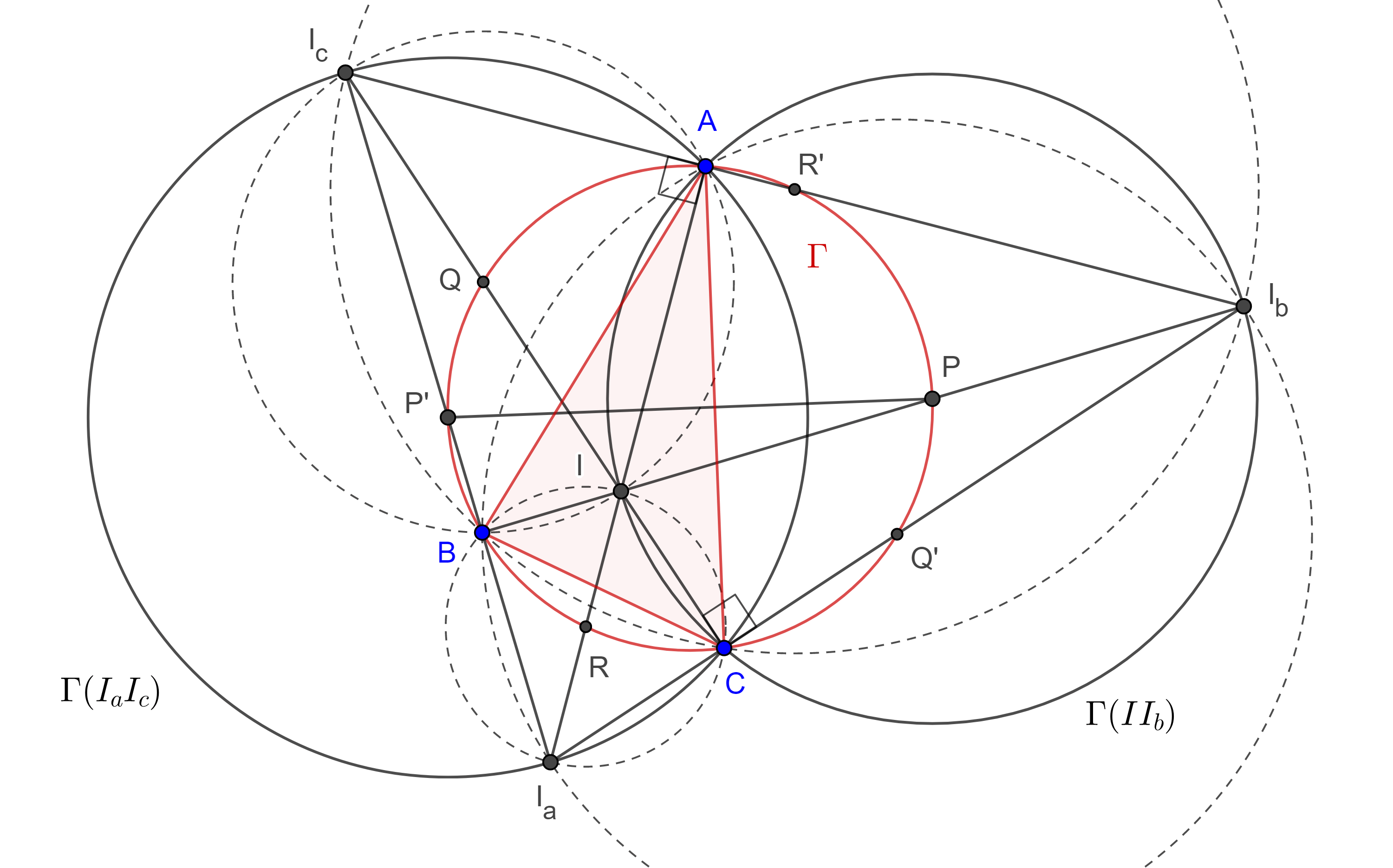
Demostración. Sean $\mathrm{△}ABC$, $\mathrm{\Gamma }$ su circuncírculo, $I$, $I_a$, $I_b$ y $I_c$ sus centros tritangentes.

Consideremos la circunferencia $\mathrm{\Gamma }(I{I}_b)$ cuyo diámetro es $I{I}_b$, como las bisectrices internas y externas de $\mathrm{\angle }A$, $AI$ y $A{I}_b$ son perpendiculares entonces $A\in \mathrm{\Gamma }(I{I}_b)$, de manera análoga vemos que $C\in \mathrm{\Gamma }(I{I}_b)$.

Como $AC$ es cuerda de $\mathrm{\Gamma }(I{I}_b)$, entonces su mediatriz interseca a $I{I}_b$ en el centro $P$ de $\mathrm{\Gamma }(I{I}_b)$. Ya que $AC$ es cuerda de $\mathrm{\Gamma }$, entonces su mediatriz interseca al circuncírculo de $\mathrm{△}ABC$ en el punto medio del arco $\stackrel{⌢}{CA}$ que no contiene a $B$.

Como $I{I}_b$ es bisectriz de $\mathrm{\angle }B$ entonces $I{I}_b$ interseca al circuncírculo de $\mathrm{△}ABC$ en el punto medio del arco $\stackrel{⌢}{CA}$ que no contiene a $B$.

Por lo tanto, el centro $P$ de $\mathrm{\Gamma }(I{I}_b)$ pertenece al circuncírculo de $\mathrm{△}ABC$.

Ahora consideremos la circunferencia $\mathrm{\Gamma }(I_a{I}_c)$, cuyo diámetro es $I_a{I}_c$, como las bisectrices interna y externa de $\mathrm{\angle }A$, son perpendiculares entonces $A\in \mathrm{\Gamma }(I_a{I}_c)$, con un razonamiento análogo vemos que $C\in \mathrm{\Gamma }(I_a{I}_c)$.

Considera el punto diametralmente opuesto a $P$, $P^{\prime }$ en el circuncírculo de $\mathrm{△}ABC$ entonces $\mathrm{\angle }PB{P}^{\prime }$ es ángulo recto y como $BP$ es la bisectriz interna de $\mathrm{\angle }B$ entonces $B{P}^{\prime }$ es la bisectriz externa de $\mathrm{\angle }B$.

Como $AC$ es cuerda de $\mathrm{\Gamma }(I_a{I}_c)$ entonces su mediatriz $P{P}^{\prime }$ interseca a $I_a{I}_c$ en su punto medio.

Por lo tanto, el punto medio, $P^{\prime }$, del arco $\stackrel{⌢}{AC}$, es el punto medio del diámetro, $I_a{I}_c$, de $\mathrm{\Gamma }(I_a{I}_c)$.

Del mismo modo podemos ver que $\mathrm{\Gamma }(I{I}_c)$, $\mathrm{\Gamma }(I_b{I}_a)$ pasan por los vértices $A$, $B$ y que $\mathrm{\Gamma }(I{I}_a)$, $\mathrm{\Gamma }(I_b{I}_c)$ pasan por los vertices $C$, $B$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Puntos de contacto

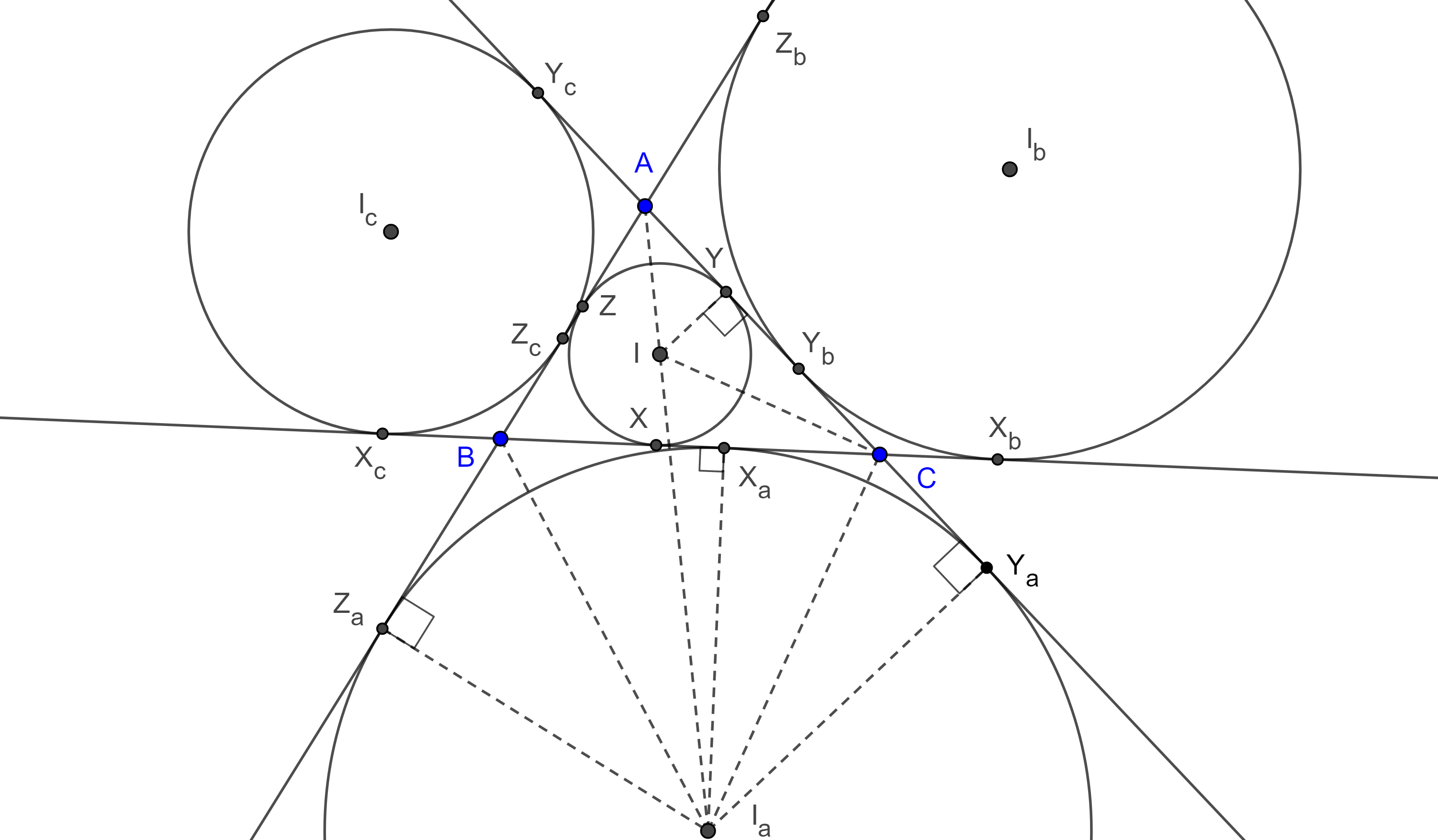
Notación. Nos referiremos a los puntos de tangencia de los círculos tritangentes $(I,r)$, $(I_a,r_a)$, $(I_b,r_b)$ y $(I_c,r_c)$ con el lado $BC$ de un triángulo $\mathrm{△}ABC$ como $X$, $X_a$, $X_b$ y $X_c$ respectivamente. Usaremos las letras $Y$ y $Z$ para los lados $AC$ y $AB$ respectivamente.

Emplearemos la letra $s$ para referirnos al semiperímetro ${\displaystyle \frac{a+b+c}{2}}$ de un triángulo $\mathrm{△}ABC$ donde $BC=a$, $AC=b$  y $AB=c$.

Proposición 1. La distancia desde el vértice de un triángulo al punto de tangencia de su circuncírculo en uno de sus lados adyacentes es igual al semiperímetro menos la longitud del lado opuesto.

Demostración. Sea $\mathrm{△}ABC$ y $(I,r)$ su circuncírculo. Como las tangentes desde un punto exterior a una circunferencia son iguales entonces $AZ=AY$, $BZ=BX$ y $CX=CY$.

Por otra parte, $AZ+BZ+BX+CX+CY+AY=c+a+b=2s$.

Por lo tanto, $AZ+BX+CX=s$.

Y así, $AY=AZ=s–a$.

Similarmente, $BZ=BX=s–b$ y $CX=CY=s–c$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 2. La distancia desde el vértice de un triángulo al punto de tangencia del excírculo opuesto, a uno de los lados adyacentes al vértice considerado es igual al semiperímetro del triángulo.

Demostración. Sea $\mathrm{△}ABC$ y $(I_a,r_a)$, $(I_b,r_b)$ y $(I_c,r_c)$ sus excentros (figura 2). Como las tangentes desde un punto exterior a una circunferencia son iguales entonces
$A{Z}_a=A{Y}_a$, $B{X}_b=B{Z}_b$ y $C{X}_c=C{Y}_c$.

Por otro lado,
$A{Z}_a+A{Y}_a=AB+B{Z}_a+AC+C{Y}_a$
$=AB+AC+B{X}_a+C{X}_a=AB+AC+BC=2s$.

Por lo tanto, $A{Z}_a=A{Y}_a=s$.

Igualmente, $B{X}_b=B{Y}_b=C{X}_c=C{Y}_c=s$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Corolario 1. $A{Z}_c=A{Y}_c=s–b$, y $A{Y}_b=A{Z}_b=s–c$.

Demostración. En la figura 2 tenemos lo siguiente:
$A{Y}_c=C{Y}_c–AC=s–AC$,
$A{Z}_b=B{Z}_b–AB=s–AB$.

Similarmente,
$B{Z}_c=B{X}_c=s–a$, $B{X}_a=B{Z}_a=s–c$,
$C{X}_a=C{Y}_a=s–b$, $C{Y}_b=C{X}_b=s–a$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Puntos isotómicos

Definición 2. Si dos puntos en uno de los lados de un triángulo equidistan al punto medio del lado considerado decimos que son puntos isotómicos.

Proposición 3. El punto de tangencia del incírculo con uno de los lados de un triángulo y el punto de tangencia del excírculo relativo al lado considerado, son puntos isotómicos.

Demostración. Por la proposición 1 y el corolario 1, tenemos que $BX=s–b=C{X}_a$ (figura 2).

Esto implica que el punto medio de $X{X}_a$ es el punto medio de $BC$, por lo tanto, $X$ y $X_a$ son puntos isotómicos.

Análogamente vemos que $Z$, $Z_c$ e $Y$, $Y_b$ son pares de puntos isotómicos.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 4. Los dos puntos de contacto de un lado de un triángulo con los dos excírculos opuestos a los vértices que pasan por ese lado son isotómicos, además la distancia entre estos dos puntos es igual a la suma de los otros dos lados.

Demostración. En la figura 2, tenemos lo siguiente:
$B{X}_c=C{X}_c–BC=s–a$, $C{X}_b=B{X}_b–BC=s–a$.

Por lo tanto, el punto medio de $X_c{X}_b$ coincide con el punto medio de $BC$.

Por otro lado, $X_c{X}_b=B{X}_c+a+C{X}_b=a+2(s–a)=2s–a=c+b$.

Igualmente, $Y_a{Y}_c=a+c$, $Z_a{Z}_b=a+b$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Radios tritangentes y área del triangulo

Proposición 5. El área de un triángulo es igual al producto del semiperímetro por el inradio.

Demostración. De la figura 2,
$(\mathrm{△}ABC)=(\mathrm{△}AIB)+(\mathrm{△}BIC)+(\mathrm{△}AIC)={\displaystyle \frac{cr}{2}}+{\displaystyle \frac{ar}{2}}+{\displaystyle \frac{br}{2}}=sr$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 6. El área de un triángulo es igual al producto de un exradio por la diferencia entre el semiperímetro y el lado relativo al excírculo considerado.

Demostración. En la figura 2,
$(\mathrm{△}ABC)=(\mathrm{△}A{I}_{a}B)+(\mathrm{△}A{I}_{a}C)–(\mathrm{△}B{I}_{a}C)$
$={\displaystyle \frac{c{r}_a}{2}}+{\displaystyle \frac{b{r}_a}{2}}–{\displaystyle \frac{a{r}_a}{2}}={\displaystyle \frac{r_a}{2}}(2s–2a)=r_a(s–a)$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Corolario 2. El reciproco del inradio es igual a la suma de los recíprocos de los exradios.

Demostración. De las proposiciones 5 y 6 se sigue que
${\displaystyle \frac{1}{r_a}}+{\displaystyle \frac{1}{r_b}}+{\displaystyle \frac{1}{r_c}}={\displaystyle \frac{(s–a)+(s–b)+(s–c)}{(\mathrm{△}ABC)}}={\displaystyle \frac{s}{(\mathrm{△}ABC)}}={\displaystyle \frac{1}{r}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 7. El área de un triángulo es igual al producto de sus lados sobre cuatro veces su circunradio.

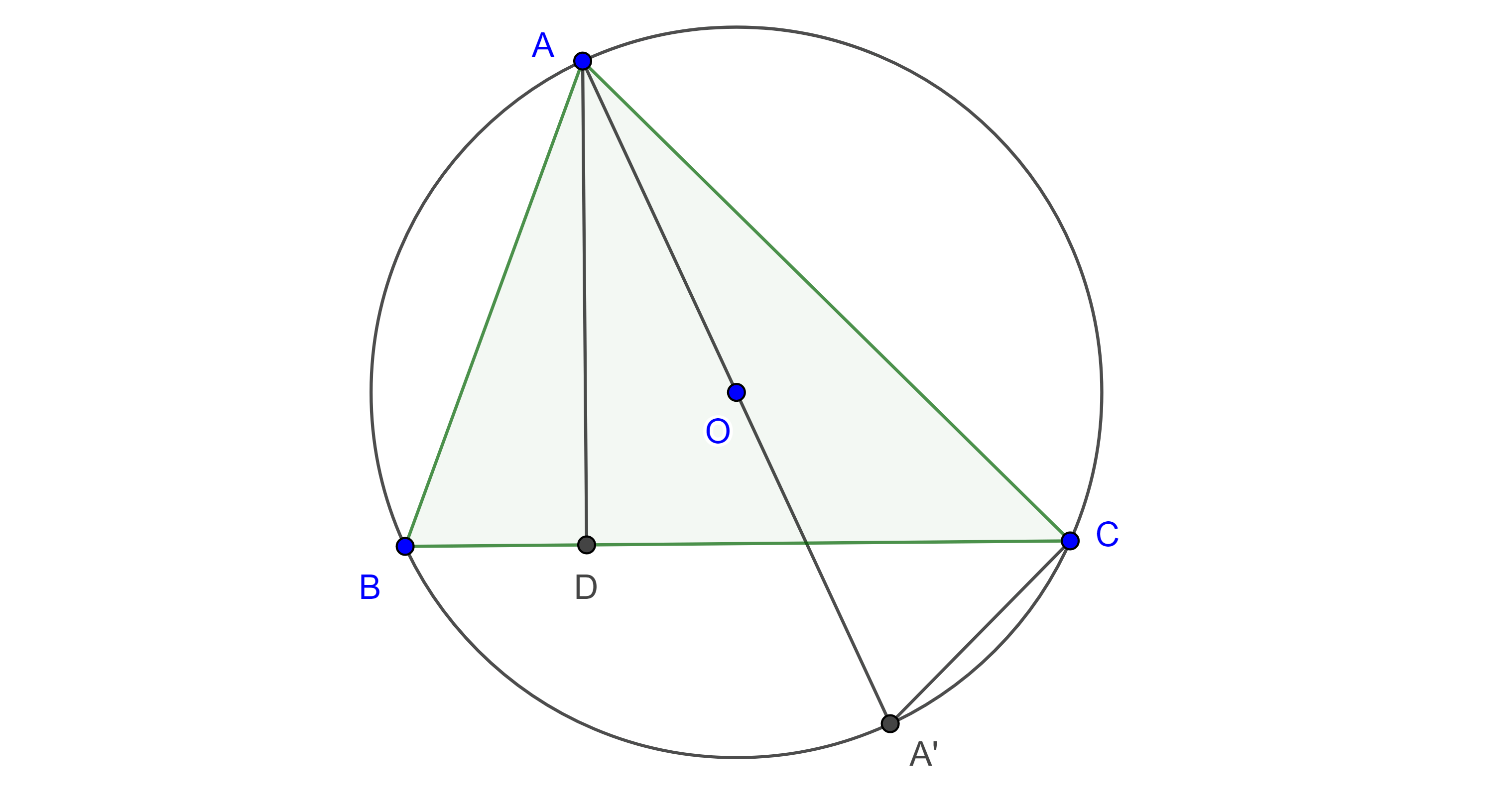
Demostración. Sean $\mathrm{△}ABC$, $(O,R)$ su circuncírculo, $D$ el pie de la altura por $A$, y $A^{\prime }$ el punto diametralmente opuesto a $A$.

$\mathrm{\angle }ABD=\mathrm{\angle }A{A}^{\prime }C$, pues abarcan el mismo arco y $\mathrm{\angle }AC{A}^{\prime }={\displaystyle \frac{\pi }{2}}$ es recto ya que $A{A}^{\prime }$ es diámetro, así que $\mathrm{△}ABD\sim \mathrm{△}A{A}^{\prime }C$, por criterio de semejanza AA.

Esto es, ${\displaystyle \frac{AB}{A{A}^{\prime }}}={\displaystyle \frac{AD}{AC}}$.

Se sigue que, $bc=2RAD$ y $abc=a2RAD=4R(\mathrm{△}ABC)$.

Por lo tanto, ${\displaystyle \frac{abc}{4R}}=(\mathrm{△}ABC)$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Formula de Herón y teorema de Carnot

Teorema 2, fórmula de Herón. Podemos calcular el área de un triángulo mediante la fórmula
$(\mathrm{△}ABC)=\sqrt{s(s–a)(s–b)(s–c)}$.

Demostración. Como $\mathrm{\angle }YCI$ y $\mathrm{\angle }{I}_{A}C{Y}_a$ son suplementarios, por criterio de semejanza AAA $\mathrm{△}YCI\sim \mathrm{△}{Y}_a{I}_{a}C$,
por lo tanto, ${\displaystyle \frac{Y_a{I}_a}{YC}}={\displaystyle \frac{Y_{a}C}{YI}}$,
es decir, ${\displaystyle \frac{r_a}{s–c}}={\displaystyle \frac{s–b}{r}}$.

También $\mathrm{△}AYI\sim \mathrm{△}A{Y}_a{I}_a$,
por lo tanto, ${\displaystyle \frac{Y_a{I}_a}{YI}}={\displaystyle \frac{A{Y}_a}{AY}}$,  
es decir, ${\displaystyle \frac{r_a}{r}}={\displaystyle \frac{s}{s–a}}$,
entonces ${\displaystyle \frac{rs}{s–a}}={\displaystyle \frac{(s–b)(s–c)}{r}}$. 

Por la proposición 5, $(\mathrm{△}ABC)=rs$,
por lo tanto, $(\mathrm{△}ABC)={\displaystyle \frac{(s–a)(s–b)(s–c)}{{\displaystyle \frac{(\mathrm{△}ABC)}{s}}}}$,
así que $(\mathrm{△}ABC{)}^2=s(s–a)(s–b)(s–c)$.

En conclusión, $(\mathrm{△}ABC)=\sqrt{s(s–a)(s–b)(s–c)}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Teorema 3, de Carnot. La suma de las distancias desde el circuncentro a los lados del triángulo es igual a la suma del circunradio y el inradio.

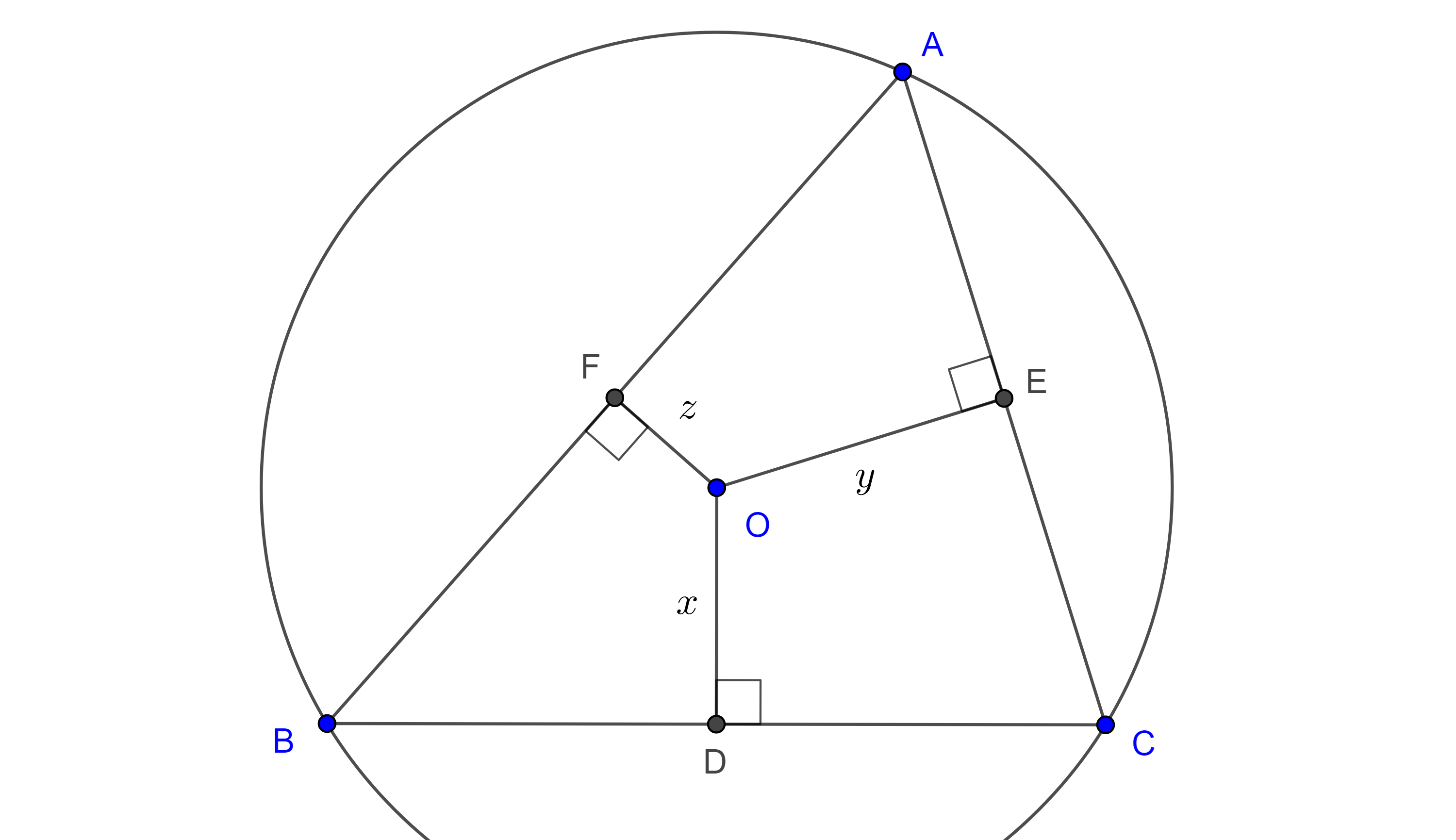
Demostración. Sea $\mathrm{△}ABC$ un triángulo acutángulo, $(O,R)$ su circuncírculo y $D$, $E$, $F$ las proyecciones de $O$ en $BC$, $AC$ y $AB$ respectivamente.

Aplicando el teorema de Ptolomeo a $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}AFOE$, $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}FBDO$ y $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ODCE$ tenemos:
$AF\times OE+AE\times OF=OA\times EF$,
$BF\times OD+BD\times OF=OB\times DF$,
$CE\times OD+CD\times OE=OC\times DE$.

Por otra parte, como $O$ está en la mediatriz de $BC$, $AC$ y $AB$ entonces $D$, $E$ y $F$ son los respectivos puntos medios y podemos aplicar el teorema del segmento medio. Si nombramos $OD=x$, $OE=y$, $OF=z$, entonces:

${\displaystyle \frac{cy}{2}}+{\displaystyle \frac{bz}{2}}={\displaystyle \frac{Ra}{2}}$,
${\displaystyle \frac{cx}{2}}+{\displaystyle \frac{az}{2}}={\displaystyle \frac{Rb}{2}}$,
${\displaystyle \frac{bx}{2}}+{\displaystyle \frac{ay}{2}}={\displaystyle \frac{Rc}{2}}$.

Sumamos las tres expresiones,

$x(c+b)+y(a+c)+z(a+b)=R(a+b+c)$
$\Rightarrow x(2s–a)+y(2s–b)+z(2s–c)=R2s$
$\Rightarrow 2s(x+y+z)–(ax+by+cz)=R2s$
$\Rightarrow 2s(x+y+z)–2(\mathrm{△}ABC)=R2s$.

De la proposición 5 tenemos $(\mathrm{△}ABC)=rs$,
por lo tanto, $2s(x+y+z)–2rs=R2s$.

Como resultado, $x+y+z=R+r$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Más adelante…

Con la ayuda de las formulas para el calculo del área de un triángulo vistas en esta entrada, en la próxima entrada mostraremos algunas desigualdades geométricas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Muestra que:
   $i)$ la bisectriz interna del ángulo de un triángulo es perpendicular al segmento que une los puntos donde las otras bisectrices internas intersecan al circuncírculo del triangulo,
   $ii)$ la bisectriz externa del ángulo de un triángulo es paralela al segmento que une los puntos donde las bisectrices externas (internas) de los otros dos ángulos intersecan al circuncírculo del triángulo.
2. Demuestra que: 
   $i)$ la suma de los catetos de un triángulo rectángulo menos la hipotenusa es igual al diámetro de su incírculo,
   $ii)$ el área de un triángulo rectángulo es igual al producto de los segmentos en los cuales la hipotenusa es dividida por el punto de tangencia de su incírculo.
3. Muestra que en la figura 2 se tienen las siguientes igualdades:
   $i)$ $X{X}_a=b–c$, $Y{Y}_b=a–c$, $Z{Z}_c=a–b$,
   $ii)$ $Z{Z}_a=Y{Y}_a=a$, $X{X}_b=Z{Z}_b=b$, $Y{Y}_c=X{X}_c=c$,
   $iii)$ $Y_b{Y}_c=Z_b{Z}_c=a$, $X_a{X}_c=Z_a{Z}_c=b$, $X_a{X}_b=Y_a{Y}_b=c$.
4. Prueba que:
   $i)$ el producto de los cuatro radios tritangentes de un triángulo es igual al cuadrado del área del triángulo $(\mathrm{△}ABC{)}^2=r{r}_a{r}_b{r}_c$
   $ii)$ el reciproco del inradio de un triángulo es igual a la suma de los recíprocos de las alturas del triangulo, ${\displaystyle \frac{1}{r}}={\displaystyle \frac{1}{h_a}}+{\displaystyle \frac{1}{h_b}}+{\displaystyle \frac{1}{h_c}}$,
   $iii)$ en la figura 2, ${\displaystyle \frac{AZ\times BX\times CY}{r}}=(\mathrm{△}ABC)$.
5. Demuestra que la razón entre el área de un triangulo y el area del triángulo formado por los puntos de contacto de su circuncírculo con sus lados es igual a la razón entre el inradio y el circundiámetro. En la figura 2, ${\displaystyle \frac{(\mathrm{△}XYZ)}{(\mathrm{△}ABC)}}={\displaystyle \frac{r}{2R}}$.
6. Muestra que en el teorema de Carnot, cuando $\mathrm{\angle }A$ es obtuso (figura 4), entonces $y+z–x=R+r$.
7. Sean $\mathrm{△}ABC$, $\alpha =\mathrm{\angle }BAC$, $\beta =\mathrm{\angle }CBA$, $\gamma =\mathrm{\angle }ACB$, $R$ el circunradio y $r$ el inradio, muestra que:
   $i)$ $\sin {\displaystyle \frac{\alpha }{2}}=\sqrt{{\displaystyle \frac{(s–b)(s–c)}{bc}}}$, $\sin {\displaystyle \frac{\beta }{2}}=\sqrt{{\displaystyle \frac{(s–a)(s–c)}{ac}}}$, $\sin {\displaystyle \frac{\gamma }{2}}=\sqrt{{\displaystyle \frac{(s–a)(s–b)}{ab}}}$
   $ii)$ $\cos \alpha +\cos \beta +\cos \gamma =1+{\displaystyle \frac{r}{R}}$.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Trigonometría.
• Siguiente entrada del curso: Desigualdades geométricas.
• Otros cursos.

Fuentes

• Altshiller, N., College Geometry. New York: Dover, 2007, pp 73-79, 87-91.
• Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 11-13.
• Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 86-89, 97-98.
• Quora
• Cut the Knot

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»