Archivo de la etiqueta: biyectiva

Teoría de los Conjuntos I: Funciones suprayectivas y biyectivas

Por Gabriela Hernández Aguilar

Deja un comentario

Introducción

Si tenemos dos conjuntos $X$ y $Y$ y se nos pide definir una función $f:X\to Y$ lo que debemos hacer es relacionar a cada uno de los elementos de $X$ con un único elemento de $Y$. Esta forma de proceder no garantiza que cualquier elemento de $Y$ se encuentra relacionado con algún elemento de $X$. Aquellas funciones que sí cumplan esto último les llamaremos funciones suprayectivas y será el tema que trataremos en esta entrada.

Función suprayectiva

Definición. Sea $f:X\to Y$ una función. Si $f[X]=Y$, entonces decimos que $f$ es suprayectiva.

$\square$

Teorema. Sea $f:X\to Y$ una función. Entonces los siguientes enunciados son equivalentes:

  1. $f$ es suprayectiva.
  2. Para cualquier $y\in Y$, existe $x\in X$ tal que $f(x)=y$.
  3. Para cualesquiera $h,k:Y\to Z$ tales que $h\circ f= k\circ f$, se tiene que $h=k$.

Demostración.

$1)\rightarrow 2)$

Supongamos que $f$ es suprayectiva, es decir que $f[X]=Y$. Sea $y\in Y$, entonces $y\in f[X]$ por lo que existe $x\in X$ tal que $f(x)=y$. Por lo tanto, para cualquier $y\in Y$ existe $x\in X$ tal que $f(x)=y$.

$2)\rightarrow 3)$

Sean $h,k:Y\to Z$ tales que $h\circ f=k\circ f$. Veamos que $h=k$. Sea $y\in Y$, veamos que $h(y)=k(y)$. Dado que $y\in Y$, por hipótesis tenemos que existe $x\in X$ tal que $f(x)=y$, por lo que $h(y)= h(f(x))$ y $k(y)= k(f(x))$. Luego, como $(h\circ f)(x)= h(f(x))= k(f(x))= (k\circ f)(x)$, tenemos que $h(y)= k(y)$.

$3)\rightarrow 1)$

Observemos que $f[X]\subseteq Y$, por lo que resta probar que $Y\subseteq f[X]$. Definamos $h: Y\to \set{0,1}$ y $k: Y\to \set{0,1}$ funciones dadas por $h(y)=0$ para todo $y\in Y$ y

\begin{align*}
k(y) = \left\{ \begin{array}{lcc}
0 &  \text{si} & y\in f[X]\\
1 &  \text{si}  & y \notin f[X] \\
\end{array}
\right.
\end{align*}

respectivamente.

Sea $x\in X$, entonces $f(x)\in Y$ y así, $(h\circ f)(x)= h(f(x))=0$ y $(k\circ f)(x)= k(f(x))=0$. Por lo tanto, $h\circ f=k\circ f$ y, por hipótesis $h=k$.

Si tomamos $y\in Y$, $h(y)=k(y)$. Esto significa que $k(y)=0$, por lo tanto, debe ocurrir que $y\in f[X]$.

Algunas funciones suprayectivas

Ejemplo.

La función identidad es suprayectiva. En efecto, sea $Id_X:X\to X$ la función identidad y sea $y\in X$, entonces $y\in X$ satisface $Id_X(y)= y$.

Por lo tanto, $Id_X$ es suprayectiva.

$\square$

Ejemplo.

Sea $X$ un conjunto no vacío y $f:X\to \set{c}$ una función dada por $f(x)=c$ para todo $x\in X$. Tenemos que $f$ es suprayectiva.

Dado que $c$ es el único elemento de $\set{c}$, debemos encontrar que existe $x\in X$ tal que $f(x)=c$. Como $X$ no es vacío, existe $x\in X$ y es tal que que $f(x)=c$.

$\square$

Ejemplo.

Sea $X$ un conjunto y $A\subseteq X$ un subconjunto propio de $X$ (distinto de $X$ y no vacío). La función característica de $A$ es una función suprayectiva.

Deseamos ver que para cualquier $y\in \set{0,1}$ existe $x\in X$ tal que $\chi_A(x)=y$.

Caso 1: Si $y=0$, entonces tomemos $x\in X\setminus A$ de modo que $\chi_A(x)=0$.

Caso 2: Si $y=1$, entonces tomemos $x\in A$, de modo que $\chi_A(x)=1$.

Por lo tanto, $\chi_A$ es suprayectiva.

$\square$

Composición de funciones y suprayectividad

Así como lo hicimos en la entrada anterior con respecto a la inyectividad, también podemos averiguar qué pasa con la composición de funciones con respecto a la suprayectividad. Tenemos el siguiente teorema.

Teorema. Sean $f:X\to Y$ y $g:Y\to Z$ funciones suprayectivas, $g\circ f$ es suprayectiva.

Demostración.

Sea $z\in Z$, y veamos que existe $x\in X$ tal que $(g\circ f)(x)=z$.
Dado que $g$ es suprayectiva y $z\in Z$, entonces existe $y\in Y$ tal que $g(y)=z$. Luego, como $f$ es suprayectiva y $y\in Y$, entonces existe $x\in X$ tal que $f(x)=y$, así $z=g(y)=g(f(x))$. Por lo tanto, $g\circ f$ es suprayectiva.

$\square$

Funciones biyectivas

Definición. Decimos que $f:X\to Y$ es una función biyectiva si y sólo si $f$ es inyectiva y suprayectiva.

Ejemplo.

La función identidad es biyectiva.

Verificamos en la entrada de funciones inyectivas que la función identidad es una función inyectiva, además de que en esta entrada verificamos que es suprayectiva.

$\square$

Ejemplo.

Sean $X=\set{1,2,3}$ y $Y=\set{2,4,6}$ y sea $f:X\to Y$ la función dada por $f(x)=2x$. Tenemos que $f$ es inyectiva pues es una función uno a uno, es decir, elementos distintos van a dar a elementos distintos. Más explícitamente $1$ va a dar a $2$, $2$ a $4$ y $3$ a $6$.

Además $f$ es suprayectiva, pues para cualquier $y\in Y$, existe $x\in X$ tal que $f(x)=y$. En efecto, esto sucede ya que para $2\in Y$ existe $1\in X$ tal que $f(1)=2$; para $4\in Y$ existe $2\in X$ tal que $f(2)=4$ y por último para $6\in Y$ existe $3\in X$ tal que $f(3)=6$.

$\square$

Tarea moral

Realiza la siguiente lista de ejercicios que te ayudará a fortalecer los conceptos de función inyectiva, suprayectiva y biyectiva.

  1. Sean $f:X\to Y$ y $g:Y\to Z$ funciones. Demuestra que si $g\circ f$ es suprayectiva, entonces $g$ es suprayectiva.
  2. Demuestra o da un contraejemplo del siguiente enunciado: Si $f:X\to Y$ y $g:Y\to Z$ son funciones tales que $g\circ f$ es suprayectiva, entonces $f$ es suprayectiva.
  3. Sean $X=\set{1,2,3, \cdots}$ y $Y=\set{3,4,5,\cdots}$ y sea $f:X\to Y$ dada por $f(x)=2x+3$. ¿$f$ es suprayectiva? Argumenta tu respuesta. Quizás a estas alturas tengas que ser un poco informal en términos de teoría de conjuntos, pero usa lo que conoces de las operaciones de números.

Más adelante…

Ahora que aprendimos el concepto de función inyectiva y suprayectiva tenemos las bases suficientes para hablar de funciones invertibles. Veremos funciones invertibles por la derecha e invertibles por la izquierda, cuyos conceptos resultarán equivalentes al de función suprayectiva y función inyectiva respectivamente.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Funciones inyectivas, suprayectivas y biyectivas

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

En la entrada anterior, hemos revisado la definición de las funciones matemáticas. Siguiendo con este tema, ahora vamos a estudiar tres tipos de funciones: las inyectivas, suprayectivas y finalmente las inyectivas. Hemos hablado anteriormente de las primeras dos, ahora estudiaremos algunas equivalencias de las definiciones vistas en un principio y algunos resultados interesantes.

Inyectividad entre funciones

Las definiciones que daremos al estar hablando de inyectividad y supreyactividad de funciones serán las mismas que dimos al hablar de los tipos de relaciones. Primero empezaremos hablando de la inyectividad.

Cuando estemos hablando de funciones, diremos que una función inyectiva es aquella que manda a elementos distintos en el dominio a elementos distintos en el contradominio.

Definición. Diremos que una función $f: X \rightarrow Y$ es inyectiva, si $f$ es una relación inyectiva. Es decir para cada elemento $y \in Im[f]$, existe un único $x$ tal que $(x,y) \in f$

Nota que esta es la definición de inyectividad que dimos anteriormente. El hecho de que $f$ sea una función, nos permitirá tener otra forma de ver la inyectividad, para darte cuenta de ello, observa la siguiente proposición:

Proposición. Sea $f: X \rightarrow Y$ una función. Entonces son equivalentes:

  1. $f$ es inyectiva.
  2. Para cualesquiera tres elementos $x,w \in X$ y $y \in Im[f]$ sucede que si $f(x) = y \land f(w) = y$ entonces $x=w$.

Demostración.

$1) \Rightarrow 2)$. Recordemos que una equivalencia de la inyectividad en relaciones es que si $(x,y) \in f$ y $(w,y) \in R$ entonces $x=w$. Usaremos esta equivalencia para nuestra demostración. Ahora nota que si $f(x)=y$ y $f(w)=y$ entonces $(x,f(x)) \in f$ y $(w,f(w)) \in f$. Como $f$ es inyectiva entonces $x=w$.

$2) \Rightarrow 1)$.Sean $(x,y) \in f$ y $(w,y) \in f$. Para demostrar el inciso, bastará demsotrar que $x=w$, para ello note que como $f$ es una función entonces $(x,y) = (x,f(x))$ y $(w,y) =(w,f(w))$. Ahora notemos que $f(x)=f(w)$, por hipótesis, esto significa que $x=w$.

$\square$

.

Esta última equivalencia deja más claro que una función inyectiva es aquella que envía a elementos distintos en el dominio a elementos distintos en el contradominio.

Ejemplos de funciones inyectivas son:

  • La función $f:\mathbb{Z} \rightarrow \mathbb{Z}$ donde $f(x)=x+1$, esto es debido a que si $f(x)=f(w)$ entonces $x+1=w+1$, lo que implicaría que $x=w$.
  • La función $f:\{1,2,3\} \rightarrow \{a,b,c,d,e\}$ dada por: $f=\{(1,e),(2,b),(3,c)\}$.
  • La función identidad entre cualquier conjunto $X$, dada por $f: X \Rightarrow X $ donde $f(x)=x$.

Suprayectividad entre funciones

Siguiendo con la lista de conceptos a revisar hoy, nos encontramos nuevamente con la suprayectividad, el concepto en donde todo el contradominio de la función coincide con su imagen:

Definición. diremos que una función $f:X \rightarrow Y$ es suprayectiva si $f$ es una relación suprayectiva. Es decir, si para cada $y \in Y$, existe un $x \in X$ tal que $f(x)=y$

Esta última definición es una derivación de una equivalencia que mostramos con anterioridad. Puesto que decir que para cada $y \in Y$, existe un $x \in X$ tal que $f(x)=y$, es equivalente a decir que para cada elemento $y \in Y$, existe un elemento $x \in X$ tal que $(x,y) \in f$, basta con notar que $f(x)=y$ produce la equivalencia deseada.

Algunos ejemplos de funciones suprayectivas son:

  • La función identidad $f: X \rightarrow X$. Para ello, nota que para cada $y \in X$, sucede que $(y,f(y)) \in f$, por lo que es suprayectiva, pues $f(y)=y$.
  • Sea $X =\{0\}$, entonces la función $f: \mathbb{Z} \rightarrow X$ dada por $f(n)=0$ es una función suprayectiva.
  • La función proyección $f: \mathbb{Z}^2 \rightarrow \mathbb{Z}$ dada por $f((x,y)) = x$ es suprayectiva.

Funciones biyectivas

El último concepto que revisaremos será el de funciones biyectivas. Estas funciones serán importantes porque en pocas palabras podrán «trasladar» un conjunto a otro. Definiremos a estas funciones como aquellas que son inyectivas y suprayectivas al mismo tiempo.

Definición. Sea $f: X \rightarrow Y$ una función. Diremos que $f$ es biyectiva si es inyectiva y suprayectiva.

Si una función es inyectiva, entonces manda distintos elementos del dominio a distintos elementos del contradominio. Mientras que si es suprayectiva, entonces todo el contradominio tiene su correspondencia. Así que si una función es biyectiva, entonces todo elemento del contradominio vendrá de uno y solamente un elemento del dominio. Esto significa que una función biyectiva «transforma» un conjunto en otro. A cada elemento del dominio lo vuelve uno del contradominio.

Por ejemplo, considera la función $f: X \rightarrow Y$ donde $X=\{1,2,3\}$ y $Y=\{a,b,c\}$ donde $f = \{(1,a),(2,b),(3,c)\}$. Nota que la función va de un conjunto $X$ y «traduce» cada uno de sus elementos a un elemento del conjunto $Y$. Esta es una forma en que las biyecciones nos dan información de cómo «traducir» un conjunto en otro.

Ahora considera la función $f: \mathbb{Z} \rightarrow \mathbb{Z}$ dada por $f(n)=n+1$. Esta es una función biyectiva. Y «traduce» cada número a su sucesor.

Otro ejemplo sería la función $f: \mathbb{R} \rightarrow \mathbb{R}$ dada por $f(x)=2x$. Nota que lo que hace esta función es «alejar» puntos del origen. Mientras que $f(0)=0$, a todos los números positivos los «aleja» más del origen del lado derecho, y a los número negativos los «aleja» del origen por la izquierda. Así que esta función biyectiva se podría pensar como una liga que pegamos a la mitad y jalamos por ambos lados hasta que cada lado mida el doble de lo que medía antes. Esta es una forma en que pasamos de una liga normal a una liga estirada, si cada punto de la recta real, fuera un pedazo de la liga, entonces «traducimos» ese punto estirando la liga.

Con estos ejemplos, vimos como una función biyectiva es una traductora de puntos, mandando cada punto del dominio a uno del contradominio, y cada punto del dominio tiene su propia traducción en el contradominio sin que otro punto del dominio comparta su traducción.

Así es como hemos revisado los tres tipos de funciones principales que usarás en muchas áreas de las matemáticas. La inyectividad nos dice que a cada elemento de la imagen de una función solo le corresponde una del dominio. La supreyactividad nos dice que la imagen de una función es igual al contradominio de la función. Mientras que la biyectividad nos habla de traducciones, o formas de ver un conjunto reflejado en otro conjunto.

Más adelante…

En la siguiente entrada daremos el paso de hablar de una función a más de una función, y esto lo haremos componiendo funciones. En un principio se pueden pensar las composiciones como mandar un elemento de un conjunto a otro conjunto mediante una función y después mandar este elemento a otro conjunto mediante otra función. Verás que será útil las composiciones cuando estemos hablando de distintas funciones entre conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Da un ejemplo de una función inyectiva pero no suprayectiva.
  2. Sea $X$ un conjunto y $Y$ un subconjunto de $X$. La función inclusión está dada por $f: Y \rightarrow X$ donde $f(y)=y$.
    1. Demuestra que la función inclusión es inyectiva.
    2. Da condiciones necesarias para que la función inclusión sea biyectiva.
  3. Considera la función $f: \mathbb{Z} \rightarrow \mathbb{Z}$ dada por $f(n) = an +b$. ¿Para qué valores $a,b$ la función es biyectiva?
  4. Demuestra que una función $f: X \rightarrow Y$ es biyectiva si y solo si para cualquier subconjunto $A \subset X$ sucede que $f[X \setminus A] = Y \setminus f[A] $.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Cálculo Diferencial e Integral I: Funciones inyectivas, sobreyectivas y biyectivas. Función inversa

Por Karen González Cárdenas

Deja un comentario

Introducción

Anteriormente, vimos las operaciones que podemos llevar a cabo entre las funciones. Ahora revisaremos las características que debe cumplir una función para poder determinar si es inyectiva, sobreyectiva o biyectiva. De igual manera, definiremos el concepto de función inversa.

Definición de función inyectiva

Definición (1): Sea $f: A \rightarrow B$ una función. Decimos que $f$ es inyectiva si para cualesquiera dos elementos distintos en $A$, la función le asocia elementos distintos en $B$, es decir,
$$x_{1} \neq x_{2} \Rightarrow f(x_{1}) \neq f(x_{2})$$
para cualesquiera $x_{1}, x_{2} \in A$.

Definición (2): Sea $f: A \rightarrow B$ una función. Decimos que $f$ es inyectiva si para cualesquiera dos elementos iguales en $B$, provienen de dos elementos iguales en $A$ bajo la función, es decir,
$$f(x_{1}) = f (x_{2}) \Rightarrow x_{1} = x_{2}$$
para cualesquiera $x_{1}, x_{2} \in A$.

Ejemplo

Sea $f: (-\infty,-1] \rightarrow \r$ definida como:
$$f(x)=11- \sqrt{x^{2}-4x-5}\quad\text{.}$$

Tomemos $x_{1}, x_{2} \in (-\infty,-1]$ tales que $f(x_{1}) = f(x_{2})$. Así queremos probar que $x_{1}=x_{2}$.
Como $f(x_{1}) = f(x_{2})$ tenemos que:
\begin{align*}
11- \sqrt{x_{1}^{2}-4x_{1}-5} &=11- \sqrt{x_{2}^{2}-4x_{2}-5}\\
– \sqrt{x_{1}^{2}-4x_{1}-5} &=- \sqrt{x_{2}^{2}-4x_{2}-5} \quad \text{sumando $11$}\\
\sqrt{x_{1}^{2}-4x_{1}-5} &=\sqrt{x_{2}^{2}-4x_{2}-5} \quad \text{multiplcando por $-1$}\\
\sqrt{(x_{1}-2)^{2}-9} &=\sqrt{(x_{2}-2)^{2}-9} \quad \text{factorizando}\\
\sqrt{(x_{1}-2)^{2}} &=\sqrt{(x_{2}-2)^{2}}\\
|x_{1}-2| &=|x_{2}-2|\quad \text{quitando la raíz cuadrada}\\
x_{1}-2 &= x_{2}-2\\
x_{1}&= x_{2}\quad \text{sumando 2}
\end{align*}

De lo anterior vemos que $f$ es inyectiva.

Definición de función sobreyectiva

Definición (1): Sea $f: A \rightarrow B$ una función. Decimos que $f$ es sobreyectiva si todo elemento en $B$ proviene de algún elemento en $A$ bajo la función, es decir, para todo $y \in B$ existe $x \in A$ tal que:
$$f(x)=y\quad\text{.}$$

Definición (2): Sea $f: A \rightarrow B$ una función. Decimos que $f$ es sobreyectiva si
$$Im_{f}=Codom_{f}\quad\text{.}$$

Ejemplo

Un ejemplo sería la función tangente, ya que su $Im_{f}= \mathbb{R} $ y su $Codom_{f}= \mathbb{R}$, más adelante veremos su definición con mayor detenimiento:
$$f(x)=tan(x)\quad\text{.}$$

Definición de función biyectiva

Definición: Sea $f: A \rightarrow B$ una función. Decimos que $f$ es biyectiva si cumple con ser inyectiva y sobreyectiva.

Ejemplo

Sea $f: \r \rightarrow \r$ definida como:
$$Id(x)=x\quad\text{.}$$

Veremos que esta función es inyectiva:
Tomemos $x_{1}, x_{2} \in \r$ distintos, queremos ver que $f(x_{1}) \neq f(x_{2})$. Como tenemos que:
$$f(x_{1})= x_{1},$$
$$f(x_{2})= x_{2}\quad\text{.}$$
Y como sabemos $x_{1} \neq x_{2}$ se sigue así:
$$f(x_{1})\neq f(x_{2})\quad\text{.}$$
Por lo que $Id(x)$ es inyectiva.

Ahora vemos que también cumple ser sobreyectiva:
Consideremos $y \in \r$. Por definición de la función identidad tenemos que:
$$y=Id(y)\quad\text{.}$$
Así vemos que cumple ser sobreyectiva.

De lo anterior podemos concluimos que $Id(x)$ es una función biyectiva.

Proposición

Proposición: Si tomamos las funciones $g: A \rightarrow B$ y $f: B \rightarrow C$ se cumple que:

  1. $f$ inyectiva y $g$ inyectiva $\quad \Rightarrow \quad f \circ g$ es inyectiva.
  2. $f$ sobreyectiva y $g$ sobreyectiva $\quad \Rightarrow \quad f \circ g$ es sobreyectiva.
  3. $f$ biyectiva y $g$ biyectiva $\quad \Rightarrow \quad f \circ g$ es biyectiva.

Demostración:

  1. Tomemos $x_{1}, x_{2} \in A$ tales que $f \circ g (x_{1})= f \circ g (x_{2})$. Queremos probar que:
    $x_{1}=x_{2}$.
    Observemos que por hipótesis tenemos que:
    $$f(g(x_{1}))= f(g(x_{2}))$$
    donde $g(x_{1}), g(x_{2}) \in B$.
    Como $f$ es una función inyectiva entonces se cumple:
    $$g(x_{1})=g(x_{2})\quad\text{.}$$
    Y al ser $g$ inyectiva obtenemos:
    $$x_{1}=x_{2}\quad\text{.}$$
  2. Como $f \circ g : A \rightarrow C$ por lo que tomemos $c \in C$. Queremos ver que existe $a \in A$ tal que $f(a)=c$.
    Ya sabemos que $f: B \rightarrow C$ es sobreyectiva entonces existe $b \in B$ tal que:
    $$f(b)=c\quad\text{.}$$
    Recordemos que $g: A \rightarrow B$ al ser sobreyectiva ocurre que existe $a \in A$ tal que:
    $$g(a)=b\quad\text{.}$$
    De lo anterior al sustituir en la composición de funciones se sigue:
    \begin{align*}
    f \circ g(a)&=f(g(a))\\
    &=f(b)\\
    &=c
    \end{align*}
  3. Se queda como ejercicio de tarea moral.

$\square$

Función inversa

Definición (función invertible): Sea $f: A \rightarrow B$ una función. Decimos que $f$ es invertible si y sólo si existe una función $g: B \rightarrow A$ tal que cumple las siguientes condiciones:

  • $g \circ f = Id_{A}$
  • $f \circ g = Id_{B}$

A continuación veremos una equivalencia que nos será de utilidad para poder decir si una función es invertible:

Teorema: Consideremos a $f: A \rightarrow B$ una función. Decimos que:
$f$ es Invertible $\Leftrightarrow f$ es biyectiva.
Demostración:
$\Rightarrow ):$ Tomemos $f$ invertible, así por definición existe una función $g: B \rightarrow A$ tal que cumple:

  • $g \circ f = Id_{A}$
  • $f \circ g = Id_{B}$

Debemos probar que $f$ es biyectiva, por lo que debemos verificar que sea inyectiva y sobreyectiva:

Inyectiva: Sean $x_{1} , x_{2} \in A$ tales que $f(x_{1})= f (x_{2})$ por lo que $g(f(x_{1}))=g( f (x_{2}))$ al ser $g$ función. Reescribiendo lo anterior tenemos lo siguiente:
\begin{align*}
g(f(x_{1}))=g( f (x_{2})) &\Rightarrow (g \circ f)(x_{1})=(g \circ f)(x_{2})\\
&\Rightarrow Id_{A}(x_{1})=Id_{A}(x_{2}) \tag{por definición de $g$}\\
&\Rightarrow x_{1}= x_{2}
\end{align*}

$\therefore f$ es inyectiva
Sobreyectiva: Sea $y \in B$. Debido a que $Id_{B}$ es sobreyectiva tenemos que $Id_{B}(y)=y$. De lo anterior tenemos:
\begin{align*}
Id_{B}(y)=y &\Rightarrow f \circ g (y)= y\\
&\Rightarrow f(g(y))=y\\
&\Rightarrow g(y) \in A
\end{align*}
$\therefore f$ es sobreyectiva
De todo lo anterior concluimos que $f$ es biyectiva.

$\Leftarrow ):$ Sea $f: A \rightarrow B$ una función biyectiva. De este modo para todo $y \in B$ existe $x \in A$ tal que:
$$f(x)=y$$
ya que $f$ es sobreyectiva. De igual manera cumple ser inyectiva por lo que esa $x$ es única.

Consideremos la función $g: B \rightarrow A$ tal que:
$$g(y)=x \Leftrightarrow f(x)=y\quad\text{.}$$
Por lo que al realizar la siguiente composición de funciones tenemos:
$$ (g \circ f)(x)=g(f(x)) =g(y)=x = Id_{A}(x),$$
$$(f \circ g)(y)= f(g(y))= f(x)=y = Id_{B}(y)$$\quad\text{.}
Vemos que esto cumple la definición de ser invertible.
$\therefore f$ es una función invertible.

$\square$

Definición: Sea $f: A \rightarrow B$ entonces:

  • $f$ tiene inversa izquierda si existe $g: B \rightarrow A$ tal que $g \circ f=Id_{A}$.
  • $f$ tiene inversa derecha si existe $h: B \rightarrow A$ tal que $f\circ h=Id_{B}$.

Definición (función inversa): Si $f: A \rightarrow B$ es invertible donde $g: B \rightarrow A$ que cumple lo anterior. Decimos que $f^{-1}=g$ es la inversa de $f$.

Corolario: Si $f: A \rightarrow B$ es una función invertible entonces $f^{-1}$ también es biyectiva.

Demostración:
Como $f$ es invertible por definición cumple:

  • $f^{-1} \circ f =Id_{A}$
  • $f \circ f^{-1}=Id_{B}$

Por lo que cumple ser inyectiva y sobreyectiva.

$\square$

Del resultado anterior observamos que $f^{-1}$ es función inversa al componer por la derecha y por la izquierda.

Teorema: Si $f: A \rightarrow B$ entonces es equivalente lo siguiente:

  • $f$ es una función inyectiva
  • $f$ tiene inversa izquierda

Teorema: Si $f: A \subseteq \r \rightarrow \r$ entonces es equivalente lo siguiente:

  • $f$ es una función suprayectiva
  • $f$ tiene inversa derecha

Más adelante

En la siguiente entrada veremos otras características que las funciones pueden cumplir para clasificarse como pares o impares. Veremos su definición formal, algunos ejemplos y resultados.

Tarea moral

  • Demuestra que $f: [0, \infty) \rightarrow [0, \infty)$ definida como:
    $$f(x)= x^{2}$$
    es inyectiva.
  • Argumenta porque la función $f: \r \rightarrow \r$ definida como:
    $$f(x)= x^{2}$$
    no es inyectiva.
  • Demuestra que $f: \r \rightarrow \r$ definida como:
    $$f(x)= -2x+1$$
    es inyectiva.
  • Prueba que si $f$ y $g$ son funciones biyectivas entonces $f \circ g$ es biyectiva.
  • Demuestra la siguiente igualdad:
    $$(f \circ g)^{-1}= f^{-1} \circ g^{-1}$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: El tamaño de los naturales y de cada natural

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En la entrada pasada, demostramos que todo número natural es el conjunto formado por los elementos $\{0,1,…,n-1\}$. Esto nos dice intuitivamente que cada número natural $n$, tiene exactamente $n$ elementos. Pero, de modo formal, ¿qué quiere decir que un conjunto tenga $n$ elementos? Esto lo precisaremos en esta entrada. Más aun, siguiendo esta idea, definiremos que quiere decir que un conjunto sea infinito. Después, veremos las propiedades que los conjuntos finitos e infinitos tienen.

El tamaño de los conjuntos

A la hora de pensar en determinar el tamaño de un conjunto, uno podría aventurarse y empezar a contar los elementos de este uno por uno. Esta forma de aproximar el problema no sólo parece muy laboriosa, sino que también presenta el problema de que no todos los conjuntos tienen la propiedad de que se pueda enlistar a sus elementos (aunque no lo definimos aún, seguramente has escuchado que el conjunto $\mathbb{R}$ de números reales no cumple esta propiedad).

De entrada, parecería que el problema de catalogar a los conjuntos por su tamaño es más complicado de lo que parece. Sin embargo, hay una idea famosa que viene a salvar la situación.

Imagina que eres el acomodador de una sala de cine con una cantidad desconocida de asientos (incluso posiblemente infinita) y que quieres sentar en ellos a un cierto conjunto de espectadores (cuya cantidad también se desconoce). Como dijimos anteriormente, la labor de contar todos los asientos de la sala podría ser demasiado complicada. ¿Cómo podríamos cerciorarnos de que cada espectador podrá tener un asiento?

La respuesta es inusualmente sencilla. La mejor forma de cerciorarse de que todos puedan sentarse, es pidiéndoles que se sienten. Si logran hacerlo de modo que a cada asistente le toque exactamente un asiento y no sobren asientos, podremos decir que hay el mismo número de personas que de lugares.

Notemos que de esta forma no necesitamos saber de forma explícita cuántas sillas hay, ni cuantas personas asistieron a la función, para saber que hay la misma cantidad de personas que de sillas. Formalmente hablando, hemos dado una relación entre el conjunto de personas y el de asientos.

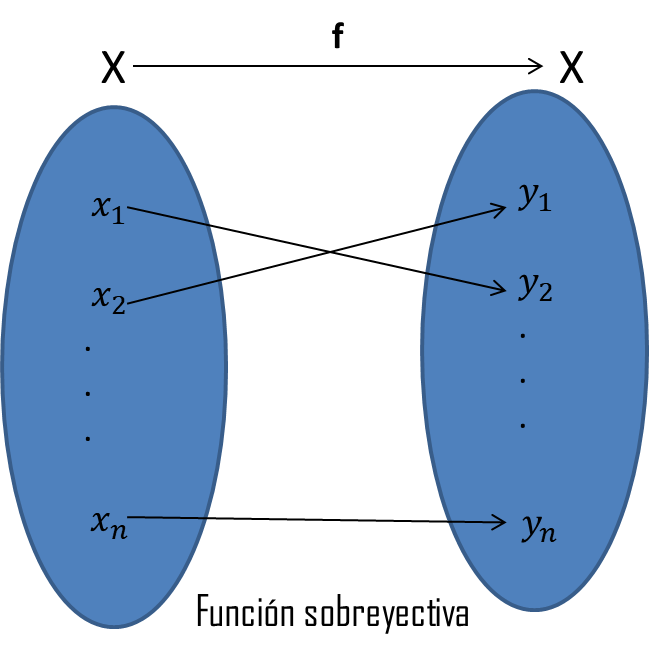
Recordemos que a una relación entre conjuntos se le llama función si a cada elemento de nuestro dominio le corresponde uno y solo un elemento del codominio. Más aún, si a todo elemento del codominio, está relacionado con uno del dominio, la función se llamará suprayectiva. Si una función satisface que los elementos del codominio se relacionan con a lo más un elemento del dominio, se le llama función inyectiva. Cuando ambas condiciones se satisfacen, diremos que la función es biyectiva.

Nota que en el ejemplo de la sala de cine, si logramos hacer que todos los asistentes se sienten sin que sobre alguna silla, entonces la función que damos es una función biyectiva. Con estas observaciones, introducimos la siguiente definición.

Definición. Diremos que dos conjuntos $A$ y $B$ tienen la misma cantidad de elementos, o la misma cardinalidad, si existe una función biyectiva entre ellos. En este caso escribimos $\vert A\vert=\vert B \vert$.

El tamaño del conjunto $\mathbb{N}$

Aunque los conjuntos finitos parecen ser más cercanos a nuestra realidad, será más interesante definir primero qué son los conjuntos infinitos. Para ello usaremos una de las propiedades «raras» que estos tienen.

Definición. Diremos que un conjunto $X$ es infinito si existe un subconjunto propio $Y$ de $X$ y una función $f:X\to Y$ biyectiva entre ambos conjuntos.

Recuerda que un subconjunto propio es cualquier subconjunto que no sea el conjunto original. En otras palabras, un conjunto es infinito si tiene el mismo tamaño que alguno de sus subconjuntos propios.

Definición. Diremos que un conjunto es finito si no es infinito.

La propiedad que usamos para caracterizar a los conjuntos infinitos fue muy novedosa cuando se enunció por primera vez. Incluso con los años fue el origen de aparentes paradojas al sentido común. Si el tema te parece interesante, puedes leer o ver algún vídeo sobre el famoso Hotel de Hilbert.

Con nuestra definición lista, empezaremos a catalogar los conjuntos que ya conocemos en finitos e infinitos.

Teorema. El conjunto $\mathbb{N}$ de números naturales es infinito.

Demostración. Para demostrar esto, consideraremos el conjunto $\mathbb{N}\setminus\{0\}$. Este es un subconjunto propio de $\mathbb{N}$. Tomemos la función $\sigma:\mathbb{N}\to \mathbb{N}\setminus\{0\}$. De acuerdo con la definición de conjunto infinito hay que demostrar que $\sigma$ es biyectiva, es decir, que es inyectiva y suprayectiva.

El hecho de que el codominio esté bien definido y que $\sigma$ sea inyectiva, fue demostrado en la entrada La construcción de los naturales, a la hora de probar los axiomas de Peano. La prueba de la suprayectividad se dejó como un ejercicio moral en la entrada de Principio de inducción y teoremas de recursión, ya que se usó para la prueba del teorema de Recursión débil. De cualquier forma, a continuación damos esa prueba.

Demostraremos que $\{0\}\cup \sigma(\mathbb{N})$ es inductivo. Evidentemente $0\in\mathbb{N}$ , y si $n\in \{0\}\cup\sigma(\mathbb{N})$, entonces es trivial que $\sigma(n)\in\sigma(\mathbb{N})$. Entonces $\{0\}\cup \sigma(\mathbb{N})=\mathbb{N}$, por lo que $\sigma(n)$ sí es suprayectiva y por lo tanto biyectiva. Con esto se concluye la prueba.

$\square$

La idea de determinar si dos conjuntos tienen la misma cantidad de elementos usando funciones se puede extender un poco más. La usaremos a continuación para definir cuándo un conjunto tiene al menos tantos elementos como otro.

Definición. Decimos que un conjunto $A$ tiene a lo más tantos elementos como un conjunto $B$ si existe una función inyectiva $f:A\to B$. En este caso, escribimos $\vert A\vert\leq \vert B \vert$.

Todo número natural es finito

Como hemos visto, los conjuntos infinitos se comportan de forma inesperada. Sin embargo los conjuntos finitos sí se comportarán de una forma más intuitiva. El teorema siguiente ejemplifica esto.

Teorema. Si $A$ es un conjunto finito, y $f:A\to A$, entonces son equivalentes las siguientes tres afirmaciones:

  1. $f$ es biyectiva
  2. $f$ es inyectiva
  3. $f$ es suprayectiva

Demostración. Evidentemente, $1)\Rightarrow 2)$ y $1)\Rightarrow 3)$. Si logramos demostrar la equivalencia entre $2)$ y $3)$ terminaremos, pues al tener uno, tendríamos el otro y por lo tanto tendríamos ambas partes de la definición de biyectividad.

$2)\Rightarrow 3)$ Supongamos que $f$ es inyectiva y supongamos que $f$ no es suprayectiva. Entonces $f:A\to f(A)$ es una biyección de $A$ con un subconjunto propio, lo cual diría que $A$ es infinito. Esto es una contradicción, así que $f$ debe ser suprayectiva.

$3)\Rightarrow 2)$ Si $f$ es suprayectiva, entonces tiene inversa derecha, es decir, existe $g:A\to A$ tal que $f\circ g=Id_A$. A partir de esta igualdad se puede probar que $g$ es inyectiva. En efecto, si $g(a)=g(b)$, entonces $f(g(a))=f(g(b))$, pero entonces $a=b$. Por la implicación del párrafo anterior, $g$, también es suprayectiva. Pero con esto se puede mostrar que $f$ es inyectiva. Si tenemos $a$ y $b$ tales que $f(a)=f(b)$, tomemos $c$ y $d$ tales que $g(c)=a$ y $g(d)=b$. De aquí, $c=f(g(c))=f(g(d))=d$ y por lo tanto $a=g(c)=g(d)=b$.

$\square$

Sigamos estudiando propiedades de los conjuntos infinitos. El siguiente resultado es bastante intuitivo: si le quitamos un elemento a un conjunto infinito, sigue siendo infinito. La demostración es algo elaborada pues debemos hacerla a partir de nuestras definiciones.

Lema 1. Si $X$ es un conjunto infinito y $x\in X$, entonces $X\setminus \{x\}$ también es un conjunto infinito.

Demostración. Sea $f:X\to A $ una biyección de $X$ a un subconjunto propio $A$. Tenemos que considerar dos casos: que $x\notin A$ o que $x\in A$. Comencemos con el caso $x\notin A$.

Para mostrar que $X\setminus \{x\}$ es infinito, utilizaremos como subconjunto a $A\setminus\{f(x)\}$ y como función a la restricción de $f$ a $X\setminus\{x\}$. Debemos demostrar que $A\setminus\{f(x)\}$ es un subconjunto propio de $X\setminus \{x\}$ y que dicha restricción es una biyección.

Lo primero sucede ya que $$A\setminus\{f(x)\}\subsetneq A\subseteq X\setminus \{x\}.$$ El hecho de que $f:X\setminus \{x\}\to A\setminus\{f(x)\}$ sea una biyección es consecuencia directa de que originalmente $f:X\to A $ era una biyección. Los detalles quedan como tarea moral.

Si por el contrario $x\in A$, como $A\subsetneq X$ debe existir $x’\in X\setminus A$. Consideremos la función

\begin{align*}
&g: & &X & &\longrightarrow & (A\cup \{x’&\})\setminus \{x\}& \\
& & &y & &\mapsto & f(&y) &\text{ si } y\neq f^{-1}(x) \\
& & f^{-1}&(x) & &\mapsto & &x’ &
\end{align*}

Veamos que $g$ es una biyección entre $X$ y $(A\cup \{x’\})\setminus \{x\}$. Lo primero que notamos es que el codominio está bien definido ya que para todo $y\in X$ se tiene que $g(y)\neq x$ (¿por qué?).

Además es inyectiva, ya que si $g(y)=g(z)$, con $y\neq f^{-1}(x)\neq z$, entonces se tiene que $f(y)=g(y)=g(z)=f(z)$, y por la inyectividad de $f$ se tiene que $y=z$. Mientras que si $y=f^{-1}(x)$, tenemos que $g(y)=x’=g(z)$ si $z\neq f^{-1}(x)$, tendríamos que $x’=f(z)$, por lo que $x’\in A$ lo cual es absurdo, entonces $z=f^{-1}(x)=y$, así $g$ es efectivamente inyectiva.

Para probar que es suprayectiva, consideremos $z\in(A\cup \{x’\})\setminus \{x\}$. Si $z=x’$, entonces $g(f^{-1}(x))=x’$, mientras que si $z\in A\setminus \{x\}$, por la suprayectvidad de $f$, debe de existir $y$ tal que $f(y)=z$. Además $y\neq f^{-1}(x)$ ya que si lo fuera $f(f^{-1}(x))=x=z$, lo cual sería absurdo. Se tiene entonces que $g(y)=f(y)=z$.

Con esto probamos que $g$ es una biyección de $X$ a un subconjunto propio al que no pertenece $x$. Para concluir, aplicamos el primer caso.

$\square$

Usando el lema anterior es fácil dar un corolario importante sobre conjuntos finitos, cuya prueba queda como un ejercicio.

Corolario. Si $X$ es un conjunto finito, y $x$ es un conjunto arbitrario, entonces $X\cup \{x\}$ es también un conjunto finito.

Armados con este corolario, podemos dar uno de los teoremas importantes de esta entrada.

Teorema. Si $n$ es un natural, entonces $n$ es un conjunto finito.

Demostración. Procedamos por inducción. Si $n=0$, entonces $n=\emptyset$, entonces $n$ no tiene subconjuntos propios con los que pueda biyectarse, ya que no tiene subconjuntos propios. Entonces por vacuidad el vacío es finito.

Supongamos que $n$ es un natural finito. Debemos demostrar que $\sigma(n) $ es también finito. Pero como $\sigma(n)=n\cup\{n\}$, el paso inductivo es consecuencia del corolario anterior. Con esto concluimos la inducción.

$\square$

Caracterizando los conjuntos finito e infinitos

Ya probamos que cada número natural es finito y que el conjunto de todos los naturales es infinito. Lo siguiente que haremos es ver que estos conjuntos nos sirven para catalogar a todos los demás conjuntos en finitos o infinitos. Comenzamos con un lema bastante intuitivo: si con conjunto tiene un subconjunto infinito, entonces es infinito.

Lema 2. Si $X$ es infinito y $X\subset Y$ entonces $Y$ también es infinito.

Demostración. Como $X$ es infinito, existe una biyección $f$ entre $X$ y uno de sus subconjuntos propios $A$. Consideremos entonces $(Y\setminus X)\cup A\subsetneq Y$, y demos una biyección entre $Y$ y este conjunto dada por

\begin{align*}
&g: & &Y & &\longrightarrow &(Y\setminus &X)\cup A & \\
& & &y & &\mapsto & &y &\text{ si } y\notin Y\setminus X\\
& & &x & &\mapsto & f(&x) &\text{ si } x\in X
\end{align*}

Probaremos que esta función es una biyección. Primero, veamos que es inyectiva. Esto se debe a que si $g(x)=g(y)$ y $x\in X$, entonces $g(y)=g(x)=f(x)\in A\subset X$, entonces $g(y)$ está en $X$, y como $Y\setminus X$ es enviado en si mismo, debe pasar que $y$ también está en $X$, por lo que $f(y)=g(y)=f(x)$ y por la inyectividad de $f$, tenemos que $y=x$. Por el contrario, si $x\notin X$, se tiene que $g(x)=x=g(y)$ entonces $g(y)\notin X$, por lo que $y$ tampoco puede estar en $X$, así, $g(y)=y=x$.

Veamos ahora que la función es suprayectiva. Si $z\in(Y\setminus X)\cup A$, consideremos dos casos: $z\in Y\setminus X$ en cuyo caso $g(z)=z$, o $z\in A$, por lo que por la suprayectividad de $f$, debemos tener que existe $x\in X$ tal que $z=f(x)=g(x)$. Así, $g$ es suprayectiva y por lo tanto es una biyección..

$\square$

Ahora sí, pasamos a demostrar los teoremas con los que concluiremos la entrada.

Teorema. El conjunto de números naturales es el conjunto infinito más pequeño, es decir, que si $X$ es un conjunto infinito, entonces $\vert\mathbb{N}\vert\leq\vert X\vert$.

Demostración. Como $X$ es infinito, debe ser distinto del vacío. Así, existe $x_0\in X$. Consideremos el conjunto $X\setminus \{x_0\}$, por el lema 1 que demostramos, este es de nuevo infinito. Una vez más, no es vacío, entonces existe $x_1\in X\setminus \{x_0\}$, y el conjunto $X\setminus\{x_0,x_1\}=(X\setminus \{x_0\})\setminus\{x_1\}$ será de nuevo infinito. Procediendo de manera recursiva, podemos dar una función

\begin{align*}
h: &\mathbb{N} \to X \\
& n \mapsto x_n
\end{align*}

tal que todos los $x_n$ son distintos entre sí (esto se puede demostrar inductivamente). Pero entonces $h$ es una función inyectiva de $\mathbb{N}$ al conjunto $X$, que es precisamente nuestra definición de que $\vert\mathbb{N}\vert\leq \vert X\vert $.

$\square$

El regreso del teorema anterior es evidentemente cierto, es decir que si un conjunto $X$ cumple que $\vert\mathbb{N}\vert\leq \vert X\vert $, entonces $X$ es infinito. Queda como ejercicio demostrarlo.

Para finalizar la entrada, damos un resultado análogo al anterior, para conjuntos finitos.

Teorema. Si $X$ es un conjunto finito, entonces existe $n\in\mathbb{N}$ tal que $\vert X\vert =\vert n\vert$.

Demostración. Si $X=\emptyset$, entonces $\vert\emptyset\vert= \vert X\vert $. Si $X$ no es vacío, entonces existe $x_0\in X$. Consideremos entonces $X\setminus \{x_0\}$. Si este conjunto es vacío, significa que $X=\{x_0\}$ y claramente podríamos biyectarlo con el conjunto $\sigma(0)=\{0\}$. Si por el contrario, $X\setminus \{x_0\}\neq \emptyset$, podemos elegir $x_1\in X\setminus \{x_0\}$ y verificar la misma condición.

Necesariamente debemos de terminar en algún momento pues, de otro modo, podremos usar el teorema de recursión para construir una función inyectiva de $\mathbb{N}$ a $X$. Esto diría que $X$ sería infinito, lo cual sería absurdo.

Entonces debe ocurrir que existe una $n$ tal que $X\setminus\{x_0,x_1,…,x_n\}$ es vacío, por lo que $X=\{x_0,x_1,…,x_n\}$, y por lo tanto podemos biyectarlo con $\sigma(n)$.

$\square$

Más adelante…

Así como los conjuntos transitivos, la teoría que se desarrolla al estudiar las cardinalidades de los conjuntos es un área de estudio importante en la teoría de conjuntos. Aunque no lo veremos a profundidad, la teoría que acabamos de desarrollar es suficiente para comparar la cardinalidad de la mayoría de los conjuntos que veamos con total precisión. Esto será cierto para, conjuntos como $\mathbb{Z}$ (el de los números enteros) o $\mathbb{Q}$ (el de los números racionales). No será sino hasta que definamos el conjunto de números reales que tendremos un conjunto con una cardinalidad estrictamente mayor que la de $\mathbb{N}$.

En la siguiente entrada definiremos el orden de los naturales, para lo cual de nuevo pensaremos a los números naturales como conjuntos. Más aún, las propiedades que estudiamos en la entrada pasada, serán de suma importancia a la hora de definir el buen orden de un conjunto. Esta es una propiedad que usamos anteriormente sin prueba, cuando demostramos el teorema de Recursión.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Supón que diriges un hotel con tantas habitaciones como números naturales. Supón que todas tus habitaciones se encuentran ocupadas, y de repente llega una persona solicitando un cuarto. ¿Cómo puedes hospedarlo sin desalojar a ningún cliente? Supón ahora que después llega un camión con tantas personas como números naturales, todas buscando un cuarto. ¿De qué forma puedes acomodarlos a ellos y a todos los clientes ya hospedados?
  2. Completa los detalles de la prueba del lema 1.
  3. Demuestra el corolario de la entrada: Si $X$ es un conjunto finito, y $x$ es un conjunto arbitrario, entonces $X\cup \{x\}$ es también un conjunto finito.
  4. Demuestra que si $X$ es tal que $\vert\mathbb{N}\vert\leq \vert X\vert $, entonces $X$ es infinito.
  5. Demuestra por inducción que si $X$ es infinito y $A$ es un subconjunto con $k$ elementos, entonces $X\setminus A$ es infinito. Si $A$ tiene tantos elementos como naturales, ¿el resultado sigue siendo cierto?

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Lineal I: Transformaciones lineales en bases, conjuntos independientes y generadores

Por Leonardo Ignacio Martínez Sandoval

11 respuestas

Introducción

El objetivo de esta entrada es entender qué efecto tienen las transformaciones lineales en bases, en conjuntos linealmente independientes y en conjuntos generadores. En la siguiente lista recordamos brevemente estas nociones:

  • Una transformación lineal $T:V\to W$ entre espacios vectoriales $V$ y $W$ es una función que «abre sumas» (es decir $T(x+y)=T(x)+T(y)$) y «saca escalares» (es decir $T(cx)=cT(x)$). Recuerda que es necesario que $V$ y $W$ estén sobre el mismo campo, cosa que asumiremos cuando hablemos de transformaciones lineales.
  • Un conjunto de vectores $\{v_1,\ldots, v_n\}$ en $V$ es linealmente independiente si la única combinación lineal de ellos que da $0$ es la trivial, osea en la que todos los coeficientes son $0$.
  • Si cualquier vector de un espacio vectorial $V$ puede escribirse como combinación lineal de un conjunto de vectores $S=\{v_1,\ldots,v_n\}$, entonces decimos que $S$ genera a $V$.
  • Un conjunto de vectores en $V$ es base si es linealmente independiente y genera a $V$.

La idea de esta entrada es entender lo siguiente:

  • ¿Cuándo las imágenes de linealmente independientes/generadores/bases son linealmente independientes/generadores/bases tras aplicar una transformación lineal?
  • ¿Cómo saber si una transformación lineal es inyectiva?
  • ¿Cómo el efecto de transformaciones lineales en bases nos permite determinar exactamente qué le hacen al resto de los vectores?

Exploración

Tomemos espacios vectoriales $V$, $W$ y una transformación lineal $T:V\to W$. Si comenzamos con un conjunto $S=\{v_1,\ldots,v_n\}$ de vectores en $V$ que es linealmente independiente (o generador, o base) en $V$, ¿cuándo sucede que $T(S)=\{T(v_1),\ldots,T(v_n)\}$ es linealmente independiente (o generador, o base, respectivamente) en $W$?

Esto definitivamente no sucede siempre. La tranformación $Z:\mathbb{R}^3\to \mathbb{R}[x]$ que manda a todo vector $(x,y,z)$ al polinomio $0$ es una transformación lineal. Sin embargo, a la base canónica $\{e_1,e_2,e_3\}$ la manda al conjunto $\{0,0,0\}=\{0\}$, que no es un conjunto ni linealmente independiente, ni generador de los polinomios con coeficientes reales.

De esta forma, tenemos que pedirle más a la transformación $T$ para que preserve las propiedades mencionadas.

Intuitivamente, si la imagen de $T$ no cubre a todo $W$, entonces los vectores de la forma $T(v)$ con $v$ en $V$ no deberían de poder generar a $W$. Así, para que $T$ mande generadores a generadores, tiene que pasar que «$T$ pase por todo $W$». Esta noción queda capturada formalmente al pedir que $T$ sea suprayectiva.

Del mismo modo, también intuitivamente si «$T$ manda elementos distintos al mismo elemento», entonces perderemos familias linealmente independientes al aplicarla. Así, para preservar conjuntos linealmente independientes, necesitamos que vectores distintos vayan a valores distintos. En términos formales, necesitamos que $T$ sea inyectiva.

Resultados principales de transformaciones lineales en bases, generadores y linealmente independientes

El primer resultado es que los requisitos que descubrimos intuitivamente en la sección pasada son suficientes.

Teorema. Sea $T:V\to W$ una transformación lineal y $S=\{v_1,\ldots,v_n\}$ un conjunto de vectores de $V$. Entonces:

  • Si $T$ es inyectiva y $S$ es linealmente independiente, entonces $T(S)$ es linealmente independiente.
  • Cuando $T$ es suprayectiva y $S$ es generador, entonces $T(S)$ es generador.
  • Si $T$ es biyectiva y $S$ es base, entonces $T(S)$ es base.

Demostración. Comencemos suponiendo que $T$ es inyectiva y $S$ es linealmente independiente. Entonces $T(v_1),\ldots,T(v_n)$ son todos distintos. Tomemos una combinación lineal de elementos de $T(S)$ igual a cero, es decir, $$a_1T(v_1)+a_2T(v_2)+\ldots+a_nT(v_n)=0.$$ Debemos mostrar que todos los coeficientes son iguales a cero. Como $T$ es transformación lineal, podemos juntar las sumas y productos escalares como sigue: $$T(a_1v_1+a_2v_2+\ldots+a_nv_n)=0=T(0).$$

Como $T$ es inyectiva, esto implica que $$a_1v_1+a_2v_2+\ldots+a_nv_n=0,$$ pero como $S$ es linealmente independiente, concluimos que $$a_1=\ldots=a_n=0.$$ Así, $T(S)$ es linealmente independiente.

Supongamos ahora que $T$ es suprayectiva y $S$ es generador. Tomemos un $w\in W$. Como $T$ es suprayectiva, existe $v\in V$ tal que $T(v)=w$ y como $S$ es generador, existen $a_1,\ldots,a_n$ tales que $$a_1v_1+\ldots+a_nv_n=v.$$ Aplicando $T$ en ambos lados, abriendo las sumas y sacando escalares obtenemos que $$a_1T(v_1)+\ldots+a_nT(v_n)=T(v)=w.$$ Así, todo elemento de $W$ se puede escribir como combinación lineal de elementos de $T(S)$, como queríamos.

Finalmente, supongamos que $T$ es biyectiva y $S$ es base. Como $T$ es inyectiva y $S$ linealmente independiente, entonces $T(S)$ es linealmente independiente. Como $T$ es suprayectiva y $S$ generador, entonces $T(S)$ es generador. Así, $T(S)$ es base.

$\square$

Una consecuencia fudamental del resultado anterior es que si $V$ y $W$ son espacios de dimensión finita y existe una transformación lineal inyectiva $T:V\to W$, entonces $\dim(V)\leq \dim(W)$. En efecto, si $B$ es base de $V$ y $T$ es inyectiva, entonces $T(B)$ es linealmente independiente en $W$ y sabemos que $W$ tiene a lo más $\dim(W)$ vectores linealmente independientes, así que $\dim(V)=|B|=|T(B)|\leq \dim(W)$. De manera similar, si existe una transformación lineal $T:V\to W$ suprayectiva, entonces $\dim(V)\geq \dim(W)$. Demuestra esto. ¿Qué pasa con las dimensiones si existe una transformación lineal biyectiva entre $V$ y $W$?

¿Cuándo una transformación lineal es inyectiva?

El teorema anterior también sugiere que es importante saber cuándo una transformación lineal es inyectiva, suprayectiva o ambas. Resulta que en el caso de la inyectividad hay un criterio que nos ayuda.

Proposición. Sean $V$ y $W$ espacios vectoriales. Una transformación lineal $T:V\to W$ es inyectiva y si sólo si el único vector $v$ de $V$ tal que $T(v)=0$ es el vector $v=0$. En otras palabras $T$ es inyectiva si y sólo si $\ker(T)=\{0\}$.

Demostración. Sean $V$ y $W$ espacios vectoriales y $T:V\to W$ una transformación lineal. Recordemos que sabemos que $T(0)=0$.

Si $T$ es inyectiva y $T(x)=0$, entonces $T(x)=T(0)$ y por inyectividad $x=0$, de modo que $x$ es el único vector que va a $0$ bajo $T$.

Si el único vector que bajo $T$ va a $0$ es el $0$ y tenemos que $T(x)=T(y)$, entonces usando que $T$ es lineal tenemos que $0=T(y)-T(x)=T(y-x)$. Así, por hipótesis $y-x=0$, es decir, $x=y$. Con esto queda mostrado que $T$ es inyectiva.

$\square$

Transformaciones lineales en bases dan toda la información

Conociendo los valores de una transformación lineal en algunos vectores, es posible determinar el valor de la transformación en otros vectores que son combinación lineal de los primeros. Considera el siguiente ejemplo.

Problema. La transformación lineal $T:M_2(\mathbb{R})\to\mathbb{R}^2$ cumple que $T\begin{pmatrix}
1 & 1\\
0 & 0
\end{pmatrix}=(1,0)$, $T\begin{pmatrix}
0 & 1 \\
0 & 1
\end{pmatrix}=(0,-1)$, $T\begin{pmatrix}
0 & 0\\
1 & 1
\end{pmatrix}=(-1,0)$ y $T\begin{pmatrix}
1 & 0\\
1 & 0
\end{pmatrix}=(0,1)$. Determina el valor de $T\begin{pmatrix} 3 & 3\\ 3 & 3\end{pmatrix}$.

Intenta resolver el problema por tu cuenta antes de ver la solución. Para ello, intenta poner a la matriz $\begin{pmatrix} 3 & 3\\ 3 & 3\end{pmatrix}$ como combinación lineal de las otras matrices y usar que $T$ es lineal.

Solución. Sean $A$, $B$, $C$ y $D$ las matrices de las cuales conocemos cuánto vale $T$ en ellas y $E$ la matriz con puros $3$’s. Queremos determinar el valor de $T(E)$. Notemos que $E=\frac{3}{2}(A+B+C+D)$. Como $T$ es transformación lineal, tenemos que

\begin{align*}
T(E)&=\frac{3}{2}(T(A)+T(B)+T(C)+T(D))\\
&=\frac{3}{2}((1,0)+(0,-1)+(-1,0)+(0,1))\\
&=(0,0).
\end{align*}

$\square$

En este problema lo que sirvió para encontrar el valor de $T(E)$ fue poner a la matriz $E$ como combinación lineal de las matrices $A,B,C,D$. De hecho, para cualquier matriz que sea combinación lineal de las matrices $A,B,C,D$, pudiéramos haber hecho lo mismo.

A partir de esta observación, podemos intuir que al conocer el efecto de transformaciones lineales en bases, podemos saber qué le hacen a cada elemento del espacio vectorial. El siguiente teorema enuncia esto de manera formal y dice un poco más.

Teorema. Sean $V$, $W$ espacios vectoriales, $B=\{v_1,v_2,\ldots,v_n\}$ una base de $V$ y $w_1,w_2,\ldots, w_n$ vectores cualesquiera de $W$. Entonces, existe una y sólo una transformación lineal $T:V\to W$ tal que $$T(v_1)=w_1,\quad T(v_2)=w_2, \quad \ldots, \quad T(v_n)=w_n.$$

Demostración. Probemos primero la parte de existencia. Como $B$ es base, cualquier vector $v$ de $V$ se puede escribir como $$a_1v_1+a_2v_2+\ldots+a_nv_n.$$ Construyamos la función $T:V\to W$ tal que $$T(v)=a_1w_1+a_2w_2+\ldots+a_nw_n.$$

Como para cada $i=1,\ldots,n$ tenemos que la combinación lineal de $v_i$ en términos de $B$ es $v_i=1\cdot v_i$, tenemos que $T(v_i)=1\cdot w_i=w_i$, que es una de las cosas que queremos. La otra que queremos es que $T$ sea lineal. Mostremos esto. Si $$v=a_1v_1+a_2v_2+\ldots+a_nv_n$$ y $$w=b_1v_1+b_2v_2+\ldots+b_nv_n,$$ entonces $$v+w=(a_1+b_1)v_1+
(a_2+b_2)v_2+\ldots+ (a_n+b_n)v_n,$$ y por definición $$T(v+w)=(a_1+b_1)w_1+ (a_2+b_2)w_2+\ldots+ (a_n+b_n)w_n.$$ Notemos que el lado derecho es igual a $T(v)+T(w)$, de modo que $T$ abre sumas. De manera similar se puede mostrar que $T$ saca escalares.

Esbocemos ahora la demostración de la unicidad. Supongamos que $T$ y $T’$ son transformaciones lineales de $V$ a $W$ tales que $T(v_i)=T'(v_i)=w_i$ para toda $i=1,\ldots,n$. Tenemos que mostrar que $T(v)=T'(v)$ para toda $v$. Para ello procedemos como en el problema antes de este teorema: escribimos a $v$ como combinación lineal de elementos de $B$. Esto se puede hacer de una única forma. El valor de $T(v)$ a su vez depende únicamente de $w_1,\ldots,w_n$ y de la los coeficientes en combinación lineal. El de $T'(v)$ también. Por lo tanto son iguales.

$\square$

Una consecuencia del teorema anterior, en la que no es necesario enunciar a las imágenes de la base, es la siguiente.

Corolario. Sean $V$ y $W$ espacios vectoriales, $B$ una base de $V$, y $T$ y $T’$ transformaciones lineales de $V$ a $W$. Si $T(v)=T'(v)$ para toda $v\in B$, entonces $T(v)=T'(v)$ para toda $v\in V$.

Más adelante…

Las propiedades que demostramos en esta entrada se usan con tanta frecuencia que muchas veces se aplican sin siquiera detenerse a argumentar por qué son válidas. Por esta razón, es importante que te familiarices con ellas. Otra ventaja de conocerlas a profundidad es que muchas veces ayudan a dar demostraciones sencillas o elegantes para algunos problemas. Finalmente, los hechos que aquí mostramos los usaremos prácticamente sin demostración en las siguientes entradas, en donde desarrollaremos la teoría de la forma matricial de transformaciones lineales.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • Encuentra qué le hace al vector $(7,3)$ una transformación lineal $T:\mathbb{R}^2\to \mathbb{R}$ tal que $T(2,1)=20$ y $T(7,2)=5$.
  • Determina si las matrices $A,B,C,D$ del problema de la entrada son una base para $M_2(\mathbb{R})$. Si no son una base, ¿cuál es la dimensión del subespacio que generan?
  • En el último teorema se afirma que la función que construimos saca escalares. Muestra esto.
  • De ese mismo teorema, escribe los detalles de que dicha función es única.
  • Demuestra el corolario enunciado en la entrada.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»