Archivo de la etiqueta: generador

Álgebra Lineal I: Bases y dimensión de espacios vectoriales

Por Ayax Calderón

10 respuestas

Introducción

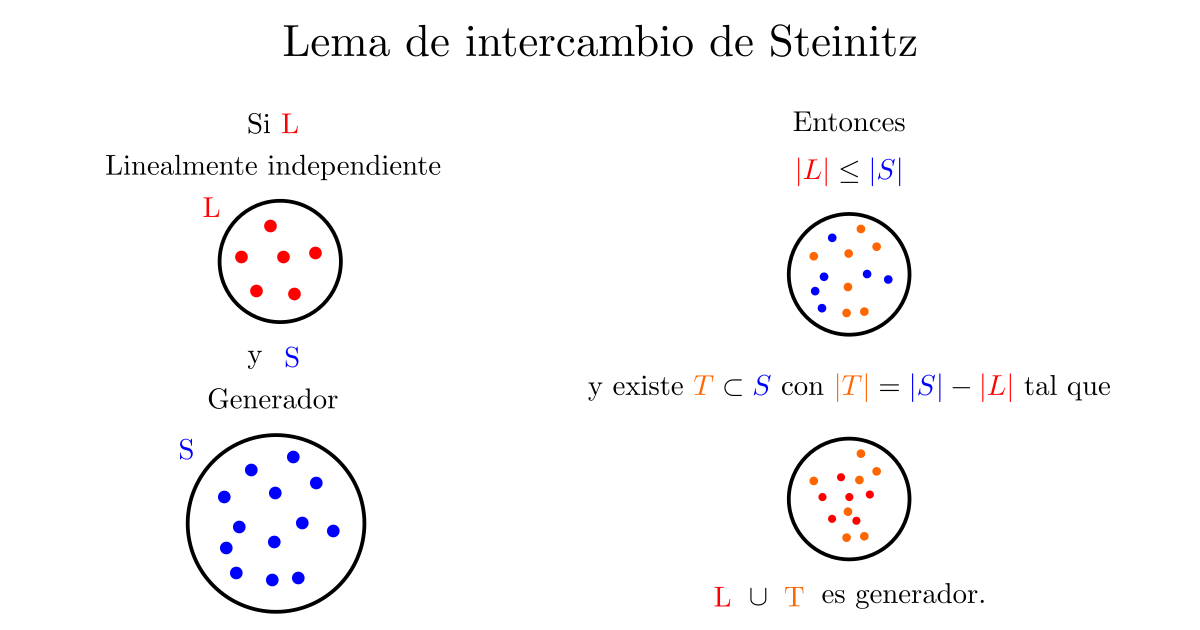
Ya hablamos de conjuntos generadores y de independencia lineal. Además, ya platicamos también del lema de intercambio de Steinitz. Con estas herramientas, tenemos todo a nuestra disposición para desarrollar la teoría de dimensión de espacios vectoriales.

Para espacios vectoriales en general, esto puede no resultar tan sencillo. Por esta razón, para este tema nos enfocaremos en el caso en el que la dimensión es finita. Sin embargo, también veremos ejemplos de espacios que no son así, y hablaremos un poco de cómo son.

Espacios de dimensión finita

Definición. Se dice que un espacio vectorial es de dimensión finita si tiene un conjunto generador con una cantidad finita de elementos.

Otra forma de interpretar la definición anterior es la siguiente:
$V$ es un espacio vectorial de dimensión finita si existe una familia finita de vectores $v_1, v_2, \dots , v_n \in V$ tal que todos los vectores en $V$ se pueden expresar como combinación lineal de dicha familia. Por ejemplo, los espacios $F^n, \hspace{2mm} M_{m,n}(F), \hspace{2mm}$ y $\hspace{2mm} \mathbb{R}_n[x]$ son de dimensión finita. Sin embargo, no todos los espacios vectoriales son de dimensión finita, de hecho la mayoría no lo son.

Problema. Demuestra que el espacio vectorial $V$ de todos los polinomios con coeficientes reales no es un espacio vectorial sobre $\mathbb{R}$ de dimensión finita.

Demostración. Supongamos que $V$ tiene un conjunto generador finito, entonces existen polinomios $p_1,p_2,\dots,p_n\in V$ tales que $V=\text{span}(p_1,p_2,\dots,p_n)$. Sea $d=\max\{deg(p_1), \dots, deg(p_n)\}$. Como todos los $p_i$ tienen grado a lo más $d$, entonces cualquier combinación lineal de $p_1,p_2,\dots,p_n$ también tiene grado a lo más $d$. Se sigue que todo vector en $V$ tiene grado a lo más $d$, pero eso es imposible, pues $deg(x^{d+1})=d+1>d$. Por lo tanto $V$ no es de dimensión finita.

$\square$

Nos gustaría definir la dimensión de un espacio vectorial. Para ilustrar esto es bueno pensar primero en $\mathbb{R}^n$ para distintos valores de $n$. Una linea (digamos $\mathbb{R}$) debería tener dimensión $1$, un plano (digamos $\mathbb{R}^2$) debería tener dimensión 2, y en general $\mathbb{R}^n$ debería tener dimensión $n$.

Antes de profundizar más en esto, es conveniente mencionar algunas definiciones y problemas prácticos para generar una mejor intuición sobre el rumbo que estamos a punto de tomar.

Definición. Una base de un espacio vectorial $V$ es un subconjunto $B$ de $V$ tal que $B$ es linealmente independiente y generador.

Ejemplos.

  • El conjunto $B=\{e_1,\ldots,e_n\}$ de vectores canónicos en $\mathbb{F}^n$ es una base. Esto se puede verificar con lo que hicimos al inicio del curso, cuando mostramos que cualquier vector $v$ en $\mathbb{F}^n$ se puede escribir de manera única como $v=x_1e_1+\ldots+x_ne_n$ con $x_1,\ldots,x_n$ escalares. Como existe al menos una forma, entonces $\text{span}(B)=F^n$. Como es única, en particular la única forma de escribir al vector $0$ es si $x_1=\ldots=x_n=0$. Esto muestra que $B$ es generador y linealmente independiente.
  • El conjunto $B=\{E_{ij}\}$ de matrices canónicas en $M_{m,n}(F)$ es una base.
  • El conjunto $1,x,\ldots,x^n$ es una base de $\mathbb{R}_n[x]$.

Encontrar bases de subespacios

Como los subespacios de espacios vectoriales también son espacios vectoriales, entonces también tiene sentido hablar de si un conjunto de vectores es base para un subespacio. Veamos ahora varios problemas para entender mejor esto.

Problema 1. Dada la matriz $A\in M_2(\mathbb{R})$
\begin{align*}
A=\begin{pmatrix}
2 & 0\\
0 & 3
\end{pmatrix}
\end{align*}
encuentra una base para el subespacio $U$ de $M_2(\mathbb{R})$ definido por
\begin{align*}
U=\{X\in M_2(\mathbb{R}): XA=AX\}.
\end{align*}

Solución. Considera la matriz $X=\begin{pmatrix}
a_1 & a_2\\
a_3 & a_4\end{pmatrix}$. Entonces $X\in U$ si y sólo si $XA=AX$, lo anterior lo escribimos como
\begin{align*}
\begin{pmatrix}
2a_1 & 3 a_2\\
2a_3 & 3a_4
\end{pmatrix} = \begin{pmatrix}
2a_1 & 2 a_2\\
3a_3 & 3a_4
\end{pmatrix}.
\end{align*}
De la igualdad anterior obtenemos que $a_2=a_3=0$. Por lo tanto
\begin{align*}
U=\left\{\begin{pmatrix}
a_1 & 0\\
0 & a_4\end{pmatrix}:a_1,a_4\in \mathbb{R}\right\}.
\end{align*}

Este es un primer paso, pues nos permite poner al subespacio $U$ en una forma en la que es más fácil de entender. Ahora es más fácil encontrar una base para $U$. Proponemos al siguiente conjunto de dos matrices:
\begin{align*}
B=\left\{ \begin{pmatrix}
1 & 0\\
0 & 0\end{pmatrix} , \begin{pmatrix}
0&0\\
0 & 1\end{pmatrix}\right\}.
\end{align*}

Por un lado, este es un conjunto generador para $U$, pues cualquier elemento de $U$ se puede escribir como combinación lineal de elementos en $B$ como sigue: $$\begin{pmatrix} a_1 & 0 \\ 0 & a_4 \end{pmatrix}=a_1 \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} + a_4 \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}.$$

Por otro lado, $B$ es un conjunto linealmente independiente pues si $a$ y $b$ son escalares que tan una combinación lineal igual a cero entonces tendríamos $$\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} = a \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} + b \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} a & 0 \\ 0 & b \end{pmatrix}.$$

Igualando la primera y última matriz entrada a entrada, tenemos que $a=b=0$.

$\triangle$

Es importante que revises el problema anterior con profundidad, pues da una idea de cómo encontrar una base $B$ de un subespacio $U$ de un espacio vectorial $V$. Una receta que funciona en algunos casos es la siguiente:

  • Entender bien el subespacio $U$ del que hay que dar una base.
  • Expresar a $U$ en términos simples.
  • Ver cómo son los vectores de $U$, y de ahí proponer una base $B$. Para esta parte hay que jugar un poco con conjuntos de vectores, para ver si son suficientes para generar y no son demasiados como para ya no ser linealmente independientes.
  • Mostrar que $B$ genera a $U$.
  • Mostrar que $B$ es linealmente independiente en $V$.

Veamos más ejemplos.

Problema 2. Determina una base para el subespacio $U$ de $\mathbb{R}^4$ dado por
\begin{align*}
U=\{(a,b,c,d)\in \mathbb{R}^4:a+b=0, c=2d\}.
\end{align*}

Solución. Como $b=-a$ y $c=2d$, entonces
\begin{align*}
U=\{(a,-a,2d,d)\in \mathbb{R}^4:a,d\in \mathbb{R}\}=\{av_1+dv_2|a,d\in \mathbb{R}\},
\end{align*}
donde $v_1=(1,-1,0,0)$ y $v_2=(0,0,2,1)$. Por lo tanto $v_1,v_2$ generan a $U$. También son linealmente independientes, pues la relación $av_1+dv_2=0$ es equivalente a $(a,-a,2d,d)=(0,0,0,0)$ e implica $a=d=0$.Se sigue que $\{v_1,v_2\}$ es una base para $U$.

$\triangle$

Problema 3. Considera los subespacios $U,V$ de $\mathbb{R}^4$ definidos por
\begin{align*}
U=\{(x,y,z,w)\in\mathbb{R}^4:y+z+w=0\}
\end{align*}
y
\begin{align*}
V=\{(x,y,z,w)\in\mathbb{R}^4:x=-y, \hspace{2mm}z=2w\}.
\end{align*}
Encuentra una base para cada uno de los subespacios $U,V$ y $U\cap V$ de $\mathbb{R}^4$.

Solución. Expresando a $w$ en términos de $y$ y $z$, obtenemos
\begin{align*}
U&=\{(x,y,z,-y-z)|y,z\in\mathbb{R}\}\\
&=\{xu_1+yu_2+zu_3|x,y,z \in \mathbb{R}\},
\end{align*}
donde $u_1=(1,0,0,0), u_2=(0,1,0,-1)$ y $u_3=(0,0,1,-1)$.

Veamos si $u_1,u_2,u_3$ son linealmente independientes. La igualdad $xu_1+yu_2+zu_3=0$ es equivalente a $(x,y,z,-y-z)=(0,0,0,0)$ e implica $x=y=z=0$. Por lo tanto, los vectores $u_1,u_2,u_3$ son linealmente independientes y forman una base de $U$.

Ahora, para $V$. Es fácil ver que
\begin{align*}
V&=\{(-y,y,2w,w)| y,w\in\mathbb{R}\}\\
&=\{yv_1+wv_2| y,w\in \mathbb{R}\},
\end{align*}
donde $v_1=(-1,1,0,0) \hspace{2mm}$ y $v_2=(0,0,2,1)$.

Nuevamente, $v_1, v_2$ son linealmente independientes, pues la relación $yv_1+wv_2=0$ es equivalente a $(-y,y,2w,w)=(0,0,0,0)$ e implica $y=w=0$. Por lo tanto $v_1,v_2$ forman una base de $V$.

Finalmente, el vector $(x,y,z,w)\in\mathbb{R}^4$ pertenece a $U\cap V$ si y sólo si
\begin{align*}
x=-y, \hspace{3mm} z=2w, \hspace{3mm} y+z+w=0.
\end{align*}
Se sigue que $x=3w, \hspace{2mm} z=2w \hspace{2mm}$ y $y=-3w$, o bien
\begin{align*}
(x,y,z,w)=(3w,-3w,2w,w)=w(3,-3,2,1).
\end{align*}
Por lo tanto $\{(3,-3,2,1)\}$ es una base de $U \cap V$.

$\triangle$

Problema 4. Sea $V$ el espacio de funciones $f:\mathbb{R}\longrightarrow \mathbb{R}$ generado por las funciones en $B=\{1,x\mapsto \sin (2x), x\mapsto \cos(2x)\}$.

a) Demuestra que $B$ es una base de $V$.
b) Demuestra que $x\mapsto \sin ^2 (x)$ es una función en $V$ y exprésala como combinación lineal de los elementos de $B$.

Solución. a) . Como $V$ es el generado de $B$, por definición $B$ es generador. Así, basta demostrar que los vectores en $B$ son linealmente independientes. En otras palabras, queremos ver que si $a,b,c$ son números reales tales que
\begin{align*}
a+b\sin (2x) + c\cos (2x)=0
\end{align*}
para todo $x\in \mathbb{R}$, entonces $a=b=c=0$.

Tomando $x=0$ se obtiene que $a+c=0$. Si tomamos $x=\frac{\pi}{2}$ obtenemos $a-c=0$. Por lo tanto $a=c=0$. Finalmente, si tomamos $x=\frac{\pi}{4}$ obtenemos $b=0$.

b) Para cada $x\in\mathbb{R}$ se tiene
\begin{align*}
\cos (2x)&=2\cos^2(x)-1\\
&=2(1-\sin^2(x))-1\\
&=1-2\sin^2(x),
\end{align*}
por lo tanto
\begin{align*}
\sin^2(x)=\frac{1-\cos (2x)}{2}.
\end{align*}
Por lo tanto $x\mapsto \sin^2(x)$ pertence a $V$ y lo expresamos como combinación lineal de los elementos de $B$ de la siguiente manera:
\begin{align*}
\sin^2(x)=\frac{1}{2}\cdot 1 + 0\cdot \sin(2x) – \frac{1}{2} \cos (2x).
\end{align*}

$\square$

Dimensión finita y bases

Ahora veamos un teorema muy importante en la teoría de la dimensión de espacios vectoriales.

Teorema. Sea $V$ un espacio vectorial de dimensión finita. Entonces
a) $V$ contiene una base con una cantidad finita de elementos.
b) Cualesquiera dos bases de $V$ tienen el mismo número de elementos (en particular, cualquier base tiene una cantidad finita de elementos).

Demostración. a) Como $V$ es de dimensión finita, entonces tiene al menos un conjunto generador finito. Sea $B$ un conjunto generador de $V$ con el menor número posible de elementos. Vamos a demostrar que $B$ es una base para $V$. $B$ ya es conjunto generador porque así lo escogimos, sólo falta probar que es linealmente independiente.

Supongamos por el contrario que $B$ no es linealmente independiente, entonces existe $v\in B$ tal que $v\in \text{span}(B\backslash \{v\})$. Por lo tanto $$\text{span}(B\setminus\{v\})=\text{span}(B)=V.$$

Pero eso es imposible pues $B$ se tomó de tamaño mínimo. Por lo tanto $B$ es linealmente independiente. Se sigue el resultado deseado.

b) Sea $B$ una base con una cantidad finita de elementos, digamos $n$. Sea $B’$ otra base de $V$. Por definición de base, $B’$ es linealmente independiente y $B$ es un conjunto generador con $n$ elementos.

Por el lema de Steinitz, $B’$ es finito y tiene a lo más $n$ elementos. Lo anterior nos muestra que cualquier base tiene a lo más $n$ elementos. De hecho, si $B’$ tiene $d$ elementos, el lema de Steinitz garantiza que $n\leq d$.

Ahora volvemos a aplicar el mismo argumento que antes, pero pensando a $B$ como linealmente independiente y a $B’$ como generador. Concluimos que $k\leq d$. De este modo, $k=d$ y por lo tanto toda base de $V$ tiene la misma cantidad de elementos.

$\square$

El resultado anterior justifica que la siguiente definición esté bien hecha.

Definición. Sea $V$ un espacio vectorial de dimensión finita. Definimos la dimensión $dim V$ de $V$ como el número de elementos de una base de $V$.

Ejemplos y problemas de dimensión

Ejemplo 1. Considera el espacio vectorial $\mathbb{R}^n$ y su base canónica $B=\{e_1,e_2,\dots , e_n\}$. Como $B$ es base y tiene $n$ elementos, entonces $dim(\mathbb{R}^n)=n$.

$\triangle$

Ejemplo 2. Considera el espacio vectorial $\mathbb{R}_n[x]$ de polinomios con coeficientes reales y grado a lo más $n$. Una base para $\mathbb{R}_n[x]$ es $\{1,x,\dots, x^n\}$, por lo tanto $dim(\mathbb{R}_n[x])=n+1$.

$\triangle$

Ejemplo 3. Considera el espacio vectorial $M_{m,n}(\mathbb{R})$. Sea $E_{ij}\in M_{m,n}(\mathbb{R})$ la matriz cuya entrada $(i,j)$ es $1$ y el resto de sus entradas son $0$. Entonces $B=\{E_{ij}| 1\leq i \leq m, 1\leq j \leq n \}$ es una base para $M_{m,n}(\mathbb{R})$. Así, $\dim(M_{m,n}(\mathbb{R}))=mn$.

$\triangle$

Problema 4. Encuentra una base y la dimensión del subespacio
\begin{align*}
V=\{(a,2a)|a\in \mathbb{R}\}\subset \mathbb{R}^2.
\end{align*}

Solución. Notemos que $V=\text{span}((1,2))$, pues $(a,2a)=a(1,2)$. Como $(1,2)\neq (0,0)$, entonces $B=\{(1,2)\}$ es una base de $V$. Por lo tanto $\dim(V)=1$.

$\triangle$

Un lema útil para demostrar que algo es base

Para finalizar esta entrada demostraremos otro teorema muy importante en la teoría de la dimensión de espacios vectoriales. En este resultado usamos de nuevo de manera repetida el lema de intercambio de Steinitz.

Teorema. Sea $V$ un espacio vectorial de dimensión finita $n$. Entonces
a) Cualquier conjunto linealmente independiente de vectores de $V$ tiene a lo más $n$ elementos.
b) Cualquier conjunto generador de $V$ tiene al menos $n$ elementos.
c) Si $S$ es un subconjunto de $V$ con $n$ elementos, entonces las siguientes afirmaciones son equivalentes:

  1. $S$ es linealmente independiente.
  2. $ S $ es un conjunto generador.
  3. $S$ es una base de $V$.

Demostración. Sea $V$ una base de $B$. Por definición $B$ tiene $n$ elementos.

a) Como $B$ es un conjunto generador con $n$ elementos, por el lema de intercambio se tiene que cualquier conjunto linealmente independiente tiene a lo más $n$ elementos.

b) Sea $S$ un conjunto generador de $V$ y supongamos que $S$ tiene $d<n$ elementos. Como $B$ es linealmente independiente, entonces por el lema de intercambio se tiene que $n \leq d$, lo cual sería una contradicción.

c) Es claro que (3) implica (1) y (2), por lo que solamente probaremos que (1) implica (3) y que (2) implica (3).

Supongamos que $S$ es linealmente independiente, entonces por el lema de intercambio de Steintz podemos agregar $n-n=0$ vectores a $S$ de manera que el nuevo conjunto es generador. Claramente el nuevo conjunto es $S$ mismo, pues no le agregamos nada. Por lo tanto $S$ es un conjunto generador y como estamos bajo el supuesto de que $S$ es linealmente independiente, entonces $S$ es una base de $V$.

Ahora supongamos que $S$ es un conjunto generador que no es linealmente independiente. Entonces existe $v\in S$ tal que $v\in \text{span}(S\setminus \{v\})$. Se sigue que $S\setminus \{v\}$ es un conjunto generador de $n-1$ elementos (al generar a $v$, genera todo lo que generaba $S$). Pero esto contradice el inciso b). Por lo tanto $S$ es linealmente independiente y por lo tanto es una base de $V$.

$\square$

El resultado anterior nos permite pensar a las bases de un espacio vectorial como los conjuntos linealmente independientes «más grandes», o bien como los conjuntos generadores «más chicos». En la siguiente entrada veremos ejemplos prácticos del uso del teorema anterior.

Más adelante…

A partir de la definición de dimensión, más adelante construiremos la noción de rango, que nos permite decir «qué tanta información guarda una matriz». La dimensión ayuda también a comprender cuándo hay cierto tipo de transformaciones lineales entre espacios vectoriales. Una aplicación más de la dimensión es que en muchos casos queremos probar afirmaciones para todos los espacios vectoriales de dimensión finita. Como la dimensión nos permite asociar a cada uno de estos un entero, muchas de estas demostraciones se pueden hacer por inducción.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • En todos los problemas en donde se hable de subespacios, verifica que en efecto los conjuntos dados son subespacios del espacio vectorial mencionado.
  • En todos los ejemplos y problemas en los que se menciona que algo es base, verifica que en efecto se tiene un conjunto que es generador y linealmente independiente.
  • Sea $V$ un espacio vectorial sobre $\mathbb{C}$ y de dimensión $n$. Demuestra que si ves a $V$ como un espacio vectorial sobre $\mathbb{R}$, entonces $\dim(V)=2n$.
  • Sea $V$ un espacio vectorial de dimensión finita y $W$ un subespacio de $V$. Demuestra que $W$ es de dimensión finita, que $\dim(W)\leq \dim(V)$ y que la igualdad se da si y sólo si $W=V$.
  • Sean $W_1,W_2$ subespacios de un espacio vectorial $V$ con dimensiones $m$ y $n$, respectivamente, con $m\geq n$.
    a) Demuestra que $\dim(W_1\cap W_2)\leq n$.
    b) Demuestra que $\dim(W_1 + W_2)\leq m+n$.
  • Encuentra la dimensión del subespacio de matrices en $M_n(\mathbb{R})$ que son simétricas.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Transformaciones lineales en bases, conjuntos independientes y generadores

Por Leonardo Ignacio Martínez Sandoval

11 respuestas

Introducción

El objetivo de esta entrada es entender qué efecto tienen las transformaciones lineales en bases, en conjuntos linealmente independientes y en conjuntos generadores. En la siguiente lista recordamos brevemente estas nociones:

  • Una transformación lineal $T:V\to W$ entre espacios vectoriales $V$ y $W$ es una función que «abre sumas» (es decir $T(x+y)=T(x)+T(y)$) y «saca escalares» (es decir $T(cx)=cT(x)$). Recuerda que es necesario que $V$ y $W$ estén sobre el mismo campo, cosa que asumiremos cuando hablemos de transformaciones lineales.
  • Un conjunto de vectores $\{v_1,\ldots, v_n\}$ en $V$ es linealmente independiente si la única combinación lineal de ellos que da $0$ es la trivial, osea en la que todos los coeficientes son $0$.
  • Si cualquier vector de un espacio vectorial $V$ puede escribirse como combinación lineal de un conjunto de vectores $S=\{v_1,\ldots,v_n\}$, entonces decimos que $S$ genera a $V$.
  • Un conjunto de vectores en $V$ es base si es linealmente independiente y genera a $V$.

La idea de esta entrada es entender lo siguiente:

  • ¿Cuándo las imágenes de linealmente independientes/generadores/bases son linealmente independientes/generadores/bases tras aplicar una transformación lineal?
  • ¿Cómo saber si una transformación lineal es inyectiva?
  • ¿Cómo el efecto de transformaciones lineales en bases nos permite determinar exactamente qué le hacen al resto de los vectores?

Exploración

Tomemos espacios vectoriales $V$, $W$ y una transformación lineal $T:V\to W$. Si comenzamos con un conjunto $S=\{v_1,\ldots,v_n\}$ de vectores en $V$ que es linealmente independiente (o generador, o base) en $V$, ¿cuándo sucede que $T(S)=\{T(v_1),\ldots,T(v_n)\}$ es linealmente independiente (o generador, o base, respectivamente) en $W$?

Esto definitivamente no sucede siempre. La tranformación $Z:\mathbb{R}^3\to \mathbb{R}[x]$ que manda a todo vector $(x,y,z)$ al polinomio $0$ es una transformación lineal. Sin embargo, a la base canónica $\{e_1,e_2,e_3\}$ la manda al conjunto $\{0,0,0\}=\{0\}$, que no es un conjunto ni linealmente independiente, ni generador de los polinomios con coeficientes reales.

De esta forma, tenemos que pedirle más a la transformación $T$ para que preserve las propiedades mencionadas.

Intuitivamente, si la imagen de $T$ no cubre a todo $W$, entonces los vectores de la forma $T(v)$ con $v$ en $V$ no deberían de poder generar a $W$. Así, para que $T$ mande generadores a generadores, tiene que pasar que «$T$ pase por todo $W$». Esta noción queda capturada formalmente al pedir que $T$ sea suprayectiva.

Del mismo modo, también intuitivamente si «$T$ manda elementos distintos al mismo elemento», entonces perderemos familias linealmente independientes al aplicarla. Así, para preservar conjuntos linealmente independientes, necesitamos que vectores distintos vayan a valores distintos. En términos formales, necesitamos que $T$ sea inyectiva.

Resultados principales de transformaciones lineales en bases, generadores y linealmente independientes

El primer resultado es que los requisitos que descubrimos intuitivamente en la sección pasada son suficientes.

Teorema. Sea $T:V\to W$ una transformación lineal y $S=\{v_1,\ldots,v_n\}$ un conjunto de vectores de $V$. Entonces:

  • Si $T$ es inyectiva y $S$ es linealmente independiente, entonces $T(S)$ es linealmente independiente.
  • Cuando $T$ es suprayectiva y $S$ es generador, entonces $T(S)$ es generador.
  • Si $T$ es biyectiva y $S$ es base, entonces $T(S)$ es base.

Demostración. Comencemos suponiendo que $T$ es inyectiva y $S$ es linealmente independiente. Entonces $T(v_1),\ldots,T(v_n)$ son todos distintos. Tomemos una combinación lineal de elementos de $T(S)$ igual a cero, es decir, $$a_1T(v_1)+a_2T(v_2)+\ldots+a_nT(v_n)=0.$$ Debemos mostrar que todos los coeficientes son iguales a cero. Como $T$ es transformación lineal, podemos juntar las sumas y productos escalares como sigue: $$T(a_1v_1+a_2v_2+\ldots+a_nv_n)=0=T(0).$$

Como $T$ es inyectiva, esto implica que $$a_1v_1+a_2v_2+\ldots+a_nv_n=0,$$ pero como $S$ es linealmente independiente, concluimos que $$a_1=\ldots=a_n=0.$$ Así, $T(S)$ es linealmente independiente.

Supongamos ahora que $T$ es suprayectiva y $S$ es generador. Tomemos un $w\in W$. Como $T$ es suprayectiva, existe $v\in V$ tal que $T(v)=w$ y como $S$ es generador, existen $a_1,\ldots,a_n$ tales que $$a_1v_1+\ldots+a_nv_n=v.$$ Aplicando $T$ en ambos lados, abriendo las sumas y sacando escalares obtenemos que $$a_1T(v_1)+\ldots+a_nT(v_n)=T(v)=w.$$ Así, todo elemento de $W$ se puede escribir como combinación lineal de elementos de $T(S)$, como queríamos.

Finalmente, supongamos que $T$ es biyectiva y $S$ es base. Como $T$ es inyectiva y $S$ linealmente independiente, entonces $T(S)$ es linealmente independiente. Como $T$ es suprayectiva y $S$ generador, entonces $T(S)$ es generador. Así, $T(S)$ es base.

$\square$

Una consecuencia fudamental del resultado anterior es que si $V$ y $W$ son espacios de dimensión finita y existe una transformación lineal inyectiva $T:V\to W$, entonces $\dim(V)\leq \dim(W)$. En efecto, si $B$ es base de $V$ y $T$ es inyectiva, entonces $T(B)$ es linealmente independiente en $W$ y sabemos que $W$ tiene a lo más $\dim(W)$ vectores linealmente independientes, así que $\dim(V)=|B|=|T(B)|\leq \dim(W)$. De manera similar, si existe una transformación lineal $T:V\to W$ suprayectiva, entonces $\dim(V)\geq \dim(W)$. Demuestra esto. ¿Qué pasa con las dimensiones si existe una transformación lineal biyectiva entre $V$ y $W$?

¿Cuándo una transformación lineal es inyectiva?

El teorema anterior también sugiere que es importante saber cuándo una transformación lineal es inyectiva, suprayectiva o ambas. Resulta que en el caso de la inyectividad hay un criterio que nos ayuda.

Proposición. Sean $V$ y $W$ espacios vectoriales. Una transformación lineal $T:V\to W$ es inyectiva y si sólo si el único vector $v$ de $V$ tal que $T(v)=0$ es el vector $v=0$. En otras palabras $T$ es inyectiva si y sólo si $\ker(T)=\{0\}$.

Demostración. Sean $V$ y $W$ espacios vectoriales y $T:V\to W$ una transformación lineal. Recordemos que sabemos que $T(0)=0$.

Si $T$ es inyectiva y $T(x)=0$, entonces $T(x)=T(0)$ y por inyectividad $x=0$, de modo que $x$ es el único vector que va a $0$ bajo $T$.

Si el único vector que bajo $T$ va a $0$ es el $0$ y tenemos que $T(x)=T(y)$, entonces usando que $T$ es lineal tenemos que $0=T(y)-T(x)=T(y-x)$. Así, por hipótesis $y-x=0$, es decir, $x=y$. Con esto queda mostrado que $T$ es inyectiva.

$\square$

Transformaciones lineales en bases dan toda la información

Conociendo los valores de una transformación lineal en algunos vectores, es posible determinar el valor de la transformación en otros vectores que son combinación lineal de los primeros. Considera el siguiente ejemplo.

Problema. La transformación lineal $T:M_2(\mathbb{R})\to\mathbb{R}^2$ cumple que $T\begin{pmatrix}
1 & 1\\
0 & 0
\end{pmatrix}=(1,0)$, $T\begin{pmatrix}
0 & 1 \\
0 & 1
\end{pmatrix}=(0,-1)$, $T\begin{pmatrix}
0 & 0\\
1 & 1
\end{pmatrix}=(-1,0)$ y $T\begin{pmatrix}
1 & 0\\
1 & 0
\end{pmatrix}=(0,1)$. Determina el valor de $T\begin{pmatrix} 3 & 3\\ 3 & 3\end{pmatrix}$.

Intenta resolver el problema por tu cuenta antes de ver la solución. Para ello, intenta poner a la matriz $\begin{pmatrix} 3 & 3\\ 3 & 3\end{pmatrix}$ como combinación lineal de las otras matrices y usar que $T$ es lineal.

Solución. Sean $A$, $B$, $C$ y $D$ las matrices de las cuales conocemos cuánto vale $T$ en ellas y $E$ la matriz con puros $3$’s. Queremos determinar el valor de $T(E)$. Notemos que $E=\frac{3}{2}(A+B+C+D)$. Como $T$ es transformación lineal, tenemos que

\begin{align*}
T(E)&=\frac{3}{2}(T(A)+T(B)+T(C)+T(D))\\
&=\frac{3}{2}((1,0)+(0,-1)+(-1,0)+(0,1))\\
&=(0,0).
\end{align*}

$\square$

En este problema lo que sirvió para encontrar el valor de $T(E)$ fue poner a la matriz $E$ como combinación lineal de las matrices $A,B,C,D$. De hecho, para cualquier matriz que sea combinación lineal de las matrices $A,B,C,D$, pudiéramos haber hecho lo mismo.

A partir de esta observación, podemos intuir que al conocer el efecto de transformaciones lineales en bases, podemos saber qué le hacen a cada elemento del espacio vectorial. El siguiente teorema enuncia esto de manera formal y dice un poco más.

Teorema. Sean $V$, $W$ espacios vectoriales, $B=\{v_1,v_2,\ldots,v_n\}$ una base de $V$ y $w_1,w_2,\ldots, w_n$ vectores cualesquiera de $W$. Entonces, existe una y sólo una transformación lineal $T:V\to W$ tal que $$T(v_1)=w_1,\quad T(v_2)=w_2, \quad \ldots, \quad T(v_n)=w_n.$$

Demostración. Probemos primero la parte de existencia. Como $B$ es base, cualquier vector $v$ de $V$ se puede escribir como $$a_1v_1+a_2v_2+\ldots+a_nv_n.$$ Construyamos la función $T:V\to W$ tal que $$T(v)=a_1w_1+a_2w_2+\ldots+a_nw_n.$$

Como para cada $i=1,\ldots,n$ tenemos que la combinación lineal de $v_i$ en términos de $B$ es $v_i=1\cdot v_i$, tenemos que $T(v_i)=1\cdot w_i=w_i$, que es una de las cosas que queremos. La otra que queremos es que $T$ sea lineal. Mostremos esto. Si $$v=a_1v_1+a_2v_2+\ldots+a_nv_n$$ y $$w=b_1v_1+b_2v_2+\ldots+b_nv_n,$$ entonces $$v+w=(a_1+b_1)v_1+
(a_2+b_2)v_2+\ldots+ (a_n+b_n)v_n,$$ y por definición $$T(v+w)=(a_1+b_1)w_1+ (a_2+b_2)w_2+\ldots+ (a_n+b_n)w_n.$$ Notemos que el lado derecho es igual a $T(v)+T(w)$, de modo que $T$ abre sumas. De manera similar se puede mostrar que $T$ saca escalares.

Esbocemos ahora la demostración de la unicidad. Supongamos que $T$ y $T’$ son transformaciones lineales de $V$ a $W$ tales que $T(v_i)=T'(v_i)=w_i$ para toda $i=1,\ldots,n$. Tenemos que mostrar que $T(v)=T'(v)$ para toda $v$. Para ello procedemos como en el problema antes de este teorema: escribimos a $v$ como combinación lineal de elementos de $B$. Esto se puede hacer de una única forma. El valor de $T(v)$ a su vez depende únicamente de $w_1,\ldots,w_n$ y de la los coeficientes en combinación lineal. El de $T'(v)$ también. Por lo tanto son iguales.

$\square$

Una consecuencia del teorema anterior, en la que no es necesario enunciar a las imágenes de la base, es la siguiente.

Corolario. Sean $V$ y $W$ espacios vectoriales, $B$ una base de $V$, y $T$ y $T’$ transformaciones lineales de $V$ a $W$. Si $T(v)=T'(v)$ para toda $v\in B$, entonces $T(v)=T'(v)$ para toda $v\in V$.

Más adelante…

Las propiedades que demostramos en esta entrada se usan con tanta frecuencia que muchas veces se aplican sin siquiera detenerse a argumentar por qué son válidas. Por esta razón, es importante que te familiarices con ellas. Otra ventaja de conocerlas a profundidad es que muchas veces ayudan a dar demostraciones sencillas o elegantes para algunos problemas. Finalmente, los hechos que aquí mostramos los usaremos prácticamente sin demostración en las siguientes entradas, en donde desarrollaremos la teoría de la forma matricial de transformaciones lineales.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • Encuentra qué le hace al vector $(7,3)$ una transformación lineal $T:\mathbb{R}^2\to \mathbb{R}$ tal que $T(2,1)=20$ y $T(7,2)=5$.
  • Determina si las matrices $A,B,C,D$ del problema de la entrada son una base para $M_2(\mathbb{R})$. Si no son una base, ¿cuál es la dimensión del subespacio que generan?
  • En el último teorema se afirma que la función que construimos saca escalares. Muestra esto.
  • De ese mismo teorema, escribe los detalles de que dicha función es única.
  • Demuestra el corolario enunciado en la entrada.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

El lema de intercambio de Steinitz

Por Leonardo Ignacio Martínez Sandoval

7 respuestas

Introducción

En esta entrada platicaré de un lema muy útil en álgebra lineal, sobre todo cuando se están definiendo las nociones de base y de dimensión para espacios vectoriales de dimensión finita. Se trata del lema de intercambio de Steinitz.

Supondré que el lector ya sabe un poco de álgebra lineal, pero muy poquito. Basta con saber la definición de espacio vectorial. Lo demás lo definiremos sobre el camino.

El nombre del lema es en honor al matemático alemán Ernst Steinitz. Sin embargo, personalmente a mi me gusta pensarlo como el lema del «regalo de vectores», por razones que ahorita platicaremos. El enunciado es el siguiente:

Teorema (Lema de intercambio de Steinitz). Sea $V$ un espacio vectorial. Tomemos un conjunto finito y linealmente independiente $L$ de $V$, y un conjunto finito y generador $S$ de $V$. Supongamos que $L$ tiene $m$ elementos y que $S$ tiene $n$ elementos. Entonces:

  • $m\leq n$
  • Se puede tomar un subconjunto $T$ de $S$ de tamaño $n-m$ tal que $L\cup T$ sea generador de $V$.

En pocas palabras, «cualquier conjunto linealmente independiente tiene a lo mucho tantos elementos como cualquier conjunto generador y, además, cualquier generador le puede regalar vectores al linealmente independiente para volverlo generador».

De manera esquemática, está pasando lo siguiente:

Diagrama del lema de intercambio de Steinitz
Diagrama del lema de intercambio de Steinitz

Lo que haremos es hablar de las definiciones necesarias para entender el lema, hablar de la intuición detrás, dar un par de ejemplos y luego dar la demostración. La presentación está ligeramente basada en el libro de álgebra lineal de Titu Andreescu.

Definiciones e intuición

Sea $V$ un espacio vectorial sobre un campo $F$.

Si tenemos vectores $v_1,\ldots,v_n$ de $V$ y escalares $a_1,\ldots,a_n$ en $F$, podemos considerar al vector formado por multiplicar los vectores por los escalares correspondientes y sumarlos todos, es decir al vector $v$ dado por la expresión $a_1v_1+\cdots+a_nv_n$ . En este caso, decimos que $v$ es una combinación lineal de $v_1,\ldots,v_n$, o a veces que $v_1,\ldots,v_n$ generan a $v$.

Un conjunto $S=\{v_1,v_2,\ldots,v_n\}$ de vectores de $V$ es generador si para cualquier $v$ de $V$ existen escalares $a_1,\ldots,a_n$ en $F$ para los cuales $v=a_1v_1+\cdots+a_nv_n$. Dicho de otra forma, «$S$ es generador si cualquier vector del espacio vectorial es combinación lineal de vectores de $S$».

De esta definición es fácil ver que si $S$ es un conjunto generador y $T$ es un conjunto que contiene a $S$ (es decir, $T\supset S$), entonces $T$ también es generador: simplemente para cualquier $v$ usamos la combinación lineal que tenemos en $S$ y al resto de los vectores (los de $T\setminus S$) les ponemos coeficientes cero.

Un conjunto $L=\{w_1,w_2,\ldots,w_m\}$ de vectores de $V$ es linealmente independiente si la única combinación lineal de vectores de $L$ que da $0$ es aquella en la que todos los escalares son $0$. Dicho de otra forma, «$L$ es linealmente independiente si $a_1w_1+\ldots+a_mw_m=0$ implica que $a_1=a_2=\ldots=a_m=0$.»

Con los conjuntos linealmente independientes pasa lo contrario a lo de los generadores. Si $L$ es un conjunto linealmente independiente y $M$ está contenido en $L$ (es decir, ahora $M\subset L$), entonces $M$ es linealmente independiente. Esto sucede pues cualquier combinación lineal de $M$ también es una combinación lineal de $L$. Como no hay ninguna combinación lineal no trivial de elementos de $L$ que sea igual a cero, entonces tampoco la hay para $M$.

Los párrafos anteriores dejan la idea de que «los conjuntos generadores tienen que ser grandes» y que «los conjuntos linealmente independientes tienen que ser chiquitos». El lema de intercambio de Steinitz es una manera en la que podemos formalizar esta intuición.

Como los conjuntos generadores son «grandes», entonces son bien buena onda y bien generosos. Tienen muchos elementos. Como los conjuntos linealmente independientes son «chiquitos», entonces necesitan elementos. Lo que dice el lema de intercambio de Steinitz es que si tenemos a un generador $S$ y a un linealmente independiente $L$, entonces $S$ tiene más elementos y que puede regalar al linealmente independiente $L$ algunos elementos $T$ para que ahora $L\cup T$ tenga tantos elementos como tenía $S$ y además se vuelva generador. Una cosa importante es que no cualquier subconjunto $T$ funciona. Este tiene que estar bien elegido.

Ejemplo concreto del lema de intercamio de Steinitz

Veamos un ejemplo muy concreto. Supongamos que nuestro espacio vectorial es $\mathbb{R}^3$, osea, los vectores con $3$ entradas reales. Tomemos a los siguientes conjuntos de vectores:

  • $L=\{(1,2,3), (0,3,0)\}$
  • $S=\{(0,1,0), (1,0,0), (0,0,-1), (2,4,6)\}$

Por un lado, el conjunto $L$ es linealmente idependiente. Una combinación lineal $a(1,2,3)+b(0,3,0)=(0,0,0)$ implica de manera directa que $a=0$ (por la primer o tercer coordenadas) y de ahí $b=0$ (por la segunda coordenada).

Por otro lado, el conjunto $S$ es generador, pues con $(0,0,-1)$ podemos obtener a $(0,0,1)$ como combinación lineal, de modo que $S$ genera a los tres de la base canónica y por tanto genera a todo $\mathbb{R}^3$.

Notemos que en efecto $L$ tiene menos elementos que $S$. Además, el lema de intercambio de Steinitz garantiza que $S$ puede pasarle $|S|-|L|=4-2=2$ elementos a $L$ para volverlo generador. Pero hay que ser cuidadosos. Si le regala los elementos $(0,1,0)$ y $(2,4,6)$, entonces no funciona (se puede verificar que este conjunto no genera a $\mathbb{R}^3$). Pero si le regala, por ejemplo, los elementos $(1,0,0)$ y $(0,0,-1)$ entonces ahora sí generará (se puede argumentar viendo que entonces ahora genera a los tres de la base canónica).

Demostración del lema de intercambio de Steinitz

Pasemos ahora a la demostración del lema de Steinitz. Lo demostraremos por inducción en la cantidad de elementos que tiene $L$, el linealmente independiente. Si $|L|=m=0$, entonces claramente $m=0\leq n$, y además $S$ le puede pasar $n-0=n$ elementos (todos) a $L$ y volverlo generador.

Supongamos entonces que es cierta la siguiente afirmación.

Hipótesis inductiva Sea $V$ un espacio vectorial. Tomemos un conjunto finito y linealmente independiente $L$ de $V$, y un conjunto finito y generador $S$ de $V$. Supongamos que $L$ tiene $m$ elementos y que $S$ tiene $n$ elementos. Entonces:

  • $m\leq n$
  • Se puede tomar un subconjunto $T$ de $S$ de tamaño $n-m$ tal que $L\cup T$ sea generador de $V$.

Para el paso inductivo, tomemos $L=\{w_1,w_2,\ldots,w_m,w_{m+1}\}$ un linealmente independiente de $V$ y $S=\{v_1,v_2,\ldots,v_n\}$ un generador de $V$. Aplicándole la hipótesis inductiva al linealmente independiente $L’=L\setminus \{w_{m+1}\}=\{w_1,\ldots,w_m\}$ y al generador $S$, tenemos que:

  • $m\leq n$
  • Se puede tomar un subconjunto $T’=\{s_1,s_2,\ldots,s_{n-m}\}$ de $S$ tal que $L’\cup T’= \{w_1,w_2,\ldots,w_m,s_1,\ldots,s_{n-m}\}$ sea generador de $V$.

Como $L’\cup T’$ es generador, entonces podemos poner a $w_{m+1}$ como combinación lineal de elementos de $L’\cup T’$, es decir, existen $a_1,\ldots, a_m, b_1,\ldots,b_{n-m}$ tales que $$w_{m+1}=a_1w_1+\ldots+a_mw_m+b_1s_1+\ldots+b_{n-m}s_{n-m}.$$

Ya sabemos que $m\leq n$. Si $m=n$, la combinación lineal anterior no tendría ningún $s_i$, y entonces sería una combinación lineal no trivial para los elementos de $L$, lo cual es una contradicción pues $L$ es linealmente independiente. Entonces $m\neq n$ y $m\leq n$, así que $m+1\leq n$, que era el primer punto que queríamos probar.

También, como $L$ es linealmente independiente, no se vale que todos los $b_i$ sean iguales a cero. Sin perder generalidad, podemos suponer que $b_1\neq 0$. Así, $s_1$ se puede despejar como combinación lineal en términos de $w_1,\ldots,w_n,w_{n+1}, s_2,\ldots,s_{n-m}$ y por lo tanto $L\cup (T’\setminus \{s_1\})$ genera lo mismo que $L’\cup T’$, que era todo $V$. Así, $T:=T’\setminus \{s_1\}$ es el subconjunto de $S$ de tamaño $n-(m+1)$ tal que $L\cup T$ es generador. Esto termina la prueba del lema.

Algunas aplicaciones

El lema de intercambio de Steinitz se puede utilizar para probar varias afirmaciones con respecto a bases de un espacio vectorial de dimensión finita.

Un espacio vectorial es de dimensión finita si tiene un conjunto generador con una cantidad finita de elementos. Una base de un espacio vectorial es un conjunto que sea simultáneamente generador y linealmente independiente.

Las siguientes afirmaciones se siguen directamente del lema de Steinitz.

  1. Todas las bases de un espacio vectorial finito tienen la misma cantidad de elementos.
  2. En un espacio vectorial de dimensión $d$:
    • Todo conjunto linealmente independiente tiene a lo más $d$ elementos.
    • Todo conjunto generador tiene al menos $d$ elementos.
  3. Si $S$ es un conjunto con $n$ vectores de un espacio vectorial de dimensión $n$, entonces las siguientes tres afirmaciones son equivalentes:
    • El conjunto $S$ es base.
    • $S$ es linealmente independiente.
    • $S$ es generador.

Como primer ejemplo, haremos (1). Tomemos $B_1$ y $B_2$ bases de un espacio vectorial de dimensión finita $B$. Pensando a $B_1$ como linealmente independiente y a $B_2$ como generador, tenemos $|B_1|\leq |B_2|$. Pensando a $B_2$ como linealmente independiente y a $B_1$ como generador, tenemos $|B_2|\leq |B_1|$. Así, $|B_1|=|B_2|$.

Como segundo ejemplo, haremos una parte de (3). Suponiendo que $S$ es un conjunto de $n$ vectores de un espacio vectorial de dimensión $n$, veremos que su independencia lineal implica $S$ es base. Sea $B$ una base de $V$. Por el lema de Steinitz, podemos pasar $|B|-|S|=n-n=0$ elementos de $B$ a $S$ para volverlo generador. Es decir, $S$ ya es generador. Como además es linealmente independiente, entonces es base.

El resto de las demostraciones son igual de sencillas, como puedes verificar.

Más adelante…

El lema de Steinitz es la herramienta clave para definir dar la definición de dimensión de espacios vectoriales en el caso de dimensión finita. Lo usaremos una y otra vez. Por esta razón, es muy recomendable repasar su demostración y entender a profundidad qué dice.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Replica por tu cuenta la demostración del lema de Steinitz hasta que te sientas cómodo con los argumentos.
  • En el ejemplo que se dio de la aplicación del lema de Steinitz, ¿cuáles son todas las posibilidades de $2$ elementos que se pueden pasar para que $L$ se convierta en generador?
  • Usa el lema de Steinitz para demostrar el resto de consecuencias que mencionamos.
  • ¿Qué te dice el lema de Steinitz cuando $L$ y $S$ son inicialmente del mismo tamaño?
  • Muestra que en el lema de Steinitz la hipótesis de que $L$ sea finito no es necesaria, es decir, que incluso sin esta hipótesis se pueden mostrar todas las conclusiones.

Entradas relacionadas

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario:

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»