Introducción
En la entrada anterior [Enlace entrada anterior] se introdujo la esencia del concepto de transformaciones y que estaremos viendo diversos tipos de transformaciones, pero para que no trabajemos en un espacio desconocido, en ésta entrada hablaremos de nociones básicas de funciones que debemos tener presentes para luego definir formalmente el concepto de qué es una transformación.
Funciones
Sean $E$ y $F$ dos conjuntos no vacíos, denominaremos función de un conjunto $E$ en un conjunto $F$ (o función definida en $E$ con valores en $F$) a una regla o ley $f$ que a todo elemento $x \in E$ le pone en correspondencia un determinado elemento $f(x) \in F$.
Al conjunto de los elementos $x \in E$ les llamamos dominio o argumento de la función $f$ y normalmente su notación es $Dom(f)$. Al conjunto de los elementos $f(x) \in F$ le llamamos rango o imagen y se denota por $Im(f)$. Además se encuentra el conjunto $F$ del contradominio, el cual contiene al rango.
A una función la designamos por lo general con la letra $f$ o con el símbolo $f: E \longrightarrow F$, que nos señala que $f$ aplica el conjunto $E$ en $F$. También podemos emplear la notación $x \mapsto f(x)$ para indicarnos que al elemento $x$ le corresponde el elemento $f(x)$. Cabe mencionar que en la mayoría de los casos las funciones se definen mediante igualdades, las cuales describen la ley de correspondencia.
Ejemplo 1. Podemos decir que la función $f$ está definida mediante la igualdad $f(x) = \sqrt{ x^2 + 1}$, $x \in [a,b]$. Si $y$ es la notación general de los elementos del conjunto $F$, o sea $F = \{y\}$, la aplicación $f: E \longrightarrow F$ se escribe en forma de la igualdad $y = f(x)$, y decimos entonces que la función se encuentra dada en su forma explícita.
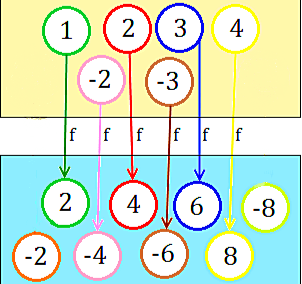
Ejemplo 2. Mediante la siguiente imagen vamos a obtener $Domf$, $Imf$ y el $Codf$.
Podemos ver que $Domf$ es el conjunto formado por $\{1, -2, 2, -3, 3, 4\} $. La $Imf$ es $\{2, -4, 4, -6, 6, 8\}$ y el $Codf$ es $\{-2,2,-4,4,-6,6,8,-8\}$. Podemos darnos cuenta que no necesariamente la $Imf$ debe coincidir siempre con el $Codf$.
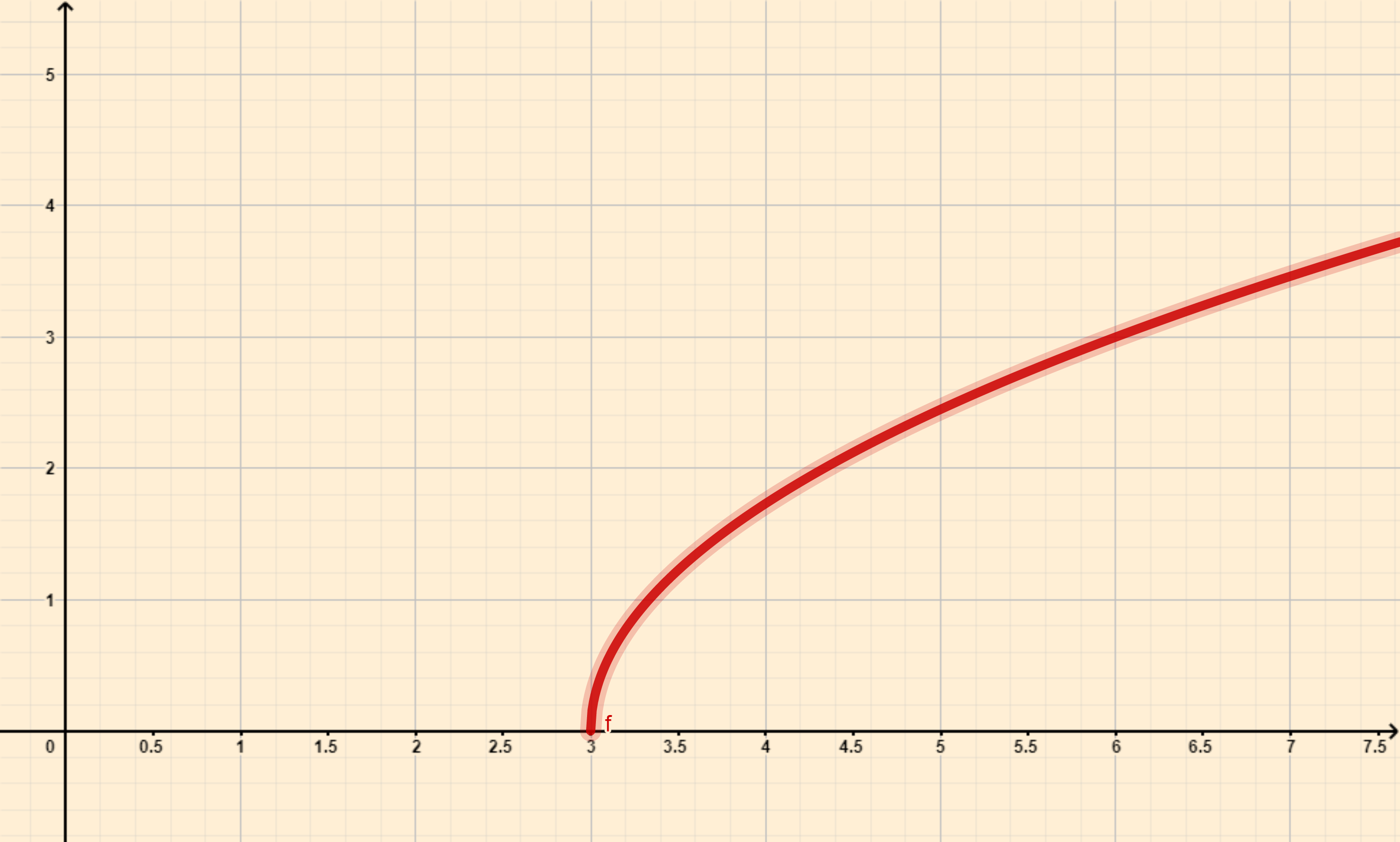
Ejemplo 3. Sea la función definida por la ecuación $y = \sqrt{3 – 9x}$. Debido a que la función es una raíz cuadrada, $y$ es función de $x$ sólo para $3-9x \geq 0$; pues para cualquier $x$ que satisfaga esta desigualdad, se determina un valor único de $y$. Procedemos a resolver la desigualdad:
\begin{align*}
3-9x & \geq 0,\\
3 & \geq 9x,\\
\dfrac{3}{9} & \geq x,\\
\dfrac{1}{3} & \geq x.
\end{align*}
Sin embargo si $x > \dfrac{1}{3}$, obtenemos la raíz cuadrada de un número negativo y en consecuencia no existe un número real $y$. Por tanto $x$ debe estar restringida a $\dfrac{1}{3} \geq x $. Concluimos que el $Domf$ es el intervalo $\left(- \infty, \dfrac{1}{3}\right]$ y la $Imf$ es $[0, + \infty).$
Función inyectiva, sobreyectiva y biyectiva
Definición. Una función $f: E \longrightarrow F$ se denomina:
- Inyectiva si $f(x) = f(x’)$ implica que $x = x’$. Otra forma de expresarlo es que no existen dos elementos de $E$ con una misma imagen ($x \neq x $ implica que $f(x) \neq f(x’)$).
- Suprayectiva o sobreyectiva si $\forall y \in F$ existe $x \in E$ tal que $f(x)=y$. Es decir que todos los elementos del conjunto $F$ son imagen de algún elemento de $E$.
- Biyectiva si la función cumple ser inyectiva y suprayectiva.
Problema 1. Consideren la función $f: \mathbb{R} \longrightarrow \mathbb{R} $ definida por $f(x) = \dfrac{3x-1}{x+3}$ y determinen su dominio y si es biyectiva.
Solución. Veamos el dominio de la función, para que la función racional $f(x) = \dfrac{3x-1}{x+3}$ no se indetermine debe cumplirse que:
\begin{align*}
x+3 & \neq 0,\\
x & \neq -3,\\
\therefore Domf & = \mathbb{R} – \{-3 \}.\\
\end{align*}
Ahora veamos si $f$ es biyectiva. Sean $a,b \in \mathbb{R} – \{ -3 \}$, para que $f$ sea inyectiva debe cumplir que $f(x) = f(x’)$ implica que $x = x’$, por ello:
\begin{equation*}
f(a) = f(b) \hspace{0.5cm} \Longrightarrow \hspace{0.5cm} \dfrac{3a-1}{a+3} = \dfrac{3b-1}{b+3}.\\
\end{equation*}
Resolviendo:
\begin{align*}
(3a-1)(b+3) &= (3b-1)(a+3),\\
3ab + 9a – b -3 &= 3ab +9b -a -3,\\
10a &= 10b,\\
a &= b.
\end{align*}
Por tanto $f$ es inyectiva. Ahora veamos si $f$ es suprayectiva, sean $x, y \in E$ entonces:
\begin{align*}
f(x) = f(y) \hspace{0.5cm} &\Longrightarrow \hspace{0.5cm} y = \dfrac{3x-1}{x+3},\\
\end{align*}
Resolviendo
\begin{align*}
y(x+3) &= 3x-1,\\
yx +3y &= 3x-1,\\
yx-3x &= -3y-1,\\
x(y-3) &= -3y-1,
\end{align*}
y despejando a $x$
\begin{align*}
x &= \dfrac{-3y-1}{y-3},\\
x &= \dfrac{3y+1}{3-y},
\end{align*}
y como $3-y \neq 0$, entonces $y \neq 3$. En consecuencia $y \in \mathbb{R} – \{3 \}$. Pero al estar definida $f$ por $f: \mathbb{R} \longrightarrow \mathbb{R}$, tenemos que $f$ no es suprayectiva.
\begin{align*}
\therefore f \text{ no es biyectiva}.
\end{align*}
Composición de funciones y funciones inversas.
Definición. Dadas las funciones $f: A \longrightarrow B$ y $g: B \longrightarrow C$ , donde la imagen de $f$ está contenida en el dominio de $g$, se define la función composición $(g \circ f): A \longrightarrow C$ como $(g \circ f)(x) = g(f(x)),$ para todos los elementos $x$ de $A$.
La composición de funciones se realiza aplicando dichas funciones en orden de derecha a izquierda, de manera que en $(g \circ f)(x)$ primero actúa la función $f$ y luego la $g$ sobre $f(x)$.
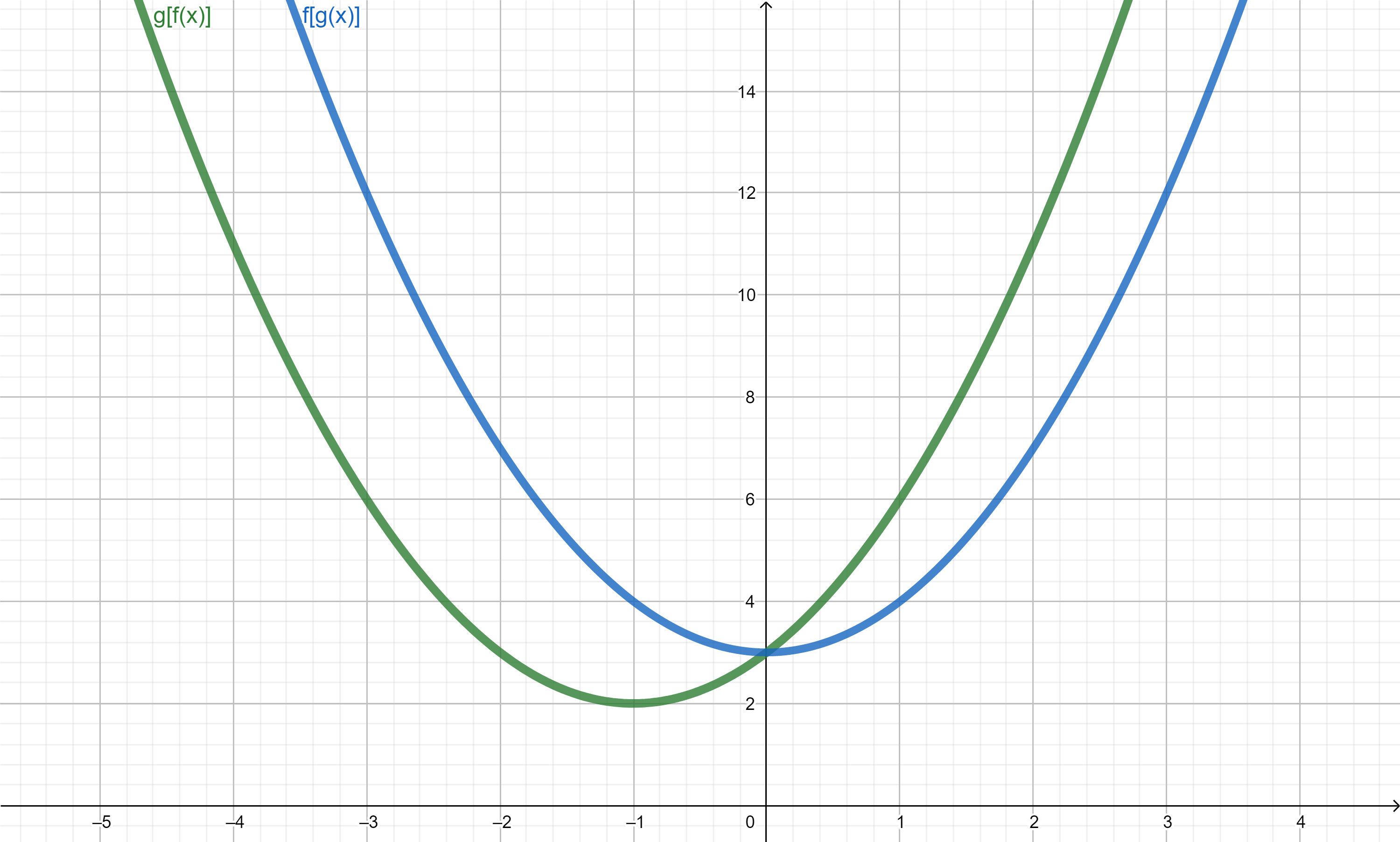
Ejemplo 4. Sean las funciones $f$ y $g$ tales que $f(x)=x+1$ y $g(x) = x^2 +2$, calcularemos las funciones composición $(g \circ f)(x)$ y $(f \circ g)(x)$. Tenemos para $(g \circ f)(x)$
\begin{align*}
(g \circ f)(x) = g[f(x)] &= g(x+1),\\
&= (x+1)^2 + 2,\\
&= x^2 +2x +1 +2,\\
&= x^2 + 2x +3.
\end{align*}
Y para $(f \circ g)(x)$
\begin{align*}
(f \circ g)(x) = f[g(x)] &= f(x^2+2),\\
&= (x^2 + 2) + 1,\\
&= x^2 + 3.\\
\end{align*}
Observemos que la composición no es conmutativa pues las funciones $(f \circ g)$ y $(g \circ f)$ no son iguales.
Definición. Llamaremos función inversa de $f$ a otra función $f^{-1}$ que cumple que si $f(x)=y$, entonces $f^{-1}(y)=x$.
Sólo es posible determinar la función inversa $f^{-1}: B \longrightarrow A$ si y sólo si $f: A \longrightarrow B$ es biyectiva.
Notemos que la función inversa $f^{-1}: B \longrightarrow A$ también es biyectiva y cumple:
\begin{align*}
f^{-1}(f(x)) &= x, \hspace{0.2cm} \forall x \in A,\\
f(f^{-1}(y)) &= y, \hspace{0.2cm} \forall y \in B.
\end{align*}
Dicho de otro modo,
\begin{align*}
f^{-1} \circ f &= id_{A},\\
f \circ f^{-1} &= id_{B},
\end{align*}
donde $id_{A}$ e $id_{B}$ son las funciones identidad de $A$ y $B$ respectivamente. Es decir, son las funciones $id_{A}: A \longrightarrow A$ definida por $id_{A}(x) = x$ e $id_{B}: B \longrightarrow B$ definida por $id_{B}(y) = y$.
Concepto formal de transformación
Ahora hemos llegado a la definición de nuestro interés.
Definición. Una transformación en un plano A es una función biyectiva $f: A \longrightarrow A$ del plano en sí mismo.
Llamaremos transformación en el plano, a toda función que hace corresponder a cada punto del plano, otro punto del mismo.
Tarea moral
Vamos a realizar unos par de ejercicios para repasar y practicar los conceptos que vimos en esta entrada.
Ejercicio 1. Consideren la siguiente función $f: \mathbb{R} \longrightarrow \mathbb{R}$ definida por $f(x) = \dfrac{3x-1}{x+3}$ y determinen su dominio, si ella es inyectiva, suprayectiva y la inversa de $f$.
Ejercicio 2. Sean $f: X \longrightarrow Y$ y $g: Y \longrightarrow Z$ funciones, demuestren que
(1) Si $f$ y $g$ son inyectivas, entonces $g \circ f$ es inyectiva.
(2) Si $g \circ f$ es suprayectiva, entonces $g$ es suprayectiva.
Más adelante
En esta entrada vimos las nociones básicas de funciones que nos llevaron a definir formalmente el concepto de una transformación. Dicho concepto nos permitirá comenzar a trabajar en la siguiente entrada con unos primeros conjuntos cuyas propiedades hacen que tengan un nombre especial: los grupos de transformaciones.
Enlaces
- Página principal del curso:
- Entrada anterior del curso:
- Siguiente entrada del curso: