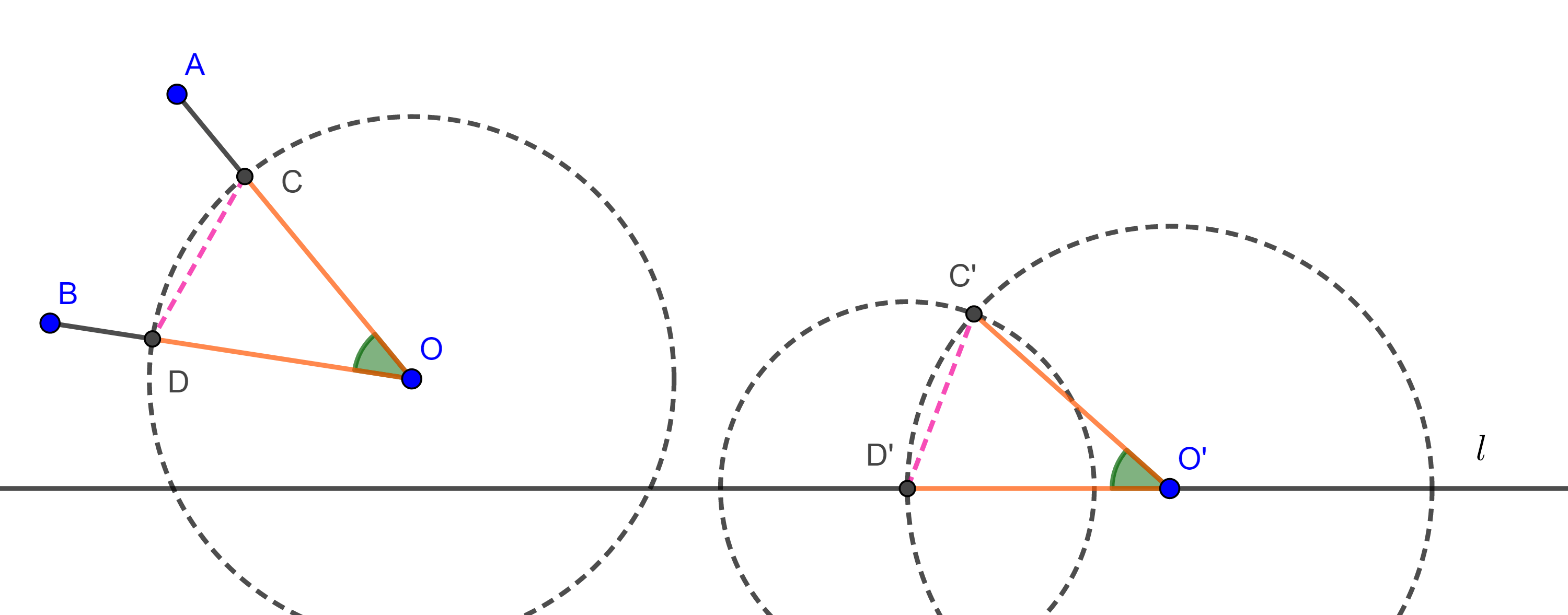Geometría Moderna I: Desigualdad del triángulo y lugar geométrico

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta ocasión estudiaremos una propiedad muy importante de los triángulos, la desigualdad del triángulo que básicamente nos dice que la distancia mas corta entre dos puntos es el segmento de recta que los une, también veremos lo que es un lugar geométrico y mostraremos un par de ejemplos importantes.

Desigualdad del triángulo

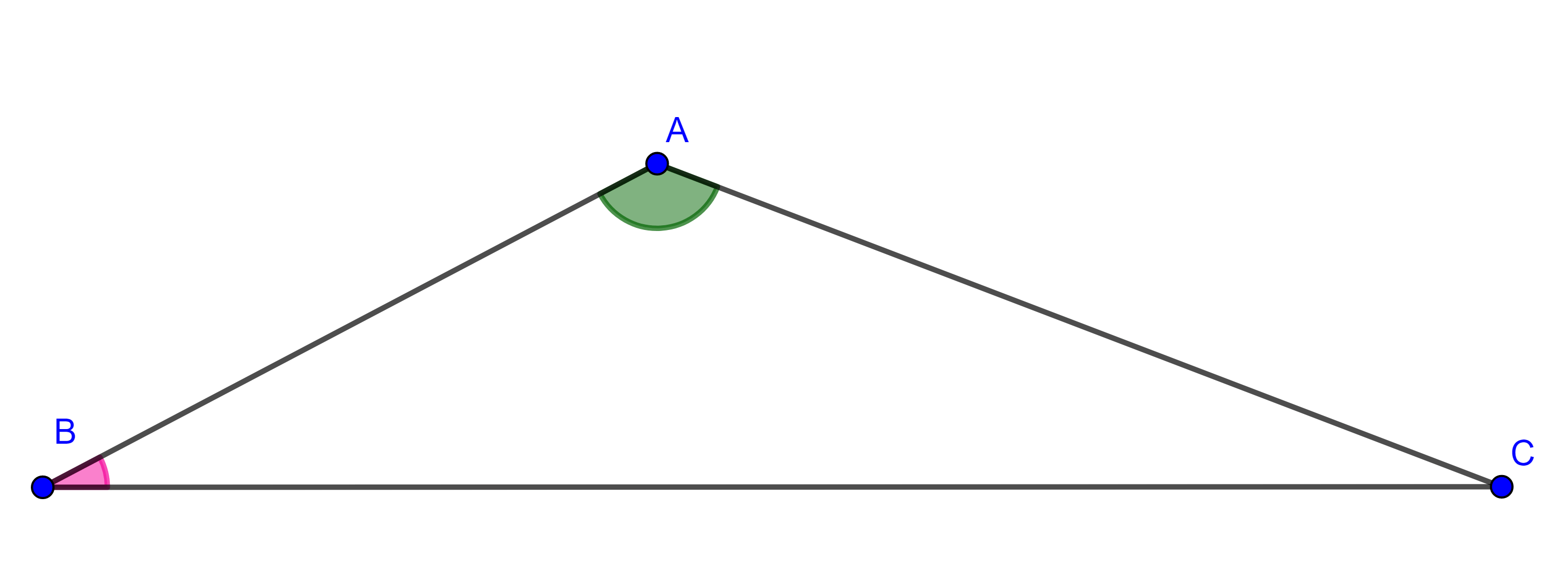
Proposición 1. En todo triángulo al mayor de los lados se opone el mayor de los ángulos.

Demostración. Sea $\triangle ABC$ tal que $AB > AC$, debemos mostrar que $\angle C > \angle B$.

Figura 1

Como $AB > AC$, podemos construir un punto $D \in AB$ tal que $AD = AC$, ya que $\triangle ADC$ es isósceles, por la proposición de la entrada anterior, se cumple $\angle CDA = \angle ACD$, de aquí se sigue que:

$\begin{equation} \angle C = \angle ACB > \angle ACD = \angle DCA. \end{equation}$

Como $\angle ADC$ es un ángulo exterior de $\triangle DBC$, entonces $\angle ADC$ es mayor que los ángulos internos de $\triangle DBC$, no adyacentes a él, en particular

$\begin{equation} \angle ADC > CBD = \angle B. \end{equation}$

De $(1)$ y $(2)$ se sigue que $\angle C > \angle B$.

$\blacksquare$

Corolario. En todo triángulo el ángulo mayor es opuesto al lado mayor.

Demostración. Sea $\triangle ABC$ tal que $\angle A > \angle B$, por demostrar que $BC > AC$. Supongamos lo contrario.

Figura 2

Caso 1. Si $BC = AC$, entonces $\triangle ABC$ es isósceles por lo que $\angle A = \angle B$, lo que es una contradicción a nuestra hipótesis.

Caso2. Si $BC < AC$, entonces por la proposición anterior $\angle B > \angle A$, esto nuevamente contradice la hipótesis.

Por lo tanto, no queda otra opción más que $\angle A > \angle B$.

$\blacksquare$

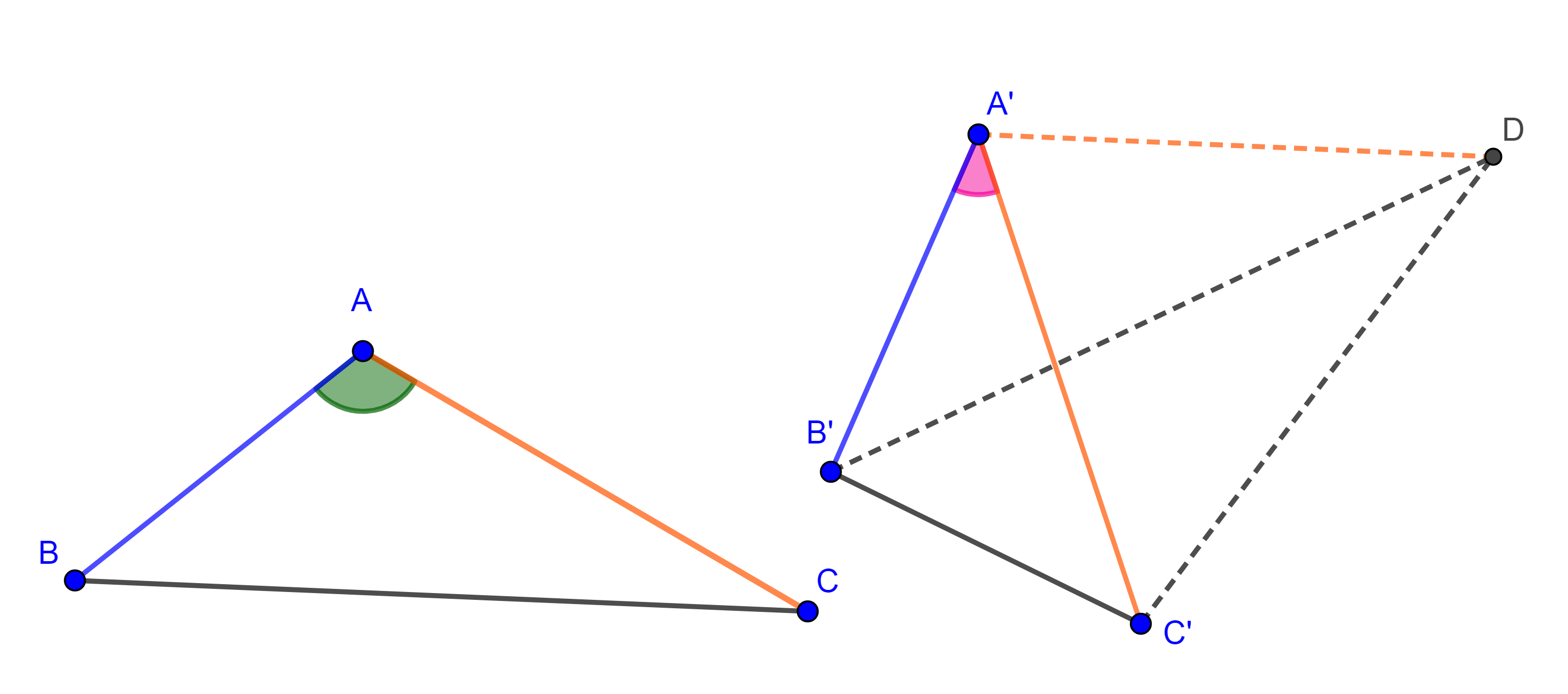
Proposición 2. Si dos lados de un triángulo son iguales a dos lados de un segundo triángulo, pero el ángulo comprendido entre el primer par de lados es mayor que el ángulo formado por los lados del segundo triangulo, entonces el lado restante del primer triángulo será mayor al tercer lado del segundo triangulo.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB = A’B’$, $AC = A’C’$ y $\angle A > \angle A’$, por demostrar que $BC > B’C’$.

Figura 3

Sobre $A’B’$ y tomando como vértice $A’$ construimos un ángulo igual a $\angle A$, y construimos $D$ tal que $A’D = AC$, entonces por criterio LAL, $\triangle ABC \cong \triangle A’B’D$ por lo que $B’D = BC$.

Notemos que $\triangle C’A’D$ es isósceles, entonces $\angle DC’A = \angle A’DC’$.

Ahora en $\triangle DC’B’$ tenemos $\angle DC’B’ = \angle A’C’B’ + \angle DC’A$,
$\Rightarrow \angle DC’B’ > \angle DC’A = \angle A’DC’$.

Pero $\angle A’DC’ = \angle A’DB’ + \angle B’DC’$,
$\Rightarrow \angle A’DC’ > \angle B’DC’$.

Por transitividad, $\angle DC’B’ > \angle B’DC’$.

Aplicando el corolario obtenemos $B’D > B’C’$, pero $B’D = BC$,
$\Rightarrow BC > B’C’$.

$\blacksquare$

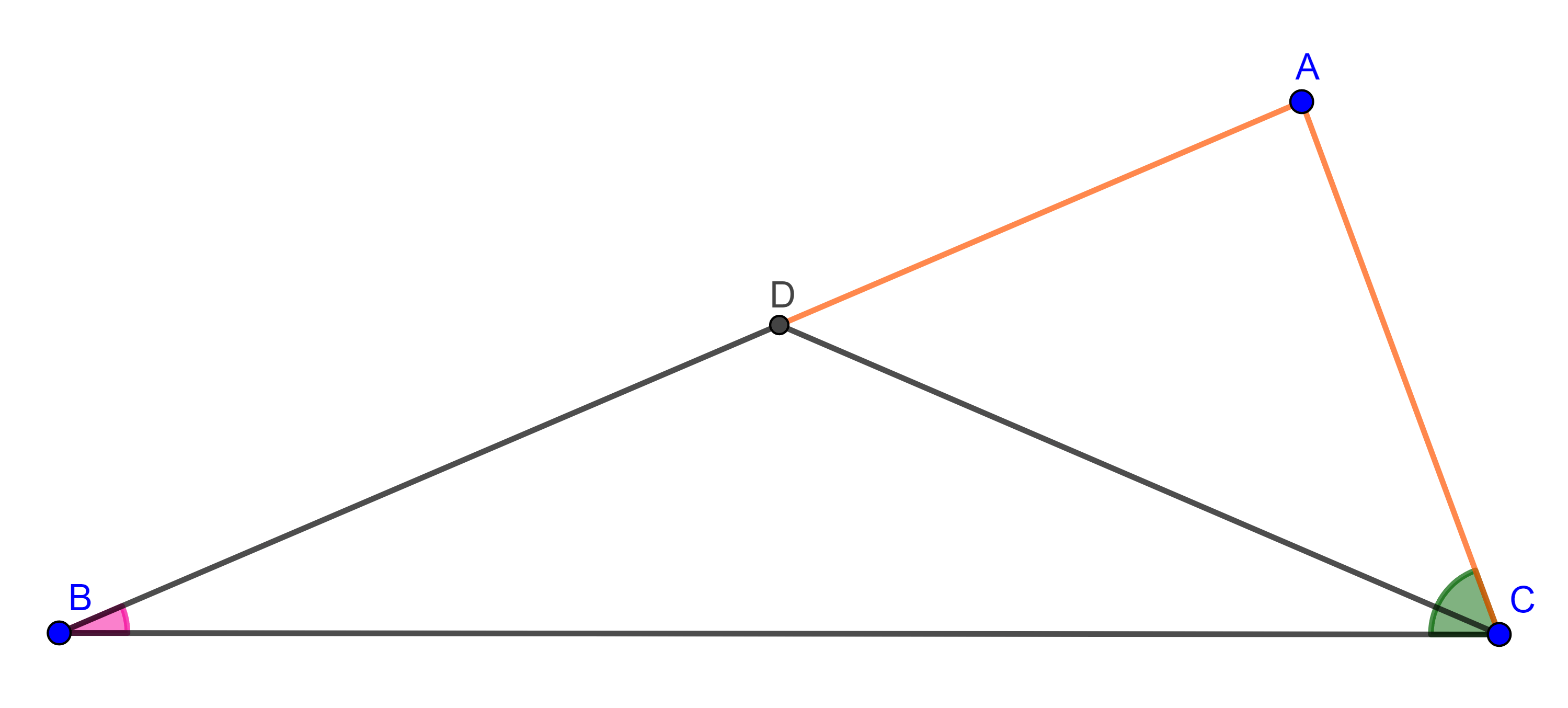
Teorema 1, desigualdad del triángulo. Para todo triangulo se cumple que la suma de cualesquiera dos de sus lados es mayor al lado restante.

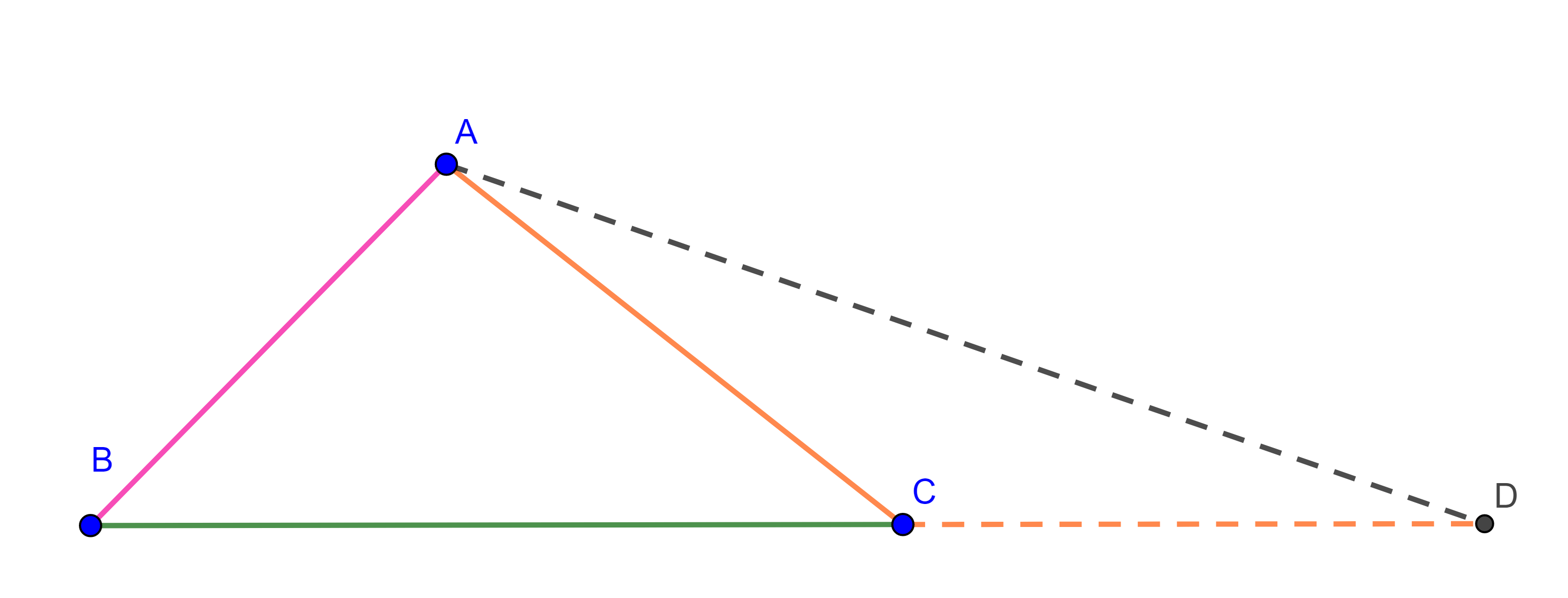
Demostración. Sea $\triangle ABC$, sobre la recta que pasa por $B$ y $C$, construimos un punto $D$ tal que $CD = AC$.

Figura 4

Como $\triangle ACD$ es isósceles, $\angle CAD = \angle ADC$, entonces en $\triangle ABD$ tenemos $\angle BAD > \angle CAD = \angle ADC = \angle ADB$, por el corolario anterior $BD > AB$.

Pero $BD = BC + CD = BC + AC$, por lo tanto, $AC + BC > AB$.

Las otras desigualdades, $AB + BC > AC$ y $AB + AC > BC$, se muestran de manera similar.

$\blacksquare$

El reciproco de este teorema también es cierto y lo mostramos a continuación.

Construcción de un triángulo y un ángulo

Teorema 2. Si $a$, $b$ y $c$ son tres números positivos tales que $a + b > c$, $a + c > b$ y $b + c > a$, entonces es posible construir un triángulo de lados $a$, $b$ y $c$.

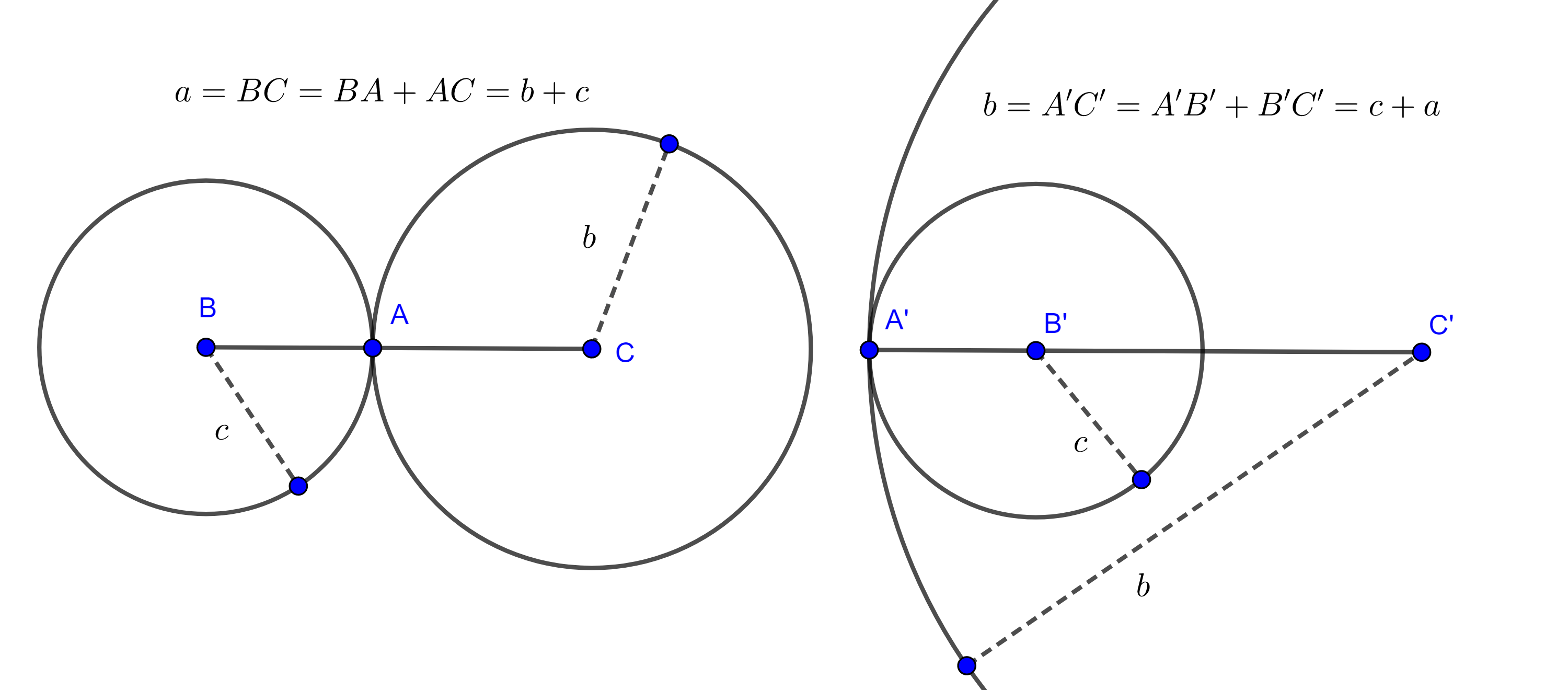
Demostración. Construyamos un segmento $BC$ de longitud $a$, trazamos una circunferencia con centro en $B$ y radio $c$ $(B, c)$, trazamos otra circunferencia con centro en $C$ y radio $b$ $(C, b)$.

$(B, c)$ y $(C, b)$ se intersecan en dos puntos, sea $A$ uno de estos puntos. $AB = c$ por ser radio de $(B, c)$, $AC = b$ por ser radio de $(C, b)$ y $BC = a$ por construcción.

Figura 5

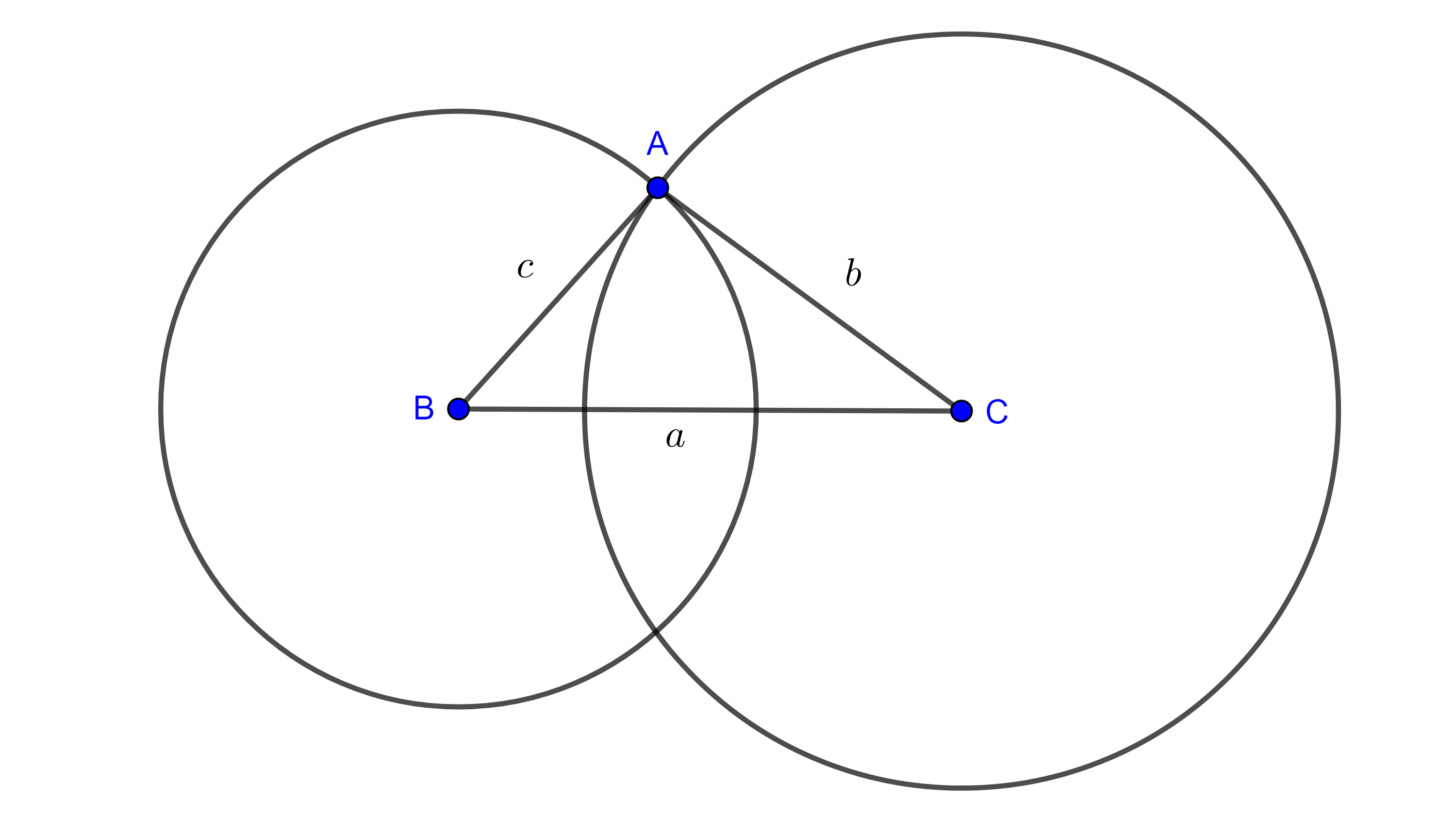
Notemos que si $(B, c)$ y $(C, b)$ se intersecaran en un solo punto entonces la intersección estaría sobre $BC$ o su extensión, y en tal caso se tendría alguna de las siguientes igualdades
$a = b + c$, $b = a + c$ o $c = a + b$, figura 6.

Figura 6

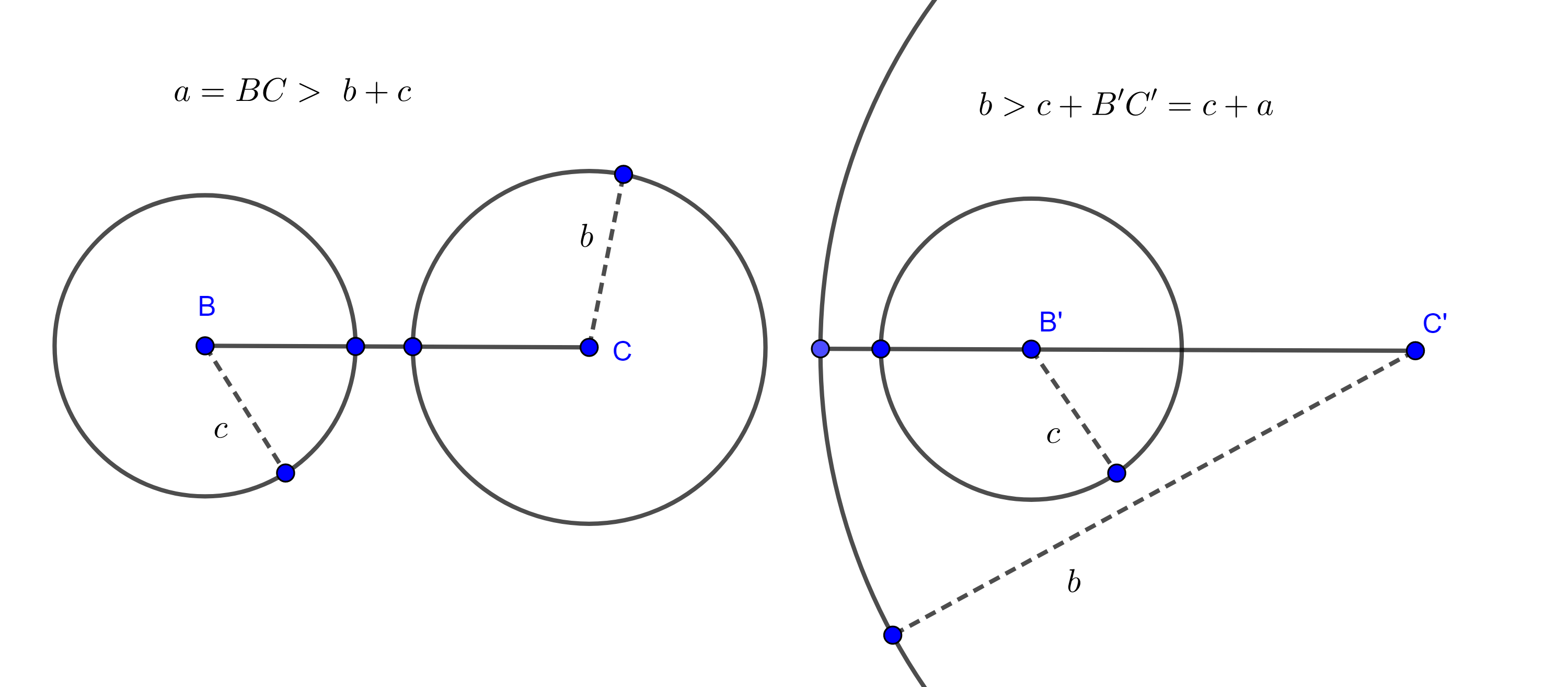
Y si $(B, c) \cap (C, b) = \varnothing$, entonces alguna de las cantidades seria mayor que la suma de las otras dos, $a > b + c$, $b > a + c$ o $c > a + b$, figura 7, lo que sería una contradicción a nuestras hipótesis.

Figura 7

Por lo tanto, $\triangle ABC$ es el triángulo buscado.

$\blacksquare$

Problema. Sobre una recta dada construir un ángulo igual a un ángulo dado.

Solución. Sea $\angle AOB$ el ángulo dado y $l$ la recta dada.

Con centro en $O$ y radio arbitrario $r > 0$ trazamos una circunferencia $(O, r)$ que corte a $OA$ en $C$ y a $OB$ en $D$.

Figura 8

Tomamos $O’ \in l$ y construimos una circunferencia con centro en $O’$ y radio $r$, $(O’, r)$, tomamos una de las intersecciones de $l$ con $(O’, r)$, digamos $D’$, trazamos otra circunferencia con centro en $D’$ y radio $CD$, $(D’, CD)$, sea $C’$ una de las intersecciones de $(O’, r)$ con $(D´, CD)$, entonces por criterio LLL $\triangle COD \cong \triangle C’O’D’$

Por lo tanto, $\angle AOB = \angle C’O’D’$.

$\blacksquare$

Lugar geométrico

Un lugar geométrico es un conjunto de puntos que cumplen un conjunto de condiciones dadas. Para probar que una figura geométrica es un lugar geométrico por lo general la prueba se divide en dos partes.

  • Probar que todos los puntos que satisfacen las condiciones pertenecen a la figura.
  • Probar que todos los puntos que pertenecen a la figura satisfacen las condiciones.

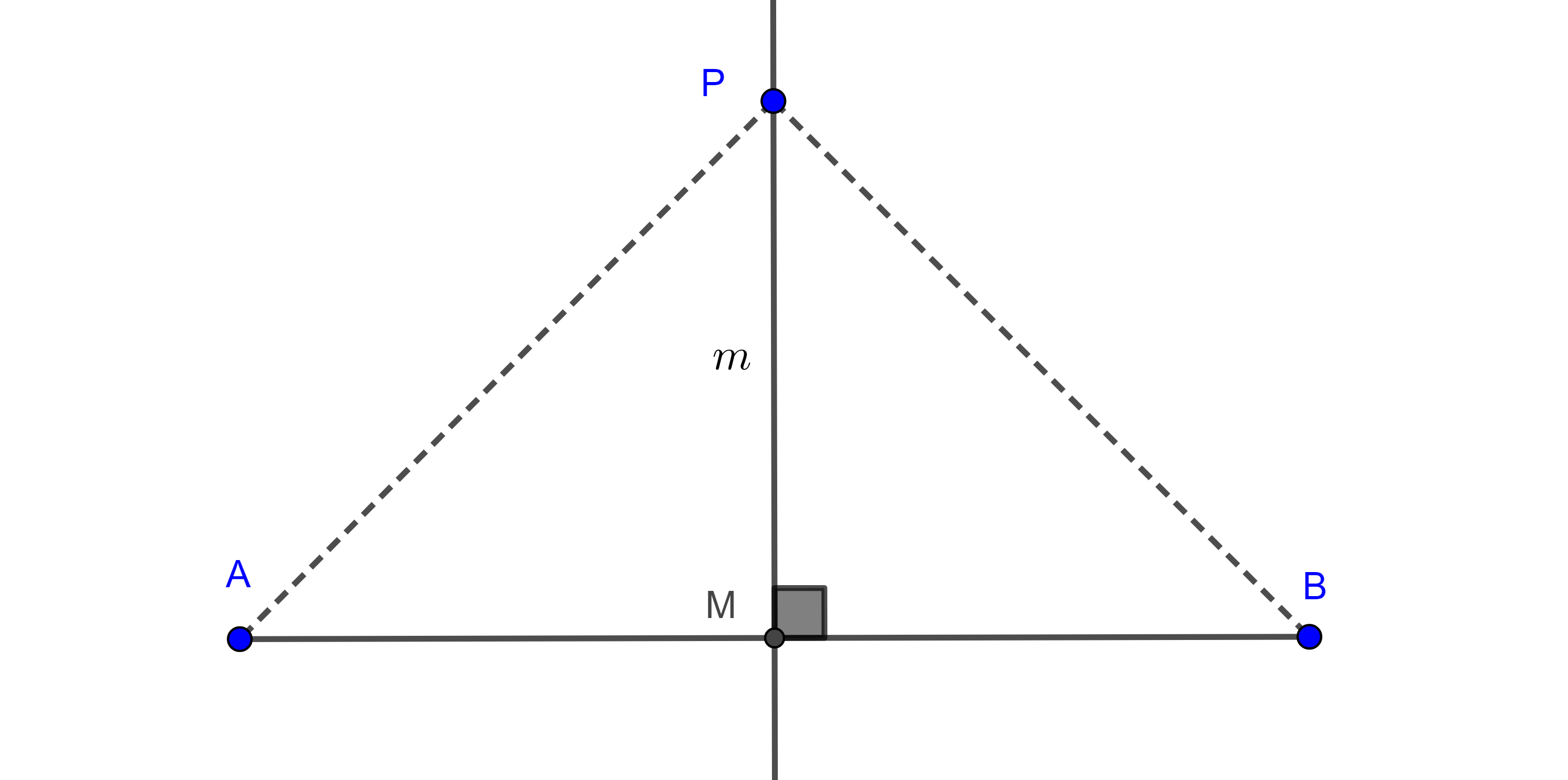
Teorema 3. El lugar geométrico de los puntos que equidistan a dos puntos dados, es la mediatriz del segmento que une los puntos dados.

Demostración. Sean $AB$ un segmento dado, $M$ el punto medio y $m$ la mediatriz de $AB$ respectivamente.

Figura 9

Primero vemos que los puntos en la mediatriz de $AB$  equidistan de $A$ y $B$.

Sea $P \in m$, por definición de mediatriz, $m \cap AB = M$ y $l \perp AB$.

Entonces por criterio LAL (lado, ángulo, lado), $\triangle PMA \cong \triangle PMB$, en consecuencia, $PA = PB$.

$\blacksquare$

Ahora veamos que todos los puntos que equidistan de $A$ y $B$, son los puntos en la mediatriz $m$ de $AB$.

Sea $P$ un punto que satisface las condiciones dadas, entonces $PA = PB$ y así $\triangle APB$ es isósceles, en la entrada anterior vimos que la mediatriz de un triángulo isósceles, pasa por el vértice que comparten los lados iguales, por lo tanto, $P \in m$.

$\blacksquare$

Definición. Definimos la distancia de un punto $P$ a una recta $l$ como la distancia entre $P$ y el pie de la perpendicular trazada desde $P$ a $l$.

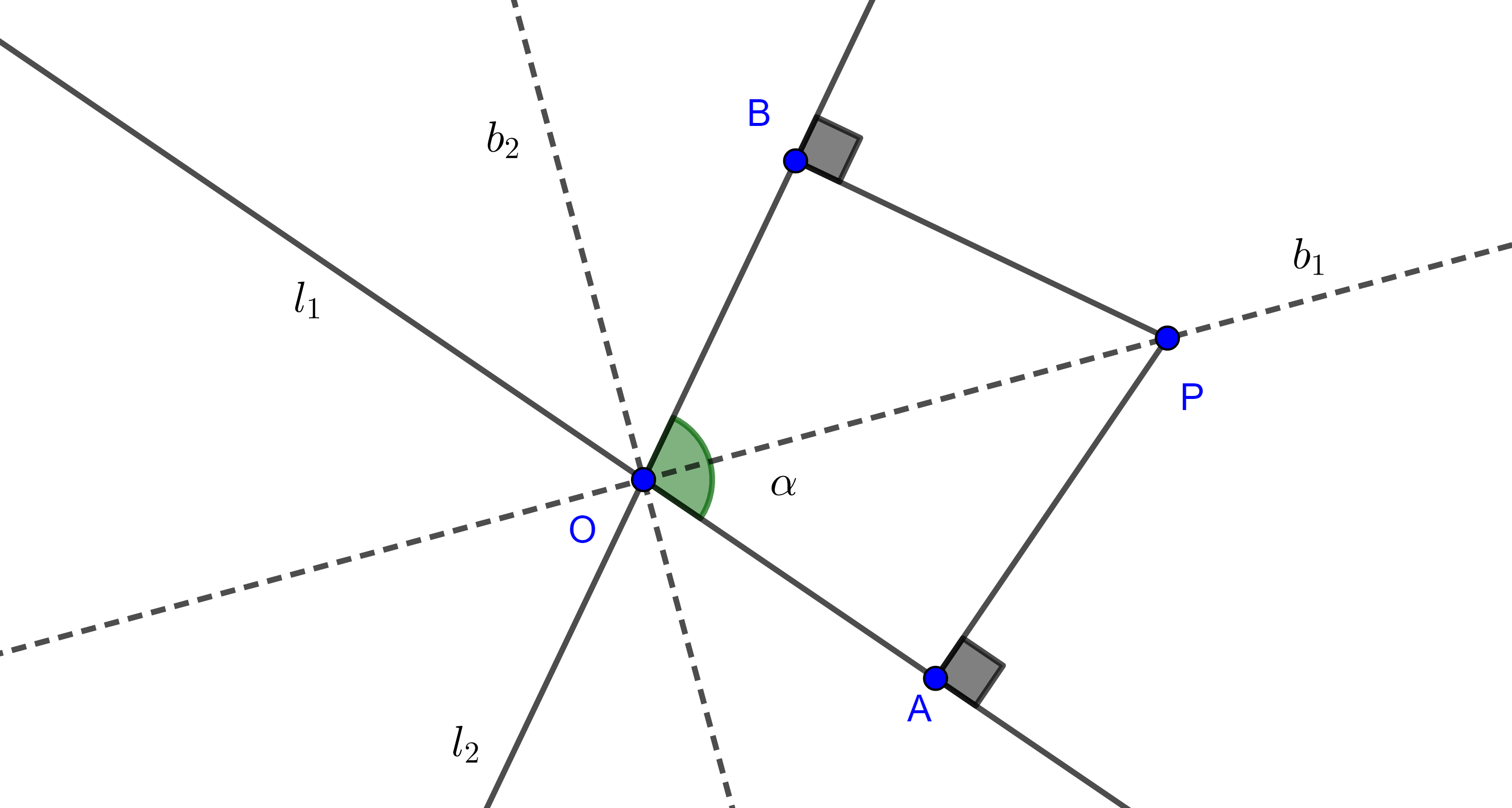
Teorema 4. El lugar geométrico de los puntos que equidistan a dos rectas que se intersecan son las bisectrices de los ángulos formados por las rectas.

Demostración. Sean $l_{1}$ y $l_{2}$, dos rectas que se intersecan en $O$, consideremos $b_{1}$ la bisectriz de uno de los ángulos formados por $l_{1}$ y $l_{2}$, digamos $\alpha$, y sea $b_{2}$ la bisectriz del ángulo suplementario a $\alpha$.

Primero veamos que todos los puntos en la bisectriz de $\alpha$ equidistan a $l_{1}$ y $l_{2}$.

Figura 10

Sea $P \in b_{1}$, y sean $A$ y $B$ las intersecciones de las perpendiculares trazadas desde $P$ a $l_{1}$ y $l_{2}$ respectivamente.

Como $b_{1}$ es bisectriz, $\angle AOP = \angle POB$, además $\angle PAO = \angle OBP = \dfrac{\pi}{2}$, como la suma de los ángulos internos de todo triángulo es constante entonces $\angle OPA = \angle BPO$.

Entonces en los triángulos $\triangle PAO$ y $\triangle PBO$, $\angle AOP = \angle POB$, $\angle OPA = \angle BPO$ y $OP$ es un lado común.

Por criterio LAL, $\triangle PAO \cong \triangle PBO$, por lo tanto $PA = PB$, así la distancia de $P$ a $l_{1}$ y a $l_{2}$ es la misma.

De manera análoga podemos ver que los puntos en $b_{2}$ son equidistantes a $l_{1}$ y $l_{2}$.

$\blacksquare$

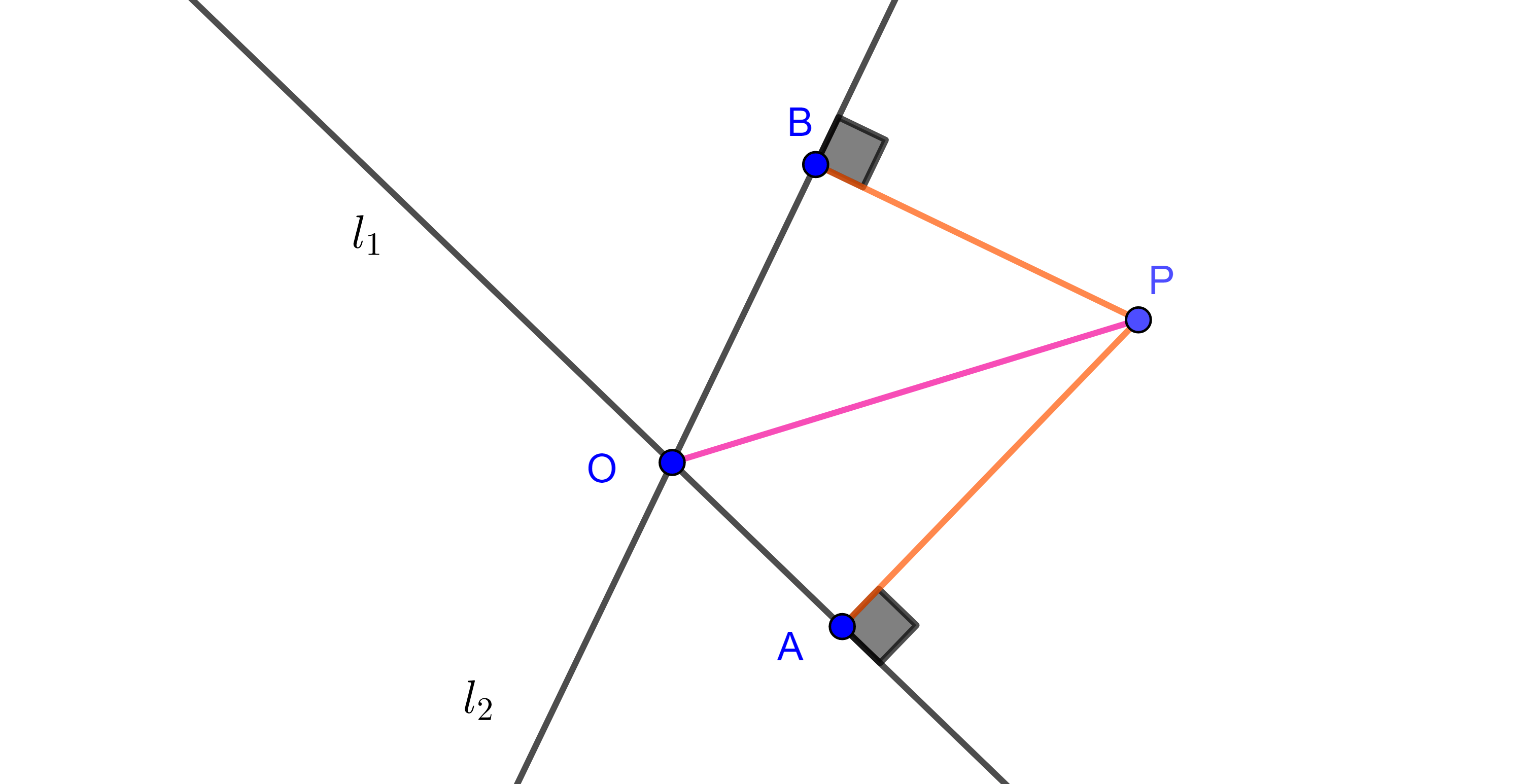
Ahora mostremos que todos los puntos que son equidistantes a $l_{1}$ y $l_{2}$ pertenecen a $b_{1}$ o $b_{2}$.

Sea $P$ un punto que satisface que $PA = PB$, donde $A$ y $B$ son los pies de las perpendiculares trazadas desde $P$ a $l_{1}$ y $l_{2}$ respectivamente.

Figura 11

Entonces $\triangle PAO$ y $\triangle PBO$ son triángulos rectángulos donde la hipotenusa es la misma, y por hipótesis tienen un cateto igual, $PA = PB$, por criterio hipotenusa – cateto $\triangle PAO \cong \triangle PBO$, en particular $\angle AOP =\angle POB$.

Notemos que las dos rectas dividen al plano en cuatro regiones distintas y en cada región podemos hacer el mismo procedimiento, pero dos rectas que se intersecan solo tienen dos bisectrices distintas.

Por lo tanto si $PA = PB$, entonces $P \in b_{1}$ o $P \in b_{2}$.

$\blacksquare$

Más adelante…

En al siguiente entrada estudiaremos a los paralelogramos y sus propiedades.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB = A’B’$, $AC = A’C’$ y $BC > B’C’$, muestra que $\angle A > \angle A’$.
  2. Sea $\square ABCD$ un cuadrado y $O$ un punto en el plano muestra que $OA < OB + OC + OD$.
  3. Sean $\triangle ABC$ y $A’$ un punto en el interior del triángulo, muestra que $AB + AC > A’B + A’C$ y que $\angle BA’C > \angle BAC$.
  4. En un poblado situado junto a un rio, cuyo borde es totalmente recto, hay un incendio en un punto $A$, la estación de bomberos se encuentra en un punto $B$ del mismo lado del río donde se dio el incendio, los bomberos necesitan pasar primero por el río para abastecerse de agua. ¿Qué punto $P$ en el borde del río hace que el trayecto $BP + PA$ sea mínimo?
  5. Muestra que si dos circunferencias se intersecan en un solo punto entonces el punto pertenece al segmento que une los centros o a su extensión.
  6. $i)$ Dados una recta y un punto en ella construye la perpendicular a la recta por el punto dado.
    $ii)$ Dados una recta y un punto fuera de ella construye la paralela a la recta por el punto dado.
    $iii)$ Dados una recta y un punto fuera de ella construye la perpendicular a la recta por el punto dado.
  7. $i)$ Dados una recta y un numero $a > 0$ encuentra el el lugar geométrico de los puntos cuya distancia a la recta es $a$.
    $ii)$ ¿Cuál es el lugar geométrico de los puntos cuya distancia a una circunferencia dada $(O, r)$ es una constante dada $b > 0$?

Entradas relacionadas

Fuentes

  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 9-12, 44-54.
  • Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 16-18.
  • Geometría interactiva
  • Geometry Help

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Lineal II: Demostración del teorema de Cayley-Hamilton

Por Julio Sampietro

8 respuestas

Introducción

En esta entrada demostraremos el teorema de Cayley-Hamilton. Daremos dos demostraciones de sabores muy diferentes. La primera demostración explota las propiedades de la matriz adjunta, mientras que la segunda echa mano de las familias especiales de las cuales calculamos el polinomio característico.

Primera demostración

La primera demostración del teorema de Cayley-Hamilton usa algunas propiedades de la matriz adjunta. Recordamos el teorema y lo demostramos a continuación:

Teorema. (Cayley-Hamilton)

Para cualquier matriz $A\in M_n(F)$ se cumple que

\begin{align*}
\chi_A(A)=O_n.
\end{align*}

Demostración. Sea $A\in M_n(F)$ y sea $B=XI_n-A\in M_n(K)$ dónde $K=F(X)$ es el campo de fracciones racionales en la variable $X$. Es decir, un elemento de $K$ es un cociente de la forma

\begin{align*}
\frac{A(X)}{B(X)}, \hspace{2mm} A(X),B(X)\in F[X]
\end{align*}

con $B$ no idénticamente cero.

Sea $C$ la matriz adjunta de $B$, es decir $C=\operatorname{adj}(B)$. Sus entradas son (por definición) los determinantes de las matrices de tamaño $(n-1)$ cuyas entradas son a su vez polinomios de grado a lo más $1$. Es decir cada entrada de $C$ es un polinomio de grado a lo más $n-1$. Luego, sea

\begin{align*}
c_{ij}= c_{ij}^{(0)}+c_{ij}^{(1)}X+\dots+c_{ij}^{(n-1)} X^{n-1}
\end{align*}

la $(i,j)$-ésima entrada de $C$, con $c_{ij}^{(0)},\dots, c_{ij}^{(n-1)}\in F$. Sea $C^{(k)}$ la matriz cuyas entradas son $c_{ij}^{(k)}$. Entonces

\begin{align*}
C=C^{(0)}+C^{(1)}X+\dots+ C^{(n-1)}X^{n-1}.
\end{align*}

Ahora, recuerda que

\begin{align*}
B\cdot C=B \cdot \operatorname{adj}(B)=\det(B)\cdot I_n=\chi_A(X)\cdot I_n.
\end{align*}

Es decir

\begin{align*}
(X I_n-A)\cdot \left(C^{(0)}+C^{(1)}X+\dots+C^{(n-1)}X^{n-1}\right)=\chi_A(X)\cdot I_n.
\end{align*}

Por otro lado, si escribimos a $\chi_A(X)$ como $\chi_A(X)=X^{n}+u_{n-1}X^{n-1}+\dots + u_0\in F[X]$, la igualdad anterior se convierte en

\begin{align*}
&-AC^{(0)}+(C^{(0)}-AC^{(1)})X+ (C^{(1)}-AC^{(2)})X^2+\dots + (C^{(n-2)}-AC^{(n-1)})X^{n-1}\\ &+C^{(n-1)}X^{n}= u_0 I_n+\dots + u_{n-1}I_nX^{n-1}+I_nX^{n}.
\end{align*}

Identificando los términos de cada coeficiente llegamos a

$$\left\{\begin{matrix}
-AC^{(0)}&= u_0 I_n,\\ C^{(0)}-AC^{(1)}&= u_1 I_n,\\ \vdots & \\ C^{(n-2)}-AC^{(n-1)}&=u_{n-1}I_n,\\ C^{(n-1)}&=I_n.
\end{matrix}\right.$$

Comenzando con la última igualdad, tenemos que $C^{(n-1)}=I_n$. Sustituyendo en la anterior llegamos a que $C^{(n-2)}=A+u_{n-1}I_n$, e inductivamente se cumple que

\begin{align*}
C^{(n-j-1)}=A^{j}+u_{n-1}A^{j-1}+\dots+u_1 I_n.
\end{align*}

En particular

\begin{align*}
C^{(0)}=A^{n-1}+u_{n-1}A^{n-2}+\dots+u_1 I_n.
\end{align*}

Multiplicando ambos lados por $A$ y usando que $-AC^{(0)}=u_0 I_n$ finalmente llegamos a

\begin{align*}
A^{n}+u_{n-1}A^{n-1}+\dots+ u_0 I_n=O_n.
\end{align*}

Pero esta igualdad no es nada más que $\chi_A(A)=O_n$, lo que concluye la prueba.

$\square$

Segunda demostración

Para la segunda demostración enunciaremos el teorema de una manera distinta pero equivalente (¿por qué?). Usaremos una estrategia fundada en el cálculo de polinomios característicos de familias conocidas de una entrada previa.

Teorema. (Cayley-Hamilton)

Sea $V$ un espacio vectorial de dimensión finita sobre $F$ y sea $T:V\to V$ una transformación lineal. Entonces $\chi_T(T)=0$.

Demostración. La idea es reducir el problema a transformaciones lineales para las que podemos calcular $\chi_T$ fácilmente. Sin embargo, los detalles son un poco complicados.

Fijemos $x\in V$. Para $m\geq 0$ fijamos

\begin{align*}
W_m=\operatorname{Span}(T^0(x), T^1(x), \dots, T^{m}(x)).
\end{align*}

Nota como $W_0\subset W_1\subset \dots \subset V$ y que $\dim W_m\leq \dim W_{m+1}\leq \dim V$ para todo $m\geq 0$. Entonces debe existir algún $m$ mínimo tal que $\dim W_{m-1}=\dim W_m$. Entonces como $W_{m-1}\subset W_{m}$ se tiene que $W_{m-1}=W_{m}$. Luego $T^{m}(x)\in W_{m-1}$, es decir existe una combinación lineal

\begin{align*}
T^{m}(x)=\sum_{k=0}^{m-1} a_k T^{k}(x).
\end{align*}

Nota que esto implica que $W_{m-1}$ es estable bajo $T$. Como $m$ es mínimo, los vectores $T^{0}(x),\dots, T^{m-1}(x)$ deben ser linealmente independientes: en efecto, si no lo fueran existiría una relación de dependencia entre $T^{m-1}(x)$ y términos de grado menor y así $\dim W_{m-1}=\dim W_{m-2}$ y entonces $m$ no sería mínimo. Por lo tanto forman una base para $W_{m-1}$ y respecto a esta base la matriz asociada a $T\vert_{W_{m-1}}$ es

\begin{align*}
A=\begin{pmatrix} 0 & 0 & 0 &\dots & 0 & a_0\\ 1 & 0 & 0 & \dots & 0 & a_1\\ 0 & 1 & 0 & \dots & 0 & a_2\\ \vdots & \vdots &\vdots &\ddots &\vdots &\vdots\\ 0 & 0 & 0 & \dots & 1 & a_{m-1}\end{pmatrix}.
\end{align*}

El polinomio característico de matrices como esta lo calculamos en esta entrada y es igual a $X^{m}-a_{m-1}X^{m-1}-\dots -a_0$. Entonces

\begin{align*}
\chi_{T\vert_{W_{m-1}}}(T)(x)= T^{m}(x)-\sum_{k=0}^{m-1}a_k T^{k}(x)=0.
\end{align*}

Pero como $W_{m-1}$ es $T-$estable, el polinomio característico de $T\vert_{W_{m-1}}$ divide al polinomio característico de $T$ (este es un ejercicio en la tarea moral de esta entrada) y por tanto $\chi_T(T)(x)=0$. Como $x$ fue arbitrario concluimos que $\chi_T(T)$ es la transformación cero.

$\square$

Más adelante…

En la próxima entrada veremos aplicaciones del teorema de Cayley-Hamilton.

Tarea moral

  1. Supón que $T:V\to V$ es una transformación lineal y $V$ es de dimensión finita. Demuestra que si $W$ es un subespacio $T$-estable de $V$ entonces $\chi_{T\vert_{W}}(X)$ divide a $\chi_{T}(X)$. Sugerencia. Considera una base de $W$, extiéndela a una base de $V$. ¿Cómo se ve la matriz asociada a $T$ en esta base?
  2. Explica por qué las dos versiones que dimos del teorema de Cayley-Hamilton son equivalentes.
  3. Demuestra la propiedad de la matriz adjunta que se menciona en la primera demostración.
  4. Sean $A,B,C\in M_2(\mathbb{C})$ matrices tales que $AC=CB$ y $C\neq O_n$. Demuestra que para cualquier polinomio $P$ se cumple que $P(A)C=CP(B)$. Usando esto y escogiendo un polinomio adecuado, deduce que $A$ y $B$ tienen un eigenvalor en común. Sugerencia: Usa el teorema de Cayley-Hamilton.
  5. Sea la matriz
    \begin{align*}
    A=\begin{pmatrix}
    0 & 2 & 0\\
    1 & 1 & -1\\
    -1 & 1& 1
    \end{pmatrix}.
    \end{align*}
    Usa el teorema de Cayley-Hamilton para calcular $A^{1000}$. Sugerencia: El teorema de Cayley-Hamilton te debería dar una relación entre algunas potencias de $A$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Cálculo Diferencial e Integral I: Repaso. Inducción matemática

Por Karen González Cárdenas

4 respuestas

Introducción

En el curso de Álgebra Superior I se presenta al conjunto de los números naturales ($\mathbb{N}$). Posteriormente, en el curso de Álgebra Superior II se habla mucho más de ellos: se construyen a partir de teoría de conjuntos y se muestran desde los fundamentos muchas de sus propiedades.

Nosotros no nos enfocaremos en los aspectos anteriores, pero sí aprovecharemos que dicho conjunto posee una propiedad muy importante: el principio de inducción matemática. Como mencionamos en la entrada pasada, este método de demostración es aplicado frecuentemente en las pruebas en las que se desea probar que alguna propiedad se satisface para todos los números naturales.

En Cálculo Diferencial e Integral I haremos uso de la Inducción matemática constantemente, por lo que en esta entrada haremos una revisión a lo necesario para nuestro curso.

Efecto dominó

Imagina que te han regalado una cantidad infinita de fichas de dominó y que has decidido acomodarlas en una fila, una tras otra. Tu propósito al terminar de acomodarlas es dejar caer todas las fichas, por ello consideras empujar la primera ficha para que, al caer ésta, choque con la segunda provocando su caída, y así sucesivamente.

El riesgo del Efecto Dominó: Micro triangulaciones y sus ventajas en Trabajos de Investigación

Una vez que has decidido poner en marcha tu plan y empujas la ficha 1, te comienzas a preguntar: ¿Cómo puedo asegurar que la ficha 1,000 caerá si sólo he visto caer las primeras 50 fichas? ¿Y que hay de la ficha 1,000,000?

El Principio de Inducción es el que daría respuesta a tu pregunta. El razonamiento de este principio sustenta que si sabes que el procedimiento se ha cumplido para las primeras 50 fichas, en consecuencia cada ficha irá cayendo al final para cualquier ficha que consideres.

Ahora que tenemos una noción de su comportamiento, veremos la definición formal.

Principio de Inducción matemática

Cada autor decide si el conjunto de los números naturales considerará o no al cero como uno de sus elementos. En nuestro caso, tomaremos al cero como un número natural de aquí en adelante.

Definición: Sea $P$ una propiedad y $n\in \mathbb{N}$. Decimos que la propiedad $P$ es válida para todos los naturales si tenemos que:

  1. La propiedad $P$ se cumple para $0$.
  2. Si la propiedad $P$ se cumple para $n \Rightarrow$ la propiedad también se cumple para $n + 1$.

El punto número 1 es conocido como Base de Inducción. El antecedente del punto número 2 es llamado Hipótesis de Inducción y su consecuente Paso Inductivo. En algunos problemas basta con demostrar la afirmación únicamente cuando $n\geq 1$. En estos casos, la base de inducción debe de cumplirse para el natural $1$.

A continuación veremos un par de ejemplos para ver cómo funciona dicho principio.

Ejemplo: Demuestra utilizando Inducción matemática la siguiente fórmula.

$$1+2+ \ldots + n = \frac{n(n+1)}{2}, \quad \forall n\in \mathbb{N}$$

Observación: $\therefore$ se lee «por lo tanto» y $\forall$ significa «para todo».


Demostración: Haremos inducción sobre $n$.
Base de Inducción.- Verificamos que la fórmula se cumple cuando $n=1$

\begin{align*}
\frac{1(1+1)}{2}&= \frac{1(2)}{2}\\
&=\frac{2}{2}\\
&= 1
\end{align*}
Lo cual es cierto.

Hipótesis de Inducción.- Suponemos que la fórmula se cumple para cualquier $k\in \mathbb{N}$ así:
$$1+2+ \ldots + k = \frac{k(k+1)}{2}$$

Paso Inductivo.- Queremos probar que la fórmula se cumple para $k+1$, por lo que bastará probar la siguiente igualdad:
$$1+2+ \ldots + k+ (k+1) = \frac{(k+1)((k+1)+1)}{2}$$ es decir, $$1+2+ \ldots + k+ (k+1) = \frac{(k+1)(k+2)}{2}$$

Desarrollaremos el lado izquierdo de la igualdad sustituyendo lo que tenemos en la Hipótesis de Inducción, así queda lo siguiente:
\begin{align*}
1+2+ \ldots + k+ (k+1) &= \frac{k(k+1)}{2} + (k+1)\\
&= \frac{k(k+1)}{2}+ \frac{2(k+1)}{2}\\
&=\frac{k(k+1)+ 2(k+1)}{2}\\
&=\frac{(k+1)(k+2)}{2}
\end{align*}


$$\therefore 1+2+ \ldots + n = \frac{n(n+1)}{2}, \quad \forall n\in \mathbb{N}$$

$\square$

Ejemplo: Demuestra que

$2^{n} < n! \quad$ si $\quad n \geq 4$

Recordemos que $n!$ es llamado $n$ factorial y que está definido como: $n! = 1\cdot 2 \cdot \ldots \cdot (n-1)(n)$.


Demostración: Aplicando inducción sobre $n$, vemos que dada la condición de $n \geq 4$, bastaría probar que:
$$2^{n+3} < (n+3)!, \quad \forall n \in \mathbb{N}$$

La razón de considerar $n+3$ es porque queremos todos aquellos naturales mayores o iguales que 4, al sustituir valores para $n$:

\begin{align*}
n=1 &\Rightarrow 1+3\\
&\Rightarrow 4\\
\\
n=2 &\Rightarrow 2+3\\
&\Rightarrow 5\\
\\
n=3 &\Rightarrow 3+3\\
&\Rightarrow 6\\
&\vdots
\end{align*}
Notamos que los números que obtenemos lo cumplen, aún si continuáramos con dicha sustitución, por esa razón podemos proceder sin problemas.

Y ya que $n$ factorial está definido como: $n! = 1\cdot 2 \cdot \ldots \cdot (n-1)(n)$ tenemos que $4!= 4\cdot 3\cdot 2\cdot 1 =24$.

Base de Inducción.- Verificamos que la desigualdad se cumple para $n=1$. Así sustituyendo vemos:
$$2^{1+3} = 2^{4}=16$$ y que $$(1+3)! = 4! =24$$
Por lo que se cumple la desigualdad: $$2^{1+3} < (1+3)!$$

Hipótesis de Inducción.- Suponemos que la desigualdad se cumple para cualquier $k \in \mathbb{N}$.
$$2^{k+3} < (k+3)!$$

Paso Inductivo.- Queremos probar que la desigualdad se cumple para $k+1$, esto sería:
$$2^{(k+1)+3} < ((k+1)+3)!$$ que es lo mismo que, $$2^{k+4} < (k+4)!$$

Vemos que al reescribir la desigualdad anterior tenemos:
$$2\cdot 2^{k+3} < (k+3)! (k+4)$$
Por hipótesis de inducción sabemos se cumple $2^{k+3} < (k+3)!$, por lo que si se cumple la desigualdad $2< k+4$ terminamos.

$P.d:$ $$2< k+4,\quad \forall k\in \mathbb{N}$$
Demostración: Utilizaremos inducción sobre $k$.
Base Inducción.- Vemos para $k=1$ que $$2< 1+4 = 5$$ se cumple.

Hipótesis de Inducción.- Suponemos que es cierta la desigualdad $2< k+4$ para cualquier $k$.

Paso Inductivo.- Queremos probar que para $k+1$ se cumple la desigualdad $2< (k+1)+4$.
Observemos que $(k+1)+4= (k+4)+1$ que es el sucesor de $k+4$ por lo que cumple $k+4 < (k + 4)+1$.
Así haciendo uso de lo anterior y de la Hipótesis de Inducción se tiene lo siguiente:
$$2< k+4 < (k+4)+1 \quad \Rightarrow \quad2 < (k+4)+1$$
$$\therefore \quad 2 < (k+1)+4$$
$$\therefore \quad 2 < k+4 , \quad \forall k\in \mathbb{N}$$

$\square$

Por lo que ya podemos afirmar que $$2\cdot 2^{k+3} < (k+3)! (k+4).$$
Así concluimos: $$2^{n+3} < (n+3)!, \quad \forall n \in \mathbb{N}.$$

$\square$


Observación: $P.d.$ es una abreviación de «Por demostrar».

Principio de Inducción Fuerte

Existe otra forma de inducción, que debemos recordar por su utilidad, conocida como: Inducción Fuerte, que es consecuencia del Principio de Inducción que vimos antes.

Definición (Principio de Inducción fuerte): Consideremos $P$ una propiedad y $n , l \in \mathbb{N}$. Decimos que la propiedad $P$ es válida para todos los naturales si tenemos que:

  1. $P$ se cumple para $0$.
  2. Si $P$ se cumple para cualquier $l \leq n \Rightarrow P$ se cumple para $n+1$.

Ejemplo: Todos los números positivos $n >1$ son producto de primos.

Demostración: Utilizaremos Inducción fuerte sobre $n$.
Base de Inducción.- Como tenemos la condición $n>1$ consideraremos $n=2$.
Observamos que $2 = 2$ es un producto de primos ( 2 cumple la definición de ser primo).

Hipótesis de Inducción.- Supongamos que todos los números desde 2 hasta $k$ cumplen ser producto de números primos.

Paso Inductivo.- Queremos probar que $k+1$ es producto de números primos.
Recordemos que todo número es primo o compuesto, por lo que tenemos que considerar los siguientes casos.

Caso 1: $k+1$ es primo.
Como $k+1 = k+1$ se sigue que es producto de números primos y se cumple lo que queremos.

Caso 2: $k+1$ es compuesto.
Esto quiere decir que podemos expresar a $k+1$ como un producto de la siguiente manera:
$$k+1= a\cdot b$$ donde $k+1 > a \quad$ y $\quad b > 1$.
Observemos que las últimas desigualdades implican que $k \geq a,b \geq 2$, así por Hipótesis de Inducción $a$ y $b$ cumplen ser producto de números primos.
$\therefore \quad k+1$ es producto de primos.
$\therefore \quad$ Todos los números positivos $n >1$ son producto de primos.

$\square$

Más adelante

Ahora que hemos terminado con el repaso de Inducción matemática. En la siguiente entrada comenzaremos a ver un conjunto de números de suma importancia para el Cálculo: los reales.

Tarea moral

A continuación, encontrarás ejercicios en los que pondrás en práctica el Principio de Inducción matemática:

  1. Probar que: $n^{3} – n$ es un múltiplo de 6, $\forall n\in \mathbb{N}$.
  2. Utiliza inducción para probar la siguiente igualdad:
    $$1^{2}+2^{2}+\ldots + n^{2} = \frac{n(n+1)(2n+1)}{6}, \quad \forall n\in \mathbb{N}$$
  3. Demuestra que:
    $$1+3+5+7+\ldots +2n-1 = n^{2}, \quad \forall n\in \mathbb{N}$$
  4. Demuestra por inducción sobre $n$, con $r \neq 1$:
    $$1+r+r^{2}+ \ldots +r^{n} = \frac{1-r^{n+1}}{1-r}$$
  5. Utiliza inducción para probar la siguiente igualdad:
    $$2+5+8+ \ldots+ (3n-1)= \frac{n(3n+1)}{2}$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Lineal II: Teorema de Sylvester

Por Diego Ligani Rodríguez Trejo

5 respuestas

Introducción

En entradas anteriores estudiamos las formas bilineales y las cuadráticas. También vimos las matrices que las representan. Introdujimos una noción de congruencia de matrices relacionada con todo esto. Y vimos que la congruencia de matrices preserva una noción de positividad para matrices. Ahora daremos un paso más y veremos que de hecho la congruencia de matrices preserva más que sólo eso.

Para ello, introduciremos la noción de la signatura de una matriz. A grandes rasgos, esta noción nos dice «qué tan positiva» es una matriz simétrica. Para definir esta noción, lo haremos primero para las matrices diagonales. Luego lo definiremos para todas las matrices simétricas a través del teorema que demostramos la entrada anterior. Toda la discusión la haremos en el caso real. El caso complejo tiene sus versiones análogas, que quedarán descritas en los ejercicios.

Signatura de una matriz diagonal

Comenzamos con la siguiente definición.

Definición. Sea $A$ una matriz diagonal en $M_n(\mathbb{R})$. Sea $P$ la cantidad de entradas positivas en la diagonal y $N$ la cantidad de entradas negativas en la diagonal. A $(P,N)$ le llamamos la signatura de $A$.

En cierto sentido, la signatura generaliza tanto la noción de rango, como la noción de positividad y de positividad definida. Esto queda plasmado en las siguientes observaciones.

Observación. Una matriz diagonal ya está en forma escalonada reducida. Y el rango de una matriz en forma escalonada reducida coincide con la cantidad de renglones no cero. Así, si la signatura de una matriz diagonal es $(P,N)$, entonces su rango es $P+N$.

Observación. Por lo que vimos en la entrada anterior, una matriz diagonal en $M_n(\mathbb{R})$ es positiva si y sólo si ninguna de sus entradas diagonales es negativa. Esto pasa si y sólo si su signatura es de la forma $(k,0)$ para algún $0\leq k\leq n$.

Observación. Por un resultado análogo al de la entrada anterior, una matriz diagonal es $M_n(\mathbb{R})$ es positiva definida si y sólo si todas sus entradas diagonales son positivas. Esto pasa si y sólo si su signatura es $(n,0)$.

La signatura es invariante bajo congruencias

El resultado clave de esta entrada es el siguiente lema.

Lema. Sean $A$ y $B$ matrices diagonales en $M_n(\mathbb{R})$ congruentes entre sí. Entonces la signatura de $A$ y la de $B$ son iguales.

Demostración. Llamemos $(P,N)$ a la signatura de $A$ y $(Q,M)$ a la signatura de $B$.

Como $A$ y $B$ son congruentes, entonces representan a una misma forma cuadrática $q:\mathbb{R}^n\to \mathbb{R}$, pero quizás en diferentes bases. Sea $\alpha$ la base en la cual $q$ tiene matriz $A$ y $\beta$ la la base en la cual $q$ tiene matriz $B$. Sea $b$ la forma polar de $p$.

Como la signatura de $A$ es $(P,N)$, entonces $q$ es positivo (resp. negativo, cero) para $P$ (resp. $N$, $n-P-N$) elementos de la base $\alpha$. Tenemos algo análogo para $B$. Así, podemos llamar a las bases

\begin{align*}
\alpha&=\{a^+_1,\ldots,a^+_P,a^-_1,\ldots, a^-_N,a^0_1\ldots, a^0_{n-P-N}\},\\
\beta&= \{b^+_1,\ldots,b^+_Q,b^-_1,\ldots, b^-_M,b^0_1\ldots, b^0_{n-Q-M}\},\\
\end{align*}

en donde $q$ aplicado a alguno de estos elementos tiene el signo del superíndice.

Demostraremos que $P=Q$ por contradicción. Supongamos que no. Sin perder generalidad, $P>Q$. Consideremos $V$ el subespacio de $\mathbb{R}^n$ generado por los vectores $a^+_1,\ldots,a^+_P$ y $W$ el subespacio de $\mathbb{R}^n$ generado por los vectores $b^-_1,\ldots, b^-_M,b^0_1\ldots, b^0_{n-Q-M}.$ Estos espacios tienen dimensión $P$ y $n-Q$ respectivamente. Como $P>Q$, tenemos que $P+(n-Q)>Q+(n-Q)=n$. Así, los espacios $V$ y $W$ tienen intersección no trivial, y por lo menos hay un vector $v$ distinto de $0$ en $V\cap W$. ¿Cuánto vale $q(v)$?

Por un lado, $v$ está en $V$ así que es combinación lineal de elementos $a^+_i$: $$v=\sum_{i=1}^P r_i a^+_i.$$ De este modo:

\begin{align*}
q(v)=\sum_{i=1}^P r_i^2 q(a^+_i) + 2\sum_{i=1}^P\sum_{j=1}^P b(a^+_i,a^+_j).
\end{align*}

El primer sumando es positivo pues $q$ es positivo en todo $a^+_i$. El segundo sumando es cero pues cada término es $0$ por ser una entrada $(i,j)$ con $i\neq j$ de la matriz diagonal $A$. Así, $q(v)>0$.

Similarmente, $v$ está en $W$ así que es combinación lineal de elementos $b^-_i$ y elementos $b^0_i$, de donde se puede mostrar que $q(v)\leq 0$.

Hemos encontrado una contradicción que surgió de suponer $P\neq Q$, así que $P=Q$. De manera análoga se demuestra que $N=M$. Así, la signatura de $A$ y de $B$ debe ser la misma.

$\square$

Signatura para matrices simétricas

En la entrada anterior vimos que cualquier matriz simétrica en $M_n(\mathbb{R})$ es congruente a alguna matriz diagonal. Es posible que sea congruente a más de una matriz diagonal.

Definición. Sea $A$ una matriz simétrica en $M_n(\mathbb{R})$. Sea $D$ una matriz diagonal congruente a $A$. Definimos la signatura de $A$ como la signatura de $D$.

El lema de la sección anterior nos permite asegurarnos de que la siguiente definición está bien hecha. Si $A$ fuera congruente a dos matrices diagonales $D$ y $E$, entonces $D$ y $E$ serían congruentes entre sí. De este modo, la signatura de $A$ no cambia si la tomamos con respecto a $D$ o con respecto a $E$.

Pensemos que dos matrices $A$ y $B$ son congruentes entre sí. Sean $D$ y $E$ matrices diagonales congruentes a $A$ y $B$ respectivamente. Por transitividad, $D$ y $E$ son congruentes, así que tienen la misma signatura. Así, $A$ y $B$ tienen la misma signatura.

Una última observación es la siguiente. Si $A$ y $B$ son simétricas y congruentes entre sí, entonces están relacionadas mediante un producto con matrices invertibles. Como el producto por matrices invertibles no afecta el rango, concluimos que $A$ y $B$ tienen el mismo rango. Juntando esto con observaciones anteriores, una matriz simétrica $A$ de signatura $(P,N)$ tiene rango $P+N$.

Resumimos todo esto en el siguiente resultado.

Proposición. Sean $A$ y $B$ matrices simétricas.

  • Si la signatura de $A$ es $(P,N)$, entonces su rango es $P+N$.
  • Si $A$ y $B$ son congruentes, entonces tienen la misma signatura. En particular:
    • Tienen el mismo rango.
    • Si una es positiva, la otra también lo es.
    • Si una es positiva definida, la otra también lo es.

El teorema de Sylvester

Enunciemos las versiones análogas a lo anterior en términos de formas cuadráticas. Comencemos con el teorema de Gauss. Tomemos una forma cuadrática $q$ de $\mathbb{R}^n$ y escribámosla como $$q=\sum_{i=1}^r a_i l_i^2$$ con $a_1,\ldots,a_r$ reales y $l_1,\ldots,l_r$ formas lineales linealmente independientes.

Podemos quitar todos los términos con $a_i=0$ sin afectar la igualdad. Además, si $a_i$ es positivo podemos factorizarlo en $l_i^2$ para definir $m_i=(\sqrt{a_i}l_i)^2$, y si $a_i$ es negativo podemos factorizar $-a_i$ en $l_i^2$ para obtener $m_i=(\sqrt{-a_i}l_i)^2$. En otras palabras, de cualquier expresión de Gauss podemos llegar a una de la forma $$q=\sum_{i=1}^r \epsilon_i m_i^2,$$

en donde los $\epsilon_i$ son $1$ o $-1$. Si tenemos $P$ valores de $\epsilon_i$ iguales a $1$ y $N$ valores de $\epsilon_i$ iguales a $-1$ diremos que la signatura de $q$ es $(P,N)$ y que el rango de $q$ es $P+N$.

¿Por qué esto está bien definido? Porque ya vimos que cada forma de Gauss de $q$ da una base en la cual la matriz que representa a $q$ es diagonal. Las entradas de la diagonal son los coeficientes de la forma de Gauss. Dos matrices que salen así son congruentes, así que por el lema de la sección anterior tienen la misma signatura. Esto garantiza que en ambas expresiones de Gauss de las de arriba hay la misma cantidad de $1$s y $-1$s.

El gran resumen de todo esto es el siguiente teorema.

Teorema (ley de inercia de Sylvester). Sea $q$ una forma cuadrática de $\mathbb{R}^n$. Entonces existen $\epsilon_1,\ldots,\epsilon_r$ iguales a $1$ o a $-1$ y formas lineales $l_1,\ldots,l_r$ linealmente independientes tales que $$q=\sum_{i=1}^r \epsilon_i l_i^2.$$

Cualesquiera dos expresiones de este estilo tienen la misma cantidad de coeficientes positivos, y la misma cantidad de coeficientes negativos.

Dato curioso: ¿Por qué ley de inercia?

En esta entrada nos hemos referido al teorema de Sylvester de dos maneras intercambiables: teorema de Sylvester y ley de inercia de Sylvester. La intuición diría que quizás existe alguna relación con la física. Quizás es porque algún uso especial de este teorema lo hace importante para el cálculo de la inercia. Esto no es así.

El nombre, curiosamente, viene de esta frase de Sylvester:

Este número constante de signos positivos que se asocian a una función cuadrática bajo cualquier transformación […] puede ser llamado, convenientemente, su inercia, hasta que una mejor palabra sea encontrada.

J. J. Sylvester, On the Theory of the Syzygetic Relations… (1853)

Aparentemente no se encontró una mejor palabra y ahora es el térimo que se usa. Interpretando un poco lo que dice Sylvester, la inercia se refiere a la resistencia de un cuerpo de cambiar de estado. Así, tal vez Sylvester pensó en la «resistencia a cambiar» de la signatura de una forma cuadrática bajo cambios de base.

Más adelante…

Hay mucha más teoría que se puede enunciar y demostrar para formas cuadráticas en general. Por ahora detendremos nuestra exploración hasta aquí, y ya sólo nos enfocaremos en las formas bilineales simétricas y positivas, es decir, en los productos interiores. Queremos enunciar y demostrar varios resultados para espacios con producto interior y para espacios euclideanos.

Dos conceptos que estudiaremos a continuidad son el de dualidad y el de ortogonalidad. Esto nos abrirá las puertas a entender correctamente algunos tipos de transformaciones lineales muy importantes, como las transformaciones simétricas, las normales y las ortogonales.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso. Sin embargo, ayudan para repasar los conceptos vistos en esta entrada.

En los siguientes ejercicios, usa el algoritmo de Gauss para escribir cada forma como combinación cuadrática de formas lineales linealmente independientes. Además encuentra su rango y signatura.

  1. Encuentra el rango y la signatura de la forma cuadrática$q : \mathbb{R}^4 \rightarrow \mathbb{R}$ dada por
    \begin{align*} q(x,y,z,t)= xy + yz + zt+tx. \end{align*}
  2. Completa algunos detalles faltantes en las demostraciones anteriores. Por ejemplo:
    1. ¿Por qué las formas $m_i$ de la discusión del teorema de Sylvester son linealmente independientes?
    2. ¿Por qué son análogas las demostraciones faltantes en el lema que demostramos?
  3. Demuestra que cualquier matriz simétrica es congruente a una matriz diagonal cuya diagonal es de la forma $1,\ldots,1,-1\ldots,-1,0,\ldots,0$.
  4. Enuncia y demuestra un resultado análogo al lema principal de esta entrada, pero para matrices con entradas complejas. Recuerda que en este caso debes usar matrices hermitianas y las congruencias son a través de usar una matriz invertible y su traspuesta conjutada.
  5. Enuncia y demuestra una ley de inercia de Sylvester para formas cuadráticas hermitianas.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Ecuaciones Diferenciales I: Soluciones a las ecuaciones diferenciales

Por Omar González Franco

Deja un comentario

Las matemáticas son la puerta y la llave a la ciencia.
– Roger Bacon

Introducción

En la entrada anterior vimos lo que son las ecuaciones diferenciales (ED), en particular las ecuaciones diferenciales ordinarias (EDO) con las que trabajaremos a lo largo del curso. Vimos también como clasificarlas por tipo, orden y linealidad.

Mencionábamos que lo que nos interesa al tener una ecuación diferencial es hallar la función involucrada que depende de la variable independiente, hallar dicha función significa que hemos resuelto la ecuación diferencial y a la función encontrada la llamaremos función solución, o simplemente solución. Antes de aprender a resolver ecuaciones diferenciales, en esta entrada estudiaremos las propiedades mismas de una solución.

Soluciones de ecuaciones diferenciales

Una función $f$ es solución si para una ecuación diferencial ordinaria de $n$-ésimo orden cumple lo siguiente.

$$F(x, f(x), f^{\prime}(x), \cdots, f^{(n)}(x)) = 0 \tag{1} \label{1}$$

para toda $x \in \delta$. En este curso supondremos que una solución $f$ es una función con valores reales, es decir, $\delta \in \mathbb{R}$.

El intervalo de solución $\delta$ también es conocido como intervalo de definición, intervalo de existencia, intervalo de validez o dominio de la solución y puede ser un intervalo abierto $(a, b)$, un intervalo cerrado $[a, b]$, un intervalo infinito $(a, \infty)$, etcétera.

Ejemplo: Verificar que la función

$$f(x) = y = \dfrac{1}{x}$$

es solución de la ecuación diferencial

$$x \dfrac{dy}{dx} + y = 0$$

Solución: Consideremos la función $y = \dfrac{1}{x}$ para toda $x \neq 0$. La derivada de esta función es

$$\dfrac{dy}{dx} = -\dfrac{1}{x^{2}}$$

para toda $x \neq 0$. Sustituyamos estas funciones en la ecuación diferencial y verifiquemos que se satisface la igualdad.

\begin{align*}
x \dfrac{dy}{dx} + y &= x \left( -\dfrac{1}{x^{2}} \right) + \dfrac{1}{x} \\
&= -\dfrac{1}{x} + \dfrac{1}{x} \\
&= 0
\end{align*}

Como hemos recuperado la ecuación diferencial decimos que en efecto $y = \dfrac{1}{x}$ es solución. Observemos que la solución no está definida para $x = 0$, sin embargo, al ser solución significa que es una función definida en un intervalo $\delta$ en el que es derivable y satisface la ecuación, esto indica que $y$ es solución en cualquier intervalo que no contenga al $0$.

Como observación notemos que la función $f(x) = y = 0$ y la derivada correspondiente $\dfrac{dy}{dx} = 0$, también satisfacen la misma ecuación diferencial, entonces decimos que dicha ecuación diferencial tiene solución trivial.

Como podemos notar, tanto la función $y = \dfrac{1}{x}$, como la función constante $y = 0$, son solución de la misma ecuación diferencial, ¡esto significa que una ecuación diferencial puede tener más de una solución!.

$\square$

Curva solución de una ecuación diferencial

Las soluciones de las ecuaciones diferenciales ordinarias de una variable dependiente son funciones de una variable independiente, por lo tanto se pueden graficar en el plano $XY$. De acuerdo a la definición de solución, y al ejemplo anterior, es importante hacer una distinción entre el dominio de una función (los valores para los cuales la función está definida) y un intervalo de solución.

Si $f(x)$ es solución de una ecuación diferencial, entonces $f(x)$ es derivable, lo que también significa que es continua en su intervalo de definición $\delta$, esto es necesario para ser solución y no siempre va a ocurrir para todo el dominio de la función $f$. Puede haber diferencia entre la gráfica de la función $f(x)$ y la gráfica de la solución $f(x)$. En el ejemplo anterior el dominio de la función $y = \dfrac{1}{x}$ es $D = \mathbb{R} -\{0\}$, mientras que el intervalo de solución es cualquier intervalo que no contenga al $0$, por ejemplo $\delta = (-\infty, -1)$, $\delta = (5, 100)$ o $\delta = (1, \infty)$, etcétera. El intervalo de solución no necesita ser igual al dominio de la función $f(x)$.

Gráfica de la función $y = \dfrac{1}{x}$.
Curva solución definida por $y = \dfrac{1}{x}$ en el intervalo $\delta = (1, 100)$.

Ejemplo: Comprobar que la función

$$f(x) = y = \dfrac{1}{4 -x^{2}}$$

es solución de la ecuación diferencial

$$\dfrac{dy}{dx} = 2xy^{2}$$

y determinar al menos un intervalo de solución.

Solución: La función dada es

$$y = \dfrac{1}{4 -x^{2}}$$

La derivada de esta función es

$$\dfrac{dy}{dx} = \dfrac{2x}{(4 -x^{2})^{2}}$$

Esta ecuación se puede reescribir de la siguiente manera:

$$\dfrac{dy}{dx} = \dfrac{2x}{(4 -x^{2})^{2}} = 2x \dfrac{1}{(4 -x^{2})^{2}} = 2x \left(\dfrac{1}{4 -x^{2}}\right) ^{2} = 2xy^{2}$$

Esto es,

$$\dfrac{dy}{dx} = 2xy^{2}$$

Efectivamente, la función dada es solución de la ecuación diferencial.

Ahora debemos determinar un intervalo de solución, para hacerlo podemos comenzar por determinar el dominio de la función. La función $y = \dfrac{1}{4 -x^{2}}$ no está definida cuando $4 = x^{2}$, es decir, cuando $x = 2$ o $x = -2$, por lo tanto el dominio de la función es

$$D = (-\infty, -2) \cup (-2, 2) \cup (2, \infty)$$

Gráfica de la función $\dfrac{1}{4 -x^{2}}$.

El intervalo de solución es cualquiera que no contenga al $-2$ ni al $2$, el ejercicio nos pide determinar al menos un intervalo de solución, podemos entonces considerar el intervalo abierto$\delta = (2, \infty)$ como el intervalo de solución.

Curva solución en el intervalo $ \delta = (2, \infty)$.

$\square$

Soluciones explícitas y soluciones implícitas

Recordemos que una función es explícita si se puede escribir como $y = f(x)$, es decir, si la variable dependiente se puede escribir en términos de la variable independiente, mientras que una función implícita esta dada por la forma $f(x, y) = 0$. Ya sabemos que las soluciones de las ecuaciones diferenciales son funciones por lo que estos conceptos se pueden extender a estas soluciones.

Una solución explicita $y = f(x)$ la podemos manejar, evaluar y derivar usando las reglas usuales. Más adelante nos encontraremos con soluciones en las que no es factible obtener la forma explicita y tendremos que hallar al menos una forma implícita de la solución.

Ejemplo: Verificar que la relación

$$x^{2} + y^{2} = 100$$

es una solución implícita de la ecuación diferencial

$$\dfrac{dy}{dx} = -\dfrac{x}{y}$$

y determinar las soluciones explícitas.

Solución: Primero notemos que, de acuerdo a la definición de solución implícita, la relación dada se puede escribir como

$$G(x, y) = x^{2} + y^{2} -100 = 0$$

Derivemos esta ecuación implícitamente.

\begin{align*}
\dfrac{d}{dx} \left( x^{2} + y^{2} -100 \right) &= \dfrac{d}{dx} (0) \\
\dfrac{d}{dx} (x^{2}) + \dfrac{d}{dx} (y^{2}) -\dfrac{d}{dx} (100) &= \dfrac{d}{dx} (0) \\
2x + \dfrac{d}{dy}y^{2}\dfrac{dy}{dx} -0 &= 0 \\
2x + 2y \dfrac{dy}{dx} &= 0
\end{align*}

De la última relación despejamos $\dfrac{dy}{dx}$ obteniendo así la ecuación diferencial $\dfrac{dy}{dx} = -\dfrac{x}{y}$. Por lo tanto $x^{2} + y^{2} = 100$ es una solución implícita. El intervalo de solución es $\delta = (-10, 10)$.

Gráfica de la solución implícita $x^{2} + y^{2} = 100$

La relación $x^{2} + y^{2} = 100$ es una solución implícita ya que no es de la forma $y = f(x)$, sin embargo se puede obtener la solución explícita con sólo despejar a $y$.

$$y = \pm \sqrt{100 -x^{2}}$$

Pero notemos que ahora tenemos dos soluciones.

$$y_{1} = \sqrt{100 -x^{2}} \hspace{1cm} y \hspace{1cm} y_{2} = -\sqrt{100 -x^{2}}$$

Estas funciones satisfacen respectivamente $x^{2} + y_{1}^{2} = 100$ y $x^{2} + y_{2}^{2} = 100$, además de la ecuación diferencial. Por lo tanto, ambas son soluciones explícitas en el mismo intervalo $\delta = (-10, 10)$ .

En las siguientes gráficas se muestran las curvas solución de cada solución explícita.

Curva solución $y_{1} = \sqrt{100 -x^{2}}$.
Curva solución $y_{2} = -\sqrt{100 -x^{2}}$.

Observamos que cada solución explícita corresponde a un tramo de la solución implícita y ambas forman dicha solución.

$\square$

Con este ejemplo vemos que es importante entender las circunstancias del problema para poder determinar la solución adecuada de la ecuación diferencial. En este caso la solución implícita involucra a las dos soluciones explícitas y nos permite conocer más acerca del problema. Cabe mencionar que no siempre será necesario o posible obtener la solución explícita, en el ejemplo fue sencillo obtener la función $y$ en términos de $x$, pero no siempre será el caso y obtener la solución implícita $G(x, y) = 0$ será suficiente.

Otro punto importante a observar es que al derivar la constante $100$ se obtiene un cero, eso significa que, independientemente del valor de la constante, al derivar siempre vamos a obtener un cero, considerando esto, la forma más general de expresar la solución anterior es

$$x^{2} + y^{2} = c$$

donde $c$ es una constante arbitraria. Si derivamos obtendremos nuevamente la ecuación diferencial

$$\dfrac{dy}{dx} = -\dfrac{x}{y}$$

Debido a que hay una infinidad de valores que puede tomar $c$ (en el campo de los reales), entonces significa que la ecuación diferencial ¡tiene infinitas soluciones!.

En efecto, una ecuación diferencial puede tener una infinidad de soluciones, así que dependerá del problema o de las condiciones, la solución que debamos considerar. A pesar de que una ecuación diferencial puede tener infinitas soluciones es posible encontrar un solución general que considere todas las posibilidades.

Familias de soluciones

Al resolver una ecuación diferencial de primer orden

$$F(x, y , y^{\prime}) = 0 \label{2} \tag{2}$$

normalmente se obtiene una solución que contiene una sola constante arbitraria $c$.

Este concepto se puede extender a una ecuación diferencial de orden $n$

$$F(x, y, y^{\prime}, \cdots, y^{(n)}) = 0 \label{4} \tag{4}$$

en este caso la solución

$$G(x, y, c_{1}, c_{2}, \cdots, c_{n}) = 0 \label{5} \tag{5}$$

corresponde a una familia de soluciones $n$-paramétrica.

En el ejemplo que vimos, la relación

$$x^{2} + y^{2} = c$$

corresponde a la solución general de la ecuación diferencial

$$\dfrac{dy}{dx} = – \dfrac{x}{y}$$

mientras que la relación

$$x^{2} + y^{2} = 100$$

corresponde a una posible solución, en este caso decimos que es una solución particular.

Concluyamos esta entrada con un último ejemplo.

Ejemplo: Mostrar que la función

$$y(x) = 3x^{2} + c_{1}x + c_{2}$$

con $c_{1}$ y $c_{2}$ constantes arbitrarias, es solución general de la ecuación diferencial

$$\dfrac{d^{2}y}{dx^{2}} = 6$$

Solución: Derivemos dos veces la función dada y veamos si obtenemos la ecuación diferencial. Derivando una vez obtenemos lo siguiente.

\begin{align*}
\dfrac{dy}{dx} &= \dfrac{d}{dx}(3x^{2}) + \dfrac{d}{dx}(c_{1}x) + \dfrac{d}{dx}(c_{2}) \\
&= 2(3x) + c_{1} + 0 \\
&= 6x + c_{1}
\end{align*}

La primer derivada es

$$ \dfrac{dy}{dx} = 6x + c_{1}$$

Derivemos nuevamente esta función.

\begin{align*}
\dfrac{d^{2}y}{dx^{2}} &= \dfrac{d}{dx}(6x) + \dfrac{d}{dx}(c_{1}) \\
&= 6 + 0 \\
&= 6
\end{align*}

Efectivamente

$$\dfrac{d^{2}y}{dx^{2}} = 6$$

Por lo tanto, la función

$$y(x) = 3x^{2} + c_{1}x + c_{2}$$

es solución de la ecuación diferencial. Sabemos que es la solución general porque satisface a la ecuación diferencial de segundo orden y contiene dos constantes arbitrarias. Una posible solución particular sería la función

$$y(x) = 3x^{2} + 10x -5$$

o

$$y(x) = 3x^{2} -0.2x + 155$$

etcétera. En este caso no hay restricción de valores para $x$ por lo que el intervalo de solución puede ser cualquiera en $\mathbb{R}$ o bien $\delta = \mathbb{R}$

$\square$

Hemos concluido la entrada.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  1. Comprobar que las siguientes funciones $y = f(x)$ son solución de la correspondiente ecuación diferencial y establecer un adecuado intervalo de solución $\delta$.
  • $2 \dfrac{dy}{dx} + y = 0$; $\hspace{1cm}$ $y = e^{-x/2}$
  • $\dfrac{d^{2}y}{dx^{2}} -6\dfrac{dy}{dx} + 13y = 0$; $\hspace{1cm}$ $y = e^{3x} \cos{(2x)}$
  • $(y -x) \dfrac{dy}{dx} = y -x + 8$; $\hspace{1cm}$ $y = x + 4\sqrt{x + 2}$
  1. Comprobar que las siguientes familias de soluciones son solución de la correspondiente ecuación diferencial y establecer un adecuado intervalo de solución $\delta$.
  • $\dfrac{dy}{dx} = y(1 -y)$; $\hspace{1cm}$ $y = \dfrac{c_{1}e^{x}}{1 + c_{1}e^{x}}$
  • $\dfrac{d^{2}y}{dx^{2}} -4\dfrac{dy}{dx} + 4y = 0$; $\hspace{1cm}$ $y = c_{1}e^{2x} + c_{2}xe^{2x}$

Más adelante…

Ahora ya conocemos algunas características de las funciones solución de las ecuaciones diferenciales ordinarias. Sabemos que existen soluciones generales, o familias de soluciones, de una ecuación diferencial, sin embargo en algunas situaciones nos veremos en la necesidad de conocer una solución particular debido a condiciones prescritas según el problema que estemos estudiando, a estas condiciones prescritas las llamamos condiciones iniciales (o valores iniciales) y serán las que establezcan una solución particular que nos sirva para modelar nuestro problema.

En la siguiente entrada estudiaremos soluciones con condiciones iniciales y revisaremos algunos problemas del mundo real que involucran ecuaciones diferenciales ordinarias.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»