Introducción

En esta entrada estudiaremos los criterios de congruencia para triángulos, los cuales estaremos usando a lo largo del curso, nos apoyaremos en las transformaciones rígidas las cuales presentamos a continuación.

Definición 1. Decimos que dos triángulos distintos $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ son congruentes y lo denotamos como $\mathrm{△}ABC\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$, si los lados y los ángulos correspondientes son iguales, esto es,

• $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime }$, $\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime }$, $\mathrm{\angle }C=\mathrm{\angle }{C}^{\prime }$ y
• $AB=A^{\prime }{B}^{\prime }$, $BC=B^{\prime }{C}^{\prime }$, $AC=A^{\prime }{C}^{\prime }$.

Definición 2. Una transformación rígida es una función del plano en sí mismo, o un subconjunto de él, donde la preimagen y la imagen son congruentes.

Una reflexión en una recta es una transformación rígida que manda a todo punto en la preimagen con su punto simétrico respecto a la recta.

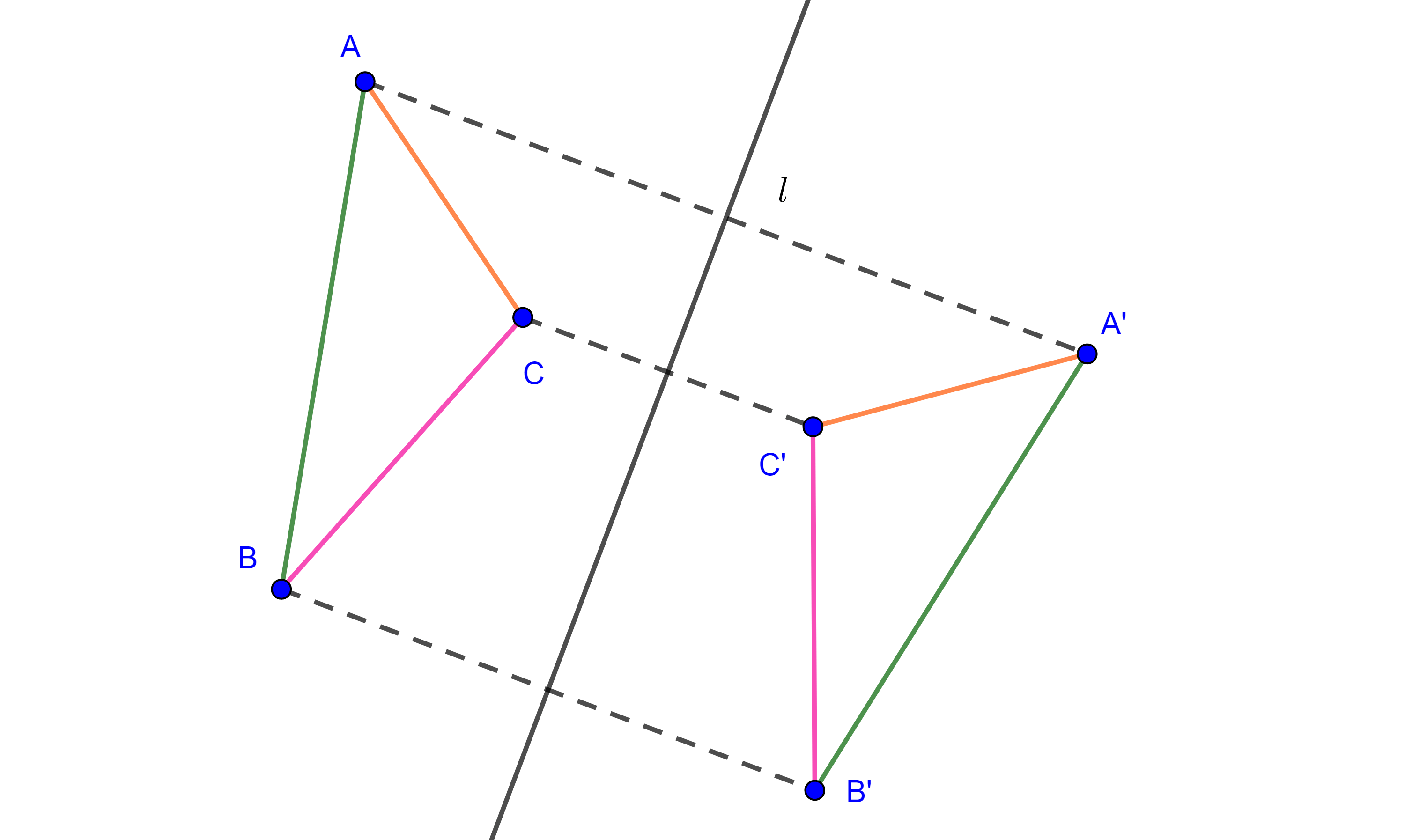
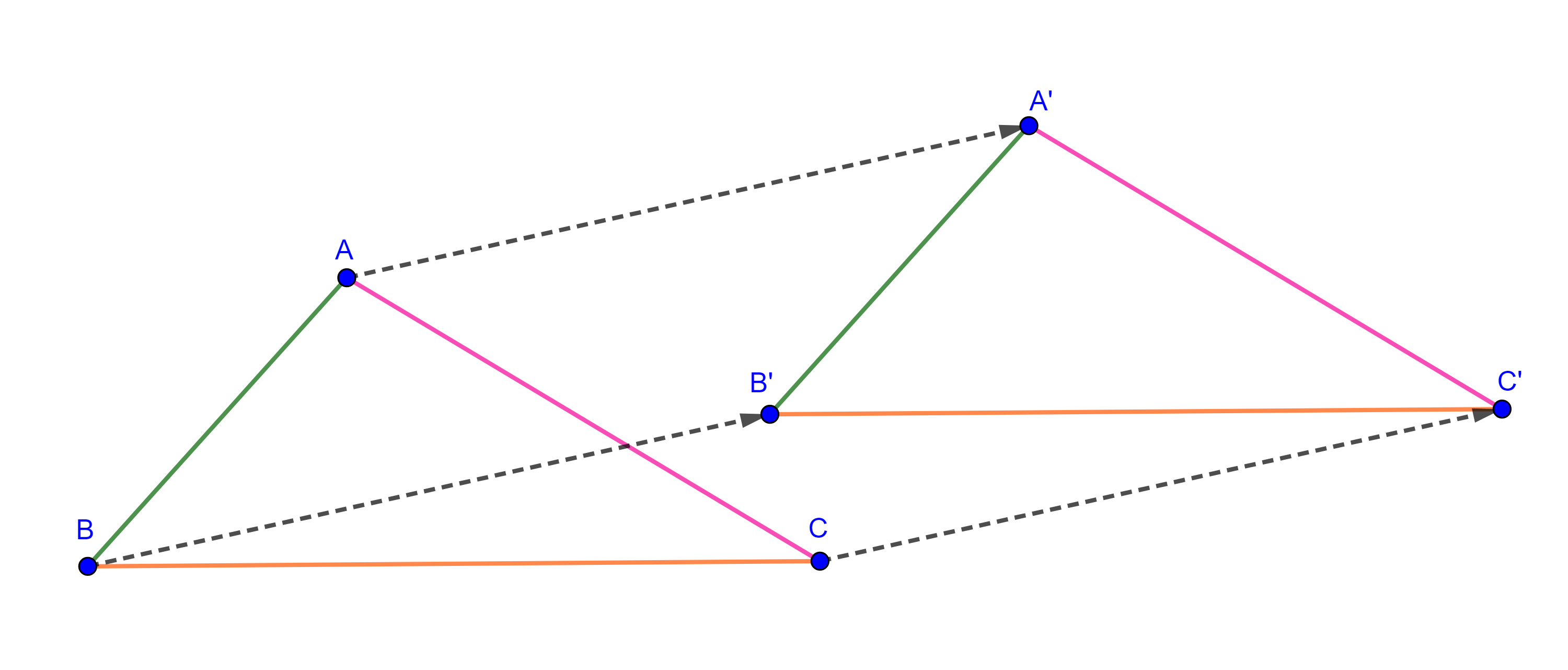
Una traslación es una transformación rígida que mueve a todos los puntos en la preimagen una distancia constante en una dirección especifica.

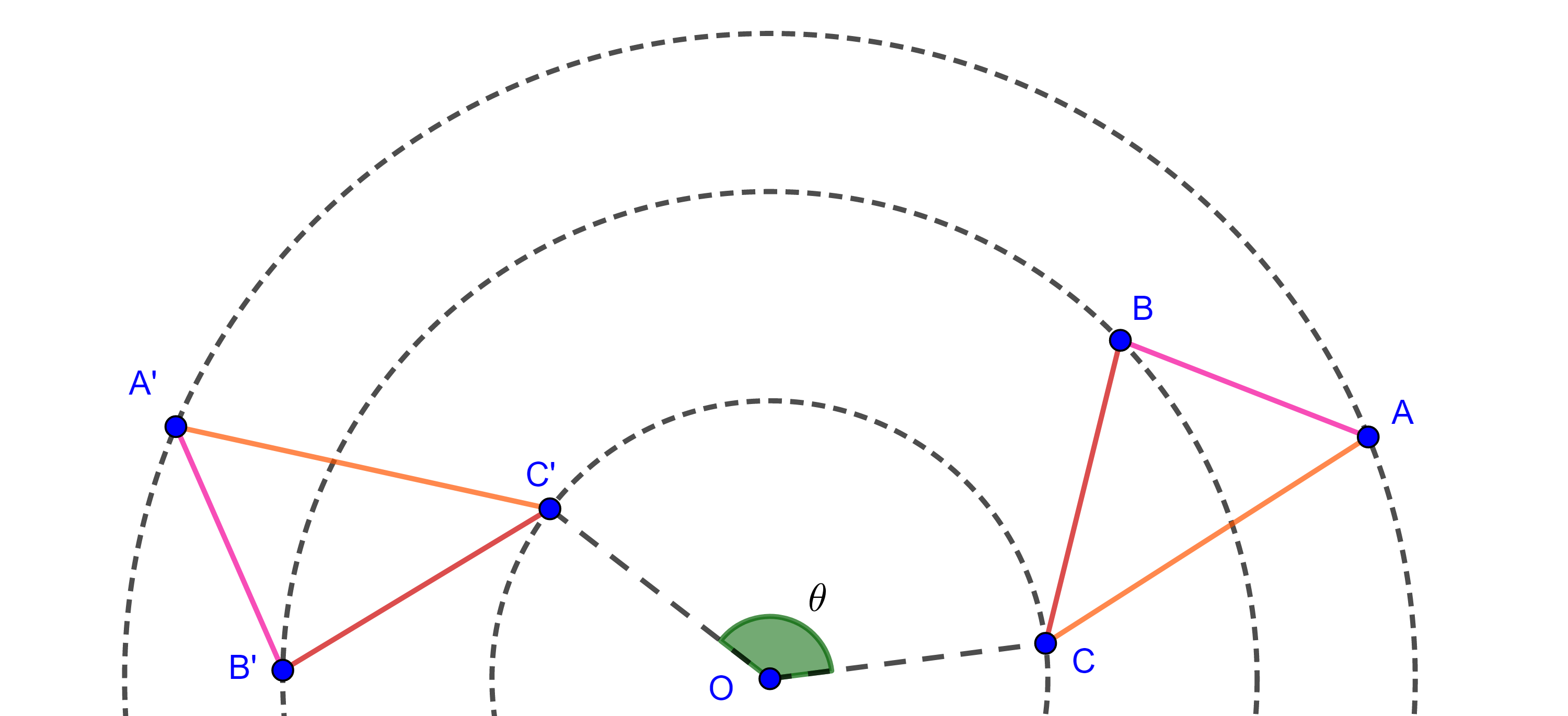
Una rotación es una transformación rígida donde todos los puntos en la preimagen giran alrededor de un punto fijo en un ángulo constante.

Criterio lado, ángulo, lado (LAL)

Teorema 1, de congruencia lado, ángulo, lado. Si en un triángulo dos de sus lados y el ángulo interior que estos forman, son iguales a dos lados y el ángulo interior comprendido entre ellos de un segundo triángulo entonces los triángulos son congruentes.

Demostración. Sean $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ tales que $AB=A^{\prime }{B}^{\prime }$, $AC=A^{\prime }{C}^{\prime }$ y $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime }$, debemos mostrar que $BC=B^{\prime }{C}^{\prime }$, $\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime }$ y $\mathrm{\angle }C=\mathrm{\angle }{C}^{\prime }$.

La idea es superponer los ángulos $\mathrm{\angle }BAC$ y $\mathrm{\angle }{B}^{\prime }{A}^{\prime }{C}^{\prime }$ de la siguiente manera, hacemos una composición de transformaciones rígidas para que $A$ y $A^{\prime }$ coincidan y los segmentos $AB$ y $A^{\prime }{B}^{\prime }$  se superpongan.

Entonces como $AB=A^{\prime }{B}^{\prime }$ los puntos $B$ y $B^{\prime }$ coincidirán, ahora como $\mathrm{\angle }BAC=\mathrm{\angle }{B}^{\prime }{A}^{\prime }{C}^{\prime }$ los segmentos $AC$ y $A^{\prime }{C}^{\prime }$ quedaran sobrepuestos, si no es así entonces hacemos una reflexión a través de $AB$ para que esto suceda.

Como $AC$ y $A^{\prime }{C}^{\prime }$  tienen la misma longitud sucederá que $C$ y $C^{\prime }$ coincidirán, de esta manera los segmentos $BC$ y $B^{\prime }{C}^{\prime }$ coincidirán pero también los pares de ángulos ($\mathrm{\angle }CBA$, $\mathrm{\angle }{C}^{\prime }{B}^{\prime }{A}^{\prime }$) y ($\mathrm{\angle }ACB$, $\mathrm{\angle }{A}^{\prime }{C}^{\prime }{B}^{\prime }$) coincidirán.

Por lo tanto, por la noción común numero 4 (cosas que coinciden una con otra son iguales entre sí), tendrán la misma magnitud,
$BC=B^{\prime }{C}^{\prime }$, $\mathrm{\angle }CBA=\mathrm{\angle }{C}^{\prime }{B}^{\prime }{A}^{\prime }$, $\mathrm{\angle }ACB=\mathrm{\angle }{A}^{\prime }{C}^{\prime }{B}^{\prime }$.

Como resultado, $\mathrm{△}ABC\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Notemos que el procedimiento de “superponer” las figuras no se menciona en los axiomas de Euclides ni en las nociones comunes, así que este es un ejemplo de que los postulados de Euclides son incompletos como lo mencionábamos en la entrada anterior.

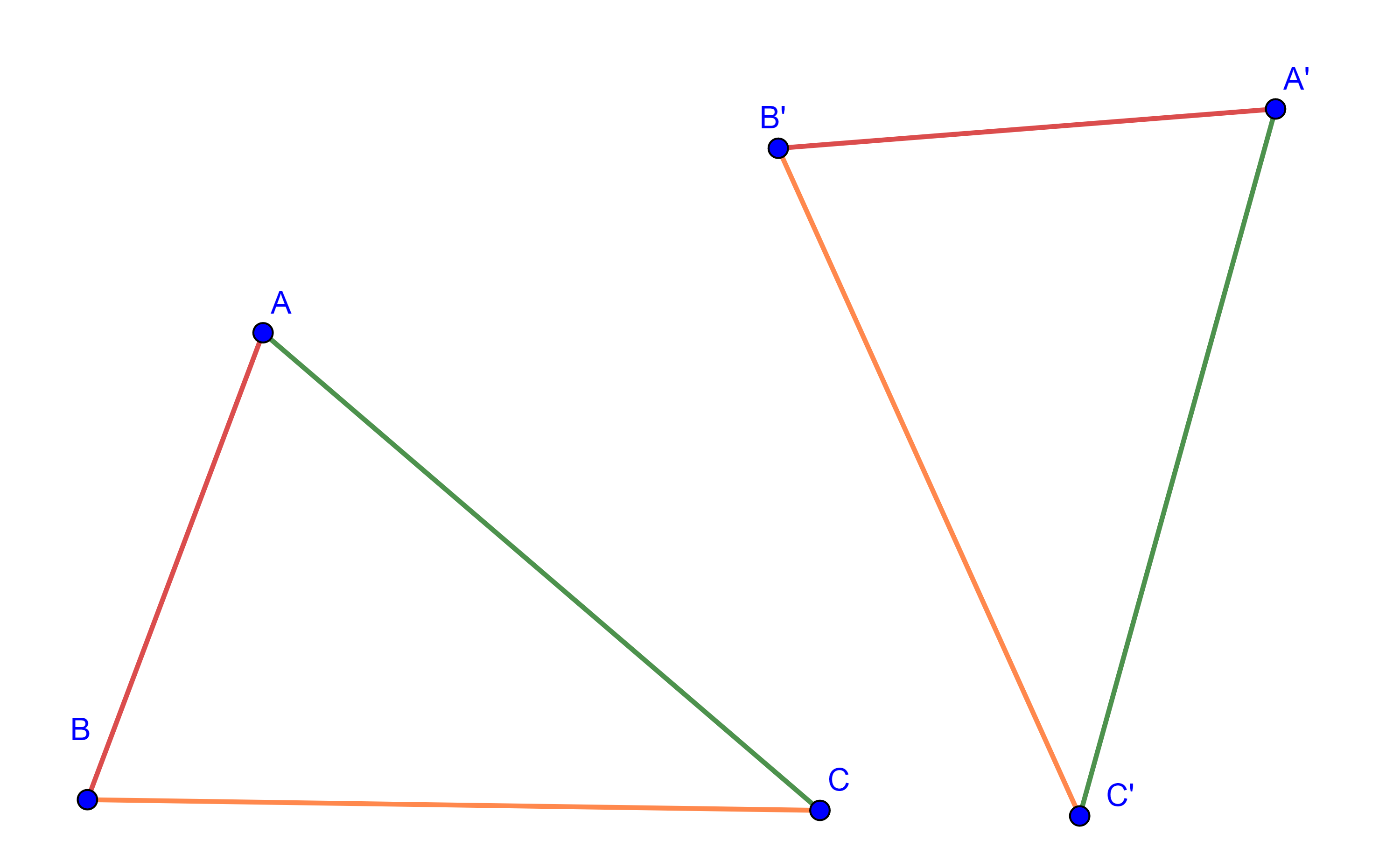
En el siguiente interactivo se ilustra un caso particular de como con una traslación y una rotación podemos superponer dos triángulos.

Criterio lado, lado, lado (LLL)

Definición 3. La mediatriz de un segmento es la recta perpendicular al segmento y que pasa por su punto medio, es decir, lo biseca.

La bisectriz de un ángulo es la recta que pasa por el vértice del ángulo y lo divide en dos ángulos iguales. Notemos que en un triángulo hay tres bisectrices internas y tres bisectrices externas.

Decimos que un vértice y un lado de un triángulo son opuestos si el lado no contiene al vértice. La altura de un triángulo, es el segmento que une uno de sus vértices con el pie de la perpendicular al lado opuesto.

La mediana de un triángulo es el segmento que une un vértice con el punto medio del lado opuesto.

Proposición. Los ángulos internos de un triángulo isósceles, que no son aquel comprendido entre los lados iguales, son iguales entre sí, además, la bisectriz del ángulo interior formado por los lados iguales, la altura trazada por ese vértice, la mediana y mediatriz del lado opuesto coinciden.

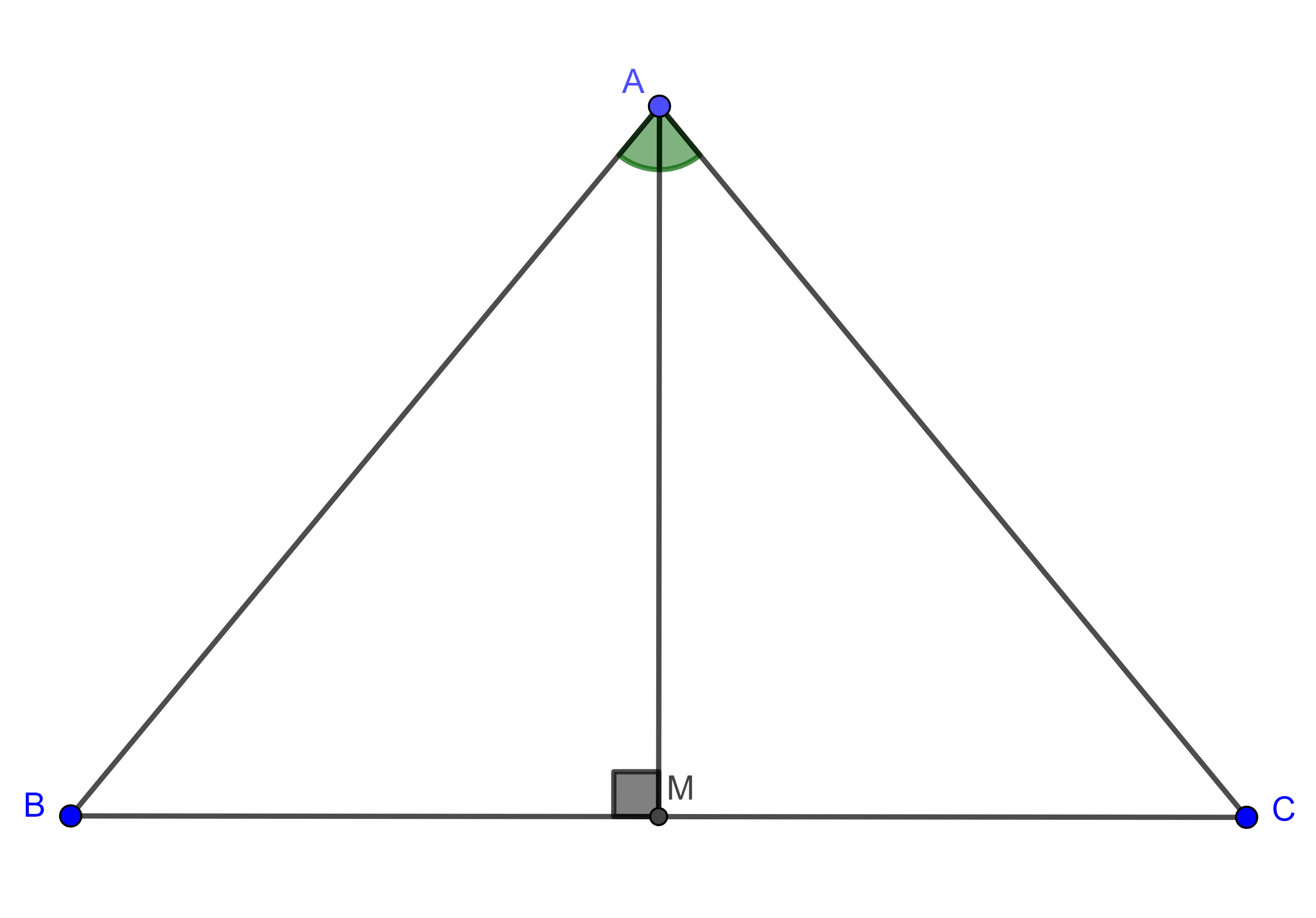
Demostración.  Sea $\mathrm{△}ABC$ un triángulo isósceles con $AB=AC$ y tracemos la bisectriz de $\mathrm{\angle }A$, sea $M$ el punto en donde la bisectriz corta al lado opuesto.

Los triángulos $\mathrm{△}AMB$ y $\mathrm{△}AMC$ tienen dos lados iguales, $AB=AC$ por hipótesis y $AM$ es un lado en común, además $\mathrm{\angle }BAM=\mathrm{\angle }MAC$ por ser $AM$ bisectriz, por criterio LAL los triángulos son congruentes.

Por lo tanto, $BM=CM$, $\mathrm{\angle }AMB=\mathrm{\angle }CMA$ y $\mathrm{\angle }B=\mathrm{\angle }C$
esta última igualdad es la primera de las afirmaciones que se quería mostrar.

Por otro lado, como $BM=CM$, entonces $M$ es punto medio de $BC$ por lo que $AM$ es mediana.

Ahora, como $\mathrm{\angle }AMB+\mathrm{\angle }CMA=\pi$ y $\mathrm{\angle }AMB=\mathrm{\angle }CMA$, entonces $AM$ es perpendicular a $BC$ y así $AM$ es mediatriz y altura.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

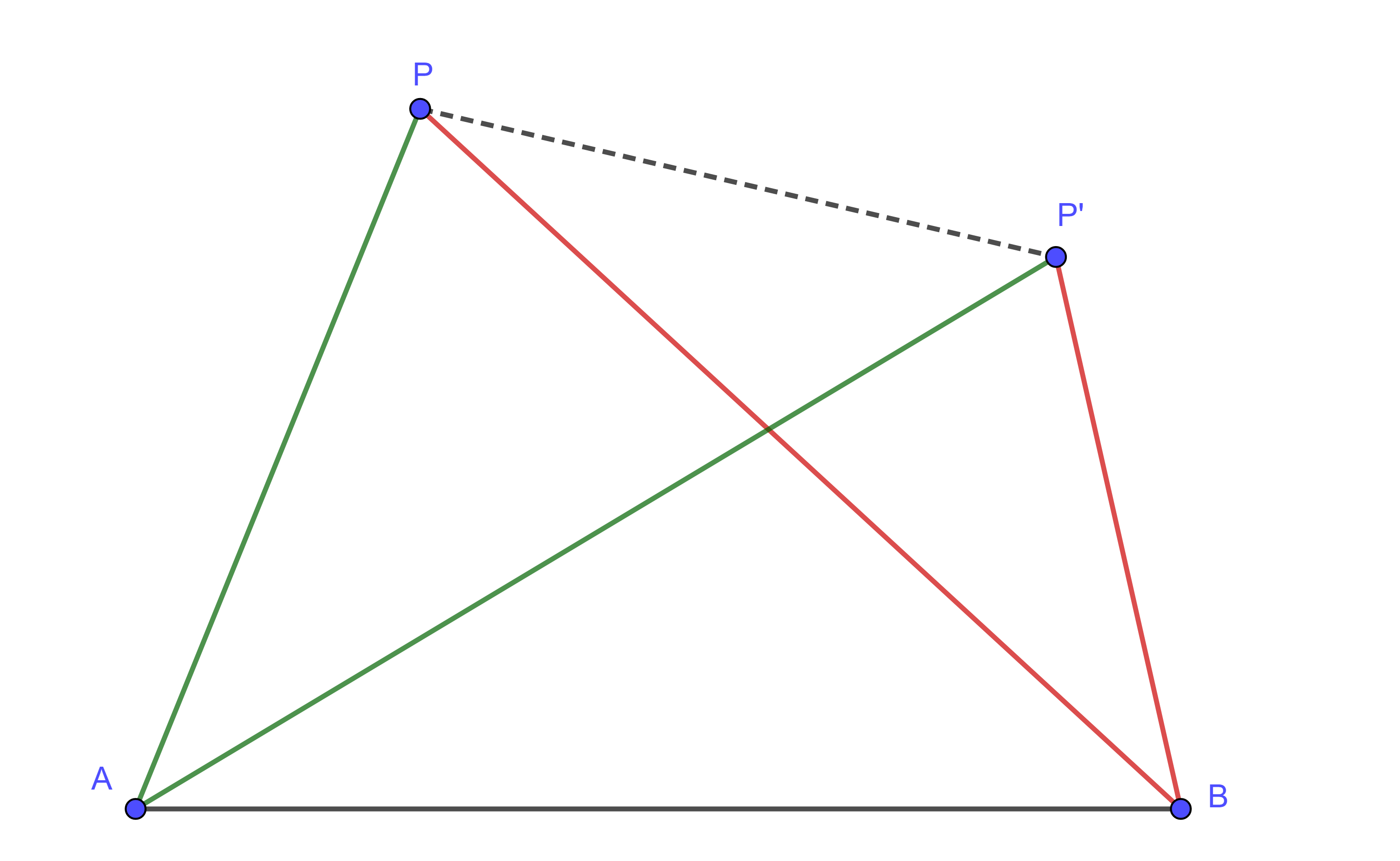
Lema. Dado un segmento $AB$ y un punto $P$ no colineal con $A$ y $B$, no existe otro punto $P^{\prime }$ diferente de $P$ y en el mismo semiplano que $P$ respecto de $AB$, tal que $AP=A{P}^{\prime }$ y $BP=B{P}^{\prime }$.

Demostración. Por reducción al absurdo, supongamos que existe $P^{\prime }\ne P$ talque $AP=A{P}^{\prime }$ y $BP=B{P}^{\prime }$, entonces consideremos los triángulos isósceles, $\mathrm{△}PAP$´ y $\mathrm{△}PB{P}^{\prime }$.

Por la proposición anterior $\mathrm{\angle }AP{P}^{\prime }=\mathrm{\angle }P{P}^{\prime }A$ y $\mathrm{\angle }BP{P}^{\prime }=\mathrm{\angle }P{P}^{\prime }B$.

Pero $\mathrm{\angle }AP{P}^{\prime }=\mathrm{\angle }APB+\mathrm{\angle }BP{P}^{\prime }=\mathrm{\angle }APB+\mathrm{\angle }P{P}^{\prime }B$,
$\Rightarrow AP{P}^{\prime }>P{P}^{\prime }B$.

Por otro lado, $\mathrm{\angle }P{P}^{\prime }B=\mathrm{\angle }P{P}^{\prime }A+\mathrm{\angle }A{P}^{\prime }B$,
$\Rightarrow P{P}^{\prime }B>P{P}^{\prime }A$.

De las últimas dos desigualdades concluimos que $AP{P}^{\prime }>P{P}^{\prime }A$, lo cual es una contradicción al axioma de tricotomía pues vimos que $AP{P}^{\prime }=P{P}^{\prime }A$.

Por lo tanto, no existe $P^{\prime }$ distinto de $P$ tal que $AP=A{P}^{\prime }$ y $BP=B{P}^{\prime }$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Teorema 2, de congruencia lado, lado, lado. Si los lados de un triángulo son iguales a los lados de otro triángulo, entonces los triángulos son congruentes.

Demostración. Sean $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ tales que $AB=A^{\prime }{B}^{\prime }$, $BC=B^{\prime }{C}^{\prime }$ y $AC=A^{\prime }{C}^{\prime }$, veamos que los ángulos respectivos tienen la misma magnitud.

Hagamos la composición de transformaciones rígidas necesaria para para hacer coincidir los puntos $B$ y $B^{\prime }$ de manera que los segmentos $BC$ y $B´C^{\prime }$ se sobrepongan.

Como $BC=B^{\prime }{C}^{\prime }$ entonces $C$ y $C^{\prime }$ coincidirán.

Ahora realizamos otra composición de transformaciones rígidas para que $A$ y $A^{\prime }$ se encuentren en el mismo semiplano respecto de $BC$ y $B^{\prime }{C}^{\prime }$, que ahora son el mismo segmento.

Por el lema anterior, como $AB=A^{\prime }{B}^{\prime }$ y $AC=A^{\prime }{C}^{\prime }$, no es posible que $A\ne A^{\prime }$, por lo tanto, coinciden, como $\mathrm{△}ABC$ y $\mathrm{△}A´B´C´$ coinciden, por la noción común número 4, todas sus magnitudes son iguales, por lo que $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime }$, $\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime }$ y $\mathrm{\angle }C=\mathrm{\angle }{C}^{\prime }$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Problema. Dado un ángulo construir su bisectriz.

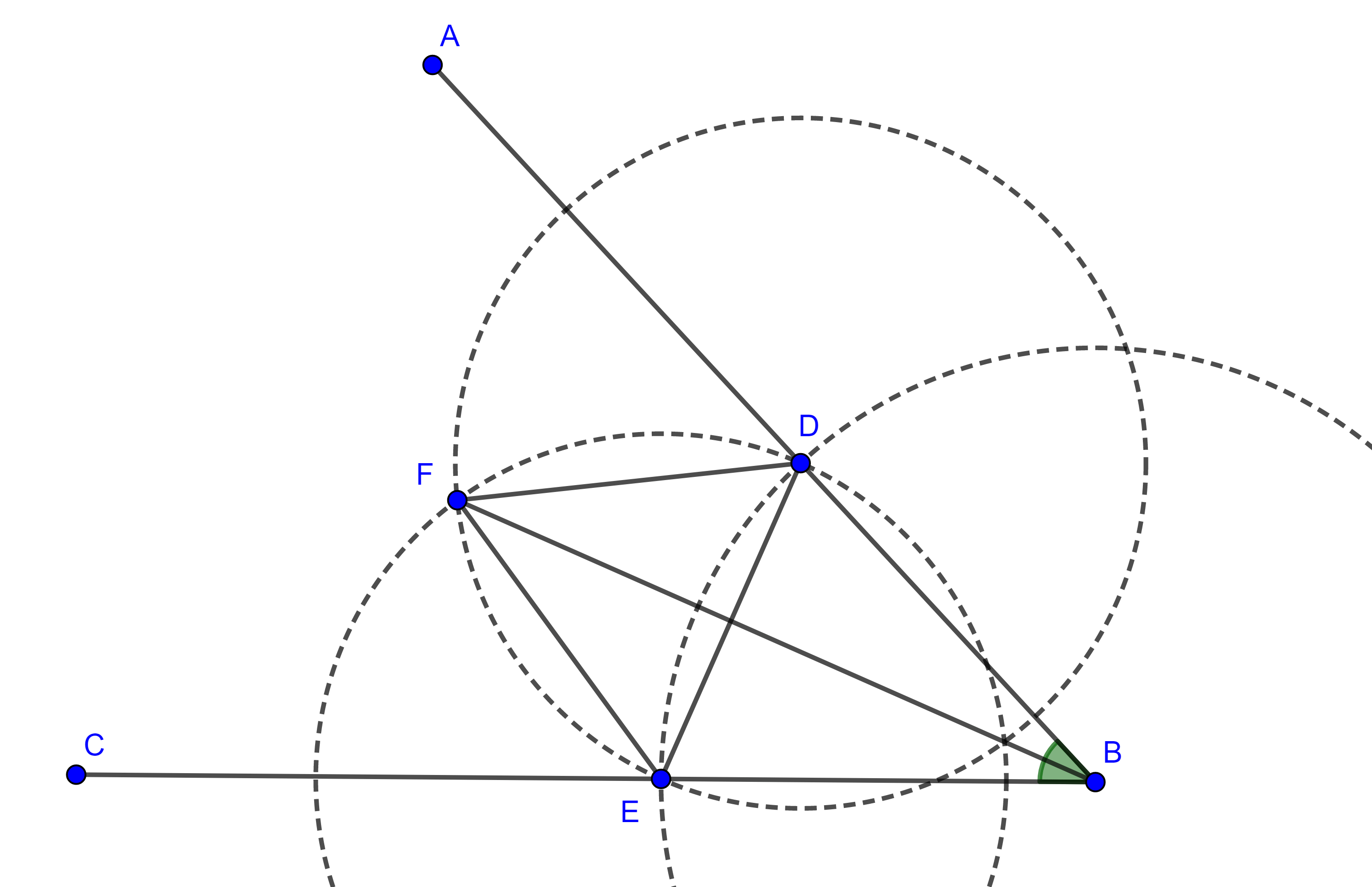
Solución. Sea $\mathrm{\angle }ABC$ el ángulo dado, trazamos una circunferencia de radio arbitrario pero positivo que corta a $AB$ en $D$ y a $BC$ en $E$.

Ahora construimos un triángulo equilátero sobre $DE$, como lo hicimos en la primera entrada, cuyo tercer vértice será $F$.

Veamos que $BF$ es la bisectriz de $\mathrm{\angle }ABC$. Tenemos que $BD=BE$, pues son radios de una misma circunferencia, $DF=EF$, ya que $\mathrm{△}DEF$ es equilátero por construcción, por LLL $\mathrm{△}BDF\cong \mathrm{△}BEF$, en consecuencia $\mathrm{\angle }DBF=\mathrm{\angle }FBE$, por lo tanto, $BF$ es bisectriz de $\mathrm{\angle }ABC$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Criterio ángulo, lado, ángulo (ALA)

Teorema 3, de congruencia ángulo, lado, ángulo. Si dos ángulos y el lado comprendido entre ellos de un triángulo son iguales a dos ángulos y el lado comprendido entre ellos de otro triangulo, entonces los triángulos son congruentes.

Demostración. Sean $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ tales que $\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime }$, $\mathrm{\angle }C=\mathrm{\angle }{C}^{\prime }$ y $BC=B^{\prime }{C}^{\prime }$.

Como la suma de los ángulos internos de todo triangulo es $\pi$ entonces
$\mathrm{\angle }A+\mathrm{\angle }B+\mathrm{\angle }C=\pi =\mathrm{\angle }{A}^{\prime }+\mathrm{\angle }{B}^{\prime }+\mathrm{\angle }{C}^{\prime }$
$\Rightarrow A=A^{\prime }$.

Si cualquier otro par de lados correspondientes fuese igual entonces por LAL, los triángulos serian congruentes. Supongamos lo contrario para llegar a una contradicción, es decir, que $AC\ne A^{\prime }{C}^{\prime }$ y $AB\ne A^{\prime }{B}^{\prime }$.

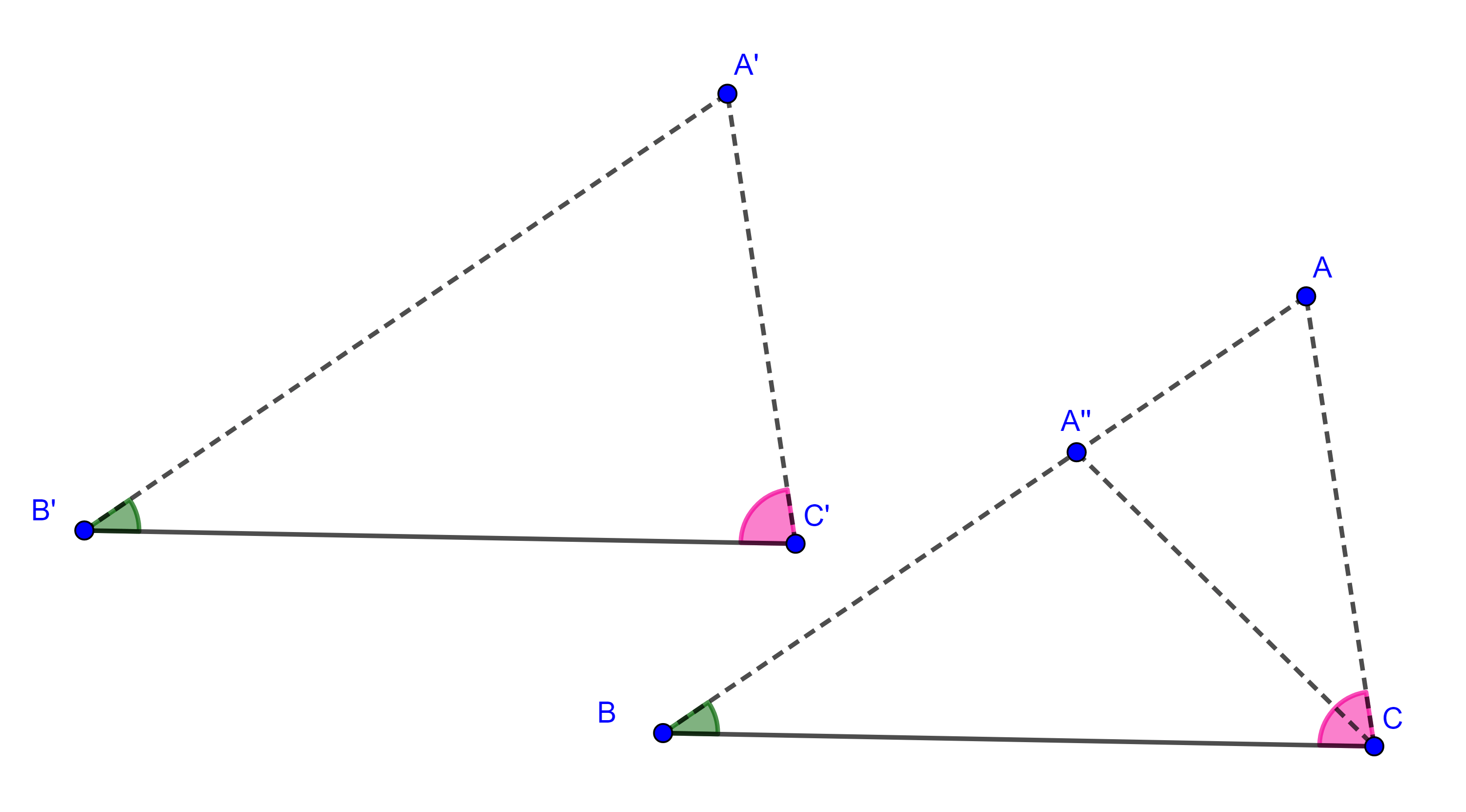
Sin pérdida de generalidad supongamos que $AC>A^{\prime }{C}^{\prime }$.

Construimos sobre $AC$ un punto $A^{″}$ tal que $A^{″}B=A^{\prime }{B}^{\prime }$, entonces $\mathrm{△}{A}^{″}BC\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ por LAL, por lo que $\mathrm{\angle }{A}^{″}CB=\mathrm{\angle }{A}^{\prime }{C}^{\prime }{B}^{\prime }$.

Por hipótesis, $\mathrm{\angle }ACB=\mathrm{\angle }{A}^{\prime }{C}^{\prime }{B}^{\prime }$ así que $\mathrm{\angle }ACB=\mathrm{\angle }{A}^{″}CB$, pero $\mathrm{\angle }ACB>\mathrm{\angle }{A}^{″}CB$, lo que es una contradicción.

Por lo tanto, $AC=A^{\prime }{C}^{\prime }$ y por LAL, $\mathrm{△}ABC\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Criterio hipotenusa, cateto

Definición 4. En un triángulo rectángulo a los lados que forman el ángulo recto le llamamos catetos y al lado opuesto al ángulo recto le llamamos hipotenusa.

Teorema 4. De congruencia hipotenusa, cateto. Si la hipotenusa y un cateo de un triángulo rectángulo son iguales a la hipotenusa y un cateto de otro triángulo rectángulo, entonces los triángulos son congruentes.

Demostración. Sean $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ tales que $\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime }={\displaystyle \frac{\pi }{2}}$, $AB=A^{\prime }{B}^{\prime }$ y $AC=A^{\prime }{C}^{\prime }$.

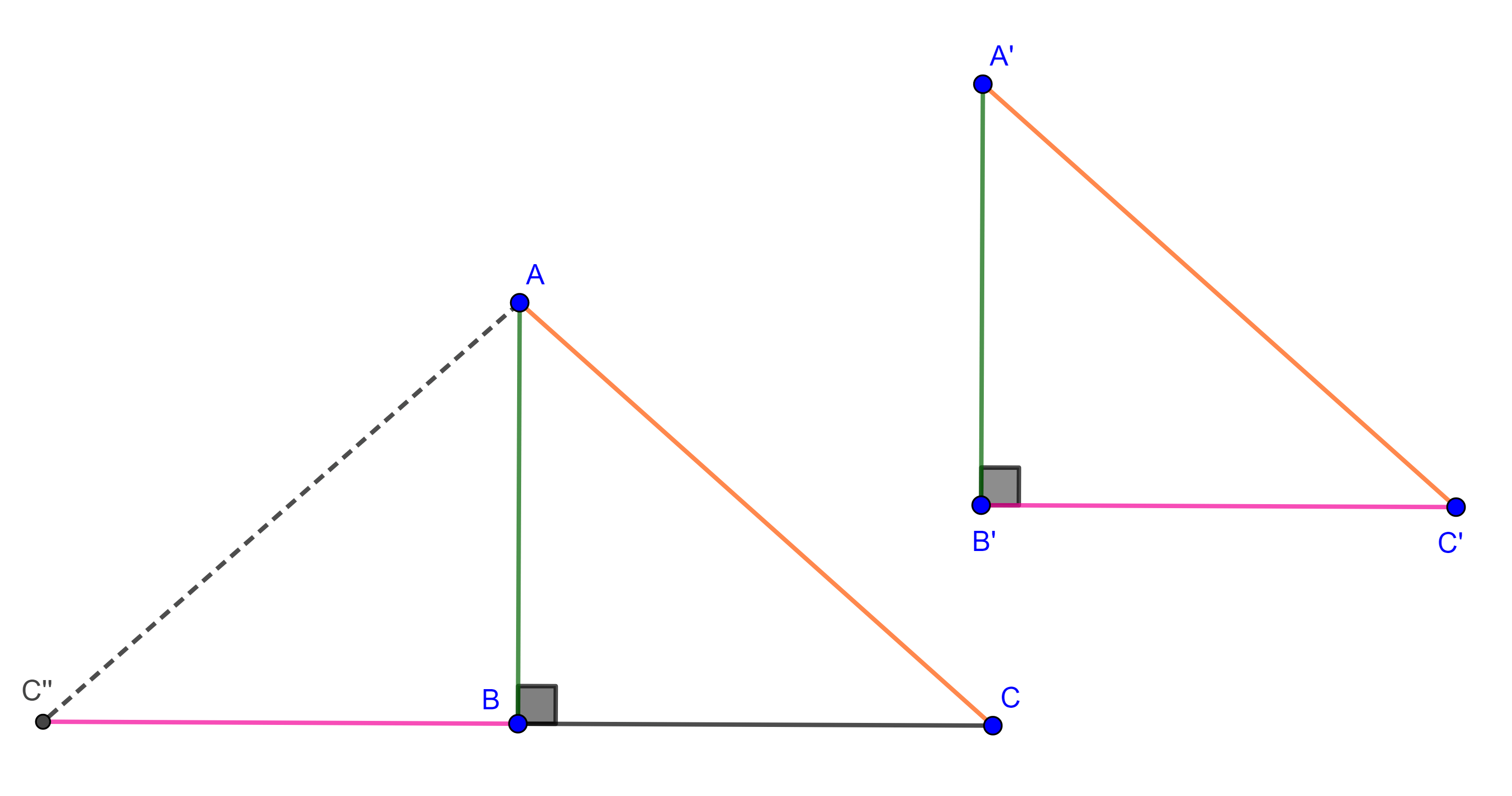
Sobre la recta determinada por $B$ y $C$ construimos un punto $C^{″}$ del lado opuesto a $C$ respecto a $B$, tal que $B{C}^{″}=B^{\prime }{C}^{\prime }$.

Entonces por LAL, $\mathrm{△}AB{C}^{″}\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$, por lo tanto, $A{C}^{″}=A^{\prime }{C}^{\prime }$, por hipótesis $AC=A^{\prime }{C}^{\prime }$, así que $AC=A{C}^{″}$.

Como $\mathrm{△}{C}^{″}AC$ es isósceles y por construcción $AB$ es la altura trazada desde $A$, por la proposición, $AB$ coincide con la mediatriz de $C^{″}C$, por lo que $B{C}^{″}=BC$, pero $B{C}^{″}=B^{\prime }{C}^{\prime }$ por construcción, por lo tanto, $BC=B^{\prime }{C}^{\prime }$, finalmente por LLL, $\mathrm{△}ABC\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Más adelante…

En la siguiente entrada estudiaremos la desigualdad del triangulo y su reciproco, presentaremos el concepto de lugar geométrico y mostraremos un par de ejemplos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Muestra que si se hacen dos reflexiones sucesivas con respecto a dos rectas paralelas, el resultado es una traslación.
2. Muestra que si se hacen dos reflexiones sucesivas con respecto a dos rectas concurrentes, se obtiene una rotación con respecto al punto de intersección entre las rectas.
3. $i)$ Muestra que si un triangulo tiene dos ángulos iguales, entonces los lados opuestos a estos ángulos también son iguales.
   $ii)$ Muestra que los ángulos internos de un triángulo equilátero son iguales.
4. Si dos rectas distintas se intersecan forman 4 ángulos, prueba que las bisectrices de ángulos opuestos por el vértice son la misma y que las bisectrices de ángulos adyacentes son perpendiculares.
5. Dado un segmento, construye su mediatriz.
6. Demuestra sin usar el quinto postulado (lo que implica que los ángulos interiores de todo triangulo suman dos ángulos rectos), que todo ángulo exterior de un triángulo es mayor que cualquiera de los ángulos interiores no adyacentes a el.
7. Muestra con un ejemplo que el criterio LLA en general no se cumple, es decir, cuando dos triángulos diferentes tienen dos lados y un ángulo correspondientes iguales, pero el ángulo no es el que forman los lados correspondientes iguales.

Entradas relacionadas

• Ir a Geometría Moderna I
• Entrada anterior del curso: Postulados de Euclides.
• Siguiente entrada del curso: Desigualdad del triángulo y lugar geométrico.

Fuentes

• Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 10-16.
• Math Bits Notebook
• Geometría interactiva
• Geometry Help
• Math Open Reference
• Math is Fun

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»