Ninguna investigación humana puede ser llamada verdadera
ciencia si no puede ser demostrada matemáticamente.
– Leonardo da Vinci
Introducción
En la entrada anterior estudiamos algunas propiedades de las soluciones de las ecuaciones diferenciales ordinarias, en particular vimos que una ecuación diferencial puede tener infinitas soluciones y el intervalo de solución puede ser cualquiera en el que la función esté definida, sea derivable $n$ veces y cuyas derivadas sean continuas. En esta entrada estudiaremos cómo obtener una solución particular de una solución general dados unos valores prescritos conocidos como condiciones iniciales y veremos la importancia de saber elegir el intervalo de solución en estos casos particulares.
En esta entrada también estudiaremos algunos problemas del mundo real que involucran ecuaciones diferenciales, a través de estos problemas introduciremos la idea de ecuación diferencial como modelo matemático. Los problemas que estudiaremos tienen el objetivo de presentar el análisis que debemos hacer al intentar modelar un problema usando ecuaciones diferenciales y no con el propósito de resolver el problema mismo, pues resolverlo significa determinar las soluciones de las ecuaciones diferenciales que surjan y hasta este momento aún no hemos visto métodos de resolución.
Problema con valores iniciales
$$\dfrac{d^{(n)}y}{dx^{(n)}} = f(x, y, y^{\prime}, \cdots, y^{(n –1)}) \label{1} \tag{1}$$ sujeto a que se cumpla $$y(x_{0}) = y_{0}, \hspace{0.5cm} y^{\prime}(x_{0}) = y_{1}, \hspace{0.5cm} \cdots, \hspace{0.5cm} y^{(n -1)}(x_{0}) = y_{n -1} \label{2} \tag{2}$$ donde $y_{0}, y_{1}, \cdots, y_{n -1}$ son contantes reales arbitrarias dadas, se llama problema con valores iniciales (PVI), o problema con valores iniciales de $n$-ésimo orden.
$$y(x_{0}) = y_{0}, \hspace{0.5cm} y^{\prime}(x_{0}) = y_{1}, \hspace{0.5cm} \cdots, \hspace{0.5cm} y^{(n -1)}(x_{0}) = y_{n -1}$$ se llaman condiciones iniciales.
De manera resumida podemos decir que un problema con valores iniciales es la ecuación diferencial acompañada de condiciones iniciales.
En el caso de ecuaciones diferenciales de primer y segundo orden tendríamos el siguiente PVI respectivamente:
- Resolver $\dfrac{dy}{dx} = f(x, y)$ $\hspace{1.2cm}$ sujeto a $\hspace{0.5cm}$ $y(x_{0}) = y_{0}$
- Resolver $\dfrac{d^{2}y}{dx^{2}} = f(x, y, y^{\prime})$ $\hspace{0.5cm}$ sujeto a $\hspace{0.5cm}$ $y(x_{0}) = y_{0}$ $\hspace{0.3cm}$ y $\hspace{0.3cm}$ $y^{\prime}(x_{0}) = y_{1}$
Geométricamente un PVI de primer orden significa que estamos buscando una solución $y(x)$ de la ecuación diferencial en un intervalo $\delta$ que contenga a $x_{0}$ tal que su gráfica pase por el punto $(x_{0}, y_{0})$.
En el caso del PVI de segundo orden estamos buscando una solución $y(x)$ de la ecuación diferencial en un intervalo $\delta$ que contenga a $x_{0}$ de tal manera que su gráfica no sólo pase por el punto $(x_{0}, y_{0})$, sino que también la pendiente a la curva en ese punto tenga como valor $m = y_{1}$.
En la entrada anterior vimos que las soluciones generales tienen constantes arbitrarias, las condiciones iniciales de un PVI nos permitirá determinar el valor de dichas contantes para obtener una solución particular, pues con frecuencia resolver un problema con valores iniciales de $n$-ésimo orden implica primero determinar una familia $n$-paramétrica de soluciones de la ecuación diferencial dada y después usando las $n$ condiciones iniciales en $x_{0}$ determinar los valores numéricos de las $n$ constantes de la familia. Es importante mencionar que la solución particular obtenida debe estar definida en algún intervalo $\delta$ que contenga al punto inicial $x_{0}$. Veamos un ejemplo.
Ejemplo: Considerar la solución general
$$y(x) = c_{1} e^{2x} + c_{2} e^{-x} + c_{3}e^{3x}$$
de la ecuación diferencial
$$y^{\prime \prime \prime} -4 y^{\prime \prime} + y^{\prime} +6y = 0$$
(Más adelante en el curso estudiaremos la forma de obtener este tipo de soluciones). Encontrar la solución particular dadas las siguientes condiciones iniciales:
$$y(0) = 4, \hspace{1cm} y^{\prime}(0) = -1, \hspace{1cm} y \hspace{1cm} y^{\prime \prime}(0) = 0$$
Solución: Como tarea moral verifica que en efecto la función dada es solución de la ecuación diferencial, por ahora asumiremos que lo es.
Tenemos un problema con valores iniciales, así que la solución está sujeta a las condiciones iniciales, lo que debemos hacer para obtener la solución particular no es más que aplicar las condiciones iniciales. En este caso $x_{0} = 0$, la primera condición inicial nos dice que se debe satisfacer $y(x_{0}) = y(0) = 4$, entonces evaluemos la solución en $x_{0} = 0$ y el resultado lo igualamos a $4$.
\begin{align*}
y(0) &= c_{1} e^{2(0)} + c_{2} e^{-0} + c_{3}e^{3(0)} \\
&= c_{1} + c_{2} + c_{3} \\
&= 4
\end{align*}
El resultado de aplicar la primera condición inicial es
$$y(0) = c_{1} + c_{2} + c_{3} = 4$$
Para aplicar la segunda condición inicial necesitamos la derivada de la solución general, dicha función es
$$y^{\prime}(x) = 2c_{1}e^{2x} -c_{2}e^{-x} + 3c_{3}e^{3x}$$
Apliquemos la segunda condición inicial, $y^{\prime}(0) = -1$.
\begin{align*}
y^{\prime}(0) &= 2c_{1} e^{2(0)} -c_{2} e^{-0} + 3c_{3}e^{3(0)} \\
&= 2c_{1} -c_{2} + 3c_{3} \\ &
= -1
\end{align*}
El resultado de aplicar la segunda condición inicial es
$$y^{\prime}(0) = 2c_{1} -c_{2} + 3c_{3} = -1$$
Finalmente, para aplicar la tercera condición inicial necesitamos la segunda derivada de la solución general, esto es
$$y^{\prime \prime}(x) = 4c_{1}e^{2x} + c_{2}e^{-x} + 9c_{3}e^{3x}$$
Apliquemos la condición inicial $y^{\prime \prime}(0) = 0$.
\begin{align*}
y^{\prime \prime}(0) &= 4c_{1} e^{2(0)} + c_{2} e^{-0} + 9c_{3}e^{3(0)} \\
&= 4c_{1} + c_{2} + 9 c_{3} \\
&= 0
\end{align*}
El resultado de aplicar la tercera condición inicial es
$$y^{\prime \prime}(0) = 4c_{1} + c_{2} + 9c_{3} = 0$$
De las ecuaciones obtenidas de aplicar las condiciones iniciales formamos el siguiente sistema de ecuaciones.
\begin{align*}
c_{1} + c_{2} + c_{3} &= 4 \\
2c_{1} -c_{2} + 3c_{3} &= -1 \\
4c_{1} + c_{2} + 9c_{3} &= 0
\end{align*}
Intenta resolver el sistema de ecuaciones usando el método que gustes. Una vez que lo resuelvas notarás que los valores para las incógnitas son:
$$c_{1} = \dfrac{10}{3}, \hspace{1cm} c_{2} = \dfrac{29}{12} \hspace{1cm} y \hspace{1cm} c_{3} = -\dfrac{7}{4}$$
Sólo basta sustituir estos valores en la solución general de la ecuación diferencial para obtener la solución particular. Por lo tanto, la solución particular sujeta a las condiciones iniciales es:
$$y(x) = \dfrac{10}{3} e^{2x} + \dfrac{29}{12} e^{-x} -\dfrac{7}{4}e^{3x}$$
$\square$
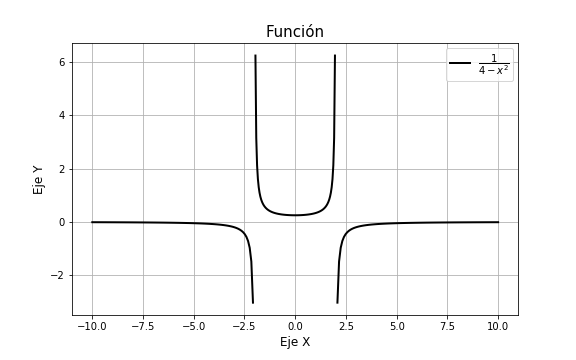
En la entrada anterior vimos que el intervalo de solución $\delta$ no es necesariamente el dominio de la función, sino que podemos tomar cualquier intervalo en el que la solución es derivable $n$ veces con derivadas continuas en ese intervalo, en el caso de los problemas con valores iniciales es necesario que el punto $x_{0}$ pertenezca al intervalo de solución $\delta$, esto en ocasiones establecerá un intervalo limitado para la solución, así que debemos tener cuidado con los valores en los que la solución particular está definida. Para visualizar este hecho retomemos el ejemplo visto en la entrada anterior donde mostramos que la función
$$y(x) = \dfrac{1}{4 -x^{2}}$$
es solución de la ecuación diferencial
$$\dfrac{dy}{dx} = 2xy^{2}$$
Realicemos este mismo ejercicio, pero ahora visto como un problema de valores iniciales y veamos la importancia de elegir correctamente el intervalo solución.
Ejemplo: La ecuación diferencial
$$\dfrac{dy}{dx} = 2xy^{2}$$
tiene como solución general a la función
$$y(x) = -\dfrac{1}{x^{2} + c_{1}}$$
Determinar la solución particular dada la condición inicial
$$y(0) = \dfrac{1}{4}$$
Solución: La solución general es
$$y(x) = -\dfrac{1}{x^{2} + c_{1}}$$
Aplicando la condición inicial obtenemos lo siguiente.
$$y(0) = -\dfrac{1}{0^{2} + c_{1}} = -\dfrac{1}{c_{1}} = \dfrac{1}{4}$$
De la última igualdad obtenemos $c_{1} = -4$, sustituyendo en la solución general se tiene
\begin{align*}
y(x) = -\dfrac{1}{x^{2} + c_{1}} = -\dfrac{1}{x^{2} -4} = \dfrac{1}{4 -x^{2}}
\end{align*}
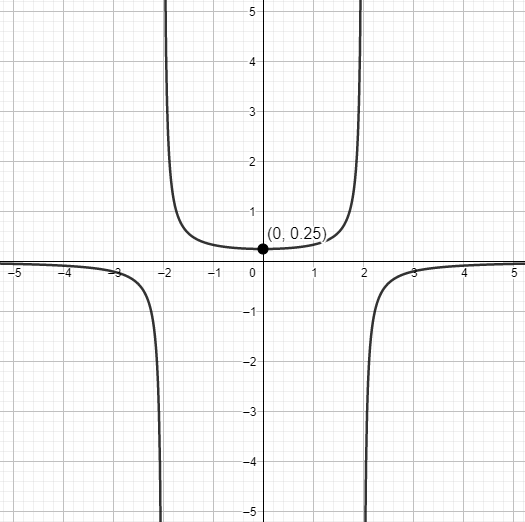
Así que la solución particular
$$y(x) = \dfrac{1}{4 -x^{2}}$$
corresponde a un PVI de $\dfrac{dy}{dx} = 2xy^{2}$ con la condición inicial $y(0) = \dfrac{1}{4}$. En la entrada anterior mostramos la gráfica de esta función.
Pero ahora el intervalo de solución debe ser aquel en el que $x_{0} = 0 \in \delta$. El intervalo más grande que puede tomar la solución particular es $\delta = (-2, 2)$, pues es el intervalo donde está el punto $x_{0} = 0$ y donde la solución es continua. ¡La condición inicial ha restringido el intervalo de solución!
$\square$
Con este ejemplo vemos que las condiciones iniciales establecen un intervalo de solución especifico, en ocasiones (como en el primer ejemplo visto en esta entrada) no habrá mayor problema con el intervalo si la función es derivable y por tanto continua es todo su dominio. Es recomendable primero determinar en donde la solución está definida (encontrar su dominio) y posteriormente revisar si se trata sólo de una solución general o si hay condiciones iniciales que determinarán una solución particular.
Existencia de una solución única
Al trabajar con problemas con valores iniciales debemos hacernos dos preguntas importantes. ¿Existe la solución del problema? y si existe la solución, ¿es única?. Más adelante estudiaremos las ecuaciones diferenciales de primer orden y retomaremos con mayor profundidad este tema, por ahora sólo vamos a enunciar un teorema que da las condiciones suficientes para garantizar la existencia y unicidad de una solución de un PVI de primer orden.
$$\dfrac{dy}{dx} = f(x, y) \label{3} \tag{3}$$ donde $f(x, y)$ está definida en una región rectangular $U$ en el plano $XY$, la región está definida por $a \leq x \leq b$, $c \leq y \leq d$ y contiene al punto $(x_{0}, y_{0})$ en su interior. Si $f(x, y)$ satisface las condiciones:
Entonces existe algún intervalo $\delta_{0}: (x_{0} -h, x_{0} + h)$, $h > 0$, contenido en $[a, b]$, y una función única $y(x)$, definida en $\delta_{0}$, que satisface la condición inicial $y(x_{0}) = y_{0}$.
Dicho de otra manera, las condiciones para la existencia de soluciones son:
- Continuidad de $f(x, y)$ en $U$.
- Acotamiento de $f(x, y)$ por $U$.
Y las condiciones para la unicidad son:
- Continuidad de $f(x, y)$ y $\dfrac{\partial f}{\partial y}$ en $U$.
- Acotamiento de $f(x, y)$ y $\dfrac{\partial f}{\partial y}$ por $U$.
Estas condiciones son suficientes, pero no necesarias, puede existir una solución única que satisface $y(x_{0}) = y_{0}$, pero que no cumple con alguna de las condiciones anteriores o que no cumple con ninguna.
Problemas que se modelan con ecuaciones diferenciales
Las matemáticas permiten modelar muchos de los fenómenos que ocurren en en mundo real, a esta descripción matemática de un sistema de fenómenos se le denomina modelo matemático y se construyen con la intención de representar algunas características del fenómeno para después hacer predicciones. Es cierto que esto puede ser un proceso muy difícil ya que implica que las hipótesis que hagamos deben ser descritas en fórmulas muy precisas que nos permitan predecir lo que ocurrirá. Una vez construido un modelo, las predicciones se deben comparar con los datos del sistema, dependerá de la compatibilidad entre las hipótesis y las predicciones lo que defina si debemos confiar en el modelo o debemos mejorar nuestras suposiciones.
En el caso de las ecuaciones diferenciales, éstas nos permiten modelar sistemas que evolucionan con el tiempo o sistemas que implican una razón de cambio de una o más variables. En este curso consideraremos a un modelo matemático como una ecuación diferencial o un sistema de ecuaciones diferenciales que describen el comportamiento de un fenómeno que estemos estudiando. Una vez que hemos formulado un modelo matemático surge el reto de resolver las ecuaciones diferenciales para saber si la solución es consistente con los hechos conocidos acerca del comportamiento del sistema y si no lo es debemos repetir un proceso de modelado en el que vamos ajustando las hipótesis, identificamos nuevas variables o incluso incluimos leyes empíricas que se puedan aplicar al sistema.
Hasta ahora ya hemos estudiado algunas ecuaciones diferenciales, sabemos cómo verificar cuando una función es solución y hemos estudiado algunas de sus propiedades. Para concluir esta entrada vamos a analizar algunos problemas del mundo real que son modelados con ecuaciones diferenciales. En esta parte nos enfocaremos en la forma en la que surgen las ecuaciones dado un problema y no nos preocuparemos por resolverlas, pues esto es algo que aún desconocemos.
Propagación de una enfermedad contagiosa
Recientemente hemos tenido la experiencia de observar cómo es que una enfermedad contagiosa se puede propagar en la población. En términos muy generales intentemos modelar la propagación de una enfermedad contagiosa a través de una comunidad de personas que han estado en contacto con personas enfermas.
Definamos a $x(t)$ como el número de personas que están enfermos en un cierto tiempo $t$ y sea $y(t)$ el número de personas que aún no han sido expuestas al contagio en ese momento $t$. Es claro que la razón $\dfrac{dx}{dt}$ con la que se propaga la enfermedad debe ser proporcional al número de encuentros o interacciones entre los dos grupos de personas. Si suponemos que el número de interacciones es conjuntamente proporcional a $x(t)$ y $y(t)$, entonces un modelo puede ser
$$\dfrac{dx}{dt} = cxy \label{4} \tag{4}$$
donde $c$ es la constante de proporcionalidad. Consideremos una comunidad con una población fija de $n$ personas, si inicialmente nadie tiene la enfermedad entonces $y = n$, pero si a esa comunidad llega una persona enferma $x = 1$, entonces podemos construir la siguiente relación.
$$x + y = n + 1 \label{5} \tag{5}$$
de donde podemos despejar a $y$ como
$$y = n + 1 -x$$
y sustituir en el modelo.
$$\dfrac{dx}{dt} = cx(n + 1 -x) \label{6} \tag{6}$$
Esta última ecuación sería el modelo que describe la propagación de la enfermedad a través del tiempo. Una condición inicial sería que en el momento en el que llego la persona enferma a la comunidad comenzó a propagarse la enfermedad, esto es, $x(0) = 1$.
$\square$
Ley de enfriamiento de Newton
La ley de enfriamiento de Newton establece que la razón de cambio de la temperatura $T(t)$ de un cuerpo con respecto al tiempo $t$ es proporcional a la diferencia entre la temperatura del cuerpo $T(t)$ y la temperatura del medio ambiente $T_{m}$. Esta ley puede ser modelada con la siguiente ecuación diferencial.
$$\dfrac{dT}{dt} = -k(T -T_{m}) \label{7} \tag{7}$$
donde $k > 0$ es la contante de proporcionalidad y $T_{m}$ es la temperatura del medio ambiente considerada también una constante. Si podemos resolver esta ecuación encontraríamos una función que podría predecir la temperatura del cuerpo en cualquier tiempo $t$.
Sin embargo, sin resolver la ecuación podemos notar que si $T > T_{m}$, entonces $\dfrac{dT}{dt} < 0$, lo que significa que el cuerpo se estaría enfriando, pues la función $T(t)$ sería una función decreciente mientras avanza el tiempo. Por otro lado, si $T < T_{m}$, entonces $\dfrac{dT}{dt} > 0$, es decir la función $T(t)$ sería una función creciente en el tiempo lo que físicamente significa que el cuerpo se esta calentando.
$\square$
Cuerpos en caída
Consideremos un objeto que es lanzado desde lo alto de un edificio, el problema que queremos analizar es hallar la forma de conocer la posición del objeto con respecto al suelo en algún tiempo $t$ después de ser lanzado y antes de tocar el suelo. Por convención consideremos que la dirección hacía arriba es positiva.
Analicemos la situación. Consideremos un edificio de altura $r_{0}$, desde esa altura se lanza un objeto de masa $m$, la velocidad inicial con la que es lanzado es $v_{0}$. El objeto al caer esta sometido a la fuerza de gravedad, la segunda ley de Newton nos dice que cuando la fuerza neta $F$ que actúa sobre un cuerpo no es cero, entonces la fuerza neta es proporcional a su aceleración $a$, estas cantidades están relacionadas por la ecuación
$$F = ma \label{8} \tag{8}$$
con $m$ la masa del cuerpo, si el objeto esta en caída la fuerza neta será su peso.
$$F = -W \label{9} \tag{9}$$
El signo menos es porque el peso del objeto es una fuerza dirigida hacia abajo. Recordando que el peso está dado como
$$W = mg \label{10} \tag{10}$$
donde $m$ es la masa del objeto y $g$ es la aceleración debido a la gravedad de la tierra, usando entonces la segunda ley de Newton podemos establecer que
$$F = ma = -mg = -W$$
es decir $a = -g$. Recordemos que la aceleración de un objeto corresponde a la tasa de cambio de la velocidad y que a su vez la velocidad es la tasa de cambio de la posición del objeto, es decir, la aceleración es la segunda derivada de la posición con respecto al tiempo, si $r(t)$ es la posición del objeto, entonces
$$a(t) = \dfrac{d^{2}r}{dt^{2}} = \ddot{r}(t) \label{11} \tag{11}$$
Por lo tanto, la ecuación diferencial que modela nuestro problema es
$$\dfrac{d^{2}r}{dt^{2}} = -g \label{12} \tag{12}$$
Las condiciones iniciales son claras, al tiempo $t = 0$ el objeto se encuentra en la posición mas alta del edificio es decir $r(0) = r_{0}$ y la velocidad con la que es lanzada al tiempo $t = 0$ es $v(0) = \dot{r}(0) = v_{0}$. Resolviendo la ecuación diferencial y obteniendo la solución particular podremos predecir la posición del objeto con respecto al suelo a cualquier tiempo $t$ antes de caer por completo.
$\square$
Modelo logístico de la población
Este es uno de los modelos más estudiados y representativos al estudiar ecuaciones diferenciales. Lo que se quiere estudiar es el crecimiento de una población, queremos crear un modelo que prediga el crecimiento que puede haber en una población en función de su entorno y los recursos limitados a los que están sujetos. Para comenzar con este estudio se pueden considerar las siguientes hipótesis.
- Si la población es pequeña, la tasa de crecimiento de la población es proporcional a su tamaño.
- Si la población es demasiado grande para ser soportada por su entorno y recursos, la población disminuirá, en este caso la tasa de crecimiento será negativa.
Las variables involucradas en este problema son las siguientes:
Por supuesto el tiempo $t$ es la variable independiente en la que queremos predecir. Otra variable es la población $P$, esta variable es dependiente del tiempo $P = P(t)$, $k$ será el parámetro que corresponde a la razón de crecimiento en el caso de poblaciones pequeñas y $N$ será otro parámetro que establece cuando la población comienza a ser demasiado grande. El parámetro $N$ se conoce como capacidad de soporte del entorno. De acuerdo a las hipótesis anteriores, estamos suponiendo que $P(t)$ crece si $P(t) < N$ y decrece si $P(t) > N$. Ahora que conocemos las variables que estarán presente en el modelo, matemáticamente podemos escribir a las hipótesis como:
- $\dfrac{dP}{dt} = kP$ $\hspace{0.5cm}$ si $P$ es pequeña.
- $\dfrac{dP}{dt} < 0$ $\hspace{0.8cm}$ si $P$ es grande, tal que $P > N$
Queremos una expresión (ecuación diferencial) que involucre ambas hipótesis. Supongamos que la ecuación que buscamos es de la forma
$$\dfrac{dP}{dt} = k \alpha P \label{13} \tag{13}$$
Donde $\alpha$ es una función que debe acoplarse a las hipótesis. Para que satisfaga la primea hipótesis debe ocurrir que $\alpha$ sea cercano a $1$ cuando $P$ es pequeño y que $\alpha < 0$ cuando $P > N$. La expresión más simple que satisface esto es
$$\alpha = 1 -\dfrac{P}{N} \label{14} \tag{14}$$
Podemos notar que si $P = 0$, entonces $\alpha = 1$ y si $P > N$, entonces $\alpha < 0$. Por lo tanto, la ecuación diferencial que describe esta situación es:
$$\dfrac{dP}{dt} = k \left(1 -\dfrac{P}{N}\right) P \label{15} \tag{15}$$
Éste es el modelo logístico de la población con velocidad de crecimiento $k$ y capacidad de soporte $N$. Como podemos notar es una ecuación diferencial no lineal y su solución la analizáremos con detalle más adelante en el curso.
$\square$
Sistemas Depredador – Presa
Para concluir estudiemos otro de los modelos más estudiados en ecuaciones diferenciales, el modelo depredador – presa. En el mundo ninguna especie vive aislada y sus interacciones pueden proporcionar algunos de los modelos más interesantes por estudiar. El problema que analizaremos es en el que una especie se come a otra, con fines ilustrativos consideremos a la especie depredador como zorros y a la especie presa como conejos. Llamemos $Z(t)$ a la variable dependiente que describe el número de zorros que hay en una cierta región y sea $C(t)$ otra variable dependiente que describe el número de conejos que hay en esa misma región, ambas funciones son dependientes del tiempo $t$. Nuestras hipótesis tienen que ser tales que describan el aumento o disminución de ambas poblaciones de acuerdo a las interacciones que hay entre zorros y conejos, es claro que si hay muchos conejos los zorros tendrán alimento y su población crecerá, mientras que la de conejos disminuirá y por otro lado, si hay pocos conejos la población de zorros disminuirá (morirán por falta de alimento), mientras que la de conejos aumentará. Las hipótesis que consideraremos son las siguientes:
- Si no hay zorros presentes, los conejos se reproducen a una tasa proporcional a su población y no les afecta la sobrepoblación.
- Los zorros se comen a los conejos y la razón a la que los conejos son devorados es proporcional a la tasa a la que los zorros y conejos interactúan.
- Sin conejos que comer, la población de zorros disminuirá a una tasa proporcional a ella misma.
- La tasa de nacimientos de los zorros crece en proporción al número de conejos comidos por zorros que, por la segunda hipótesis, es proporcional a la tasa a la que los zorros y conejos interactúan.
Las variables que tenemos hasta ahora son el tiempo $t$ y las poblaciones $Z(t)$ y $C(t)$, para satisfacer las hipótesis necesitamos de parámetros que las modelen. Los parámetros que consideraremos son los siguientes:
- $a$ es el coeficiente de la tasa de crecimiento de conejos.
- $b$ es la constante de proporcionalidad que mide el número de interacciones conejos-zorros en las que el conejo es devorado.
- $c$ es el coeficiente de la tasa de muertes de zorros.
- $d$ es la constante de proporcionalidad que mide el beneficio a la población de zorros de un conejo devorado.
Tomaremos la convención de que todos estos parámetros son positivos. En este caso particular tenemos dos variables dependientes del tiempo por lo tanto será necesario encontrar dos ecuaciones que modelen al sistema. Para que sea más intuitivo entender el modelo vamos a mostrar las ecuaciones que modelan el sistema y veamos por qué son así.
\begin{align*}
\dfrac{dC}{dt} &= aC -bCZ \\
\dfrac{dZ}{dt} &= -cZ + dCZ \label{16} \tag{16}
\end{align*}
La primer hipótesis nos habla de una relación proporcional en el crecimiento de la población de conejos cuando no hay zorros presentes, de ahí el término $aC$ de la primer ecuación, lo mismo ocurre con la tercera hipótesis, pero en este caso se trata de un decremento de población de zorros tras la falta de conejos, por ello el signo menos en el término $-cZ$ de la segunda ecuación. Por otro lado, la segunda y cuarta hipótesis nos habla de una interacción entre los zorros y los conejos, esta interacción puede ser modelada con el producto $CZ$, con este producto hacemos que la interacción aumente si $C$ o $Z$ aumentan, pero desaparece si $C = 0$ o $Z = 0$, así en el caso de la segunda hipótesis los conejos son devorados de manera proporcional a la interacción entre zorros y conejos, por ello agregamos el término $-bCZ$ en la primer ecuación, el signo menos indica que el número de conejos debe disminuir, pues están siendo devorados, así mismo, la cuarta hipótesis nos habla de un crecimiento en el número de zorros al comer conejos, esta interacción es modelada con el término $dCZ$, en este caso es positivo ya que los zorros están aumentando en número. Este análisis es lo que le da sentido al modelo (\ref{16}) que hemos creado.
Algo interesante que notamos es que ahora tenemos dos ecuaciones diferenciales que modelan el fenómeno. Cuando hay dos o más ecuaciones diferenciales decimos que es un sistema de ecuaciones diferenciales, en este caso este sistema de ecuaciones lo llamamos sistema de primer orden de ecuaciones diferenciales ordinarias, se dice también que el sistema es acoplado porque las tasas de cambio $\dfrac{dC}{dt}$ y $\dfrac{dZ}{dt}$ dependen tanto de $C$ como de $Z$. Los sistemas de ecuaciones diferenciales será un tema que estudiaremos en la tercera unidad del curso.
Una solución al modelo que hemos construido consiste en encontrar un par de funciones $C(t)$ y $Z(t)$ que describan las poblaciones de conejos y zorros como funciones del tiempo. Como el sistema es acoplado, no podemos determinar cada una de esas funciones de forma aislada, sino que debemos resolver ambas ecuaciones diferenciales de forma simultánea, sin embargo en este caso no es posible determinar de modo explícito formulas para $C(t)$ y $Z(t)$, no pueden ser expresadas en términos de funciones conocidas tales como polinomios, senos, cosenos, exponenciales, etcétera. Más adelante veremos que las funciones $C(t)$ y $Z(t)$ existen, pero entonces, ¿cómo conocerlas?. En la siguiente entrada estudiaremos un método cualitativo de las ecuaciones diferenciales que puede ser un método que nos ayude en estos casos, por ejemplo.
$\square$
Por supuesto estos son sólo algunos problemas ilustrativos en los que las ecuaciones diferenciales modelan algún fenómeno natural, pero la cantidad de fenómenos que involucran ecuaciones diferenciales son enormes y un tanto el objetivo es que conforme vayamos aprendiendo seamos capaces de construir nuestros propios modelos sobre algún fenómeno que observemos a nuestro alrededor.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- Dada la ecuación diferencial y su solución general, verificar que la función $y(x)$ es solución, determinar la solución particular dadas las condiciones iniciales y determinar el intervalo de solución $\delta$ en donde puede estar definida dicha solución.
- $\dfrac{dy}{dx} = y^{2}, \hspace{1cm} y(x) = \dfrac{1}{c_{1} -x}, \hspace{1cm} y(1) = 2$.
- $\dfrac{dy}{dx} + y = 0, \hspace{1cm} y(x) = c_{1}e^{-x}, \hspace{1cm} y(0) = 2$.
- $\dfrac{d^{2}y}{dx^{2}} + y = 0, \hspace{1cm} y(x) = c_{1} \cos(x) + c_{2} \sin(x), \hspace{1cm} y(0) = -1 \hspace{0.5cm} y \hspace{0.5cm} y^{\prime}(0) = 8$.
- Considerar el modelo de población
$\dfrac{dP}{dt} = 0.4 P \left( 1 -\dfrac{P}{230} \right)$
donde $P(t)$ es la población en el tiempo $t$.
- ¿Para qué valores de $P$ está en equilibrio la población?.
- ¿Para qué valores de $P$ está creciendo la población?.
- ¿Para qué valores de $P$ está decreciendo la población?.
- El sistema
$\dfrac{dx}{dt} = ax -by\sqrt{x}$
$\dfrac{dy}{dt} = cy\sqrt{x}$
ha sido propuesto como un modelo para un sistema depredador – presa de dos especies particulares de microorganismos (con $a$, $b$ y $c$ parámetros positivos).
- ¿Qué variable, $x(t)$ o $y(t)$, representa a la población depredadora? y ¿qué variable representa a la población presa?.
- ¿Qué le pasa a la población depredadora si la presa se extingue?.
Más adelante…
Más adelante aprenderemos a resolver ecuaciones diferenciales ordinarias de primer orden de forma analítica, una vez que estemos listos puede ser conveniente regresar a esta entrada e intentar resolver las ecuaciones diferenciales que modelan cada uno de los problemas vistos para extrapolar en los resultados.
Pero antes de estudiar métodos analíticos estudiaremos un método geométrico o mejor conocido como método cualitativo de las ecuaciones diferenciales que nos permitirá describir las soluciones sin conocer explícitamente la forma analítica de las funciones solución.
Entradas relacionadas
- Página principal del curso: Ecuaciones Diferenciales I
- Entrada anterior del curso: Soluciones a las ecuaciones diferenciales
- Siguiente entrada del curso: Campos de pendientes y su ecuación diferencial asociada
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»