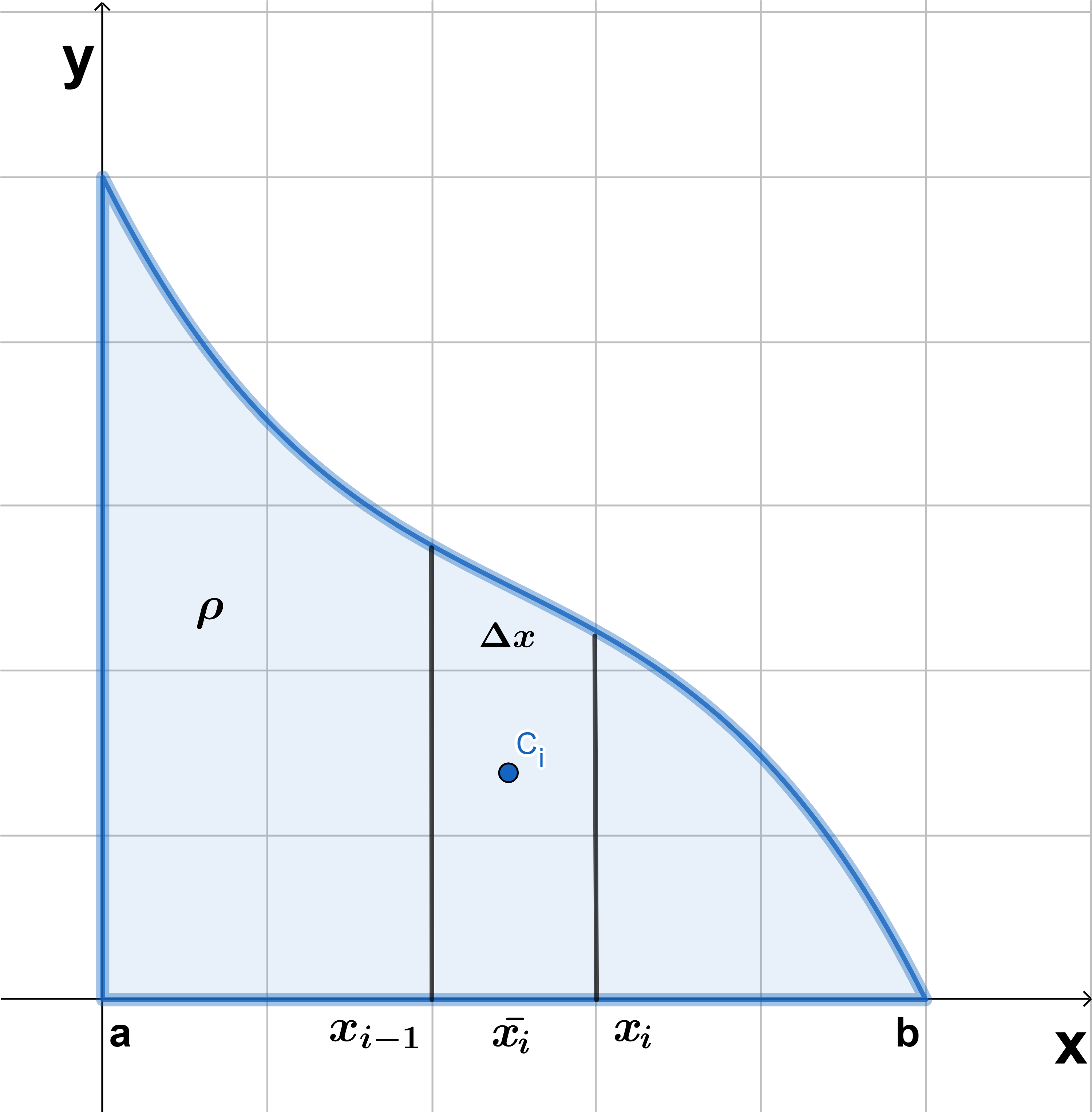Introducción
En la sección anterior vimos como calcular el momento y el centro de masa con ayuda de la integral, en esta sección revisaremos el concepto de trabajo en el área de la física como una aplicación más de la integración.
Trabajo
Consideremos una partícula $P$ en un plano, que se mueve una distancia $d$ a lo largo de una curva $C$ como resultado de la aplicación de una fuerza externa $F$, que es función de la posición de la partícula en el espacio, es decir, $F=F(x)$ y sea $dx$ un desplazamiento infinitesimal experimentado por la partícula en un intervalo de tiempo $dt$, se define el trabajo infinitesimal $dW$ a la fuerza $F$ durante el desplazamiento infinitesimal $dx$ al producto escalar $F \cdot dx$ esto es:
$$dW=F \cdot dx$$
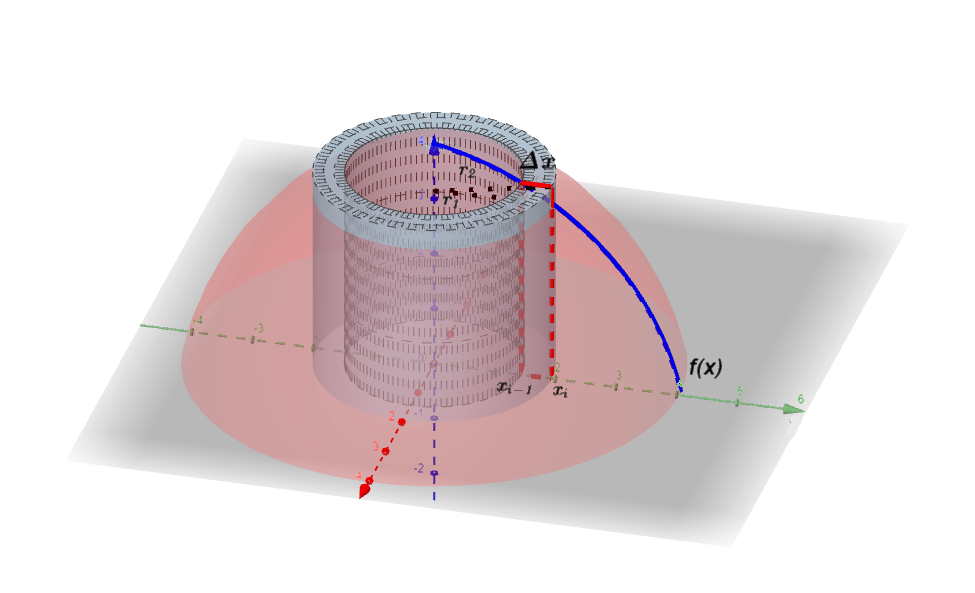
Ahora, supongamos que la partícula $P$ recorre una trayectoria en el espacio a lo largo del eje $x$, para determinar el trabajo que se realiza sobre esta partícula en un desplazamiento a lo largo de las posiciones $a$ y $b$, hacemos una partición en el intervalo $[a, b]$ en $n$ subintervalos con puntos extremos $x_{0}, x_{1}, …., x_{n}$ e igual ancho $\Delta x$. Sea $x^{*}_{i^{}}$ un punto en el subintervalo $[x_{i-1}, x_{i}]$, si $F$ es continua en el intervalo $[a,b]$ entonces podemos aproximar el trabajo como una suma dada como:
$$Trabajo \approx \sum_{i=1}^{n}F(x^{*}_{i^{}})\Delta x$$
Por tanto, se define el trabajo efectuado al mover una partícula u objeto en el intervalo $[a, b]$ como el límite cuando $n \to \infty$ como:
$$W=\lim_{n \to \infty}\sum_{i=1}^{n}F(x^{*}_{i^{}})\Delta x=\int_{a}^{b}F(x)dx \tag{1}$$
En el sistema internacional de unidades $(SI)$, el trabajo se mide en Joules $(J)$.
Ley de Hooke
La ley de Hooke nos dice que la fuerza necesaria para estirar o comprimir un resorte a una cierta longitud a partir de su estado de equilibrio, es proporcional a $x$, es decir:
$$F=-kx \tag{2}$$
Donde $k$ es la constante del resorte o constante de fuerza del resorte, esta constante $k$ es una característica propia del resorte. Nótese que $k$ es positiva.
Ejemplos
- Cuando una partícula se ubica una distancia $x$ pies del origen, una fuerza de $x^{2}+2x$ libras actúa sobre ella. ¿Cuánto trabajo se efectúa al moverla desde $x=1$ hasta $x=3$?
De la definición del trabajo $(1)$, tenemos que:
$$W=\int_{1}^{3}(x^{2}+2x)dx=\left [ \frac{x^{3}}{3}+x^{2} \right ]\bigg|_{1}^{3}=\frac{3^{3}}{3}+3^{2}-\frac{1}{3}-1=\frac{50}{3}$$
Por tanto, el trabajo realizado es: $16.6 Ib.pie.$
- Una partícula eléctrica $q_{1}$ está en reposo con una carga de $2C$ efectúa un trabajo sobre otra partícula eléctrica $q_{2}$ a una distancia de $20$ cm. con carga $1C$. ¿Cuánto trabajo se efectúa al moverla a $40$ cm.?
En este caso, la fuerza de la particula $q_{1}$ que actua sobre la particula $q_{2}$ es la fuerza de Coulomb, que se define como:
$$F=k\frac{q_{1}q_{2}}{r^{2}}$$
Donde $k$ es la constante de Coulomb.
Para calcular el trabajo efectuado tenemos que:
$$W=\int_{a}^{b}F(x)dx=\int_{0.2}^{0.4}k\frac{q_{1}q_{2}}{r^{2}}dr=\int_{0.2}^{0.4}k\frac{(2C)(1C)}{r^{2}}dr=2C^{2}k\int_{0.2}^{0.4}\frac{dr}{r^{2}}$$
$$=2C^{2}k\left [ -\frac{1}{r} \right ]\bigg|_{0.2}^{0.4}=2C^{2}k \left(2.5 \frac{1}{m} \right)$$
Como $k=9\cdot 10^{9}\frac{Nm^{2}}{C^{2}}$, entonces:
$$W=4.5\cdot 10^{10}J$$
- Una fuerza de $40N$ se requiere para retener un resorte desde su longitud natural de 10 cm. a una longitud de 15 cm. ¿Cuánto trabajo se hace al estirar el resorte de 15 a 18 cm.?
Tenemos un resorte, de acuerdo con la ley de Hooke $(2)$ que nos dice que $F=-kx$ donde $k$ se denomina constante del resorte, la fuerza que se requiere para mantener el resorte estirado $x$ metros más allá de su longitud natural es $f(x)=-kx$.
Primero calculamos $k$, vemos que cuando el resorte se pasa de $10$ a $15$ cm, la cantidad estirada es $5 cm =0.05m$ lo que quiere decir que: $f(0.05)=40$, de modo que:
$$ f(0.05)=0.05k=40 \Rightarrow k=\frac{40}{0.05}=800$$
El trabajo hecho para estirar el resorte de 15 a 18 cm es:
$$W=\int_{0.05}^{0.08} (800)xdx=800\left [ \frac{x^{2}}{2} \right ]\bigg|_{0.05}^{0.08}=400\left [ (0.08)^{2}-(0.05)^{2} \right ]=1.56J$$
Tarea moral
Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Un resorte tiene una longitud natural de 1m. una fuerza de 24N lo estira hasta una longitud de 1.8m.
- a Determinar la constante $k$ del resorte.
- ¿Cuánto trabajo se requerirá para estirar el resorte hasta 2m mas que su longitud natural?
- ¿Hasta que longitud se estirara el resorte si le aplicamos una fuerza de 45?
- Una cubeta de 5 Ib se eleva desde el piso, jalándola con una cuerda de 20 pies a una velocidad constante. La cuerda pesa 0.08 $ib/pie$. ¿Cuánto trabajo se realiza al subir la cubeta y la cuerda?
- Una partícula se desplaza a lo largo del eje x impulsada por una fuerza que mide $\frac{10}{(1+x)^{2}}$ libras en un punto a x pies del origen. Calcule el trabajo realizado al mover la partícula desde el origen a una distancia de 9 pies.
- Una fuerza de 2N estirara una banda elástica 2 cm (0.02m. Suponiendo que en este caso se cumple la ley de Hooke, ¿Cuánto se estirara la banda al aplicarle una fuerza de 4N? ¿Cuánto trabajo se realizara para estirar la banda esa longitud?
- Cuando una partícula de masa m esta en $(x,0)$, es estirada hacia el origen con una fuerza de magnitud $\frac{k}{x^{2}}$. Si la partícula parte del reposo en $x=b$ y no actúa sobre ella ninguna otra fuerza, determine el trabajo realizado sobre ella cuando llega a $x=a, 0< a<b$.
Más adelante…
En esta entrada vimos la aplicación de la integral en el área de la física con ejemplos sencillos, dando la definición de trabajo y la definición de la ley de Hooke, en la siguiente entrada veremos otra aplicación en la física que es la definición de fuerza y presión en la hidrostática.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral II.
- Entrada anterior del curso: Cálculo Diferencial e Integral II: Centro de masa y momentos – El blog de Leo (nekomath.com)
- Siguiente entrada del curso: Cálculo Diferencial e Integral II: Fuerza y presión hidrostática – El blog de Leo (nekomath.com)