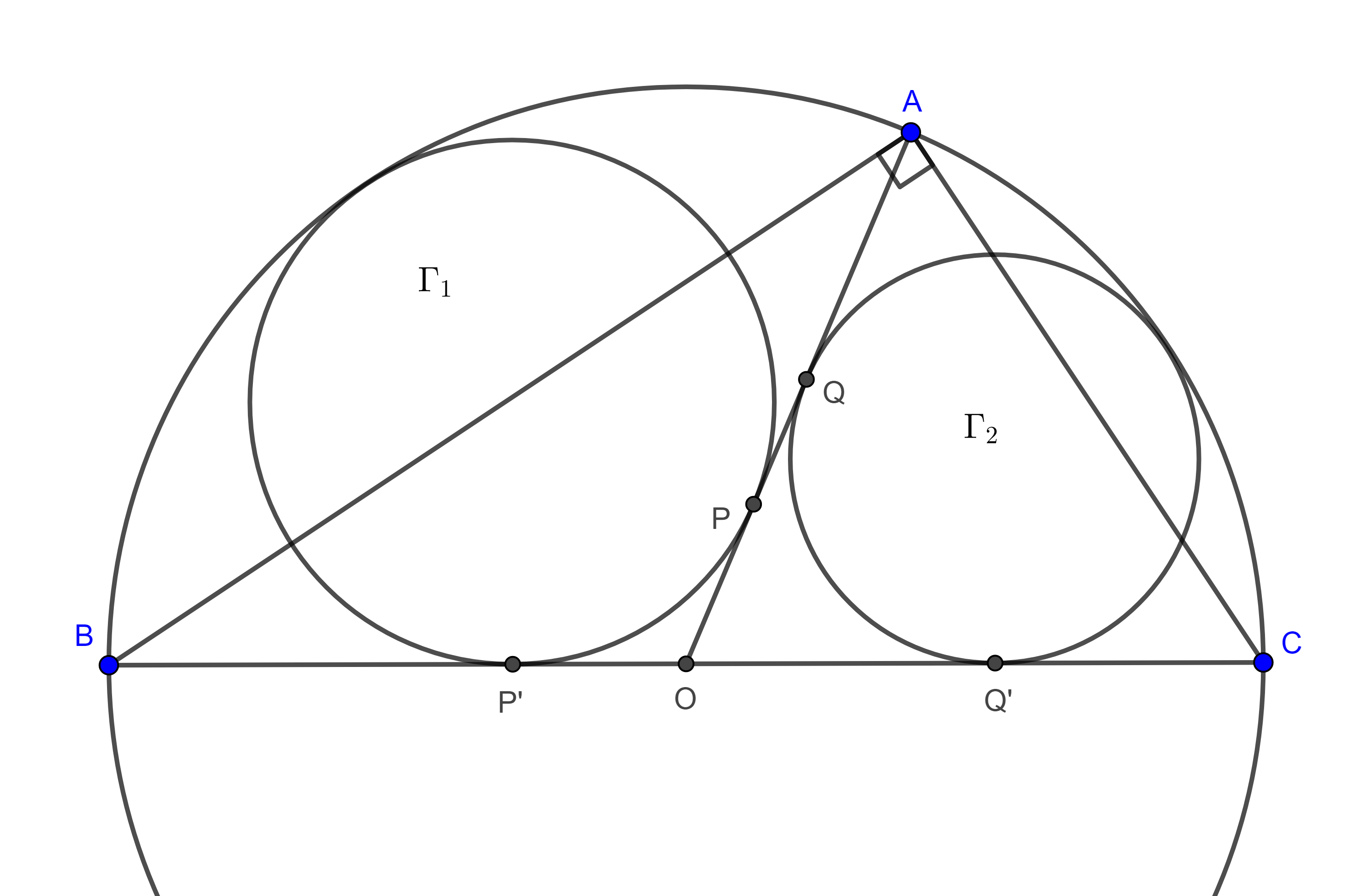Introducción
En esta ocasión demostraremos el teorema generalizado de Ptolomeo conocido como teorema de Casey, el cual nos dice que los vértices del cuadrilátero cíclico, al que hace mención el teorema de Ptolomeo, pueden ser considerados como circunferencias de radio distinto de cero, y los lados o diagonales del cuadrilátero cíclico se pueden pensar como segmentos tangentes entre dos circunferencias.
Tangente común a dos circunferencias
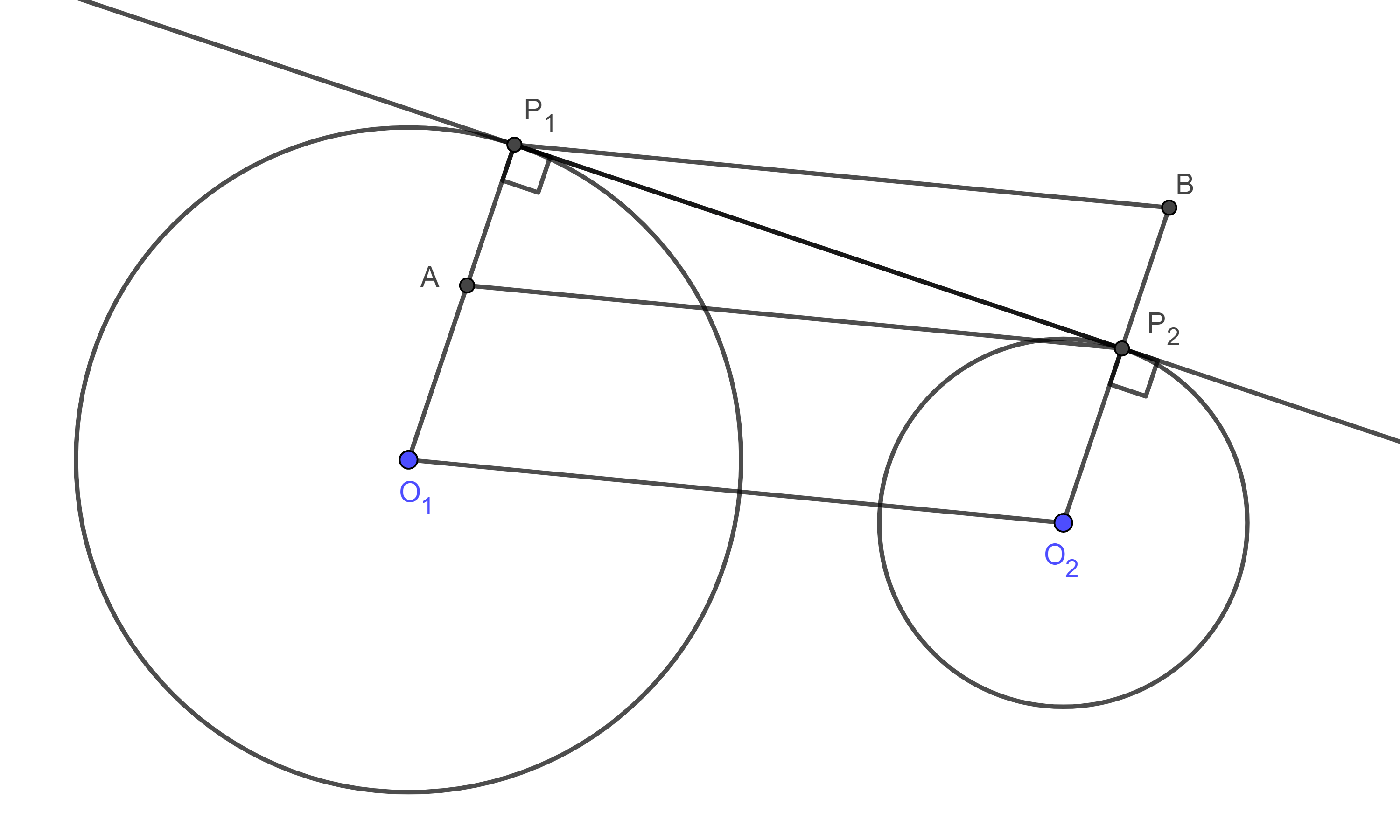
Proposición 1. Sean $(O_{1}, R_{1})$, $(O_{2}, R_{2})$, dos circunferencias tal que ninguna contiene a la otra y $P_{1}$, $P_{2}$ los puntos en que una recta es tangente a ambas circunferencias, entonces:
$i)$ Si $P_{1}P_{2}$ es exterior, es decir, no cruza el segmento $O_{1}O_{2}$ (figura 1),
$P_{1}P_{2}^2 = O_{1}O_{2}^2 – (R_{1} – R_{2})^2$,
$ii)$ Si $P_{1}P_{2}$ es interior, es decir, interseca al segmento $O_{1}O_{2}$ (figura 2),
$P_{1}P_{2}^2 = O_{1}O_{2}^2 – (R_{1} + R_{2})^2$.
Demostración. Sin pérdida de generalidad supongamos $R_{1} \geq R_{2}$.
$i)$ Sean $A$ la intersección de $O_{1}P_{1}$ con la paralela a $O_{1}O_{2}$ desde $P_{2}$, $B$ la intersección de $O_{2}P_{2}$ con la paralela a $O_{1}O_{2}$ desde $P_{1}$.
Como $O_{1}P_{1} \perp P_{1}P_{2}$ y $O_{2}P_{2} \perp P_{1}P_{2}$ entonces $O_{1}P_{1} \parallel O_{2}P_{2}$.
Por lo tanto, $\square P_{1}O_{1}O_{2}B$, $\square P_{1}AP_{2}B$ y $\square AO_{1}O_{2}P_{2}$ son paralelogramos.
En consecuencia,
$P_{1}B = O_{1}O_{2}$ y $P_{2}B = AP_{1} = R_{1} -AO_{1} = R_{1} – R_{2}$.
Como $\angle BP_{2}P_{1} = \dfrac{\pi}{2}$ podemos aplicar el teorema de Pitágoras a $\triangle BP_{2}P_{1}$.
$P_{1}P_{2}^2 = P_{1}B^2 – P_{2}B^2 = O_{1}O_{2}^2 – (R_{1} – R_{2})^2$.
$\blacksquare$
$ii)$ Sea $C$ la intersección de $O_{2}P_{2}$ con la paralela a $P_{1}P_{2}$ desde $O_{1}$.
Como $O_{1}C \parallel P_{1}P_{2}$ y $P_{1}P_{2} \perp O_{2}P_{2}$ entonces $\angle O_{1}CO_{2} = \dfrac{\pi}{2}$, además $\square CO_{1}P_{1}P_{2}$ es un rectángulo.
Por lo tanto,
$CO_{1} = P_{1}P_{2}$ y $CP_{2} = O_{1}P_{1} = R_{1}$.
Como resultado de aplicar el teorema de Pitágoras a $\triangle O_{1}CO_{2}$ obtenemos,
$P_{1}P_{2}^2 = CO_{1}^2 = O_{1}O_{2}^2 – CO_{2}^2$
$= O_{1}O_{2}^2 – (CP_{2} + P_{2}O_{2})^2 = O_{1}O_{2}^2 – (R_{1} + R_{2})^2$.
$\blacksquare$
Teorema de Casey
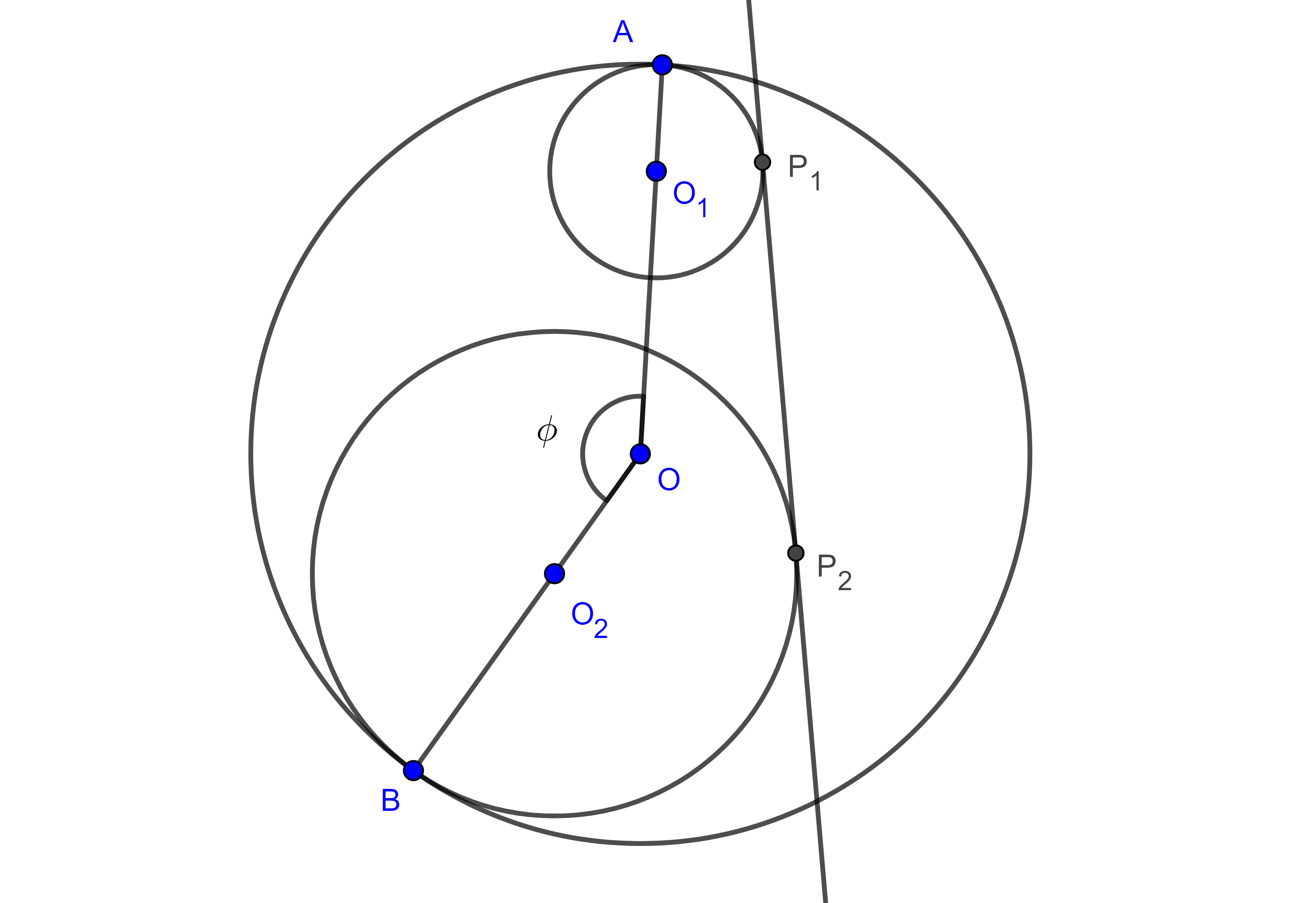
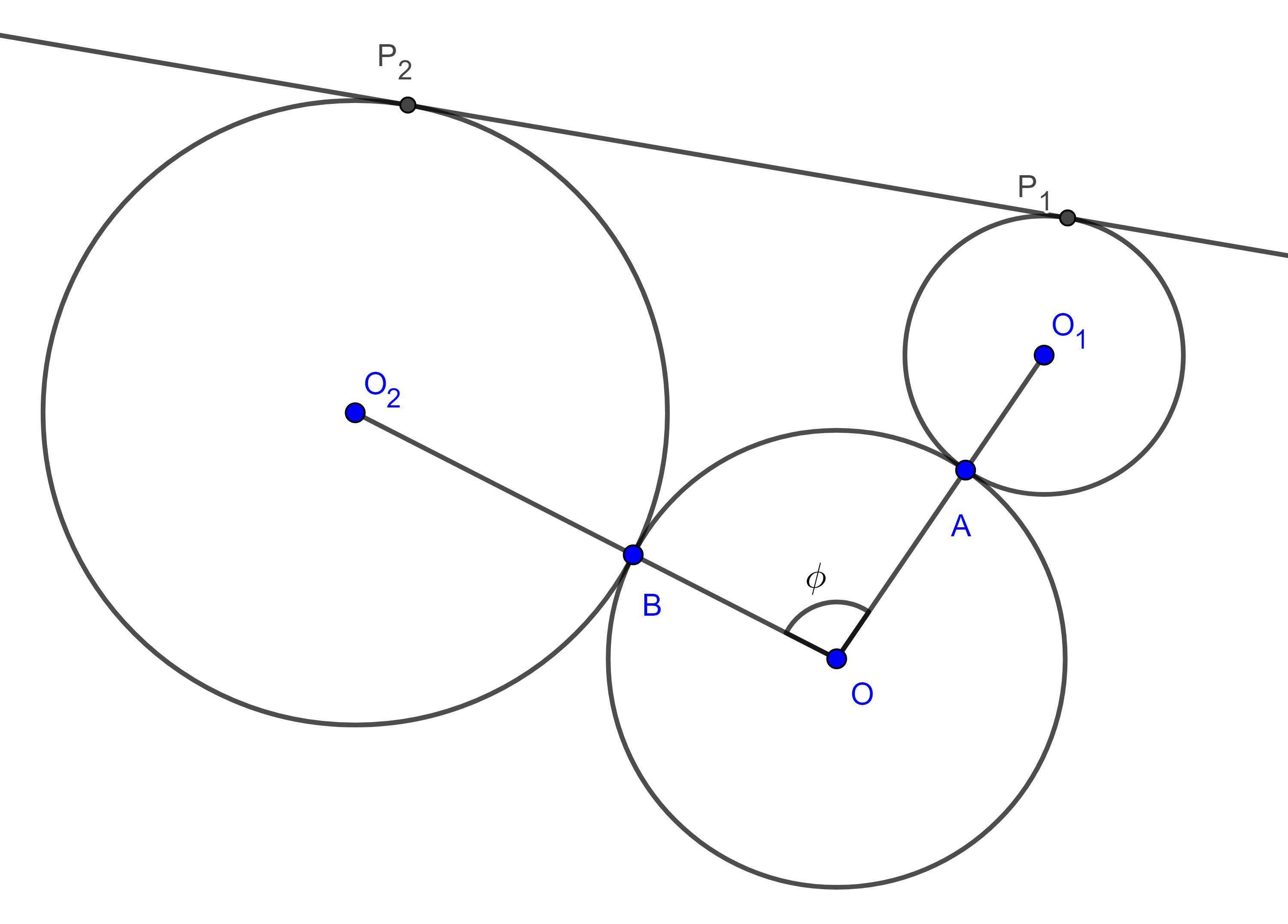
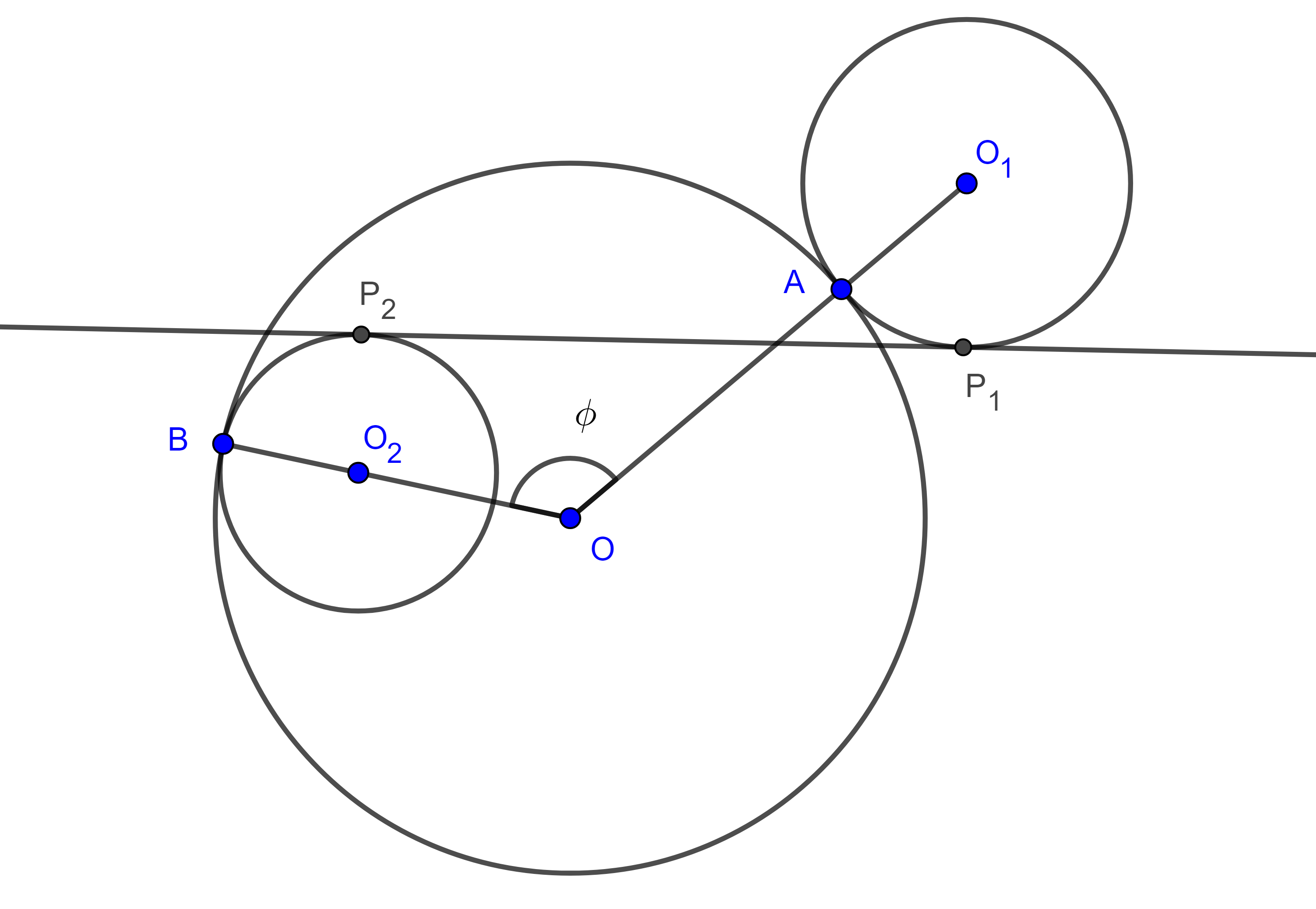
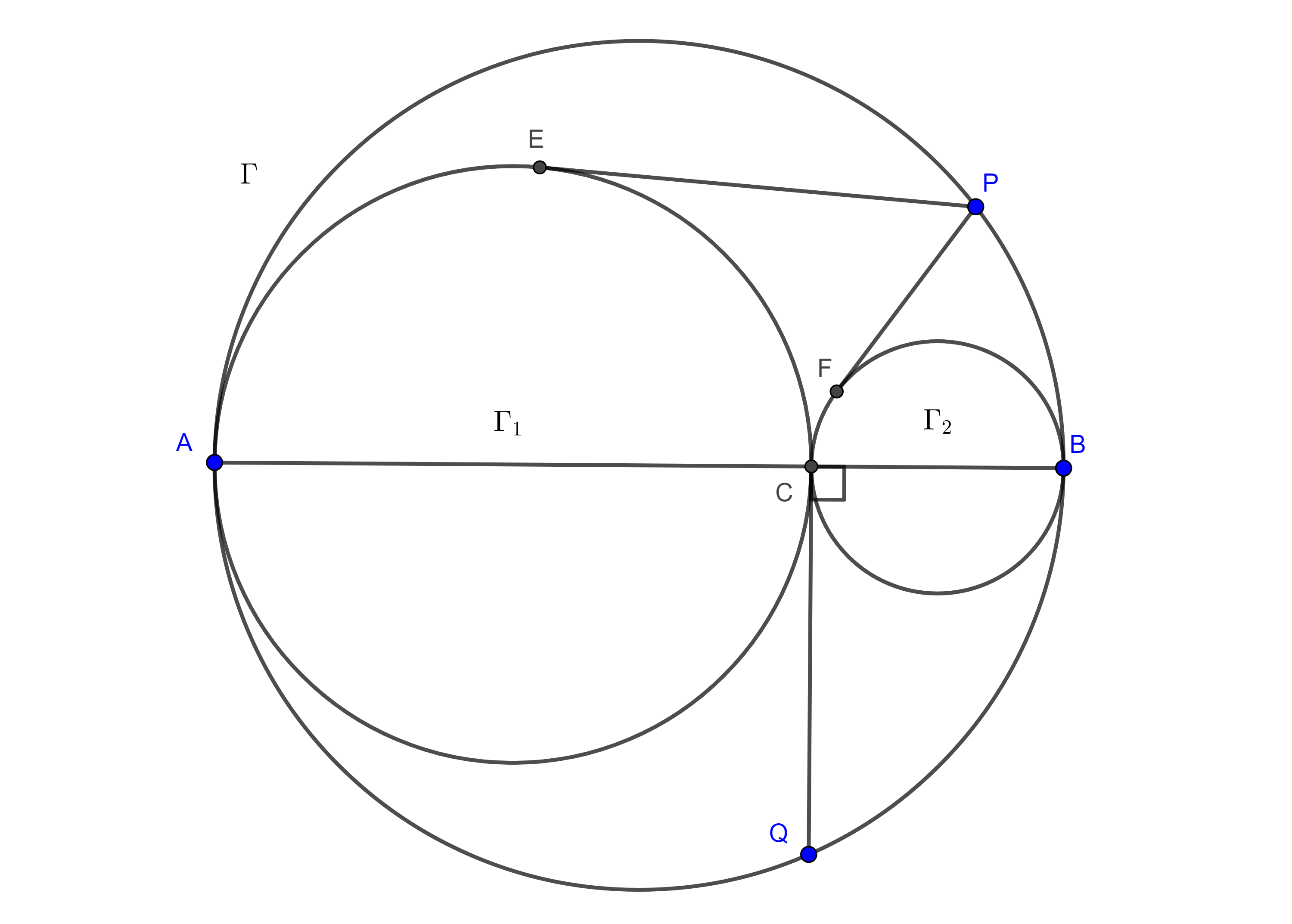
Proposición 2. Sean $(O_{1}, R_{1})$, $(O_{2}, R_{2})$, dos circunferencias tangentes a una tercera circunferencia $(O, R)$, en dos puntos distintos $A$ y $B$ respectivamente, considera $P_{1}$, $P_{2}$ los puntos en que una recta es tangente a $(O_{1}, R_{1})$ y a $(O_{2}, R_{2})$, entonces:
$i)$ Si $(O_{1}, R_{1})$, $(O_{2}, R_{2})$, son interiores a $(O, R)$ y $P_{1}P_{2}$ es exterior (figura 3),
$P_{1}P_{2} = \dfrac{AB}{R} \sqrt{(R – R_{1})(R – R_{2})}$,
$ii)$ Si $(O_{1}, R_{1})$, $(O_{2}, R_{2})$, son exteriores a $(O, R)$ y $P_{1}P_{2}$ es exterior (figura 4),
$P_{1}P_{2} = \dfrac{AB}{R} \sqrt{(R + R_{1})(R + R_{2})}$,
$iii)$ Si $(O_{1}, R_{1})$ es exterior, $(O_{2}, R_{2})$ es interior a $(O, R)$ y $P_{1}P_{2}$ es interior (figura 5),
$P_{1}P_{2} = \dfrac{AB}{R} \sqrt{(R + R_{1})(R – R_{2})}$.
Demostración. Sea $\phi = \angle AOB$.
$i)$ Aplicamos la ley de cosenos a $\triangle O_{1}OO_{2}$ y a $\triangle AOB$,
$O_{1}O_{2}^2 = O_{1}O^2 + O_{2}O^2 – 2O_{1}O \times O_{2}O \cos \phi$
$\begin{equation} = (R – R_{1})^2 + (R – R_{2})^2 – 2(R – R_{1})(R – R_{2})\cos \phi. \end{equation}$
$AB^2 = AO^2 + BO^2 – 2AO \times BO \cos \phi = 2R^2 – 2R^2\cos \phi$
$\Leftrightarrow$
$\begin{equation} \cos \phi = 1 – \dfrac{AB^2}{2R^2}. \end{equation}$
Por la proposición anterior parte $i)$ y de las ecuaciones $(1)$ y $(2)$ tenemos
$P_{1}P_{2}^2 = O_{1}O_{2}^2 – (R_{1} – R_{2})^2$
$= (R – R_{1})^2 + (R – R_{2})^2 – 2(R – R_{1})(R – R_{2})(1 – \dfrac{AB^2}{2R^2}) – (R_{1} – R_{2})^2$
$= R^2 – 2RR_{1} + R_{1}^2 + R^2 – 2RR_{2} + R_{2}^2 – 2(R^2 – RR_{2} – RR_{1} + R_{1}R_{2})$
$+ 2(R – R_{1})(R – R_{2})\dfrac{AB^2}{2R^2} – (R_{1} – R_{2})^2$
$= (R – R_{1})(R – R_{2})(\dfrac{AB^2}{R^2})$.
Por lo tanto,
$P_{1}P_{2} = \dfrac{AB}{R} \sqrt{(R – R_{1})(R – R_{2})}$.
$ii)$ y $iii)$ se muestran con un razonamiento similar.
$\blacksquare$
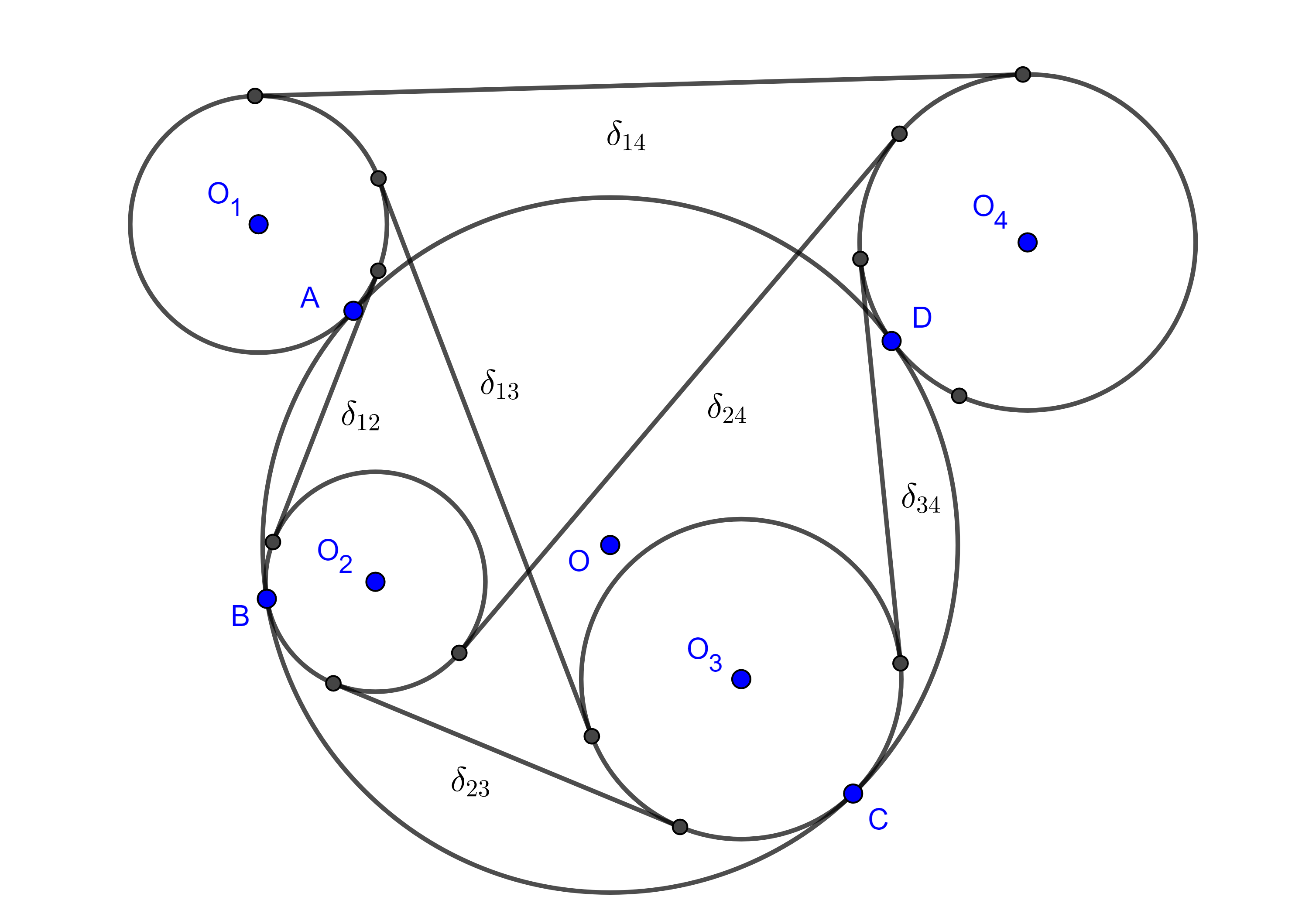
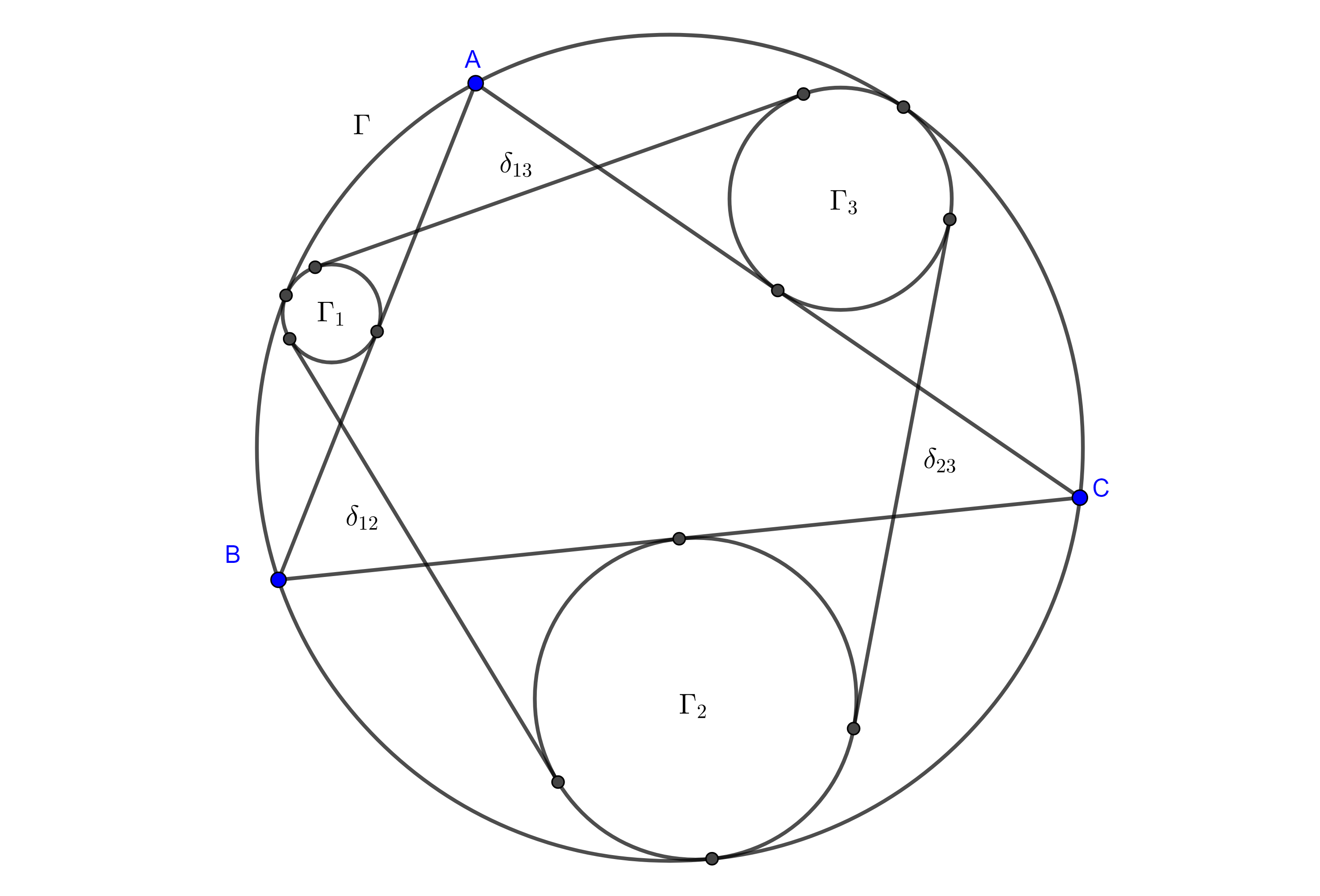
Teorema de Casey. Sean $(O_{i}, R_{i})$, $i = 1, 2, 3, 4$ circunferencias tangentes a una quinta circunferencia $(O, R)$, respectivamente en los puntos $A$, $B$, $C$ y $D$, en ese orden (figura 6), y denotemos como $\delta_{ij}$ a la medida de la tangente común a $(O_{i}, R_{i})$ y $(O_{j}, R_{j})$ la cual tomaremos como exterior si ambas circunferencias son interiores a $(O, R)$ o si ambas son exteriores a $(O, R)$, pero si una es interior y la otra es exterior a $(O, R)$ entonces tomaremos el segmento de la tangente interior a ambas circunferencias.
Bajo estas condiciones se verifica la siguiente igualdad
$\delta_{12} \delta_{34} + \delta_{14}\delta_{23} = \delta_{13}\delta_{24}$.
Demostración. Mostraremos el caso en que dos circunferencias son interiores y dos son exteriores a $(O, R)$, todos los demás casos son análogos.
Tenemos que sustituir el valor de cada segmento de tangente de acuerdo a la proposición 2 y recordar que por el teorema de Ptolomeo, $AB \times CD + AD \times BC = AC \times BD$.
$\delta_{12} \delta_{34} + \delta_{14}\delta_{23}$
$= \dfrac{AB}{R} \sqrt{(R + R_{1})(R – R_{2})} \dfrac{CD}{R} \sqrt{(R + R_{4})(R – R_{3})}$
$+ \dfrac{BC}{R} \sqrt{(R – R_{2})(R – R_{3})} \dfrac{AD}{R} \sqrt{(R + R_{1})(R + R_{4})}$
$= \dfrac{ AB \times CD + AD \times BC }{R} \sqrt{(R + R_{1})(R – R_{2})(R + R_{4})(R – R_{3})}$
$=\dfrac{ AC \times BD }{R} \sqrt{(R + R_{1})(R – R_{2})(R + R_{4})(R – R_{3})}$
$= \dfrac{AC}{R} \sqrt{(R + R_{1})(R – R_{3})} \dfrac{BD}{R} \sqrt{(R + R_{4})(R – R_{2})}$
$= \delta_{13}\delta_{24}$.
$\blacksquare$
Notemos que cuando las 4 circunferencias tangentes a $(O, R)$ tienen radio igual a $0$, el resultado es el teorema de Ptolomeo.
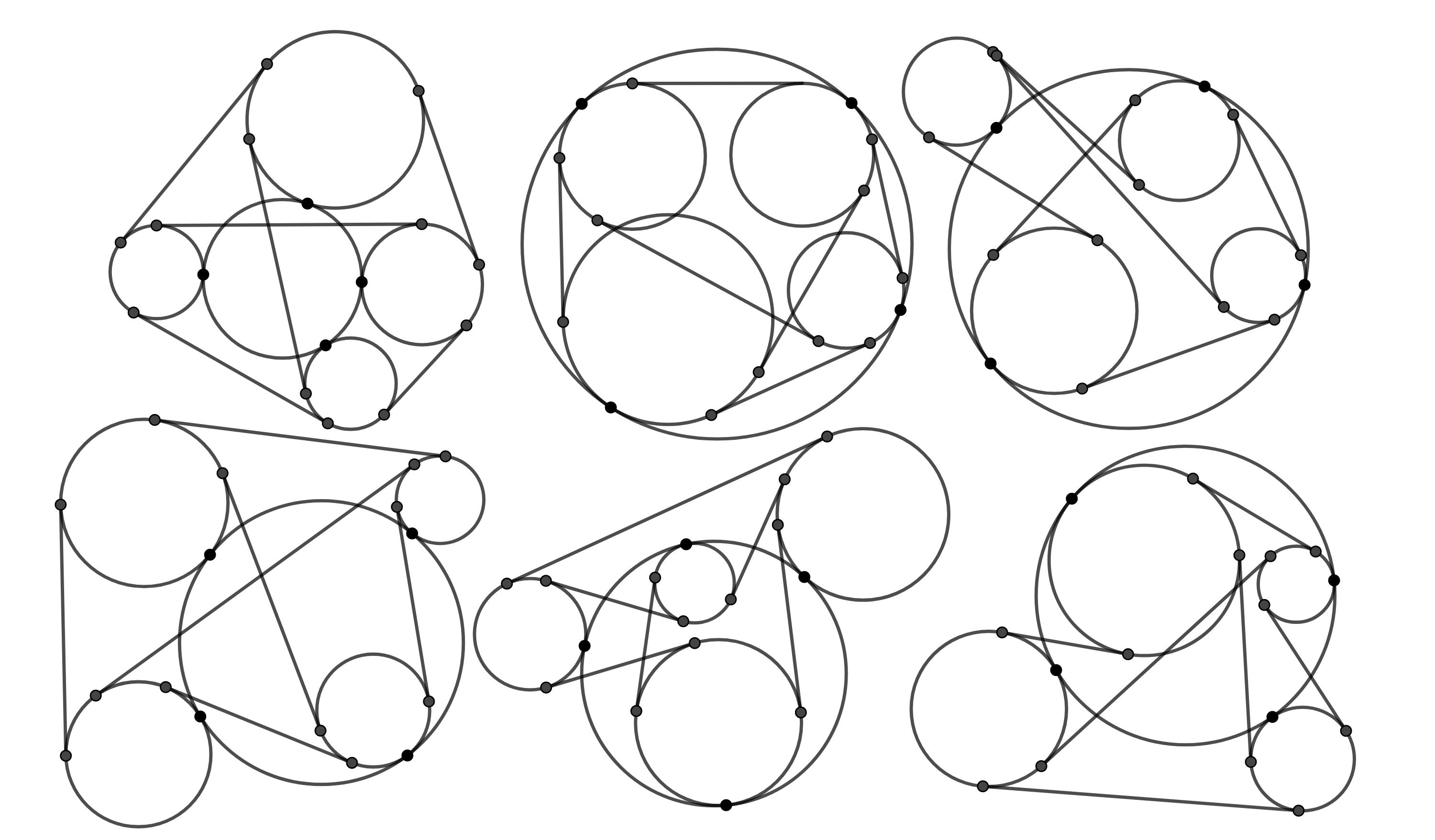
En la siguiente figura se ilustran todos los posibles casos del teorema de Casey.
Problemas
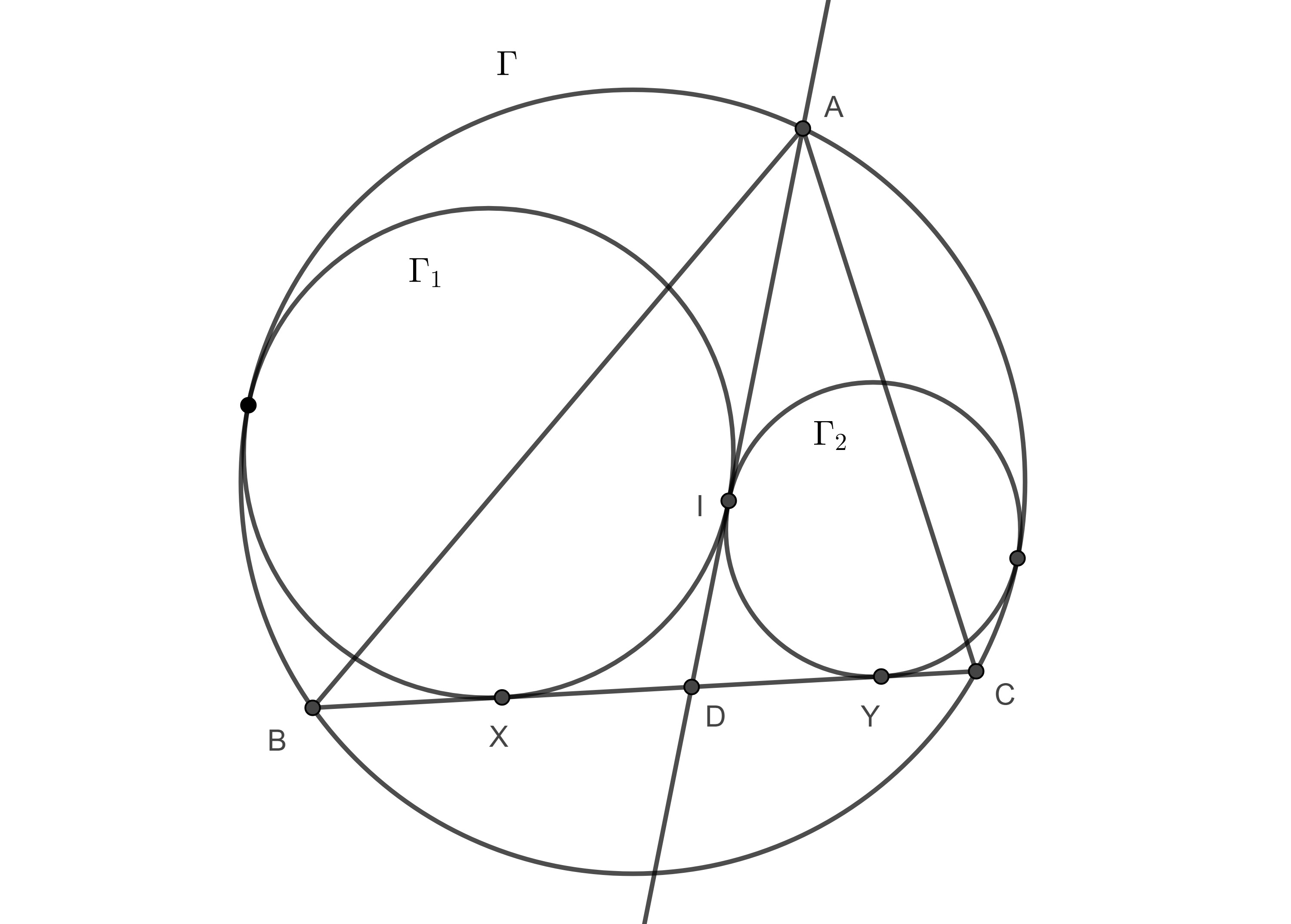
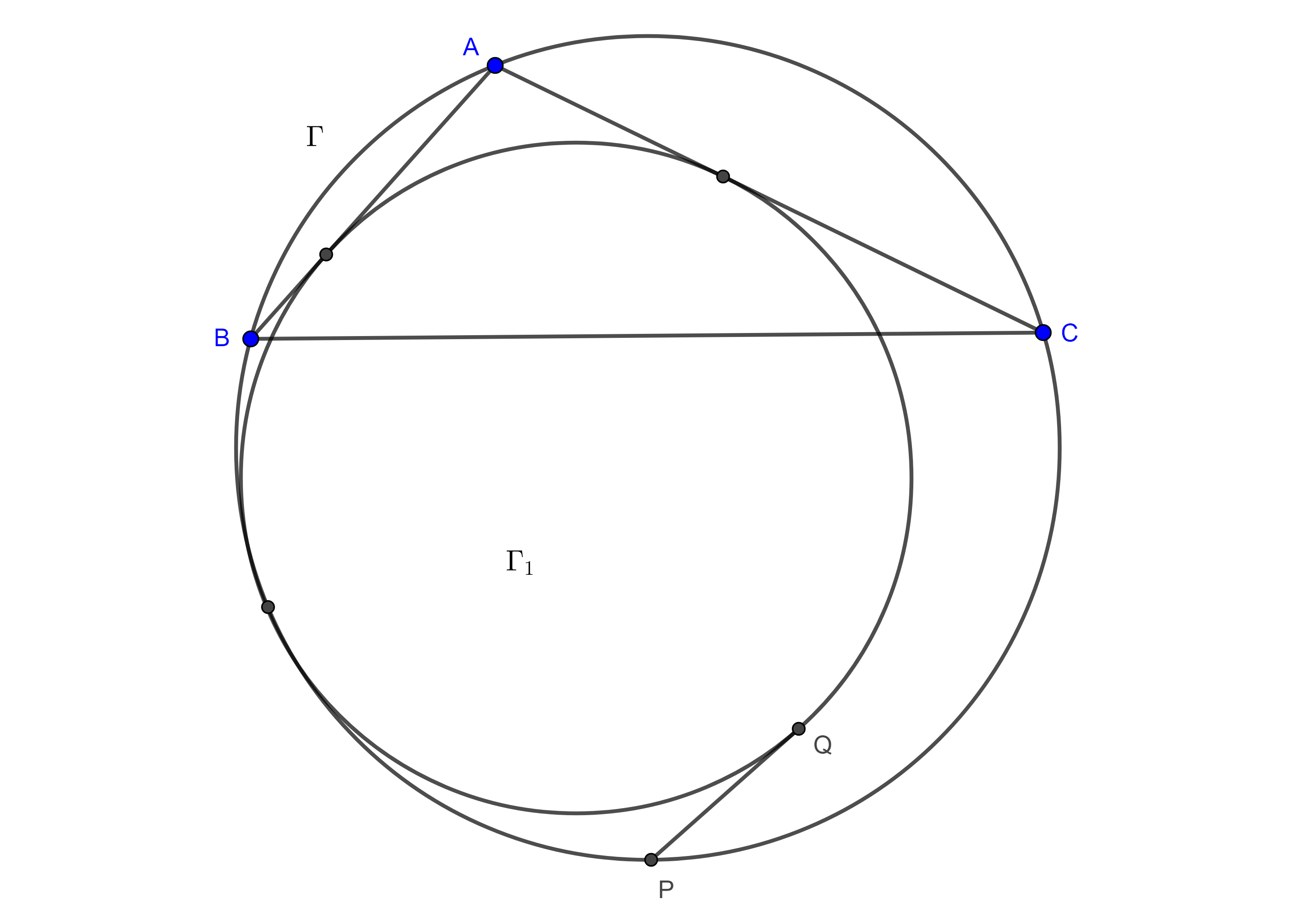
Problema 1. Sean $\Gamma_{1}$, $\Gamma_{2}$, dos circunferencias tangentes entre si (exteriormente) en $I$ y al mismo tiempo son tangentes a una tercera circunferencia $\Gamma$ (interiormente), consideremos la recta tangente a $\Gamma_{1}$, $\Gamma_{2}$ por $I$ y su intersección, $A$, con $\Gamma$ y otra tangente exterior común a $\Gamma _{1}$, $\Gamma _{2}$, en $X$, $Y$ respectivamente la cual interseca a $\Gamma$ en $B$ y $C$ (figura 8). Entonces $I$ es el incentro de $\triangle ABC$.
Demostración. Sea $D = BC \cap AI$, entonces $DX = DI = DY$.
Consideremos los puntos $A$, $B$ y $C$ como circunferencias de radio $0$.
Como resultado de aplicar el teorema de Casey a $(A, 0)$, $\Gamma_{1}$, $(B, 0)$, y $(C, 0)$ tangentes a $\Gamma$, obtenemos,
$\begin{equation} AI \times BC + BX \times AC = AB \times XC = AB \times (2DI + CY). \end{equation}$
Hacemos lo mismo con los círculos $(A, 0)$, $(B, 0)$, $(C, 0)$ y $\Gamma_{2}$ tangentes a $\Gamma$.
$\begin{equation} AB \times CY + AI \times BC = AC \times BY = AC \times (BX + 2DI). \end{equation}$
Restamos $(4)$ a $(3)$
$BX \times AC – AB \times CY = 2 AB \times DI + AB \times CY – 2 AC \times DI – AC \times BX$
$\Leftrightarrow AC \times DI + AC \times BX = AB \times DI + AB \times CY$
$\Leftrightarrow AC \times BD = AC(DI + BX) = AB(DI + CY) = AB \times CD$.
En consecuencia,
$\begin{equation} \dfrac{BD}{CD} = \dfrac{AB}{AC}. \end{equation}$
Por el reciproco del teorema de la bisectriz, la última igualdad nos dice que $AD$ es bisectriz de $\angle A$.
Ahora sumamos $(4)$ y $(3)$
$2AI \times BC + BX \times AC + AB \times CY$
$= 2AB \times DI + AB \times CY + 2AC \times DI + AC \times BX$
$\Leftrightarrow AI \times BC = AB \times DI + AC \times DI$.
En consecuencia,
$\dfrac{AI}{DI} = \dfrac{AB + AC}{BC}$.
Por otra parte, de $(5)$ tenemos
$\dfrac{BD}{CD} = \dfrac{AB}{AC}$
$\Leftrightarrow \dfrac{BC}{CD} = \dfrac{BD + CD}{CD} = \dfrac{AB + AC}{AC}$
$\Leftrightarrow \dfrac{AC}{CD} = \dfrac{AB + AC}{BC}$.
Por lo tanto, $\dfrac{AI}{DI} = \dfrac{AC}{CD}$, se sigue que $CI$ es bisectriz de $\angle C$.
Como resultado, $I$ es el incentro de $\triangle ABC$.
$\blacksquare$
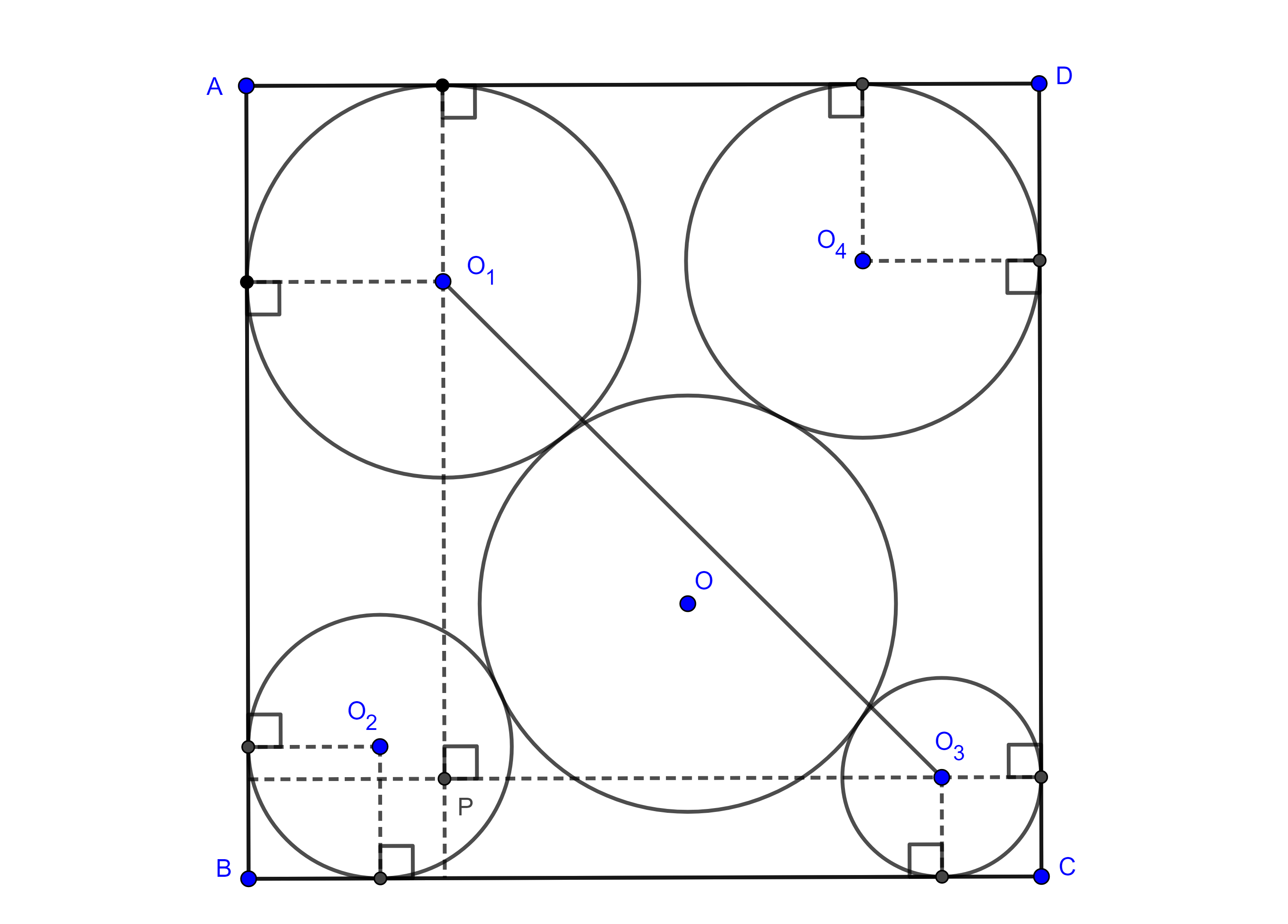
Problema 2. Sea $\square ABCD$ un cuadrado y $(O, R)$ un círculo en el interior de $\square ABCD$, y consideremos $(O_{i}, R_{i})$, $i = 1,2,3,4$ cuatro circunferencias cada una tangente a dos lados del cuadrado y a $(O, R)$ al mismo tiempo, encuentra una representación del lado del cuadrado en términos de los $R_{i}$, con $i = 1,2,3,4$.
Solución. Por construcción, cada lado del cuadrado es tangente a dos circunferencias así que si $\delta_{ij}$ denota la longitud del segmento tangente común a dos circunferencias entonces,
$\delta_{12} = AB – R_{1} – R_{2}$,
$\delta_{23} = AB – R_{2} – R_{3}$,
$\delta_{34} = AB – R_{3} – R_{4}$,
$\delta_{14} = AB – R_{1} – R_{4}$.
Para calcular $\delta_{13}$ consideremos $P$ la intersección de la perpendicular a $BC$ por $O_{1}$, con la perpendicular a $AB$ por $O_{3}$ entonces $\triangle O_{1}PO_{3}$ es rectángulo y por el teorema de Pitágoras
$O_{1}O_{3}^2 = 2(AB – R_{1} – R_{3})^2$.
Por la proposición 1 parte $i)$ tenemos que
$\delta_{13}^2 = O_{1}O_{3}^2 – (R_{1} – R_{3})^2 = 2(AB – R_{1} – R_{3})^2 – (R_{1} – R_{3})^2$.
Por lo tanto,
$\delta_{13} = \sqrt{2(AB – R_{1} – R_{3})^2– (R_{1} – R_{3})^2}$.
Igualmente vemos que $\delta_{24} = \sqrt{2(AB – R_{2} – R_{4})^2 – (R_{2} – R_{4})^2}$.
Aplicamos el teorema de Casey a $(O_{i}, R_{i})$ $i = 1, 2, 3, 4$ tangentes a $(O, R)$
$\delta_{12}\delta_{34} + \delta_{14}\delta_{32} = \delta_{13}\delta_{24}$
$= (AB – R_{1} – R_{2})( AB – R_{3} – R_{4}) + (AB – R_{2} – R_{3})( AB – R_{1} – R_{4})$
$= \sqrt{2(AB – R_{1} – R_{3})^2 – (R_{1} – R_{3})^2}\sqrt{2(AB – R_{2} – R_{4})^2 – (R_{2} – R_{4})^2}$.
Despejando $AB$ se puede llegar a la expresión
$AB = \dfrac{2(R_{1}R_{3} – R_{2}R_{4}) + \sqrt{2(R_{1} – R_{2}) (R_{1} – R_{4}) (R_{3} – R_{2}) (R_{3} – R_{4}) }}{R_{1} – R_{2} + R_{3} – R_{4}}$.
No se desarrollará este último procedimiento por ser largo, para llegar al resultado solo hay que desarrollar los productos y después reagrupar para despejar $AB$.
$\blacksquare$
Problema 3. Sean $\triangle ABC$ un triángulo rectángulo con $\angle BAC =\dfrac{\pi}{2}$, $(O, R)$ su circuncírculo, considera dos circunferencias $\Gamma_{1}$ tangente a $OA$ en $P$, a $OB$ y a $(O, R)$ (internamente) y $\Gamma_{2}$ tangente a $OA$ en $Q$, a $OC$ y a $(O, R)$ (internamente). Muestra que $\dfrac{AB}{AC} = \dfrac{AP}{AQ}$.
Demostración. Sean $P’$ y $Q’$ los puntos de tangencia de $\Gamma_{1}$ y $\Gamma_{2}$ con $OB$ y $OC$ respectivamente, entonces $OP = OP’$ por ser segmentos tangentes a $\Gamma_{1}$ trazados desde $O$.
Igualmente vemos que $OQ = OQ’$.
Como $\triangle ABC$ es rectángulo y $BC$ es la hipotenusa, entonces $O$ es el punto medio de $BC$.
Por lo tanto, $R = OB = OA = OC$.
Como resultado obtenemos, $AP = BP’$ y $AQ = CQ’$.
Ahora aplicamos el teorema de Casey a los círculos $(A, 0)$, $\Gamma_{1}$, $(B, 0)$ y $\Gamma_{2}$ tangentes a $(O, R)$.
$AP \times BQ’ + AQ \times BP’ = AB \times P’Q’$
$\Leftrightarrow AP(BQ’ + AQ) = AB \times P’Q’$
Por lo tanto,
$\begin{equation} AP \times BC = AB \times P’Q’. \end{equation}$
Hacemos lo mismo para $A$, $\Gamma_{1}$, $C$ y $\Gamma_{2}$ tangentes a $(O, R)$.
$AP \times CQ’ + AQ \times CP’ = AC \times P’Q’$
$\Leftrightarrow AQ(AP + CP’) = AC \times P’Q’$.
Por lo tanto,
$\begin{equation} AQ \times BC = AC \times P’Q’. \end{equation}$
Haciendo el cociente de $(6)$ sobre $(7)$ obtenemos el resultado buscado, $\dfrac{AP}{AQ} = \dfrac{AB}{AC}$.
$\blacksquare$
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Completa la prueba de la proposición 2 parte $ii)$ y $iii)$.
- Sean $l_{1}$ y $l_{2}$ dos rectas paralelas y tangentes a una circunferencia $(O, R)$, considera otras dos circunferencias, $(O_{1}, R_{1})$ tangente a $l_{1}$ y a $(O, R)$, y $(O_{2}, R_{2})$ tangente a $l_{2}$, y a las primeras dos circunferencias $(O, R)$, $(O_{1}, R_{1})$. Muestra que $R = 2 \sqrt{R_{1}R_{2}}$.
- Sean $AB$ el diámetro de una circunferencia $\Gamma$, $P$, $Q \in \Gamma$ en arcos distintos respecto de $AB$, trazamos $C$ el pie de la perpendicular a $AB$ trazada desde $Q$ y considera $\Gamma_{1}$, $\Gamma_{2}$ dos circunferencias de diámetro $AC$ y $CB$ respectivamente. Sean $PE$ y $PF$ segmentos tangentes a $\Gamma_{1}$ y $\Gamma_{2}$ respectivamente. Prueba que $PE + PF = PQ$.
- Sean $\triangle ABC$ y $\Gamma$ su circuncírculo con $AB = c$, $BC = a$ y $AC = b$, considera $\Gamma_{1}$, $\Gamma_{2}$ y $\Gamma_{3}$ círculos tangentes a $AB$, $BC$ y $AC$ respectivamente en sus puntos medios y al mismo tiempo tangentes al arco $\overset{\LARGE{\frown}}{AB}$, $\overset{\LARGE{\frown}}{BC}$ y $\overset{\LARGE{\frown}}{CA}$ respectivamente, denota $\delta_{ij}$ al segmento de tangente exterior y común a $\Gamma_{i}$, $\Gamma_{j}$. Muestra que $\delta_{ij} = \dfrac{a + b + c}{4}$, $i, j = 1, 2, 3$, $i \neq j$.
- Considera $\triangle ABC$ y su circuncírculo $\Gamma$, sea $\Gamma_{1}$ una circunferencia tangente a $AB$ en $P$, a $AC$ en $Q$ y a $\Gamma$ internamente, muestra que el punto medio de $PQ$ es el incentro de $\triangle ABC$.
- Sean $\triangle ABC$ y $\Gamma$ su circuncírculo con $AC > AB$. Una circunferencia $\Gamma_{1}$ es tangente a $AB$, $AC$ y al circuncírculo internamente, $P$ es el punto medio del arco $\overset{\LARGE{\frown}}{BC}$ y $\overline{PQ}$ es un segmento tangente a $\Gamma_{1}$. Muestra que $\dfrac{PQ}{PA} = \dfrac{AC – AB}{AC + AB}$.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Cuadrilátero bicéntrico.
- Otros cursos.
Fuentes
- Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 45-54.
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 251-258.
- Luis Gonzáles., Casey’s Theorem and its applications. 2011.
- Kin Y. Li. The Hong Kong University of Sience and Technology. Mathematical Excalibur. 2012, Vol 16 No. 5.
- Wolfram MathWorld
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»