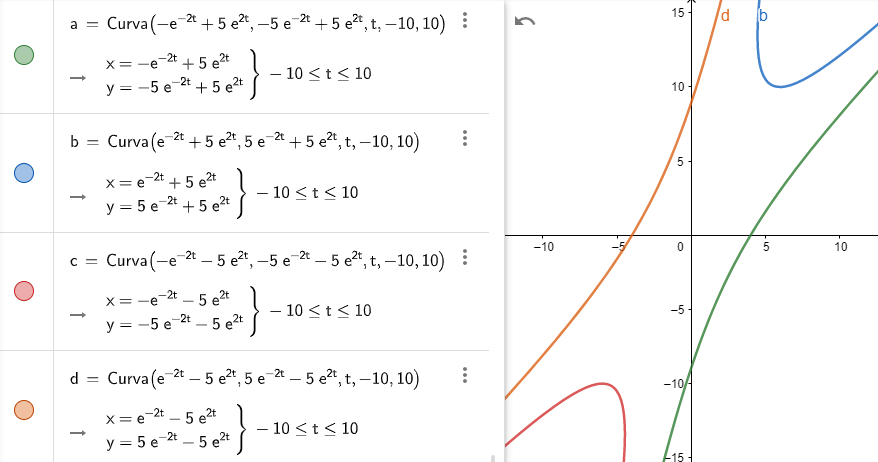Introducción
Como se ha mencionado anteriormente el objetivo de introducir ideas de álgebra lineal en cálculo diferencial es poder establecer una transformación lineal que sea la mejor aproximación lineal en un punto a una función dada. Esto nos ayudará a entender a la función dada en el punto en términos de otra función «más simple». Pero así mismo, las transformaciones lineales pueden ellas mismas pensarse en términos de transformaciones más sencillas. En esta entrada revisaremos esta idea y la conectaremos con la noción de eigenvectores.
Por un lado, recordaremos cómo es que una transformación lineal puede ser representada mediante una matriz una vez que se ha elegido una base del espacio vectorial. Luego, hablaremos de cómo elegir, de entre todas las bases, aquella que nos de una representación matricial lo más sencilla posible.
Representación matricial de las transformaciones lineales
Comencemos esta entrada repasando la importante relación entre transformaciones lineales y matrices. Denotaremos como $\mathcal{L}(\mathbb{R}^n,\mathbb{R}^m)$ al espacio vectorial de transformaciones lineales de $\mathbb{R}^n$ a $\mathbb{R}^m$.
Si tomamos cualquier transformación lineal $T\in \mathcal{L}(\mathbb{R}^n,\mathbb{R}^m)$, entonces los valores de $T$ en cualquier vector de $\mathbb{R}^n$ quedan totalmente determinados por los valores de $T$ en los elementos de alguna base $\beta$ para $\mathbb{R}^n$. Tomemos $\gamma=\{\bar{w}_{1},\dots ,\bar{w}_{m}\}$ una base ordenada para $\mathbb{R}^m$, y $\beta=\{\bar{e}_{1},\dots ,\bar{e}_{n}\}$ una base ordenada para $\mathbb{R}^n$. Para cada $\bar{e}_{k}$ tenemos:
$$\begin{equation} T(\bar{e}_{k})=\sum_{i=1}^{m}t_{ik}\bar{w}_{i} \end{equation},$$
para algunos escalares $t_{1k},\dots ,t_{mk}$ que justo son las componentes de $T(\bar{e}_{k})$ en la base $\gamma$. Con estos escalares, podemos considerar la matriz: \[ \text{Mat}_{\gamma,\beta}(T)= \begin{pmatrix} t_{11} & \dots & t_{1n} \\ \vdots & \ddots & \vdots \\ t_{m1} & \dots & t_{mn} \end{pmatrix} \]
Esta es llamada la representación matricial de la transformación $T$ con respecto a las bases $\beta$ y $\gamma$. Esta matriz ayuda a calcular $T$ en cualquier vector de $\mathbb{R}^n$ como explicamos a continuación.
Para cada $\bar{v}\in \mathbb{R}^n$, podemos expresarlo como combinación lineal de elementos de la base $\beta$ digamos que $\bar{v}=\sum_{i=1}^{n} v_{i}\bar{e}_{i}$. Mediante estos coeficientes, podemos entonces asociar a $\bar{v}$ al siguiente vector columna de $\mathbb{R}^n$ \[ [\bar{v}]_{\beta}=\begin{pmatrix} v_{1} \\ \vdots \\ v_{n} \end{pmatrix}, \]
al que llamamos el vector de coordenadas de $\bar{v}$ con respecto a la base $\beta$.
Realicemos por un lado el siguiente cálculo:
\[ \text{Mat}_{\gamma,\beta}(T)[\bar{v}]_{\beta}=\begin{pmatrix} t_{11} & \dots & t_{1n}\\ \vdots & \ddots & \vdots \\ t_{m1} & \dots & t_{mn} \end{pmatrix} \begin{pmatrix} v_{1} \\ \vdots \\ v_{n} \end{pmatrix}=\begin{pmatrix} \displaystyle\sum_{k=1}^{n}t_{1k}v_{k} \\ \vdots \\ \displaystyle\sum_{k=1}^{n}t_{mk}v_{k}.\end{pmatrix} \]
Por otro lado tenemos lo siguiente:
\begin{align*}
T(\bar{v})&=T \left( \sum_{k=1}^{n}v_{k}\bar{e}_{k} \right)\\&=\sum_{k=1}^{n}v_{k}T(\bar{e}_{k})\\&=\sum_{k=1}^{n}v_{k}T\left( \sum_{i=1}^{m}t_{ik}\bar{w}_{i} \right)\\&=\sum_{i=1}^{m}\left( \sum_{k=1}^{n}v_{k}t_{ik} \right)\bar{w}_{i}.
\end{align*}
Juntando ambos cálculos: \[ [T(\bar{v})]_{\gamma}=\begin{pmatrix} \sum_{k=1}^{n}v_{k}t_{1k} \\ \vdots \\ \sum_{k=1}^{n}v_{k}t_{mk} \end{pmatrix} = \text{Mat}_{\gamma,\beta}(T)[\bar{v}]_{\beta}.\]
En otras palabras, aplicar $T$ a un vector $\bar{v}$ equivale a multiplicar $\text{Mat}_{\gamma,\beta}$ por el vector columna asociado a $\bar{v}$ en la base $\beta$, en el sentido de que tras hacer este producto recuperamos el vector de coordenadas para $T(\bar{v})$ en la base $\gamma$.
Isomorfismo entre transformaciones lineales y matrices
Con las operaciones de suma y multiplicación por escalar que vimos en la entrada de Matrices, se tiene que $M_{m,n}\left( \mathbb{R} \right)$ es un espacio vectorial sobre $\mathbb{R}$. De igual manera $\mathcal{L}(\mathbb{R}^n,\mathbb{R}^m)$ es un espacio vectorial sobre $\mathbb{R}$ con las siguientes operaciones:
- Si $T$ y $U$ son dos transformaciones, la transformación $T+U$ es aquella que envía a todo vector $\bar{v}\in \mathbb{R}^n$ al vector $T(\bar{v})+U(\bar{v})$.
- Si $r\in \mathbb{R}$ la transformación $rT$ es la que a todo $\bar{v}\in \mathbb{R}^n$ lo envía al vector $rT(\bar{v})$.
Queda como ejercicio que verifiques que esto dota efectivamente a $\mathcal{L}(\mathbb{R}^n,\mathbb{R}^m)$ de la estructura de espacio vectorial.
A continuación veremos que estos dos espacios vectoriales son, prácticamente, el mismo. Lo que haremos es construir una función $$\Phi :M_{m,n}\left( \mathbb{R} \right) \to\mathcal{L}(\mathbb{R}^n,\mathbb{R}^m)$$ que sea biyectiva y que preserve las operaciones de suma y de producto escalar.
Para ello, tomemos una base $\beta=\{\bar{e}_1,\ldots,\bar{e}_n\}$ de $\mathbb{R}^{n}$ y una base $\gamma=\{\bar{u}_1,\ldots,\bar{u}_m\}$ de $\mathbb{R}^m$. Tomemos una matriz $A\in M_{m,n}(\mathbb{R})$. Explicaremos a continuación cómo construir la transformación $\Phi(A)$, para lo cual diremos qué hace con cada elemento de la base $\beta$. Tomaremos aquella transformación lineal $T_A\in \mathcal{L}(\mathbb{R}^n,\mathbb{R}^m)$ tal que
$$T_A(\bar{e}_j)=\sum_{i=1}^n a_{ij} \bar{u}_i.$$
Tomamos entonces $\Phi(A)=T_A$. Veamos que $\Phi$ tiene todas las propiedades que queremos.
- $\Phi$ es suprayectiva. Si tenemos una transformación $T:\mathbb{R}^n\to \mathbb{R}^m$, entonces por la construcción anterior se tiene que su forma matricial $A:=\text{Mat}_{\gamma,\beta}(T)$ justo cumple $T_A=T$, de modo que $\Phi(A)=T$.
- $\Phi$ es inyectiva. Si $A$ y $B$ son matrices distintas, entonces difieren en alguna entrada, digamos $(i,j)$. Pero entonces $T_A$ y $T_B$ difieren ya que $T_A(\bar{e}_j)\neq T_B(\bar{e}_j)$ ya que en las combinaciones lineales creadas hay un coeficiente distinto. Así, $\Phi(A)\neq \Phi(B)$.
- $\Phi $ es lineal. Para $r\in \mathbb{R}$, $A$ y $B$ matrices con entradas $a_{ij}$ y $b_{ij}$, respectivamente, se cumple que $\Phi \left( rA+B \right)=T_{(rA+B)}$ y entonces se satisface para cada $j=1,\dots ,n$ lo siguiente:
\begin{align*}
(rA+B)[\bar{e}_{j}]_{\beta}&=rA[\bar{e}_{j}]_{\beta}+B[\bar{e}_{j}]_{\beta}\\&=r[T_A(\bar{e}_{i})]_{\gamma}+[T_{B}(\bar{e}_{i})]_{\gamma}.
\end{align*}
Por tanto para cada $\bar{e}_{i}$ tenemos que $$T_{(rA+B)}(\bar{e}_{i})=rT_{A}(\bar{e}_{i})+T_{B}(\bar{e}_{i})$$ y en consecuencia $$T_{(rA+B)}=rT_{A}+T_{B}.$$ Así $$\Phi (rA+B)=r\Phi (A)+\Phi(B).$$
Todo lo anterior implica que $M_{m,n}\left( \mathbb{R} \right)\simeq \mathcal{L}(\mathbb{R}^n,\mathbb{R}^m)$, es decir, que ambos espacios vectoriales son isomorfos.
En búsqueda de una matriz sencilla
Por lo que hemos platicado hasta ahora, a cada transformación lineal le corresponde una matriz, y viceversa. De hecho, esta asociación respeta operaciones como la suma y el producto por escalar. Esta equivalencia está dada a partir de la función $\Phi$ encontrada en la sección anterior.
Si $\Phi $ es biyectiva, ¿por qué hablamos entonces de encontrar una representación matricial simple para una transformación lineal $T$? Esto parecería no tener sentido, pues a cada transformación le corresponde una y sólo una matriz. Sin embargo, esto es cierto únicamente tras haber fijado las bases $\beta$ y $\gamma$ para $\mathbb{R}^n$ y $\mathbb{R}^m$, respectivamente. Así, dependiendo de la elección de las bases las representaciones matriciales cambian y si tenemos una transformación lineal $T$, es posible que querramos encontrar bases $\beta$ y $\gamma$ en donde la representación matricial sea sencilla.
Nos enfocaremos únicamente en transformaciones lineales que van de un espacio vectorial a sí mismo. Tomemos entonces $T:\mathbb{R}^n\to \mathbb{R}^n$ y una base $\beta$ de $\mathbb{R}^n$. Por simplicidad, escribiremos $\text{Mat}_{\beta, \beta}(T)$ simplemente como $\text{Mat}_{\beta}(T)$. Hay propiedades de $T$ que podemos leer en su matriz $\text{Mat}_{\beta}(T)$ y que no dependen de la base $\beta$ que hayamos elegido. Si con una base $\beta$ especial resulta que $\text{Mat}_{\beta}(T)$ es muy sencilla, entonces podremos leer estas propiedades de $T$ muy fácilmente. Un ejemplo es la siguiente proposición, la cual queda como tarea moral.
Proposición. La transformación lineal $T:\mathbb{R}^n\to\mathbb{R}^n$ es invertible si y sólo si $\text{Mat}_{\beta}(T)$ es invertible.
Si $A=\text{Mat}_{\beta}(T)$ fuera muy muy sencilla, por ejemplo, si fuera una matriz diagonal, entonces podríamos saber la invertibilidad de $T$ sabiendo la invertibilidad de $A$, y la de $A$ sería muy fácil de ver pues por ser matriz diagonal bastaría hacer el producto de las entradas de su diagonal para obtener su determinante y estudiar si es distinto de cero.
Motivados por el ejemplo anterior, estudiemos la siguiente pregunta: ¿toda transformación lineal se puede representar con una matriz diagonal? Si una transformación lineal se puede representar de esta manera, diremos que es diagonalizable.
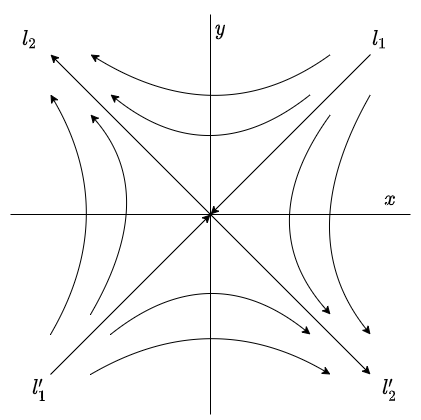
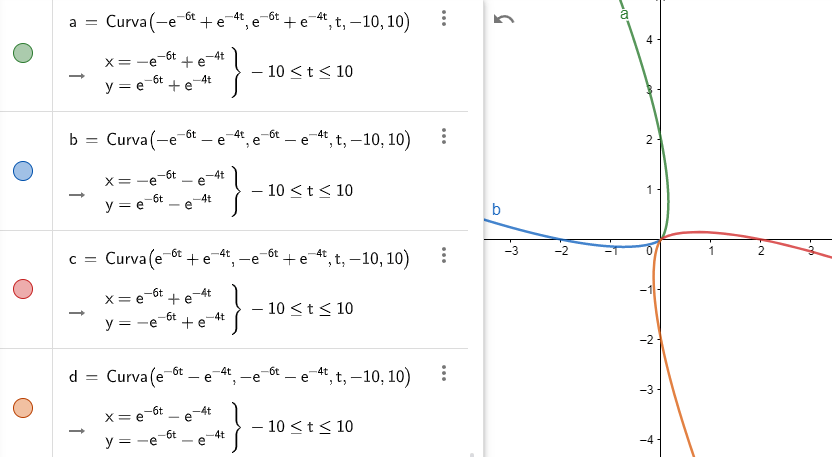
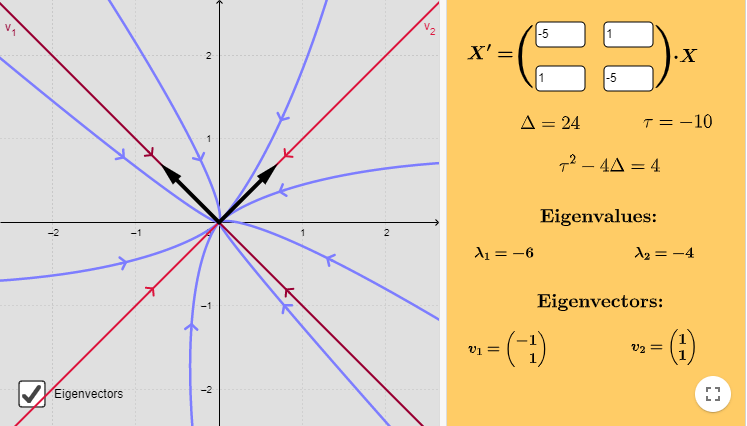
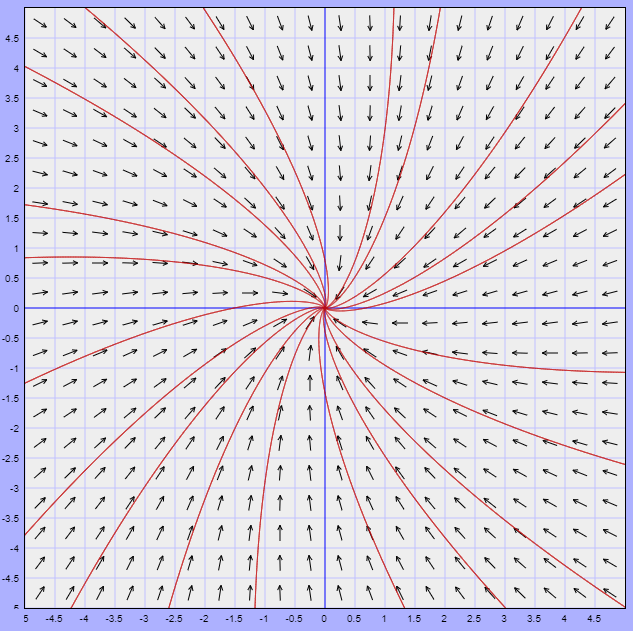
Eigenvalores, eigenvectores y eigenespacios
En lo que sigue repasaremos el aparato conceptual que nos permitirá dar una respuesta parcial de cuándo una matriz es diagonalizable. Un tratamiento mucho más detallado se puede encontrar aquí en el blog, en el curso de Álgebra Lineal II, comenzando con la entrada Eigenvectores y eigenvalores.
Para nuestro repaso, debemos introducir algunos conceptos y estudiarlos.
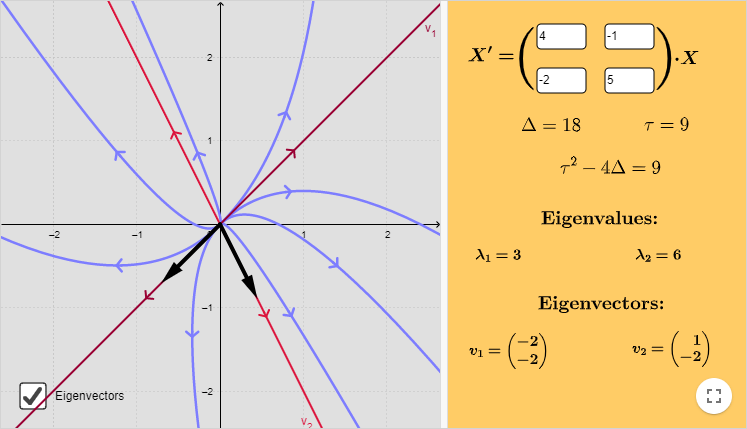
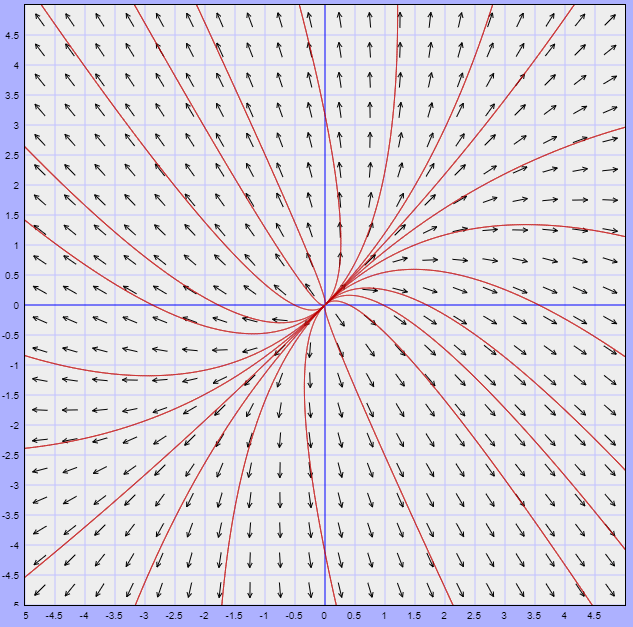
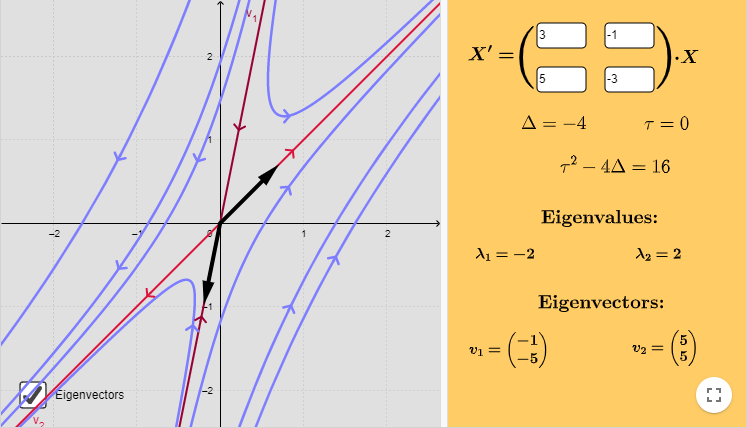
Definición. Sea $T:\mathbb{R}^n\rightarrow \mathbb{R}^n$ una transformación lineal. Diremos que un escalar $r \in \mathbb{R}$ es un eigenvalor de $T$ si existe $\bar{v}\in \mathbb{R}^n\setminus\{ \bar{0} \}$ tal que $T(\bar{v})=r\bar{v}$. A dicho vector $\bar{v}$ le llamaremos un eigenvector de $T$ con eigenvalor asociado $r$.
Dado un eigenvector $\bar{v}\in \mathbb{R}^n$, sólo hay un eigenvalor correspondiente a éste. Si $T(\bar{v})=r\bar{v}$ y $T(\bar{v})=t\bar{v}$, entonces $r\bar{v}=t\bar{v}$ de donde $(r-t)\bar{v}=\bar{0}$. Como $\bar{v}\neq \bar{0}$, se sigue que $r=t$.
Por otro lado, para un eigenvalor $r$ puede haber más de un eigenvector con eigenvalor asociado $r$. Consideremos para un eigenvalor $r$ el conjunto $E(r)=\{ \bar{v}\in V |T(\bar{v})=r\bar{v}\}$. Notemos que $\bar{0}\in E(r)$ y también todos los eigenvectores de $r$ están en $E(r)$. Además, $E(r)$ es un subespacio de $\mathbb{R}^n$, pues si $\bar{u},\bar{v} \in E(r)$, y $a\in \mathbb{R}$, tenemos
\begin{align*}
T(a\bar{u}+\bar{v})&=aT(\bar{u})+T(\bar{v})\\
&=a(r\bar{u})+(r\bar{v})\\
&=r(a\bar{u}+\bar{v}),
\end{align*}
lo cual implica que $a\bar{u}+\bar{v} \in E(r)$.
Definición. Para una transformación lineal $T:\mathbb{R}^n\to \mathbb{R}^n$ y un eigenvalor $r$ de $T$ llamaremos a
$$E(r)=\{ \bar{v}\in V |T(\bar{v})=r\bar{v}\}$$
el eigenespacio de $T$ correspondiente a $r$.
Cuando tenemos eigenvectores correspondientes a eigenvalores distintos, cumplen algo especial.
Proposición. Si $\bar{v}_{1}, \dots ,\bar{v}_{l}$ son eigenvectores de una transformación lineal $T:\mathbb{R}^n \rightarrow \mathbb{R}^n$ con eigenvalores correspondientes $r_{1}, \dots ,r_{l}$ distintos entonces $\bar{v}_{1}, \dots ,\bar{v}_{l}$ son linealmente independientes.
Demostración. La ruta para establecer la demostración de este teorema será por inducción sobre $l$. Para un conjunto con sólo un eigenvector el resultado es evidente (¿por qué?). Supongamos cierto para cualquier subconjunto de $l-1$ eigenvectores que pertenecen a eigenespacios distintos. Sean $\bar{v}_{1}, \dots ,\bar{v}_{l}$ eigenvectores en distintos eigenespacios y consideremos $\alpha _{1}, \dots ,\alpha_{l}$ escalares tales que:
\begin{equation}
\label{eq:comb-cero}
\sum_{k=1}^{l}\alpha _{k}\bar{v}_{k}=\bar{0}.
\end{equation}
Aplicamos $T$ a la igualdad anterior. Usando que cada $\bar{v}_{k}$ es eigenvector correspondiente al eigenvalor $r_{k}$ obtenemos:
\begin{align*}
\bar{0}=T(\bar{0})&=T\left(\sum_{k=1}^{l}\alpha _{k}\bar{v}_{k} \right)\\&=\sum_{k=1}^{l}\alpha _{k}T(\bar{v}_{k})\\&=\sum_{k=1}^{l}\alpha _{k}r_{k}\bar{v}_{k}.
\end{align*}
Es decir,
\begin{equation}
\label{eq:aplicarT}
\textbf{0}=\sum_{k=1}^{l}\alpha _{k}r_{k}\bar{v}_{k}
\end{equation}
Multipliquemos \eqref{eq:comb-cero} por $r_{l}$ y restemos el resultado de \eqref{eq:aplicarT} para obtener que
\begin{align*}
\bar{0}=\bar{0}-\bar{0}&=\sum_{k=1}^{l}\alpha _{k}r_{k}\bar{v}_{k}-r_{l}\sum_{k=1}^{l}\alpha _{k}\bar{v}_{k}\\&=\sum_{k=1}^{l-1}\alpha _{k}(r_{k}-r_{l})\bar{v}_{k}.
\end{align*}
Tenemos entonces:
\[ \sum_{k=1}^{l-1}\alpha _{k}(r_{k}-r_{l})\bar{v}_{k}=\bar{0}.\]
Ya que por hipótesis de inducción $\bar{v}_{1}, \dots ,\bar{v}_{l-1}$ son linealmente independientes entonces $\alpha _{k}(r_{k}-r_{l})=0$ para todo $k$, pero los eigenvalores son todos distintos entre sí por lo tanto para todo $k$ de $1$ a $l-1$ se tiene $r_{k}-r_{l}\neq 0$ y así $\alpha _{k}=0$. Finalmente, usando \eqref{eq:comb-cero} obtenemos $\alpha_l=0$. Por lo tanto $\bar{v}_{1}, \dots ,\bar{v}_{l}$ son linealmente independientes.
$\square$
Eigenvectores y transformaciones diagonalizables
Recuerda que dijimos que una transformación lineal $T:\mathbb{R}^n\to \mathbb{R}^n$ es diagonalizable si existe una base $\beta$ de $\mathbb{R}^n$ tal que $\text{Mat}_{\beta}(T)$ es una matriz diagonal. El siguiente resultado conecta las dos ideas que hemos estado explorando: los eigenvectores y la representabilidad sencilla de $T$.
Teorema. Sea $T:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ transformación lineal. Una matriz $T$ es diagonalizable si y sólo si existe una base de $\mathbb{R}^n$ conformada por eigenvectores de $T$.
En realidad la demostración consiste únicamente en entender correctamente cómo se construyen las matrices para una base dada.
Demostración. $\Rightarrow )$ Supongamos que $T$ tiene una representación matricial que es una matriz diagonal $A:=\text{Mat}_{\beta}(T)=\text{diag}(r_{1}, \dots ,r_{n})$ con respecto a la base $\beta=\{\bar{v}_{1}, \dots ,\bar{v}_{n}\}$. Afirmamos que para cada $j=1,\ldots,n$ se tiene $\bar{v}_j$ es eigevector de eigenvalor $r_j$. En efecto, la forma en la que se construyó la matriz $A$ nos dice que
\begin{align*}
T(\bar{e}_j)&=\sum_{i=1}^n a_{ij} \bar{e}_i \\&= a_{jj} \bar{e}_j \\&= r_j \bar{e}_j,
\end{align*}
en donde estamos usando que las entradas $a_{ij}$ de la matriz son cero si $i\neq j$ (por ser diagonal), y son $r_j$ si $i=j$. Por supuesto, como $\bar{e}_j$ forma parte de una base, tampoco es el vector cero. Así, $\bar{e}_j$ es eigenvector de eigenvalor $\bar{e}_j$.
$\Leftarrow )$ Supongamos ahora que $\bar{v}_{1},\dots ,\bar{v}_{n}$ son una base $\beta$ de $\mathbb{R}^n$ conformada por eigenvectores de $T$ con eigenvalores asociados, digamos, $r_{1},\dots ,r_{n}$. Aquí se puede mostrar que $\text{Mat}_\beta(T)$ es diagonal. Queda como tarea moral hacer las cuentas.
$\square$
Hay una situación particular en la que podemos aprovechar el teorema anterior de manera inmediata: cuando la transformación tiene $n$ eigenvalores distintos. Esta consecuencia queda establecida en el siguiente resultado.
Corolario. Toda transformación lineal $T:\mathbb{R}^n\rightarrow \mathbb{R}^n$ tiene a lo más $n$ eigenvalores distintos. Si $T$ tiene exactamente $n$ eigenvalores distintos, entonces los eigenvectores correspondientes forman una base para $\mathbb{R}^n$ y la matriz de $T$ relativa a esa base es una matriz diagonal con los eigenvalores como elementos diagonales.
Demostración. Queda como tarea moral. Como sugerencia, recuerda que mostramos arriba que los eigenvectores de eigenvalores distintos son linealmente independientes.
$\square$
Al parecer los eigenvalores, eigenvectores y eigenespacios de una transformación lineal son cruciales para poder expresarla de manera sencilla. ¿Cómo los encontramos? Esto lo veremos en la siguiente entrada.
Antes de concluir, mencionamos que hay otro teorema crucial sobre diagonalización de matrices. Diremos que una matriz $P\in M_n(\mathbb{R})$ es ortogonal si $P^tP=I$.
Teorema (el teorema espectral). Sea $A\in M_n(\mathbb{R})$ una matriz simétrica. Entonces, existe una matriz ortogonal $P$ tal que $PAP^t$ es una matriz diagonal.
El teorema anterior nos dice no únicamente que la matriz $A$ es diagonalizable, sino que además es diagonalizable mediante un tipo muy especial de matrices. Un estudio y demostración de este teorema queda fuera de los alcances de nuestro curso, pero puedes revisar, por ejemplo la entrada teorema espectral del curso de Álgebra Lineal I que tenemos en el blog.
Más adelante…
Lo que haremos en la siguiente entrada es desarrollar un método para conocer los eigenvalores de una matriz. A partir de ellos podremos encontrar sus eigenvectores. Y en ciertos casos especiales, esto nos permitirá mostrar que la transformación es diagonalizable y, de hecho, nos dará la base para la cual la matriz asociada es diagonal.
Tarea moral
- Considera la transformación lineal de $\mathbb{R}^{3}$ en $\mathbb{R}^{2}$, dada como $T(x,y,z)=(x+y,z+y)$. Encuentra su representación matricial con las bases canónicas de $\mathbb{R}^3$ y $\mathbb{R}^2$. Luego, encuentra su representación matricial con las bases $\{(1,2,3),(1,0,1),(0,-1,0)\}$ de $\mathbb{R}^3$ y $\{(1,1),(1,-1)\}$ de $\mathbb{R}^2$.
- Considera la siguiente matriz: \[ \begin{pmatrix} 1 & 0 & 2 & 3 \\ 0 & -1 & 0 & 2 \\ \end{pmatrix}\] Da una transformación lineal $T:\mathbb{R}^4\to \mathbb{R}^2$ y ciertas bases $\beta$ de $\mathbb{R}^4$ y $\gamma$ de $\mathbb{R}^2$ para las cuales esta matriz sea la representación matricial de $T$ en las bases $\beta$ y $\gamma$.
- Fija bases $\beta$, $\gamma$ y $\delta$ para $\mathbb{R}^n$, $\mathbb{R}^m$ y $\mathbb{R}^l$. Considera dos transformaciones lineales $T:\mathbb{R}^n\to \mathbb{R}^m$ y $S:\mathbb{R}^m\to \mathbb{R}^l$. Demuestra que:
$$\text{Mat}_{\delta, \beta} (S \circ T) = \text{Mat}_{\delta,\gamma}(S) \text{Mat}_{\gamma, \beta} (T).$$
En otras palabras que la «composición de transformaciones corresponde al producto de sus matrices». - Sea $T:\mathbb{R}^n\to\mathbb{R}^n$ una transformación lineal y $\beta$ una base de $\mathbb{R}^n$. Demuestra que $T$ es biyectiva si y sólo si $\text{Mat}_{\beta}(T)$ es invertible.
- Verifica que los vectores $\bar{v}_1,\ldots,\bar{v}_n$ dados en el último teorema en efecto ayudan a dar una representación matricial diagonal para $T$.
- La demostración del último corolario es un conjunto de sencillas consecuencias de las definiciones y teoremas desarrollados en esta entrada con respecto a los eigenvalores y eigenvectores. Realiza esta demostración.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral III
- Entrada anterior del curso: Sistemas de ecuaciones lineales
- Entrada siguiente del curso: Polinomio característico