Profundiza lo suficiente en cualquier cosa y encontrarás las matemáticas.
– Dean Schlicter

Introducción

En la entrada anterior comenzamos a desarrollar formalmente la teoría cualitativa de las ecuaciones diferenciales, en particular estudiamos algunos sistemas lineales y no lineales autónomos planos, es decir, con dos ecuaciones diferenciales.

Ahora sabemos cómo obtener un bosquejo del campo vectorial asociado al sistema y dibujar algunas trayectorias de forma tangente a los vectores, esto sin siquiera conocer explícitamente las soluciones del sistema. También sabemos identificar los puntos de equilibrio de un sistema y clasificarlos como estables, asintóticamente estables o inestables. Según sea la naturaleza del punto de equilibrio tendremos más información sobre las soluciones del sistema, al menos de forma cualitativa.

En esta entrada haremos un análisis más detallado sobre las trayectorias que se forman en el plano fase y que representan soluciones particulares del sistema. Veremos, además, una forma relativamente sencilla de obtener las trayectorias sin apoyarnos del campo vectorial asociado y es ¡resolviendo una ecuación de primer orden!.

Trayectorias de un sistema autónomo

Recordemos que los sistemas que estamos estudiando son de la forma

\begin{align*}
x^{\prime} &= \dfrac{dx}{dt} = F_{1}(x, y) \\
y^{\prime} &= \dfrac{dy}{dt} = F_{2}(x, y) \label{1} \tag{1}
\end{align*}

Hasta ahora en el plano fase hemos trazado trayectorias descritas por las soluciones de un sistema autónomo guiándonos por el campo vectorial asociado. En esta ocasión desarrollaremos otro método para obtenerlas y es resolviendo una ecuación de primer orden.

Supongamos que

$$Y(t) = (x(t), y(t)) \label{2} \tag{2}$$

es una solución del sistema (\ref{1}) que no permanece constante en el tiempo, es decir, que no se trata de una solución de equilibrio y además la derivada $\dfrac{dx}{dt}$ es distinta de cero en $t = t_{0}$, entonces en un entorno del punto $x_{1} = x(t_{0})$ se verifica que

$$\dfrac{dy}{dx} = \dfrac{dy}{dt} \dfrac{dt}{dx} = \dfrac{F_{2}(x, y)}{F_{1}(x, y)}$$

Por lo tanto, la trayectoria de esa solución verifica la ecuación diferencial de primer orden

$$\dfrac{dy}{dx} = \dfrac{F_{2}(x, y)}{F_{1}(x, y)} \label{3} \tag{3}$$

En el caso en el que $\dfrac{dx}{dt}$ sea cero para todo $t$, se tendrá que verificar que $\dfrac{dy}{dt}$ no siempre sea nula, por lo que la trayectoria de esa solución verifica, análogamente, la ecuación diferencial

$$\dfrac{dx}{dy} = \dfrac{F_{1}(x, y)}{F_{2}(x, y)} \label{4} \tag{4}$$

En cualquier caso, las trayectorias se podrán determinar resolviendo una ecuación diferencial de primer orden.

Más adelante veremos algunos ejemplos.

Propiedades cualitativas de las trayectorias

Las propiedades cualitativas de las trayectorias nos permiten obtener información sobre el comportamiento de las soluciones. Algunas de las propiedades más importantes se enuncian a continuación.

• Cada trayectoria del plano fase representa infinitas soluciones del sistema autónomo.

Demostración: Sea $Y(t) = (x(t), y(t))$ una solución de (\ref{1}), entonces se cumple que

$$\dfrac{dY}{dt} = (x^{\prime}, y^{\prime}) = (F_{1}(x, y), F_{2}(x, y))$$

Para ahorrar notación escribiremos

$$F(Y(t)) = (F_{1}(x, y), F_{2}(x, y))$$

de manera que el sistema se puede escribir como

$$\dfrac{dY}{dt} = F(Y(t)) \label{6} \tag{6}$$

Definamos la función auxiliar $\phi(t) = F(Y(t))$, entonces la ecuación anterior se puede escribir como

$$\dfrac{dY}{dt}(t) = \phi(t) \label{7} \tag{7}$$

Las dos funciones $\dfrac{dY}{dt}(t)$ y $\phi(t)$ coinciden en todo instante. Sea $c$ una constante, en particular deben coincidir en $t + c$, esto es

$$\dfrac{dY}{dt}(t + c) = \phi(t + c) = F(Y(t + c)) \label{8} \tag{8}$$

Pero $\dfrac{dY}{dt}$ evaluada en $t + c$ es igual a la derivada de $\hat{Y}(t) = Y(t + c)$ evaluada en $t$, esto es

$$\dfrac{d}{dt} Y(t + c) = F(Y(t + c))$$

o bien,

$$\dfrac{d\hat{Y}}{dt} = F(\hat{Y}(t)) \label{9} \tag{9}$$

Por lo tanto, la función $\hat{Y}(t) = Y(t + c)$ es otra solución del sistema.

$\square$

Este teorema es valido para cada $c \in \mathbb{R}$ lo que muestra que cada una de las trayectorias del plano fase puede representar infinitas soluciones del sistema.

Por ejemplo, una solución del sistema

\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= 2xy
\end{align*}

es

$$x(t) = \tan(t), \hspace{1cm} y(t) = \sec^{2}(t)$$

Por el teorema anterior, las funciones

$\hat{x}(t) = \tan(t + c), \hspace{1cm} \hat{y}(t) = \sec^{2}(t + c)$

también son solución del mismo sistema y ambas trazan la misma trayectoria en el plano fase, sin embargo no coinciden en el mismo punto al momento de evaluar en $t = t_{0}$.

Para el caso lineal se puede verificar explícitamente el teorema anterior.

Sea $\mathbf{Y}^{\prime} = \mathbf{AY}$ un sistema lineal, sabemos que toda solución $\mathbf{Y}(t)$ de esta ecuación es de la forma

$$\mathbf{Y}(t) = e^{\mathbf{A}t} \mathbf{K} \label{10} \tag{10}$$

para algún vector constante $\mathbf{K}$, notemos que

$$\mathbf{Y}(t + c) = e^{\mathbf{A}(t + c)} \mathbf{K} = e^{\mathbf{A}t} e^{\mathbf{A}c} \mathbf{K}$$

Esto es cierto, ya que

$$(\mathbf{A}t) \mathbf{A}c = \mathbf{A}c(\mathbf{A}t)$$

para cualesquiera valores de $t$ y $c$. Sea el vector constante $\mathbf{C} = e^{\mathbf{A}c}\mathbf{K}$, entonces la solución anterior se puede escribir como

$$\mathbf{Y}(t + c) = e^{\mathbf{A}t} \mathbf{C} \label{11} \tag{11}$$

Por lo tanto, $\mathbf{Y}(t + c)$ es también una solución de $\mathbf{Y}^{\prime} = \mathbf{AY}$.

Una observación más es que el teorema anterior no es válido si la función $F$ depende explícitamente de $t$. Supongamos que $Y(t)$ es una solución de la ecuación diferencial no autónoma

$$Y^{\prime} = F(t, Y(t)) \label{12} \tag{12}$$

Evaluando en $t + c$, se tiene

$$Y^{\prime}(t + c) = F(t + c, Y(t + c)) \label{13} \tag{13}$$

por consiguiente, la función $Y(t + c)$ satisface la ecuación diferencial

$$Y^{\prime} = F(t + c, Y) \label{14} \tag{14}$$

y tal ecuación es diferente de la ecuación no autónoma (\ref{12}).

• Existencia y unicidad de las trayectorias.

Demostración: Sea $Y_{0} = (x_{0}, y_{0})$ un punto cualquiera en el espacio fase y sea $Y = \phi(t)$ la solución del problema de valores iniciales

$$Y^{\prime} = F(x, y), \hspace{1cm} Y(0) = Y_{0} \label{15} \tag{15}$$

La trayectoria de esta solución pasa por el punto $Y_{0}$, de manera que existe al menos una trayectoria a través de cada punto $Y_{0}$, esto muestra la existencia. Supongamos ahora que la trayectoria de alguna otra solución $Y = \psi(t)$ también pasa por el punto $Y_{0}$, esto significa que existe $t_{0} \neq 0$, tal que $\psi(t_{0}) = Y_{0}$. Por el teorema anterior se tiene que la función

$$Y = \psi(t + t_{0})$$

es también una solución del sistema. Notemos que $\psi(t + t_{0})$ y $\phi(t)$ tienen el mismo valor en $t = 0$, tal valor es

$$\psi(t_{0}) = \phi(0) = Y_{0} \label{16} \tag{16}$$

Dadas las hipótesis del teorema y el resultado (\ref{16}) estamos en condiciones de aplicar el teorema de existencia y unicidad de los sistemas de ecuaciones diferenciales, por este teorema se tiene que $\psi(t + t_{0})$ es igual a $\phi(t)$ para todo $t \in \mathbb{R}$. Esto implica que las trayectorias de $\phi(t)$ y $\psi(t)$ son idénticas quedando demostrada la unicidad de las trayectorias.

$\square$

Observemos que si $\hat{Y}_{0}$ es un punto de la trayectoria de $\phi(t)$, es decir, $\hat{Y}_{0} = \phi(t_{1})$ para alguna $t_{1}$, entonces $\hat{Y}_{0}$ está también en la trayectoria de $\psi(t)$, ya que

$$\hat{Y}_{0} = \phi (t_{1}) = \psi(t_{1} + t_{0}) \label{17} \tag{17}$$

Recíprocamente, si $\hat{Y}_{0}$ es un punto de la trayectoria de $\psi(t)$, es decir, existe $t_{2}$, tal que $\psi (t_{2}) = \hat{Y}_{0}$, entonces $ \hat{Y}_{0} $ está también en la trayectoria de $\phi (t)$, ya que

$$\hat{Y}_{0} = \psi(t_{2}) = \phi (t_{2} -t_{0}) \label{18} \tag{18}$$

En la entrada anterior vimos que los puntos de equilibrio estables se caracterizan por que las trayectorias cercanas a dicho punto nunca llegan a él, dichas curvas solían ser cerradas, veremos a continuación que las curvas cerradas son periódicas.

• Las trayectorias cerradas corresponden a soluciones periódicas.

Demostración: Sea $Y = \phi(t)$ una solución de (\ref{1}) y supongamos que

$$\phi(t_{0} + T) = \phi(t_{0})$$

para algún par de números $t_{0}$ y $T$. Por el primer teorema, la función

$$\psi(t) = \phi (t + T)$$

es también una solución de (\ref{1}) que coincide con $\phi(t)$ en el tiempo $t = t_{0}$. Por el teorema de existencia y unicidad de los sistemas de ecuaciones diferenciales se satisface que $\psi(t) = \phi(t + T)$ es idénticamente igual a $\phi(t)$, por lo tanto

$$\phi(t + T) = \phi(t)$$

$\square$

Explícitamente vemos que si $(x(t), y(t))$ es una solución del sistema (\ref{1}), que en dos instantes $t_{0}$ y $t_{0} + T$ toma el mismo valor, entonces

$$(x(t), y(t)) = (x(t + T), y(t + T)) \label{21} \tag{21}$$

para todo $t \in \mathbb{R}$, es decir $(x(t), y(t))$ es periódica.

Concluiremos esta entrada realizando algunos ejemplos.

Ejemplo: Describir las trayectorias del sistema no lineal

\begin{align*}
x^{\prime} &= y(1 -x^{2} -y^{2}) \\
y^{\prime} &= -x(1 -x^{2} -y^{2})
\end{align*}

Solución : El objetivo de este ejercicio es caracterizar a las soluciones del sistema de forma cualitativa aplicando lo que conocemos hasta ahora.

Lo primero que haremos será determinar los puntos de equilibrio del sistema, dichos puntos se obtienen de resolver el siguiente sistema

\begin{align*}
y(1- x^{2} -y^{2}) &= 0 \\
-x(1 -x^{2} -y^{2}) &= 0
\end{align*}

Vemos que $(x, y) = (0, 0)$ es un punto de equilibrio y todo punto de la circunferencia

$$x^{2} + y^{2} = 1$$

es también un punto de equilibrio.

Ahora podemos determinar las trayectorias del sistema analíticamente resolviendo una ecuación diferencial de primer orden, de acuerdo a (\ref{3}) dicha ecuación es

$$\dfrac{dy}{dx} = \dfrac{-x(1 -x^{2} -y^{2})}{y(1 -x^{2} -y^{2})} = -\dfrac{x}{y}$$

Resolvamos la ecuación diferencial

$$\dfrac{dy}{dx}= -\dfrac{x}{y}$$

Apliquemos separación de variables.

\begin{align*}
y dy &= -xdx \\
\int y dy &= -\int x dx \\
\dfrac{y^{2}}{2} &= -\dfrac{x^{2}}{2} + k \\
x^{2} + y^{2} &= c^{2}
\end{align*}

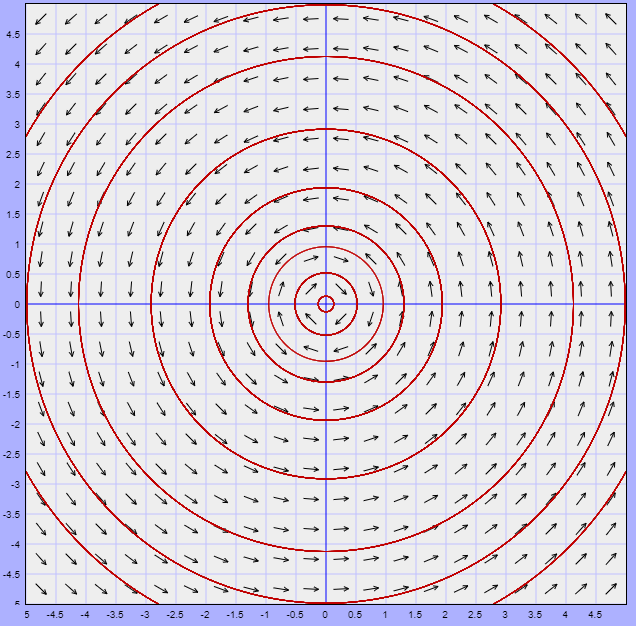
En donde $c^{2}$ engloba todas las constantes. Notamos que las trayectorias corresponden a circunferencias concéntricas de radio $c$, tal que $c\neq 1$. El plano fase se ve de la siguiente forma.

Efectivamente las trayectorias son circunferencias concéntricas lo que significa que son periódicas ya que cada cierto tiempo $T$ vuelven al mismo punto de inicio $t_{0}$, sin embargo al no conocer explícitamente las soluciones $x(t)$ y $y(t)$ no no es posible determinar el valor del periodo $T$.

Notemos también que las trayectorias para $c < 1$ giran en la dirección de las manecillas del reloj, mientras que las trayectorias para $c > 1$ giran en la dirección opuesta. Es claro que todos los puntos de equilibrio son estables ya que ninguna trayectoria tiende a ellos, pero las que están cerca a ellos permanecen cerca para todo $t \in \mathbb{R}$.

$\square$

Ejemplo: Mostrar que las soluciones de la siguiente ecuación diferencial de segundo orden son periódicas.

$$\dfrac{d^{2}z}{dt^{2}} + z + z^{5} = 0$$

Solución: Lo primero que haremos será escribir la ecuación de segundo orden en un sistema de dos ecuaciones de primer orden. Sean

$$x = z \hspace{1cm} y \hspace{1cm} y = \dfrac{dx}{dt} = \dfrac{dz}{dt}$$

Y de la ecuación diferencial vemos que

$$\dfrac{d^{2}z}{dt^{2}} = \dfrac{dy}{dt} = -x -x^{5}$$

Entonces el sistema es

\begin{align*}
\dfrac{dx}{dt} &= y \\
\dfrac{dy}{dt} &= -x -x^{5}
\end{align*}

Para conocer la forma explícita de las trayectorias escribamos al sistema como una ecuación de primer orden y resolvámosla.

$$\dfrac{dy}{dx} = \dfrac{-x -x^{5}}{y}$$

La ecuación es separable.

\begin{align*}
y dy &= -(x + x^{5})dx \\
\int y dy &= -\int (x + x^{5}) dx \\
\dfrac{y^{2}}{2} &= -\dfrac{x^{2}}{2} + \dfrac{x^{6}}{6} + k
\end{align*}

Las trayectorias están definidas por la ecuación

$$\dfrac{y^{2}}{2} + \dfrac{x^{2}}{2} -\dfrac{x^{6}}{6} = c^{2}$$

Esta ecuación define una curva cerrada para cada valor de $c$ en el plano $XY$ y como el único punto de equilibrio es el origen, entonces toda solución es periódica. El plano fase se ve de la siguiente forma.

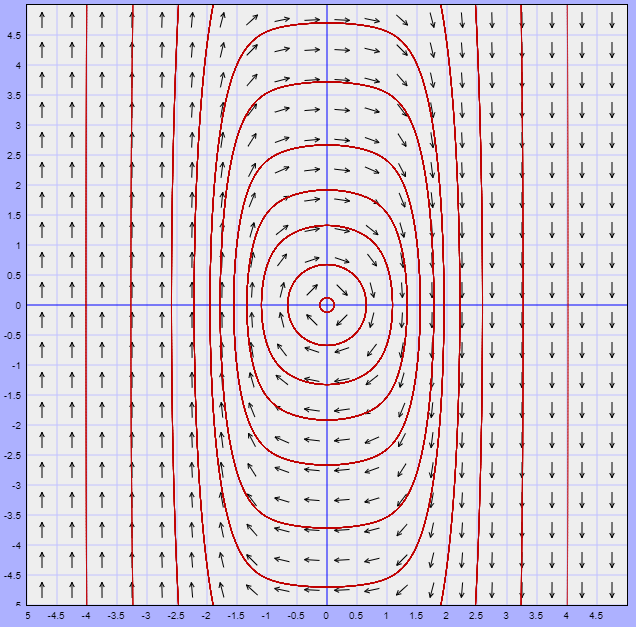
Gráficamente observamos que efectivamente las soluciones son periódicas, sin embargo no es posible calcular el periodo de ninguna solución particular.

$\square$

Ejemplo: Demostrar cualitativamente que las soluciones $Y(t) = (x(t), y(t))$ del sistema

\begin{align*}
x^{\prime} &= x^{2} + y \sin(x) \\
y^{\prime} &= -1+xy + \cos(y)
\end{align*}

que comienzan en el primer cuadrante $(x > 0, y> 0)$ deben permanecer en él para todo $t \in \mathbb{R}$.

Solución: Este es un ejemplo que nos muestra que no siempre puede ser sencillo obtener las trayectorias resolviendo una ecuación de primer orden, en este caso la ecuación a resolver sería

$$\dfrac{dy}{dx} = \dfrac{-1+xy + \cos(y)}{x^{2} + y \sin(x)}$$

Sin embargo, el ejercicio nos pide demostrarlo cualitativamente. La función vectorial $F$ es

$$F(x, y) = (x^{2} + y \sin(x), -1+xy + \cos(y))$$

El plano fase con el campo vectorial asociado y las trayectorias sobre el primer cuadrante se ilustra a continuación.

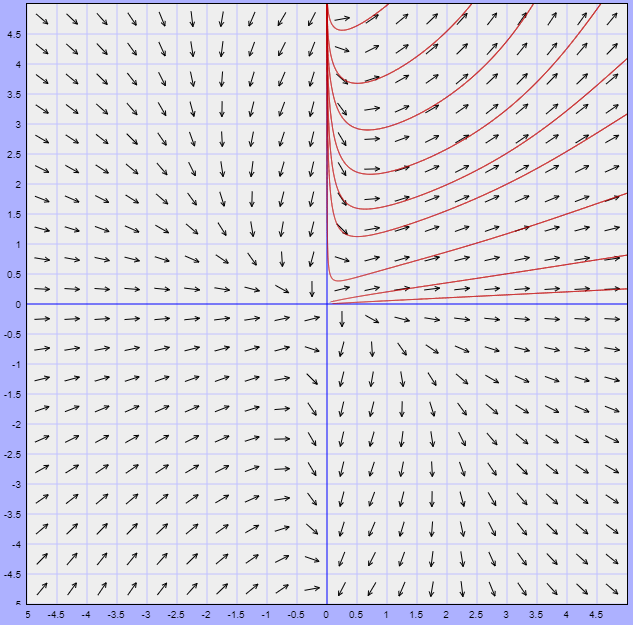
Al menos geométricamente logramos observar que todas las trayectorias que comienzan en el primer cuadrante permanecen en él para todo $t \in \mathbb{R}$, esto significa que las soluciones siempre permanecerán positivas para $x > 0$ y $y > 0$.

$\square$

Para concluir estudiemos el movimiento de un péndulo como ejemplo.

Ejemplo: La ecuación de movimiento del péndulo es

$$\dfrac{d^{2} \theta}{dt^{2}} + \dfrac{g}{l} \sin(\theta) = 0 \label{22} \tag{22}$$

en donde $l$ es la longitud del hilo del péndulo, $\theta$ el ángulo que forma el hilo con la vertical y $g$ la aceleración de la gravedad.

Analizar el movimiento del péndulo.

Solución: Primero comprendamos el fenómeno. Estamos considerando un péndulo simple en el cual si desplazamos la partícula desde la posición de equilibrio hasta que el hilo forme un ángulo $\theta$ con la vertical, y luego la soltamos partiendo del reposo, el péndulo oscilará en un plano bajo la acción de la gravedad. Las oscilaciones tendrán lugar entre las posiciones extremas $\theta$ y $-\theta$, simétricas respecto a la vertical, a lo largo de un arco de circunferencia cuyo radio es la longitud $l$ del hilo.

Comencemos por escribir la ecuación del péndulo en una sistema de dos ecuaciones de primer orden. Sean

$$x = \theta \hspace{1cm} y \hspace{1cm} y = \dfrac{d \theta}{dt} = \dfrac{dx}{dy}$$

Y de la ecuación del péndulo obtenemos que

$$\dfrac{d^{2} \theta}{dt^{2}} = \dfrac{dy}{dt} = -\dfrac{g}{l} \sin(x)$$

Entonces el sistema correspondiente es

\begin{align*}
\dfrac{dx}{dt} &= y \\
\dfrac{dy}{dt} &= -\dfrac{g}{l} \sin(x)
\end{align*}

La función vectorial $F$ es

$$F(x, y) = \left( y, -\dfrac{g}{l} \sin(x) \right)$$

Los puntos de equilibrio son los puntos tal que

\begin{align*}
y &= 0 \\
-\dfrac{g}{l} \sin(x) &= 0
\end{align*}

De la primer ecuación tenemos $y = 0$ y de la segunda notamos que para que $\sin(x) = 0$ se debe cumplir que $x = k \pi$ con $k$ una constante entera, por tanto el sistema tiene infinitos puntos de equilibrio y son de la forma $(k\pi ,0)$ con $k\in \mathbb{Z}$.

Consideremos los puntos de equilibrio $(0,0)$ y $(\pi ,0)$. El primer punto indica que

$$x = \theta = 0 \hspace{1cm} y \hspace{1cm} y = \dfrac{d \theta}{dt} = 0$$

En este caso el péndulo se encuentra en reposo en la posición de equilibrio y no hay desplazamiento ya que la velocidad es nula.

En el caso del segundo punto crítico se tiene que

$$x = \theta = \pi \hspace{1cm} y \hspace{1cm} y = \dfrac{d \theta}{dt} = 0$$

Por tanto, el ángulo de desplazamiento es $\pi$, y la velocidad nuevamente es nula. En cualquiera de estas dos situaciones el péndulo continuará así indefinidamente. Sin embargo, estos dos puntos de equilibrio son diferentes. Cuando nos encontramos en la situación de equilibrio $(0,0)$, ante cualquier pequeño cambio de la situación (cambio de posición o de velocidad), el sistema presentará pequeñas oscilaciones, mientras que cuando nos encontramos en la situación de equilibrio $(\pi, 0)$, estos pequeños cambios harán que el sistema presente una notable desviación. Estas características indican que el punto de equilibrio $(0, 0)$ es estable, mientras que el punto de equilibrio $(\pi, 0)$ es inestable.

A continuación se muestra el plano fase del sistema en el cual podemos observar las trayectorias para distintas soluciones particulares $(x(t), y(t))$ y lo que sucede alrededor de los puntos de equilibrio.

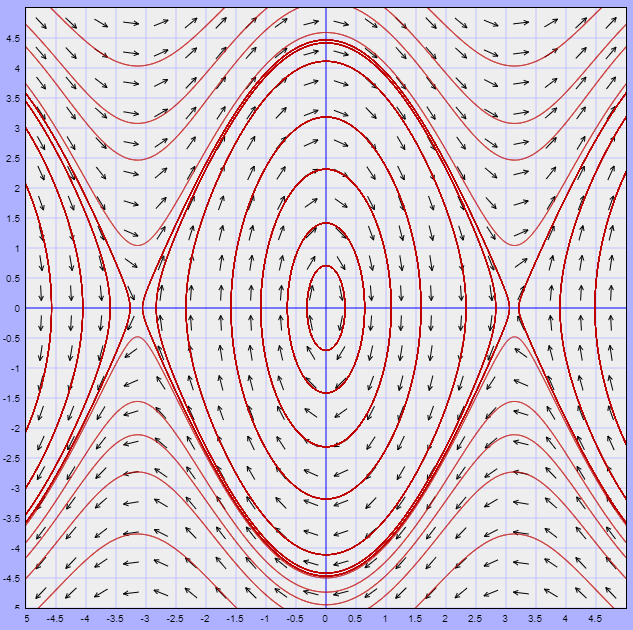
El plano fase muestra geométricamente que las soluciones para valores de $x = \theta$ pequeños el movimiento es periódico y deja de serlo conforme nos acercamos a los puntos de equilibrio $(-\pi, 0)$ o $(\pi, 0)$. Esto tiene sentido, pues la ecuación del péndulo (\ref{22}) no corresponde a un movimiento armónico simple debido a la presencia de la función seno, sin embargo para oscilaciones de pequeña amplitud en los que el ángulo es suficientemente pequeño se puede hacer la aproximación $\sin(\theta) \approx \theta$, en este caso la ecuación del péndulo se reduce a

$$l \dfrac{d^{2} \theta}{dt^{2}} + g \theta = 0 \label{23} \tag{23}$$

la cual corresponde a una ecuación de movimiento armónico simple refiriéndose al movimiento angular en lugar del movimiento rectilíneo.

La solución de la ecuación (\ref{23}) es

$$\theta = A \sin(\omega t + \phi) \label{24} \tag{24}$$

Donde,

$$\omega = \sqrt{\dfrac{g}{l}} \label{25} \tag{25}$$

es la frecuencia angular. El periodo será, entonces

$$T = 2 \pi \sqrt{\dfrac{l}{g}} \label{26} \tag{26}$$

y $A$ y $\phi$ son constantes correspondientes a la amplitud angular y a la fase inicial del movimiento, respectivamente y son determinadas por las condiciones iniciales.

$\square$

Con esto concluimos esta entrada.

En las próximas entradas revisaremos nuevamente los sistemas lineales homogéneos y el método de valores y vectores propios para hacer un análisis desde una perspectiva cualitativa.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Para las demostraciones cualitativas puedes usar la herramienta que hemos estado utilizando.

1. Demostrar cualitativamente que todas las soluciones $Y(t) = (x(t), y(t))$ del sistema
   
   $x^{\prime} = y(e^{x} -1)$
   $y^{\prime} = x + e^{y}$
   
   que comienzan en el semiplano derecho $(x > 0)$ deben permanecer en él para todo $t \in \mathbb{R}$.

2. Demostrar cualitativamente que todas las soluciones $Y(t) = (x(t), y(t))$ del sistema
   
   $x^{\prime} = 1 + x^{2} + y^{2}$
   $y^{\prime} = xy + \tan(y)$
   
   que comienzan en el semiplano superior $(y > 0)$ deben permanecer en él para todo $t \in \mathbb{R}$.

3. Demostrar cualitativamente que todas las soluciones $Y(t) = (x(t), y(t))$ del sistema
   
   $x^{\prime} = -1 -y + x^{2}$
   $y^{\prime} = x + xy$
   
   que empiezan en el interior del círculo unitario $x^{2} + y^{2} = 1$ deben permanecer en él para todo $t \in \mathbb{R}$.

4. Demostrar que todas las soluciones del sistema de ecuaciones
   
   $x^{\prime} = y(1 + x^{2} + y^{2})$
   $y^{\prime} = -2x(1 + x^{2} + y^{2})$
   
   son de la forma $\dfrac{1}{2}y^{2} + x^{2} = c^{2}$, es decir, las trayectorias son una familia de elipses.

5. Demostrar que alrededor del punto de equilibrio las soluciones de las siguientes ecuaciones de segundo orden son periódicas.

• $\dfrac{d^{2}z}{dt^{2}} + z^{3} = 0$

• $\dfrac{d^{2}z}{dt^{2}} + \dfrac{z}{1 + z^{2}} = 0$

Más adelante…

En la unidad anterior desarrollamos el método de valores y vectores propios para resolver sistemas lineales homogéneos, vimos que existen distintos casos de acuerdo al valor que tomen los valores propios y el método de resolución para cada caso es relativamente distinto. En las siguientes entradas estudiaremos nuevamente estos sistemas con la adición de que ahora estudiaremos el tipo de trayectorias que genera cada sistema en el plano fase y veremos la dependencia que tienen éstas con el valor que tomen los valores propios.

Entradas relacionadas

• Página principal del curso: Ecuaciones Diferenciales I
• Entrada anterior del curso: Sistemas autónomos, puntos de equilibrio y su estabilidad
• Siguiente entrada del curso: Teoría cualitativa de los sistemas lineales homogéneos – Valores propios reales y distintos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»