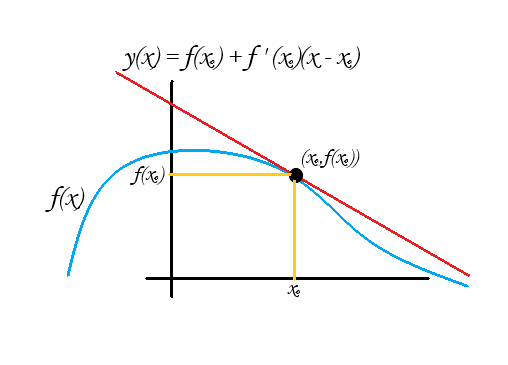Introducción
Así como en la segunda unidad del curso, en esta unidad cubriremos nuevamente algunos temas de álgebra lineal que son importantes para el cálculo de varias variables. Nuevamente, daremos una exposición un poco superficial, pues se espera que estos temas sean cubiertos a profundidad en un curso de Álgebra Lineal 1 que se lleve en paralelo. Una posibilidad es tomar de manera paralela el curso aquí en el blog, en el siguiente enlace: Álgebra Lineal I, en donde hay una exposición más holgada de los temas que revisaremos en las siguientes entradas.
Comenzaremos esta entrada mencionando la importancia de las matrices como herramienta matemática en el estudio de las funciones de $\mathbb{R}^n$ en $\mathbb{R}^m$. Revisaremos también las distintas operaciones que podemos ejecutar sobre ellas. Hablaremos de operaciones binarias y elementales. Cada una de ellas tiene sus propósitos particulares.
Importancia de las matrices en cálculo diferencial e integral
Recordemos algunos conceptos del curso de Cálculo Diferencial e Integral 1. Comencemos con una función $f:D\subset \mathbb{R} \to \mathbb{R}$ una función derivable en el punto $x_{0} \in D$. La derivada de la función $f$ en el punto $x_{0}$ es un número que representa la pendiente de la recta tangente a la gráfica de la función en el punto $(x_{0},f (x_{0})) $. La recta en cuestión tiene por ecuación $y(x) =f ( x_{0})+f'(x_{0})(x-x_{0}) $. Observa que la función $y$ citada es una función lineal. No necesariamente es una transformación lineal, pues puede desplazar al origen. Sin embargo la llamamos «la mejor aproximación lineal a $f$ en el punto $x_{0}$». A grandes rasgos, recibe este nombre pues la función $f$ cerca de un punto dado $x_{0}$ toma valores muy cercanos a los que tomaría $y(x)$ cerca de ese mismo punto.
En el estudio de las funciones reales, así como en sus aplicaciones, es mucho mas fácil auxiliarnos de aproximaciones lineales para investigar y conocer las propiedades locales o en ciertas vecindades del punto a tratar. Las aproximaciones lineales son ecuaciones de rectas, las cuales poseen propiedades muy nobles y bastante tratables. Esta técnica de trabajar problemas de funciones reales (derivables) con lineas rectas, usando la mejor aproximación lineal en el punto dado también es usada para las funciones de $\mathbb{R}^n$ en $\mathbb{R}^m$, usando transformaciones lineales con las cuales se trabajará en las siguientes secciones.
La técnica será casi igual a la usada para las funciones de una variable real: hallaremos una transformación lineal la cual podremos usar para tener la mejor aproximación lineal a la función en un punto dado de su dominio. De aquí es natural que introduzcamos a las matrices en $M_{m,n}(\mathbb{R})$, pues las transformaciones lineales de $\mathbb{R}^n$ en $\mathbb{R}^m$ pueden ser representadas por matrices una vez que hayamos elegido las bases para los espacios vectoriales $\mathbb{R}^n$ y $\mathbb{R}^m$. Además, hay propiedades de transformaciones lineales que se pueden entender fácilmente en términos de matrices. Por ejemplo, la composición y producto escalar de transformaciones lineales tienen sus correspondientes operaciones en matrices, repectivamente la multiplicación de matrices y producto por escalar.
Definición de matriz
Recuerda que nuestra exposición está condensada pues los temas pueden consultarse a detalle en otras entradas de este blog. Específicamente, para el tema de matrices puedes considerar esta entrada para un tratamiento más detallado.
Definición. Sean $m$ y $n$ números naturales. Una matriz de $n$ filas y $m$ columnas con entradas en los números reales es un arreglo rectangular de la siguiente forma:
$$A=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\end{pmatrix}.$$
Al conjunto de todas las matrices de $n$ filas y $m$ columnas con entradas en los números reales lo denotaremos por $M_{m,n}(\mathbb{R})$. Si $m=n$, usaremos la notación simplificada $M_n(\mathbb{R})$.
Es posible formalizar todavía más a las matrices, pensando en los conjuntos $[m]=\{1,2,\ldots,m\}$ y $[n]=\{1,2,\ldots,n\}$, y tomando una matriz como una función $A:[n]\times[m]\to\mathbb{R}$. Sin embargo, usualmente no tomaremos esta definición, y nos apegaremos a las definiciones dadas arriba.
Operaciones binarias relacionadas con matrices
Hablaremos de tres operaciones binarias relacionadas con matrices, las cuales son útiles para nuestros propósitos en cálculo, pues hay algunas operaciones entre funciones que se corresponden con ellas. Las operaciones que discutiremos son el producto por escalar, la suma de matrices y el producto de matrices. Respectivamente, estas corresponderán, en cierto sentido, al producto por escalar, suma de funciones y composición de funciones. Puedes revisar esta entrada para conocer detalle como se dan algunas de estas correspondencias.
Definición. La suma de matrices es una operación binaria que toma dos matrices con la misma cantidad de filas, y con la misma cantidad de columnas. Si la matriz $A$ tiene entradas $a_{ij}$ y la matriz $B$ tiene entradas $b_{ij}$, su suma está definida como la matriz $A+B$ cuyas entradas son $a_{ij}+b_{ij}$, es decir, las matrices se suman entrada a entrada. Pensada de esta manera, la suma es una función $+:M_{m,n}(\mathbb{R})\times M_{m,n}(\mathbb{R}) \to M_{m,n}(\mathbb{R})$.
Podemos ver esta operación también en los arreglos correspondientes:
\begin{align*}
A+B&=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} & \cdots & b_{1n}\\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \cdots & b_{mn}\end{pmatrix}\\
&:=\begin{pmatrix} a_{11}+b_{11} & a_{12}+b_{12} & \cdots & a_{1n}+b_{1n}\\ a_{21}+b_{21} & a_{22}+b_{22} & \cdots & a_{2n}+b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}+b_{m1} & a_{m2}+b_{m2} & \cdots & a_{mn}+b_{mn}\end{pmatrix}
\end{align*}
Definición. El producto matriz por escalar es una operación binaria que toma un número real $r$ y una matriz $A$. A la pareja $(r,A)$ le asigna otra matriz que denotaremos por $rA$. Si las entradas de $A$ son $a_{ij}$, las de $rA$ son $ra_{ij}$. En otras palabras, cada una de las entradas de $A$ se multiplica por $r$, de modo que en el arreglo se ve de la siguiente manera:
$$rA=\begin{pmatrix} ra_{11} & ra_{12} & \cdots & ra_{1n}\\ ra_{21} & ra_{22} & \cdots & ra_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ ra_{m1} & ra_{m2} & \cdots & ra_{mn}\end{pmatrix}.$$
De esta manera, el producto matriz por escalar es una operación binaria
$$\cdot: \mathbb{R} \times M_{m,n}(\mathbb{R})\to M_{m,n}(\mathbb{R}).$$
Definición. Finalmente, tenemos el producto de matrices. Para multiplicar dos matrices $A$ y $B$, necesitamos que la cantidad de columnas de $A$ sea igual a la cantidad de filas de $B$. Así, $A$ es una matriz de, digamos $m\times n$ y $B$ es una matriz de, digamos $n\times p$. Su producto será una matriz de $m\times p$. Si $A$ tiene entradas $a_{ij}$ y $B$ tiene entradas $b_{jk}$, entonces la matriz producto $AB$ tendrá entradas dadas por la siguiente regla del producto:
\begin{align*}
c_{ik}&=\sum_{j=1}^n a_{ij}b_{jk}\\
&=a_{i1}b_{1k}+a_{i2}b_{2k}+\ldots+a_{in}b_{nk}.
\end{align*}
Esto nos dice que el producto de matrices es entonces una operación binaria
$$\cdot: M_{m,n}(\mathbb{R})\times M_{n,p}(\mathbb{R})\to M_{m,p}(\mathbb{R}).$$
Operaciones elementales de matrices
Las operaciones elementales involucran únicamente una matriz. Usualmente son usadas para resolver sistemas de ecuaciones lineales, una vez que estos se han pasado a su forma matricial. Así mismo, las operaciones elementales ayudan a hallar representaciones mas sencillas de ciertas transformaciones lineales.
Definición. Dada una matriz $A$, una transposición de renglones consiste en elegir dos de los renglones de $A$ e intercambiarlos.
Definición. Dada una matriz $A$, un reescalamiento consiste en elegir un renglón y un número real $r\neq 0$, y substituir al renglón por aquel que se obtiene al multiplicar cada entrada del renglón por $r$.
Definición. Dada una matriz $A$, una transvección consiste en elegir dos renglones $u$ y $v$ de la matriz y un escalar $r$, y sustituir al renglón $v$ por el renglón $v+ru$ (aquí pensamos a $u$ y $v$ como vectores para efectuar las operaciones).
Las operaciones elementales son fundamentales en la teoría de matrices pues a partir de ellas siempre podemos llevar cualquier matriz a una forma muy sencilla, que definimos a continuación.
Definición. Una matriz $A$ está en forma escalonada reducida si suceden las siguientes cosas:
- Aquellas filas de $A$ que consisten de puros ceros, están hasta abajo.
- En aquellas filas que no sean de puros ceros, la primera entrada (de izquierda a derecha) que no sea igual a cero (a la que llamaremos pivote) es igual a $1$.
- Si una fila está arriba de otra y ambas tienen pivote, entonces el pivote de la de arriba está más a la izquierda que el pivote de la de abajo.
- Si una entrada de la matriz es pivote (de alguna fila), entonces es la única entrada distinta de cero de la columna en la que está.
En este enlace puedes encontrar una exposición más detallada de este tipo de matrices
Ejemplo. Consideremos la siguiente matriz: $$\begin{pmatrix} 0 & 5 & 3 \\ 3 & 7 & 0 \\ 0 & 0 & 1 \end{pmatrix}.$$
El pivote del primer renglón es 5, del segundo 3, y del tercero 1. Esta matriz no está en forma escalonada reducida pues no todos sus pivotes son iguales a $1$. Tampoco esta en forma escalonada reducida pues el pivote de la tercera fila (la entrada $1$), no es la única entrada distinta de cero en su columna, pues en esa columna también hay un $3$.
$\triangle$
Ejemplo. Las siguientes matrices sí están en forma escalonada reducida:
\[ \begin{pmatrix} 1 & 5 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\hspace{2cm} \begin{pmatrix} 0 & 1 & -2 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{pmatrix}\hspace{2cm} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \]
$\triangle$
Quizás el teorema más fundamental de la teoría de matrices es el teorema de reducción gaussiana, que enunciamos a continuación.
Teorema. Cualquier matriz $A\in M_{m,n}(\mathbb{R})$ puede ser llevada a forma escalonada reducida mediante la aplicación de algunas operaciones elementales.
Mas adelante…
Como ya lo hemos mencionado las matrices serán usadas para representar transformaciones lineales. Las transformaciones lineales nos ayudarán a introducir la noción de derivabilidad en varias variables. Y ello nos permitirá aproximar fácilmente cualquier función $f:\mathbb{R}^n\to \mathbb{R}^m$.
De esta manera, un conocimiento amplio de las matrices repercute en un conocimiento amplio de las transformaciones lineales, lo cual a su vez nos da más información en cuanto a las funciones de $\mathbb{R} ^n$ en $\mathbb{R} ^m$. Para seguir haciendo hincapié en las nociones de matrices que más nos interesan, en la siguiente entrada revisaremos un importante número asociado a cada matriz cuadrada: el determinante.
Tarea moral
- Consideremos las matrices $A,B$ de la siguiente manera: \[ A=\begin{pmatrix} 3 & 2 & 0 \\ 2 & 7 & 0 \\ 1 & 0 & 0 \end{pmatrix}\hspace{1cm} B=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \] Encuentra una matriz $X$ que resuelva la siguiente ecuación: \[ 5X + A = B. \]
- Aplica operaciones elementales sucesivas para llevar la siguiente matriz a una matriz escalonada reducida: \[ \begin{pmatrix} 1 & 4 & 0 \\ 3 & 0 & -5 \\ 0 & 0 & -1 \\ 6 & 5 & 0 \end{pmatrix}.\]
- Considera a la matriz identidad $I_4\in M_{4}(\mathbb{R})$ donde $I_{ij}=0$ para $i\neq j$, y $I_{ij}=1$ en otro caso. Aplica las siguiente operaciones elementales y toma nota del resultado para el siguiente ejercicio:
- Una transposición de los renglones $1$ y $3$.
- Un reescalamiento por $-1$ al renglón $2$
- Una transvección usando los renglones $2$ y $1$, y el escalar $4$.
- Aplica las mismas operaciones del punto anterior a la matriz del Ejercicio 2. Toma nota de los resultados.
- Finalmente multiplica cada una de matrices del Ejercicio 3 por la izquierda con la matriz del Ejercicio 2. Compara con los resultados obtenidos en el Ejercicio 4. ¿Qué observas?
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral III
- Entrada anterior del curso: Polinomio de Taylor para campos escalares
- Entrada siguiente del curso: Determinantes