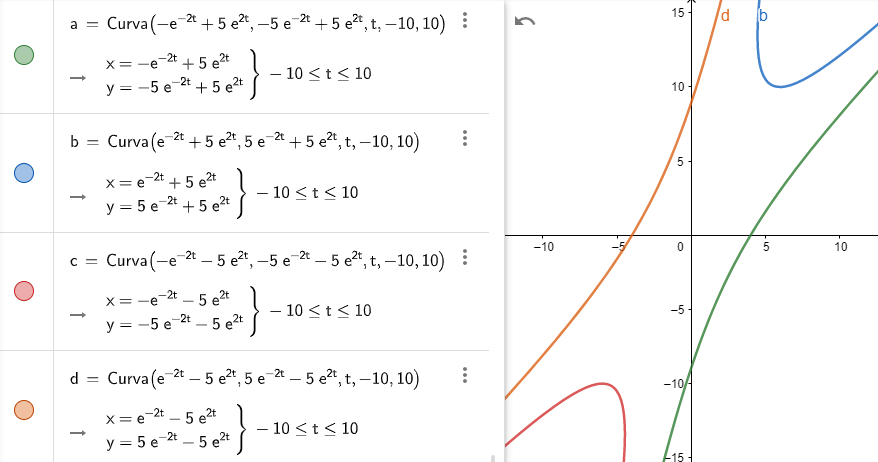Las matemáticas son el juez supremo;
de sus decisiones no hay apelación.
– Tobias Dantzig
Introducción
Ahora que conocemos algunas de las propiedades cualitativas más importantes a analizar de los sistemas autónomos compuestos por dos ecuaciones diferenciales, dedicaremos las siguientes entradas a estudiar exclusivamente los sistemas lineales homogéneos, logrando hacer una conexión entre la unidad 3 y la unidad 4 del curso.
Esta y las siguientes entradas serán el complemento cualitativo del método de valores y vectores propios para resolver sistemas lineales homogéneos, con la restricción de que los sistemas que estudiaremos estarán compuestos por dos ecuaciones diferenciales ya que son el tipo de sistemas en los que conjuntamente podemos hacer una descripción geométrica en $\mathbb{R}^{2}$, concretamente en el plano fase o plano $XY$.
En la primera entrada de esta unidad mostramos los casos posibles de acuerdo al valor que pueden tomar los valores propios, dichos casos pueden ser
Valores propios reales y distintos:
- $\lambda_{1} < \lambda_{2} < 0$.
- $\lambda_{1} > \lambda_{2} > 0$.
- $\lambda_{1} < 0$ y $\lambda_{2} > 0$.
Valores propios complejos:
- $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha < 0$.
- $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha = 0$.
- $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha > 0$.
Valores propios repetidos:
- $\lambda_{1} = \lambda_{2} < 0$.
- $\lambda_{1} = \lambda_{2} > 0$.
Valores propios nulos:
- $\lambda_{1} = 0$ y $\lambda_{2} < 0$.
- $\lambda_{1} = 0$ y $\lambda_{2} > 0$.
- $\lambda_{1} = \lambda_{2} = 0$.
Dedicaremos esta entrada al caso exclusivo en el que los valores propios son reales y distintos.
Sistemas lineales
El sistema lineal autónomo que estudiaremos es
\begin{align*}
x^{\prime} &= ax + by \\
y^{\prime} &= cx+dy \label{1} \tag{1}
\end{align*}
Si se definen las matrices
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
x^{\prime} \\ y^{\prime}
\end{pmatrix}, \hspace{1cm} \mathbf{Y} = \begin{pmatrix}
x \\ y
\end{pmatrix} \hspace{1cm} y \hspace{1cm} \mathbf{A} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix}$$
entonces el sistema se puede escribir como
$$\mathbf{Y}^{\prime} = \mathbf{AY} \label{2} \tag{2}$$
Por otro lado, si consideramos la función vectorial
$$F(x, y) = (F_{1}(x, y), F_{2}(x, y)) \label{3} \tag{3}$$
en donde,
$$F_{1}(x, y) = ax + by \hspace{1cm} y \hspace{1cm} F_{2}(x, y) = cx + dy \label{4} \tag{4}$$
entonces el sistema autónomo (\ref{1}) se puede escribir, alternativamente, como
$$Y^{\prime} = F(x, y) \label{5} \tag{5}$$
Veremos que el plano fase del sistema depende casi por completo de los valores propios de la matriz $\mathbf{A}$ y habrá diferencias notables si los valores propios de $\mathbf{A}$ cambian de signo o se vuelven imaginarios.
Sean $\lambda_{1}$ y $\lambda_{2}$ los dos valores propios reales de $\mathbf{A}$, tal que $\lambda_{1} \neq \lambda_{2}$, recordemos que la solución general para este caso es de la forma
$$\mathbf{Y}(t) = c_{1}e^{\lambda_{1} t} \mathbf{K}_{1} + c_{2}e^{\lambda_{2} t} \mathbf{K}_{2} \label{6} \tag{6}$$
En donde $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ son los vectores propios de $\mathbf{A}$ y $c_{1}$ y $c_{2}$ son constantes arbitrarias que se determinan a partir de las condiciones iniciales del problema.
Comencemos por estudiar el caso en el que los valores propios son negativos.
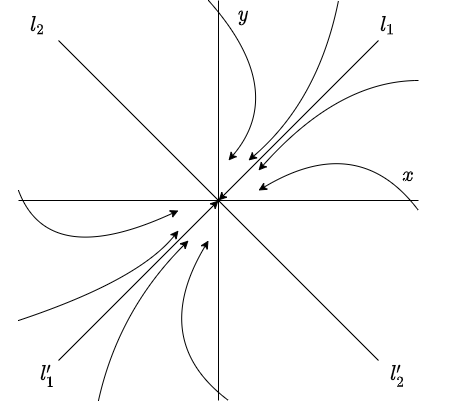
Valores propios negativos
Caso 1: $\lambda_{1} < \lambda_{2} < 0$.
Sean $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ los vectores propios de $\mathbf{A}$ con valores propios $\lambda_{1}$ y $\lambda_{2}$, respectivamente. La solución general está dada por (\ref{6}), sin embargo es conveniente hacer un análisis por separado de las soluciones linealmente independientes
$$\mathbf{Y}_{1}(t) = c_{1}e^{\lambda_{1} t} \mathbf{K}_{1} \hspace{1cm} y \hspace{1cm} \mathbf{Y}_{2}(t) = c_{2}e^{\lambda_{2} t} \mathbf{K}_{2}$$
Comencemos por trazar en el plano $XY$, o plano fase, cuatro semirrectas, dos de ellas $l_{1}$ y $l_{2}$ siendo paralelas a $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$, respectivamente, mientras que las semirrectas $l^{\prime}_{1}$ y $l^{\prime}_{2}$ paralelas a $-\mathbf{K}_{1}$ y $-\mathbf{K}_{2}$, respectivamente.
Consideremos primero la solución
$$\mathbf{Y}_{1}(t) = c_{1}e^{\lambda_{1} t} \mathbf{K}_{1} \label{7} \tag{7}$$
Esta solución es siempre proporcional a $\mathbf{K}_{1}$ y la constante de proporcionalidad $c_{1}e^{\lambda_{1} t}$ varía de $\pm \infty$ a cero, dependiendo de si $c_{1}$ es positiva o negativa. Por lo tanto, la trayectoria de esta solución es la semirrecta $l_{1}$ para $c_{1} > 0$, y la semirrecta $l^{\prime}_{1}$ para $c_{1} < 0$. Análogamente, la trayectoria de la solución
$$\mathbf{Y}_{2}(t) = c_{2}e^{\lambda_{2} t} \mathbf{K}_{2} \label{8} \tag{8}$$
es la semirrecta $l_{2}$ para $c_{2} > 0$ y la semirrecta $l^{\prime}_{2}$ para $c_{2} < 0$.
Consideremos ahora la solución general (\ref{6}).
$$\mathbf{Y}(t) = c_{1}e^{\lambda_{1} t} \mathbf{K}_{1} + c_{2}e^{\lambda_{2} t} \mathbf{K}_{2}$$
Notemos que toda solución $\mathbf{Y}(t)$ tiende al punto $(0, 0)$ cuando $t \rightarrow \infty$. Por lo tanto, toda trayectoria de (\ref{1}) tiende al origen cuando $t$ tiende a infinito.
Observemos que $e^{\lambda_{2} t} \mathbf{K}_{2}$ es muy pequeño comparado con $e^{\lambda_{1} t} \mathbf{K}_{1}$ cuando $t$ es grande (recordemos que $\lambda_{1} < \lambda_{2} < 0$). Por lo tanto, para $c_{1} \neq 0$, $\mathbf{Y}(t)$ se aproxima cada vez más a $c_{1} e^{\lambda_{1} t} \mathbf{K}_{1}$ conforme $t \rightarrow \infty $, esto implica que la tangente a la trayectoria de $\mathbf{Y}(t)$ tiende a $l_{1}$ si $c_{1}$ es positiva y a $l^{\prime}_{1}$, si $c_{1}$ es negativa.
Con todas estas características el plano fase de (\ref{1}), para el caso en el que los valores propios son negativos, tiene la forma que se presenta en la siguiente figura.
Observamos que todas las trayectorias, con excepción de una sola recta, tienden al origen. En este caso se dice que el punto de equilibrio $Y_{0} = (0, 0)$ de (\ref{1}) es un nodo atractor y su estabilidad es asintóticamente estable.
Una última observación es que la trayectoria de toda solución $\mathbf{Y}(t)$ de (\ref{1}) tiende al origen cuando $t$ tiende a infinito, sin embargo ese punto no pertenece a la trayectoria de ninguna solución no trivial $\mathbf{Y}(t)$.
Veamos ahora que ocurre cuando los valores propios son positivos.
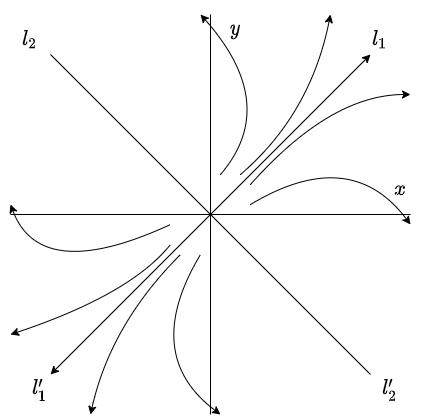
Valores propios positivos
Caso 2: $0 < \lambda_{1} < \lambda_{2}$.
Para este caso se hace análogamente el mismo análisis que en el caso anterior, de modo que el plano fase es exactamente el mismo, excepto que el sentido de las trayectorias es el opuesto. El plano fase se muestra a continuación.
Como las soluciones se alejan del punto de equilibrio $Y_{0} = (0, 0)$ de (\ref{1}), se dice que dicho punto es un nodo repulsor e inestable.
Antes de realizar algunos ejemplos concluyamos con el caso en el que un valor propio es negativo, mientras que el otro es positivo.
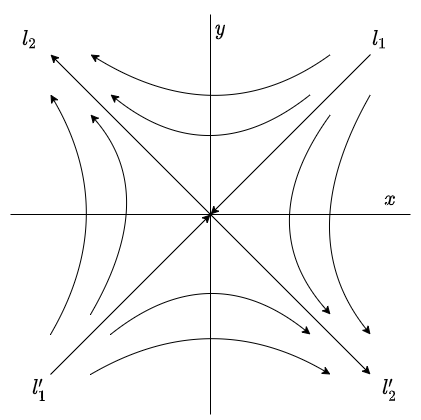
Valores propios con signos opuestos
Caso 3: $\lambda_{1} < 0 < \lambda_{2}$.
Sean nuevamente $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ los vectores propios de $\mathbf{A}$ con valores propios $\lambda_{1}$ y $\lambda_{2}$, respectivamente.
De forma similar que en los casos anteriores, comencemos por trazar en el plano $XY$ cuatro semirrectas, dos de ellas $l_{1}$ y $l_{2}$ siendo paralelas a $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$, respectivamente, mientras que las semirrectas $l^{\prime}_{1}$ y $l^{\prime}_{2}$ paralelas a $-\mathbf{K}_{1}$ y $-\mathbf{K}_{2}$, respectivamente.
Consideremos nuevamente las soluciones linealmente independientes por separado.
$$\mathbf{Y}_{1}(t) = c_{1}e^{\lambda_{1} t} \mathbf{K}_{1} \hspace{1cm} y \hspace{1cm} \mathbf{Y}_{2}(t) = c_{2}e^{\lambda_{2} t} \mathbf{K}_{2}$$
En el caso de la solución
$$\mathbf{Y}_{1}(t) = c_{1}e^{\lambda_{1} t} \mathbf{K}_{1}$$
la trayectoria es $l_{1}$ para $c_{1} > 0$ y $l^{\prime}_{1}$ para $c_{1} < 0$, mientras que la trayectoria de la solución
$$\mathbf{Y}_{2}(t) = c_{2} e^{\lambda_{2} t} \mathbf{K}_{2}$$
es $l_{2}$ para $c_{2} > 0$ y $l^{\prime}_{2}$ para $c_{2} < 0$.
Notemos que la solución $c_{1} e^{\lambda_{1} t} \mathbf{K}_{1}$ tiende al origen $(0, 0)$ cuando $t \rightarrow \infty$, mientras que la solución $c_{2} e^{\lambda_{2} t} \mathbf{K}_{2}$ con $c_{2} \neq 0$ es no acotada conforme $t \rightarrow \infty$.
Por otro lado, observemos que $e^{\lambda_{1} t} \mathbf{K}_{1}$ es muy pequeño comparado con $e^{\lambda_{2} t} \mathbf{K}_{2}$ cuando $t$ crece mucho. Por lo tanto, toda solución $\mathbf{Y}(t)$ de (\ref{1}) con $c_{2} \neq 0$ es no acotada cuando $t$ tiende a infinito y su trayectoria tiende a $l_{2}$ o a $l^{\prime}_{2}$. De forma similar notamos que $e^{\lambda_{2} t} \mathbf{K}_{2}$ es muy pequeño comparado con $e^{\lambda_{1} t} \mathbf{K}_{1}$ cuando $t$ crece mucho con signo negativo. Por lo tanto, la trayectoria de cualquier solución $\mathbf{Y}(t)$ de (\ref{1}) con $c_{1} \neq 0$ tiende a $l_{1}$ o a $l^{\prime}_{1}$ cuando $t$ tiende a menos infinito.
Por lo tanto, en el caso en el que los valores propios tienen signos opuestos, el plano fase, con las características mencionadas, tiene la siguiente forma.
Es posible observar que el plano fase se asemeja a una silla de montar cerca del origen, por esta razón se dice que el punto de equilibrio $Y_{0} = (0, 0)$ de (\ref{1}) es un punto silla y es inestable.
Para concluir con la entrada realicemos un ejemplo por cada caso analizado. En los ejemplos de esta y las próximas entradas estaremos usando las herramientas antes proporcionadas para visualizar el plano fase y el campo vectorial asociado. Puedes usarlas tu mismo para comprobar los resultados o visualizar otros sistemas.
Caso 1: $\lambda_{1} < \lambda_{2} < 0$.
Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
-5 & 1 \\ 1 & -5
\end{pmatrix} \mathbf{Y}$$
Solución: Primero resolvamos el sistema analíticamente. Determinemos los valores propios.
$$\begin{vmatrix}
-5 -\lambda & 1 \\ 1 & -5 -\lambda
\end{vmatrix} = (-5 -\lambda)^{2} -1 = \lambda^{2} + 10 \lambda + 24 = (\lambda + 6)(\lambda + 4) = 0$$
Las raíces son $\lambda_{1} = -6$ y $\lambda_{2} = -4$. Determinemos los vectores propios. La primer ecuación a resolver es
$$(\mathbf{A} + 6 \mathbf{I}) \mathbf{K} = \mathbf{0}$$
o bien,
$$\begin{pmatrix}
1 & 1 \\ 1 & 1
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Inmediatamente vemos que $k_{1} = -k_{2}$. Sea $k_{2} = 1$, entonces $k_{1} = -1$, así el primer vector propio es
$$\mathbf{K}_{1} = \begin{pmatrix}
-1 \\ 1
\end{pmatrix}$$
Para el segundo vector propio resolvemos la ecuación
$$(\mathbf{A} + 4 \mathbf{I}) \mathbf{K} = \mathbf{0}$$
o bien,
$$\begin{pmatrix}
-1 & 1 \\ 1 & -1
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
En este caso $k_{1} = k_{2}$. Sea $k_{1} = 1 = k_{2}$, entonces el segundo vector propio es
$$\mathbf{K}_{2} = \begin{pmatrix}
1 \\ 1
\end{pmatrix}$$
Por lo tanto, la solución general del sistema es
$$\mathbf{Y}(t) = c_{1} e^{-6t} \begin{pmatrix}
-1 \\ 1
\end{pmatrix} + c_{2} e^{-4t} \begin{pmatrix}
1 \\ 1
\end{pmatrix}$$
Separemos la soluciones en las funciones $x(t)$ y $y(t)$.
\begin{align*}
x(t) &= -c_{1}e^{-6t} + c_{2}e^{-4t} \\
y(t) &= c_{1}e^{-6t} + c_{2}e^{-4t}
\end{align*}
Analicemos las soluciones cualitativamente.
Lo primero que sabemos es que el punto de equilibrio $Y_{0} = (0, 0)$ es un nodo atractor estable lo que implica que todas las soluciones tienden al origen, pero nunca llegan a él ya que dicho punto no pertenece a ninguna solución.
Las rectas paralelas a los vectores propios $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ están definidas por las funciones $y(x) = -x$ y $y(x) = x$, respectivamente. La forma de comprobarlo es considerando las soluciones linealmente independientes por separado.
$$\mathbf{Y}_{1}(t) = c_{1} e^{-6t} \begin{pmatrix}
-1 \\ 1
\end{pmatrix}$$
y
$$\mathbf{Y}_{2}(t) = c_{2} e^{-4t} \begin{pmatrix}
1 \\ 1
\end{pmatrix}$$
En el caso de la solución $\mathbf{Y}_{1}(t)$ las soluciones son
\begin{align*}
x(t) &= -c_{1}e^{-6t} \\
y(t) &= c_{1}e^{-6t}
\end{align*}
De donde es claro que $y = -x = c_{1}e^{-6t}$. De forma similar, de la segunda solución $\mathbf{Y}_{2}(t)$ se obtienen las soluciones
\begin{align*}
x(t) &= c_{2}e^{-4t} \\
y(t) &= c_{2}e^{-4t}
\end{align*}
De donde $y = x = c_{2}e^{-4t} $.
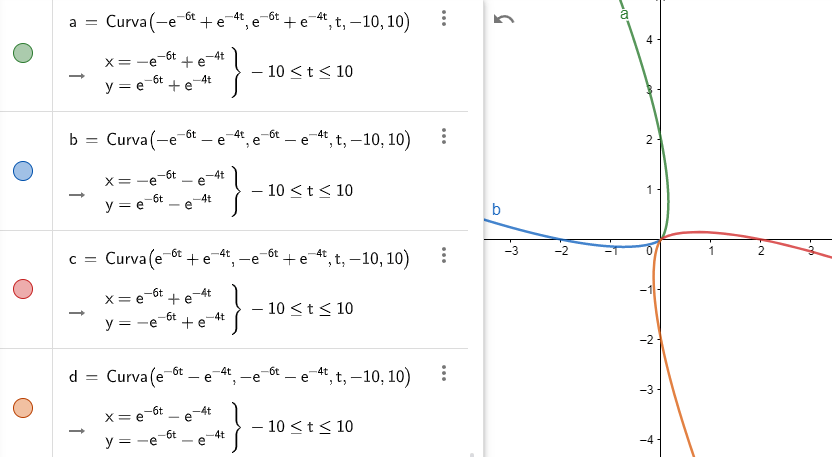
Todas las trayectorias se trazarán de acuerdo a la función paramétrica
$$f(t) = (-c_{1}e^{-6t} + c_{2}e^{-4t}, c_{1}e^{-6t} + c_{2}e^{-4t})$$
Tracemos como ejemplo $4$ trayectorias correspondientes a los siguientes casos:
- $c_{1} = 1$, $c_{2} = 1 \hspace{1.3cm} \rightarrow \hspace{1cm} f(t) = (-e^{-6t} + e^{-4t}, e^{-6t} + e^{-4t})$
- $c_{1} = 1$, $c_{2} = -1 \hspace{1cm} \rightarrow \hspace{1cm} f(t) = (-e^{-6t} -e^{-4t}, e^{-6t} -e^{-4t})$
- $c_{1} = -1$, $c_{2} = 1 \hspace{1cm} \rightarrow \hspace{1cm} f(t) = (e^{-6t} + e^{-4t}, -e^{-6t} + e^{-4t})$
- $c_{1} = -1$, $c_{2} = -1 \hspace{0.7cm} \rightarrow \hspace{1cm} f(t) = (e^{-6t} -e^{-4t}, -e^{-6t} -e^{-4t})$
La gráfica en el plano $XY$ de las cuatro trayectorias anteriores, cerca del origen, se muestra a continuación.
Por supuesto hay infinitas trayectorias, una para cada posible par de valores $c_{1}$ y $c_{2}$.
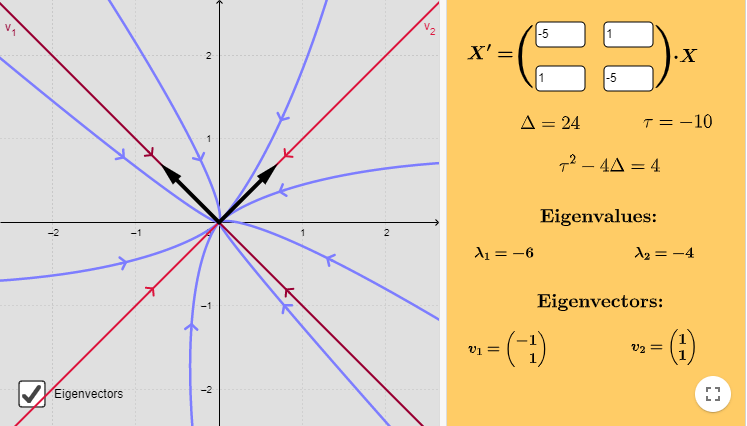
En la parte izquierda de la siguiente figura se encuentra el plano fase del sistema con algunas trayectorias, los vectores propios de $\mathbf{A}$ y las rectas paralelas a dichos vectores. En el lado derecho se encuentra el sistema que estamos analizando y el valor de los eigenvalores y eigenvectores.
En la figura anterior también se encuentran los datos $\Delta = 24$ y $\tau = -10$, estos valores corresponden al valor del determinante y la traza de $\mathbf{A}$, respectivamente. Por el momento no tenemos que preocuparnos por estos valores, sin embargo más adelante veremos que nos serán de mucha utilidad cuando estudiemos el llamado plano traza – determinante.
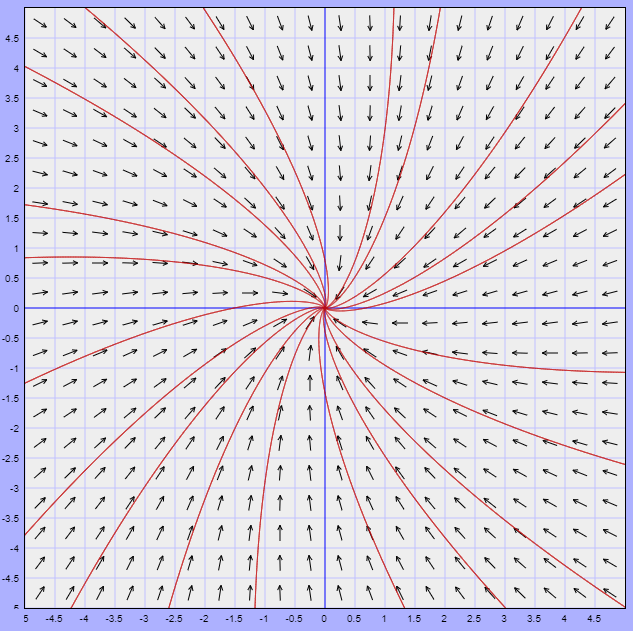
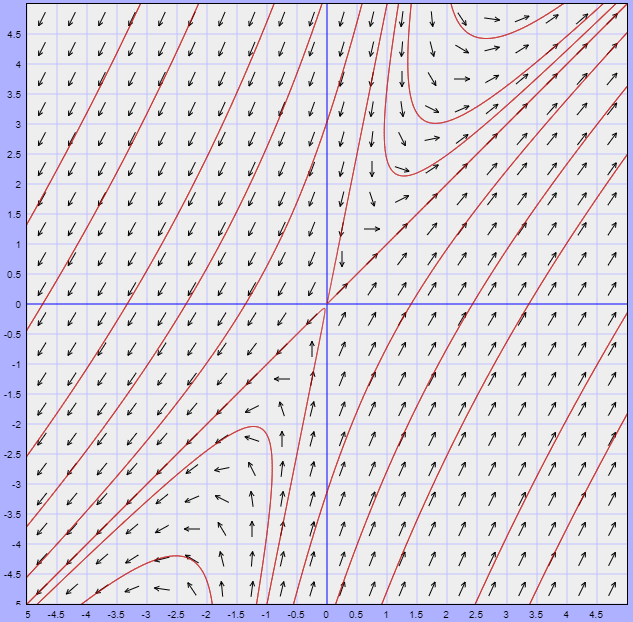
Para concluir con el ejemplo determinemos el campo vectorial asociado. La función $F(x, y)$ en este caso es
$$F(x, y) = (-5x + y, x -5y)$$
El campo vectorial asociado junto con algunas trayectorias se muestra a continuación.
$\square$
Caso 2: $0 < \lambda_{1} < \lambda_{2}$.
Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
4 & -1 \\ -2 & 5
\end{pmatrix} \mathbf{Y}$$
Solución: Determinemos los valores propios.
$$\begin{vmatrix}
4 -\lambda & -1 \\ -2 & 5 -\lambda
\end{vmatrix} = (4 -\lambda)(5 -\lambda) -2 = \lambda^{2} -9 \lambda + 18 = (\lambda -3)(\lambda -6) = 0$$
Las raíces son $\lambda_{1} = 3$ y $\lambda_{2} = 6$. Determinemos los vectores propios. La primer ecuación a resolver es
$$(\mathbf{A} -3 \mathbf{I}) \mathbf{K} = \mathbf{0}$$
o bien,
$$\begin{pmatrix}
1 & -1 \\ -2 & 2
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Resolviendo el sistema se obtiene que $k_{1} = k_{2}$, elegimos convenientemente $k_{1} = -2 = k_{2}$, tal que el primer vector propio es
$$\mathbf{K}_{1} = \begin{pmatrix}
-2 \\ -2
\end{pmatrix}$$
Para obtener el segundo vector propio resolvemos la ecuación
$$(\mathbf{A} -6 \mathbf{I}) \mathbf{K} = \mathbf{0}$$
o bien,
$$\begin{pmatrix}
-2 & -1 \\ -2 & -1
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
En este caso se obtiene que $-2k_{1} = k_{2}$. Elegimos $k_{1} = 1$, entonces $k_{2} = -2$ y así el segundo vector propio es
$$\mathbf{K}_{2} = \begin{pmatrix}
1 \\ -2
\end{pmatrix}$$
Por lo tanto, la solución general es
$$\mathbf{Y}(t) = c_{1} e^{3t} \begin{pmatrix}
-2 \\ -2
\end{pmatrix} + c_{2} e^{6t} \begin{pmatrix}
1 \\ -2
\end{pmatrix}$$
Escribamos la solución en términos de las funciones $x(t)$ y $y(t)$.
\begin{align*}
x(t) &= -2c_{1}e^{3t} + c_{2}e^{6t} \\
y(t) &= -2c_{1}e^{3t} -2c_{2}e^{6t}
\end{align*}
Comencemos por determinar las funciones que definen las rectas paralelas a los vectores propios, para ello consideremos por separado las soluciones linealmente independientes
$$\mathbf{Y}_{1}(t) = c_{1} e^{3t} \begin{pmatrix}
-2 \\ -2
\end{pmatrix}$$
y
$$\mathbf{Y}_{2}(t) = c_{2} e^{6t} \begin{pmatrix}
1 \\ -2
\end{pmatrix}$$
De la solución $\mathbf{Y}_{1}(t)$ tenemos las soluciones
\begin{align*}
x(t) &= -2c_{1}e^{3t} \\
y(t) &= -2c_{1}e^{3t}
\end{align*}
De donde vemos que $y = x = -2c_{1}e^{3t}$, por tanto la recta paralela a $\mathbf{K}_{1}$ se define por la función $y(x) = x$. Por otro lado, de la solución $\mathbf{Y}_{2}(t)$ se tiene las soluciones
\begin{align*}
x(t) &= c_{2}e^{6t} \\
y(t) &= -2c_{2}e^{6t}
\end{align*}
En este caso vemos que $y = -2x = -2c_{2}e^{6t}$, por tanto la recta paralela al vector propio $\mathbf{K}_{2}$ esta definida por la función $y(x) = -2x$.
La función paramétrica que nos permite trazar las trayectorias es
$$f(t) = (-2c_{1}e^{3t} + c_{2}e^{6t}, -2c_{1}e^{3t} -2c_{2}e^{6t})$$
Si lo deseas intenta graficar algunas trayectorias para algunos valores de $c_{1}$ y $c_{2}$ como lo hicimos en el ejemplo anterior.
El plano fase del sistema indicando algunas trayectorias, los vectores propios y las rectas paralelas a estos vectores, se muestra a continuación.
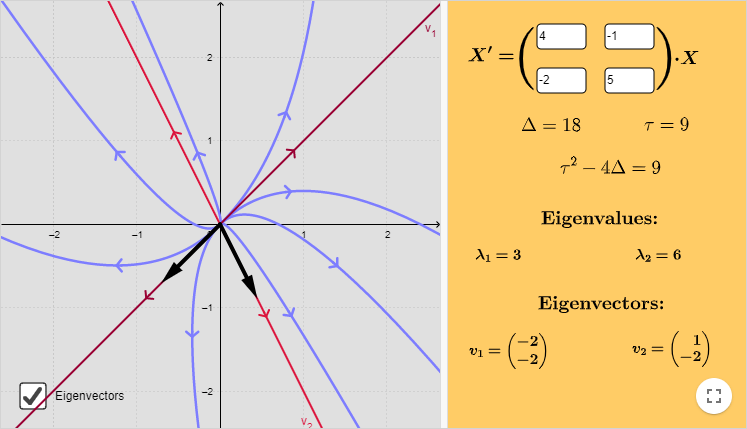
Se puede observar que las trayectorias son un poco similares a las del ejemplo anterior con la diferencia de que el sentido es el opuesto, de forma que el punto de equilibrio $Y_{0} = (0, 0)$ es nodo repulsor inestable.
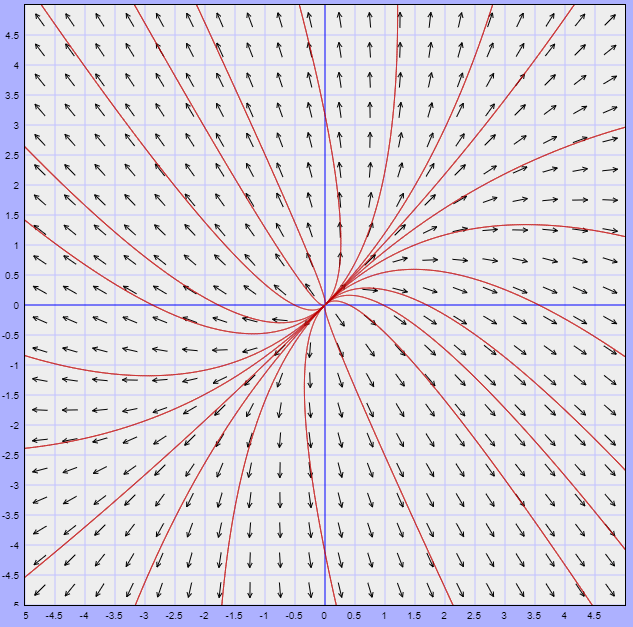
El campo vectorial asociado está dado por la función vectorial
$$F(x, y) = (4x -y, -2x + 5y)$$
El campo vectorial con algunas trayectorias se muestra a continuación.
$\square$
Concluyamos con un ejemplo del tercer caso.
Caso 3: $\lambda_{1} < 0 < \lambda_{2}$.
Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
3 & -1 \\ 5 & -3
\end{pmatrix} \mathbf{Y}$$
Solución: Determinemos los valores propios.
$$\begin{vmatrix}
3 -\lambda & -1 \\ 5 & -3 -\lambda
\end{vmatrix} = (3 -\lambda )( -3 -\lambda ) + 5 = \lambda {2} -4 = (\lambda -2)(\lambda + 2) = 0$$
Las raíces son$\lambda_{1} = -2$ y $\lambda_{2} = 2$. Determinemos los vectores propios. Para el primer vector resolvamos la ecuación
$$(\mathbf{A} + 2 \mathbf{I}) \mathbf{K} = \mathbf{0}$$
o bien,
$$\begin{pmatrix}
5 & -1 \\ 5 & -1
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Vemos que $5k_{1} = k_{2}$. Sea $k_{1} = -1$, tal que $k_{2} = -5$, así el primer vector propio es
$$\mathbf{K}_{1} = \begin{pmatrix}
-1 \\ -5
\end{pmatrix}$$
Para obtener el segundo vector propio resolvemos
$$(\mathbf{A} -2 \mathbf{I}) \mathbf{K} = \mathbf{0}$$
o bien,
$$\begin{pmatrix}
1 & -1 \\ 5 & -5
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Tenemos que $k_{1} = k_{2}$. Sea $k_{1} = 5 = k_{2}$, entonces el segundo vector propio es
$$\mathbf{K}_{2} = \begin{pmatrix}
5 \\ 5
\end{pmatrix}$$
Por lo tanto, la solución general es
$$\mathbf{Y}(t) = c_{1} e^{-2t} \begin{pmatrix}
-1 \\ -5
\end{pmatrix} + c_{2} e^{2t} \begin{pmatrix}
5 \\ 5
\end{pmatrix}$$
o bien,
\begin{align*}
x(t) &= -c_{1} e^{-2t} + 5c_{2} e^{2t} \\
y(t) &= -5c_{1}e^{-2t} + 5c_{2}e^{2t}
\end{align*}
Las soluciones linealmente independientes son
$$\mathbf{Y}_{1}(t) = c_{1} e^{-2t} \begin{pmatrix}
-1 \\ -5
\end{pmatrix}$$
y
$$\mathbf{Y}_{2}(t) = c_{2} e^{2t} \begin{pmatrix}
5 \\ 5
\end{pmatrix}$$
cuyas soluciones en términos de las funciones $x(t)$ y $y(t)$ son, respectivamente
\begin{align*}
x(t) &= -c_{1} e^{-2t} \\
y(t) &= -5c_{1}e^{-2t}
\end{align*}
y
\begin{align*}
x(t) &= 5c_{2} e^{2t} \\
y(t) &= 5c_{2}e^{2t}
\end{align*}
La recta paralela al vector propio $\mathbf{K}_{1}$ está definida por la función $y(x) = 5x$, mientras que la recta paralela al vector propio $\mathbf{K}_{2}$ está definida por la función $y(x) = x$.
Las trayectorias son trazadas de acuerdo a la función paramétrica
$$f(t) = (-c_{1} e^{-2t} + 5c_{2} e^{2t}, -5c_{1} e^{-2t} + 5c_{2} e^{2t})$$
Consideremos nuevamente los siguientes casos:
- $c_{1} = 1$, $c_{2} = 1 \hspace{1.3cm} \rightarrow \hspace{1cm} f(t) = (-e^{-2t} + 5e^{2t}, -5e^{-2t} + 5e^{2t})$
- $c_{1} = 1$, $c_{2} = -1 \hspace{1cm} \rightarrow \hspace{1cm} f(t) = (-e^{-2t} -5e^{2t}, -5e^{-2t} -5e^{2t})$
- $c_{1} = -1$, $c_{2} = 1 \hspace{1cm} \rightarrow \hspace{1cm} f(t) = (e^{-2t} + 5e^{2t}, 5e^{-2t} + 5e^{2t})$
- $c_{1} = -1$, $c_{2} = -1 \hspace{0.7cm} \rightarrow \hspace{1cm} f(t) = (e^{-2t} -5e^{2t}, 5e^{-2t} -5e^{2t})$
La gráfica en el plano $XY$ de las cuatro trayectorias anteriores, cerca del origen, se muestra a continuación.
Observemos cuidadosamente que ocurre en los casos límite.
Consideremos la función
$$f(t) = (x(t), y(t)) = (-e^{-2t} + 5e^{2t}, -5e^{-2t} + 5e^{2t})$$
Conforme $t$ crece el término $-e^{-2t}$ se hace muy pequeño comparado con el término $5e^{2t}$, de manera que si $t \rightarrow \infty$, entonces $x(t) \rightarrow 5e^{2t}$, de forma similar el término $-5e^{-2t}$ se hace muy pequeño en comparación con el término $5e^{2t}$, es decir, si $t \rightarrow \infty$, entonces $y(t) \rightarrow 5e^{2t}$. Esto nos permite notar que si $t \rightarrow \infty$, entonces $y \rightarrow x$. Por el contrario, si $t \rightarrow -\infty$, entonces $y \rightarrow 5x$. En la gráfica anterior vemos este comportamiento para la trayectoria verde.
Intenta hacer este mismo análisis para las tres trayectorias restantes de la gráfica anterior y logra notar que en los casos límites las trayectorias tienden a las rectas paralelas a los vectores propios.
En la siguiente figura se muestra el plano fase indicando algunas trayectorias, los vectores propios y las rectas paralelas a estos vectores.
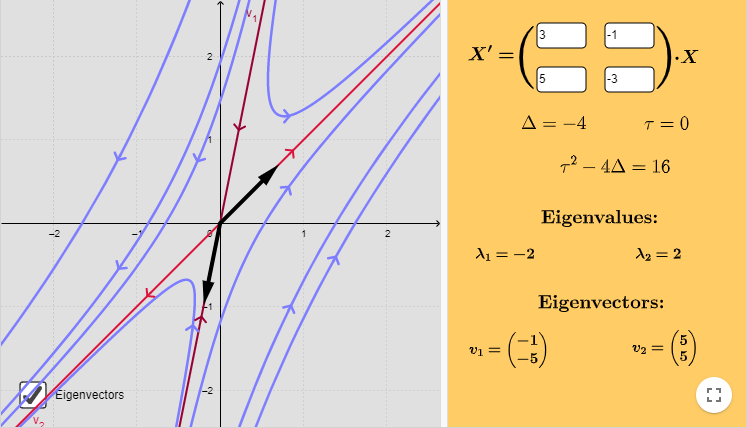
Efectivamente, el punto de equilibrio $Y_{0} = (0, 0)$ es un punto silla y es inestable.
Finalmente apreciemos el campo vectorial asociado, definido por la función vectorial
$$F(x, y) = (3x -y, 5x -3y)$$
$\square$
Con esto concluimos esta entrada. En la siguiente entrada veremos que ocurre si los valores y vectores propios son complejos.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- Resolver los siguientes sistemas lineales y hacer un análisis cualitativo de las soluciones.
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
1 & -2 \\ 3 & -4
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
2 & 2 \\ 1 & 3
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
3 & -2 \\ 2 & -2
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
0 & -1 \\ 8 & -6
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
2 & 1 \\ 1 & 2
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
1 & 2 \\ 4 & 3
\end{pmatrix} \mathbf{Y}$
Más adelante…
Concluimos con el caso en el que los valores propios de la matriz $\mathbf{A}$ son reales y distintos.
En la siguiente entrada haremos un análisis muy similar a como lo hicimos en esta entrada, pero en el caso en el que los valores propios de la matriz $\mathbf{A}$ son complejos. Veremos que en este caso existen soluciones que son periódicas.
Entradas relacionadas
- Página principal del curso: Ecuaciones Diferenciales I
- Entrada anterior del curso: Propiedades cualitativas de las trayectorias
- Siguiente entrada del curso: Teoría cualitativa de los sistemas lineales homogéneos – Valores propios complejos
- Video relacionado al tema: Plano fase para sistemas lineales con valores propios reales distintos no nulos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»