Todas las verdades de las matemáticas están vinculadas entre si.
– Adrien-Marie Legendre

Introducción

Hemos estudiado algunas propiedades de las soluciones de una ecuación diferencial, estas funciones son expresiones analíticas que nos son útiles para describir una solución de una ecuación diferencial, sin embargo no siempre es necesario obtener dicha expresión analítica para lograr describir las soluciones. En este entrada haremos un análisis geométrico (o cualitativo) sobre ecuaciones diferenciales ordinarias de la forma

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{dy}{dx}}=f(x,y(x))\end{array}$$

Campos de pendientes

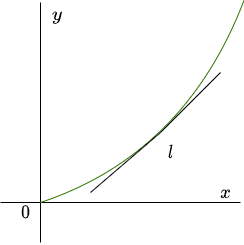
Recordemos que geométricamente la derivada ${\displaystyle \frac{dy}{dx}}$ de una función derivable $y=y(x)$ corresponde a la pendiente de las rectas tangentes en cada punto de la gráfica de la función $y(x)$, este resultado nos será de utilidad para intentar describir cualitativamente las soluciones de una ecuación diferencial de la forma normal ($\text{1}$).

De acuerdo a la definición de solución de una ecuación diferencial, la función $y(x)$ es necesariamente derivable y por tanto continua en un intervalo $\delta$, esto nos garantiza que la curva solución en $\delta$ no tiene cortes y debe tener una recta tangente en cada punto $(x,y(x))$.

Si la función $y(x)$ es solución, entonces tiene una gráfica en el plano $XY$, la gráfica corresponde a la curva solución y la pendiente en cada punto está dada por

$$m={\displaystyle \frac{dy}{dx}}=f(x,y)$$

Es así que para cada punto $(x,y)$ en el plano $XY$ se le puede asociar una número dado por la función razón que corresponderá a la pendiente de la recta tangente de una curva solución que pasa por ese punto $(x,y)$.

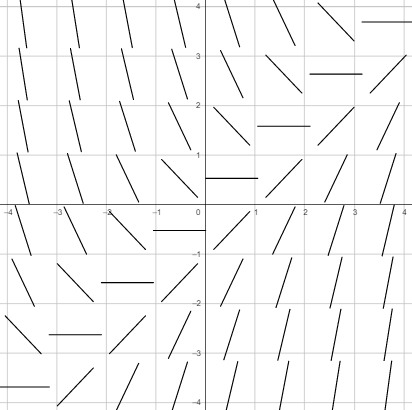
Por lo tanto, podemos construir en el plano $XY$ un conjunto de elementos lineales dados por el valor de la función razón en cada punto $(x,y)$. Veamos un ejemplo.

Ejemplo: Visualizar los elementos lineales de la ecuación diferencial

$${\displaystyle \frac{dy}{dx}}=x-y$$

Solución: En este caso la función razón es

$$f(x,y)=x-y$$

$x$ y $y$ pueden tomar cualquier valor en $\mathbb{R}$. En la siguiente tabla tenemos algunos valores para $x$ y $y$. En la primera fila tenemos los valores de $x$ en el intervalo $(-4,4)$ en pasos de una unidad, mientras que en la primer columna tenemos los valores de $y$ en el intervalo $(-4,4)$ en pasos de una unidad, el resto de valores corresponde al valor de la función razón $f(x,y)=x-y$ evaluada en los valores correspondientes. Por ejemplo si $x=-2$ y $y=4$, entonces

$$f(x,y)=x-y=-2-4=-6$$

tal como se indica en la tabla.

Con ayuda de esta tabla podemos construir un conjunto de elementos lineales con pendiente según el valor de la función razón (recordemos que una recta de $45°$ tiene pendiente $m=1$).

Aumentando el número de valores para $x$ y $y$ en los rangos $(-4,4)$ se puede obtener un conjunto mayor de elementos lineales.

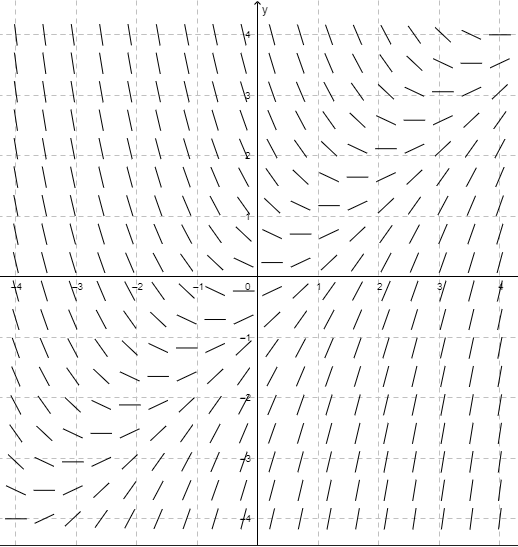
Es posible notar un patrón en esta última imagen. Anteriormente mencionamos que el valor de la función razón $f(x,y)$ es el valor de la pendiente de la recta tangente en un punto $(x,y)$ de la curva solución de la ecuación diferencial ($\text{1}$), en este caso los elementos lineales corresponden a las rectas tangentes de las curvas solución de la ecuación diferencial

$${\displaystyle \frac{dy}{dx}}=x-y$$

Es decir, los elementos lineales son tangentes a funciones $y(x)$ ¡que son solución de la ecuación diferencial!, basta trazar curvas a lo largo de los elementos lineales para hallar gráficamente las soluciones.

Ya vimos que una ecuación diferencial puede tener infinitas soluciones, o bien una familia de soluciones, en este caso, en la gráfica se muestran $4$ curvas solución correspondientes a $4$ soluciones $y=y(x)$ particulares, cada una se obtiene de distintas condiciones iniciales.

Lo importante que debemos rescatar es que, a pesar de no tener la forma explícita (o implícita) de la función solución $y=y(x)$, gráficamente ¡ya conocemos las posibles gráficas de las curvas solución de la ecuación diferencial dada!. También es importante notar que el signo de la pendiente nos dice si la curva es creciente o decreciente, esto debido al resultado de cálculo en donde si ${\displaystyle \frac{dy}{dx}}>0$ o ${\displaystyle \frac{dy}{dx}}<0$ para toda $x$ en un intervalo $\delta$, entonces la función derivable $y=y(x)$ es creciente o decreciente en $\delta$, respectivamente.

Como ejercicio moral verifica que la solución general de la ecuación diferencial dada es

$$y(x)=x-1+{\displaystyle \frac{c}{e^x}}$$

Posteriormente usa un graficador de funciones y traza la gráfica de la solución general dándole valores arbitrarios a la constante $c$ y compara los resultados con los obtenidos en la imagen anterior.

De acuerdo a la imagen se puede notar que las $4$ curvas solución que se muestran corresponden a los valores iniciales

$$y(3)=-4y(-3)=0,y(1)=2,yy(-2)=-4$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

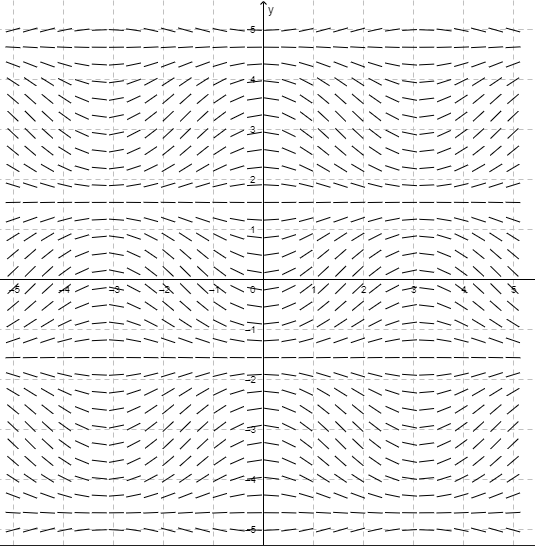
Las imágenes anteriores corresponden al campo de pendientes de la ecuación diferencial

$${\displaystyle \frac{dy}{dx}}=x-y$$

Un campo de pendientes indica el flujo de las soluciones y facilita el trazo de cualquier solución particular, la dirección del campo indica el aspecto o forma de una familia de curvas solución de la ecuación diferencial dada, esto permite observar a simple vista aspectos cualitativos de la solución, por ejemplo regiones en el plano donde la solución presenta un comportamiento poco común.

En este contexto una curva solución también es llamada curva integral.

Método de las isóclinas

Ahora somos capaces de esbozar campos de pendientes de ecuaciones diferenciales de la forma ($\text{1}$), sin embargo es un proceso muy tardado si se piensa hacer a mano ya que hay que ir evaluando punto a punto del plano para obtener el valor de la pendiente en dicho punto y así poder dibujar un elemento lineal, esto puede ser mucho más rápido si se utilizan programas computacionales que lo realicen.

Existe un método que nos permite dibujar elementos lineales de forma eficiente sin necesidad de ir evaluando punto a punto, este método es conocido como el método de las isóclinas.

En otras palabras, una isóclina es una curva de nivel de la función $f(x,y)$, es decir

$$\begin{array}{}\text{(2)}& f(x,y)=k\end{array}$$

donde $k$ es una constante arbitraria, si sustituimos ($\text{2}$) en ($\text{1}$), obtenemos

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{dy}{dx}}=k\end{array}$$

Con esta ecuación vemos que en efecto para todas las soluciones $y=y(x)$ va a haber puntos donde la pendiente ${\displaystyle \frac{dy}{dx}}$ sera la misma, una constante.

Con este método sólo basta encontrar las isóclinas de una ecuación diferencial y sobre ellas dibujar elementos lineales que tengan la misma pendiente obteniendo así el campo de pendientes y por tanto las curvas solución. Para que quede más claro construyamos las isóclinas de la ecuación diferencial del ejemplo anterior.

Ejemplo: Hallar las isóclinas y el campo de pendientes de la ecuación diferencial

$${\displaystyle \frac{dy}{dx}}=x-y$$

Solución: Comencemos por igualar la función razón a una constante.

$${\displaystyle \frac{dy}{dx}}=x-y=k$$

Despejemos la función dependiente $y$ en términos de la variable independiente y la constante.

$$y=y(x)=x-k$$

Es claro que es la ecuación de una recta, para cada valor arbitrario de $k$ se obtiene una recta distinta, lo importante es que a lo largo de toda esa recta hay elementos lineales con la misma pendiente, sólo basta evaluar un punto de cada isóclina en la función razón y obtendremos el valor de la pendiente para toda la isóclina.

En la imagen vemos que a lo largo de cada isóclina (en este caso rectas marcadas de verde) los elementos lineales tienen la misma pendiente recuperando así el campo de pendientes que habíamos obtenido anteriormente.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Este método es muy útil si lo que queremos es esbozar un campo de pendientes a mano. Una vez obtenido el campo de pendientes procedemos a dibujar las curvas solución como lo hicimos con anterioridad.

Método de Euler

El análisis geométrico que acabamos de hacer está íntimamente relacionado con un método numérico fundamental para aproximar soluciones de una ecuación diferencial de la forma ($\text{1}$) acompañada de una condición inicial, dicho método es conocido como método de Euler. Consideremos el problema con condición inicial

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{dy}{dx}}=f(x,y),y(x_0)=y_0\end{array}$$

Debido a que $f(x,y)$ es dada, entonces podemos trazar su campo de pendientes en el plano $XY$, esto nos permite colocarnos en el punto $(x_0,y_0)$ y comenzar a dar pequeños pasos dictados por las tangentes de dicho campo.

Comenzamos por elegir un tamaño de paso $\mathrm{\Delta }x$ pequeño de tal manera que la pendiente de la solución aproximada se actualice cada $\mathrm{\Delta }x$ unidades de $x$, es decir, en cada paso nos movemos $\mathrm{\Delta }x$ unidades a lo largo del eje $x$. El tamaño de $\mathrm{\Delta }x$ determina la exactitud de la solución, así como el número de cálculos que son necesarios para obtener la aproximación.

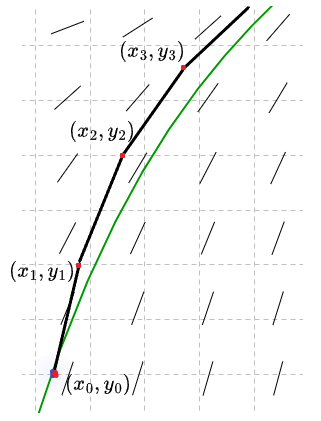
Imaginemos que nos colocamos en el punto $(x_0,y_0)$, el primer paso es hacia el punto $(x_1,y_1)$, donde

$$\begin{array}{}\text{(5)}& x_1=x_0+\mathrm{\Delta }x\end{array}$$

El punto $(x_1,y_1)$ se encuentra sobre la línea que pasa por $(x_0,y_0)$ y cuya pendiente esta dada por el campo de pendiente en dicho punto, o bien, por $f(x_0,y_0)$. Una vez que estemos en $(x_1,y_1)$ repetimos el procedimiento, damos nuevamente un paso cuyo tamaño a lo largo del eje $x$ es $\mathrm{\Delta }x$ y cuya dirección esta determinada por el campo de pendientes en $(x_1,y_1)$, esto nos permitirá llegar al punto $(x_2,y_2)$, donde

$$\begin{array}{}\text{(6)}& x_2=x_1+\mathrm{\Delta }x\end{array}$$

El punto $(x_2,y_2)$ está sobre el segmento de línea que comienza en $(x_1,y_1)$ y tiene pendiente $f(x_1,y_1)$. Repetimos este procedimiento para llegar al punto $(x_3,y_3)$, tal como se ilustra en la siguiente figura.

En la figura vemos en verde la gráfica de una solución y en segmentos negros los pasos que el método de Euler establece para aproximarnos a la solución. Geométricamente, el método genera una secuencia de pequeños segmentos de línea que conectan $(x_n,y_n)$ con $(x_{n+1},y_{n+1})$. Notemos que en casa paso cometemos un error, si el tamaño de $\mathrm{\Delta }x$ es suficiente pequeño, los errores no resultarán demasiado grandes conforme avanzamos y la gráfica resultante será cercana a la solución buscada.

Para llevar a cabo el método de Euler, necesitamos una fórmula que determine $(x_{n+1},y_{n+1})$ a partir de $(x_n,y_n)$. Al especificar el tamaño del paso $\mathrm{\Delta }x$ determinamos que, de forma general

$$\begin{array}{}\text{(7)}& x_{n+1}=x_n+\mathrm{\Delta }x,\end{array}$$

Para obtener $y_{n+1}$ a partir de $(x_n,y_n)$ usamos la ecuación diferencial. La pendiente de la solución de la ecuación ($\text{1}$) en el punto $(x_n,y_n)$ es $f(x_n,y_n)$, el punto $(x_{n+1},y_{n+1})$ se determina suponiendo que éste se encuentra sobre la línea que pasa por $f(x_n,y_n)$.

Podemos determinar $y_{n+1}$ de la siguiente fórmula de pendiente.

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{y_{n+1}-y_n}{x_{n+1}-x_n}}=f(x_n,y_n),\end{array}$$

Usando ($\text{7}$) se puede escribir lo siguiente:

$$\begin{array}{rl}{\displaystyle \frac{y_{n+1}-y_n}{\mathrm{\Delta }x}}& =f(x_n,y_n)\\ y_{n+1}-y_n& =f(x_n,y_n)\mathrm{\Delta }x\end{array}$$

Esto es

$$\begin{array}{}\text{(9)}& y_{n+1}=y_n+f(x_n,y_n)\mathrm{\Delta }x,\end{array}$$

Por lo tanto, dada la condición inicial $y(x_0)=y_0$ y el tamaño del paso $\mathrm{\Delta }x$, el punto $(x_{n+1},y_{n+1})$ se determina a partir del punto precedente $(x_n,y_n)$ usando la ecuación diferencial para determinar valor de la pendiente $f(x_n,y_n)$ y utilizando las ecuaciones ($\text{7}$) y ($\text{9}$).

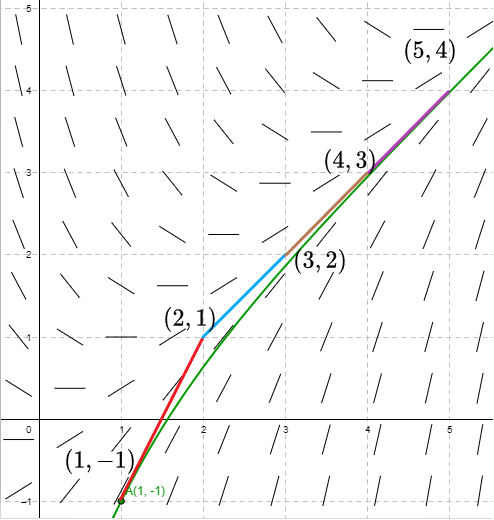
Ejemplo: Determinar una aproximación de la solución del siguiente PVI:

$${\displaystyle \frac{dy}{dx}}=x-y,y(1)=-1$$

Solución: Ya conocemos el campo de pendientes de la ecuación diferencial ${\displaystyle \frac{dy}{dx}}=x-y$. En este caso buscamos una aproximación a la solución particular que pasa por el punto $(x_0,y_0)=(1,-1)$. Para usar el método de Euler, propongamos un paso de unidad 1, es decir, $\mathrm{\Delta }x=1$. La función razón es

$$f(x,y)=x-y$$

Entonces,

$$f(x_0,y_0)=f(1,-1)=1-(-1)=2$$

Sustituyamos en las ecuaciones ($\text{7}$) y ($\text{9}$):

$$\begin{array}{rl}{x}_1& =x_0+\mathrm{\Delta }x=1+1=2\\ y_1& =y_0+f(x_0,y_0)\mathrm{\Delta }x=-1+2(1)=1\end{array}$$

Por lo tanto, $(x_1,y_1)=(2,1)$. Ahora vemos que

$$f(x_1,y_1)=f(2,1)=2-1=1$$

Nuevamente aplicamos ($\text{7}$) y ($\text{9}$):

$$\begin{array}{rl}{x}_2& =2+1=3\\ y_2& =1+1(1)=2\end{array}$$

Por lo tanto, $(x_2,y_2)=(3,2)$. Continuando verificamos que $f(3,2)=3-2=1$, entonces

$$\begin{array}{rl}{x}_3& =3+1=4\\ y_3& =2+1(1)=3\end{array}$$

El nuevo punto obtenido es $(x_3,y_3)=(4,3)$. Uno más, $f(4,3)=4-3=1$.

$$\begin{array}{rl}{x}_4& =4+1=5\\ y_4& =3+1(1)=4\end{array}$$

Así, $(x_4,y_4)=(5,4)$.

Este proceso se sigue indefinidamente hasta hallar una gráfica aproximada de la solución buscada. En la siguiente figura se muestra la curva solución y los pasos obtenidos usando el método de Euler.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Dos casos especiales

Hemos trabajado con la ecuación diferencial

$${\displaystyle \frac{dy}{dx}}=f(x,y(x))$$

Es posible que ocurra que la función razón sólo dependa de la variable dependiente $y(x)$, o sólo de la variable independiente $x$, es decir, tener las ecuaciones diferenciales

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{dy}{dx}}=f(y)\end{array}$$

o

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{dy}{dx}}=f(x)\end{array}$$

Más adelante veremos que estas ecuaciones son más fácil de resolver analíticamente debido a que son lo que se conoce como ecuaciones separables, pero por ahora vamos a hacer un análisis cualitativo como lo hemos estado haciendo en esta entrada.

Campo de pendientes para ${\displaystyle \frac{dy}{dx}}=f(x)$

El hecho de tener la ecuación diferencial

$${\displaystyle \frac{dy}{dx}}=f(x)$$

en su forma normal nos permite reconocer que la pendiente de un elemento lineal en cualquier punto es la misma que la de cualquier otro punto con la misma coordenada $x$.

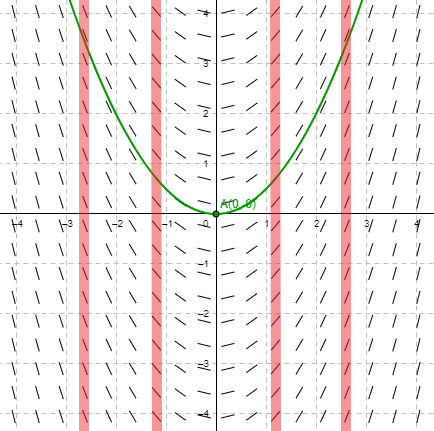
En la imagen tenemos como ejemplo el campo de pendientes de la ecuación diferencial

$${\displaystyle \frac{dy}{dx}}=f(x)=x$$

La curva verde representa una curva solución y notamos que a lo largo de las líneas verticales (líneas rojas) todos los elementos lineales tienen la misma pendiente.

Geométricamente podemos decir que en un campo de pendientes si los elementos lineales sobre cada línea vertical del dominio en consideración son paralelos, entonces la ecuación diferencial correspondiente es de la forma ($\text{10}$).

Campo de pendientes para ${\displaystyle \frac{dy}{dx}}=f(y)$

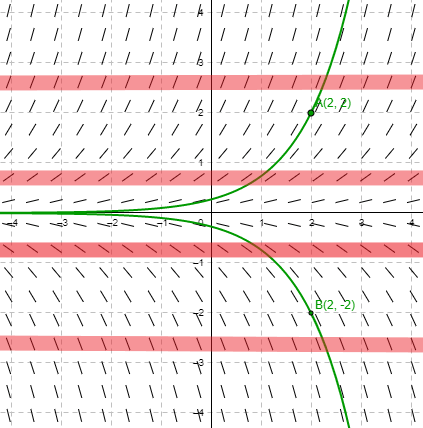
En el caso en el que la función razón sólo depende de la variable dependiente $y$ los elementos lineales de un campo de pendientes van a tener la misma pendiente en dos puntos diferentes con la misma coordenada $y$, es decir, el campo de pendientes es paralelo a lo largo de cada línea horizontal.

En la imagen tenemos como ejemplo el campo de pendientes de la ecuación diferencial

$${\displaystyle \frac{dy}{dx}}=f(y)=y$$

Las curvas verdes corresponden a soluciones de la ecuación, mientras que las líneas rojas sólo intentan hacer notar que las pendientes de los elementos lineales para un valor de $y$ son las mismas.

Hasta aquí concluimos la entrada, en la siguiente continuaremos explorando más sobre la teoría cualitativa de este tipo de ecuaciones diferenciales.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

1. Esbozar el campo de pendientes de las siguientes ecuaciones diferenciales. Hacerlo a mano en una hoja de papel usando el método de las isóclinas y posteriormente verifica tu resultado usando algún programa computacional. Una vez construido el campo de pendientes trazar tres curva solución aproximadas, donde cada una pase por cada uno de los puntos indicados.

• ${\displaystyle \frac{dy}{dx}}=1-y$ $$ Puntos: $(0,3)$, $$ $(-2,-1)$, $$ $(0,1)$.

• ${\displaystyle \frac{dy}{dx}}=x^2-y-2$ $$ Puntos: $(-1,1)$, $$ $(4,0)$, $$ $(0,-2)$.

• ${\displaystyle \frac{dy}{dx}}=xy$ $$ Puntos: $(0,1)$, $$ $(1,-2)$, $$ $(-3,2)$.

2. Considerando el ejercicio anterior, en cada ecuación diferencial dada elegir una condición inicial y usando el método de Euler determinar una solución aproximada. Se recomienda calcular al menos 5 puntos.

3. Dados los siguientes campos de pendientes, determinar la opción qué indica la ecuación diferencial que corresponde al campo de pendientes. Justificar la respuesta.

• a) ${\displaystyle \frac{dy}{dx}}=\sin (x)+\cos (x)$; $$ b) ${\displaystyle \frac{dy}{dx}}=\sin (x)\cos (x)$; $$ c) ${\displaystyle \frac{dy}{dx}}=2\sin (x)$

• a) ${\displaystyle \frac{dy}{dx}}=x^2+y^2$; $$ b) ${\displaystyle \frac{dy}{dx}}=5y^2$; $$ c) ${\displaystyle \frac{dy}{dx}}=x^2-y^2$

Más adelante…

En la siguiente entrada continuaremos con las descripciones cualitativas de las soluciones de una ecuación diferencial, en particular estudiaremos con mayor detalle las ecuaciones de la forma

$${\displaystyle \frac{dy}{dx}}=f(y)$$

llamadas ecuaciones diferenciales autónomas.

Entradas relacionadas

• Página principal del curso: Ecuaciones Diferenciales I
• Entrada anterior del curso: Ecuaciones diferenciales como modelos matemáticos
• Siguiente entrada del curso: Ecuaciones diferenciales autónomas

• Video relacionado al tema: Campo de pendientes asociado a una ecuación diferencial, curvas integrales y método de las isóclinas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»