Las matemáticas son la creación más poderosa y bella del espíritu humano.
– Stefan Banach

Introducción

Con esta entrada culminaremos el estudio de los sistemas lineales. En la unidad 3 hicimos un estudio analítico y en esta unidad un estudio cualitativo, aunque reducido a un sistema compuesto por dos ecuaciones, esto con el fin de hacer al mismo tiempo un estudio geométrico en el plano.

A continuación presentamos un breve resumen de los visto en las entradas anteriores.

Clasificación de los planos fase y los puntos de equilibrio

El sistema que estudiamos todo este tiempo fue

\begin{align*}
x^{\prime} &= ax + by \\
y^{\prime} &= cx + dy \label{1} \tag{1}
\end{align*}

Este sistema lo podemos escribir en forma matricial como

$$\begin{pmatrix}
x^{\prime} \\ y^{\prime}
\end{pmatrix} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \begin{pmatrix}
x \\ y
\end{pmatrix} \label{2} \tag{2}$$

Si

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
x^{\prime} \\ y^{\prime}
\end{pmatrix}, \hspace{1cm} \mathbf{Y} = \begin{pmatrix}
x \\ y
\end{pmatrix} \hspace{1cm} y \hspace{1cm} \mathbf{A} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix}$$

entonces el sistema (\ref{2}) se escribe como

$$\mathbf{Y}^{\prime} = \mathbf{AY} \label{3} \tag{3}$$

Vimos que la naturaleza y estabilidad del punto de equilibrio quedó caracterizada por los valores propios de la matriz $\mathbf{A}$ del sistema.

El único punto de equilibrio de los sistemas lineales es el origen $Y_{0} = (0, 0)$, siempre que el determinante de $\mathbf{A}$ sea distinto de cero. En la entrada anterior teníamos que $|\mathbf{A}| = 0$, es por ello que obtuvimos infinitos puntos de equilibrio y es que el hecho de que tengamos valores propios nulos es un caso especial y poco común.

En el caso en el que no hay valores propios nulos, sabemos que en función del comportamiento de las trayectorias en relación con el punto de equilibrio aislado $Y_{0} = (0, 0)$, este punto se denominará: nodo, punto silla, centro, foco, atractor o repulsor. Recordemos cuando se da cada caso.

1. El punto de equilibrio es un nodo.
   
   Este caso ocurre cuando los valores propios $\lambda_{1}$ y $\lambda_{2}$ son reales y del mismo signo.

• Si $\lambda_{1} < \lambda_{2} < 0$, entonces todas las trayectorias se acercan al origen, de manera que el punto de equilibrio es un nodo atractor y será asintóticamente estable.

• Si $\lambda_{1} > \lambda_{2} > 0$, entonces todas las trayectorias se alejan del origen, por tanto, el punto de equilibrio es un nodo repulsor y será inestable.

2. El punto crítico es un punto silla.
   
   Este caso se presenta cuando los valores propios $\lambda_{1}$ y $\lambda_{2}$ son reales y de distinto signo.

• Si $\lambda_{1} < 0$ y $\lambda_{2} > 0$ ocurre que dos trayectorias rectas se acercan al origen y otras dos trayectorias rectas se separan de él, mientras que el resto de trayectorias al pasar cerca del origen inmediatamente se alejan de él. Esto nos permite concluir que todo punto silla es inestable.

3. El punto crítico es un centro.
   
   Este caso se presenta cuando los valores propios son imaginarios puros.

• Si $\lambda_{1} = i \beta$ y $\lambda_{2} = -i \beta$, entonces las trayectorias serán curvas cerradas que rodean al origen, en general tienen forma de elipses, de modo que ninguna trayectoria tiende a él cuando $t \rightarrow + \infty $ o $t \rightarrow -\infty $, esto hace que el punto de equilibrio sea estable, pero no asintóticamente estable.

4. El punto crítico es un foco.
   
   En este caso los valores propios son complejos conjugados y tienen parte real no nula.

• Si $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha < 0$, entonces las trayectorias son curvas en forma de espiral que, conforme $t \rightarrow + \infty$ todas se acercan al origen, es por ello que el punto de equilibrio es asintóticamente estable.

• Si $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha > 0$, entonces las trayectorias son curvas en forma de espiral que, conforme $t \rightarrow + \infty$ todas se separan del origen, es por ello que el punto de equilibrio es inestable.

5. El punto crítico es un atractor o un repulsor.
   
   Este caso se presenta cuando un sistema lineal tiene valores propios reales, del mismo signo, pero además iguales.

• Si $\lambda_{1} = \lambda_{2} < 0$, entonces las trayectorias tienden hacia el origen en forma de rayos o curvas dependiendo de si es posible determinar dos vectores propios o uno propio y otro generalizado. En este caso el punto de equilibrio es un atractor y es asintóticamente estable.

• Si $\lambda_{1} = \lambda_{2} > 0$, entonces las trayectorias se alejan el origen en forma de rayos o curvas dependiendo de si es posible determinar dos vectores propios o uno propio y otro generalizado. En este caso el punto de equilibrio es un repulsor y es inestable.

6. Los puntos críticos son una recta.
   
   En este caso particular hay infinitos puntos de equilibrio, todos sobre una recta y ocurre cuando uno o ambos valores propios son cero.

Como podemos ver, las características de las trayectorias y de los puntos de equilibrio en el plano fase quedan determinadas por los valores propios de la matriz de coeficientes $\mathbf{A}$. Sin embargo, estas características también se pueden describir en términos de la traza $T$ y del determinante $D$ de la matriz de coeficientes $A$, veamos como es esto.

La traza y el determinante de la matriz de coeficientes

Consideremos la matriz de coeficientes

$$\mathbf{A} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \label{4} \tag{4}$$

Sabemos que la traza de una matriz se define como la suma de los elementos de la diagonal principal de dicha matriz. En nuestro caso, la traza de $\mathbf{A}$ es

$$T = Tr(\mathbf{A}) = a + d \label{5} \tag{5}$$

Por otro lado, el determinante de la matriz $\mathbf{A}$ es

$$D = |\mathbf{A}| = ad -bc \label{6} \tag{6}$$

Consideremos la ecuación característica de $\mathbf{A}$.

$$|\mathbf{A} -\lambda \mathbf{I}| = \begin{vmatrix}
a -\lambda & b \\ c & d -\lambda
\end{vmatrix} = 0 \label{7} \tag{7}$$

El polinomio característico es

$$P(\lambda) = (a -\lambda)(d -\lambda) -bc = \lambda^{2} -(a + d) \lambda + (ad -bc) \label{8} \tag{8}$$

Si sustituimos las ecuaciones (\ref{5}) y (\ref{6}) en la ecuación característica se tiene

$$\lambda^{2} -T \lambda + D = 0 \label{9} \tag{9}$$

Las raíces de esta ecuación cuadrática son

$$\lambda_{1} = \dfrac{T + \sqrt{T^{2} -4D}}{2} \hspace{1cm} y \hspace{1cm} \lambda_{2} = \dfrac{T -\sqrt{T^{2} -4D}}{2} \label{10} \tag{10}$$

Hemos logrado escribir a los valores propios de $\mathbf{A}$ en términos de la traza y del determinante de la misma matriz $\mathbf{A}$.

De tarea moral, usando (\ref{10}) calcula explícitamente las operaciones $(\lambda_{1} + \lambda_{2})$ y $(\lambda_{1} \cdot \lambda_{2})$ y verifica que se satisfacen las siguientes relaciones importantes.

$$T = \lambda_{1} + \lambda_{2} \label{11} \tag{11}$$

y

$$D = \lambda_{1} \lambda_{2} \label{12} \tag{12}$$

Es decir, la traza y el determinante de $\mathbf{A}$ también se pueden escribir en términos de los valores propios de $\mathbf{A}$.

El análisis cualitativo que hemos hecho a lo largo de las últimas entradas ha sido en función de los valores propios, recordemos que las posibilidades son

Valores propios reales y distintos:

• $\lambda_{1} < \lambda_{2} < 0$.
• $\lambda_{1} > \lambda_{2} > 0$.
• $\lambda_{1} < 0$ y $\lambda_{2} > 0$.

Valores propios complejos:

• $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha < 0$.
• $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha = 0$.
• $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha > 0$.

Valores propios repetidos:

• $\lambda_{1} = \lambda_{2} < 0$.
• $\lambda_{1} = \lambda_{2} > 0$.

Valores propios nulos

• $\lambda_{1} = 0$ y $\lambda_{2} < 0$.
• $\lambda_{1} = 0$ y $\lambda_{2} > 0$.
• $\lambda_{1} = \lambda_{2} = 0$.

Sin embargo, ahora podemos analizar cada caso pero en función de los valores de la traza $T$ y el determinante $D$ de $\mathbf{A}$, ya que inmediatamente podemos notar de (\ref{10}) que los valores propios de $\mathbf{A}$ son complejos si $T^{2} -4D < 0$, son repetidos si $T^{2} -4D = 0$, y son reales y distintos si $T^{2} -4D > 0$.

El plano Traza – Determinante

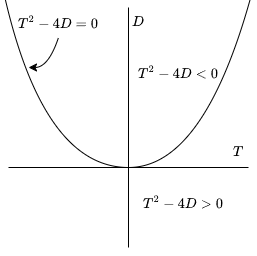
Comenzaremos a hacer un nuevo bosquejo para los sistemas lineales examinando el conocido plano traza – determinante. El eje $T$ corresponderá a la línea horizontal y representa a la traza, mientras que el eje $D$ corresponderá a la vertical y representa al determinante. En este plano la curva

$$T^{2} -4D = 0$$

o su equivalente,

$$D(T) = \dfrac{T^{2}}{4} \label{13} \tag{13}$$

es una parábola con concavidad hacia arriba. Arriba de ésta encontramos $T^{2} -4D < 0$, y abajo de ella $T^{2} -4D > 0$, tal como se muestra en la siguiente figura.

Para usar este plano, calculamos primero $T$ y $D$ para una matriz $\mathbf{A}$ dada y luego localizamos el punto $(T, D)$ en el plano. De forma inmediata podremos visualizar si los valores propios son reales, repetidos o complejos, dependiendo de la posición de $(T, D)$ respecto a la parábola.

Ejemplo: Determinar el tipo de valores propios que tiene el siguiente sistema lineal.

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
4 & 5 \\ -2 & 6
\end{pmatrix} \mathbf{Y}$$

Solución: La matriz de coeficientes es

$$\mathbf{A} = \begin{pmatrix}
4 & 5 \\ -2 & 6
\end{pmatrix}$$

Vemos que

$$T = 4 + 6 = 10$$

y

$$D = 4(6) -5(-2) = 24 + 10 = 34$$

Ahora bien

$$T^{2} -4D = (10)^{2} -4(34) = 100 -136 = -36$$

Como $T^{2} -4D < 0$, entonces inmediatamente concluimos que los valores propios son complejos conjugados. Ahora bien, aún no sabemos si se trata de un centro o algún tipo de espiral, pero por el momento no nos preocupemos por ello.

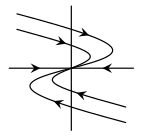
Sólo con el fin de conocer el tipo de soluciones que tiene el sistema, su plano fase es el siguiente.

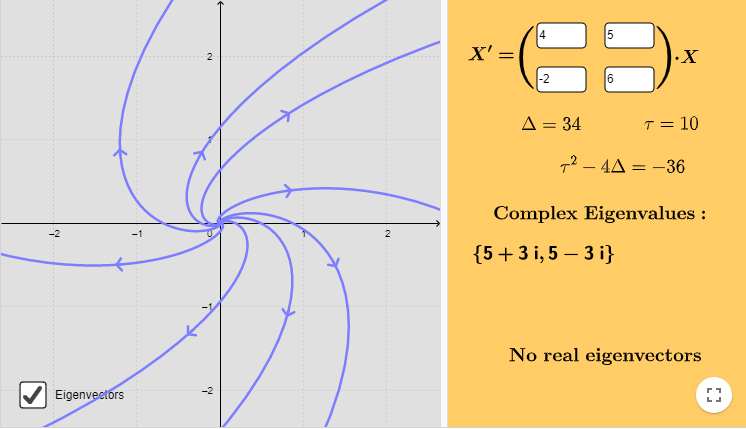
Las trayectorias del sistema corresponden a espirales y el punto de equilibrio es un foco inestable. Observa que la figura ya nos da los valores de la traza, el determinante y el discriminante, aunque con una notación distinta.

Ahora puedes regresar a visualizar los planos fase de todos los ejemplos que hicimos en las 4 entradas anteriores y poner más atención en los valores de la traza y el determinante.

$\square$

Por su puesto que podemos hacer mucho más en el plano traza – determinante. Por ejemplo, desearíamos no sólo saber si los valores propios de $\mathbf{A}$ son complejos, repetidos o reales, sino que también conocer si tienen parte real nula o distinta de cero o si son reales positivos, negativos o de distinto signo, etcétera.

A continuación haremos un análisis más detallado sobre las raíces (\ref{10}) y veremos que tipo de información nos proporciona sobre los sistemas lineales.

Recordemos que los valores propios de $\mathbf{A}$, en términos de la traza y el determinante de $\mathbf{A}$ son

$$\lambda_{1} = \dfrac{T + \sqrt{T^{2} -4D}}{2} \hspace{1cm} y \hspace{1cm} \lambda_{2} = \dfrac{T -\sqrt{T^{2} -4D}}{2}$$

Atendiendo a los diferentes valores de $T$ y $D$, se tiene:

1. Si $T^{2} -4D < 0$, entonces los valores propios $\lambda_{1}$ y $\lambda_{2}$ son complejos conjugados con parte real igual a $T /2$. Se tienen los siguientes casos:

• Los valores propios son imaginarios puros si $T = 0$ (centro y estabilidad).

• Los valores propios tienen parte real negativa cuando $T < 0$ (foco y estabilidad asintótica).

• Los valores propios tienen parte real positiva cuando $T > 0$ (foco e inestabilidad).
  
  Si consideramos el plano traza – determinante y denotamos por $O$ al origen podremos asegurar que por encima de la parábola $T^{2} -4D = 0$ se tiene:

• En el eje $OD$ se presentan los centros y hay estabilidad.

• A la izquierda del eje $OD$ se presentan los focos y hay estabilidad asintótica.

• A la derecha del eje $OD$ también se presentan focos, pero hay inestabilidad.

2. Si $D < 0$, entonces se tiene $T^{2} -4D > T^{2}$. En este caso los valores propios son reales y de distinto signo, lo que significa que se presentarán puntos silla e inestabilidad. En el plano traza – determinante los encontraremos por debajo del eje $T$.

3. Si $D > 0$ y $T^{2} -4D \geq 0$, entonces los valores propios son reales y tienen el mismo signo que $T$. Los casos posibles son:

• Si $T < 0$, se tiene:
  • Cuando $T^{2} -4D = 0$, los valores propios son iguales y negativos (atractor y estabilidad asintótica).
  • Cuando $T^{2} -4D > 0$, los valores propios son reales, distintos y negativos (nodo atractor y estabilidad asintótica).

• Si $T > 0$, se tiene:
  • Cuando $T^{2} -4D = 0$, los valores propios son iguales y positivos (repulsor e inestabilidad).
  • Cuando $T^{2} -4D > 0$, los valores propios son reales, distintos y positivos (nodo repulsor e inestabilidad).

4. Si $D = 0$, entonces uno o ambos valores propios son cero. Los siguientes casos se obtienen directamente de (\ref{11}) y (\ref{12}).

• Si $T = 0$ (origen), entonces ambos valores propios son cero (recta de puntos de equilibrio y trayectorias paralelas a dicha recta).

• Si $T > 0$, entonces un valor propio es cero y el otro es positivo (recta de puntos de equilibrio inestables y trayectorias rectas que se alejan de la recta de puntos de equilibrio).

• Si $T < 0$, entonces un valor propio es cero y el otro es negativo (recta de puntos de equilibrio asintóticamente estables y trayectorias rectas que tienden a la recta de puntos de equilibrio).

¡Todo lo que hemos aprendido sobre sistemas lineales homogéneos compuestos por dos ecuaciones diferenciales de primer orden con coeficientes constantes, incluyendo todas las características anteriores, se resume en el siguiente diagrama!.

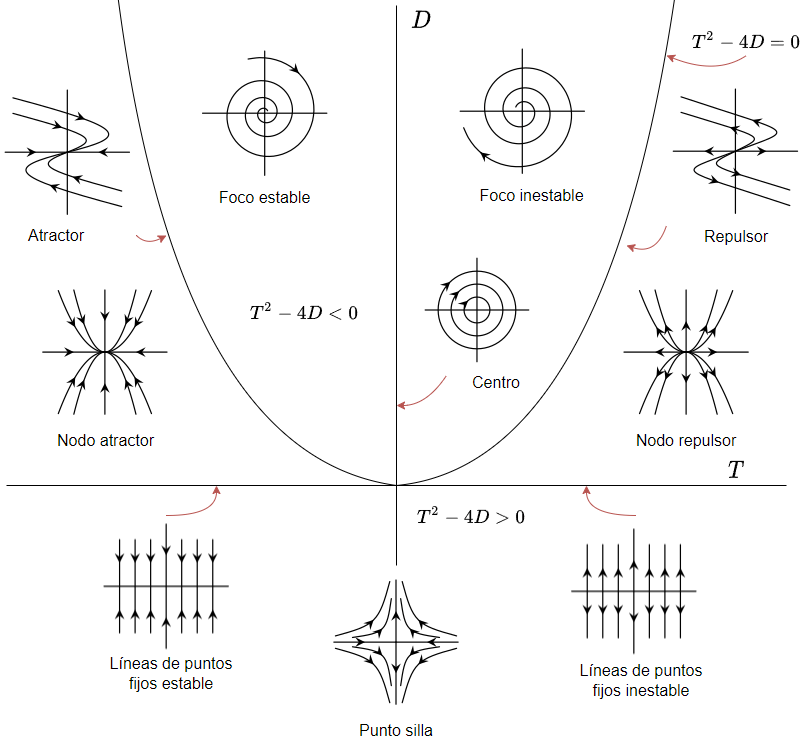
Veamos un ejemplo.

Ejemplo: Caracterizar el siguiente sistema lineal.

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
3 & -4 \\ 1 & -1
\end{pmatrix} \mathbf{Y}$$

Solución: La matriz de coeficientes es

$$\mathbf{A} = \begin{pmatrix}
3 & -4 \\ 1 & -1
\end{pmatrix}$$

Vemos que

$$T = 3 + (-1) = 2$$

y

$$D = 3(-1) -(-4)(1) = -3 + 4 = 1$$

tenemos, entonces

$$T^{2} -4D = (2)^{2} -4(1) = 4 -4 = 0$$

Como $T > 0$, $D > 0$ y $T^{2} -4D = 0$, vamos al punto 3 y deducimos que el sistema lineal tiene valores propios iguales y positivos. De acuerdo a las ecuaciones (\ref{11}) y (\ref{12}) se tiene el siguiente sistema.

\begin{align*}
T &= 2 = \lambda_{1} + \lambda_{2} \\
D &= 1 = \lambda_{1}\lambda_{2}
\end{align*}

De la primer ecuación obtenemos $\lambda_{1} = 2 -\lambda_{2}$, sustituyendo en la segunda ecuación se tiene

$$1 = (2 -\lambda_{2}) \lambda_{2}$$

de aquí obtenemos la ecuación cuadrática

$$\lambda_{2}^{2} -2 \lambda_{2} + 1 = 0$$

Las raíces son

$$\lambda_{2} = \dfrac{2 \pm \sqrt{4 -4}}{2} = 1$$

La única raíz es $\lambda_{2} = 1$, sustituyendo en cualquier ecuación del sistema obtenemos que $\lambda_{1} = 1$. Por lo tanto, el único valor propio de la matriz $\mathbf{A}$ es $\lambda = 1$ (iguales y positivos, tal como lo habíamos deducido).

Si vamos al plano traza – determinante, como $T > 0$ y $D > 0$, entonces estamos en el primer cuadrante, pero además $T^{2} -4D = 0$, así que estamos situados sobre la parábola del primer cuadrante, exactamente en el punto $(T, D) = (2, 1)$, esto nos permite concluir que el plano fase del sistema corresponde a repulsor.

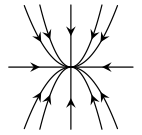
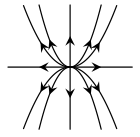
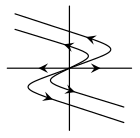
El plano fase del sistema es el siguiente.

Efectivamente se trata de un repulsor.

$\square$

Debido a que cada punto del plano traza – determinante representa un plano fase distinto, el plano traza – determinante es un ejemplo de lo que se conoce como plano paramétrico.

El plano paramétrico

El plano traza – determinante es un ejemplo de un plano paramétrico. Los elementos de la matriz $\mathbf{A}$ son parámetros que se pueden ajustar, cuando esos elementos cambian, la traza y el determinante de la matriz también se modifican y el punto $(T, D)$ se mueve en el plano paramétrico. Cuando este punto entra en las diversas regiones del plano traza – determinante, debemos imaginar que los retratos fase asociados también experimentan transformaciones.

El plano traza – determinante es un esquema de clasificación del comportamiento de todas las posibles soluciones de sistemas lineales.

En este enlace se tiene acceso a una herramienta visual del plano paramétrico. En él se puede mover el punto $(T, D)$ a lo largo de las diferentes regiones del plano traza – determinante a la vez que visualizamos el tipo de planos fase que se generan. ¡Pruébalo y diviértete!

Con esto concluimos el estudio de los sistemas lineales. Cabe mencionar que el plano traza – determinante no da una información completa sobre el sistema lineal tratado.

Por ejemplo, a lo largo de la parábola $T^{2} -4D = 0$ tenemos valores propios repetidos, pero no podemos determinar si tenemos uno o varios vectores propios linealmente independientes. para saberlo es preciso calcularlos.

De modo similar, no podemos determinar la dirección en que las soluciones se mueven alrededor del origen si $T^{2}-4D < 0$. Por ejemplo, las dos matrices

$$\mathbf{A} = \begin{pmatrix}
0 & 1 \\ -1 & 0
\end{pmatrix} \hspace{1cm} y \hspace{1cm} \mathbf{B} = \begin{pmatrix}
0 & -1 \\ 1 & 0
\end{pmatrix}$$

tienen traza $T = 0$ y determinante $D = 1$, pero las soluciones del sistema $\mathbf{Y}^{\prime} = \mathbf{AY}$ se mueven alrededor del origen en el sentido de las manecillas del reloj, mientras que las soluciones de $\mathbf{Y}^{\prime} = \mathbf{BY}$ viajan en el sentido opuesto.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

1. Hacer un análisis cualitativo de los siguientes sistemas lineales apoyándose de la traza y el determinante de la matriz de coeficientes $\mathbf{A}$, así como del plano traza – determinante. Es decir, de acuerdo al valor de la traza $T$, el determinante $D$ y el discriminante $T^{2} -4D$, determinar que tipo de valores propios tiene el sistema, así como el tipo de plano fase y estabilidad del punto de equilibrio.

• $\mathbf{Y}^{\prime} = \begin{pmatrix}
  5 & 4 \\ -2 & 3
  \end{pmatrix} \mathbf{Y}$

• $\mathbf{Y}^{\prime} = \begin{pmatrix}
  2 & -1 \\ -2 & 3
  \end{pmatrix} \mathbf{Y}$

• $\mathbf{Y}^{\prime} = \begin{pmatrix}
  1 & 1 \\ 4 & 1
  \end{pmatrix} \mathbf{Y}$

• $\mathbf{Y}^{\prime} = \begin{pmatrix}
  1 & -1 \\ 1 & 3
  \end{pmatrix} \mathbf{Y}$

• $\mathbf{Y}^{\prime} = \begin{pmatrix}
  6 & 3 \\ 2 & 1
  \end{pmatrix} \mathbf{Y}$

• $\mathbf{Y}^{\prime} = \begin{pmatrix}
  2 & -5 \\ 2 & 2
  \end{pmatrix} \mathbf{Y}$

Más adelante…

Estamos cerca de concluir el curso. En las próximas entradas estudiaremos de manera cualitativa a los sistemas no lineales compuestos por dos ecuaciones diferenciales de primer orden.

En particular, en la siguiente entrada veremos que alrededor de un punto de equilibrio de un sistema no lineal las trayectorias son muy parecidas a las de un sistema lineal lo que nos permitirá observar el comportamiento que tienen las soluciones del sistema no lineal, al menos cerca de un punto de equilibrio.

Entradas relacionadas

• Página principal del curso: Ecuaciones Diferenciales I
• Entrada anterior del curso: Teoría cualitativa de los sistemas lineales homogéneos – Valores propios nulos
• Siguiente entrada del curso: Linealización de los puntos de equilibrio de sistemas no lineales

• Video relacionado al tema: El plano traza-determinante

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»