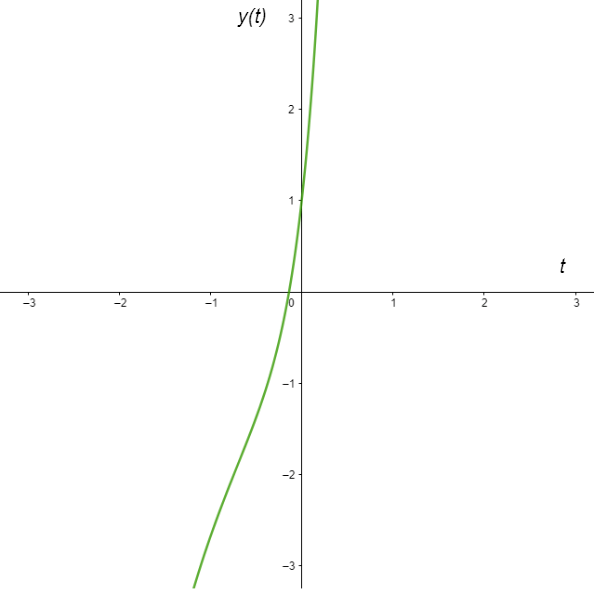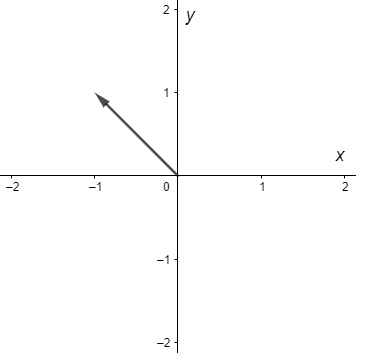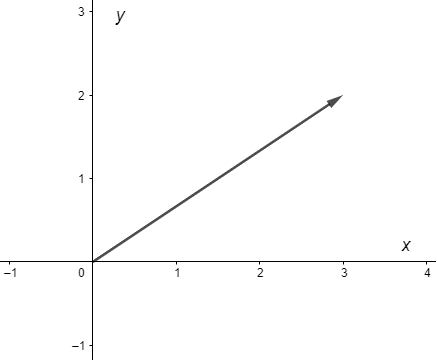No hay rama de la matemática, por lo abstracta que sea, que no
pueda aplicarse algún día a los fenómenos del mundo real.
– Lobachevski
Introducción
¡Bienvenidos a la cuarta y última unidad del curso de Ecuaciones Diferenciales I!.
En esta unidad estudiaremos a las ecuaciones diferenciales ordinarias desde una perspectiva cualitativa y geométrica. En particular, estudiaremos las propiedades cualitativas de los sistemas de ecuaciones diferenciales de primer orden que vimos en la unidad anterior y, como sabemos, las ecuaciones de orden superior se pueden reducir a sistemas de ecuaciones de primer orden, lo que significa que en nuestro estudio también estaremos revisando las propiedades cualitativas de algunas de las ecuaciones vistas en la unidad 2.
La teoría cualitativa ya no es nueva para nosotros, pues en la primera unidad estudiamos desde esta perspectiva a las ecuaciones de primer orden. Recordemos que una ecuación diferencial de primer orden se puede ver, en su forma normal, como
$$\dfrac{dy}{dx} = f(x, y(x)) = f(x, y) \label{1} \tag{1}$$
Y una ecuación diferencial autónoma como
$$\dfrac{dy}{dx} = f(y(x)) = f(y) \label{2} \tag{2}$$
En esta última ecuación la variable independiente no aparece explícitamente.
Sobre la ecuación (\ref{1}) definimos los conceptos de elementos lineales, campo de pendientes, curvas integrales e isóclinas y sobre la ecuación (\ref{2}) definimos conceptos como puntos de equilibrio o puntos críticos, esquema de fases, líneas de fase, así como atractores, repulsores y nodos. Muchos de estos conceptos los generalizaremos a los sistemas lineales, además de algunos otros conceptos nuevos que definiremos.
En esta entrada daremos una introducción intuitiva al análisis cualitativo y geométrico de los sistemas lineales y a partir de la siguiente entrada comenzaremos a formalizar la teoría.
Sistemas lineales
Recordemos que un sistema de ecuaciones diferenciales de primer orden es de la forma
\begin{align*}
y_{1}^{\prime}(t) &= F_{1}(t, y_{1}, y_{2}, \cdots, y_{n}) \\
y_{2}^{\prime}(t) &= F_{2}(t, y_{1}, y_{2}, \cdots, y_{n}) \\
&\vdots \\
y_{n}^{\prime}(t) &= F_{n}(t, y_{1}, y_{2}, \cdots, y_{n}) \label{3} \tag{3}
\end{align*}
En forma vectorial se puede escribir como
$$\mathbf{Y}^{\prime}(t) = \mathbf{F}(t, \mathbf{Y}(t)) \label{4} \tag{4}$$
Si el sistema es lineal, entonces se puede escribir, en su forma normal, como
\begin{align*}
y_{1}^{\prime}(t) &= a_{11}(t)y_{1} + a_{12}(t)y_{2} + \cdots + a_{1n}(t)y_{n} + g_{1}(t) \\ y_{2}^{\prime}(t) &= a_{21}(t)y_{1} + a_{22}(t)y_{2} + \cdots + a_{2n}(t)y_{n} + g_{2}(t) \\ &\vdots \\
y_{n}^{\prime}(t) &= a_{n1}(t)y_{1} + a_{n2}(t)y_{2} + \cdots + a_{nn}(t)y_{n} + g_{n}(t) \label{5} \tag{5}
\end{align*}
En esta unidad estudiaremos a detalle la propiedades cualitativas de los sistemas lineales compuestos por dos ecuaciones diferenciales de primer orden homogéneas con coeficientes constantes por muchas razones, las cuales comentaremos al final de la entrada. Dicho sistema lo podemos escribir de la siguiente forma.
\begin{align*}
x^{\prime}(t) &= ax(t) + by(t) \\
y^{\prime}(t) &= cx(t) + dy(t) \label{6} \tag{6}
\end{align*}
En donde $a, b, c$ y $d$ son constantes. Si definimos
$$\mathbf{Y}^{\prime}(t) = \begin{pmatrix}
x^{\prime}(t) \\ y^{\prime}(t)
\end{pmatrix}, \hspace{1cm} \mathbf{Y}(t) = \begin{pmatrix}
x(t) \\ y(t)
\end{pmatrix} \hspace{1cm} y \hspace{1cm} \mathbf{A} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix}$$
entonces el sistema (\ref{6}) se puede escribir como
$${\mathbf{Y}}'(t) = \mathbf{AY}(t) \label{7} \tag{7}$$
Esta es la forma común con la que estuvimos trabajando en la unidad anterior. Si ahora definimos las funciones
$$F_{1}(t, x, y) = ax(t) + by(t) \hspace{1cm} y \hspace{1cm} F_{2}(t, x, y) = cx(t) + dy(t) \label{8} \tag{8}$$
y definimos el vector compuesto por estas funciones
$$\mathbf{F}(t, x, y) = \begin{pmatrix}
F_{1}(t, x, y) \\ F_{2}(t, x, y)
\end{pmatrix} \label{9} \tag{9}$$
entonces podemos escribir al sistema (\ref{6}) como
$$\mathbf{Y}^{\prime}(t) = \mathbf{F}(t, x, y) \label{10} \tag{10}$$
De (\ref{7}) y (\ref{10}), se obtiene que
$$\mathbf{F}(t, x, y) = \mathbf{AY}(t) \label{11} \tag{11}$$
Esta es una nueva forma de ver un sistema lineal, sin embargo nuestro interés está en hacer un análisis cualitativo y geométrico, así que es conveniente ver a la ecuación (\ref{11}) como una función de varias variables definida en un dominio $U$.
Observemos que el sistema lineal (\ref{6}) no depende explícitamente de la variable $t$, por lo que podemos escribir
\begin{align*}
x^{\prime} &= ax + by \\
y^{\prime} &= cx + dy \label{12} \tag{12}
\end{align*}
Y ahora podemos escribir
$$F_{1}(x, y) = ax + by \hspace{1cm} y \hspace{1cm} F_{2}(x, y) = cx + dy \label{13} \tag{13}$$
Es claro que $F_{1}: \mathbb{R}^{2} \rightarrow \mathbb{R}$ y $F_{2}: \mathbb{R}^{2} \rightarrow \mathbb{R}$, es decir las funciones $F_{1}$ y $F_{2}$ son funciones de dos variables cuyo dominio está formado por puntos con $2$ coordenadas y la función asocia a cada punto un número real determinado. La gráfica de estas funciones está en $\mathbb{R}^{3}$. Ahora bien, se puede definir la función
$$F(x, y) = (F_{1}(x, y), F_{2}(x, y)) = (ax + by, cx + dy) \label{14} \tag{14}$$
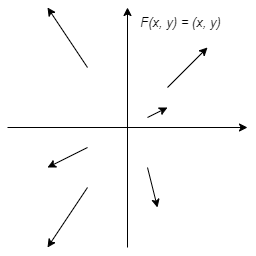
En este caso $F: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$, así que ya no podemos visualizar su gráfica, sin embargo existe una técnica en la que en un mismo plano a cada elemento $(x, y) \in \mathbb{R}^{2}$ lo dibujamos como un punto y a $F(x, y)$ como un vector colocado sobre ese punto $(x, y)$. Por ejemplo, la función
$$F(x, y) = (x, y)$$
se puede visualizar como
Este tipo de bosquejos es lo que conocemos como campos vectoriales.
Finalmente consideremos las soluciones del sistema lineal (\ref{12}). En este caso lo que obtendremos al resolver el sistema serán dos funciones $x(t)$ y $y(t)$ definidas como $x: \mathbb{R} \rightarrow \mathbb{R}$ y $y: \mathbb{R} \rightarrow \mathbb{R}$. Lo que deseamos es graficar de alguna manera estas dos funciones en el mismo plano en el que se bosqueja el campo vectorial $F(x, y)$, para hacerlo definimos la función
$$f(t) = (x(t), y(t)) \label{15} \tag{15}$$
Vemos que $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$, es decir, dado un valor para $t$ las soluciones $x(t)$ y $y(t)$ toman un valor particular que sirven como entrada de la función $f$ y ésta devuelve un sólo valor.
Para tener una visualización de $f$ consideremos como ejemplo la función
$$f(t) = (t, t^{2})$$
con $t \in [-2, 2]$, es decir,
$$x(t) = t \hspace{1cm} y \hspace{1cm} y(t) = t^{2}$$
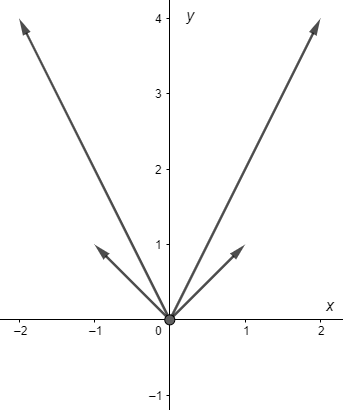
Consideremos algunos valores particulares
- $t = -2 \hspace{0.7cm} \rightarrow \hspace{1cm} f(-2) = (-2, 4)$.
- $t = 2 \hspace{1cm} \rightarrow \hspace{1cm} f(2) = (2, 4)$.
- $t = -1 \hspace{0.7cm} \rightarrow \hspace{1cm} f(-1) = (-1, 1)$.
- $t = 1 \hspace{1cm} \rightarrow \hspace{1cm} f(1) = (1, 1)$.
Para visualizar estos datos lo que vamos a hacer es dibujar vectores que parten del origen hacía las coordenadas $(x(t), y(t))$ obtenidas, tal como se muestra en la siguiente figura.
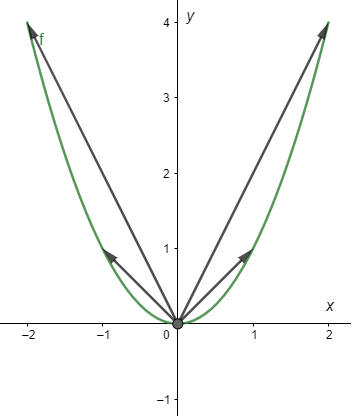
$f(t)$ será la curva que trazará la punta del vector a medida que $t$ tiene distintos valores. Siguiendo con el mismo ejemplo $f(t) = (t, t^{2})$ para $t \in [-2, 2]$, la curva que traza $f$ se ve de la siguiente forma.
Observemos que $f(t) = (t, t^{2})$ no es más que la parametrización de la parábola $y(x) = x^{2}$ en el intervalo $[-2, 2]$. Es por ello que diremos que $f(t)$ es una función paramétrica.
Recordemos que un sistema de ecuaciones paramétricas permite representar una curva o superficie en el plano o en el espacio mediante una variable $t$ llamada parámetro que recorre un intervalo de números reales, considerando cada coordenada de un punto como una función dependiente del parámetro.
Concluiremos esta entrada con un ejemplo para visualizar cómo es que esta nueva forma de ver el problema de resolver un sistema lineal nos ayudará a obtener información cualitativa del mismo.
Análisis cualitativo y geométrico
Ejemplo: Hacer un análisis cualitativo y geométrico del siguiente sistema lineal homogéneo.
\begin{align*}
x^{\prime} &= 2x + 3y \\
y^{\prime} &= 2x + y \label{16} \tag{16}
\end{align*}
Solución: Primero resolvamos el sistema de forma tradicional, es decir, analíticamente.
La matriz de coeficientes es
$$\mathbf{A} = \begin{pmatrix}
2 & 3 \\ 2 & 1
\end{pmatrix} \label{17} \tag{17}$$
Los valores propios se obtienen de resolver la siguiente ecuación característica.
$$|\mathbf{A} -\lambda \mathbf{I})| = \begin{vmatrix}
2 -\lambda & 3 \\ 2 & 1-\lambda
\end{vmatrix} = \lambda^{2} -3 \lambda -4 = (\lambda + 1)(\lambda -4) = 0$$
Resolviendo se obtiene que los valores propios son
$$\lambda_{1} = -1 \hspace{1cm} y \hspace{1cm} \lambda_{2} = 4$$
Determinemos los vectores propios.
Para $\lambda_{1} = -1$, debemos resolver
$$(\mathbf{A} + \mathbf{I}) \mathbf{K} = \mathbf{0}$$
El sistema de ecuaciones que se obtiene es
\begin{align*}
3k_{1} + 3k_{2} &= 0 \\
2k_{1} + 2k_{2} &= 0
\end{align*}
De donde $k_{1} = -k_{2}$. Si elegimos $k_{2} = 1$, se obtiene $k_{1} = -1$ y entonces el primer vector propio es
$$\mathbf{K}_{1} = \begin{pmatrix}
-1 \\ 1
\end{pmatrix}$$
Para $\lambda_{2} = 4$, debemos resolver
$$(\mathbf{A} -4\mathbf{I}) \mathbf{K} = \mathbf{0}$$
El sistema de ecuaciones que se obtiene es
\begin{align*}
-2k_{1} + 3k_{2} &= 0 \\
2k_{1} -3k_{2} &= 0
\end{align*}
Se ve que $k_{1} = \dfrac{3}{2}k_{2}$, así si $k_{2} = 2$, entonces $k_{1} = 3$ y por tanto el segundo vector propio es
$$\mathbf{K}_{2} = \begin{pmatrix}
3 \\ 2
\end{pmatrix}$$
Las soluciones linealmente independientes son
$$\mathbf{\mathbf{Y}}_{1}(t) = \begin{pmatrix}
-1 \\ 1
\end{pmatrix} e^{ -t} \hspace{1cm} y \hspace{1cm}
\mathbf{\mathbf{Y}}_{2}(t) = \begin{pmatrix}
3 \\ 2
\end{pmatrix}e^{4t} \label{18} \tag{18}$$
Y por lo tanto, la solución general del sistema lineal es
$$\mathbf{\mathbf{Y}}(t) = c_{1} \begin{pmatrix}
1 \\ -1
\end{pmatrix} e^{ -t} + c_{2} \begin{pmatrix}
3 \\ 2
\end{pmatrix} e^{4t} \label{19} \tag{19}$$
Si dejamos de usar la notación matricial podemos escribir a las soluciones como
$$x(t) = c_{1} e^{-t} + 3c_{2} e^{4t} \hspace{1cm} y \hspace{1cm} y(t) = -c_{1}e^{-t} + 2c_{2} e^{4t} \label{20} \tag{20}$$
Hasta aquí es hasta donde hemos llegado con lo visto en la unidad anterior, ahora veamos el comportamiento de estas soluciones geométricamente.
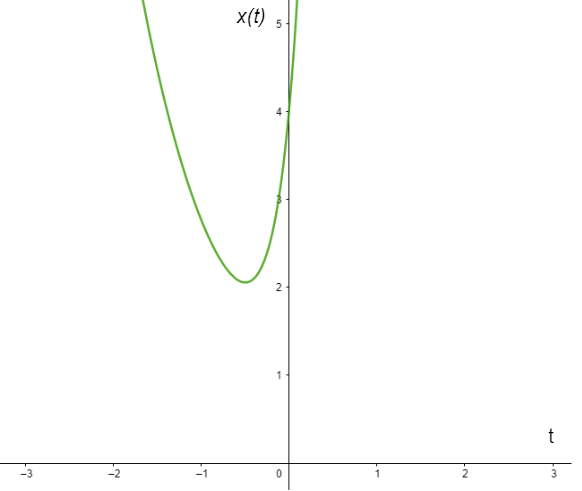
Obtuvimos dos funciones, cada una de ellas depende de la variable $t$ de forma que la primer función la podemos graficar en el plano $XT$, mientras que la segunda en el plano $YT$.
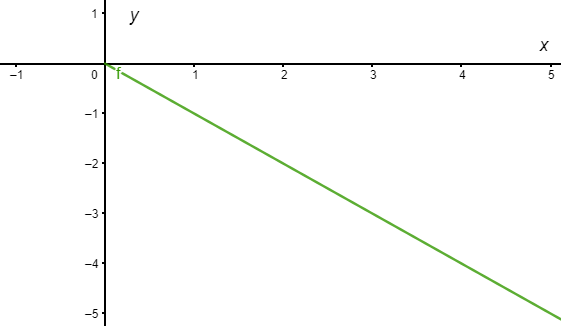
La gráfica de $x(t)$ para $c_{1} = c_{2} = 1$ se ve de la siguiente forma.
Por otro lado, la gráfica de $y(t)$ para $c_{1} = c_{2} = 1$ se ve de la siguiente forma.
De acuerdo a (\ref{15}), la función paramétrica es
$$f(t) = (c_{1}e^{-t} + 3c_{2}e^{4t}, -c_{1}e^{-t} + 2c_{2}e^{4t}) \label{21} \tag{21}$$
Para el caso particular en el que $c_{1} = c_{2} = 1$ la función paramétrica es
$$f(t) = (e^{-t} + 3e^{4t}, -e^{-t} + 2 e^{4t}) \label{22} \tag{22}$$
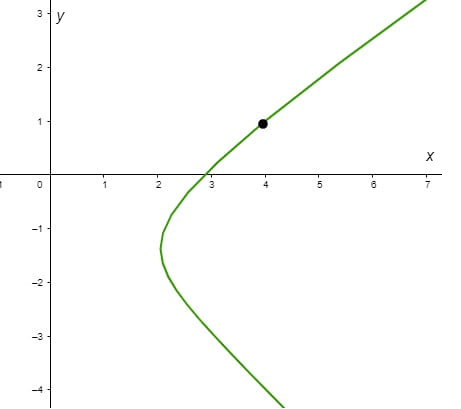
Grafiquemos en el plano $XY$ la trayectoria de esta función.
Como ejemplo, si $t = 0$, entonces $x(0) = 4$ y $y(0) = 1$, tal coordenada $(4, 1)$ corresponde al punto mostrado en el plano $XY$, así la trayectoria se forma por el conjunto de puntos $(x(t), y(t))$ correspondientes a cada valor $t \in \mathbb{R}$.
Las tres gráficas anteriores corresponden a la solución particular en la que $c_{1} = c_{2} = 1$, así cada solución particular producirá tres curvas distintas en tres planos distintos.
Nos centraremos especialmente en el plano $XY$ o también llamado plano fase. Cada una de las curvas que se pueden formar en el plano fase correspondientes a valores específicos de $c_{1}$ y $c_{2}$ se llama trayectoria.
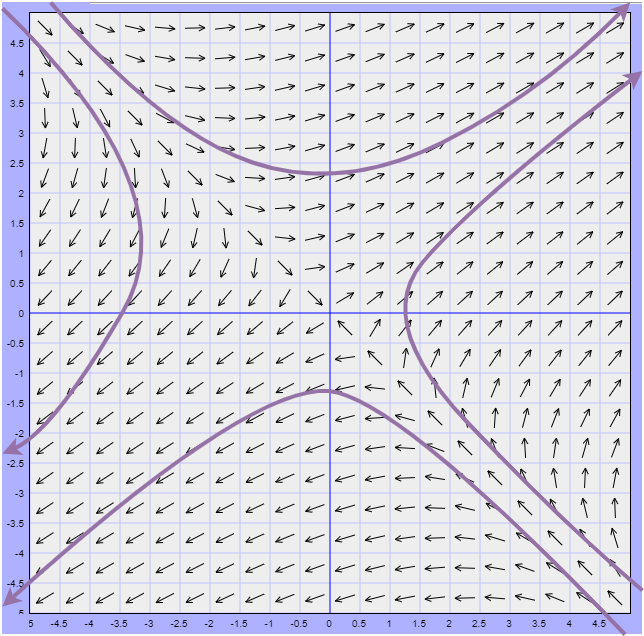
En el siguiente plano fase se muestra un conjunto de trayectorias definidas por (\ref{21}) para distintos valores de $c_{1}$ y $c_{2}$.
Al conjunto de trayectorias representativas en el plano fase se llama diagrama fase.
Consideremos las soluciones independientes (\ref{18}).
$$\mathbf{\mathbf{Y}}_{1} = \begin{pmatrix}
-1 \\ 1
\end{pmatrix} e^{ -t} \hspace{1cm} y \hspace{1cm}
\mathbf{\mathbf{Y}}_{2} = \begin{pmatrix}
3 \\ 2
\end{pmatrix}e^{4t}$$
Y notemos lo siguiente.
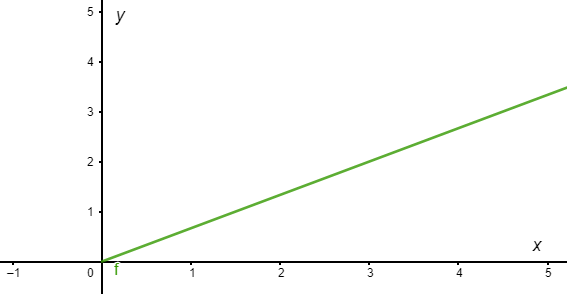
De $\mathbf{Y}_{2}$ se obtienen las funciones
$$x(t) = 3e^{4t} \hspace{1cm} y \hspace{1cm} y(t) = 2e^{4t} \label{23} \tag{23}$$
De manera que la función $y(t)$ se puede escribir en términos de $x$ como
$$y(x) = \dfrac{2}{3}x$$
con $x > 0$ y cuya gráfica en el plano $XY$ corresponde a una recta en el primer cuadrante con pendiente $\dfrac{2}{3}$.
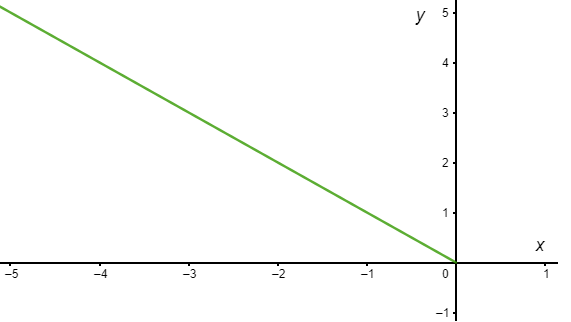
De forma similar, si consideramos la solución $-\mathbf{Y}_{1}$ se obtienen las funciones
$$x(t) = e^{-t} \hspace{1cm} y \hspace{1cm} y(t) = -e^{t} \label{24} \tag{24}$$
De forma que $y$ en términos de $x$ se ve como
$$y(x) = -x$$
Para $x < 0$ en el plano $XY$ tendremos una recta en el segundo cuadrante con pendiente $-1$.
Consideremos ahora la solución $-\mathbf{Y}_{2}$ cuyas funciones son
$$x(t) = -3e^{4t} \hspace{1cm} y \hspace{1cm} y(t) = -2e^{4t} \label{25} \tag{25}$$
En este caso,
$$y(x) = \dfrac{2}{3}x$$
con $x < 0$, la gráfica corresponde a una recta de pendiente $ \dfrac{2}{3}$ en el tercer cuadrante.
Y finalmente de $\mathbf{Y}_{1}$ se obtienen las funciones
$$x(t) = -e^{-t} \hspace{1cm} y \hspace{1cm} y(t) = e^{-t} \label{26} \tag{26}$$
tal que,
$$y(x) = -x$$
con $x > 0$ y cuya gráfica es una recta de pendiente $-1$ en el cuarto cuadrante.
Lo interesante es que cada vector propio se puede visualizar como un vector bidimensional que se encuentra a lo largo de una de estas semirrectas.
Por ejemplo el vector propio
$$\mathbf{K}_{1} = \begin{pmatrix}
-1 \\ 1
\end{pmatrix}$$
corresponde al siguiente vector en el plano $XY$.
Mientras que el vector propio
$$\mathbf{K}_{2} = \begin{pmatrix}
3 \\ 2
\end{pmatrix}$$
corresponde al vector
A continuación se muestran las cuatro semirrectas anteriores y los vectores propios unitarios
$$\hat{\mathbf{K}}_{1} = \dfrac{\mathbf{K}_{1}}{\left\| \mathbf{K}_{1} \right\|} \hspace{1cm} y \hspace{1cm} \hat{\mathbf{K}}_{2} = \dfrac{\mathbf{K}_{2}}{\left\| \mathbf{K}_{2} \right\|}$$
sobre el mismo plano fase de antes.
El vector propio $\hat{\mathbf{K}}_{2}$ se encuentra junto con $y = \dfrac{2}{3}x$ en el primer cuadrante y $\hat{\mathbf{K}}_{1}$ se encuentra junto con $y =-x$ en el segundo cuadrante.
Notamos que en el plano fase las trayectorias tienen flechas que indican dirección. Para saber la dirección de las trayectorias nos apoyaremos en el campo vectorial asociado.
Definamos las funciones $F_{1}$ y $F_{2}$ de acuerdo a (\ref{13}).
$$F_{1}(x, y) = 2x + 3y, \hspace{1cm} y \hspace{1cm} F_{2}(x, y) = 2x + y \label{27} \tag{27}$$
Entonces la función $F(x, y)$ correspondiente es
$$F(x, y) = (2x + 3y, 2x + y) \label{28} \tag{28}$$
El campo vectorial será descrito por esta función. Como vimos al inicio de la entrada, para cada punto $(x, y)$ del plano fase anclaremos un vector cuya punta termina en la coordenada dada por la suma vectorial $(x, y) + F(x, y)$. Por ejemplo si $x = 0$ y $y = 1$, entonces nos situaremos en la coordenada $(0, 1)$ del plano fase, evaluando en la función $F(x, y)$ se obtiene el punto $F(0, 1) = (3, 1)$, entonces la punta del vector que parte de $(0, 1)$ terminará en la coordenada $(0, 1) + (3, 1) = (3, 2)$.
Como ejemplo dibujemos los vectores correspondientes a las siguientes evaluaciones.
$$F(0, 1) = (3, 1), \hspace{1cm} F(0, -2) = (-6, -2), \hspace{1cm} F(-3, 0) = (-6, -6)$$
$$F(0, 3) = (9, 3), \hspace{1cm} F(2, -2) = (-2, 2), \hspace{1cm} F(3, -1) = (3, 5)$$
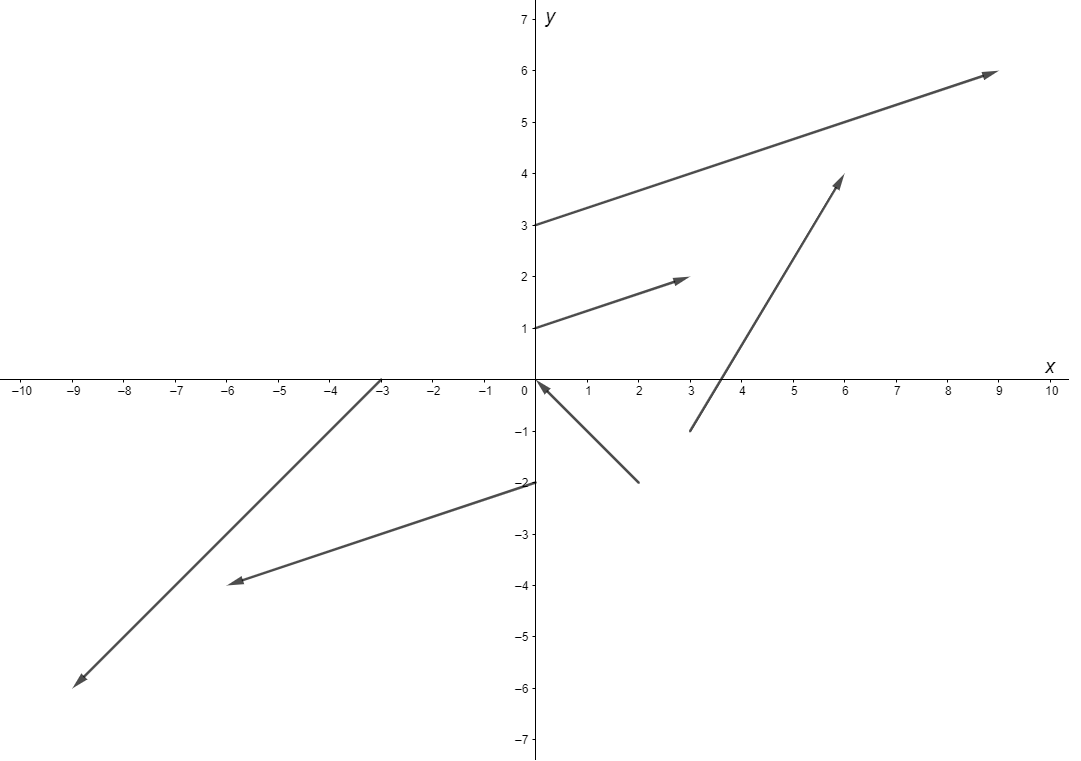
Como se puede notar, si dibujáramos todos los vectores para cada punto $(x, y)$ tendríamos un desastre de vectores, todos de distintos tamaños atravesándose entre sí y no habría forma de observar el patrón que esconde el campo vectorial. Para solucionar este problema existe la convención de escalar todos los vectores a un mismo tamaño, por su puesto esto ya no representa correctamente al campo vectorial, pero sí que es de mucha ayuda visualmente y se convierte en sólo una representación del campo vectorial.
En nuestro ejemplo la función
$$F(x, y) = (2x + 3y, 2x + y)$$
se representa por el siguiente campo vectorial.
Cómo $F(x, y) = (x^{\prime}, y^{\prime})$, entonces los vectores del campo vectorial deben ser tangentes a las trayectorias formadas por la función paramétrica $f(t) = (x(t), y(t))$. Concluimos entonces que las soluciones del sistema lineal serán trayectorias cuyos vectores del campo vectorial son tangentes a dichas trayectorias.
Una característica observable del campo vectorial es que los vectores tienden a alejarse del origen, veremos más adelante que el origen no sólo es una solución constante $x = 0$, $y = 0$ (solución trivial) de todo sistema lineal homogéneo de $2$ ecuaciones lineales, sino que también es un punto importante en el estudio cualitativo de dichos sistemas.
Si pensamos en términos físicos, las puntas de flecha de cada trayectoria en el tiempo $t$ se mueven conforme aumenta el tiempo. Si imaginamos que el tiempo va de $-\infty$ a $\infty$, entonces examinando la solución
$$x(t) = c_{1}e^{ -t} + 3c_{2}e^{4t}, \hspace{1cm} y(t) = -c_{1}e^{ -t} + 2c_{2}e^{4t}, \hspace{1cm} c_{1} \neq 0, \hspace{0.4cm} c_{2} \neq 0$$
muestra que una trayectoria o partícula en movimiento comienza asintótica a una de las semirrectas definidas por $\mathbf{Y}_{1}$ o $ -\mathbf{Y}_{1}$ (ya que $e^{4t}$ es despreciable para $t \rightarrow -\infty$) y termina asintótica a una de las semirrectas definidas por $\mathbf{Y}_{2}$ o $ -\mathbf{Y}_{2}$ (ya que $e^{-t}$ es despreciable para $t \rightarrow \infty$).
El plano fase obtenido representa un diagrama de fase que es característico de todos los sistemas lineales homogéneos de $2 \times 2$ con valores propios reales de signos opuestos.
$\square$
Hemos concluido con el ejemplo. Lo que nos muestra este ejemplo es que es posible hacer un desarrollo geométrico sobre un sistema lineal, sin embargo esto sólo es posible si es un sistema con dos ecuaciones, ya que si aumenta el número de ecuaciones también aumentará el número de dimensiones y ya no seremos capaz de obtener gráficas. Es posible extender el plano fase a tres dimensiones (espacio fase para un sistema lineal con $3$ ecuaciones), pero nos limitaremos sólo a los sistemas de $2$ ecuaciones para hacer más sencilla la tarea. También es importante mencionar que podremos hacer este análisis siempre y cuando los coeficientes sean constantes y las ecuaciones no dependan explícitamente de la variable independiente $t$.
Con este método geométrico será posible estudiar el comportamiento de las soluciones sin la necesidad de resolver el sistema, incluso con este método podremos estudiar sistemas no lineales para los cuales aún no conocemos algún método para resolverlos.
Finalmente veremos que las propiedades del plano fase quedarán determinadas por los valores propios del sistema, de manera que en las siguientes entradas haremos un análisis para cada una de las posibilidades que existen, tales posibilidades son:
Valores propios reales y distintos:
- $\lambda_{1} < \lambda_{2} < 0$.
- $\lambda_{1} > \lambda_{2} > 0$.
- $\lambda_{1} < 0$ y $\lambda_{2} > 0$ (como en nuestro ejemplo).
Valores propios complejos:
- $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha < 0$.
- $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha = 0$.
- $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$ con $\alpha > 0$.
Valores propios repetidos:
- $\lambda_{1} = \lambda_{2} < 0$.
- $\lambda_{1} = \lambda_{2} > 0$.
Valores propios nulos:
- $\lambda_{1} = 0$ y $\lambda_{2} < 0$.
- $\lambda_{1} = 0$ y $\lambda_{2} > 0$.
- $\lambda_{1} = \lambda_{2} = 0$.
En las próximas entradas estudiaremos a detalle cada uno de estos casos.
En este enlace se tiene acceso a una excelente herramienta para visualizar el plano fase de sistemas lineales de dos ecuaciones homogéneas con coeficientes constantes y en este enlace se puede visualizar el campo vectorial asociado, además de algunas trayectorias del sistema dando clic sobre el campo vectorial.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- En la unidad anterior resolviste de tarea moral los siguientes sistemas lineales. En este caso realiza un desarrollo geométrico como lo hicimos en esta entrada e intenta describir el comportamiento de las soluciones en el plano fase. Dibuja a mano algunos vectores del campo vectorial y algunas trayectorias sobre el mismo plano fase, posteriormente verifica tu resultado visualizando el espacio fase y el campo vectorial usando los enlaces proporcionados anteriormente.
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
6 & -3 \\ 2 & 1
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
1 & -3 \\ -2 & 2
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
-3 & 2 \\ -1 & -1
\end{pmatrix}\mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
-1 & 3 \\ -3 & 5
\end{pmatrix}\mathbf{Y}$
¿Qué características distintas identificas entre los planos fase de cada uno de los sistemas anteriores?.
Más adelante…
Esta entrada nos ha servido de introducción al estudio geométrico y cualitativo de los sistemas lineales. En la siguiente entrada formalizaremos lo que vimos en esta entrada para posteriormente hacer un análisis más detallado sobre los distintos tipos de sistemas tanto lineales como no lineales que se puedan presentar.
Entradas relacionadas
- Página principal del curso: Ecuaciones Diferenciales I
- Entrada anterior del curso: Teorema de existencia y unicidad para sistemas de ecuaciones diferenciales de primer orden
- Siguiente entrada del curso: Sistemas autónomos, puntos de equilibrio y su estabilidad
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»