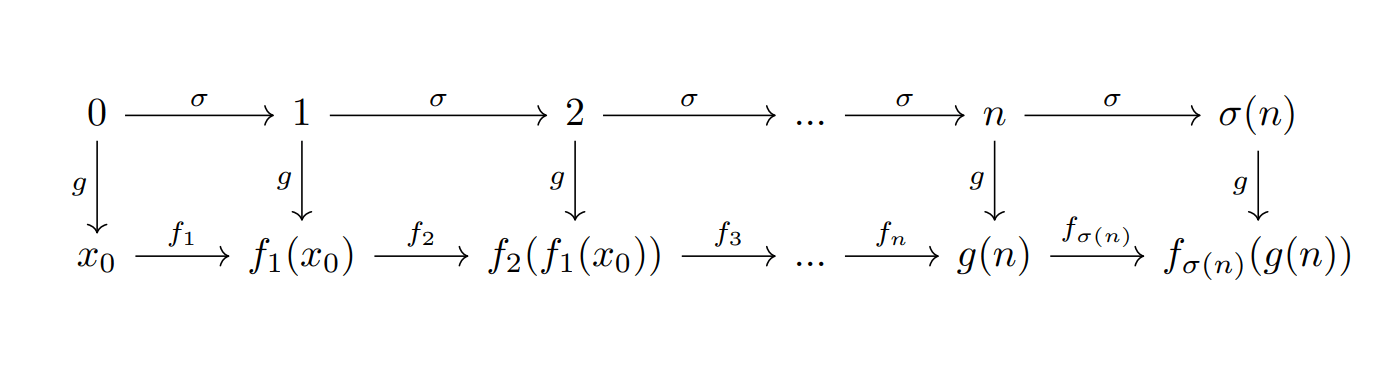Archivo de la etiqueta: inducción

Álgebra Superior II: Definición de la suma y sus propiedades básicas

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

Para continuar con nuestra tarea de construir las operaciones más elementales de los números naturales, en esta entrada definimos la conocida operación suma. Un buen ejercicio antes de empezar con el contenido de la entrada, es pensar ¿Cómo podemos definir la suma de dos números enteros? De nuevo nos encontramos con el problema de intentar definir formalmente algo que ha sido intuitivo para nosotros durante la mayor parte de nuestra vida.

Sin embargo, todo el trabajo que hicimos en las entradas anteriores, especialmente en la demostración del teorema de Recursión, nos servirán para poder dar una definición precisa de qué es la suma. Además, usando el principio de Inducción, podremos demostrar las propiedades que nos han sido tan familiares desde hace mucho tiempo.

La idea intuitiva de la suma

La primera forma en la que aprendimos a sumar, al menos de manera intuitiva y tal vez limitada, fue usando nuestros dedos. Ocuparemos esta idea como hilo conductor, para poder llegar a la definición recursiva de la suma. Con esta forma de pensar, si queríamos sumar $3+4$, poníamos frente a nosotros nuestras manos con los dedos abajo, e instantáneamente mencionábamos la palabra «tres«. Después estirábamos un primer dedo y al mismo tiempo, mencionábamos la palabra «cuatro» (a quien ahora conocemos como el sucesor de $3$), después alzábamos un segundo dedo y decíamos «cinco» (el sucesor de $4$) , y continuábamos de la misma manera hasta que tuviéramos cuatro dedos totalmente extendidos; momento en el cual, decíamos el resultado: «siete«.

Analicemos un poco qué es lo que queremos decir con «continuábamos de la misma manera«. Entre cada número que contábamos, varias cosas pasaban por nuestra mente. Al mencionar un número, lo primero que hacíamos era cerciorarnos que aún tuviéramos extendidos menos dedos de los que queríamos añadir. Si esta condición se satisfacía, teníamos que grabarnos el número que habíamos mencionado justo en ese instante (el olvidar dicho número, tenía como consecuencia empezar el procedimiento desde el inicio), después alzábamos el siguiente dedo, y mencionábamos el sucesor del número memorizado (es por esto que recordar ese número era tan importante). Muy a grandes rasgos esto es lo mismo que lo que haremos de manera formal.

Definición de la suma

Esperamos que en los párrafos anteriores puedas encontrar una analogía entre el algoritmo que usábamos para sumar cotidianamente, y el método recursivo que describiremos a continuación. Antes de precisar la definición de la suma, hay que aclarar que no definiremos «de golpe» qué quiere decir «sumar dos números». Más bien, lo que haremos es, para cada natural, decir qué quiere decir «sumarle otro». Lo haremos de esta manera pues esto es lo que nos permite hacer el teorema de Recursión. Así, para cada número natural $m$ (fijo) obtendremos una función que nos sume a ese número fijo, una cantidad arbitraria.

Definición: Sea $m\in\mathbb{N}$. Definimos la función $s_{m}:\mathbb{N}\longrightarrow\mathbb{N}$, como la única función que satisface las propiedades siguientes:

  1. $s_{m}(0)=m$.
  2. $s_{m}(\sigma(n))=\sigma(s_{m}(n))$.

Denotaremos $s_{m}(n)$ como $m+n$.

Vale la pena hacer un par de comentarios de la definición anterior. Primero mencionamos que esta definición depende totalmente del teorema de Recursión Débil. Si regresas al enunciado del teorema, podemos notar que la función $s_m$ se obtiene tomando $X=\mathbb{N}$, $x_{0}=m$, $f=\sigma$ y $g=s_{m}$.

En segundo lugar, hay que remarcar que a pesar de nuestra intuición, los papeles de $m$ y $n$ en la expresión $m+n$, no son intercambiables. Por definición $m+n=s_{m}(n)$, mientras que $n+m=s_{n}(m)$. A primera vista, estos valores no tienen por qué coincidir. Veremos que en efecto esta y otras propiedades sí son válidas, para que posteriormente podamos utilizarlas de manera directa.

Aprender a sumar cero

De aquí en adelante probaremos varias propiedades de la suma. Debido a la definición recursiva de esta función, la mayor herramienta que ocuparemos es el principio de Inducción.

Antes de lanzarnos a demostrar la primer propiedad, nota que directamente de las definiciones de las funciones $s_{m}$ y de la notación que estamos usando, se tiene que $m+0=s_m(0)=m$. Ahora nos gustaría ver que también $0+m=m$, pero como aún no sabemos que la suma sea conmutativa, tendremos que probarlo por inducción.

Proposición: Para todo $n\in\mathbb{N}$ se tiene que $s_{0}(n)=n$, es decir, $0+n=n$

Demostración. Como se mencionó, procedamos por inducción sobre $n$.

Base inductiva: Por el punto (1) de la definición de $s_0$, tenemos que s_{0}(0)=0.

Hipótesis inductiva: Supongamos que para algún $n\in\mathbb{N}$, se tiene que $s_{0}(n)=n$.

Paso inductivo: Demostremos que $s_{0}(\sigma(n))=\sigma(n)$.

La demostración se sigue de la siguiente cadena de igualdades, las cuales justificamos una a una abajo:

\begin{align*}
s_{0}(\sigma(n))&=\sigma(s_{0}(n)) \\&\overset{\text{H.I.}}{=}\sigma(n).
\end{align*}

La primera igualdad sucede por el punto (2) de la definición de $s_0$. La segunda igualdad sucede por la hipótesis inductiva, lo cual estamos indicando con un «H.I.» sobre el símbolo de igualdad.

Esto termina el paso inductivo y entonces la proposición se vale para todos los naturales.

$\square$

Así, ya sabemos «sumar cero».

Aprender a sumar uno

Veamos ahora que nuestra intuición de «sumar uno» en efecto coincide de manera formal con «ir al sucesor».

Observación: Tenemos la siguiente cadena de igualdades \[n+1=s_{n}(1)=s_{n}(\sigma(0))=\sigma(s_{n}(0))=\sigma(n).\]

La primera es por nuestra elección de notación. La segunda por la definición del símbolo 1, pues simplemente es el sucesor de 0. La tercera es por el punto (2) de la definición de $s_n$. Finalmente, la última es por el punto (1) de la definición de $s_n$.

$\triangle$

Proposición: Para todo $n\in\mathbb{N}$ se tiene que $s_{1}(n)=\sigma(n)$, es decir, que al juntarlo con la observación anterior obtenemos $1+n=\sigma(n)=n+1$.

Demostración. Demostremos que $s_1(n)=\sigma(n)$ por inducción sobre $n$. Tenemos que $s_{1}(0)=1=\sigma(0)$ por el punto (1) de la definición de $s_1$ y por la definición de 1. Esto muestra que la igualdad se cumple en el caso base $n=0$.

Nuestra hipótesis de inducción es suponer que $s_{1}(n)=\sigma(n)$ y a partir de ella debemos demostrar que $s_{1}(\sigma(n))=\sigma(\sigma(n))$. Esto lo logramos mediante la siguiente cadena de igualdades:

\begin{align*}
s_{1}(\sigma(n))&=\sigma(s_{1}(n))\\ &= \sigma(\sigma(n))
\end{align*}

La primera igualdad se debe al punto (2) de la definición de $s_1$. La segunda, a la hipótesis inductiva.

$\square$

La suma es asociativa

Con los resultados probados en las dos secciones anteriores, continuamos ahora probando propiedades más interesantes de la suma. Aunque las aprendimos desde la educación básica, ahora será momento de justificar por qué se deducen de lo que hemos construido. Empezamos por la asociatividad.

Proposición (asociatividad): Si $a, b, n$, son naturales arbitrarios, entonces $(a+b)+n=a+(b+n)$.

Como es usual, aquí los paréntesis significan «hacer esa operación primero». Si quisiéramos usar la notación formal, tendríamos que enunciar la asociatividad como $$s_{a+b}(n)=s_a(s_b(n)),$$ y cuando hagamos la demostración aprovecharemos la definición de estas funciones $s_{a+b}$, $s_a$ y $s_b$.

Demostración. Procedamos por inducción. Tenemos tres variables naturales. ¿Sobre cuál hacemos inducción? Esto es una decisión importante y el hacer una elección incorrecta puede dificultar la prueba o impedir concluirla. Haremos inducción sobre $n$, pero te recomendamos que intentes hacerlo sobre las otras variables para detectar las dificultades que pueden surgir.

Base inductiva: $(a+b)+0=a+b=a+(b+0)$. En el primer paso usamos el punto (1) de la definición de $s_{a+b}$ y en el segundo usamos el punto (1) de la definición de $s_b$.

Hipótesis inductiva: Supongamos que $(a+b)+n=a+(b+n)$. Recuerda que en una prueba inductiva sólo se hace la hipótesis inductiva para un valor fijo de $n$, pero lo que se quiere suponer es que se vale para todo valor de $n$. Así, no estamos suponiendo que cualquier $n$ pueda asociarse con cualesquiera dos números, solo estamos suponiendo que una $n$ fija puede asociarse con los valores fijos de $a$ y de $b$; más aún, el orden de $a$ y $b$ importa, ya que no hemos demostrado aún la conmutatividad.

Paso inductivo: Demostremos que $(a+b)+\sigma(n)=a+(b+\sigma(n))$.

Hagamos esto mediante la siguiente cadena de igualdades:

\begin{align*}
(a+b)+\sigma(n)&=\sigma((a+b)+n)\\
&\overset{\text{H.I}}{=}\sigma(a+(b+n))\\
&=a+\sigma(b+n)\\
&=a+(b+\sigma(n)).
\end{align*}

Aquí las igualdades se siguen, respectivamente, de la definición de $s_{a+b}$, de la hipótesis inductiva, de la definición de $s_a$ y de la definición de $s_b$. Con esto, concluimos la prueba del paso inductivo y con ello la prueba por inducción.

$\square$

En la demostración anterior ya no estamos siendo tan específicos con exactamente qué parte de la definición de las funciones estamos usando. Sin embargo, te sugerimos completar estos detalles pues te ayudarán a entender mucho mejor por qué cada uno de los pasos tiene su justificación.

La suma es conmutativa

Otra de las propiedades de la suma que nos enseñan en educación básica es que «el orden de los factores no afecta el resultado». Esto tiene un nombre en matemáticas formales: conmutatividad. El objetivo de la siguiente proposición es demostrar que en efecto la suma es conmutativa.

Proposición (conmutatividad): Si, $n, m$ son naturales, entonces $n+m=m+n$.

En términos de las funciones que construimos mediante el teorema de recursión esto se ve como $s_n(m)=s_m(n)$.

Demostración. De nuevo, procedamos por inducción sobre $n$, por la misma razón remarcamos que entonces $m$ es un número arbitrario pero fijo.

Base inductiva. Por la primer proposición que probamos, tenemos que $0+m=m=m+0$.

Hipótesis de Inducción: Supongamos que $n$ cumple que $n+m=m+n$.

Paso inductivo: Demostremos que $\sigma(n)+m=m+\sigma(n)$.

Hagamos esto mediante la siguiente cadena de igualdades:

\begin{align*}
m+\sigma(n)&=\sigma(m+n)\\
&\overset{H.I.}{=}\sigma(n+m)\\
&=n+\sigma(m)\\
&=n+(1+m)\\
&=(n+1)+m\\
&=\sigma(n)+m.
\end{align*}

Como siempre, es importante justificar cada igualdad. Pero ahora es tu turno. ¿Cuáles son las justificaciones de cada una de estas igualdades? Nota que algunas serán las definiciones, algunas serán la notación que estamos usando y finalmente otras se deducen de propiedades que ya demostramos (como la asociatividad).

$\square$

La suma se cancela

Imagina por un momento que tenemos una igualdad del estilo $x+8=y+8$ en los números naturales. Nos gustaría poder concluir que $x=y$. Sin embargo, no podemos hacer el «truco tradicional» de «restar 8» en cada lado de la igualdad para cancelar al 8, pues en los naturales no existe la operación de resta. Nos encontraremos con ella más adelante, hasta que trabajemos con los números enteros.

Aunque no podamos restar, de cualquier forma podemos realizar cancelaciones de este estilo. La siguiente proposición formaliza este hecho.

Proposición (cancelación por la derecha): Si, $a, b, n$ son naturales, tales que $a+n=b+n$, entonces $a=b$.

Demostración. Como ya esperábamos, sean $a$ y $b$ arbitrarios, y procedamos por inducción sobre $n$.

Base inductiva. Si $a+0=b+0$, por definición de $s_a$ y $s_b$ obtenemos $a=b$.

Hipótesis inductiva. Supongamos que $n$ es tal que cada vez que tengamos $a+n=b+n$, obtenemos que $a=b$.

Paso inductivo. Demostremos que si $a+\sigma(n)=b+\sigma(n)$, entonces $a=b$.

Entonces supongamos que $a+\sigma(n)=b+\sigma(n)$. Por definición $a+\sigma(n)=\sigma(a+n)$ y $b+\sigma(n)=\sigma(b+n)$. Por nuestra hipótesis tendríamos entonces que $\sigma(a+n)=\sigma(b+n)$. Usando el cuarto axioma de Peano, obtendríamos entonces que $a+n=b+n$. Finalmente, la hipótesis inductiva nos garantiza que entonces $a=b$, como buscábamos.

$\square$

Podemos enunciar el resultado anterior en una forma un poco más «funcional».

Corolario: Las funciones $s_{m}$ con $m\in \mathbb{N}$ son inyectivas.

Demostración: Con todas las herramientas que hemos desarrollado, ya no será necesario ocupar la inducción.

Si $s_{m}(a)=s_{m}(b)$, por la conmutatividad de la suma, tenemos que $s_{m}(a)=s_{a}(m)$ y $s_{m}(b)=s_{b}(m)$. Esto quiere decir que $a+m=b+m$, y por la proposición anterior, $a=b$.

$\square$

Con esto hemos demostrado las propiedades más fundamentales de la suma, a partir de las cuales podremos probar muchas más.

Resumen de propiedades de la suma

Para recapitular, en esta entrada demostramos las siguientes propiedades de la suma y por lo tanto podremos usarlas directamente de aquí en adelante:

  • Para todo $n$ natural, se tiene $0+n=n=n+0$.
  • Para todo $n$ natural, se tiene $1+n=\sigma(n)=n+1$.
  • Para $m$ y $n$ naturales cualesquiera, se tiene $m+n=n+m$.
  • Para $l,m,n$ naturales cualesquiera, se tiene que $l+(m+n)=(l+m)+n$.
  • Para $l,m,n$ naturales cualesquiera, si $m+l=n+l$, entonces $m=n$.

Más adelante…

Ya que conocemos las propiedades de la suma, podemos pasar a definir el producto, y análogamente, a como lo hicimos antes, estudiaremos sus propiedades usando el principio de Inducción.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra que si $a, b\in \mathbb{N}$, y $a+b=0$, entonces $a=b=0$.
  2. Demuestra que si $a+a=b+b$, entonces $a=b$. ¡Ten cuidado! En los números naturales no se vale «dividir», así que más bien tendrás que hacer una prueba inductiva.
  3. Sean $m,n,l$ naturales cualesquiera. Demuestra, usando sólo las propiedades que ya mostramos (ya sin inducción), que todas las siguientes expresiones son iguales:
    \begin{align*}
    m+(n+l)\\
    (l+m)+n\\
    n+(m+l)\\
    (n+l)+m\\
    \end{align*}
  4. ¿Cuáles de las funciones $s_{m}$ tienen inversa? ¿Qué significa esto?
  5. Antes de dominar las tablas de multiplicar de memoria, ¿Cómo multiplicabas? Ocupa esta idea para motivar una definición recursiva del producto de números naturales.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Principio de inducción y teoremas de recursión

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

Inducción y recursión son dos conceptos similares con los que seguramente te has topado en tu formación matemática, e incluso tal vez antes. Muchas veces se llegan a confundir ambos conceptos, ya que ambos tienen una fuerte relación con el 5° axioma de Peano.

Aunque lo detallaremos a lo largo de la entrada, el principio de Inducción es una propiedad de los números naturales, que nos sirve para demostrar que todos los naturales satisfacen una propiedad. Es decir, es una estrategia de demostración. En contraste, la recursión es un resultado que justifica el hecho de poder dar una definición para todos los naturales, basándonos en la definición de su antecesor. En otras palabras, es una estrategia de definición.

Al final de la entrada demostraremos el teorema de recursión débil, en cuya prueba, podremos apreciar cómo es que depende directamente del Principio de inducción.

Pruebas por inducción

Recordemos el 5° axioma de Peano, el cual probamos en la entrada pasada que se satisface en nuestro modelo:

Si $S\subset \mathbb{N}$ satisface que

  • $0\in S$ y
  • si $n\in S$, implica que $\sigma(s)\in S$,

entonces $S=\mathbb{N}$.

Como hemos mencionado en entradas anteriores, esta proposición es muy similar al principio de Inducción que probablemente hayas ocupado desde el curso de Álgebra Superior I. Más aún, en la entrada pasada, seguimos la misma estrategia que en otros cursos, a la hora de ocupar el 5° axioma. Efectivamente, la equivalencia entre ambos resultados es casi inmediata, y como ejemplo ilustrativo, probaremos el Principio de Inducción a partir del 5° axioma de Peano.

Proposición (Principio de Inducción): Sea $P(n)$ una propiedad, es decir, una proposición matemática que depende de un entero $n$. Si se tiene que:

  1. $P(0)$ es verdadera y
  2. cada vez que $P(n)$ es cierto, también lo es $P(n+1)$,

entonces P(n) es cierta para todos los números naturales.

Demostración. Sea $P(n)$ una propiedad que satisface 1. y 2. y consideremos el conjunto $S:=\{n\in\mathbb{N}: P(n)\text{es verdadera}\}$.

Como $P(0)$ es verdadera, entonces $0\in S$.

Tomemos $n\in S$, entonces $P(n)$ es verdadera, y por 2., tenemos que $P(n+1)$ es verdadera; es decir, $n+1\in S$. Por el 5° Axioma de Peano, se tiene que $S=\mathbb{N}$, por lo que por la definición de $S$, se tiene que $P(n)$ es cierta para cada $n\in \mathbb{N}$

$\square$

Definiciones por recursión

Una de nuestras primeras ideas para poder construir a $\mathbb{N}$, fue intentar construir a mano cada elemento. Para esto, dimos una definición de lo que significaba el $0$ y el sucesor de un número. Después empezamos a iterar una y otra vez la función sucesor para obtener el sucesor del último número encontrado. Discutimos por qué es que esta idea no sería el mejor camino (sólo nos permite llegar hasta una cantidad finita de naturales), por lo tuvimos que introducir el Axioma del Infinito para resolver el problema. Veamos la analogía entre esta idea y el siguiente ejemplo intuitivo.

Ejemplo: Definamos la función factorial de un número natural, como:

  • $0!=1$
  • $(n+1)!=(n!)(n+1)$

Entonces, $3!:=(2!)(3)=(1!)(2)(3)=(0!)(1)(2)(3)=(1)(1)(2)(3)=6$.

Recordemos que al definir a los naturales, necesitábamos conocer un número para poder definir su sucesor. Aquí sucede lo mismo: en la definición de factorial necesitamos conocer quién es el factorial de un número para poder definir el factorial de su sucesor. A este tipo de definiciones se les conoce como definiciones recursivas, ya que para definir algo para un número, necesitamos tener conocimiento del valor de la función en los números anteriores.

Queda una pregunta muy importante. Si a los naturales no los pudimos definir de manera recursiva, ¿por qué podemos afirmar que la función factorial sí existe? A continuación enunciaremos algunos teoremas que nos garantizarán que sí podemos hacer este tipo de definiciones recursivas en nuestro modelo. Daremos una versión fuerte y una versión débil. Demostraremos la versión débil, pues basta para mucho de lo que queremos definir en los naturales (sumas, productos, potencias).

Las siguientes secciones son un poquito técnicas. Si las puedes seguir por completo, es fantástico. Pero incluso si no es así, basta con que en el fondo te quedes con la idea importante detrás: sí se vale definir de manera recursiva. Más adelante podrás regresar a este tema y entenderlo por completo.

Los teoremas de la recursión

Antes de la demostración principal de esta entrada, enunciaremos los teoremas que nos importan y hablaremos de manera intuitiva de lo que dicen. Hay dos versiones que veremos: una fuerte y una débil. Aunque parece que dicen cosas diferentes, en realidad son equivalentes. Será muy claro que la versión fuerte «implica» a la débil. Pero luego, en los problemas de tarea moral, se esbozará cómo ver que la versión débil se puede utilizar para demostrar la fuerte.

Teorema (Recursión Fuerte): Sea $X$ un conjunto y $x_{0}\in X$. Supongamos que tenemos varias funciones (una por cada natural $i$)

$$\{f_i:X\to X\}_{i\in\mathbb{N}\setminus \{0\}}.$$

Entonces existe una única función $g:\mathbb{N}\to X$ tal que:

  • $g(0)=x_{0}$
  • $g(\sigma(n))=f_{\sigma(n)}(g(n))$.

¿Qué es lo que quiere decir este teorema? Para responder esta pregunta veamos el siguiente diagrama:

Nuestro diagrama empieza en $0$, el cual queremos que sea mandado a algún $x_{0}\in X$, para la definición de los demás números, ocupamos la segunda característica que esperamos que $g$ satisfaga. Por ejemplo $g(1)=g(\sigma(0))=f_{1}(g(0))=f_{1}(x_{0})$. Este análisis coincide con lo que nos presenta el primer cuadro de flechas del diagrama anterior, que nos presenta los dos caminos que debe satisfacer $g$, para que sea la función que queremos. Como da lo mismo si «primero aplicamos $\sigma$ y luego $g$», a que si «primero aplicamos $g$ y luego $f_1$», decimos que el primer cuadrado del diagrama conmuta.

Análogamente, ya que conocemos la definición de $g(1)$ podemos fijarnos en el segundo cuadro, para poder definir $g(2)$ (de nuevo, conmuta) y seguir «recursivamente» para cualquier número natural.

Ejemplo: ¿Qué conjunto, y qué funciones necesitamos para definir el factorial?

Consideremos $X=\mathbb{N}$, definiremos intuitivamente (ya que aún no lo hemos definido formalmente), $f_{i}:\mathbb{N}\longrightarrow \mathbb{N}$, como $f_{i}(n)=i\cdot n$, es decir, el producto por $i$.

El teorema de Recursión Fuerte, nos dice que existe una única función $g$ tal que

  • $g(0)=1$
  • $g(\sigma(n))=f_{\sigma(n)}(g(n))=\sigma(n)\cdot g(n)$

Denotemos $n!:=g(n)$. Entonces tenemos que $\sigma(n)!=n!\cdot \sigma(n)$, justo como queremos.

$\triangle$

El teorema de Recursión Débil y su demostración

El teorema de Recursión Débil tiene un enunciado parecido al teorema de recursión fuerte y puede ser visto como una consecuencia directa del teorema anterior pues se obtiene de la versión fuerte tomando $f_{1}=f_{2}=\ldots=f_{n}=\ldots$

Teorema (Recursión Débil): Sea $X$ un conjunto y $x_{0}\in X$. Supongamos que tenemos una función $f:X\to X$. Entonces existe una única función $g:\mathbb{N}\to X$ tal que:

  • $g(0)=x_{0}$
  • $g(\sigma(n))=f(g(n))$.

Para concluir con esta entrada, probaremos el teorema de Recursión Débil. Antes de hacer esto introducimos un concepto auxiliar y una propiedad de los naturales.

Recordemos que como conjunto, $m=\{0,1,…,m-1\}$, lo que sugiere la siguiente definición.

Definición: Si $n,m\in \mathbb{N}$, decimos que $n<m$ si $n\in m$.

Puede probarse que esta relación en $\mathbb{N}$ es un orden total, y que sastisface la siguiente propiedad.

Teorema (Principio el Buen Orden): Sea $S\subset\mathbb{N}$ un conjunto no vacío, es decir $S\neq \emptyset$. Entonces $S$ tiene un elemento mínimo. Es decir, existe $n\in S$ tal que $n<m$ para todo $m\in S\setminus\{n\}$.

La prueba del Principio del Buen Orden y más propiedades de $<$ serán estudiadas con mayor detalle en entradas posteriores. Con esto en mente demostramos el teorema de Recursión Débil.

Demostración. Recordemos que por definición, toda función con dominio $A$ y codominio $B$, es un subconjunto de $A\times B$, por lo que una buena idea es analizar el conjunto $\wp(\mathbb{N}\times X)$, definamos

\[\Re:=\{R\in\wp(\mathbb{N}\times X)\mid (0,x_{0})\in R \text{ y si }(n,x)\in R\text{, entonces }(\sigma(n),f(x))\in R\}\]

Esta definición se ve terriblemente complicada. Pero la intuición es clara: $\Re$ tiene a todas las posibles colecciones de parejas de $\mathbb{N}\times X$ que cumplen lo que queremos. El problema es que muchas de ellas no son funciones y tenemos que «arreglar esto».

Probablemente, notarás alguna similitud entre el conjunto $\Re$ y el conjunto de los subconjuntos inductivos (que se menciona en La construcción de los naturales). Siguiendo esta analogía, definiremos $g:=\bigcap \Re$ (podemos hacer esta intersección ya que $\Re$ no es vacío pues $\mathbb{N}\times X$ está en $\Re$).

  • Demostremos que $g\in \Re$:

Por las propiedades de la intersección, tenemos que $g\subset\mathbb{N}\times X$, por lo que $g\in \wp(\mathbb{N}\times X)$. Veamos que $(0,x_{0})\in g$. Sea $R\in\Re$ arbitrario, entonces $(0,x_{0})\in R$, por lo que $(0,x_{0})\in\bigcap \Re=g$. Por último, si $(n,x)\in g$, demostremos que $(\sigma(n),f(x))\in g$, para esto, sea $R\in \Re$ arbitrario, como $(n,x)\in g$, entonces $(n,x)\in R$, por lo que $(\sigma(n),f(x))\in R$. Es decir, $(\sigma(n), f(x))\in\bigcap \Re=g$. Por todo lo anterior, $g\in\Re$.

  • Veamos ahora que $Dom(g)=\mathbb{N}$:

Usemos el quinto axioma de Peano, como $(0,x_{0})\in g$, entonces $0\in Dom(g)$. Supongamos ahora que $n\in Dom(g)$ y demostremos que $\sigma(n)\in Dom(g)$, por la hipótesis de inducción, existe $x\in X$ tal que $(n,x)\in g$, y como $g\in\Re$, tenemos que $(\sigma(n),f(x))\in g$, pero esto quiere decir que $\sigma(n)\in Dom(g)$. Entonces $Dom(g)$ es inductivo, entonces $Dom(g)=\mathbb{N}$.

  • Demostremos ahora que $g$ sí es función. Para esto, tenemos ver que «cada natural se va a un sólo elemento», en símbolos, si $(n,x),(n,y)\in g$ entonces $n=m$.

Aquí es donde ocuparemos el Principio del Buen Orden. Consideremos $S:=\{n\in\mathbb{N}\mid (n,x),(n,y)\in g \text{ y } x\neq y \}$. Procedamos por contradicción, supongamos que $S\neq\emptyset$, entonces, $S$ tiene un elemento mínimo, denotémoslo por $n$.

Si $n=0$, entonces existe $x\in X$ tal que $(0,x)\in X$ y $x\neq x_{0}$. Entonces consideremos $g’=g\setminus\{(0,x)\}$. Notemos que $g’\in\Re$, ya que $(0,x_{0})\in g’$, ya que $(0,x_{0})\neq (0,x)$. Además si $(k,a)\in g’$, entonces $(k,a)\in g$, por lo que $(\sigma(k),f(a))\in g$, y como $0$ nunca es el sucesor de otro número, tenemos que $(\sigma(k),f(a))\neq(0,x)$, por lo tanto $(\sigma(k),f(a))\in g’$, es decir, $g’\in \Re$, lo que implica que $g=\bigcap \Re\subset g’=g\setminus\{(0,x)\}$ lo cual es absurdo, por lo que $n\neq 0$.

Como $n\neq 0$, debemos tener que existe $m$ tal que $\sigma(m)=n$ ¿Por qué?. Y como $n$ es el mínimo en $S$, tenemos que $m\not\in S$, es decir, existe un único $x\in X$ tal que $(m,x)\in g$, esto implica que $(\sigma(m),f(x))=(n,f(x))\in g$, y como $n\in S$, debe existir $y\in X$, $y\neq f(x)$ tal que $(n,y)\in g$. Análogamente a como lo hicimos antes, consideremos $g’=g\setminus (n,y)$ y veamos que $g’\in \Re$. Como $(n,y)\neq(0,x_{0})$, tenemos que $(0,x_{0})\in g’$. Más aún, si $(k,a)\in g’$, demostremos que $(\sigma(k),f(a))\in g’$, para esto supongamos que no.

Como $(k,a)\in g’$, tenemos que $(k,a)\in g$, por lo que $(\sigma(k),f(a))\in g$, esto implica que $(\sigma(k),f(a))=(n,y)$ ya que este es el único elemento de $g$ que no está en $g’$. Como $\sigma(k)=n=\sigma(m)$, concluimos, por la inyectividad de $\sigma$, que $k=m$. Esto quiere decir que $(k,a)=(m,a)\in g$, pero recordando que $x$ es el único elemento relacionado con $m$, concluimos que $x=a$, en síntesis, $(k,a)=(m,x)$, por lo que $(\sigma(k),f(a))=(\sigma(m),f(x))=(n,f(x))\neq(n,y)$. Esto implica que $(\sigma(k), f(a))\in g’$, contradiciendo nuestra suposición de que no lo estaba.

Entonces hemos probado que $(0,x_{0})\in g’$ y que cada vez que $(k,a)\in g’$, también lo está $(\sigma(k), f(a))$. Esto quiere decir que $g’\in\Re$, y como lo hicimos anteriormente, tendremos que $g=\bigcap \Re\subset g’=g\setminus\{(n,y)\}$, lo cual es una contradicción. Esto quiere decir, que suponer que $S$ tiene un elemento mínimo, es absurdo, por lo que $S=\emptyset$. Lo que traducido quiere decir que para todo $n\in\mathbb{N}$, existe un único $x\in X$ tal que $(n,x)\in g$. Es decir, que $g$ sí es una función.

  • Demostremos que $g$ satisface las dos propiedades del Teorema.

Ya vimos que $g\in \Re$, por lo que $g(0)=x_{0}$. Sea ahora $n\in \mathbb{N}$ y $x=g(n)$, de nuevo, como $g\in\Re$, tenemos que $g(\sigma(n))=f(x)=f(g(n))$.

  • Por último, demostremos la unicidad de $g$.

Si $h:\mathbb{N}\longrightarrow X$ es otra función que satisface las características del Teorema, consideremos $A=\{n\in\mathbb{N}\mid h(n)=g(n)\}$, como $h(0)=x_{0}=g(0)$. Tenemos que $0\in A$. Supongamos que $n\in A$. Tendríamos entonces que $h(\sigma(n))=f(h(n))=f(g(n))=g(\sigma(n))$, es decir que $\sigma(n)\in A$, por lo que $A$ es inductivo, y por consiguiente, $A=\mathbb{N}$. En resumen, $h$ y $g$, coinciden en dominio, codominio y regla de correspondencia, entonces $h=g$, como debíamos probar.

$\square$

La demostración del teorema de Recursión Fuerte requiere de algunos detalles adicionales, pero puede deducirse del teorema de Recursión Débil. Dejamos esto como uno de los problemas de la tarea moral.

Más adelante…

El teorema de Recursión será la mayor herramienta que tendremos para poder darle una forma más familiar a los números naturales, ya que las operaciones de suma y multiplicación, que veremos en la siguiente entrada, tendrán una definición recursiva.

Y así como el teorema de la Recursión nos permitirá definir, usaremos continuamente el principio de Inducción para poder demostrar las numerosas propiedades que estas operaciones tienen.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra el 5° Axioma de Peano a partir del Principio de Inducción.
  2. Demuestra que si $n\neq 0$ entonces existe $m$ tal que $\sigma(m)=n$.
  3. ¿Qué función $g$, satisface que $g(0)=1$ y $g(\sigma(n))=2\cdot g(n)$? ¿Qué función $f$ estamos ocupando?
  4. ¿Qué conjunto y que función nos permitiría definir la sucesión de Fibonacci $a_{n+2}=a_{n+1}+a_{n}$ usando el Teorema de Recursión?
  5. Demuestra el Teorema de Recursión Fuerte, usando el Débil. Sugerencia: Considera, $F(n,x):\mathbb{N}\times X\longrightarrow \mathbb{N}\times X$, como $F(n,x)=(\sigma(n),f_{\sigma(n)}(x))$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: La construcción de los naturales

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En la entrada pasada presentamos los axiomas de Peano como una formalización de por qué los naturales se comportan como nuestra intuición nos indica. Sin embargo, también vimos que, por si mismos, los axiomas de Peano no nos dicen cómo hacer una construcción de los naturales a partir de conceptos previos. Para intentar lograr esto, introdujimos la definición del sucesor de un conjunto arbitrario y empezamos a iterarla en el conjunto vacío para generar una lista de conjuntos, que relacionamos con los números naturales que conocemos.

Por último, notamos que ocupar esta idea, al menos de forma directa, tiene el problema de dar «pasitos muy chicos», que no nos permitirían acabar nunca de definir a todos los números naturales y, en consecuencia, que no nos dejaría definir en sí el conjunto de los naturales.  Es por eso que en esta entrada acabaremos, de una vez por todas, con el problema de definir con precisión el conjunto de números naturales. Veremos que, en efecto, esta construcción que haremos se apega no sólo a nuestra intuición, sino también a los axiomas de Peano.

Conjuntos inductivos

Antes de empezar con la tarea de definir a los números naturales, recordamos la definición del sucesor de un conjunto.

Definición. Si $A$ es un conjunto, definimos el sucesor de $A$, como $\sigma(A):=A\cup \{A\}$.

El conjunto que queremos definir es el conjunto $\mathbb{N}$ de números naturales. Como mencionamos en las entrada pasada, buscamos de manera formal lograr que \[\mathbb{N}=\{\emptyset,\sigma(\emptyset),\sigma(\sigma(\emptyset)),…\},\] por lo que $\mathbb{N}$ satisfaría dos propiedades que englobamos en la siguiente definición.

Definición. Diremos que un conjunto $S$ es inductivo si cumple que:

  1. $\emptyset\in S$ y
  2. si $X\in S$, entonces $\sigma(X)\in S$.

Notemos que estas dos propiedades son muy similares a los dos primeros axiomas de Peano.

Hay que remarcar que aunque no sabemos que exista un conjunto tal que sus elementos son $\emptyset,\sigma(\emptyset),\sigma(\sigma(\emptyset)),…$, en caso de que sí existiera, sería un hecho que tal conjunto sería inductivo.

Otro posible ejemplo de un conjunto inductivo podría verse como \[\{…\sigma(\sigma(\{\{\emptyset\}\})), \sigma(\{\{\emptyset\}\}), \{\{\emptyset\}\},\emptyset,\sigma(\emptyset),\sigma(\sigma(\emptyset)),…\}.\]

Intuitivamente podemos notar que si $S$ es un conjunto inductivo, entonces, $\mathbb{N}\subset S$, por lo que uno podría aventurarse y definir a los naturales como $$\{x:  x \text{ está en todo conjunto inductivo}\}.$$

Sin embargo, los axiomas que de teoría de conjuntos que tenemos hasta ahora no nos permiten saber si se puede construir un conjunto así.

¿Qué es lo que sí nos permiten hacer los axiomas de teoría de conjuntos? Si tenemos una colección de conjuntos, podemos hacer la intersección de todos ellos. Esto motiva la siguiente proposición acerca de la intersección de conjuntos inductivos.

Proposición. Si $B\neq\emptyset$ es un conjunto tal que todos sus elementos son conjuntos inductivos, entonces $\bigcap {B}$ es también un conjunto inductivo.

Demostración. Como $B\neq\emptyset$, sabemos que la intersección sí es un conjunto. Veamos que este conjunto es inductivo. Antes de hacer esto recordemos que, por definición, los elementos de $\bigcap{B}$ son precisamente, todos los $x$ tales que $x\in Y$ para todo $Y\in B$.

Para ver que $\bigcap B$ es inductivo, necesitamos verificar que cumpla las dos características de la definición:

  1. Veamos primero que $\emptyset\in\bigcap B$.
    Sea $Y\in B$ arbitrario. Como los elementos de $B$ son inductivos, $\emptyset\in Y$, y como $Y$ es arbitrario, podemos concluir que $\emptyset$ está en todos los elementos de $B$. Esta es justo la definición de que $\emptyset\in \bigcap B$.
  2. Veamos ahora que $x\in \bigcap B \Rightarrow \sigma(x)\in \bigcap B$.
    Sea $x\in \bigcap B$ y sea $Y\in B$. Como $x\in\bigcap B$, entonces $x\in Y$ y como $Y$ es inductivo, $\sigma(x)\in Y$. De nuevo, como $Y$ fue arbitrario, se sigue que $\sigma(x)$ está en todos los elementos de B, por lo que $\sigma(x)\in\bigcap B$.

Con esto demostramos que $\bigcap B$ es inductivo.

$\square$

En otras palabras, «la intersección arbitraria de conjuntos inductivos es un conjunto inductivo».

El axioma del infinito y la construcción de los naturales

Por todo lo escrito anteriormente, y meditando el hecho de que si partimos de los primeros axiomas de la teoría de conjuntos, sólo podemos crear conjuntos con una cantidad finita de elementos, parece ser que la existencia de un conjunto como los naturales no puede ser deducida con las herramientas que tenemos. Esto en efecto es así. Por ello, debemos introducir un nuevo axioma de la teoría de conjuntos.

Axioma (del infinito). Existe un conjunto inductivo.

El axioma del infinito no nos garantiza inmediatamente la existencia de $\mathbb{N}$, ya que como se vio en un ejemplo más arriba, $\mathbb{N}$ no es el único conjunto inductivo. Sin embargo, esta es la última pieza que necesitamos para poder dar la construcción de los naturales. Hacemos esto a continuación.

Sea $A$ algún conjunto inductivo (que nos garantiza el axioma del infinito), y consideremos $B=\{X\subset A \mid X \text{ es inductivo}\}$ (¿por qué $B$ es un conjunto?). Notemos que $A\in B$ por lo que $B$ es no vacío, por lo tanto, podemos pensar en su intersección, $\bigcap B$. Como los elementos de $B$ son conjuntos inductivos, por la proposición anterior concluimos que $\bigcap B$ es inductivo. A esta intersección la denotaremos como $\mathbb{N}_{A}$. ¡Ya apareció por primera vez el símbolo de números naturales! Pero tiene algo adicional: usamos un subíndice $A$ ya que, a primera vista, su construcción depende del conjunto inductivo $A$ con el que empezamos. Sin embargo, justamente, el paso siguiente será ver que $\mathbb{N}_{A}$ no depende de $A$.

Para ello, primero hacemos la observación de que si $Y\subset A$ es inductivo, entonces $\mathbb{N}_{A}\subset Y$, la cual te dejamos corroborar usando las propiedades de la intersección. Dicho esto, probamos lo siguiente.

Proposición. Si $C$ es otro conjunto inductivo, entonces $\mathbb{N}_{A}= \mathbb{N}_{C} $.

Demostración. Consideremos $\mathbb{N}_{A} \cap \mathbb{N}_{C} $, el cual sabemos que es un conjunto inductivo. Como $\mathbb{N}_{A} \cap \mathbb{N}_{C} \subset A$, por la observación anterior, concluimos que $\mathbb{N}_{A} \subset \mathbb{N}_{A} \cap \mathbb{N}_{C} $. Como la intersección está contenida en cada intersecando, $\mathbb{N}_{A} \subset \mathbb{N}_{A} \cap \mathbb{N}_{C}\subset\mathbb{N}_{A} $, por lo que $\mathbb{N}_{A} = \mathbb{N}_{A} \cap \mathbb{N}_{C} $. Haciendo las mismas observaciones para $\mathbb{N}_{C}$, concluimos que $\mathbb{N}_{A} = \mathbb{N}_{A} \cap \mathbb{N}_{C}= \mathbb{N}_{C} $, con lo que concluimos la prueba.

$\square$

Como sabemos ahora que el conjunto $\mathbb{N}_{A}$ no depende del conjunto $A$ inductivo con el que empecemos, finalmente podemos definir al conjunto de números naturales.

Definición. Si $A$ es algún conjunto inductivo, definimos al conjunto de los números naturales $\mathbb{N}$ como $\mathbb{N}:=\mathbb{N}_{A}$. Definimos al cero como $0:=\emptyset$ y la función sucesor para los naturales como $\sigma:\mathbb{N}\to \mathbb{N}$ tal que $\sigma(n)=n\cup \{n\}$.

Nuestra construcción de los naturales cumple los axiomas de Peano

Para concluir esta entrada veremos que la construcción de los naturales que dimos en efecto da un modelo para los axiomas de Peano. En realidad, la construcción de la función sucesor, la noción de conjunto inductivo y la forma en la que creamos $\mathbb{N}$ fueron todas ellas siempre motivadas por estas ideas, por lo que no deberá ser difícil probar que en verdad todo funciona como queremos.

Teorema. El conjunto $\mathbb{N}$ junto con el $0$ y la función $\sigma$ que definimos satisfacen los cinco axiomas de Peano.

Demostración. Veamos que se verifican los cinco axiomas de Peano.

Axioma 1. $0\in\mathbb{N}$.

Como $\mathbb{N}$ es inductivo, $0=\emptyset\in\mathbb{N}$.

Axioma 2. Si $n\in \mathbb{N}$, entonces $\sigma(n)\in\mathbb{N}$.

Si $n\in\mathbb{N}$, como $\mathbb{N}$ es inductivo, se sigue que $\sigma(n)\in\mathbb{N}$.

Axioma 3. Para toda $n\in\mathbb{N}$ se tiene que $\sigma(n)\neq 0$.

Como $\sigma(n)=n\cup\{n\}$, tenemos que $n\in\sigma(n)$ por lo que $\sigma(n)\neq\emptyset=0$.

Axioma 4. Si $\sigma(n)=\sigma(m)$, entonces $n=m$.

Como $\sigma(n)=\sigma(m)$ y $n\in\sigma(n)$, entonces $n\in\sigma(m)= m\cup\{m\}$. Como $n$ está en una unión, hay dos opciones: $n\in\{m\}$ o $n\in m$. Si $n\in \{m\}$, entonces $n=m$ y concluimos.

En otro caso, $n\in m$. Veamos que podemos decir de $m$. Procediendo análogamente, podemos notar que $m=n$ o $m\in n$. En el primer caso, llegamos a lo que queremos. El segundo caso es imposible, pues tendríamos $n\in m\in n$ lo cual contradice el axioma de regularidad de teoría de conjuntos.

Axioma 5. Si $S\subset\mathbb{N}$ tal que $0\in S$ y $n\in S \Rightarrow \sigma(n)\in S$, entonces $S=\mathbb{N}$.

Notemos que las hipótesis de $S$ implican que éste es un conjunto inductivo. Por ello, $\mathbb{N}=\mathbb{N}_{S}\subset S\subset \mathbb{N}$. Esta cadena de contenciones implica la igualdad $\mathbb{N}=S$.

$\square$

Notemos que todos los axiomas salieron de forma casi inmediata de la definición de $\mathbb{N}$ o de la definición de $\sigma$, justo como esperábamos.

Más adelante…

Ya dimos la construcción de los naturales. También vimos que en verdad funcionan como esperábamos. nuestro siguiente objetivo será definir una suma, un producto y un orden en $\mathbb{N}$. Así como lo hicimos con los axiomas de Peano, veremos que nuestras definiciones coincidirán con las propiedades que conocemos.

Para hacer esto seguiremos pensando simultáneamente tanto en la definición conjuntista que hemos dado de los naturales, como en los axiomas de Peano. Especialemente usaremos el quinto axioma de manera repetida. Veremos cómo este axioma es básicamente el principio de inducción que conocimos en Álgebra Superior I. También veremos cómo nos ayuda a demostrar el teorema de recursión, el cual a su vez la herramienta que necesitaremos para definir con toda formalidad la suma y producto en los naturales.

Tarea moral

  1. Completa los detalles faltantes de la construcción de los naturales. En particular, sobre por qué el conjunto $B$, de los conjuntos inductivos de $A$, sí existe. Necesitarás usar un axioma muy específico de la teoría de conjuntos.
  2. Demuestra que si $x\subset y\subset\sigma(x) $, entonces $y=x$ o $y=\sigma(x)$.
  3. Si aún no estás tan acostumbrado a las intersecciones arbitrarias, considera un conjunto inductivo $A$ y la siguiente definición: $$\mathbb{N}’:=\{x\in A:  x \text{ está en todo conjunto inductivo}\}.$$ ¿Cómo se relaciona el axioma del infinito, con el hecho de que esto sí sea un conjunto?
  4. Esboza una demostración de que $\mathbb{N}’=\mathbb{N}$.
  5. Usa el quinto axioma de Peano para demostrar que para cualquier natural $n$ se cumple que $$\sigma(n)=\{0, 1, 2, …, n\}.$$
    Sugerencia. Considera el conjunto $S\subseteq \mathbb{N}$ de enteros $n$ para los cuales la afirmación anterior es cierta. Demuestra que $S$ es inductivo y usa el quinto axioma para concluir que $S=\mathbb{N}$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Introducción al curso y a los números naturales

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

El curso de Álgebra Superior I tuvo como principal objetivo darte las herramientas necesarias para poder entender, a grandes rasgos, la teoría que sustenta las primeras asignaturas con las que te encuentras a nivel universitario en tu trayectoria matemática. Por esta razón, en el temario se incluyeron los temas de lógica, demostraciones, teoría de conjuntos, números naturales, inducción matemática, conteo y espacios vectoriales.

Sin embargo, quedaron abiertas algunas preguntas. Por ejemplo: ¿cómo sabemos que los conjuntos con los que trabajamos existen?, ¿qué es en el fondo el conjunto de números reales que usamos en los espacios vectoriales? o ¿por qué funciona el principio de inducción?

En este sentido, el curso de Álgebra Superior II es la continuación de Álgebra Superior I. El objetivo de este curso será responder estas preguntas que en el curso anterior quedaron sin responder. Con esto en mente, usaremos las herramientas de la teoría de conjuntos que desarrollamos con anterioridad para estudiar qué son los números naturales, los enteros y hasta los complejos. Haremos una escala en cada tema para poder entender a profundidad las propiedades con las que hemos estado familiarizados desde educación básicas y para conocer otras propiedades que te servirán a lo largo de tu formación matemática.

En la parte final del curso, introduciremos otra estructura con la que seguramente ya estarás familiarizado gracias al curso de Cálculo Diferencial e Integral I: el anillo de polinomios con coeficientes reales (o complejos). Como en el caso de los temas anteriores, nos detendremos a estudiar las propiedades que caracterizan a este conjunto y las similitudes que podemos encontrar con algunos de los sistemas numéricos, como los números enteros.

La intuición detrás de formalizar a los números naturales

Desde la educación básica se aprende a contar. Con el pasar del tiempo, la idea de los números naturales y las características que se necesitan para contar “de uno en uno” seguramente se han hecho muy familiares en tu mente. A grandes rasgos, cuando contamos tenemos mente a los números $$0,1,2,3,4,5,6,7,\ldots.$$ De hecho, las propiedades de estos números probablemente son tan familiares que ya no reparas en ello a la hora de contar. Al cero le sigue el uno. Al uno le sigue el dos. Y así sucesivamente. Esto resulta práctico a la hora de contar, pero algo impráctico a la hora de establecer los fundamentos matemáticos de los números naturales. Por esta razón, tomémonos un momento para pensar en las propiedades que satisface este sistema numérico.

La primera característica en la que podemos pensar es que los números naturales cuentan con un elemento especial de entre todos los demás números, el primero de todos ellos. Dependiendo del contexto, el $0$ (y no el $1$) es considerado como el primer número natural y coincide con la intuición de que podemos «tener cero cosas», es decir, ninguna. Es importante que sepas que en cierto contextos (por ejemplo, otros cursos o áreas de las matemáticas) podría no serlo. La recomendación es que siempre uses la convención del área o comunidad con la que estés trabajando. En este curso el número $0$ siempre será un número natural.

Otra característica con la que seguramente estamos muy familiarizados es que si bien los números naturales tienen un comienzo (en nuestro caso, el $0$), por otra parte nunca terminan. No importa hasta qué número podamos haber contado, siempre podemos dar un paso más y avanzar al siguiente número. Cuando tenemos un natural, decimos entonces que siempre tiene un sucesor. Sabemos que sólo hay un sucesor para cada número.

Otra característica clave de los números naturales es que, a la hora de contar, nunca regresamos a un número por el cual ya pasamos; es decir, bajo ninguna circunstancia contamos $107, 108, 109, 37, ‘ldots$. Para enunciar esto formalmente, lo diremos en dos partes. Primero, el $0$ no es el sucesor de ningún número y segundo, en ninguna circunstancia, un mismo número es el sucesor de dos números diferentes.

Existe una quinta propiedad, tal vez más sutil que las anteriores, y es que si empezamos a contar desde el cero y vamos contando de uno en uno, entonces podremos alcanzar cualquier número natural, siempre que el tiempo lo permita.

Resulta que estas propiedades intuitivas son suficientes para definir muchas otras operaciones en los números naturales y para obtener una gran cantidad de propiedades. Es por esta razón que conviene incluirlas en nuestra formalización de los naturales, como discutimos a continuación.

Los axiomas de Peano para los números naturales

A finales del siglo XIX, los matemáticos empezaron a notar que a partir de algunas propiedades tan elementales como las que discutimos arriba, se podían probar las leyes de la aritmética que conocemos. En 1889, Giuseppe Peano, basado en las propiedades que acabamos de enunciar, dio un conjunto de axiomas que usó para estudiar sistemáticamente a los números naturales. Estos axiomas son:

  1. $0$ es un número natural.
  2. Si $n$ es un número natural, entonces existe un único natural, denotado $\sigma(n)$ al que llamamos su sucesor.
  3. Para todo número natural, $\sigma(n)\neq0$.
  4. Si $n,m$ son números naturales, tales que $\sigma(n)=\sigma(m)$, entonces $n=m$.
  5. Si $S$ es un subconjunto de números naturales tal que: $0$ está en $S$, y para todo $n$ en $S$, se cumple que $\sigma(n)$ está también en $S$, entonces $S$ es el conjunto de todos los naturales.

Nota que cada una de las cinco propiedades coinciden con una de las propiedades intuitivas que mencionamos antes.

Encontrando los primeros números naturales

El logro de Peano fue muy importante, ya que permitió reducir la teoría de los números naturales a solo cinco axiomas; sin embargo, aún quedan abiertas las preguntas ¿qué son los números naturales? y ¿cómo sabemos que existen? Aunque se hayan mencionado las propiedades de un objeto, no necesariamente tiene que existir tal objeto. Este fue el gran problema al que se enfrentaron los matemáticos cuando intentaron definir a un conjunto al que pertenecen todos los conjuntos.

Es por esta razón que debemos fundamentar la construcción de los números naturales en teoría que ya tengamos desarrollada. Por esta razón, a partir de este punto se aparece la teoría de los conjuntos, la cual nos permitirá definir formalmente lo que significan los símbolos que diariamente ocupamos (como el $0$), para después ver que en efecto estos conjuntos satisfacen los axiomas de Peano.

Definición: Definimos al cero como $0:=\emptyset$.

Cuando ponemos $:=$, quiere decir que estamos definiendo algo, típicamente un símbolo. Cuando veas algo así aparecer, puedes pensar que significa «esta es la primera vez que usamos el símbolo $0$, y lo que querrá decir es el conjunto vacío». Podemos pensar en esta definición como una simple ocurrencia de notación; sin embargo, es curioso notar que, pensando intuitivamente, $\emptyset$ tiene en efecto cero elementos. Más adelante veremos que los demás números naturales también satisfacen esta intuitiva coincidencia.

Definición: Dado un conjunto $A$ arbitrario, definimos el sucesor de $A$ como $\sigma(A):=A\cup\{A\}$.

Notemos que en realidad $\sigma$ no es en el sentido estricto una función ¿por qué? Más bien, lo que estamos haciendo es explicar a qué nos referimos con el símbolo $\sigma(A)$.

Considerando que hemos construido el primer número natural (el $0$) y hemos dado una forma de construir sucesores, parece una buena idea considerar \[\sigma(0)=\sigma(\emptyset)=\emptyset\cup\{\emptyset\}=\{\emptyset\}.\]

Y definir $1:= \{\emptyset\}$. Análogamente podemos pensar que \[2:=\sigma(1)=\sigma(\{\emptyset\})=\{\emptyset\}\cup\{\{\emptyset\}\}=\{\emptyset,\{\emptyset\}\}.\]

Podríamos continuar así sucesivamente. Observa que, efectivamente, los conjuntos $1$ y $2$ coinciden con la intuición de tener respectivamente $1$ y $2$ elementos.

Los «disfraces» de los números naturales

Actualmente usamos el sistema de numeración arábigo y sabemos exactamente qué quieren decir los «dibujos» $1$, $2$, $3$, $4$, etc. Si fueramos romanos, estaríamos usando los «dibujos» $I$, $II$, $III$, $IV$, etc. De manera estricta, los «dibujos» no son lo mismo que «el concepto que representan». Es decir, en el fondo, $2$ y $II$ son «disfraces distintos para el mismo concepto». Pero ninguno de esos «dibujos» es el concepto mismo, ni vive de manera formal en la teoría que estamos construyendo.

Lo que sí vive en la teoría que construimos es el $\{\emptyset,\{\emptyset\}\}$, pues a partir de los axiomas se puede garantizar su existencia. Por supuesto, en el curso usaremos los «disfraces» habituales de estos conceptos, de modo que casi siempre escribiremos $2$, $7$, $51$, etc. Sin embargo, es crucial que en todo momento tengas en cuenta que cuando escribimos esos «dibujos», en el fondo están las construcciones formales que realizaremos.

Más adelante…

Hemos empezado a definir a los números naturales a partir del $0$ (el conjunto vacío) y la función sucesor $\sigma$; sin embargo, la realidad es que el proceso que hemos descrito debe ser refinado, ya que si continuamos así, jamás acabaremos de definir la infinidad de números naturales que queremos que existan.

Incluso asumiendo que los podemos definir a todos, un segundo problema que se origina es el intentar unirlos en un solo «conjunto de los números naturales». Uno podría intentar ocupar el principio de inducción para resolver el problema. Sin embargo, recordemos que por el momento sólo contamos con los axiomas de la teoría de conjuntos, y aún no sabemos que el principio de inducción (visto como en el curso de Álgebra Superior I, o a partir de los axiomas de Peano) sea válido. Entonces, necesitaremos pensar cómo resolver el problema desde otra perspectiva.

Además, queda el problema de ver que los números naturales que definamos sí satisfagan los axiomas de Peano. También haremos esto pronto, para que a partir de ello podamos comenzar a introducir otras propiedades aritméticas y de orden.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Prueba a partir de sólo los axiomas de Peano, que $n\neq \sigma (n) $ para todo $n\in\mathbb{N}$.
  2. ¿Qué axiomas de Peano satisface el conjunto $\sigma(\mathbb{N})$, es decir, el conjunto de los números a partir del $1$?
  3. ¿Cómo será un conjunto y una función que satisfagan los axiomas 1), 2), 4) y 5) de Peano, pero que no satisfaga el 3)? ¿Puedes construir formalmente un conjunto y una función así?
  4. A partir de la definición de $\sigma(n)$ que dimos, demuestra que para todo número natural $n$ se satisface que $n\in\sigma(n)$ y que $n\subset\sigma(n)$.
  5. Demuestra que si $A$ es un conjunto, entonces $\sigma(A)$ es un conjunto. Para ello, tendrás que recordar los axiomas de teoría de conjuntos.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Seminario de Resolución de Problemas: Identidades algebraicas y binomio de Newton

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción a entradas de álgebra

Cuando en matemáticas hablamos de álgebra, se abarca una gran cantidad de ideas, que van desde el álgebra de secundaria, en la cual factorizamos, despejamos y usamos identidades algebraicas, hasta el álgebra abstracta, que estudia estructuras algebraicas más generales como grupos, anillos y campos. Todas estas ideas tienen amplias aplicaciones en la resolución de problemas. En esta entrada, y las que vendrán a continuación, veremos numerosos ejemplos de esto

Para empezar, hablaremos de álgebra en el sentido de secundaria y preparatoria. Veremos que estas ideas, aunque sencillas, son muy versátiles. Después hablaremos de polinomios y de dos resultados fundamentales en su teoría: el teorema de factorización única y el teorema de la identidad. Los polinomios abundan en las matemáticas, y un correcto entendimiento de ellos abre muchas puertas en la resolución de problemas. En una entrada final daremos algunas ideas de otras estructuras algebraicas como grupos, anillos y campos.

Más adelante en el curso hablaremos con detalle de otros dos temas relacionados con álgebra: desigualdades y álgebra lineal.

Como lo hemos hecho hasta ahora, la idea no es profundizar demasiado en el desarrollo de la teoría algebraica. Para eso, es más recomendable llevar buenos cursos de distintos tipos de álgebra a nivel superior. Aquí en el blog hay material de los cursos Álgebra Superior II y Álgebra Lineal I que imparto en la Facultad de Ciencias de la UNAM.

Identidades algebraicas

Comenzaremos hablando de identidades algebraicas. Una identidad algebraica es una igualdad que se satisface para ciertas variables, independientemente del valor que tomen. Algunos ejemplos son las igualdades que se aprenden a nivel secundaria y bachillerato:

\begin{gather*}
a^2-b^2=(a-b)(a+b),\\
a^2+2ab+b^2=(a+b)^2,\\
a^2+b^2+c^2+2ab+2bc+2ca=(a+b+c)^2,\\
a^n-b^n = (a-b)(a^{n-1}+a^{n-2}b+\ldots+ab^{n-2}+b^{n-1}).
\end{gather*}

Varias de las identidades algebraicas nos permiten desarrollar o factorizar una expresión. Factorizarla es bastante útil en problemas de teoría de números, en donde es importante conocer qué números dividen a la expresión. Desarrollarla a veces nos permite trabajar con una suma de términos simétricos, que podemos estudiar con técnicas de polinomios o con desigualdades.

Veamos algunos ejemplos.

Problema. Muestra que si $n$ es un entero, entonces $n^4-20n^2+4$ no es un número primo.

Sugerencia pre-solución. Intenta formular un problema equivalente al factorizar la expresión. Hay más de un camino por el que puedes proceder para factorizar, pero no todos te llevan a una solución. Intenta completar cuadrados de distintas formas y ve si encuentras un patrón.

Solución. Reescribimos la expresión como sigue:
\begin{align*}
n^4-20n^2+4&=n^4-4n^2+4-16n^2\\
&=(n^2-2)^2-(4n)^2\\
&=(n^2-4n-2)(n^2+4n-2).
\end{align*}

Para ver que la expresión no es un primo, basta con ver que ninguno de estos factores puede ser igual a $1$ o $-1$. Si $n^2-4n-2=1$ o $n^2+4n-2=1$, entonces $n^2=\pm 4n+3$. Trabajando módulo $4$, tendríamos $n^2\equiv 3 \pmod{4}$, lo cual es imposible.

Si $n^2-4n-2=-1$ o $n^2+4n-2=-1$, entonces sumando $6$ de ambos lados tenemos $$(n\pm 2)^2=n^2\pm 4n+4=5.$$ Esto es imposible pues $5$ no es el cuadrado de un entero. Así, $n^4-20n^2+4$ se puede factorizar en factores distintos de $1$ y $-1$ y por lo tanto no es primo.

$\square$

El siguiente problema fue parte de la 1a Olimpiada Mexicana de Teoría de Números. Veremos dos soluciones. Ambas usan ideas algebraicas, pero son distintas entre sí.

Problema. Sean $a,b,c,d$ enteros tales que

\begin{align*}
ab + bc + ca &= 1\\
ad + dc + ca &= 1\\
ab + bd + da &= 1.
\end{align*}

Determina todos los valores posibles que puede tomar $bc+cd+db$.

Sugerencia pre-solución 1. Hay varias formas de aprovechar la simetría del problema. Intenta manipular las ecuaciones para obtener información y recuerda que es importante usar que $a$, $b$, $c$ son enteros.

Solución 1. A partir de la primera y segunda ecuación, tenemos que $$ab+bc+ca=ad+dc+ca,$$

de donde $0=ad+dc-ab-bc=(a+c)(d-b)$. De aquí tenemos dos opciones: $a=-c$ o $b=d$. Si $a=-c$, de la segunda ecuación obtenemos $$1=ad+dc+ca=-c^2,$$ lo cual es imposible. Así, concluimos que $b=d$.

Por simetría, concluimos que $c=b$, así que $b=c=d$. Tras esto, las tres ecuaciones se reducen a una sola $$1=2ab+b^2=b(2a+b).$$ Las únicas factorizaciones de $1$ en enteros son $1=1\cdot 1$ o $1=(-1)(-1)$, de modo que $b=2a+b$, de donde $a=0$ y $b=\pm 1$. De cualquier forma, la expresión que buscamos es $bc+cd+db=3b^2=3$.

$\square$

Sugerencia pre-solución 2. Formula un problema equivalente sumando $a^2$ en ambos lados en cada una de las ecuaciones.

Solución 2. Sumando $a^2$ en ambos lados de la primer ecuación obtenemos $$a^2+1=a^2+ab+bc+ca=(a+b)(a+c).$$ Las otras dos ecuaciones dan expresiones simétricas. Multiplicando las tres, tenemos $$(a^2+1)(a^2+1)^2=(a+b)^2(b+c)^2(c+a)^2.$$

El lado derecho es el cuadrado de un entero, así que el izquierdo también debe serlo, de modo que $a^2+1$ debe ser el cuadrado de un entero. Pero los únicos cuadrados a distancia $1$ son $0$ y $1$, de donde $a^2+1=1$, y así $a=0$. Las ecuaciones se convierten entonces en $bc=dc=bd=1$, de donde la suma de las tres es $3$.

$\square$

Demostraciones del binomio de Newton

La siguiente es una de las identidades algebraicas más importantes.

Teorema (binomio de Newton). Para $a$ y $b$ números reales y $n$ un entero no negativo, se tiene que
\begin{align*}
(a+b)^n=\sum_{j=0}^n \binom{n}{j}a^{n-j}b^j
\end{align*}

El término de la derecha es $$a^n+\binom{n}{1}a^{n-1}b+\ldots+\binom{n}{n-1}ab^{n-1} + b^n.$$

Veamos algunas demostraciones del teorema de binomio de Newton, que usan ideas un poco distintas. La primera usa ideas combinatorias. La segunda, ideas más algebraicas. La tercera es menos general, pero usa ideas geométricas.

Demostración combinatoria

Demostración 1. Pensemos al lado izquierdo como el producto $$(a+b)(a+b)\ldots(a+b)(a+b).$$ ¿Cómo se obtienen factores al desarrollar esta expresión? En cada uno de los $n$ paréntesis hay que elegir o un $a$, o un $b$. Así, cada sumando es producto de $n$ letras.

Si elegimos $j$ veces $b$, entonces elegimos $n-j$ veces $a$. ¿De cuántas formas podemos elegir $j$ veces $b$? Tantas como subconjuntos de tamaño $j$ de un conjunto de $n$ elementos, es decir, $\binom{n}{j}$.Así, el término $a^{n-j}b^j$ aparece $\binom{n}{j}$ veces.

Para terminar, notemos que $j$ puede ir desde $0$ (no elegir ningún $b$), hasta $n$ (no elegir ningún $a$).

$\square$

La demostración anterior es combinatoria, pues está usando argumentos de conteo. Está contando de dos formas distintas los términos que aparecen en el producto desarrollado. Además, está usando la interpretación combinatoria de los coeficientes binomiales.

Demostración algebraica

Demostración 2. Si $b=0$, entonces en ambos lados tenemos $a^n$, ya que el único sumando en el que no aparece $b$ es el primero. Tenemos algo análogo si $a=0$. De otra forma, podemos asumir que $a$ y $b$ no son cero y dividir ambos lados de la igualdad que queremos entre $b^n$. Definiendo $x=a/b$, tenemos que mostrar que:

$$(x+1)^n= \sum_{j=0}^n \binom{n}{j}x^{n-j}.$$

Esta igualdad es claramente cierta para $n=0$, pues en ambos lados obtenemos $1$, y para $n=1$, pues en ambos lados obtenemos $x+1$. Procediendo por inducción (explicamos cada paso con un poco de detalles más abajo):

\begin{align*}
(x+1)^{n+1}&=(x+1)(x+1)^n\\
& = (x+1)\sum_{j=0}^n \binom{n}{j} x^{n-j}\\
&=\sum_{j=0}^n \binom{n}{j} x^{n-j+1}+\sum_{j=0}^n \binom{n}{j}x^{n-j}\\
& = \sum_{j=0}^{n+1} \binom{n}{j-1} x^{n-j}+\sum_{j=0}^{n+1} \binom{n}{j}x^{n-j}\\
&=\sum_{j=0}^{n+1}\left(\binom{n}{j-1}+\binom{n}{j}\right) x^{n-j}\\
&=\sum_{j=0}^{n+1}\binom{n+1}{j} x^{n-j}.
\end{align*}

El primer paso es claro. En el segundo usamos hipótesis inductiva. Luego, hacemos la multiplicación por $x+1$. El siguiente paso puede ser un poco confuso, pues parece que «agregamos términos», pero en la segunda suma sólo agregamos $\binom{n}{n+1}x^{-1}=0$. En la primer suma hicimos un shift o desfase: los términos que estaban antes para $j$ de $0$ a $n$, ahora están para $j$ de $1$ a $n+1$. Además, agregamos el término $\binom{n}{-1}x^{n}=0$. En el siguiente paso usamos la identidad de Pascal: $$\binom{n}{j-1}+\binom{n}{j}=\binom{n+1}{j},$$ que se puede demostrar combinatoriamente, o directamente de manera algebraica a partir de la fórmula para coeficientes binomiales.

Con esto termina la demostración por inducción.

$\square$

Esta segunda demostración es mucho más algebraica, es decir, usa ideas de cómo se manipulan las expresiones con variables. El primer paso, en el que reducimos el problema a cuando un término es $1$, se llama homogenización. En realidad no era estrictamente necesario hacerlo, pero simplifica la notación. En las sumas hicimos un shift, que es otra técnica que se usa al estudiar sumas y series.

Demostración geométrica

Daremos una última demostración del teorema del binomio de Newton, pero sólo para el caso $n=2$. Lo que tenemos que demostrar es simplemente la identidad $$(a+b)^2=a^2+2ab+b^2.$$ Para este caso, hay una bonita «demostración sin palabras»:

Binomio al cuadrado mostrado geométricamente
Demostración visual del binomio al cuadrado

Esta demostración es geométrica, pues estamos interpretando a la igualdad como una igualdad de áreas. Estamos usando una fórmula de área para cuadrados y rectángulos. Además, estamos usando que el área de una figura es aditiva, es decir, que es igual a la suma de áreas de figuras en las que queda subdividida.

Puedes elegir tu demostración favorita del binomio de Newton. Sin embargo, en resolución de problemas es importante saber proceder con varios acercamientos. Hay problemas en los que el acercamiento combinatorio, el algebraico o el geométrico es ventajoso, y por ello es mejor tener buena práctica en todos ellos.

Una aplicación del binomio de Newton en teoría de números

En entradas anteriores ya hemos usado el teorema del binomio de Newton en repetidas ocasiones, por ejemplo, en la entrada de aritmética de números complejos. Veamos un ejemplo más.

Problema. Sean $a$ y $b$ enteros primos relativos. Muestra que para todo entero positivo $n$, se tiene que $a^n$ y $b^n$ son primos relativos.

Sugerencia pre-problema. Hay varias formas de dar una solución de esto. Una es analizando a los enteros primo por primo. Sin embargo, existe una solución usando binomio de Newton y la caracterización en términos de combinaciones lineales enteras para primos relativos.

Solución. Como $a$ y $b$ son primos relativos, existe una combinación lineal entera de ellos que da $1$, digamos $$ax+by=1.$$ Elevando esta igualdad a la $2n-1$ tenemos $$1=1^{2n-1}=(ax+by)^{2n-1}.$$ Abriendo el último término con binomio de Newton queda
$$\sum_{j=0}^{n-1} \binom{2n-1}{j} a^{2n-1-j}b^j + \sum_{j=n}^{2n-1} \binom{2n-1}{j} a^{2n-1-j}b^j,$$ y factorizando $a^n$ del primer sumando y $b^n$ del segundo,
$$a^n \sum_{j=0}^{n-1} \binom{2n-1}{j} a^{n-1-j}b^j + b^n \sum_{j=n}^{2n-1} \binom{2n-1}{j} a^{2n-1-j}b^{j-n}.$$

Lo que queda a la derecha es una combinación lineal entera de $a^n$ y $b^n$ igual a $1$, y por lo tanto son primos relativos.

$\square$

Más problemas

En la siguiente entrada hablaremos de la identidad de Gauss para suma de cuadrados y de la identidad para $x^3+y^3+z^3-3xyz$, las cuales se usan frecuentemente en resolución de problemas. Además, puedes encontrar más problemas de identidades algebraicas en la Sección 4.1 del libro Problem Solving through Problems de Loren Larson.