Archivo de la etiqueta: axiomas

Álgebra Superior I: Axiomas de los conjuntos.

Por Guillermo Oswaldo Cota Martínez

Introducción

Hasta ahora, hemos introducido intuitivamente la idea de qué es un conjunto, cómo describirlos y qué representan. En esta entrada vamos a hablar de tres temas importantes para trabajar con más ideas de los conjuntos: contención, subconjuntos y conjunto potencia.

Las primeras dos van de la mano, y serán una forma de definir subcolecciones dentro de una colección (a la que ahora llamamos conjunto) y nos permitirán manejar con mayor facilidad conceptos que veremos más adelante sobre las operaciones entre conjuntos.

Mientras tanto, el conjunto potencia nos hablará de la forma de combinar elementos dentro de un mismo conjunto, que es un concepto que tiene propiedades muy interesantes.

Estos tres conceptos serán fundamentales para axiomatizar la teoría de los conjuntos.

Axiomatizando los conjuntos

En la entrada pasada, dimos una peequeña introducción a la teoría de conjuntos. Hablamos de su idea intuitiva y algunos ejemplos de su uso en otras materias. Ahora nos toca entrar un poco más en fondo a sus reglas, esto es, sus axiomas.

Para poder hablar de los conjuntos, su idea y la forma en que se manejan, vamos a establecer algunos axiomas que describirán la teoría de conjuntos. Todo objeto matemático que sigan el sistema axiomático, serán conjuntos. Para ello, primero es fundamental declarar que existen los conjuntos, de otra forma no estaríamos trabajando con nada:

Axioma 1. Existe al menos un conjunto.

Este axioma nos permitirá trabajar con conjuntos, pues nos asegurará que al menos existe un conjunto $V$ con el que podremos trabajar los siguientes axiomas. Sin este axioma, no podríamos seguir trabajando la teoría, pues no tendríamos con qué trabajar.

Los siguientes axiomas serán los que nos darán la intuición de qué se puede y no puede hacer con un conjunto.

Axioma 2. Si X es un conjunto y $P(x)$ es una proposición que depende de elementos $x \in X$, entonces:

$$\{x \in X : P(x) \text{ se cumple}\} $$

también es un conjunto.

En la entrada pasada, dimos una idea intuitiva de este axioma, que nos dice que si tenemos un conjunto $X$ y cualquier proposición $P(x)$ de elementos de $X$ entonces podemos construir nuevos conjuntos a partir de los elementos de $X$ que cumplen cierta propiedad. Por ejemplo, piensa que $X$ es el conjunto de todos los zapatos, entonces un conjunto nuevo puede formarse a partir de la proposición $P(x): $»$x$ es amarillo», entonces el nuevo conjunto $\{ x \in X : P(x) $ se cumple $\}$ es el conjunto de los zapatos amarillos. Otro ejemplo de esto, sería el conjunto de los números pares que podemos definir a partir de los números enteros $\mathbb{Z} = \{\dots,-3,-2,-1,0,1,2,3,\dots\}$. Los número pares se pueden definir como: $2\mathbb{Z} = \{x \in \mathbb{Z} : x = 2n, n \in \mathbb{Z} \}$ es decir, es el conjunto creado por los número enteros multiplicados por dos.

Creando el conjunto vacío.

Antes de seguir con los demás axiomas, vamos a mostrar una consecuencia de los dos primeros axiomas. Observa que por el primer axioma, existe al menos un conjunto al que llamaremos $X$. Y el segundo axioma nos dice que con cualquier conjunto, se puede obtener un conjunto a partir de aquellos elementos que cumplan alguna proposición que depende de elementos de $X$, entonces consideremos la siguiente propocisión:

$$P(x) : x \neq x $$

Esta proposición nos dice que un objeto $x$ no es igual a sí mismo, lo cual es imposible, ninguna cosa u objeto matemático va a cumplir esta proposición. Es decir:

$$\forall x (\neg P(x)) $$

se cumple. ¿Entonces qué conjunto será el conjunto: $\{x \in X : P(x)\} = \{x \in X : x \neq x\} $?

Pues es un conjunto que no tiene a ningún elemento, pues ningún elemento $x$ de $X$ puede cumplir esa definición. Esto no representa ninguna contradicción a algún axioma, lo que nos dice es que existe un conjunto que no tiene a ningún elemento. A este conjunto lo conocemos como conjunto vacío y lo representamos como $\emptyset$. A veces también lo encontrarás como unas llaves sin nada adentro, es decir $\{\}$.

Una vez dicho esto, vamos construyendo poco a poco más resultados, sigamos con los siguientes axiomas:

Axioma 3. Si $X$ y $Y$ son conjuntos, entonces $\{X,Y\}$ es un conjunto.

Esto nos permite «poner» conjuntos, dentro de un conjunto. Es decir, podemos hacer dos conjuntos en los que cada elemento sea un conjunto. Por ejemplo, considera $X = $ el conjunto de zapatos amarillos y $Y = $ el conjunto de los Blergs. Entonces existe el conjunto $Z=\{X,Y\}$ un conjunto que solo tiene dos elementos: el conjunto de los zapatos amarillos y el conjunto de los Blergs. OJO: un zapato amarillo NO pertenece al conjunto $Z$, lo que sí pertenece al conjunto es el conjunto de todos los zapatos amarillos. Es decir, si $x$ es un zapato amarillo, entonces $x \in X$ pero no sucede que $x \in Z$. Lo que sí sucede es $X \in Z$.

De este axioma, podemos deducir la siguiente proposición:

Proposición: Si $X$ es un conjunto entonces $\{X\}$ tambien es un conjunto.

Demostración. Sea $X$ un conjunto. No hay nada en la definición del axioma 3 que impida que $X=Y$, entonces lo que nos dice el axioma es que si tenemos dos conjuntos $X,Y$ donde $X=Y$ entonces el conjunto $W=\{X,Y\}$ es un conjunto, y podemos reescribir este como $\{X,X\}$. Ahora, recuerda que hemos dicho con anterioridad que realmente al describir a un conjunto, solo nos interesan los elementos distintos que lo conforman, es decir, está de más repetir dos veces $X$ dentro de los corchetes que representan los elementos del conjunto $W$, entonces $W=\{X\}$ es un conjunto.

$\square$

Axioma 4. Si $X$ y $Y$ son dos conjuntos, diremos que $X=Y$ (el conjunto $X$ es igual al conjunto $Y$) si tienen exactamente los mismos elementos. Esto se puede describir usando lógica proposicional de la siguiente manera:

$$\big( X=Y\big) \Leftrightarrow \forall x\big(x \in X \Leftrightarrow x \in Y \big)$$

Axioma 5. Si $X$ es un conjunto, entonces el conjunto de los elementos que pertenecen a por lo menos un elemento de $X$ forman un conjunto (unión).

Vamos a leer con más calma el axioma. Primero tenemos un conjunto $X$, digamos el conjunto de todos los grupos dentro de una universidad. Entonces un alumno de esa universidad pertenece al menos a algún grupo. De esta manera, el conjunto de todos los alumnos de la universidad, forma un conjunto. Veamos esto con notación matemática:

Sea $U$ los grupos de la universidad: $\{G_1,G_2,G_3\}$, es decir, cada elemento cada grupo está formado de estudiantes, es decir cada alumno es elemento de un grupo, digamos

$$G_1 = \{A_1,A_2,A_3\}$$

$$G_2 = \{B_1,B_2,B_3\}$$

$$G_3 = \{C_1,C_2,C_3\}$$

Entonces el axioma nos dice que el conjunto de todos los elementos (alumnos) que pertenecen al menos a un elemento de $X$ (grupos del conjunto $U$), forma otro conjunto. En nuestro caso, sería el conjunto de todos los alumnos: $\{A_1,A_2,A_3,B_1,B_2,B_3,C_1,C_2,C_3\}$.

Quizá esta idea de «los elementos de un conjunto a su vez también tienen elementos» puede ser un poco difícil de entender y quizá hasta un poco filosófica: ¿Hasta qué punto podríamos usar el raciocinio para extraer las partes que componen a un todo? Es decir: Si consideramos el conjunto de todos los zapatos: ¿Qué significa ahora que haya un elemento que pertenezca a un zapato? las respuestas pueden ser variadas, y puede que incluso se te ocurran unas distintas a otra persona que lea esto, así que velo de la siguiente forma: si tenemos la capacidad de hacer una intuición de separar un elemento de algún conjunto en sus partes, entonces podemos hacer otro conjunto con esas partes. Conforme vayas avanzando en tu carrera matemática, vas a poder ir aclarando muchas de estas ideas, volveremos a este axioma más adelante.

Para el siguiente axioma, primero introduciremos algunos conceptos:

Contención entre conjuntos

Recuerda que los conjuntos los pensamos como «colecciones de algo», pueden ser conjuntos de zapatos, conuntos de autos o conjuntos de animales, por mencionar algunos. Para introducir el axioma que sigue, primero hablaremos de la contención y para explicarlo, veamos el conjunto de unas criaturas a las que les llamamos Blorgs y nos ayudaron en la entrada anterior. Lo que tienes que saber de ellos, es que se dividen en Blargs, Blergs y Blurgs según su color (amarillo,rojo y azul respectivamente), como lo puedes ver en la siguiente imagen:

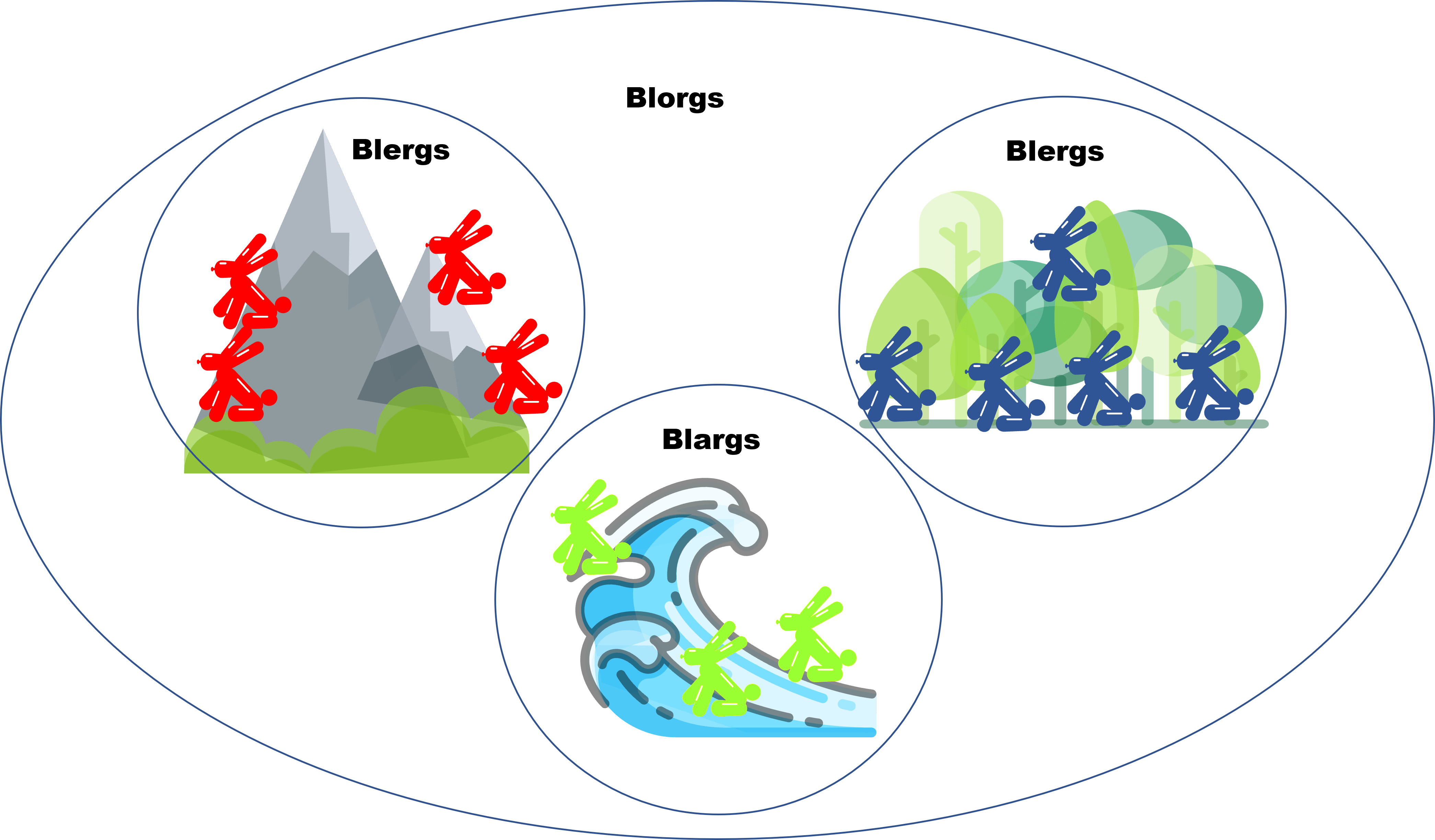
Ahora, llamemos a los 3 Blargs: «blargmino», «blargastacia» y «blargencio», de manera que el conjunto de los Blargs es:

$$\text{Blargs} = \{ \text{ blargmino, blargastacia , blargencio }\}$$.

Ahora, nota que decimos que «blargmino pertenece al conjunto de los Blorgs», pero a su vez también pertenece al conjunto de los Blargs, entonces también podríamos decir blargmino pertenece al conjunto de los Blorgs». ¿Notas que no necesitamos rigor al decir qué es y qué no es un conjunto? Con el simple hecho de poder abstraer sus partes o elementos, es suficiente. Pero ahora surge una pregunta natural: ¿Existe alguna relación entre el conjunto de los $B_a$ Blargs y el conjunto $B_o$ de todos los Blorgs? En cuyo caso, nota que:

$$\forall x(x \in B_a \Rightarrow x \in B_o) $$

Es decir, todo blarg es un blorg. Diremos entonces que los Blargs con un subconjunto de los Blorgs. Ya que todo elemento de $B_a$ está en $B_o$.

Definición. Sean $A$ y $B$ dos conjuntos. Diremos que $A$ es un subconjunto de $B$ o que $A$ está contenido en $B$ si:

$$\forall x(x \in A \Rightarrow x \in B). $$

Y lo escribiremos como $A \subset B$*

Ahora, nota que cualquier conjunto contiene al conjunto vacío.

Proposición. Sea $X$ un conjunto, entonces $\emptyset \subset X$.

Demostración. Vamos a demostrar esto por contradicción, suponiendo que $\emptyset \not \subset X$, es decir supongamos que $\neg \big( \forall x(x \in \emptyset \Rightarrow x \in X) \big) = \exists x(x \in \emptyset \land x \not \in X) $. Entonces bajo nuestra suposición, existe un elemento $x$ en $\emptyset$ pero $x \not \in X$. ¿Puedes ver porqué esto es una contraidcción? Pues estamos suponiendo que existe un elemento en $\emptyset$, pero por la forma en que definimos al conjunto vacío, esto significaría que existe un elemento $x$ que cumple que $x \neq x$, lo cual es imposible. ¿Cuál fue nuestro error? Pues suponer que no se cumplía $\emptyset \subset X$. Por lo tanto, $\emptyset \subset X$

$\square$

Axioma 6. Si $X$ es un conjunto, entonces existe un conjunto conformado por todos los subconjuntos de $X$. Nos referiremos a este conjunto como el conjunto potencia y lo denotaremos por $\mathcal P (X)$.

Nota que nuestra definición de un subconjunto $Y$ de $X$ nos pide que todo elemento de $Y$ esté en $X$, así que el conjunto potencia será aquel conjunto en el que cada elemento será un conjunto que es subconjunto de nuestro conjunto original. Pongamos un ejemplo para que lo veas mejor:

Ejemplo. Considera al conjunto $X = \{1,2,3\}$ el conjunto con los números enteros del $1$ al $3$, entonces el conjunto potencia está dado por todos sus subconjuntos: $\emptyset, \{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{1,3\},\{1,2,3\}$ es decir, el conjunto potencia de $X$ es: $$\mathcal P(X) =\{\emptyset, \{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{1,3\}, X\} $$

Con estos seis axiomas serán con los que trabajaremos, en resumen, los axiomas son los siguientes:

Axioma 1	Existe un conjunto.
Axioma 2	Podemos hacer conjuntos a partir de proposiciones que cumplen o no cumplen elementos de algún conjunto.
Axioma 3	Si $X$ y $Y$ son conjuntos, entonces $\{X,Y\}$ es un conjunto.
Axioma 4	Dos conjuntos son iguales si todos sus elementos son iguales.
Axioma 5	Existe un conjunto que tiene como elementos a todos los elementos que pertenecen a algún elemento de $X$.
Axioma 6	Para cada conjunto $X$, existe su conjunto potencia $\mathcal P (X)$ cuyos elementos son los subconjuntos de $X$.

Notas

*: Algunos autores usan la notación $\subseteq$ para detonar que «el subconjunto está contenido estrictamente o es igual», por ejemplo si decimos «X \subseteq Y» diremos que cada elemento de $X$ está en $Y$ entonces puede que $X$ sea el mismo que $Y$, nosotros nos apegaremos a la notación $\subset$ para decir que un subconjunto está contenido estrictamente o es igual, y usaremos la notación $\subsetneq$ para denotar la contención estricta, es decir, $X \subsetneq Y$ si y solo si para cada $x \in X \rightarrow x \in Y$ pero existe $y \in Y \land y \not \in X$.

Más adelante…

Ahora que ya hemos establecido las reglas que seguirán los conjuntos, es hora de hablar sobre algunas operaciones dentro de esta teoría. Sobre todo hablaremos de Intersecciones, Uniones y Complementos de conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Demuestra que las siguientes afirmaciones son equivalentes:
- $X=Y$
- $ \forall x (x \in X \Leftrightarrow x \in Y)$
- $(X \subset Y) \land (Y \subset X) $
¿Es cierto que el conjunto vacío es único?
¿Cuál es el conjunto potencia de $\{1,2,3,4\}$?
Demuestra que $X=Y$ si y solo si $\mathcal P(X) = \mathcal P(Y)$.

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Conjuntos y elementos
Siguiente entrada del curso: Problemas de conjuntos y subconjuntos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Demostraciones matemáticas (El mundo de los Blorg)

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

Esta entrada es parte de una serie de notas sobre demostraciones matemáticas. Sin embargo, para llegar a la importancia de demostrar, hablaremos previamente de un pequeño mundo en donde habitan seres fantásticos a quienes les interesa mucho la lógica y para quienes es fundamental poder deducir únicamente verdades. Este lugar lo vistaremos a lo largo de varias entradas y lo que acordemos a partir de ahora será cierto más adelante. Así que presta atención.

El mundo de los Blorgs

Antes de que pienses que te equivocaste de entrada debido al cuento que está por comenzar, déjame decirte que todo está relacionado con la teoría que hemos estado platicando. Sin embargo, antes de comenzar a aplicarla, vamos a conocer a los Blorgs.

Imagina el mundo de los Blorgs. Es un mundo paralelo al nuestro que se puede encontrar en aquel mundo que existe más allá de lo que la esquina del espejo deja ver. Es un lugar que se parece un poco al piso sobre el que estamos, despierta con casi los mismos tonos del alba por la mañana pero con algunas cosas distintas.

Para empezar estamos hablando de un mundo en el que habitan mayoritariamente criaturas llamadas Blorgs. Aquellos que alguna vez los vieron, comentan que curiosamente son pequeñas criaturas parecidas a los conejos. Y con algunas otras descripciones en mente, podríamos empezar a clasificar los Blorgs de acuerdo a distintas características como por ejemplo su dieta, su rutina, dónde viven, etc. Pero se decidió que era mejor clasificarlos según su color, y aquí es donde las cosas se ponen interesantes.

Por un lado están los Blergs, estos son las criaturas rojas que viven por las montañas. Después podemos considerar a los Blargs que son aquellos Blorgs verdes y viven debajo del mar, no son muy sociales pero es lo que hay. Finalmente están los Blurgs que son azules y prefieren vivir en el bosque. Entonces, podemos dividir a los Blorgs en sus razas: Blergs, Blargs y Blurgs. Algo importante que tenemos que decir también: ningún Blorg tiene más de un color.

Quizá sean de color distinto y vivan en lugares diferentes, pero esto no les impide tener algunas cosas en común. Por ejemplo, todos los Blurgs comen pescados, pues tienen un lago cerca de su bosque, y al ser los Blargs marinos, también comen pescados. El hecho de haber vivido tanto tiempo en terreno alto, hizo que los Blergs prefieran cultivar sus cosechas: frutos dulces y verduras siempre comen. Por alguna razón, será costumbre o creencia, todos los Blorgs comen los lunes, es decir, que cada criatura come una vez a la semana. Eso les ha ayudado a no depender tanto de la comida en el día a día. Aunque aquí es donde los Blurgs no coinciden: ellos no esperan tanto y también comen algo los viernes.

La vida siendo Blorg

Tristemente, los Blargs no pueden salir del mar, pues a pesar de ser Blorgs, el salir del agua les despinta lo verde y les quita fuerza. Es por esto que casi no hablan con sus contrapartes terrestres. Por otro lado los Blerg y los Blurg se llevan muy bien. Los Blurgs comparten la madera que tienen con los Blergs y los Blergs comparten los cultivos que hacen con los Blurgs (aunque no para comer, los Blurgs más bien usan los lindos colores de los frutos rojos para pintar).

No está de más decir que todos los Blergs son amigos de todos los Blurgs. Esto hace que los Blargs se sientan más ajenos a ellos, pues aunque sí se llevan con los Blurgs, prefieren juntarse con los delfines que viven junto a ellos. Los blurgs son amistosos con los Blargs y Blergs, y siempre están dispuestos a negociar peces a cambio de paseos a lo largo del mar. Pero nadie se queja, así es la vida siendo un Blorg.

De esta manera, podemos resumir la información que sabemos de los Blorgs en el siguiente diagrama:

Sobre Axios y demostraciones matemáticas

Una cualidad que podemos saber de los Blorgs es que ellos le llaman al lugar en donde viven «Axios» y dentro de ella, no hacen diferencia entre lo que es una característica o costumbre, ellos no tienen una palabra para cada una de ellas. En su lugar usan la palabra «Axioma«* (¿recuerdas qué significa esta palabra?). Esto quiere decir que para los Blargs, ser verdes es un axioma, al igual que para ellos hablar con delfines o comer peces es un axioma.

Así que es natural poder hacer conclusiones a partir de estos Axiomas. Por ejemplo: ¿Qué opinarías si te digo que todos los Blorgs comen peces? ¿O si te digo que todos los Blorgs que viven en montañas comen los lunes? Pues quizá puedas dar respuesta a estas preguntas intuitivamente. Pero, ¿cómo es que nos aseguramos que la respuesta es correcta o no?

En Axios no basta con decir que todos los Blorgs que viven en las montañas comen los lunes. Los Blorgs no entienden la intuición, pero nosotros sí. A ellos hay que convencerlos con demostraciones, a ellos tenemos que explicarles mediante lógica el porqué una proposición sucede. Es decir que si queremos afirmar que todos los Blorgs que viven en las montañas comen los lunes, tenemos que decir paso a paso el porqué es así. Y esto lo lograremos sólo mediante reglas de inferencia válidas. Vamos a anotar esto que acabamos de decir como una definición (¿recuerdas qué era una definición?):

Definición. Una demostración matemática es el uso de pasos lógicos usando reglas de inferencia válidas para llegar de la veracidad de ciertas hipótesis a la veracidad de una conclusión.

La intuición con inferencia

Para introducir un poco más qué van a ser las demostraciones en las matemáticas, vamos a pensar en Legos, aquellos pequeños bloques que encajan unos con otros con los que se pueden armar lo que se te ocurra. Y piensa a las reglas de inferencia como las instrucciones para armar algo.

Imagina que queremos armar un cuarto con una mesa, cama y lámpara con estas piezas. Primero, tendríamos que armar una mesa, para lo cual necesitamos armar las patas y después la superfice. Las reglas de inferencia nos van a ayudar diciéndonos: las patas hay que acomodarlas de cierta manera junto a la superficie para que se haga una mesa. Y una vez construida la mesa, ahora podemos usar otras reglas de inferencia para crear la cama y otras para la lámpara, juntando las tres partes (mesa, cama y lámpara) tendríamos hecho un cuarto.

Así, si quisiéramos «demostrar» cómo se hace un cuarto con estas piezas de Lego, tendríamos que explicar cómo se hace la lámpara, cómo se hace la cama y cómo la mesa. Esto es lo que haremos en matemáticas: construir cosas dando las instrucciones adecuadas. Incluso podríamos ir más allá: Una vez que sabemos cómo construir un cuarto, podríamos también demostrar cómo se hace una cocina y un baño. Entonces si tuviéramos ese conocimiento de cómo se hacen estos tres, podríamos construir una casa. Y después sabiendo cómo se construyen casas, podríamos crear ciudades y países enteros. Pero como todo: un paso a la vez.

Armando piezas con los Blorgs

Nuestras piezas de Lego con los Blorgs van a ser los axiomas. Ahora si le dijeramos a un Blorg que los Blorgs verdes comen peces, no nos creería. Debemos darle una demostración de esto:

Proposición. Los Blorgs verdes comen peces.

Demostración. Para empezar, vamos a notar que es una proposición del tipo «Si $x$ es un Blorg verde, entonces $x$ come peces». Esto es lo que queremos demostrar. Para ello, vamos a ir armando poco a poco el argumento con las piezas que sí conocemos:

Usaremos que todos los Blorgs verdes son Blargs. Es decir «si $x$ es un Blorg verde, entonces $x$ es un Blarg»
Usaremos que todos los Blargs comen peces. Es decir «si $x$ es un Blarg, entonces $x$ come peces»

En las demostraciones vamos a ir usando cosas que ya conocemos (en este caso los axiomas) para poder ir aplicando pasos lógicos y reglas de inferencia para llegar a la conclusión deseada. Entonces como queremos ver que todos los Blorgs verdes comen peces, entonces resulta natural «agarrar» o «elegir» un Blorg verde y ver que ese Blorg come peces (si pasa con un Blorg verde, pasará para todos los Blorgs verdes pues todos nuestros pasos lógicos aplicarán para todos los Blorgs verdes). Así que empecemos considerando a $x$ un Blorg verde . Sabemos que «si $x$ es un Blorg verde, entonces $x$ es un Blarg» entonces como nuestro $x$ es un Blorg verde, entonces es un Blarg.

Ahora, sabemos que nuestro $x$ es un Blarg, pero además sabemos que «si $x$ es un Blarg, entonces $x$ come peces» entonces también nuestro Blarg come peces. Por lo tanto los Blorgs verdes comen peces.

$\square$

¿Viste cómo es que hicimos la demostración? Si consideramos

$ P(x) : x$ es blorg verde,
$ Q(x) : x$ es blarg,
$ R(x) : x$ come peces,

entonces realmente lo que hicimos fue usar la siguiente regla de inferencia válida:

$$ \begin{array}{rl} & P \Rightarrow Q \\ & Q \Rightarrow R \\ \hline \therefore & P \Rightarrow R \end{array}.$$

La razón por la que $P\Rightarrow Q$ y $Q\Rightarrow R$ los tomamos como premisas, es porque acordamos que son axiomas. Recuerda que los axiomas los tomamos como verdaderos.

En este caso solo usamos una regla de inferencia. Más veremos cómo se pueden usar varias reglas de inferencia en una misma demostración. Apenas estamos empezando este tema, así que si aún tienes muchas dudas, no te preocupes y vuelve a leer la demostración si es necesario.

Notas

Estas son algunas anotaciones del artículo y no es necesario que las sepas, únicamente son curiosidades o temas por aparte que forman parte de cultura matemática

* Esta palabra viene del griego ἀξίωμα que significa «lo que se considera justo» y de hecho viene de la palabra ἄξιος (áxios) que significa «valioso» y en la antigua grecia se consideraban aquellas cosas que parecían evidentes y no hacía falta justificar.

Más adelante…

Apenas estamos empezando a explicar qué son estas «demostraciones matemáticas». En el mundo de la matemática no hay algo como el recetario de las demostraciones, pero hay ideas o formas de pensar los problemas que te servirán para tener una idea de por dónde empezar a pensar a la hora de demostrar. Así que en las siguientes entradas vamos a ver algunas de estas «formas» de pensar los problemas y lo haremos con ayuda de los Blorgs.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

¿Qué color necesita tener un Blorg para ser amigo de los delfines?
¿Es cierto que existe un Blorg que coma frutos rojos en viernes?
¿Qué argumentos lógicos podrías usar para demostrar que todo Blorg rojo come los lunes? ¿Y qué argumentos usarías para demostrar que si un Blorg vive en el mar, entonces no come los viernes? Finalmente, ¿puedes argumentar por que si un Blorg no es Blurg, entonces sus Blorg amigos comen los viernes?
Verifica que

$$ \begin{array}{rl} & P \Rightarrow Q \\ & Q \Rightarrow R \\ \hline \therefore & P \Rightarrow R \end{array}$$

es una regla de inferencia válida.

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Inferencias matemáticas
Siguiente entrada del curso: Demostraciones directas e indirectas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior II: La construcción de los naturales

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En la entrada pasada presentamos los axiomas de Peano como una formalización de por qué los naturales se comportan como nuestra intuición nos indica. Sin embargo, también vimos que, por si mismos, los axiomas de Peano no nos dicen cómo hacer una construcción de los naturales a partir de conceptos previos. Para intentar lograr esto, introdujimos la definición del sucesor de un conjunto arbitrario y empezamos a iterarla en el conjunto vacío para generar una lista de conjuntos, que relacionamos con los números naturales que conocemos.

Por último, notamos que ocupar esta idea, al menos de forma directa, tiene el problema de dar «pasitos muy chicos», que no nos permitirían acabar nunca de definir a todos los números naturales y, en consecuencia, que no nos dejaría definir en sí el conjunto de los naturales. Es por eso que en esta entrada acabaremos, de una vez por todas, con el problema de definir con precisión el conjunto de números naturales. Veremos que, en efecto, esta construcción que haremos se apega no sólo a nuestra intuición, sino también a los axiomas de Peano.

Conjuntos inductivos

Antes de empezar con la tarea de definir a los números naturales, recordamos la definición del sucesor de un conjunto.

Definición. Si $A$ es un conjunto, definimos el sucesor de $A$, como $\sigma(A):=A\cup \{A\}$.

El conjunto que queremos definir es el conjunto $\mathbb{N}$ de números naturales. Como mencionamos en las entrada pasada, buscamos de manera formal lograr que \[\mathbb{N}=\{\emptyset,\sigma(\emptyset),\sigma(\sigma(\emptyset)),…\},\] por lo que $\mathbb{N}$ satisfaría dos propiedades que englobamos en la siguiente definición.

Definición. Diremos que un conjunto $S$ es inductivo si cumple que:

$\emptyset\in S$ y
si $X\in S$, entonces $\sigma(X)\in S$.

Notemos que estas dos propiedades son muy similares a los dos primeros axiomas de Peano.

Hay que remarcar que aunque no sabemos que exista un conjunto tal que sus elementos son $\emptyset,\sigma(\emptyset),\sigma(\sigma(\emptyset)),…$, en caso de que sí existiera, sería un hecho que tal conjunto sería inductivo.

Otro posible ejemplo de un conjunto inductivo podría verse como \[\{…\sigma(\sigma(\{\{\emptyset\}\})), \sigma(\{\{\emptyset\}\}), \{\{\emptyset\}\},\emptyset,\sigma(\emptyset),\sigma(\sigma(\emptyset)),…\}.\]

Intuitivamente podemos notar que si $S$ es un conjunto inductivo, entonces, $\mathbb{N}\subset S$, por lo que uno podría aventurarse y definir a los naturales como $$\{x: x \text{ está en todo conjunto inductivo}\}.$$

Sin embargo, los axiomas que de teoría de conjuntos que tenemos hasta ahora no nos permiten saber si se puede construir un conjunto así.

¿Qué es lo que sí nos permiten hacer los axiomas de teoría de conjuntos? Si tenemos una colección de conjuntos, podemos hacer la intersección de todos ellos. Esto motiva la siguiente proposición acerca de la intersección de conjuntos inductivos.

Proposición. Si $B\neq\emptyset$ es un conjunto tal que todos sus elementos son conjuntos inductivos, entonces $\bigcap {B}$ es también un conjunto inductivo.

Demostración. Como $B\neq\emptyset$, sabemos que la intersección sí es un conjunto. Veamos que este conjunto es inductivo. Antes de hacer esto recordemos que, por definición, los elementos de $\bigcap{B}$ son precisamente, todos los $x$ tales que $x\in Y$ para todo $Y\in B$.

Para ver que $\bigcap B$ es inductivo, necesitamos verificar que cumpla las dos características de la definición:

Veamos primero que $\emptyset\in\bigcap B$.
Sea $Y\in B$ arbitrario. Como los elementos de $B$ son inductivos, $\emptyset\in Y$, y como $Y$ es arbitrario, podemos concluir que $\emptyset$ está en todos los elementos de $B$. Esta es justo la definición de que $\emptyset\in \bigcap B$.
Veamos ahora que $x\in \bigcap B \Rightarrow \sigma(x)\in \bigcap B$.
Sea $x\in \bigcap B$ y sea $Y\in B$. Como $x\in\bigcap B$, entonces $x\in Y$ y como $Y$ es inductivo, $\sigma(x)\in Y$. De nuevo, como $Y$ fue arbitrario, se sigue que $\sigma(x)$ está en todos los elementos de B, por lo que $\sigma(x)\in\bigcap B$.

Con esto demostramos que $\bigcap B$ es inductivo.

$\square$

En otras palabras, «la intersección arbitraria de conjuntos inductivos es un conjunto inductivo».

El axioma del infinito y la construcción de los naturales

Por todo lo escrito anteriormente, y meditando el hecho de que si partimos de los primeros axiomas de la teoría de conjuntos, sólo podemos crear conjuntos con una cantidad finita de elementos, parece ser que la existencia de un conjunto como los naturales no puede ser deducida con las herramientas que tenemos. Esto en efecto es así. Por ello, debemos introducir un nuevo axioma de la teoría de conjuntos.

Axioma (del infinito). Existe un conjunto inductivo.

El axioma del infinito no nos garantiza inmediatamente la existencia de $\mathbb{N}$, ya que como se vio en un ejemplo más arriba, $\mathbb{N}$ no es el único conjunto inductivo. Sin embargo, esta es la última pieza que necesitamos para poder dar la construcción de los naturales. Hacemos esto a continuación.

Sea $A$ algún conjunto inductivo (que nos garantiza el axioma del infinito), y consideremos $B=\{X\subset A \mid X \text{ es inductivo}\}$ (¿por qué $B$ es un conjunto?). Notemos que $A\in B$ por lo que $B$ es no vacío, por lo tanto, podemos pensar en su intersección, $\bigcap B$. Como los elementos de $B$ son conjuntos inductivos, por la proposición anterior concluimos que $\bigcap B$ es inductivo. A esta intersección la denotaremos como $\mathbb{N}_{A}$. ¡Ya apareció por primera vez el símbolo de números naturales! Pero tiene algo adicional: usamos un subíndice $A$ ya que, a primera vista, su construcción depende del conjunto inductivo $A$ con el que empezamos. Sin embargo, justamente, el paso siguiente será ver que $\mathbb{N}_{A}$ no depende de $A$.

Para ello, primero hacemos la observación de que si $Y\subset A$ es inductivo, entonces $\mathbb{N}_{A}\subset Y$, la cual te dejamos corroborar usando las propiedades de la intersección. Dicho esto, probamos lo siguiente.

Proposición. Si $C$ es otro conjunto inductivo, entonces $\mathbb{N}_{A}= \mathbb{N}_{C} $.

Demostración. Consideremos $\mathbb{N}_{A} \cap \mathbb{N}_{C} $, el cual sabemos que es un conjunto inductivo. Como $\mathbb{N}_{A} \cap \mathbb{N}_{C} \subset A$, por la observación anterior, concluimos que $\mathbb{N}_{A} \subset \mathbb{N}_{A} \cap \mathbb{N}_{C} $. Como la intersección está contenida en cada intersecando, $\mathbb{N}_{A} \subset \mathbb{N}_{A} \cap \mathbb{N}_{C}\subset\mathbb{N}_{A} $, por lo que $\mathbb{N}_{A} = \mathbb{N}_{A} \cap \mathbb{N}_{C} $. Haciendo las mismas observaciones para $\mathbb{N}_{C}$, concluimos que $\mathbb{N}_{A} = \mathbb{N}_{A} \cap \mathbb{N}_{C}= \mathbb{N}_{C} $, con lo que concluimos la prueba.

$\square$

Como sabemos ahora que el conjunto $\mathbb{N}_{A}$ no depende del conjunto $A$ inductivo con el que empecemos, finalmente podemos definir al conjunto de números naturales.

Definición. Si $A$ es algún conjunto inductivo, definimos al conjunto de los números naturales $\mathbb{N}$ como $\mathbb{N}:=\mathbb{N}_{A}$. Definimos al cero como $0:=\emptyset$ y la función sucesor para los naturales como $\sigma:\mathbb{N}\to \mathbb{N}$ tal que $\sigma(n)=n\cup \{n\}$.

Nuestra construcción de los naturales cumple los axiomas de Peano

Para concluir esta entrada veremos que la construcción de los naturales que dimos en efecto da un modelo para los axiomas de Peano. En realidad, la construcción de la función sucesor, la noción de conjunto inductivo y la forma en la que creamos $\mathbb{N}$ fueron todas ellas siempre motivadas por estas ideas, por lo que no deberá ser difícil probar que en verdad todo funciona como queremos.

Teorema. El conjunto $\mathbb{N}$ junto con el $0$ y la función $\sigma$ que definimos satisfacen los cinco axiomas de Peano.

Demostración. Veamos que se verifican los cinco axiomas de Peano.

Axioma 1. $0\in\mathbb{N}$.

Como $\mathbb{N}$ es inductivo, $0=\emptyset\in\mathbb{N}$.

Axioma 2. Si $n\in \mathbb{N}$, entonces $\sigma(n)\in\mathbb{N}$.

Si $n\in\mathbb{N}$, como $\mathbb{N}$ es inductivo, se sigue que $\sigma(n)\in\mathbb{N}$.

Axioma 3. Para toda $n\in\mathbb{N}$ se tiene que $\sigma(n)\neq 0$.

Como $\sigma(n)=n\cup\{n\}$, tenemos que $n\in\sigma(n)$ por lo que $\sigma(n)\neq\emptyset=0$.

Axioma 4. Si $\sigma(n)=\sigma(m)$, entonces $n=m$.

Como $\sigma(n)=\sigma(m)$ y $n\in\sigma(n)$, entonces $n\in\sigma(m)= m\cup\{m\}$. Como $n$ está en una unión, hay dos opciones: $n\in\{m\}$ o $n\in m$. Si $n\in \{m\}$, entonces $n=m$ y concluimos.

En otro caso, $n\in m$. Veamos que podemos decir de $m$. Procediendo análogamente, podemos notar que $m=n$ o $m\in n$. En el primer caso, llegamos a lo que queremos. El segundo caso es imposible, pues tendríamos $n\in m\in n$ lo cual contradice el axioma de regularidad de teoría de conjuntos.

Axioma 5. Si $S\subset\mathbb{N}$ tal que $0\in S$ y $n\in S \Rightarrow \sigma(n)\in S$, entonces $S=\mathbb{N}$.

Notemos que las hipótesis de $S$ implican que éste es un conjunto inductivo. Por ello, $\mathbb{N}=\mathbb{N}_{S}\subset S\subset \mathbb{N}$. Esta cadena de contenciones implica la igualdad $\mathbb{N}=S$.

$\square$

Notemos que todos los axiomas salieron de forma casi inmediata de la definición de $\mathbb{N}$ o de la definición de $\sigma$, justo como esperábamos.

Más adelante…

Ya dimos la construcción de los naturales. También vimos que en verdad funcionan como esperábamos. nuestro siguiente objetivo será definir una suma, un producto y un orden en $\mathbb{N}$. Así como lo hicimos con los axiomas de Peano, veremos que nuestras definiciones coincidirán con las propiedades que conocemos.

Para hacer esto seguiremos pensando simultáneamente tanto en la definición conjuntista que hemos dado de los naturales, como en los axiomas de Peano. Especialemente usaremos el quinto axioma de manera repetida. Veremos cómo este axioma es básicamente el principio de inducción que conocimos en Álgebra Superior I. También veremos cómo nos ayuda a demostrar el teorema de recursión, el cual a su vez la herramienta que necesitaremos para definir con toda formalidad la suma y producto en los naturales.

Tarea moral

Completa los detalles faltantes de la construcción de los naturales. En particular, sobre por qué el conjunto $B$, de los conjuntos inductivos de $A$, sí existe. Necesitarás usar un axioma muy específico de la teoría de conjuntos.
Demuestra que si $x\subset y\subset\sigma(x) $, entonces $y=x$ o $y=\sigma(x)$.
Si aún no estás tan acostumbrado a las intersecciones arbitrarias, considera un conjunto inductivo $A$ y la siguiente definición: $$\mathbb{N}’:=\{x\in A: x \text{ está en todo conjunto inductivo}\}.$$ ¿Cómo se relaciona el axioma del infinito, con el hecho de que esto sí sea un conjunto?
Esboza una demostración de que $\mathbb{N}’=\mathbb{N}$.
Usa el quinto axioma de Peano para demostrar que para cualquier natural $n$ se cumple que $$\sigma(n)=\{0, 1, 2, …, n\}.$$
Sugerencia. Considera el conjunto $S\subseteq \mathbb{N}$ de enteros $n$ para los cuales la afirmación anterior es cierta. Demuestra que $S$ es inductivo y usa el quinto axioma para concluir que $S=\mathbb{N}$.

Entradas relacionadas

Ir a: Álgebra Superior II
Entrada anterior del curso: Introducción al curso y a los números naturales
Siguiente entrada del curso: Principio de inducción y teoremas de recursión

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior I: Tipos de enunciados matemáticos

Por Leonardo Ignacio Martínez Sandoval

5 respuestas

Introducción

En esta entrada platicamos de varios tipos de enunciados con los que te vas a encontrar frecuentemente en tu trayectoria matemática a nivel universitario. Para entender correctamente las definiciones siguientes, es muy importante que ya estés familiarizado con el concepto de proposición matemática que tratamos con anterioridad.

Axiomas

En las matemáticas, los axiomas son enunciados que tomamos como verdaderos. NEs decir, son verdaderos por convención. Son el punto de partida que establece las reglas del juego de cierta área de las matemáticas.

Cuando estés en cálculo, se verán los axiomas que deben satisfacer los números reales. Cuando estés en álgebra lineal, ser verán los axiomas de espacio vectorial. En geometría moderna se verán los postulados de Euclides (que puedes pensar como axiomas). En este curso hablaremos un poco de axiomas para la teoría de conjuntos y para los números naturales.

Algunos ejemplos son los siguientes (no es necesario que entiendas exactamente qué dicen):

Para cada dos puntos, hay una línea que pasa por ellos.
Cada número natural tiene un único sucesor.
Para el neutro $e$ de un grupo $G$ y cualquier elemento $a$ en $G$, existe un elemento $b$ en $G$ tal que $ab=ba=e$.
Para cualquier colección $A_1,\ldots,A_n$ de abiertos, se tiene que $$A_1 \cap A_2 \cap \ldots A_n$$ también es abierto.

Los axiomas no requieren ser justificados o demostrados. Simplemente acordamos su validez.

Definiciones

Las definiciones no son proposiciones matemáticas y no tiene sentido decir que son verdaderas o falsas. Simplemente son enunciados que le ponen un nombre a un objeto matemático con ciertas propiedades para poder referirnos a él de manera sencilla más adelante. En ocasiones, estas definiciones hacen referencia a cómo se expresa el concepto matemático en símbolos y frecuentemente para ello se usa la palabra «denotar».

Hay varias formas en las que se pueden escribir definiciones matemáticas. Las siguientes son algunas (no es necesario que las entiendas completamente).

Un número entero es perfecto si la suma de sus divisores propios es igual a sí mismo.
Un cuadrilátero es un cuadrado si las longitudes de sus cuatro lados son iguales y los cuatro ángulos en sus vértices son rectos.
Para dos conjuntos $A$ y $B$ definimos a su unión como el conjunto que consiste de los elementos que están en cualquiera de los dos conjuntos. Lo denotamos por $A\cup B$.
Una operación binaria es asociativa si $(a\cdot b)\cdot c=a\cdot (b\cdot c)$.
Un grupo es un conjunto con una operación binaria asociativa, con neutro y con inversos.

Las definiciones son muy útiles pues ayudan a acortar el lenguaje e ir construyendo ideas más complejas e interesantes. Toma en cuenta lo siguiente con respecto a las definiciones.

Cuando se tienen enunciados del estilo «tomemos $C$ un cuadrado», o «sea $G$ un grupo», o incluso «consideremos $A\cup B$», de manera instantánea ya se pueden tomar como verdaderas todas las propiedades dadas por la definición. Así, de manera inmediata es verdadero que los lados de $C$ miden lo mismo y que $A\cup B$ tiene tanto a los elementos de $A$ como a los de $B$. También es verdadero que $G$ tiene una operación asociativa. Y por la definición de «asociativa», de manera inmediata es verdadero que $(a\cdot b)\cdot c=a\cdot (b\cdot c)$. Observa cómo se van haciendo deducciones sucesivas de hechos verdaderos.
Cuando se requiera verificar si un objeto satisface una definición, entonces hay que verificar que sean ciertas todas las propiedades enunciadas en la definición. Así, no basta ver que $C$ tiene lados iguales para ver que es un cuadrado. También hay que ver que sus ángulos son todos ellos rectos.

Proposiciones

Las proposiciones son simplemente proposiciones matemáticas en el sentido de la entrada anterior. Son enunciados matemáticos que se puede determinar si son verdaderos o falsos. Usualmente, cuando se encuentran en un curso o en un texto, es porque ya se verificó su veracidad. En estos contextos, tras enunciar una proposición se suele dar una demostración, que es un concepto del que hablaremos a profundidad más adelante.

Una vez que tenemos axiomas y definiciones, es posible empezar a relacionar distintos conceptos mediante proposiciones. A continuación se tienen algunos ejemplos:

Si un cuadrilátero tiene todos sus ángulos rectos y tiene dos lados consecutivos iguales, entonces es un cuadrado.
La suma de dos números pares siempre da un número par.
Existe una función continua que no es diferenciable.
Siempre se cumple que $(A\cup B)^c = A^c \cap B^c$.
La suma de dos números que sean múltiplos de $3$ nunca es un múltiplo de $3$.
Todas las funciones diferenciables son continuas.

Todas las proposiciones arriba enunciadas son verdaderas, excepto una de ellas. Observa que usan palabras como «y», «si… entonces…», «todas», etc. Varias de estas palabras tienen un significado matemático muy preciso que discutiremos más adelante. Después veremos cómo determinar la veracidad de algunas de estas proposiciones y qué tipo de argumentos hay que dar para demostrarlas.

Lemas

Un lema es prácticamente una proposición. Los lemas tienen este nombre más bien con un fin práctico. Lo que se está avisando es que hay que poner atención a esa proposición, pues probablemente sea utilizada como resultado auxiliar una o varias veces más adelante.

Como los lemas son proposiciones matemáticas, entonces pueden ser verdaderos o falsos. Por esta razón, para poder afirmar que un lema es verdadero, es necesario dar una demostración en donde se justifique o se deduzca desde elementos más básicos (como definiciones, axiomas o proposiciones) la validez del mismo.

Teoremas

Los teoremas también son básicamente proposiciones. Su nombre también cumple un fin práctico. Cuando se le pone el nombre de «teorema» a una proposición, es para dar a entender que es una proposición muy importante dentro de la teoría. Usualmente para llegar a un teorema se necesita probar varios resultados auxiliares.

Hay algunos teoremas que se vuelven tan relevantes que adquieren nombre propio. Algunos ejemplos de teoremas son los siguientes (son ejemplos nada más, tampoco es fundamental que entiendas exactamente qué están diciendo):

Un espacio vectorial de dimensión finita es isomorfo a su espacio dual.
Teorema de Pitágoras: En un triángulo rectángulo de catetos con longitudes $a$ y $b$ e hipotenusa $c$ se cumple que $a^2+b^2=c^2$.
Teorema de Hall: Si una familia de al menos $n+1$ convexos en $\mathbb{R}^n$ se intersecta de $n+1$ en $n+1$ elementos, entonces toda la familia se intersecta.
Teorema fundamental del álgebra: Todo polinomio no constante con coeficientes en $\mathbb{C}$ tiene por lo menos una raíz en $\mathbb{C}$.

Los investigadores en matemáticas y áreas afines se dedican a encontrar este tipo de resultados relevantes. Una frase conocida de Alfréd Rényi es: «Un matemático es una máquina que transforma café en teoremas».

Corolarios

Un corolario, de nuevo, es prácticamente una proposición. Sin embargo, en el desarrollo de la teoría matemática los corolarios usualmente son resultados que se siguen fácilmente de resultados previos, sobre todo de teoremas. A continuación, algunos ejemplos.

Un corolario del teorema de Pitágoras es «La hipotenusa es más larga que cualquiera de los catetos».
Un corolario de teorema fundamental del álgebra es «Un polinomio no constante de grado $n$ tiene exactamente $n$ raíces complejas contando multiplicidades».
Un corolario del teorema de Hall es que si en una mesa hay manchas circulares del mismo radio, y cualesquiera tres de ellas se pueden cubrir con un plato, entonces todas las manchas se pueden cubrir usando un sólo un plato.

Puedes pensar en los corolarios como la «cereza del pastel».

Conjeturas

Las conjeturas también son proposiciones matemáticas: son enunciados que se puede determinar si son verdaderos o falsos. Sin embargo, a diferencia de los lemas, proposiciones, teoremas y corolarios (que se sabe que son verdaderos), lo que ocurre con las conjeturas es que todavía no hay nadie que haya determinado si son verdaderas o falsas.

Las conjeturas juegan un papel importante en la teoría de muchas áreas de las matemáticas, pues son resultados que se espera que sean verdaderos, pero para los cuales aún es necesario el desarrollo de nuevas técnicas en la investigación matemática.

Recapitulación

En resumen, los lemas, proposiciones, teoremas y corolarios son todos ellos proposiciones matemáticas. Pueden ser verdaderas o falsas. Los que encuentres en textos y cursos prácticamente serán verdaderos. Para asegurar que son verdaderos, requieren de una demostración, es decir, de una serie de argumentos y deducciones.

Usualmente encontrarás lo que hemos platicadoen el siguiente «esquema»:

Definición -> Lema -> Proposición -> Teorema -> Corolario

Los axiomas son enunciados matemáticos que damos por hecho. Las definiciones nos ayudan a referirnos a objetos matemáticos con ciertas propiedades de manera más sencilla.

Las conjeturas son proposiciones matemáticas que todavía nadie sabe si son verdaderas o no. Los investigadores en matemáticas desarrollan nuevas técnicas para resolver estos problemas.

Más adelante…

Ya platicamos del tipo de enunciados que existen en las matemáticas y dimos algunos ejemplos. En el transcurso del curso veremos muchos ejemplos más. Después de este paréntesis, es importante que retomemos la teoría de lógica para poder hablar de algo fundamental al momento de determinar la veracidad de proposiciones matemáticas: las demostraciones. Antes de llegar ahí, es importante hablar de conectores lógicos, de cuantificadores y de condicionales.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Busca en internet por lo menos otros tres teoremas.
Investiga por lo menos otras tres conjeturas que todavía no hayan sido resueltas.
Encuentra en internet una noticia de alguna conjetura matemática que haya sido resuelta recientemente.

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Introducción al curso y proposiciones matemáticas
Siguiente entrada del curso: Conectores: negaciones, conjunciones y disyunciones

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»