Introducción
Lo primero que queremos determinar en un problema de clasificación es cuáles son los objetos que clasificaremos. En esta entrada los definimos con toda precisión: serán los polinomios cuadráticos en dos variables y las curvas cuadráticas.
Los primeros son expresiones algebraicas que mezclan a dos variables $x$ y $y$ mediante sumas y productos, pero teniendo grado dos. Las segundas son aquellos conjuntos del plano en donde se anula un polinomio cuadrático.
Polinomios cuadráticos en dos variables
Comencemos con una definición algebraica.
Definición. Un polinomio cuadrático en dos variables $P$ es una función $P:\mathbb{R}^2\to \mathbb{R}$ de la forma $$P((x,y))=Ax^2+Bxy+Cy^2+Dx+Ey+F,$$ para algunos reales $A,B,C,D,E,F$, en donde alguno de $A$, $B$ ó $C$ es distinto de cero.
En ocasiones, para abreviar «polinomio cuadrático en dos variables» simplemente usaremos las siglas «PCDV».
Ejemplo. Todas las expresiones que aparecen en las cónicas canónicas que hemos estudiado son PCDVs. Por ejemplo, la ecuación canónica de la elipse $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$ puede reescribirse como $$b^2x^2+a^2y^2-a^2b^2=0.$$ Del lado izquierdo de esta igualdad tenemos un PCDV. De manera similar, la ecuación canónica de la parábola $y^2=4px$ puede reescribirse como $y^2-4px=0$. Una vez más al lado izquierdo nos aparece un PCDV.
$\triangle$
Ejemplo. Si consideramos las dos rectas $3x+5y+1=0$ y $2x-2y+1=0$ y «multiplicamos» sus ecuaciones, entonces obtenemos de nuevo un PCDV pues el producto es:
\begin{align*}
(3x+5y+1)(2x-2y+1)&=6x^2-6xy+3x+10xy-10y^2+5y+2x-2y+1\\
&=6x^2+4xy-10y^2+5x+3y+1.
\end{align*}
$\triangle$
Curvas cuadráticas
Cuando tenemos una expresión algebraica que depende de dos variables $x$ y $y$, entonces podemos preguntarnos por cómo es la figura geométrica que se obtiene al considerar los puntos $(x,y)$ del plano que hacen que la expresión algebraica sea igual a cero. Un ejemplo de esto es cuando consideramos las expresiones del estilo $Ax+By+C$. Las parejas $(x,y)$ que hacen que esta expresión sea igual a cero forman una recta en el plano. En efecto, forman la recta en forma normal dada por la ecuación $(A,B)\cdot (x,y)=-C$, como puedes verificar.
Esta idea es mucho más general. A partir de los polinomios cuadráticos en dos variables también podemos hacernos la misma pregunta: ¿cómo se ven las parejas $(x,y)$ que anulan un polinomio cuadrático? La respuesta será importante, así que las figuras que se construyen así les damos su propio nombre.
Definición. Una curva cuadrática es el conjunto de puntos $(x,y)$ del plano que anulan a un polinomio cuadrático en dos variables $P$. En otras palabras, es un conjunto de la forma $$\mathcal{C}:=\{(x,y)\in \mathbb{R}^2: Ax^2+Bxy+Cy^2+Dx+Ey+F = 0\}.$$
A $P$ le llamamos el polinomio asociado a $\mathcal{C}$. A $\mathcal{C}$ le llamamos la curva descrita (o dada) por $P$. Quizás usaremos terminología un poco distinta, pero que siga dejando evidente que $P$ y $\mathcal{C}$ están relacionados.
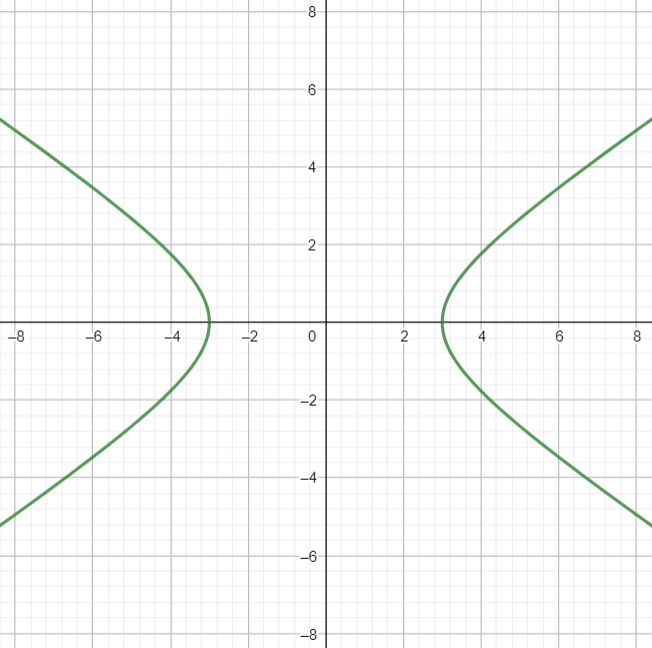
Ejemplo. Ya hemos estudiado anteriormente algunas curvas cuadráticas: las cónicas canónicas. Por ejemplo, si tomamos el PCDV $P((x,y))=4x^2-9y^2-36$ y nos preguntamos para cuáles parejas $(x,y)$ esto es igual a cero, como respuesta tenemos que son aquellas parejas $(x,y)$ tales que $ 4x^2-9y^2-36=0$, lo cual podemos reescribir como $$\frac{x^2}{9}-\frac{y^2}{4}=1.$$ Esta es la hipérbola canónica de semieje mayor $3$ y semieje menor $2$. Podemos verla en la siguiente figura.
$\triangle$
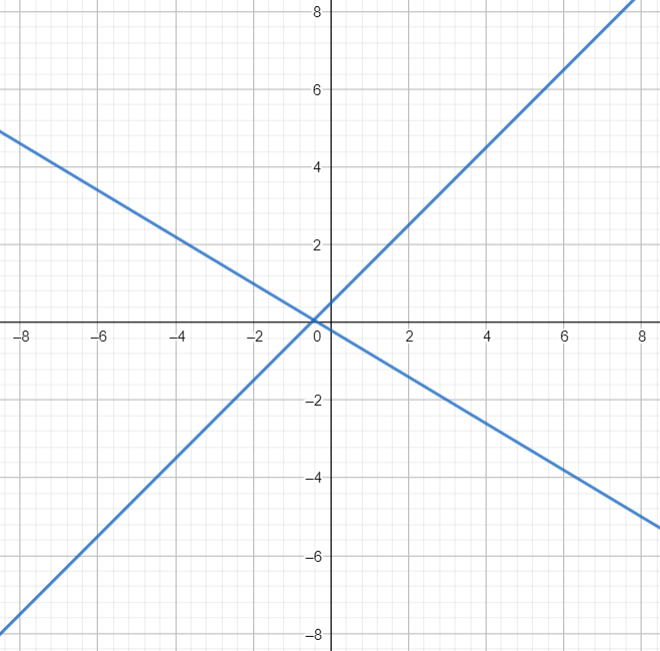
Ejemplo. ¿Qué sucede si nos fijamos en la curva descrita por el polinomio cuadrático en dos variables $$ 6x^2+4xy-10y^2+5x+3y+1$$ que construimos en un ejemplo anterior? Si recuerdas, obtuvimos este polinomio cuadrático en dos variables a partir de multiplicar dos expresiones. De esta forma, tenemos que $$ 6x^2+4xy-10y^2+5x+3y+1=0$$ si y sólo si $$ (3x+5y+1)(2x-2y+1) =0.$$ Pero el producto de dos cosas es igual a cero si y sólo si alguna es igual a cero. Así, alguna de las expresiones $3x+5y+1$ y $2x-2y+1$ debe ser igual a cero. Si la primera es cero, entonces $(x,y)$ es un punto en la recta normal $\ell_1$ de ecuación $(3,5)\cdot (x,y) = -1$. Si la segunda es cero, entonces $(x,y)$ es un punto en la recta normal $\ell_2$ de ecuación $(2,-2)\cdot(x,y) = -1$. Así, la curva cuadrática descrita por el PCDV es la unión de $\ell_1$ con $\ell_2$. Podemos verla en la siguiente figura.
$\triangle$
Forma matricial de polinomios cuadráticos en dos variables
Cuando trabajamos con rectas, nos convenía tener varias formas de expresarlas: la forma paramétrica ayudaba a determinar fácilmente el paralelismo, la forma baricéntrica nos daba fórmulas sencillas para los puntos medios, la forma normal nos permitía encontrar distancias, etc. Así mismo, cuando trabajamos con polinomios cuadráticos en dos variables es de ayuda tener más de una expresión.
Podemos reescribir un polinomio cuadrático en dos variables $$P((x,y))=Ax^2+Bxy+Cy^2+Dx+Ey+F$$ de una manera más compacta usando multiplicación matricial. Para ello, definimos $$M=\begin{pmatrix} A & \frac{B}{2} \\ \frac{B}{2} & C \end{pmatrix}, k=\begin{pmatrix} D \\ E \end{pmatrix}, v=\begin{pmatrix} x \\ y \end{pmatrix}.$$ Con esta notación, e interpretando a las matrices de $1\times 1$ como reales, tenemos que $P$ se puede reescribir de la siguiente manera: $$P(v)=v.$$
En efecto, al realizar las operaciones en el lado derecho obtenemos:
\begin{align*}
v^t M v + k^t v + F &=\begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} A & \frac{B}{2} \\ \frac{B}{2} & C \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} D & E \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + F\\
&=\begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} Ax + \frac{B}{2} y \\ \frac{B}{2} x + C y \end{pmatrix} + Dx + Ey + F\\
&=Ax^2 + Bxy + Cy^2+Dx+Ey+F.
\end{align*}
Observa que cuando pasamos un polinomio cuadrático en dos variables a forma matricial entonces siempre obtenemos una matriz $M$ simétrica.
Ejemplo. La forma matricial del PCDV que encontramos anteriormente $$6x^2+4xy-10y^2+5x+3y+1$$ es
$$ \begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} 6 & 2 \\ 2 & 10 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 5 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + 1.$$
nota que el coeficiente de $xy$ se tuvo que dividir entre $2$ para llegar a las entradas de la matriz. Es importante recordar esto al pasar de la forma en coordenadas a la forma matricial.
$\triangle$
En caso de ser necesario, también podemos pasar fácilmente de la forma matricial de un polinomio cuadrático en dos variables a su forma en coordenadas.
Ejemplo. Si comenzamos con el polinomio cuadrático en dos variables con forma matricial $$ \begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} 2 & -1 \\ -1 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 0 & -3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} – 1, $$
entonces su forma en coordenadas es $$2x^2-2xy+3y^2 – 3y -1.$$
Observa que las entradas $-1$ fuera de la diagonal principal de la matriz al salir se duplican para conformar el coeficiente de $xy$. Es importante recordar esto al pasar de forma matricial a forma en coordenadas.
$\triangle$
Más adelante…
En esta entrada definimos qué son los polinomios cuadráticos en dos variables y qué son las curvas cuadráticas.
Por un lado, mencionamos que todas las ecuaciones de cónicas canónicas que hemos visto tienen polinomios cuadráticos en dos variables. ¿Será que todas las ecuaciones de cónicas también tienen polinomios cuadráticos en dos variables? Por otro lado, vimos que algunas curvas cuadráticas son cónicas. Pero nos pasó algo un poco raro: en un ejemplo salieron dos rectas que se intersectan, que quizás estrictamente no pensamos como una cónica usual (elipse, hipérbola, parábola).
¿Cómo serán todas las curvas cuadráticas? ¿Serán sólo las cónicas usuales y algunas excepciones o podrán tener formas muy extrañas? Eso lo estudiaremos después.
También en esta entrada vimos la forma matricial de un polinomio cuadrático en dos variables. De momento, no hemos hablado de la utilidad que tiene pensar a un PCDV así. Sin embargo, en la siguiente entrada veremos que esta expresión es fundamental para ver qué sucede cuando «combinamos» un polinomio cuadrático con una transformación afín.
Tarea moral
- Usa alguna herramienta tecnológica (como GeoGebra) para trazar las curvas cuadráticas descritas por los siguientes polinomios cuadráticos en dos variables:
- $x^2-2xy+3y^2+x-5y+7$
- $3y^2+5y+x$
- $x^2+y^2-5x-5y+3$
- $xy-x-y+7$
- $-x^2+2xy-3y^2-x+5y-7$
- Sea $P:\mathbb{R}^2\to \mathbb{R}$ dada por $P((x,y))=(Ax+By+C)(Dx+Ey+F)$. Demuestra que $P$ es un polinomio cuadrático en dos variables. Luego, demuestra que:
- Si $AE-BD\neq 0$, entonces la curva cuadrática dada por $P$ es la unión de dos rectas que se intersectan.
- Si $AE-BD=0$, entones la curva cuadrática dada por $P$ es la unión de dos rectas paralelas (no necesariamente distintas).
- Demuestra que la intersección de una recta con una curva cuadrática sólo puede ser:
- Vacía,
- Un punto,
- Dos puntos, o
- Una infinidad de puntos.
- Demuestra que cualquier curva cuadrática $\mathcal{C}$ puede ser descrita a través de una infinidad de polinomios cuadráticos en dos variables.
- Considera la gráfica de la función $f(x)=\sin(x)$. ¿Será que esta gráfica es una curva cuadrática? Intenta demostrar por qué sí o por qué no.
Entradas relacionadas
- Ir a Geometría Analítica I
- Entrada anterior del curso: Introducción a resultados de clasificación
- Siguiente entrada del curso: Equivalencias afines e isométricas