Introducción
En la entrada anterior hablamos de la noción de potencia de un punto con respecto a una circunferencia. Lo que haremos ahora es tomar dos circunferencias y preguntarnos por los puntos cuya potencia a ellas coincide. Esto nos llevará a estudiar la noción de eje radical de las circunferencias.
A grandes rasgos, definiremos qué es el eje radical. Luego, mostraremos que es una recta muy específica. Después de hacer eso, estudiaremos qué sucede si tenemos tres circunferencias. Finalmente, hablaremos un poco de cómo dibujar el eje radical de dos circunferencias.
Eje radical de 2 circunferencias
La definición que nos interesa estudiar ahora es el conjunto de puntos del plano cuyas potencias a dos circunferencias coincide. La siguiente definición formaliza esto.
Definición. El eje radical de dos circunferencias no concéntricas $\mathcal{C}_1$ y $\mathcal{C}_2$ es el lugar geométrico de los puntos $P$ tales que $$\text{Pot}(P,\mathcal{C}_1)=\text{Pot}(P,\mathcal{C}_2).$$ Si un punto está en el eje radical de ellas, decimos que es equipotente a ambas.
Ejemplo.
$\triangle$
El eje radical es una recta
En esta sección demostraremos el siguiente teorema.
Teorema. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias no concéntricas de de centros $O_1$ y $O_2$. El eje radical de ellas es la recta que perpendicular a la recta $O_1O_2$, y que pasa por el punto $M$ de $O_1O_2$ que cumple $\text{Pot}(M,\mathcal{C}_1)=\text{Pot}(M,\mathcal{C}_2).$
La demostración de este teorema la dividiremos en las siguientes partes:
- Probar que existe al menos un punto $P$ en el eje radical.
- Mostrar que la proyección $M$ de dicho punto a la recta $O_1O_2$ también está en el eje radical.
- Ver que todo punto en la perpendicular a $O_1O_2$ por $M$ está en el eje radical.
- Mostrar que no existen otros puntos en el eje radical más allá de los ya localizados.
Veamos cada uno de estos puntos como una proposición por separado.
Proposición. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias no concéntricas. Existe al menos un punto $P$ en el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$.
Demostración. Vamos a dar una construcción explícita para encontrar un punto en el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$:
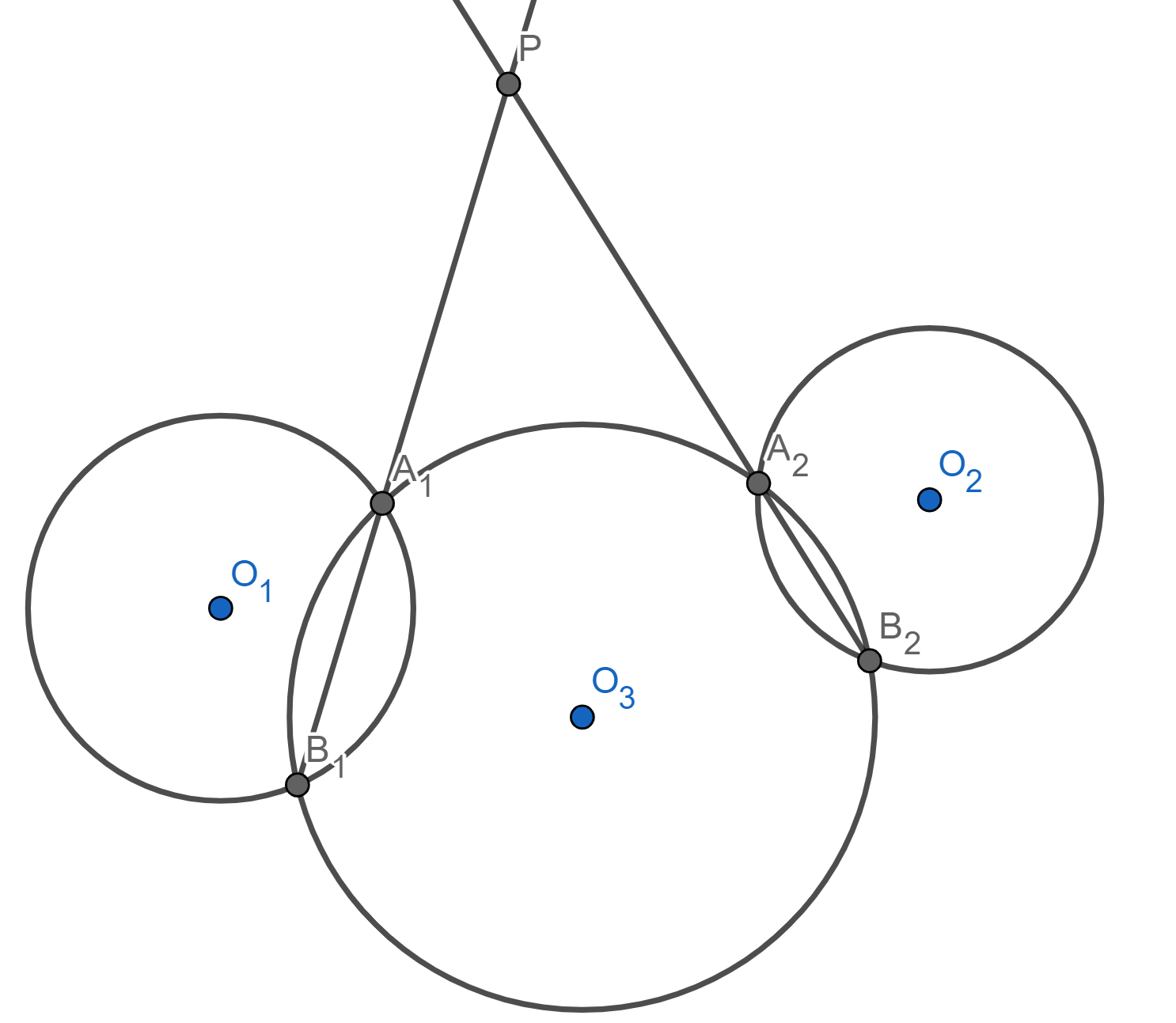
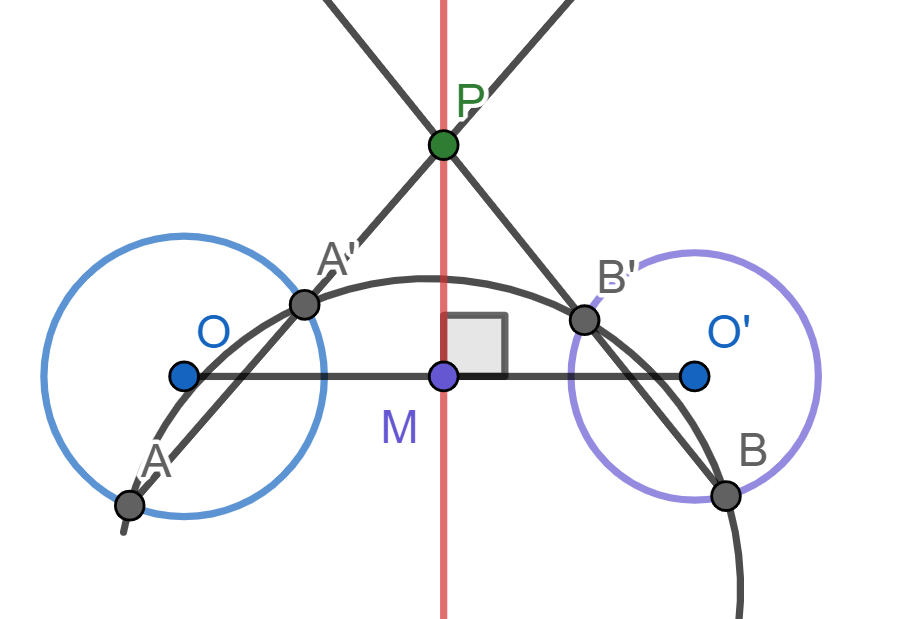
Para ello, tracemos una tercera circunferencia $\mathcal{C}_3$ que intersecte a cada una de $\mathcal{C}_1$ y $\mathcal{C}_2$ en dos puntos (una manera de hacer esto esto tomar $\mathcal{C}_3$ como el circuncírculo un punto dentro de $\mathcal{C}_1$, uno dentro de $\mathcal{C}_2$ y otro fuera de ambas).
Llamamos $A_1,B_1$ las intersecciones con $\mathcal{C}_1$ y $A_2,B_2$ las intersecciones con $\mathcal{C}_2$. Tomamos el punto $P$ como la intersección de $A_1B_1$ con $A_2B_2$ como en la siguiente figura.
Las siguientes cuentas muestran que $P$ es equipotente a ambas. Estamos usando el resultado de la entrada anterior que muestra que el cálculo de la potencia con respectoa $\mathcal{C}_3$ no depende de los puntos elegidos.
\begin{align*}
\text{Pot}(P,\mathcal{C}_1)&=PA_1 \cdot PB_1\\
&=\text{Pot}(P,\mathcal{C}_3)\\
&=PA_2 \cdot PB_2\\
&=\text{Pot}(P,\mathcal{C}_2)
\end{align*}
Por lo anterior es una realidad que existe al menos un punto en el eje radical.
$\square$
Ahora veremos que la proyección de un punto equipotente en la recta de los centros también es un punto equipotente.
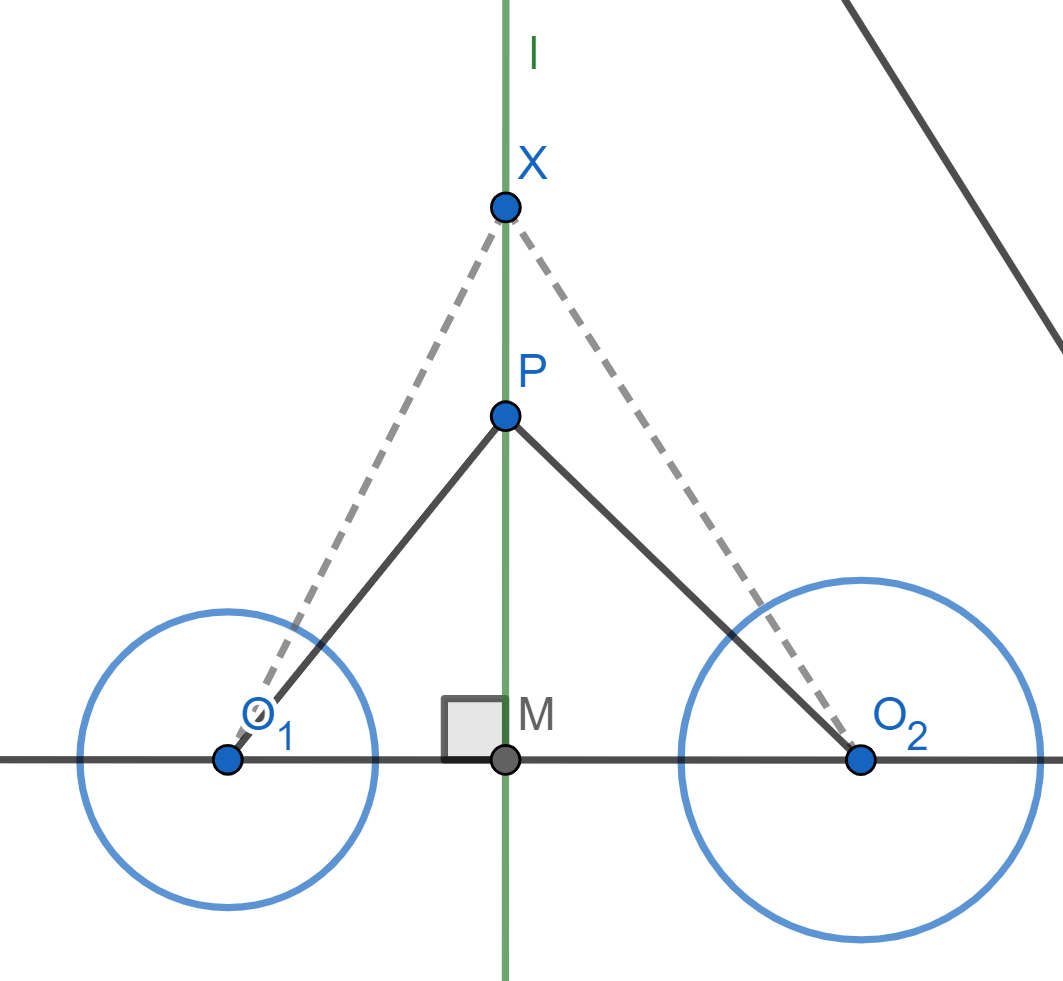
Proposición. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias no concéntricas de centros $O_1$ y $O_2$. Si $P$ es un punto equipotente con respecto a ellas y $M$ es el pie de la perpendicular desde $P$ a la recta $O_1O_2$, entonces $M$ es equipotente con respecto a las dos circunferencias.
Demostración. Sean $r_1$ y $r_2$ los radios de $\mathcal{C}_1$ y $\mathcal{C}_2$, respectivamente. Como $P$ esta en el eje radical de ambas, entonces por cómo se calcula la potencia con la distancia a los centros y el radio, tenemos que
\begin{equation}\label{eq:pot-ambos}PO_1^2 – r_1^2 = PO_2^2 – r_2^2.\end{equation}
Queremos demostrar que $M$ pertenece al eje radical, ósea $\text{Pot}(M,\mathcal{C}_1)=\text{Pot}(M,\mathcal{C}_2)$.
Tracemos los segmentos $O_1P$ y $O_2P$. Los triángulos $\triangle PMO_1$ y $\triangle PMO_2$ son rectángulos, ver la siguiente figura.
Por Pitágoras se sigue que $$PO_1^2=MO_1^2+PM^2$$ y $$PO_2^2=MO_2^2+PM^2.$$
Al sustituir en \eqref{eq:pot-ambos}, obtenemos: $$MO_1^2+PM^2-r_1^2=MO_2^2+PM^2-r_2^2.$$
Cancelando $PM^2$, se obtiene la expresión que muestra que $M$ también es equipotente a ambas circunferencias:
\begin{equation}\label{eq:Mradical}MO_1^2-r_1^2=MO_2^2-r_2^2.\end{equation}
$\square$
Ahora veremos que todos los puntos en la perpendicular por $M$ también son equipotentes.
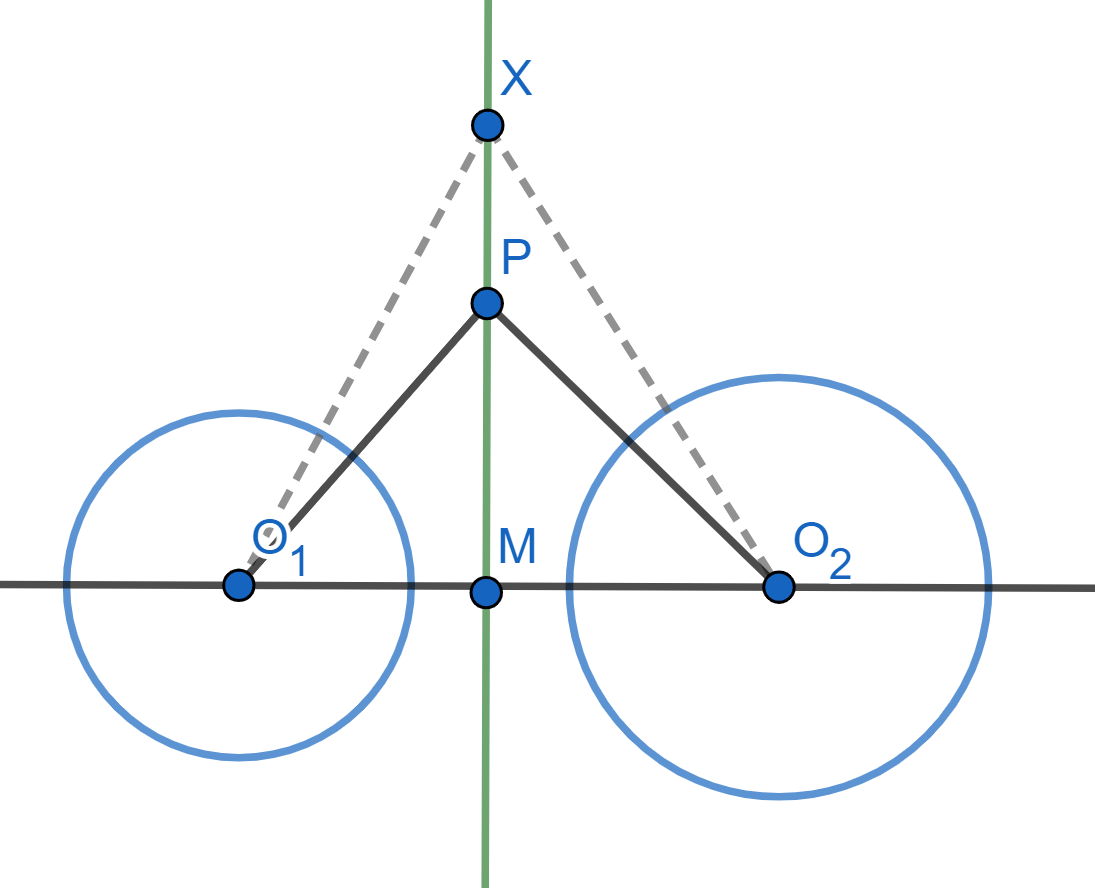
Proposición. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias no concéntricas de de centros $O_1$ y $O_2$. Si $M$ es un punto en $O_1O_2$ equipotente a ambas circunferencias, entonces todos los puntos en la perpendicular a $O_1O_2$ por $M$ también lo son.
Demostración. A la perpendicular del enunciado la llamaremos $l$. Sea $X$ un punto en $l$. Debemos mostrar que $$\text{Pot}(X,\mathcal{C}_1)=\text{Pot}(X,\mathcal{C}_2).$$
Para ello, trazamos $O_1X$ y $O_2X$.
Como los triángulos $\triangle XMO_1$ y $\triangle XMO_2$ son rectángulos, nuevamente por Pitágoras: $$XO_1^2=MO_1^2+XM^2$$ y $$XO_2^2=MO_2^2+XM^2.$$
Usando las igualdades anteriores y que $M$ está en el eje radical (específicamente, \eqref{eq:Mradical}), tenemos que:
\begin{align*}
\text{Pot}(X,\mathcal{C}_1)&=XO_1^2-r_1^2\\
&= MO_1^2+XM^2 – r_1^2\\
&=MO_2^2+XM^2 – r_2^2\\
&=XO_2^2-r_2^2\\
&=\text{Pot}(X,\mathcal{C}_2)
\end{align*}
Por lo tanto, todo punto $X$ en $l$ es un punto en el eje radical.
$\square$
Ya sólo nos falta ver que no hay más puntos equipotentes.
Proposición. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias no concéntricas de de centros $O_1$ y $O_2$. Si $M$ es un punto en $O_1O_2$ equipotente a ambas circunferencias, entonces únicamente los puntos en la perpendicular a $O_1O_2$ por $M$ son equipotentes a las circunferencias.
Demostración. Primero veremos que el único punto en $O_1O_2$ que puede funcionar es $M$. Para ello, para buscar una contradicción supongamos que otro punto $N$ en la recta $O_1O_2$, con $N\neq M$ también cumple que $\text{Pot}(N,\mathcal{C}_1)=\text{Pot}(N,\mathcal{C}_2)$. Entonces, $$NO_1^2-r_1^2=NO_2^2-r_2^2.$$
Restando a esta ecuación la ecuación \eqref{eq:Mradical}, obtenemos que $$NO_1^2-MO_1^2 = NO_2^2-MO_2^2,$$ y por diferencia de cuadrados, $$(NO_1+MO_1)(NO_1-MO_1)=(NO_2+MO_2)(NO_2-MO_2).$$
Tenemos que $NO_1-MO_1=NO_1+O_1M=NM$ y lo análogo para $O_2$, de modo que $$(NO_1+MO_1)NM=(NO_2+MO_2)NM.$$
Como $N\neq M$, tenemos $NM\neq 0$ y lo podemos cancelar. $$NO_1+MO_1=NO_2+MO_2,$$
de donde sale la cuarta igualdad de la siguiente cadena:
\begin{align*}
O_2O_1&=O_2N+NO_1\\
&=-NO_2+NO_1\\
&=-MO_1+MO_2\\
&=O_1M+MO_2\\
&=O_1O_2.
\end{align*}
Obtenemos que $O_2O_1=O_1O_2$. ¡Esto es imposible, pues son segmentos dirigidos y $O_1\neq O_2$! Esta contradicción muesta que $M$ es el único punto en $O_1O_2$ equipotente a ambas circunferencias.
Para finalizar, supongamos que existe un punto $P’$ cualquiera del plano equipotente a $\mathcal{C}_1$ y $\mathcal{C}_2$. Por la proposición de la proyección, la proyección $M’$ de $P’$ en $O_1O_2$ también es equipotente. Por lo que acabamos de mostrar, $M=M’$. Y así, $P’$ está en la perpendicular a $O_1O_2$ por $M$, como queríamos.
$\square$
Los ejes radicales por parejas de 3 circunferencias son concurrentes
Si tenemos tres circunferencias, entonces definen tres ejes radicales. Estos tres ejes radicales siempre concurren.
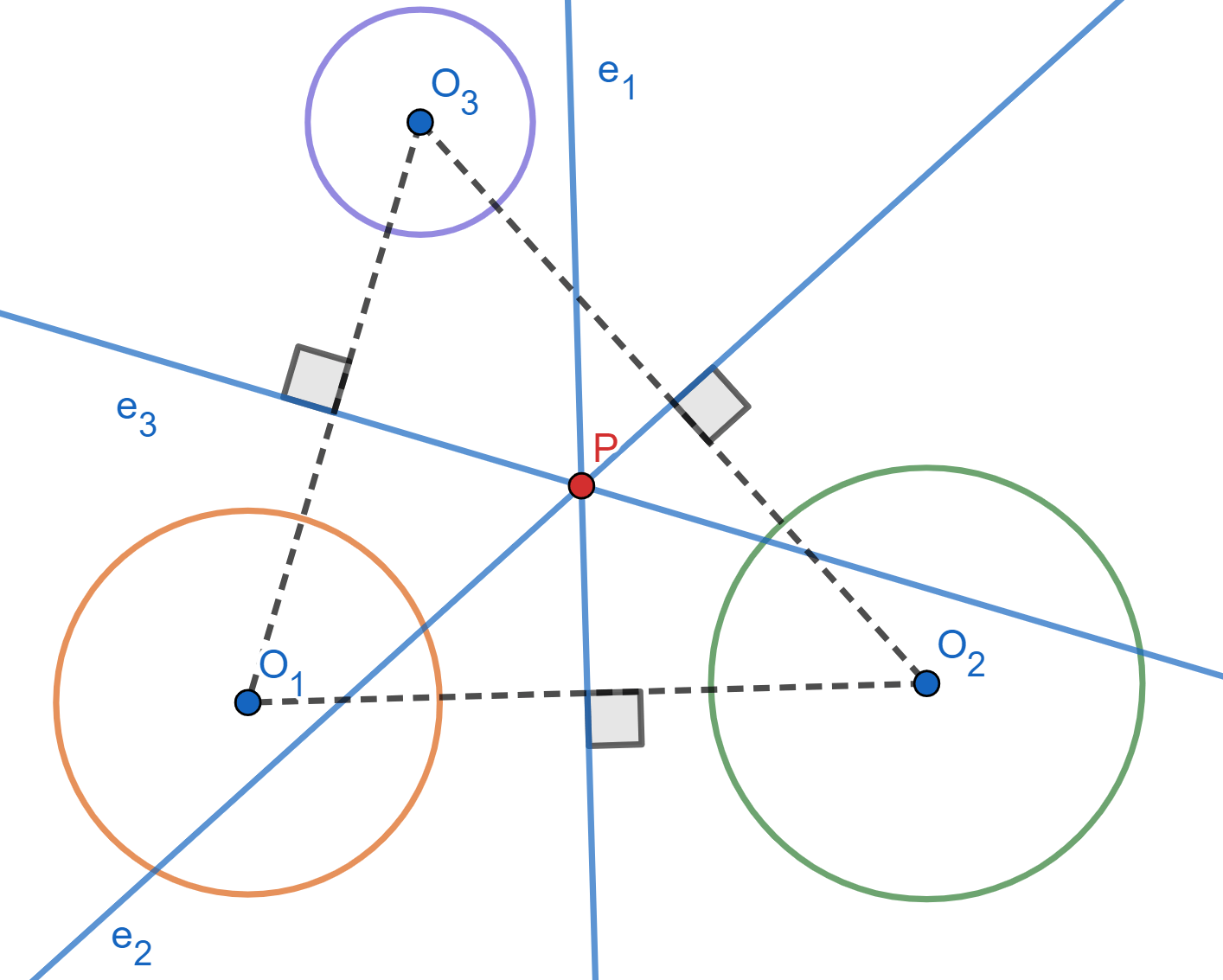
Teorema. Sean $\mathcal{C}_1$, $\mathcal{C}_2$ y $\mathcal{C}_3$ circunferencias de centros no colineales. Sea $e_1$ el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$. Sea $e_2$ el eje radical de $\mathcal{C}_2$ y $\mathcal{C}_3$. Sea $e_3$ el eje radical de $\mathcal{C}_3$ y $\mathcal{C}_1$. Las rectas $e_1,e_2,e_3$ son concurrentes.
Demostración. Consideremos 3 circunferencias $\mathcal{C}_1,\mathcal{C}_2$ y $\mathcal{C}_3$, cuyos centros son $O_1$, $O_2$ y $O_3$ no son colineales (en particular, son distintos). Tomemos los ejes radicales $e_1,e_2,e_3$ como en el enunciado.
Llamamos $P$ al punto de intersección de $e_1$ y $e_2$. Como $P$ está en $e_1$, entonces $\text{Pot}(P,\mathcal{C}_1)=\text{Pot}(P,\mathcal{C}_2)$ y como $P$ está en $e_2$, entonces $\text{Pot}(P,\mathcal{C}_2)=\text{Pot}(P,\mathcal{C}_3)$.
De esta manera, $$\text{Pot}(P,\mathcal{C}_1)=\text{Pot}(P,\mathcal{C}_3).$$ Esto muestra que también $P$ está en $e_3$. Por lo tanto, los 3 ejes radicales concurren en $P$.
$\square$
Construcción del eje radical
¿Cómo podemos dibujar el eje radical de dos circunferencias no concéntricas $\mathcal{C}_1$ y $\mathcal{C}_2$, digamos, con regla y compás? Podemos seguir la idea que usamos cuando probamos que por lo menos existe un punto en el eje radical. Sean $O_1$ y $O_2$ los centros de estas circunferencias, respectivamente.
Dibujemos una circunferencia $\mathcal{C}$ que corte a las circunferencias $\mathcal{C}_1$ y $\mathcal{C}_2$, en $A,A’$ y $B,B’$. Esto puede hacerse trazando el circuncírculo de $O_1$, $O_2$ y un punto fuera de ambas cirfunferencias. Sean $A$ y $A’$ las intersecciones de $\mathcal{C}$ con $\mathcal{C}_1$. Sean $B$ y $B’$ las intersecciones de $\mathcal{C}$ con $\mathcal{C}_2$. Tomemos $P$ la intersección de $AA’$ y $BB’$. Por lo que mostramos anteriormente, $P$ está en el eje radical de las circunferencias. Y además, también mostramos que la recta perpendicular a $O_1O_2$ por $P$ es el eje radical. Así, al trazar esta perpendicular, obtenemos el eje radical requerido.
Más adelante…
Se seguirá abordando el tema de potencia de un punto y el eje radical con respecto a las circunferencias ortogonales.
Al final de los temas de esta primera unidad se dejará unas series de ejercicios.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Poencia de un punto
- Siguiente entrada del curso: Circunferencias ortogonales