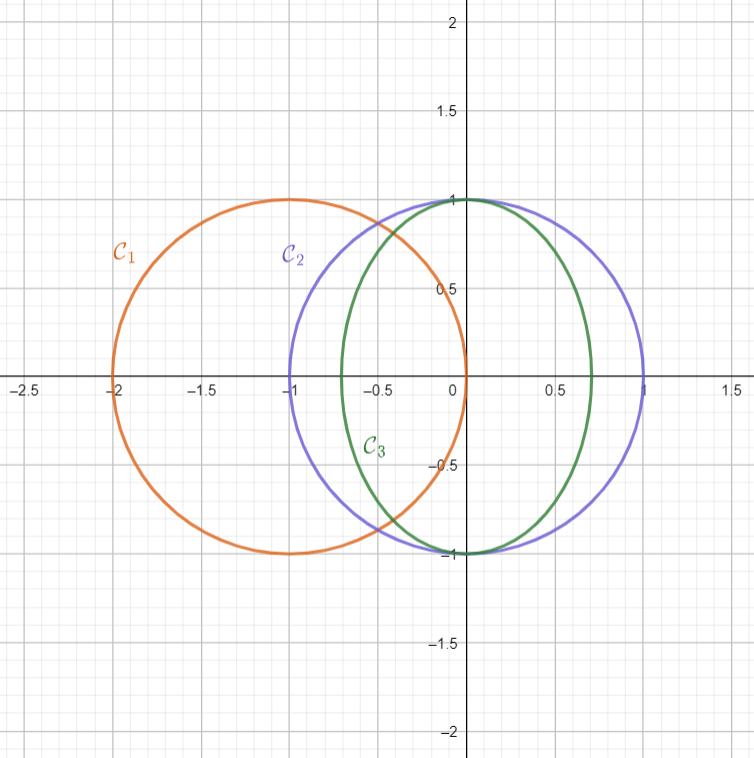Introducción

En entradas anteriores hablamos de los objetos que nos interesa clasificar: los polinomios cuadráticos y las curvas cuadráticas. Ahora hablaremos de las nociones que usaremos para considerar a dos polinomios cuadráticos o curvas cuadráticas como «equivalentes». Para ello, definiremos las nociones de «afínmente equivalentes» e «isométricametne equivalentes».

Composición de un PCDV y una transformación afín

Antes de enunciar propiamente el problema de clasificación que queremos resolver, vamos a demostrar un resultado auxiliar fundamental. A grandes rasgos, lo que nos dice es que si combinamos un polinomio cuadrático en dos variables con una transformación afín, entonces de nuevo obtenemos un polinomio cuadrático en dos variables. La demostración hará evidente cómo a veces es más útil la forma matricial de un PCDV.

Teorema. Consideremos $P:\mathbb{R}^2\to \mathbb{R}$ un polinomio cuadrático en dos variables y $T:\mathbb{R}^2\to \mathbb{R}^2$ una transformación afín dados por

\begin{align*}
P(v)&=v^t M v + k^t v + F\\
T(v)&=Av+b
\end{align*}

para $A,M$ matrices de $2\times 2$, para $k,b$ vectores columna en $\mathbb{R}^2$ y $F$ un real. Entonces $P\circ T$ es nuevamente un polinomio cuadrático en dos variables y, explícitamente,

\begin{align*}
(P\circ T)(v)= v^t(A^tMA)v + (2b^t MA + k^t A) v + P(b) .
\end{align*}

Demostración. La expresión que queremos encontrar es $(P\circ T)(v)=P(T(v))=P(Av+b)$. Para evaluar $P$, hagamos cada término poco a poco. A continuación usaremos las propiedades de la multiplicación matricial y de la transposición de matrices. Recordemos que $M$ es una matriz simétrica.

Hagamos las operaciones término a término. En el primer sumando tenemos:

\begin{align*}
(Av+b)^t M (Av+b) &= (v^tA^t+b^t) M (Av+b)\\
&=v^tA^tMAv + v^t A^t M b + b^t M A v + b^t M b\\
&=v^t(A^tMA)v + (A^t M b)^t v + (b^t M A) v + b^t M b\\
&= v^t(A^tMA)v + (b^t M^t A) v + (b^t M A) v + b^t M b \\
&= v^t(A^tMA)v + 2 (b^t M A) v + b^t M b.
\end{align*}

En el segundo sumando tenemos:

\begin{align*}
k^t(Av+b)=k^tAv + k^t b.
\end{align*}

Y el último sumando es $F$. Al sumar todo notemos que aparece un término $b^t M b + k^t b + F=P(b)$. Así, concluimos que: $$(P\circ T)(v)= v^t(A^tMA)v + (2b^t MA + k^t A) v + P(b).$$

Esto muestra que $P\circ T$ es de nuevo un polinomio cuadrático en dos variables y que la fórmula es como se establece en el enunciado del teorema.

$\square$

Aunque parezca que se hicieron varias cuentas, son muchas menos a que si usáramos la expresión en coordenadas. Además, usaremos repetidamente el resultado para ahorrarnos cuentas posteriores. Veamos un pequeño ejemplo de lo que sucede al componer una transformación afín con un PCDV.

Ejemplo. Consideremos al polinomio cuadrático en dos variables $P((x,y))=2x^2-y^2+3x+2$ y a la transformación afín $T((x,y))=(2x,y+1)$. Al realizar la composición obtenemos lo siguiente:

\begin{align*}
(P\circ T)((x,y))&=P(T((x,y))\\
&=P((2x,y+1))\\
&=2(2x)^2-(y+1)^2+3(2x)+2\\
&=4x^2-y^2-2y-1+6x+2\\
&=4x^2-y^2+6x-2y+1.
\end{align*}

En efecto, como lo afirma el teorema, obtenemos nuevamente un polinomio cuadrático en dos variables.

$\triangle$

La imagen de una curva cuadrática bajo una transformación afín

La sección anterior nos dice qué pasa si «combinamos» un polinomio cuadrático en dos variables y una transformación afín. También podemos preguntarnos qué es lo que sucede si «combinamos» una transformación afín y una curva cuadrática. Aquí lo que estamos pensando es que la transformación afín se la aplicaremos a cada punto de la curva.

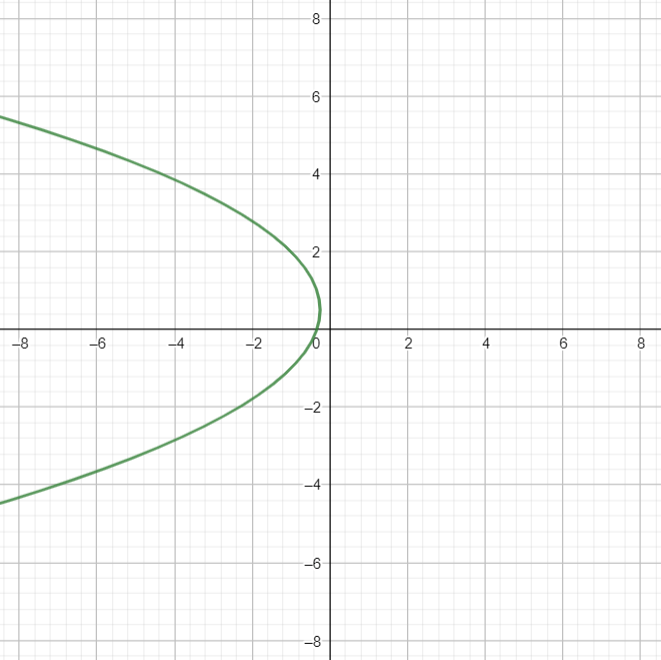
Ejemplo. Tomemos la curva cuadrática descrita por el polinomio cuadrático $y^2+3x-y+1=0$. Al trazarla en el plano obtenemos la siguiente figura.

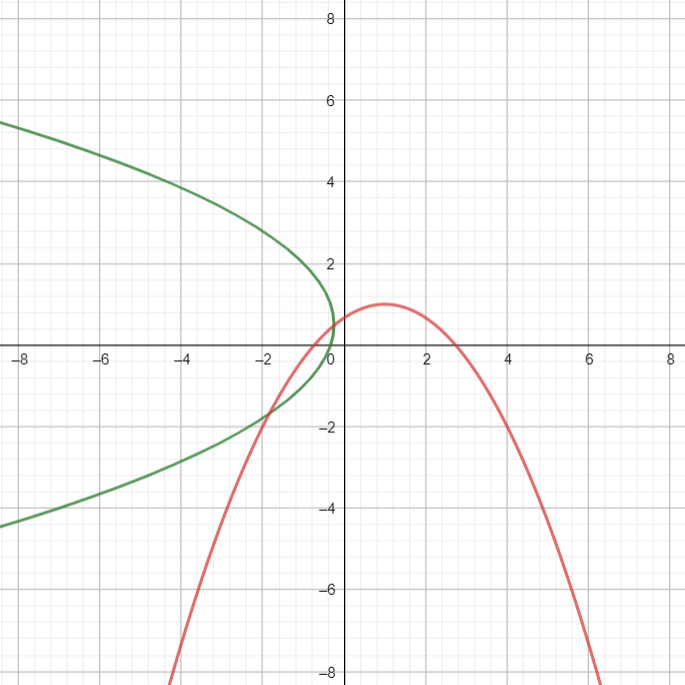
Aparentemente, obtenemos una parábola. Tomemos ahora la transformación afín $T((x,y))=(y-1,x+y)$. Al aplicar esta transformación a cada punto de la curva cuadrática anterior obtenemos la curva roja de la siguiente figura.

Aparentemente estamos obteniendo nuevamente una parábola. Entonces, parece ser que la transformación afín envió una curva cuadrática a otra curva cuadrática.

$\triangle$

Lo que sucede en el ejemplo anterior de hecho es algo que sucede en general: cuando aplicamos una transformación afín a una curva cuadrática entonces de nuevo obtenemos una curva cuadrática. Esto es lo que afirma el siguiente resultado.

Teorema. Sea $\mathcal{C}$ la curva cuadrática descrita por el polinomio cuadrático en dos variables $P$. Sea $T$ una transformación afín. Entonces $$T(\mathcal{C})=\{T((x,y)): (x,y)\in \mathcal{C}\}$$ también es una curva cuadrática. Más específicamente, es la curva cuadrática descrita por el polinomio cuadrático en dos variables $P\circ Tˆ{-1}$.

Demostración. Como $T$ es transformación afín, entonces es invertible y su inversa $Tˆ{-1}$ también es una transformación afín. Por el teorema anterior, $P\circ Tˆ{-1}$ en efecto es una transformación afín.

Tenemos que un punto $(w,z)$ pertenece a $T\mathcal{C}$ si y sólo si es de la forma $T((x,y))$ con $(x,y)$ en $\mathcal{C}$ es decir, con $P((x,y))=0$. Aplicando $Tˆ{-1}$ en $(w,z)=T((x,y))$, obtenemos que $(x,y)=Tˆ{-1}((w,z))$. Así, $(w,z)$ está en $T(\mathcal{C})$ si y sólo si $P(Tˆ{-1})((x,y))=0$. De esta manera, $T\mathcal{C}$ es precisamente el conjunto de puntos en donde se anula el PCDV $P\circ Tˆ{-1}$.

$\square$

Podemos resumir el teorema anterior como sigue: las transformaciones afines mandan curvas cuadráticas en curvas cuadráticas.

Equivalencias de polinomios y curvas cuadráticas

Al aplicar una transformación afín a un polinomio cuadrático en dos variables, de nuevo obtenemos un polinomio cuadrático. Pero no podemos ir de un polinomio cuadrático a cualquier otro haciendo esto. De hecho, es especial que esto suceda.

Definición. Diremos un polinomio cuadrático en dos variables $P$ es afínmente equivalente a otro polinomio cuadrático en dos variables $Q$ si existe una transformación afín $T$ tal que $P=Q\circ T$.

Así mismo, no cualquier curva cuadrática puede ir a cualquier otra mediante transformaciones afines. Esto es especial.

Definición Diremos que una curva cuadrática $\mathcal{C}$ es afínmente equivalente a otra curva cuadrática $\mathcal{D}$ si existe una transformación afín $T$ tal que $\mathcal{C}=D$.

Tanto en el caso de polinomios cuadráticos en dos variables, como en el caso de curvas cuadráticas, la relación de ser afínmente equivalente es una relación de equivalencia. Demostraremos esto para el caso de polinomios cuadráticos. El caso de curvas queda como tarea.

Proposición. La relación «ser afínmente equivalente a» es una relación de equivalencia para polinomios cuadráticos en dos variables.

Demostración. Debemos mostrar que la relación es reflexiva, simétrica y transitiva. La relación es reflexiva pues cualquier polinomio cuadrático en dos variables $P$ es afínmente equivalente a sí mismo a través de la transformación afín $$I((x,y))=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}+ \begin{pmatrix} 0 \\ 0 \end{pmatrix},$$ pues como simplemente es la identidad, tenemos $P \circ I = P$.

Si un polinomio $P$ es afínmente equivalente a uno $Q$, es porque existe una transformación afín $T$ tal que $P=Q\circ T$. Como $T$ es afín, su inversa también lo es, de modo que la igualdad $Q=P\circ Tˆ{-1}$ nos dice que $Q$ es afínmente equivalente a $P$. Esto muestra la simetría de la relación.

Finalmente, para la transitividad tomemos polinomios $P$, $Q$ y $R$ con $P$ afínmente equivalente $Q$ mediante una transformación afín $T$ y $Q$ afínmente equivalente a $R$ mediante una transformación afín $S$. Tenemos entonces las igualdades $P=Q\circ T$ y $Q=R\circ S$. De este modo $$P=Q\circ T = (R\circ S)\circ T=R\circ (S \circ T).$$

Como la composición de transformaciones afines es una transformación afín, entonces esto nos dice que $P$ es afínmente equivalente a $R$, como queríamos.

$\square$

Ambas nociones de equivalencia afín están muy relacionadas entre sí, aunque no son exactamente lo mismo. En la siguiente proposición veremos que la equivalencia afín de PCDVs implica la equivalencia afín de las curvas cuadráticas que describen. Sin embargo, en los ejercicios verás que hay que ser mucho más cuidadosos con el regreso.

Proposición. Si $\mathcal{C}$ y $\mathcal{D}$ son curvas curvas cuadráticas descritas por polinomios cuadráticos en dos variables $P$ y $Q$ afínmente equivalentes, entonces $\mathcal{C}$ y $\mathcal{D}$ son afínmente equivalentes.

Demostración. Como $P$ y $Q$ son afínmente equivalentes, existe una transformación afín $T$ tal que $P=Q\circ T$. Tenemos entonces que $(x,y)\in \mathcal{C}$ si y sólo si $P((x,y))=0$, lo cual sucede si y sólo si $Q(T((x,y)))=0$, si y sólo si $T((x,y))$ está en $\mathcal{D}$. Esto muestra que $\mathcal{D}=T(\mathcal{C})$.

$\square$

Con menos transformaciones es más difícil ser equivalente

Así como definimos la relación de «ser afínmente equivalente» también podríamos definir relaciones similares usando otros grupos de transformaciones. Por ejemplo:

Definición. Diremos un PCDV $P$ es isométricamente equivalente a otro PCDV $Q$ si existe una isometría $T$ tal que $P=Q\circ T$. Diremos que una curva cuadrática $\mathcal{C}$ es isométricamente equivalente a otra curva cuadrática $\mathcal{D}$ si existe una isometría $T$ tal que $\mathcal{C}=T(\mathcal{D})$

La noción de «ser isométricamente equivalentes» es, en cierto sentido «más fuerte» que la de ser «afínmente equivalentes». ¿Por qué? Porque todas las isometrías son transformaciones afines, pero lo contrario no es cierto. Así, «hay menos» isometrías que transformaciones afines. De esta forma, es «más difícil» que dos curvas cuadráticas sean isométricamente equivalentes, a que sean afínmente equivalentes. Veamos un ejemplo.

Ejemplo. Consideremos las curvas cuadráticas descritas por los siguientes polinomios:

\begin{align*}
P_1((x,y))&=x^2+2x+y^2\\
P_2((x,y))&=x^2+y^2-1\\
P_3((x,y))&=2x^2+y^2-1.
\end{align*}

Al graficarlas obtenemos respectivamente las curvas $\mathcal{C}_1, \mathcal{C}_2, \mathcal{C}_3$ en la siguiente figura. De lo que sabemos de circunferencias y elipses, tenemos que $\mathcal{C}_1$ y $\mathcal{C}_2$ son circunferencias de radio $1$ y que $\mathcal{C}_3$ es una elipse canónica con focos en el eje $y$ y centro en $(0,0)$.

Pensemos primero en equivalencia afín. Las tres curvas cuadráticas son afínmente equivalentes. Para ello, basta ver que los PCDVs que las describen son afínmente equivalentes. Para la equivalencia entre $P_1$ y $P_2$ tomamos la transformación afín $(x,y)\mapsto (x+1,y)$ y notamos que $$P_2((x+1,y))=(x+1)^2+y^2-1=x^2+2x+y^2=P_1((x,y)).$$ Para la equivalencia entre $P_2$ y $P_3$ tomamos la transformación afín $(x,y)\mapsto (\sqrt{2}x,y)$ y notamos que $$P_2((\sqrt{2}x,y))=(\sqrt{2}x)^2+y^2-1=2x^2+y^2-1=P_3((x,y)).$$ La equivalencia afín entre $P_1$ y $P_3$ se obtiene por transitividad.

Como la transformación afín $(x,y)\mapsto (x+1,y)$ es de hecho una traslación, entonces es una isometría. De esta manera, $P_1$ y $P_2$ no sólo son afínmente equivalentes, sino que también son isométricamente equivalentes. Sin embargo, es imposible encontrar una isometría que envíe $\mathcal{C}_2$ a $\mathcal{C}_3$, pues tendría que llevar a $(0,0)$ a un punto equidistante a todos los puntos de $\mathcal{C}_3$. Pero $\mathcal{C}_3$ no es una circunferencia.

En resumen:

• $\mathcal{C}_1,\mathcal{C}_2,\mathcal{C}_3$ son todas ellas afínmente equivalentes.
• $\mathcal{C}_1$ es isométricamente equivalente a $\mathcal{C}_2$.
• $\mathcal{C}_3$ no es isométricamete equivalente a $\mathcal{C}_2$, y por lo tanto tampoco a $\mathcal{C}_1$.

$\triangle$

Más adelante…

Ya dijimos qué objetos nos interesa clasificar: los polinomios cuadráticos y las curvas cuadráticas. También ya dijimos qué noción de clasificación usaremos: la equivalencia afín o la equivalencia isométrica. Estamos listos para enunciar los teoremas de clasificación que queremos demostrar. Haremos esto en la siguiente entrada. Después, en entradas posteriores, nos enfocaremos a dar la demostración poco a poco. Esto a su ves nos permitirá resolver problemas prácticos de cónicas como poder encontrar su centro o qué tan rotadas están.

Tarea moral

1. Demuestra que la relación «es afínmente equivalente a» es una relación de equivalencia para curvas cuadráticas.
2. Encuentra de manera explícita una transformación afín que ayude a ver que los polinomios cuadráticos $x^2+6x+y^2+8$ y $x^2+y^2-4y+3$ son afínmente equivalentes. ¿Son isométricamente equivalentes?
3. Demuestra que los polinomios cuadráticos en dos variables $P((x,y))=x^2+y^2+1$ y $Q((x,y))=x^2+1$ no pueden ser afínmente equivalentes. Luego, muestra que las curvas cuadráticas que definen sí son afínmente equivalentes. Como sugerencia, para ver que los polinomios no son afínmente equivalentes procede por contradicción. Supón que sí y obtén una contradicción con el coeficiente de $y^2$.
4. Muestra lo siguiente:
   1. Dos parábolas canónicas cualesquiera (i.e. descritas por ecuaciones de la forma $y=cx^2$) son afínmente equivalentes.
   2. Dos elipses canónicas cualesquiera (i.e. descritas por ecuaciones de la forma $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$) son afínmente equivalentes.
   3. Dos hipérbolas canónicas cualesquiera (i.e. descritas por ecuaciones de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$) son afínmente equivalentes.
5. Usa como ejemplo las definiciones de la entrada para definir la noción de ser «traslacionalmente equivalente». Demuestra lo siguiente:
   1. La relación «es traslacionalmente equivalente a» es una relación de equivalencia.
   2. Dos rectas son traslacionalmente equivalentes si y sólo si son paralelas.
   3. Dos circunferencias son traslacionalmente equivalentes si y sólo si son del mismo radio.
   4. Existen elipses isométricamente equivalentes, pero que no son traslacionalmente equivalentes.

Entradas relacionadas

• Ir a Geometría Analítica I
• Entrada anterior del curso: Polinomios cuadráticos y curvas cuadráticas
• Siguiente entrada del curso: Teoremas de clasificación de polinomios cuadráticos y curvas cuadráticas