Introducción

Con esta entrada comenzamos nuestra exploración de los objetos en el espacio de tres dimensiones. Lo primero que haremos es estudiar los cilindros que se construyen sobre cónicas. La mayoría de nosotros tiene una noción bastante buena sobre ellos, o por lo menos de los «cilindros usuales», en donde las secciones horizontales son círculos. Sin embargo, si bien entendemos muy bien su forma de manera intuitiva, ¿cómo los podemos representar en el lenguaje matemático?

A continuación definiremos qué entenderemos por un cilindro sobre una cónica. Veremos algunos ejemplos y luego haremos cilindros con objetos que hemos estudiado en el curso de Geometría Analítica I: con cónicas.

Definición de cilindros sobre curvas

Los cilindros que conocemos de manera intuitiva comienzan con una circunferencia y luego esta se extiende sin cambios a lo largo de un eje. Los cilindros con los que nos encontramos cotidianamente (por ejemplo, un vaso) se extienden sólo de manera acotada. Pero podemos pensar en qué sucedería si los extendemos indefinidamente. Si hacemos esto, llegamos a la siguiente definición.

Definición. Un cilindro es una superficie en $\mathbb{R}^3$ que se pueda obtener tomando un plano $\Pi$, tomando en él una curva $\mathcal{C}$ y tomando para cada punto $p$ de $\mathcal{C}$ una recta ortogonal a $\Pi$ que pase por $p$. La unión de estas rectas son el cilindro. A cada una de las rectas le llamamos una directriz del cilindro y a la curva $\mathcal{C}$ le llamamos la curva generatriz del cilindro.

Así, un cilindro es un conjunto de lineas paralelas que se encuentran «guiadas» o «dirigidas» de acuerdo a una curva plana. Podemos imaginarlo como sigue: dibujamos la curva sobre un papel, y luego sobre ella pegamos palos perpendiculares a la hoja

Cilindros a partir de cónicas

La definición de cilindro, tal y como está arriba, no restringe el tipo de cónicas que podemos tener. Sin embargo, hay una familia de cónicas que conocemos bien debido a cursos anteriores: las cónicas. Ya que podemos elegir con libertad la curva plana, pensemos en lo que sucede si usamos de las cónicas que conocemos. Para simplificar la situación, supondremos que dibujamos la cónica en el plano XY y entonces que las directrices son perpendiculares al plano $XY$, es decir, paralelas al eje $Z$. Podemos entonces hacer ejemplos de acuerdo a subfamilia de cónicas que usemos.

Cilindros elípticos

Recordemos que una elipse en el plano $XY$ puede pensarse (salvo rotaciones y traslaciones) como el lugar geométrico de los puntos $(x,y)$ que satisfacen una ecuación del estilo $$\frac{x^2}{a^2}+\frac{y^2}{b^2} =1,$$ donde $a$ y $b$ son parámetros que determinan la longitud de los ejes de la elipse.

Si ahora pensamos en todo $\mathbb{R}^3$ y nos preguntamos por el lugar geométrico de los puntos $(x,y,z)$ que satisfacen la ecuación, la respuesta es similar. Los valores de $(x,y)$ están dados por la ecuación y el valor de $z$ no está restringido de ninguna manera por la ecuación, de modo que puede ser lo que sea. ¡Hemos logrado «levantar la cónica» a líneas perpendiculares al plano $XY$!

De tener $a=b$, tendremos un cilindro circular en el origen. Si $a=b=1$, entonces es un cilindro mucho más especial, pues es uno que se obtiene de levantar la circunferencia unitaria canónica.

Por supuesto, pudimos haber comenzado con una elipse en el plano $YZ$, que tendría una ecuación del estilo $$\frac{y^2}{a^2}+\frac{z^2}{b^2} =1.$$ En este caso, el valor de $x$ sería libre, así que puede valer lo que sea. Así, esta ecuación pensada en todo $\mathbb{R}^3$ nos daría un cilindro cuya curva directriz es una elipse, y cuyas generatrices son paralelas al eje $x$.

Cilindros parabólicos

Para crear cilindros parabólicos podemos proceder de la misma manera. Para ellos, comenzamos con una parábola, por ejemplo, en el plano $XY$. Sabemos que una parábola así está dada, salvo rotaciones y traslaciones, por una ecuación del siguiente tipo: $$y^2 = 2px.$$ Una vez más, si en vez de pensar en esto como una ecuación en $\mathbb{R}^2$, la pensamos como una ecuación en $\mathbb{R}^3$, entonces el valor de $z$ es arbitrario y entonces al tomar el lugar geométrico en efecto obtenemos una línea perpendicular al plano $XY$ por cada punto de la parábola.

Cilindros hiperbólicos

La tercer familia sería la de cilindros hiperbólicos. En este caso, la curva generatriz es una hipérbola. Recordemos que salvo rotaciones y traslaciones, una hipérbola es el lugar geométrico de los puntos $(x,y)$ del plano $XY$ tales que satisfacen una ecuación del estilo $$\frac{x^2}{a^2}-\frac{y^2}{b^2} =1.$$ Al pensar a esta ecuación como una restricción para puntos $(x,y,z)$ de $\mathbb{R}^3$, obtenemos entonces un cilindro hiperbólico.

Problemas ejemplo de cilindros

Para aterrizar las ideas anteriores, veamos algunos ejemplos concretos.

Ejemplo. Tomemos el lugar geométrico de los puntos $(x,y,z) \in $ $\mathbb{R} ^3$ que cumplen con la siguiente ecuación: $$\frac{x^2}{4}+\frac{y^2}{25} = 1.$$

Podemos comenzar detectando la ausencia de la variable $z$, con lo que las generatrices serán rectas paralelas al eje $Z$. De hecho, el eje del cilindro precisamente será será el eje $Z$. Esto no siempre ocurre ya que no necesariamente el centro de la curva dada está en el origen del plano $XY$, pero debido a que no tenemos constantes que acompañen los valores $x$ o $y $ su centro no se encontrará desplazado.

¿Qué nos dicen los valores $4,25$ que acompañan a sus variables correspondientes ?Con todo en mente veamos su gráfica

Veamos desde otra perspectiva, no solo sobre el plano, sino con una vista incluyendo el otro eje coordenado obtenemos la siguiente gráfica.

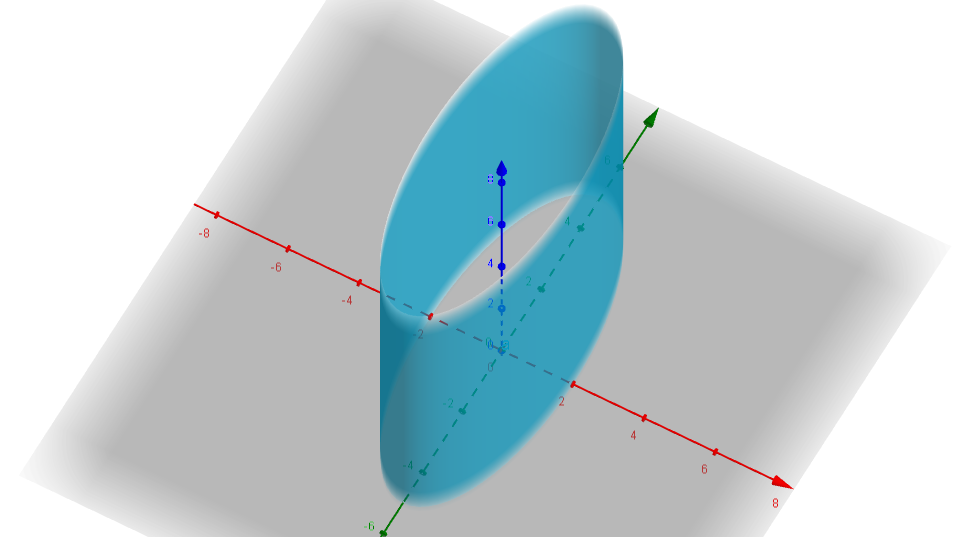
$\square$

Ejemplo. Tomemos el lugar geométrico en $\mathbb{R}^3$ de los puntos $(x,y,z)$ que cumplen la siguiente ecuación: $$y^2=6x.$$

De manera muy similar notamos que la ausencia de la variable $z$ llevara a que su directriz se encuentre en el plano $XY$ de forma que vista desde este plano:

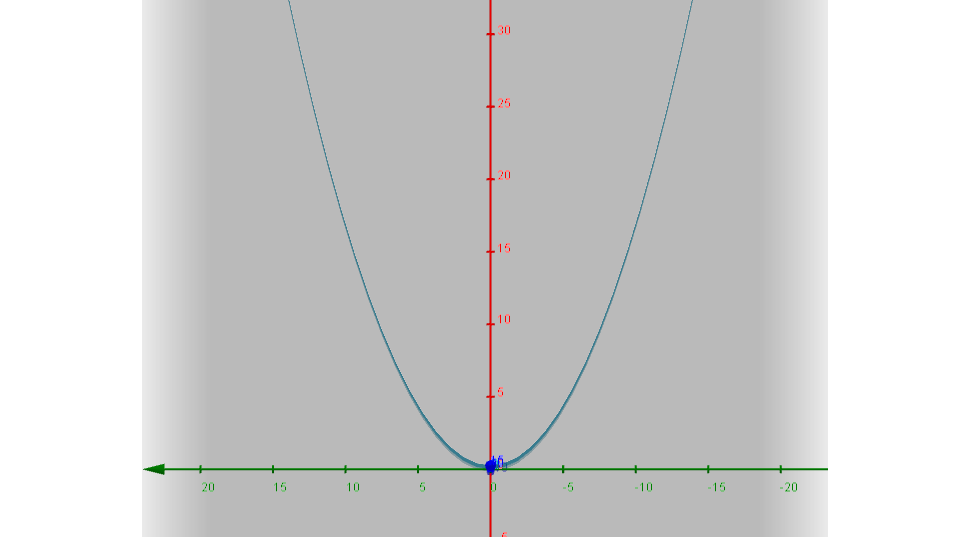
¿Puedes decir a que cónica pertenece esta gráfica?

Agregando la perspectiva con el eje faltante obtenemos:

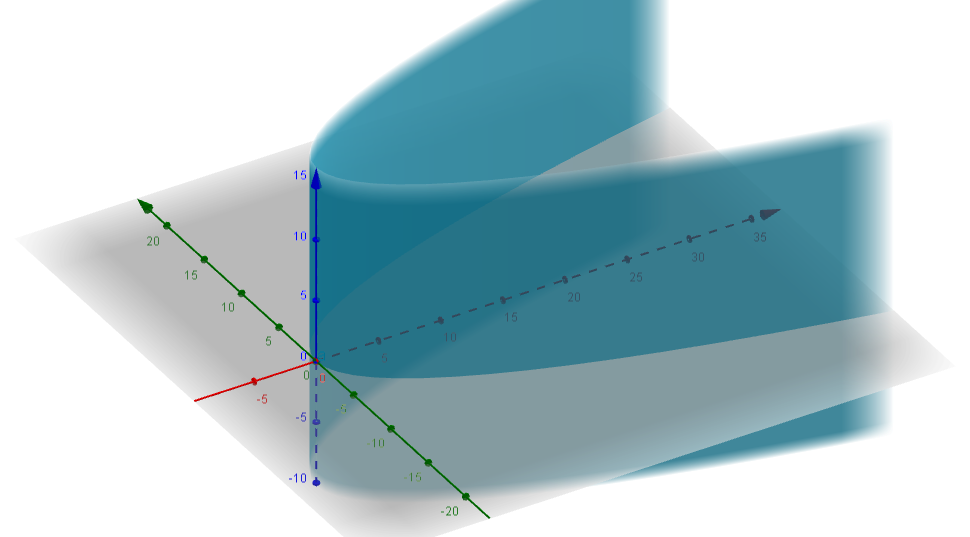
Nota importante. Como habrás notado al graficar obtenemos estas representaciones que parecen estar cortadas o seccionadas por planos paralelos al $XY$ , en realidad estos cilindros se extienden sin límite.

$\square$

Ejemplo. Para la siguiente ecuación: $$\frac{z^2}{4}-\frac{y^2}{9} = 1,$$ ¿cuál es el lugar geométrico de los puntos $(x,y,z)$ en $\mathbb{R}^3$ que la cumplen?

Notemos ahora que además de representar otro tipo de cónica tenemos ahora un cambio importante, ya no contamos de manera explicita con la $y$ en la ecuación, ¿Qué cambios conllevara esto? ¿En que plano podremos observar la cónica correspondiente?

Veamos si tu intuición fue correcta

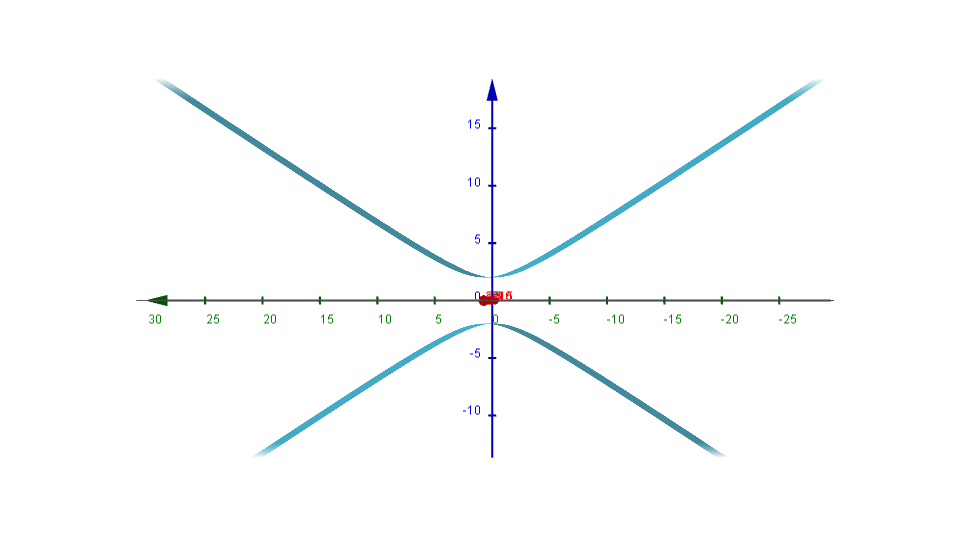
Desde otra perspectiva donde podremos ver su profundidad, tenemos ahora que las generatrices se extienden desde $- \infty$ hasta $\infty$.

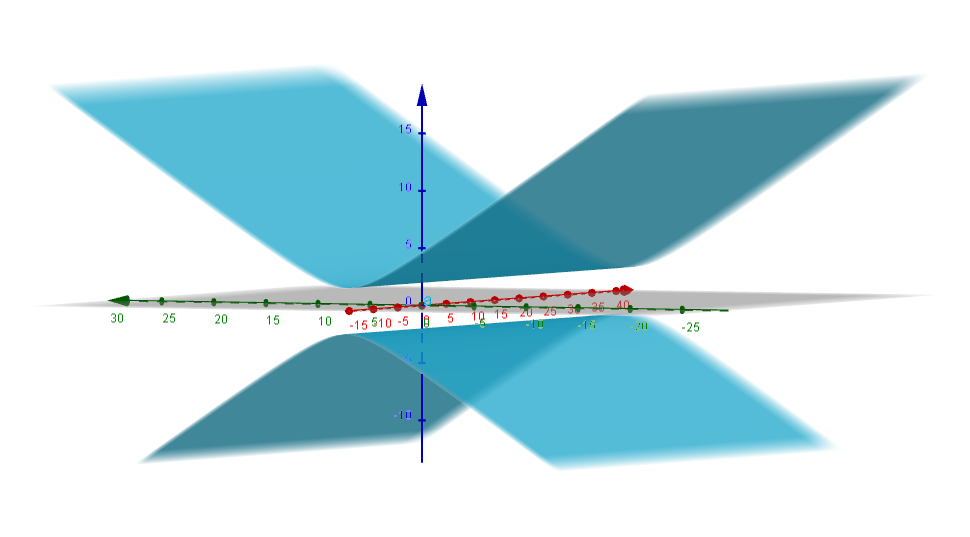
$\square$

Más adelante…

En esta primer entrada del curso hablamos de los primeros objetos geométricos de tres dimensiones que nos interesan: los cilindros con cierta curva generatriz. En la siguiente entrada veremos otra manera con la cual podemos crear un objeto de tres dimensiones a partir de rectas: las superficies de revolución. Un poco más adelante estudiaremos una versión más general de objetos que podemos obtener de esta manera: los conjuntos cero de ecuaciones de segundo grado en tres variables.

Tarea moral

Estos ejercicios te ayudaran a comprender de mejor forma los conceptos vistos.

1. Reescribe las ecuaciones de los ejemplos que dimos para que sus directrices se encuentren en diferentes planos.
   Sugerencia: Nota qué pasa con el tercer ejemplo.
2. Ahora que hemos cambiado los planos donde se encuentran las directrices, grafica estas ecuaciones, ¿Cómo cambian los cilindros? Realiza un cambio de variable para el segundo ejemplo haciendo el reemplazo $x\to x-3$. ¿Qué cambia? ¿pasa lo mismo para el primer ejemplo?
3. Determina la ecuación para un cilindro parabólico cuya parábola directriz esté contenida en el plano XY y cuyo foco sea el punto $(2, 0)$ de este plano. Hay varias de estas parábolas. Puedes usar la que gustes.
4. Gráfica los cilindros asociados a cada una de las siguientes ecuaciones:
   1. $x^2-z^2=0$.
   2. $(y-9)^2+(z-4)^2=0$.
   3. $x^2=y$.

Entradas relacionadas

• Ir a Geometría Analítica II
• Entrada siguiente del curso: