Introducción
Ya hablamos de qué es la forma canónica y la forma estándar de un problema lineal. Como platicamos, esto nos permitirá llevar los problemas que nos interesan a ciertas formas especiales a las que podremos aplicarles algunos métodos más adelante. Lo que haremos ahora es comenzar a pensar en qué quiere decir resolver un problema lineal. Para ello, recordaremos de distintos tipos de soluciones que los problemas lineales pueden tener.
Tipos de soluciones y región de factibilidad
En esta sección recordaremos los conceptos de soluciones factibles, soluciones básicas factibles (degeneradas y no degeneradas) y de región de factibilidad.
Supongamos que tenemos un problema de programación lineal en su forma canónica:
\begin{align*}
Max \quad z &= c\cdot x\\
s.a.&\\
Ax &\leq b\\
x &\geq 0,\\
\end{align*}
donde usamos la misma notación que en la entrada anterior, pero donde tomaremos $l$ variables de decisión. En particular, $x,c$ son vectores en $\mathbb{R}^n$, $b$ es un vector en $\mathbb{R}^m$ y $A$ es una matriz de entradas reales de $m\times n$. Recuerda que en la expresión anterior entendemos $0$ como el vector en $\mathbb{R}^n$ con entradas todas iguales a cero.
Este problema también tiene una forma estándar, en donde transformamos las desigualdades en igualdades introduciendo variables de sobra y de holgura.
\begin{align*}
Max \quad z &= c\cdot x\\
s.a.&\\
A’x’ &=b\\
x’ &\geq 0,\\
\end{align*}
en donde en hemos agregado $n-m$ variables de holgura al vector $x$, para obtener un vector $x’$ en $\mathbb{R}^n$, así como $n-m$ columnas a $A$ para volverla una matriz en de $m\times n$, para agregar los coeficientes de las variables de holgura que hacen que se de la igualdad.
Como recordatorio, tenemos las siguientes definiciones para los tipos de soluciones del problema lineal.
Definición. Una solución factible al problema lineal en forma canónica dado anteriormente es un vector columna $x=\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}$ que satisface las restricciones $Ax\leq b$ y $x\geq 0$. Esto se corresponde con una solución $x’$ al problema en forma estándar que satisface $A’x’= b$ y $x’\geq 0$.
Definición. La región de factibilidad del problema lineal en forma canónica es el conjunto de todas las soluciones factibles.
De entre las soluciones factibles, hay algunas que son un poco más sencillas, en el sentido de que varias de sus entradas son iguales a cero pensadas como soluciones del problema en forma estándar. En las siguientes definiciones suponemos que el rango de la matriz $A’$ es exactamente igual a $m$.
Definición. Una solución básica factible es una solución factible $x$ correspondiente a una solución $x’$ del problema en forma estándar con no más de $m$ componentes positivas. En otras palabras, $x’$ tiene al menos $n-m$ entradas iguales a cero.
Definición. Una solución básica factible no degenerada es una solución factible $x$ correspondiente a una solución $x’$ del problema en forma estándar con exactamente $m$ componentes positivas. En otras palabras, $x’$ tiene exactamente $n-m$ entradas iguales a cero.
Definición. Una solución básica factible degenerada es una solución factible $x$ correspondiente a uan solución $x’$ del problema en forma estándar con menos de $m$ componentes positivas. En otras palabras, $x’$ tiene más de $n-m$ entradas iguales a cero.
La importancia de las soluciones básicas factibles y no degeneradas es que cumplen las siguientes:
- Se puede mostrar que si un problema de programación lineal tiene óptimo, entonces dicho óptimo se alcanza para alguna solución básica factible y no degenerada.
- Las soluciones básicas factibles y no degeneradas se pueden encontrar resolviendo sistemas de ecuaciones.
- Geométricamente, las soluciones básicas factibles y no degeneradas están en vértices de la región de factibilidad.
A continuación explicaremos algunos de estos puntos con un ejemplo detallado, que te ayudará a entender la intuición detrás de estas definiciones y de su importancia.
Ejemplos de región de factibilidad y tipos de solución
Consideremos el siguiente problema de programación lineal:
\begin{align*}
Max. \quad z &= 2x_1 + 3x_2\\
s.a.&\\
&\begin{matrix}2x_1 &+ x_2 &\leq & 4\\
x_1 &+ 2x_2 &\leq &5\end{matrix}\\
&x_1, x_2 \geq 0.
\end{align*}
Antes de comenzar a estudiar la región de factibilidad, debemos verificar que está en forma canónica. En efecto, todo está en orden: el problema es de maximización, las desigualdades son $\leq$ y a las variables de decisión se les pide ser no negativas.
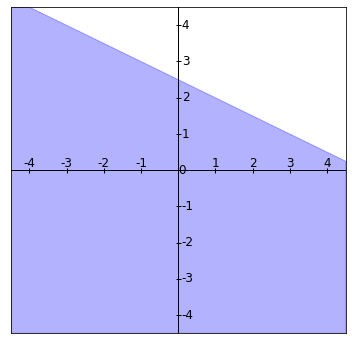
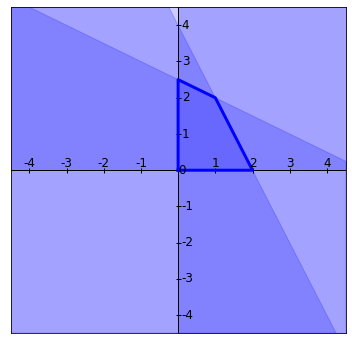
La región de factibilidad es el conjunto de todos los $(x_1,x_2)$ (en el plano $\mathbb{R}^2$) que cumplen las restricciones del problema, es decir, $2x_1 + x_2 \leq 4$, $x_1 + 2x_2 \leq 5$, $x_1\geq 0$ y $x_2\geq 0$. Para entender esto mejor, lo podemos pensar en cuatro regiones:
Región 1: La región $x_1\geq 0$, que queda a la derecha del eje $y$.
Región 2: La región $x_2\geq 0$, que queda arriba del eje $x$.
Región 3: La región $2x_1 + x_2 \leq 4$, que queda debajo de la recta $2x_1+x_2=4$.
Región 4: La región $x_1+2x_2\leq 5$, que queda por debajo de la recta $x_1+2x_2=5$.
Como queremos que $(x_1,x_2)$ satisfaga todas las restricciones simultáneamente, necesitamos que esté en la intersección de todas las regiones. Así, la región de factibilidad es en la que se intersectan todas estas regiones que acabamos de dibujar. Al sobreponerlas, obtenemos la región encerrada en la siguiente figura:
Si gustas, puedes también explorar el interactivo de GeoGebra en donde se han coloreado los complementos de las regiones para más claridad. Puedes usar el cursor para mover la figura y las herramientas de lupa para hacer acercamientos y alejamientos.
La intuición que debemos tener ahora es que el máximo de la función objetivo $2x_1+3x_2$ se tiene que alcanzar en alguno de los vértices del cuadrilátero que es la región factible. A grandes rasgos, estos vértices serán las soluciones básicas factibles y no degeneradas. Veamos dónde el álgebra nos dice esto.
Para ello, pensemos al problema en su forma estándar, tomando variables de holgura $s_1$ y $s_2$. Las restricciones que tienen las cuatro variables en conjunto son las siguientes.
\begin{align*}
2x_1 + x_2 + s_1 &= 4\\
x_1 + 2x_2 + s_2 &= 5\\
x_1, x_2, s_1, s_2 &\geq 0.
\end{align*}
La matriz $A’$ es $\begin{pmatrix}2 & 1 & 1 & 0 \\ 1 & 2 & 0 & 1 \end{pmatrix}$, que puedes verificar que tiene rango $2$. Las soluciones básicas y no degeneradas corresponden a tener en ese sistema de ecuaciones exactamente $m=2$ variables positivas, de manera que necesitamos hacer exactamente $n-m=4-2=2$ de estas variables iguales a cero. Al hacer esto, podemos resolver para las $m=2$ variables restantes. Por ejemplo, si establecemos $x_1 = 0$ y $x_2 = 0$, las ecuaciones se convierten en
\begin{align*}
s_1 = 4\\
s_2 = 5\\
x_1, x_2, s_1, s_2 \geq 0,
\end{align*}
que tiene solución única $(x_1,x_2,s_1,s_2)=(0,0,4,5)$. Así, la solución básica del problema en forma canónica es $(x_1,x_2)=(0,0)$. Hay que recordar dar la solución básica ya sólo para las variables originales, es decir, las del problema en forma canónica.
Esta solución corresponde al punto $C$ del interactivo de GeoGebra. Se puede determinar otra solución básica fijando $s_1 = 0$ y $s_2 = 0$, donde el sistema sería ahora
\begin{align*}
2x_1 + x_2 = 4\\
x_1 + 2x_2 = 5\\
x_1, x_2, s_1, s_2 \geq 0,
\end{align*}
y tras resolver las dos ecuaciones, la solución básica que se obtiene es $(x_1,x_2)=(1,2)$, que es el punto $A$ del interactivo de GeoGebra.
Podemos seguir haciendo esto. Si consideramos todas las posibilidades en las que dos variables son cero y resolvemos las ecuaciones resultantes, eso nos dará puntos $(x_1,x_2)$ en el plano. La solución óptima es la solución básica factible (punto de esquina) con el mejor valor objetivo.
En este ejemplo tenemos $\binom{4}{2} = \frac{4!}{2!2!} = 6$ formas de volver dos de las $n$ variables iguales a cero. Ya para las variables $x_1$ y $x_2$, los puntos que obtenemos son los puntos $A$, $B$, $C$, $D$ que son vértices de la región de factibilidad. Los puntos $E$ y $F$ del interactivo también son puntos básicos y no degenerados (son las otras dos intersecciones de las rectas que dibujamos), pero como no satisfacen la condición de factibilidad del problema, entonces no los podemos considerar y por lo tanto no son candidatos a dar el valor óptimo.
La siguiente tabla muestra todas las soluciones básicas y no básicas de este ejemplo:
| Variables no básicas (cero) | Variables básicas | Solución para $(x_1,x_2)$ | Punto de esquina asociado | ¿Factible? | Valor objetivo z |
| $(x_1, s_1)$ | $(s_1, s_2)$ | $(0, 0)$ | C | Sí | 0 |
| $(x_1, s_1)$ | $(x_2, s_2)$ | $(0, 4)$ | E | No | ___ |
| $(x_1, s_2)$ | $(x_2, s_1)$ | $(0, 2.5)$ | D | Sí | 7.5 |
| $(x_2, s_1)$ | $(x_1, s_2)$ | $(2, 0)$ | B | Sí | 4 |
| $(x_2, s_2)$ | $(x_1, s_1)$ | $(5, 0)$ | F | No | ___ |
| $(s_1, s_2)$ | $(x_1, x_2)$ | $(1, 2)$ | A | Sí | 8 (óptimo) |
Más adelante…
Notemos que a medida que el tamaño del problema se incrementa, enumerar todos los puntos esquina se volverá una tarea que tomaría mucho tiempo. Por ejemplo, si tuviéramos $20$ variables (ya con las de holgura) y $10$ restricciones, es necesario resolver considerar $\binom{20}{10}=184756$ formas de crear ecuaciones de $10\times 10$, y resolver cada una de ellas. Aunque esto es finito, son demasiadas operaciones. Y este en la práctica incluso es un ejemplo pequeño, ya que en la vida real hay problemas lineales que pueden incluir miles de variables y restricciones.
Por ello, se vuelve cruciar encontrar un método que atenúe esta carga computacional en forma drástica, que permita investigar sólo un subconjunto de todas las posibles soluciones factibles básicas no degeneradas (vértices de la región de factibilidad), pero que garantice encontrar el óptimo. Una idea intuitiva que debería servir es comenzar en un vértice y «avanzar en una dirección que mejore la función objetivo». Esto precisamente es la intuición detrás del método simplex, que repasaremos a continuación.
Tarea moral
- Considera el siguiente problema lineal en su forma canónica:
\begin{align*}
Max \quad z &= 2x_1 + 3x_2 \\
s.a.&\\
&\begin{matrix}x_1 &+ 3x_2 &\leq&6\\
3x_1 &+ 2x_2 &\leq &6\end{matrix}\\
&x_1, x_2 \geq 0.
\end{align*}
Sigue los pasos descritos arriba para encontrar todas sus soluciones básicas factibles y no degeneradas. Usa ello para encontrar el óptimo del problema.
- Actualiza las restricciones en el interactivo de GeoGebra que se compartió en la entrada para visualizar este problema y confirmar tus cuentas del ejercicio anterior. Para ello, deberás ir al apartado «Álgebra» del interactivo y modificar los objetos $a$ y $b$.
- Considera un problema de optimización lineal en dos variables $x$ y $y$, en forma canónica y con $m$ restricciones (desigualdades), además de las restricciones $x\geq 0$ y $y\geq 0$. Explica por qué la región de factibilidad siempre es un polígono con a lo más $m+2$ lados, y por qué entonces basta evaluar la función objetivo en a lo más $m+2$ puntos para encontrar su máximo.
- ¿Cómo se vería la región de factibilidad de un problema de optimización lineal de maximización que no tenga máximo? Explica todas las posibilidades y da ejemplos.
- Intenta usar las ideas de esta entrada para resolver los problemas de optimización lineal clásicos que hemos descrito en entradas anteriores.
Entradas relacionadas
- Ir a Investigación de Operaciones
- Entrada anterior del curso: Forma canónica y forma estándar de un problema lineal
- Entrada siguiente del curso: