Archivo de la etiqueta: optimización

Investigación de Operaciones: Soluciones básicas, factibles y no degeneradas (10)

Por Aldo Romero

Introducción

Ya hablamos de qué es la forma canónica y la forma estándar de un problema lineal. Como platicamos, esto nos permitirá llevar los problemas que nos interesan a ciertas formas especiales a las que podremos aplicarles algunos métodos más adelante. Lo que haremos ahora es comenzar a pensar en qué quiere decir resolver un problema lineal. Para ello, recordaremos de distintos tipos de soluciones que los problemas lineales pueden tener.

Tipos de soluciones y región de factibilidad

En esta sección recordaremos los conceptos de soluciones factibles, soluciones básicas factibles (degeneradas y no degeneradas) y de región de factibilidad.

Supongamos que tenemos un problema de programación lineal en su forma canónica:

\begin{align*}
Max \quad z &= c\cdot x\\
s.a.&\\
Ax &\leq b\\
x &\geq 0,\\
\end{align*}

donde usamos la misma notación que en la entrada anterior, pero donde tomaremos $l$ variables de decisión. En particular, $x,c$ son vectores en $\mathbb{R}^n$, $b$ es un vector en $\mathbb{R}^m$ y $A$ es una matriz de entradas reales de $m\times n$. Recuerda que en la expresión anterior entendemos $0$ como el vector en $\mathbb{R}^n$ con entradas todas iguales a cero.

Este problema también tiene una forma estándar, en donde transformamos las desigualdades en igualdades introduciendo variables de sobra y de holgura.
\begin{align*}
Max \quad z &= c\cdot x\\
s.a.&\\
A’x’ &=b\\
x’ &\geq 0,\\
\end{align*}

en donde en hemos agregado $n-m$ variables de holgura al vector $x$, para obtener un vector $x’$ en $\mathbb{R}^n$, así como $n-m$ columnas a $A$ para volverla una matriz en de $m\times n$, para agregar los coeficientes de las variables de holgura que hacen que se de la igualdad.

Como recordatorio, tenemos las siguientes definiciones para los tipos de soluciones del problema lineal.

Definición. Una solución factible al problema lineal en forma canónica dado anteriormente es un vector columna $x=\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}$ que satisface las restricciones $Ax\leq b$ y $x\geq 0$. Esto se corresponde con una solución $x’$ al problema en forma estándar que satisface $A’x’= b$ y $x’\geq 0$.

Definición. La región de factibilidad del problema lineal en forma canónica es el conjunto de todas las soluciones factibles.

De entre las soluciones factibles, hay algunas que son un poco más sencillas, en el sentido de que varias de sus entradas son iguales a cero pensadas como soluciones del problema en forma estándar. En las siguientes definiciones suponemos que el rango de la matriz $A’$ es exactamente igual a $m$.

Definición. Una solución básica factible es una solución factible $x$ correspondiente a una solución $x’$ del problema en forma estándar con no más de $m$ componentes positivas. En otras palabras, $x’$ tiene al menos $n-m$ entradas iguales a cero.

Definición. Una solución básica factible no degenerada es una solución factible $x$ correspondiente a una solución $x’$ del problema en forma estándar con exactamente $m$ componentes positivas. En otras palabras, $x’$ tiene exactamente $n-m$ entradas iguales a cero.

Definición. Una solución básica factible degenerada es una solución factible $x$ correspondiente a uan solución $x’$ del problema en forma estándar con menos de $m$ componentes positivas. En otras palabras, $x’$ tiene más de $n-m$ entradas iguales a cero.

La importancia de las soluciones básicas factibles y no degeneradas es que cumplen las siguientes:

Se puede mostrar que si un problema de programación lineal tiene óptimo, entonces dicho óptimo se alcanza para alguna solución básica factible y no degenerada.
Las soluciones básicas factibles y no degeneradas se pueden encontrar resolviendo sistemas de ecuaciones.
Geométricamente, las soluciones básicas factibles y no degeneradas están en vértices de la región de factibilidad.

A continuación explicaremos algunos de estos puntos con un ejemplo detallado, que te ayudará a entender la intuición detrás de estas definiciones y de su importancia.

Ejemplos de región de factibilidad y tipos de solución

Consideremos el siguiente problema de programación lineal:

\begin{align*}
Max. \quad z &= 2x_1 + 3x_2\\
s.a.&\\
&\begin{matrix}2x_1 &+ x_2 &\leq & 4\\
x_1 &+ 2x_2 &\leq &5\end{matrix}\\
&x_1, x_2 \geq 0.
\end{align*}

Antes de comenzar a estudiar la región de factibilidad, debemos verificar que está en forma canónica. En efecto, todo está en orden: el problema es de maximización, las desigualdades son $\leq$ y a las variables de decisión se les pide ser no negativas.

La región de factibilidad es el conjunto de todos los $(x_1,x_2)$ (en el plano $\mathbb{R}^2$) que cumplen las restricciones del problema, es decir, $2x_1 + x_2 \leq 4$, $x_1 + 2x_2 \leq 5$, $x_1\geq 0$ y $x_2\geq 0$. Para entender esto mejor, lo podemos pensar en cuatro regiones:

Región 1: La región $x_1\geq 0$, que queda a la derecha del eje $y$.

Región 2: La región $x_2\geq 0$, que queda arriba del eje $x$.

Región 3: La región $2x_1 + x_2 \leq 4$, que queda debajo de la recta $2x_1+x_2=4$.

Región 4: La región $x_1+2x_2\leq 5$, que queda por debajo de la recta $x_1+2x_2=5$.

Como queremos que $(x_1,x_2)$ satisfaga todas las restricciones simultáneamente, necesitamos que esté en la intersección de todas las regiones. Así, la región de factibilidad es en la que se intersectan todas estas regiones que acabamos de dibujar. Al sobreponerlas, obtenemos la región encerrada en la siguiente figura:

Si gustas, puedes también explorar el interactivo de GeoGebra en donde se han coloreado los complementos de las regiones para más claridad. Puedes usar el cursor para mover la figura y las herramientas de lupa para hacer acercamientos y alejamientos.

La intuición que debemos tener ahora es que el máximo de la función objetivo $2x_1+3x_2$ se tiene que alcanzar en alguno de los vértices del cuadrilátero que es la región factible. A grandes rasgos, estos vértices serán las soluciones básicas factibles y no degeneradas. Veamos dónde el álgebra nos dice esto.

Para ello, pensemos al problema en su forma estándar, tomando variables de holgura $s_1$ y $s_2$. Las restricciones que tienen las cuatro variables en conjunto son las siguientes.

\begin{align*}
2x_1 + x_2 + s_1 &= 4\\
x_1 + 2x_2 + s_2 &= 5\\
x_1, x_2, s_1, s_2 &\geq 0.
\end{align*}

La matriz $A’$ es $\begin{pmatrix}2 & 1 & 1 & 0 \\ 1 & 2 & 0 & 1 \end{pmatrix}$, que puedes verificar que tiene rango $2$. Las soluciones básicas y no degeneradas corresponden a tener en ese sistema de ecuaciones exactamente $m=2$ variables positivas, de manera que necesitamos hacer exactamente $n-m=4-2=2$ de estas variables iguales a cero. Al hacer esto, podemos resolver para las $m=2$ variables restantes. Por ejemplo, si establecemos $x_1 = 0$ y $x_2 = 0$, las ecuaciones se convierten en

\begin{align*}
s_1 = 4\\
s_2 = 5\\
x_1, x_2, s_1, s_2 \geq 0,
\end{align*}

que tiene solución única $(x_1,x_2,s_1,s_2)=(0,0,4,5)$. Así, la solución básica del problema en forma canónica es $(x_1,x_2)=(0,0)$. Hay que recordar dar la solución básica ya sólo para las variables originales, es decir, las del problema en forma canónica.

Esta solución corresponde al punto $C$ del interactivo de GeoGebra. Se puede determinar otra solución básica fijando $s_1 = 0$ y $s_2 = 0$, donde el sistema sería ahora

\begin{align*}
2x_1 + x_2 = 4\\
x_1 + 2x_2 = 5\\
x_1, x_2, s_1, s_2 \geq 0,
\end{align*}

y tras resolver las dos ecuaciones, la solución básica que se obtiene es $(x_1,x_2)=(1,2)$, que es el punto $A$ del interactivo de GeoGebra.

Podemos seguir haciendo esto. Si consideramos todas las posibilidades en las que dos variables son cero y resolvemos las ecuaciones resultantes, eso nos dará puntos $(x_1,x_2)$ en el plano. La solución óptima es la solución básica factible (punto de esquina) con el mejor valor objetivo.

En este ejemplo tenemos $\binom{4}{2} = \frac{4!}{2!2!} = 6$ formas de volver dos de las $n$ variables iguales a cero. Ya para las variables $x_1$ y $x_2$, los puntos que obtenemos son los puntos $A$, $B$, $C$, $D$ que son vértices de la región de factibilidad. Los puntos $E$ y $F$ del interactivo también son puntos básicos y no degenerados (son las otras dos intersecciones de las rectas que dibujamos), pero como no satisfacen la condición de factibilidad del problema, entonces no los podemos considerar y por lo tanto no son candidatos a dar el valor óptimo.

La siguiente tabla muestra todas las soluciones básicas y no básicas de este ejemplo:

Variables no básicas (cero)	Variables básicas	Solución para $(x_1,x_2)$	Punto de esquina asociado	¿Factible?	Valor objetivo z
$(x_1, s_1)$	$(s_1, s_2)$	$(0, 0)$	C	Sí	0
$(x_1, s_1)$	$(x_2, s_2)$	$(0, 4)$	E	No	___
$(x_1, s_2)$	$(x_2, s_1)$	$(0, 2.5)$	D	Sí	7.5
$(x_2, s_1)$	$(x_1, s_2)$	$(2, 0)$	B	Sí	4
$(x_2, s_2)$	$(x_1, s_1)$	$(5, 0)$	F	No	___
$(s_1, s_2)$	$(x_1, x_2)$	$(1, 2)$	A	Sí	8 (óptimo)

Más adelante…

Notemos que a medida que el tamaño del problema se incrementa, enumerar todos los puntos esquina se volverá una tarea que tomaría mucho tiempo. Por ejemplo, si tuviéramos $20$ variables (ya con las de holgura) y $10$ restricciones, es necesario resolver considerar $\binom{20}{10}=184756$ formas de crear ecuaciones de $10\times 10$, y resolver cada una de ellas. Aunque esto es finito, son demasiadas operaciones. Y este en la práctica incluso es un ejemplo pequeño, ya que en la vida real hay problemas lineales que pueden incluir miles de variables y restricciones.

Por ello, se vuelve cruciar encontrar un método que atenúe esta carga computacional en forma drástica, que permita investigar sólo un subconjunto de todas las posibles soluciones factibles básicas no degeneradas (vértices de la región de factibilidad), pero que garantice encontrar el óptimo. Una idea intuitiva que debería servir es comenzar en un vértice y «avanzar en una dirección que mejore la función objetivo». Esto precisamente es la intuición detrás del método simplex, que repasaremos a continuación.

Tarea moral

Considera el siguiente problema lineal en su forma canónica:

\begin{align*}
Max \quad z &= 2x_1 + 3x_2 \\
s.a.&\\
&\begin{matrix}x_1 &+ 3x_2 &\leq&6\\
3x_1 &+ 2x_2 &\leq &6\end{matrix}\\
&x_1, x_2 \geq 0.
\end{align*}

Sigue los pasos descritos arriba para encontrar todas sus soluciones básicas factibles y no degeneradas. Usa ello para encontrar el óptimo del problema.

Actualiza las restricciones en el interactivo de GeoGebra que se compartió en la entrada para visualizar este problema y confirmar tus cuentas del ejercicio anterior. Para ello, deberás ir al apartado «Álgebra» del interactivo y modificar los objetos $a$ y $b$.
Considera un problema de optimización lineal en dos variables $x$ y $y$, en forma canónica y con $m$ restricciones (desigualdades), además de las restricciones $x\geq 0$ y $y\geq 0$. Explica por qué la región de factibilidad siempre es un polígono con a lo más $m+2$ lados, y por qué entonces basta evaluar la función objetivo en a lo más $m+2$ puntos para encontrar su máximo.
¿Cómo se vería la región de factibilidad de un problema de optimización lineal de maximización que no tenga máximo? Explica todas las posibilidades y da ejemplos.
Intenta usar las ideas de esta entrada para resolver los problemas de optimización lineal clásicos que hemos descrito en entradas anteriores.

Entradas relacionadas

Ir a Investigación de Operaciones
Entrada anterior del curso: Forma canónica y forma estándar de un problema lineal
Entrada siguiente del curso:

Cálculo Diferencial e Integral III: Multiplicadores de Lagrange

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

En la entrada anterior buscábamos optimizar un campo escalar $f$. Retomaremos este problema, pero ahora agregando restricciones al dominio de $f$. Para ello hablaremos del método de los multiplicadores de Lagrange, el cual nos permitirá dar una solución bajo ciertas condiciones de diferenciabilidad.

Esto en general es lo mejor que podremos hacer. En realidad, los problemas de este estilo son muy difíciles y no tienen una solución absoluta. Si no tenemos las condiciones del teorema de Lagrange, es posible que se tengan que hacer cosas mucho más compliadas para obtener óptimos exactos, o bien que se tengan que hacer aproximaciones numéricas.

En la demostración del teorema de los multiplicadores de Lagrange usaremos el teorema de la función implícita, lo cual es evidencia adicional de lo importante y versátil que es este resultado.

Un ejemplo para motivar la teoría

Imagina que tenemos la función $f(x,y)=x^2+y^2$ y queremos encontrar su mínimo. Esto es muy fácil. El mínimo se da cuando $x=y=0$, pues en cualquier otro valor tenemos un número positivo. Pero, ¿Qué pasaría si además queremos que los pares $(x,y)$ que usamos satisfagan también otra condición?, por ejemplo, que cumplan $$2x^2+3y^2=10$$

En este caso, la respuesta ya no es obvia. Podríamos intentar encontrar el mínimo por inspección, pero suena que será difícil. Podríamos intentar usar la teoría de la entrada anterior, pero esa teoría no nos dice nada de qué hacer con nuestra condición.

La teoría que desarrollaremos a continuación nos permitirá respondernos preguntas de este estilo. En este ejemplo en concreto, puedes pensar que la solución se obtendrá de la siguiente manera: La ecuación $2x^2+3y^2=10$ nos dibuja una elipse en el plano, como se ve en la figura 1 imagen 3. Las curvas de nivel de la superficie dibujada por la gráfica de la función $f$ corresponden a circunferencias concéntricas, cuyo centro es el origen. Al ir tomando circunferencias cada vez mas grandes en el plano comenzando con el punto $(0,0)$ nos quedaremos con la primera que toque a la elipse, de hecho la tocará en dos puntos, digamos $(x_1 ,y_1)$ y $(x_2 ,y_2)$, donde $f(x_1 ,y_1)=f(x_2 ,y_2)$ sería el mínimo buscado, es decir el mínimo que sobre la superficie $f(x,y)$ cumple con la ecuación $2x^2+3y^2=10$.

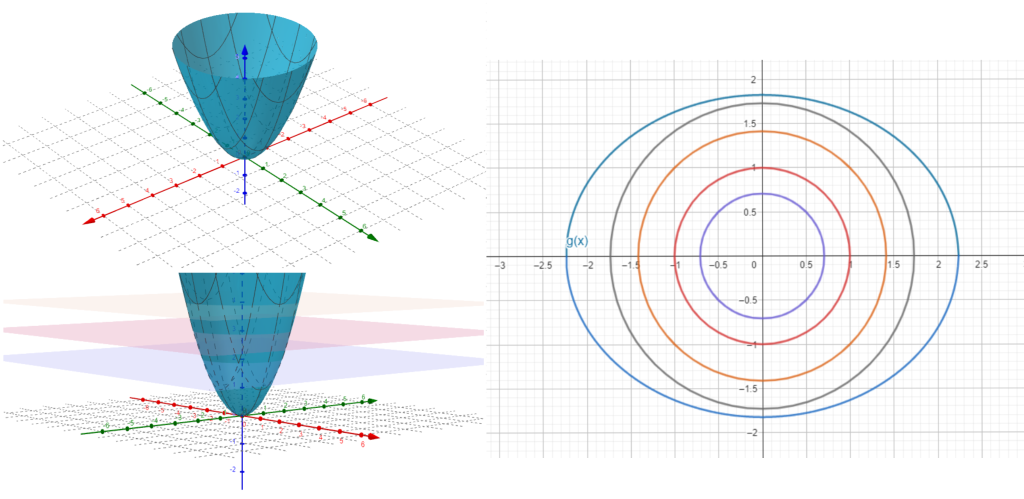
Figura 1; Imagen 1-Superior izquierda. Tenemos la gráfica de la ecuación $f(x,y)=x^2 + y^2$. Imagen 2- Inferior izquierda. Planos que intersecan a la superficie $f(x,y)$, nos dan las curvas de niver que son circunferencias concéntricas. Imagen 3- Derecha. En azul la elipse dibujada por la ecuación $2x^2 + 3y^2 =10$, y las curvas de nivel que se acercan a ella conforme cortamos mas arriba.

Pero como ahí se da una tangencia, entonces suena que justo en ese punto $(x,y)$ hay una recta simultáneamente tangente a la curva de nivel y a la elipse. Esto nos da una relación entre gradientes. El teorema de multiplicadores de Lagrange detecta y enuncia esta relación entre gradientes con precisión y formalidad, incluso cuando tenemos más de una condición. A estas condiciones también las llamamos restricciones, y están dadas por ecuaciones.

Enunciado del teorema de multiplicadores de Lagrange

A continuación enunciamos el teorema.

Teorema (multiplicadores de Lagrange). Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ es un campo escalar de clase $C^{1}$. Para $m<n$, tomamos $g_{1},\dots ,g_{m}:S\in \subset \mathbb{R}^{n}\rightarrow \mathbb{R}$ campos escalares de clase $C^{1}$ en $S$. Consideremos el conjunto $S^\ast$ donde todos los $g_i$ se anulan, es decir:

$$S^\ast=\{ \bar{x}\in S|g_{1}(\bar{x})=g_2(\bar{x})=\ldots=g_m(\bar{x})=0\}.$$

Tomemos un $\bar{x}_0$ en $S^\ast$ para el cual

$f$ tiene un extremo local en $\bar{x}_0$ para los puntos de $S^\ast$ y
$\triangledown g_{1}(\bar{x}_{0}),\dots ,\triangledown g_{m}(\bar{x}_{0})$ son linealmente independientes.

Entonces existen $\lambda _{1},\dots ,\lambda _{m}\in \mathbb{R}$, a los que llamamos multiplicadores de Lagrange tales que:

\[ \triangledown f(\bar{x}_{0})=\lambda _{1}\triangledown g_{1}(\bar{x}_{0})+\dots +\lambda _{m}\triangledown g_{m}(\bar{x}_{0}).\]

Si lo meditas un poco, al tomar $m=1$ obtenemos una situación como la del ejemplo motivador. En este caso, la conclusión es que $\triangledown f(\bar{x}_0)=\lambda \triangledown g(\bar{x}_0)$, que justo nos dice que en $\bar{x}_0$, las gráficas de los campos escalares $f$ y $g$ tienen una tangente en común.

Demostración del teorema de multiplicadores de Lagrange

Demostración. La demostración del teorema de multiplicadores de Lagrange usa varios argumentos de álgebra lineal. Esto tiene sentido, pues a final de cuentas, lo que queremos hacer es poner un gradiente ($\triangledown f(\bar{x}_0)$) como combinación lineal de otros gradientes ($\triangledown g_1(\bar{x}_0),\ldots, \triangledown g_m(\bar{x}_0)$). A grandes rasgos, lo que haremos es:

Definir un espacio $W$.
Mostrar que $\triangledown g_1(\bar{x}_0),\ldots, \triangledown g_m(\bar{x}_0)$ generan al espacio ortogonal $W^\bot$.
Mostrar que $\triangledown f(\bar{x}_0)$ es ortogonal a todo vector de $W$, por lo cual estará en $W^\bot$ y así por el inciso anterior será combinación lineal de $\triangledown g_1(\bar{x}_0),\ldots, \triangledown g_m(\bar{x}_0)$.

Para construir el espacio $W$ del que hablamos, usaremos el teorema de la función implícita y la regla de la cadena. Empecemos este argumento. Consideremos la siguiente matriz:

\[ \begin{equation} \begin{pmatrix} \frac{\partial g_{1}}{\partial x_{1}}(\bar{x}_{0}) & \dots & \frac{\partial g_{1}}{\partial x_{m}}(\bar{x}_{0}) & \frac{\partial g_{1}}{\partial x_{m+1}}(\bar{x}_{0}) & \dots & \frac{\partial g_{1}}{\partial x_{n}}(\bar{x}_{0}) \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ \frac{\partial g_{m}}{\partial x_{1}}(\bar{x}_{0}) & \dots & \frac{\partial g_{m}}{\partial x_{m}}(\bar{x}_{0}) & \frac{\partial g_{m}}{\partial x_{m+1}}(\bar{x}_{0}) & \dots & \frac{\partial g_{1}}{\partial x_{n}}(\bar{x}_{0}) \end{pmatrix}. \end{equation}\]

Dado que los vectores $\triangledown g_1(\bar{x}_0),\ldots, \triangledown g_m(\bar{x}_0)$ son linealmente independientes, el rango por renglones de esta matriz es $m$, de modo que su rango por columnas también es $m$ (tarea moral). Sin perder generalidad (quizás tras hacer una permutación de columnas, que permuta las entradas), tenemos que las primeras $m$ columnas son linealmente independientes. Así, la matriz

\[ \begin{pmatrix} \frac{\partial g_{1}}{\partial x_{1}}(\bar{x}_{0}) & \dots & \frac{\partial g_{1}}{\partial x_{m}}(\bar{x}_{0}) \\ \vdots & \ddots & \vdots \\ \frac{\partial g_{m}}{\partial x_{1}}(\bar{x}_{0}) & \dots & \frac{\partial g_{m}}{\partial x_{m}}(\bar{x}_{0}) \end{pmatrix}\]

es invertible. Hagamos $l=n-m$ y reetiquetemos las variables coordenadas $x_1,\ldots,x_m$ como $v_1,\ldots,v_m$, y las variables coordenadas $x_{m+1},\ldots,x_n$ como $u_1,\ldots, u_l$. Escribiremos $\bar{x}_0=(\bar{v}_0,\bar{u}_0)$ para referirnos al punto al que hacen referencia las hipótesis. Esto nos permite pensar $\mathbb{R}^{n}=\mathbb{R}^{m}\times \mathbb{R}^{l}$ y nos deja en el contexto del teorema de la función implícita. Como la matriz anterior es invertible, existen $U\subseteq \mathbb{R}^l$ y $V\subseteq \mathbb{R}^m$ para los cuales $\bar{u}_0\in U$, $\bar{v}_0\in V$ y hay una única función $h=(h_1,\ldots,h_m):U\to V$ de clase $C^1$ tal que para $\bar{u}\in U$ y $\bar{v}\in V$ se cumple que $g(\bar{v},\bar{u})=0$ si y sólo si $\bar{v}=h(\bar{u})$.

Definamos ahora la función $H:U\subseteq \mathbb{R}^{l}\rightarrow \mathbb{R}^{m}\times \mathbb{R}^{l}$ como $H(\bar{u})=(h(\bar{u}),\bar{u})$, la cual es de clase $C^{1}$ en $U$.

Por cómo construimos $h$, sucede que $(h(\bar{u}),\bar{u})\in S^{*}$ para toda $\bar{u}\in U$. Por definición, esto quiere decir que para toda $i=1,\ldots,m$ tenemos que $$(g_{i}\circ H)(\bar{u})=0$$ para toda $\bar{u}\in U$. Esto quiere decir que $g_i\circ H$ es una función constante y por lo tanto su derivada en $\bar{u}_0$ es la transformación $0$. Pero otra forma de obtener la derivada es mediante la regla de la cadena como sigue:

\begin{align*} D(g_{i}\circ H)(\bar{u}_{0})&=Dg_{i}(H(\bar{u}_{0}))DH(\bar{u}_{0})\\ &=Dg_{i}(\bar{v}_{0},\bar{u}_{0})DH(\bar{u}_{0}).\end{align*}

En términos matriciales, tenemos entonces que el siguiente producto matricial es igual al vector $(0,\ldots,0)$ de $l$ entradas (evitamos poner $(\bar{v}_0,\bar{u}_0)$ para simplificar la notación):

\[ \begin{equation}\begin{pmatrix} \frac{\partial g_{i}}{\partial v_{1}}& \dots & \frac{\partial g_{i}}{\partial v_{m}} & \frac{\partial g_{i}}{\partial u_{1}} & \dots & \frac{\partial g_{i}}{\partial u_{l}} \end{pmatrix}\begin{pmatrix} \frac{\partial h_{1}}{\partial u_{1}} & \dots & \frac{\partial h_{1}}{\partial u_{l}} \\ \vdots & \ddots & \vdots \\ \frac{\partial h_{m}}{\partial u_{1}} & \dots & \frac{\partial h_{m}}{\partial u_{l}} \\ 1 & \dots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \dots & 1 \end{pmatrix}\end{equation},\]

para cada $i=1,\ldots, m$. Nos gustaría escribir esta conclusión de manera un poco más sencilla, para lo cual introducimos los siguientes vectores para cada $j=1,\ldots, l$:

\[ \bar{w}_{j}=\left( \left( \frac{\partial h_{1}}{\partial u_{j}}(\bar{u}_{0}),\dots ,\frac{\partial h_{m}}{\partial u_{j}}(\bar{u}_{0}) \right), \hat{e}_{j}\right).\]

Cada uno de estos lo pensamos como vector en $\mathbb{R}^m\times \mathbb{R}^l$. Además, son $l$ vectores linealmente independientes, pues sus entradas $\hat{e}_j$ son linealmente independientes. El espacio vectorial $W$ que generan es entonces un subespacio de $\mathbb{R}^m\times \mathbb{R}^l$, con $\dim(W)=l$.

De la ecuación $(2)$ tenemos que $\triangledown g_{i}(\bar{v}_{0},\bar{u}_{0})\cdot \bar{w}_{j}=0$ para todo $i=1,\dots ,m$, y $j=1,\dots ,l$. Se sigue que $\triangledown g_{i}(\bar{v}_{0},\bar{u}_{0})\in W^{\perp}$, donde $W^{\perp}$ es el complemento ortogonal de $W$ en $\mathbb{R}^{m}\times \mathbb{R}^{l}$. Pero además, por propiedades de espacios ortogonales tenemos que

\begin{align*}
\dim(W^{\perp})&=\dim(\mathbb{R}^{m}\times \mathbb{R}^{l})-dim(W)\\
&=m+l-l\\
&=m.
\end{align*}

Así $\dim(W^{\perp})=m$, además el conjunto $\left\{ \triangledown g_{i}(\bar{v}_{0},\bar{u}_{0}) \right\}_{i=1}^{m}$ es linealmente independiente con $m$ elementos, por tanto este conjunto es una base para $W^{\perp}$. Nuestra demostración estará terminada si logramos demostrar que $\triangledown f(\bar{v}_0,\bar{u}_0)$ también está en $W^\perp$, es decir, que es ortogonal a todo elemento de $W$.

Pensemos qué pasa al componer $f$ con $H$ en el punto $\bar{u}_0$. Afirmamos que $\bar{u}_0$ es un extremo local de $f\circ H$. En efecto, $(f\circ H)(\bar{u}_0)=f(g(\bar{u}_0),\bar{u}_0)=(\bar{v}_0,\bar{u}_0)$. Si, por ejemplo $(\bar{v}_0,\bar{u}_0)$ diera un máximo, entonces los valores $f(\bar{v},\bar{u})$ para $(\bar{v},\bar{u})$ dentro de cierta bola $B_\delta(\bar{v}_0,\bar{u}_0)$ serían menores a $f(\bar{v}_0,\bar{u}_0)$. Pero entonces los valores cercanos $\bar{u}$ a $\bar{u}_0$ cumplen $(f\circ H)(\bar{u})=f(h(\bar{u}),\bar{u})$, con $(\bar{u},h(\bar{u}))$ en $S^\ast$ y por lo tanto menor a $f(\bar{v}_0,\bar{u}_0)$ (para mínimos es análogo).

Resumiendo lo anterior, $\bar{u}_{0}$ es extremo local de $f\circ H$. Aplicando lo que aprendimos en la entrada anterior, la derivada de $f\circ H$ debe anularse en $\bar{u}_0$. Pero por regla de la cadena, dicha derivada es

\begin{align*}\triangledown (f\circ H)(\bar{u}_{0})&=D(f\circ H)(\bar{u}_{0})\\ &=Df(H(\bar{u}_{0}))DH(\bar{u}_{0})\\ &=Df(h(\bar{u}_{0}),\bar{u}_{0})DH(\bar{u}_{0})\\
&=Df(\bar{v}_0,\bar{u}_{0})DH(\bar{u}_{0})
\end{align*}

Viéndolo como multiplicación de matrices, el siguiente producto es el vector $(0,0,\ldots,0)$ de $l$ entradas:

\[ \begin{pmatrix} \frac{\partial f}{\partial v_{1}} & \dots & \frac{\partial f}{\partial v_{m}} & \frac{\partial f}{\partial u_{1}} & \dots & \frac{\partial f}{\partial u_{l}} \end{pmatrix}\begin{pmatrix} \frac{\partial h_{1}}{\partial u_{1}} & \dots & \frac{\partial h_{1}}{\partial u_{l}} \\ \vdots & \ddots & \vdots \\ \frac{\partial h_{m}}{\partial u_{1}} & \dots & \frac{\partial h_{m}}{\partial u_{l}} \\ 1 & \dots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \dots & 1 \end{pmatrix}=0 \]

De donde concluimos $\triangledown f(\bar{v}_{0},\bar{u}_{0})\cdot \bar{w}_{j}=0$ para cada $j=1,\dots l$. Esto precisamente nos dice que $\triangledown f(\bar{v}_{0},\bar{u}_{0})\in W^{\perp}$. Esto es justo lo que queríamos, pues habíamos demostrado que $\left\{ \triangledown g_{i}(\bar{v}_{0},\bar{u}_{0}) \right\}_{i=1}^{m}$ es una base de $W^{\perp}$. Por ello podemos expresar a $\triangledown f(\bar{v}_{0},\bar{u}_{0})$ como combinación lineal de esta base, es decir, existen $\lambda _{1},\dots ,\lambda _{m}$ escalares tales que:

\[ \triangledown f(\bar{v}_{0},\bar{u}_{0})=\lambda _{1}\triangledown g_{1}(\bar{v}_{0},\bar{u}_{0})+\dots +\lambda _{m}\triangledown g_{m}(\bar{v}_{0},\bar{u}_{0}). \]

$\square$

¡Qué bonita demostración! Usamos el teorema de la función implícita, la regla de la cadena (dos veces), nuestros resultados para valores extremos de la entrada anterior, y un análisis cuidadoso de ciertos espacios vectoriales.

Ejemplos del método de multiplicadores de Lagrange

Veamos algunos problemas que podemos resolver con esta nueva herramienta.

Ejemplo. Determinaremos los puntos extremos de $f(x,y)=x+2y$ bajo la condición $x^{2}+y^{2}=5$. Para poner todo en términos de nuestro teorema, definimos $g(x,y)=x^{2}+y^{2}-5$. Por el teorema de multiplicadores de Lagrange, en los puntos extremos debe existir una $\lambda$ tal que $\triangledown f(x,y)=\lambda \triangledown g(x,y)$. Calculando las parciales correspondientes, debemos tener entonces

\[ \left( 1,2 \right)=\lambda \left( 2x,2y \right).\]

Adicionalmente, recordemos que se debe satisfaces $g(x,y)=0$. Llegamos entonces al sistema de ecuaciones

\[ \left \{\begin{matrix} 1-2x\lambda=0 \\ 2-2y\lambda =0 \\ x^{2}+y^{2}-5=0 \end{matrix}\right. \]

Al despejar $x$ y $y$ en ambas ecuaciones tenemos:

\[ \begin{matrix} x=\frac{1}{2\lambda} \\ y=\frac{1}{\lambda} \\ x^{2}+y^{2}-5=0 \end{matrix}.\]

Poniendo los valores de $x$ y $y$ en la tercera ecuación, llegamos a $\left( \frac{1}{2\lambda}\right)^{2}+\left( \frac{1}{\lambda}\right)^{2}-5=0$, de donde al resolver tenemos las soluciones $\lambda _{1}=\frac{1}{2}$ y $\lambda _{2}=-\frac{1}{2}$.

Al sustituir en las ecuaciones de nuestro sistema, obtenemos como puntos críticos a $(x,y)=(-1,-2)$ y $(x,y)=(1,2)$.

Si intentamos calcular el hessiano de $f$, esto no nos dirá nada (no tendremos eigenvalores sólo positivos, ni sólo negativos). Pero esto ignora las restricciones que nos dieron. Podemos hacer una figura para entender si estos puntos son máximos o mínimos. En la Figura $1$ tenemos la gráfica de $f$, intersectada con la superfice dada por $g$. Nos damos cuenta que hay un punto máximo y uno mínimo. Al evaluar, obtenemos $f(1,2)=5$ y $f(-1,-2)=-5$. Esto nos dice que el máximo en la superficie se alcanza en $(1,2)$ y el mínimo en $(-1,-2)$.

Figura 2: Ilustración del *Ejemplo 1* la función $g(x,y)=x^{2}+y^{2}-5$ esta dibujada en azul esta impone restricción a la función $f$ que dibuja un plano en el espacio.

$\triangle$

Ejemplo. Veamos cómo minimizar la expresión $$f(x,y,z)=x^{2}+y^{2}+z^{2}$$ sujetos a la condición $x+y+z=1$. Una vez más, proponemos $g(x,y,z)=x+y+z-1$ para tener la situación del teorema de multiplicadores de Lagrange. Debe pasar que $\lambda$ $\triangledown f(x,y,z)=\lambda \triangledown g(x,y,z)$. El gradiente de $g(x,y,z)$ es de puros ceros unos, así que tenemos el sistema de ecuaciones:

\[ \left \{\begin{matrix} 2x=\lambda \\ 2y=\lambda \\ 2z=\lambda \\ x+y+z-1=0 \end{matrix}\right.\]

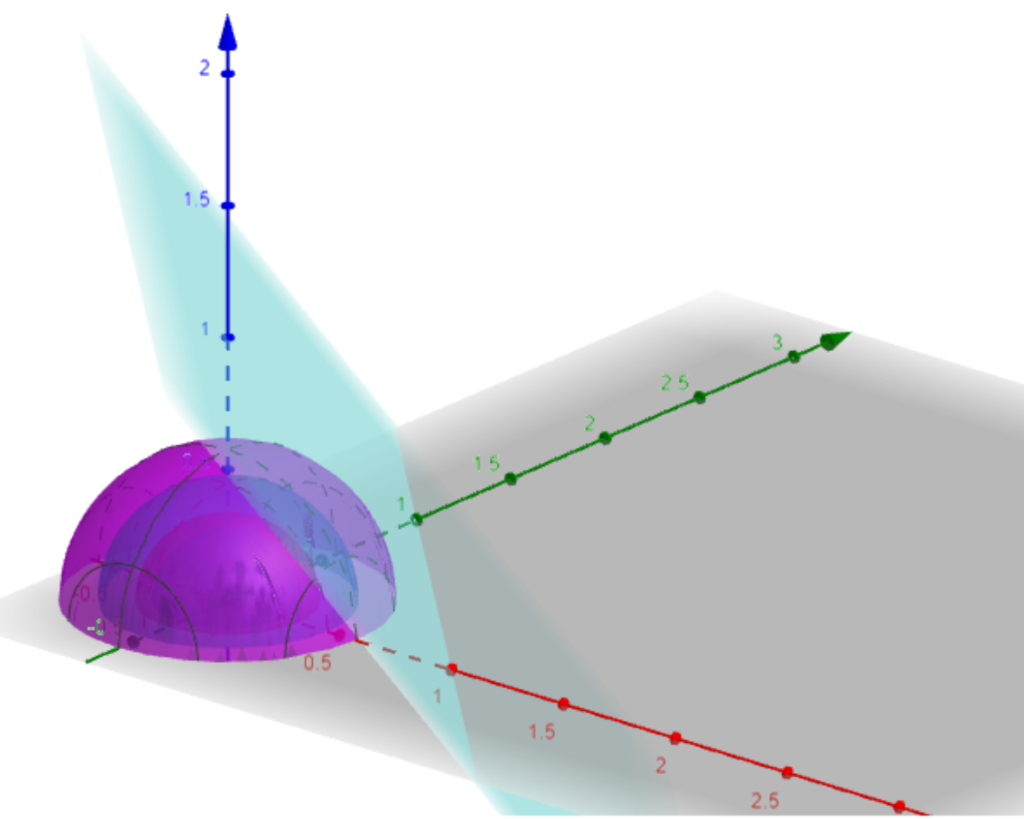
De las primeras tres ecuaciones tenemos $2x=2y=2z$ de donde $x=y=z$. Sustituyendo en la tercera ecuación, $3x-1=0$, es decir $x=y=z=\frac{1}{3}$. Ya que sólo tenemos una solución, ésta es el mínimo del conjunto de soluciones. En la figura 3 tenemos la ilustración de la solución de este problema, la esfera centrada en el origen de radio $\frac{1}{3}$ toca al plano $x+y+z=1$ en el punto $\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)$

$\triangle$

Figura 3: En azul claro el plano $x+y+z=1$, inflamos esferas centradas en el origen; desde la de radio cero vamos aumentando el radio hasta tener el radio correspondiente para el cual la esfera toque tangentemente al plano.

Más adelante…

Con esta entrada cerramos el curso de Cálculo Diferencial e Integral III. ¡¡Felicidades!! Esperamos que todas estas notas te hayan sido de ayuda para estudiar, repasar o impartir la materia. Quedamos al pendiente de cualquier duda, observación o sugerencia en la sección de comentarios de las entradas.

Tarea moral

Determina los extremos de la función $f(x,y)=xy+14$ bajo la restricción $x^{2}+y^{2}=18$
El plano $x+y+2z=2$ interseca al paraboloide $z=x^{2}+y^{2}$ en una elipse $\mathbb{E}$. Determina el punto de la elipse con el valor mayor en el eje $z$, y el punto con el valor mínimo en el mismo eje. Sugerencia: $f(x,y,z)=x+y+2z-2$, y $g(x,y,z)=x^{2}+y^{2}-z$
Determinar el máximo valor de $f(x,y,z)=x^{2}+36xy-4y^{2}-18x+8y$ bajo la restricción $3x+4y=32$
Determinar los puntos extremos de la función $f(x,y,z)=x^{2}+y^{2}+z^{2}$ bajo la restricción $xyz=4$
Demuestra que en una matriz $M$ su rango por columnas es igual a su rango por renglones. Sugerencia. Usa el teorema de reducción gaussiana. También, puedes revisar la entrada que tenemos sobre rango de matrices.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral III
Entrada anterior del curso: Puntos críticos de campos escalares

Investigación de Operaciones: Forma canónica y forma estándar de un problema lineal (9)

Por Aldo Romero

Deja un comentario

Introducción

En las entradas anteriores hemos dado ejemplos de varios problemas de aplicación que pueden ser planteados mediante un problema de programación lineal. Una vez que llegamos a un modelo, se pueden tener restricciones de los tipos $\leq$, $=$ y $\geq$. Además, puede haber restricciones de signo sobre las variables. Puede que se les pida ser no positivas, no negativas o irrestrictas (no restringidas) en signo. Lo que haremos ahora es ver cómo podemos llegar a un cierto formato (forma estándar o forma canónica).

Forma canónica de un problema lineal

A continuación introducimos el primer formato que nos facilitará el trabajo.

Definición. Se dice que un problema de programación lineal está en forma canónica si cumple simultáneamente las siguientes tres propiedades:

El problema es de maximización.
Las restricciones del problema son todas del tipo $\leq$ (menor o igual).
Las variables de decisión son no negativas.

Así, tenemos entonces que un problema en forma canónica se ve como sigue:

\begin{align*}
Max \quad z &= c_1x_1+\ldots+c_nx_n\\
s.a.&\\
&\begin{matrix} a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n \leq b_1\\
a_{21}x_1+a_{22}x_2+\ldots + a_{2n}x_n \leq b_2\\
\vdots \\
a_{m1}x_1+a_{m2}x_2+\ldots+a_{mn}x_n\leq b_n\end{matrix}\\
& x_1\geq 0, x_2\geq 0, \ldots, x_n\geq 0.
\end{align*}

En términos matriciales, esto podemos reescribirlo de manera mucho más compacta como sigue:

\begin{align*}
Max \quad z &= c\cdot x\\
s.a.&\\
Ax &\leq b\\
x &\geq 0,\\
\end{align*}

en donde:

$c=(c_1,\ldots,c_n)\in \mathbb R^n$ es el vector de costos (vector renglón)
$x = (x_1,\ldots,x_n)\in \mathbb R^n$ es el vector de variables de decisión (vector columna),
$A=[a_{ij}]$ es la matriz de restricciones, que es una matriz de $m \times n$ y
$b=(b_1,\ldots,b_m) \in \mathbb R^m$ es el vector de constantes que acotan las combinaciones lineales de variables.
Entendemos $0$ como el vector en $\mathbb{R}^n$ que consiste de puras entradas iguales a cero.

Todo problema de programación lineal puede ser expresado en forma canónica; es decir, puede definirse un problema en forma canónica equivalente a él, en el sentido de que la solución de uno nos permite encontrar la solución del otro de manera sencilla. En efecto:

Si el problema es de minimización, puede considerarse en vez de $z$ la función $z’ = -z$ y en el problema equivalente se busca maximizar $z’$.
Si una restricción es del tipo $\geq$ puede ser mutiplicada por -1 para obtener una del tipo $\leq$.
Una ecuación puede ser substituida por una desigualdad del tipo $\leq$ y otra del tipo $\geq$. Luego, la del tipo $\geq$ puede ser substituida por una del tipo $\leq$ como en el punto anterior.
Para una variable $x_i\leq 0$ puede definirse $x_i’ = -x_i$, resultando $x_i’ \geq 0$. Claramente hay una biyección entre elegir el valor de $x_i$ y $x_i’$.
Para una $x_i$ no restringida pueden ser definidas dos variables no negativas $x_i’$ y $x_i^\ast$ tales que $x_i’-x_i^\ast = x_i$. Para cualquier $x_i$ dado podemos construir dichas variables, y viceversa, para $x_i’$ y $x_i^\ast$ se puede construir $x_i$.

Ejemplo de pasar un problema a forma canónica

Transformaremos el siguiente problema a su forma canónica.
\begin{align*}
Min \quad z &= x_1-3x_2+7x_3\\
s.a.&\\
&\begin{matrix}3x_1&+x_2&+3x_3 &\leq 40\\
x_1&+9x_2&-7x_3 &\geq 50\\
5x_1&+3x_2& &= 20\\
&5x_2 &+ 8x_3 &\leq 80\end{matrix}\\
& x_1, x_2\geq 0, \quad x_3 \quad libre.\\
\end{align*}

Primeramente se definen las variables no negativas $x_3’$ y $x_3^{\ast}$, tales que $x’_3-x_3^{\ast} = x_3$, con objeto de satisfacer el punto (3) de la definición. Para satisfacer el punto (1) se considera la función:
\begin{align*}
z’ &= -z \\&= -x_1+3x_2-7x_3\\&=-x_1+3 x_2-7 x’_3+7x_3^{\ast}
\end{align*}

y se busca maximiza ésta (equivalente a minimizar $z$). Finalmente se realizan cambios en las restricciones para satisfacer el punto (2). La primera y cuarta desigualdad cumplen con la definición por lo que no se modifican (más allá de la sustitución de $x_3$ por $x’_3-x_3^{\ast}$); la segunda desigualdad se multiplica por $-1$ para obtener una del tipo $\leq$: $$ x_1 + 9x_2 – 7x_3 \geq 50 \quad \Leftrightarrow \quad -x_1 – 9x_2 + 7x_3 \leq -50.$$

Substituyendo las nuevas variables se obtiene: $$-x_1-9x_2+7x’_3-7x_3^{\ast}\leq -50.$$

Para la tercera desigualdad se tiene lo siguiente:

\begin{align*}
5x_1+3x_2 &= 20\\
&\Leftrightarrow\\
5x_1 + 3x_2 \leq 20 \quad& y \quad 5x_1 + 3x_2 \geq 20\\
&\Leftrightarrow\\
5x_1 + 3x_2 \leq 20 \quad& y \quad -5x_1 – 3x_2 \leq -20.\\
\end{align*}

Finalmente el problema queda expresado en forma canónica como:

\begin{align*}
Max \quad z’ &= -x_1+3x_2-7x’_3+7x_3^{\ast}\\
s.a.&\\
&\begin{matrix}3x_1&+x_2&+3x’_3&-3x_3^{\ast} &\leq &40\\
-x_1&-9x_2&+7x’_3&-7x_3^{\ast} &\leq &-50\\
5x_1&+3x_2 & & &\leq &20\\
-5x_1&-3x_2 & & &\leq &-20\\
&5x_2&+8x’_3&-8x_3^{\ast} &\leq &80\end{matrix}\\
&x_1, x_2, x’_3, x_3^{\ast} \geq 0.
\end{align*}

Forma estándar de un problema lineal

Definición. Se dice que un problema de programación lineal está en forma estándar si

Todas las restricciones son ecuaciones.
Todas las variables son no negativas.
La función objetivo puede pedirse que se optimice maximizándola, o minimizándola.

De esta manera, un problema en forma estándar se ve como sigue:

\begin{align*}
Max\, (\text{o } Min) \quad z &= c_1x_1+\ldots+c_nx_n\\
s.a.&\\
&\begin{matrix} a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n = b_1\\
a_{21}x_1+a_{22}x_2+\ldots + a_{2n}x_n = b_2\\
\vdots \\
a_{m1}x_1+a_{m2}x_2+\ldots+a_{mn}x_n= b_n\\
x_1\geq 0, x_2\geq 0, \ldots, x_n\geq 0.
\end{matrix}\\
\end{align*}

En notación matricial, el problema en forma canónica queda expresado de la siguiente manera:

\begin{align*}
Max\, (\text{o } Min) \quad z &= cx\\
s.a.&\\
Ax &= b\\
x &\geq 0\\
\end{align*}

en donde $c, x, A$ y $b \geq 0$ son como se mencionó antes.

Así como cualquier problema de programación lineal puede ser expresado en forma canónica, también cualquier problema de programación lineal puede expresarse en forma estándar. Una restricción del tipo $\leq$ ($\geq$) puede ser transformada en una ecuación sumando (o restando) una variable no negativa que recibe el nombre de variable de holgura (o variable de sobra).

Ejemplo de pasar un problema a forma estándar

Retomemos el problema ejemplo anterior, antes de expresarlo en forma canónica.

\begin{align*}
Min \quad z &= x_1-3x_2+7x_3\\
s.a.&\\
&\begin{matrix}3x_1&+x_2&+3x_3 &\leq 40\\
x_1&+9x_2&-7x_3 &\geq 50\\
5x_1&+3x_2& &= 20\\
&5x_2 &+ 8x_3 &\leq 80\end{matrix}\\
& x_1, x_2\geq 0, \quad x_3 \quad libre.\\
\end{align*}

Vamos a expresarlo ahora en forma estándar. Como lo hicimos anteriormente, hacemos la sustitución $x=x’_3-x_3^\ast$ para que la variable libre se convierta en dos con restricciones de ser no negativas.

Para satisfacer (1) se introducen las variables de holgura, $x_4$, $x_5$ y $x_6$ que pediremos que sean no negativas. A la primera desigualdad le sumamos $x_4$. A la quinta le sumamos $x_6$. Y finalmente, a la segunda le restamos $x_5$. Esto transforma las desigualdades en igualdades. De esta manera, el problema queda expresado de la siguiente manera:

\begin{align*}
Min \quad z &= x_1 – 3x_2+7x’_3-7x_3^\ast\\
&s.a.\\
&\begin{matrix}3x_1 &+ x_2 &+ 3x’_3 &- 3x_3^\ast &+ x_4 & & &= &40\\
x_1 &+ 9x_2 &- 7x’_3 &+ 7x_3^\ast & &- x_5 & & = &50\\
5x_1 &+ 3x_2 &&&&& &= &20\\
&5x_2 &+ 8x’_3 &- 8x_3^\ast &&&+ x_6 &= &80\end{matrix}\\
&x_1,x_2,x’_3,x_3^\ast,x_4,x_5,x_6 \geq 0.
\end{align*}

Más adelante…

Las formas que estudiamos en esta entrada nos ayudarán posteriormente para plantear soluciones para problemas de programación lineal.

Mientras tanto, en la siguiente entrada hablaremos de algunos otros conceptos relativos a la teoría de problemas lineales y posibles propiedades que puede tener una asignación de variables. Diremos qué es una solución básica, una solución factible y un punto extremo para un problema lineal.

Tarea moral

¿Cuál sería la forma estándar del problema de maximizar $x+y$ sujeto a $x-y\leq 8$ y $y\leq 0$? ¿Y su forma canónica?
Transforma el siguiente problema de programación lineal a su forma canónica y a su forma estándar:
\begin{align*}
Max \quad z &= -2x_1 + 3x_2 – 2x_3\\
&s.a.\\
&\begin{matrix}4x_1 &-x_2 &- 5x_3 &=& 10\\
2x_1 &+ 3x_2 &+ 2x_3 &\geq &12\end{matrix}\\
& x_1 \geq 0, \quad x_2, x_3 \quad irrestrictas.
\end{align*}
Revisa nuevamente las entradas anteriores y encuentra las formas canónicas y formas estándar de los problemas que hemos planteado hasta ahora.
La forma estándar (o bien la forma canónica) de un programa lineal «es equivalente» al problema original. Justifica esta afirmación formalmente. Es decir, explica por qué una solución $x_1,\ldots,x_n$ que optimiza el problema original está asociada a una solución de su forma estándar (o canónica) y viceversa.
Imagina que tenemos un sistema de ecuaciones de la forma $Ax=B$ con $A$ matriz en $M_{m,n}(\mathbb{R})$ y $b$ vector en $\mathbb{R}^m$. Queremos encontrar de todas las posibles soluciones al sistema aquella que minimiza la suma de las entradas de $x$. Plantea esto como un problema lineal y transfórmalo a su forma canónica y a su forma estándar.

Entradas relacionadas

Ir a Investigación de Operaciones
Entrada anterior del curso: El problema de la ruta más corta
Entrada siguiente del curso: Soluciones básicas, factibles y no degeneradas

Investigación de Operaciones: El problema de producción e inventario (7)

Por Aldo Romero

Deja un comentario

Introducción

Ya hemos visto algunos ejemplos en los que se plantea un problema de programación lineal a partir de un contexto específico. Hemos visto el problema de la dieta, el problema de la mochila y el problema del transporte. Hay algunos problemas que parecen un poco más complicados y que no es tan evidente desde el inicio que se pueden plantear como problemas de programación lineal. En esta ocasión veremos uno de ellos: el problema de producción e inventario.

Abundan las aplicaciones de la programación lineal para planificar la producción y para controlar inventarios. El siguiente es solo una de múltiples aplicaciones que se les puede dar a este tipo de problemas.

A grandes rasgos, el problema consiste en modelar una fábrica que necesita tener lista cierta cantidad de inventario de un producto en determinados momentos del año. La fábrica puede producir cierta cantidad de producto que depende de la temporada del año. Quizás haya temporadas en las que puede producir más de lo que necesita, pero si hace eso incurrirá en costos de almacenaje. ¿Cómo puede distribuir su producción, almacenaje y despacho la fábrica para minimizar el costo y cumplir con su compromiso de inventario? Veamos a continuación que esta situación se puede plantear en términos de un problema de programación lineal.

Ejemplo del problema de producción e inventario

Una empresa productora de videojuegos indie acaba de finalizar su último gran lanzamiento y está lista para producirlo en masa en su formato físico. La siguiente tabla indica la demanda de los primeros 3 meses de lanzamiento.

Meses transcurridos a partir del lanzamiento	0	1	2
Demanda en miles de copias del mes en curso	80	60	40
Productividad disponible del mes en curso	110	50	30

Como el primer mes de lanzamiento es el más importante, la empresa decide que se pueden producir hasta 110 mil copias ese mes, y gradualmente va a reducir su productividad a 50 mil copias el segundo mes y 30 mil el tercer mes; esto con la finalidad de enfocar más tiempo y recursos en otras producciones.

La empresa productora y las tiendas donde se venden tiene un contrato que establece en particular dos cosas:

Las tiendas tienen que tener en stock la cantidad de copias demandas cada mes, y esta cantidad de copias será las que la empresa productora entregó este mes junto con las que sobraron el mes pasado
- Si se entregan más copias que las demandadas por la tienda, se cobrará un costo de almacenamiento de \$2000 al mes por cada mil copias que están siendo almacenadas en tienda fuera de la demanda establecida.

El costo de producción de cada mil copias es de \$20000. Se desea determinar el plan de producción e inventario que satisfaga el contrato con estas tiendas a fin de minimizar los costos.

Variables de decisión

De manera intuitiva, vamos a hacer nuestras variables de decisión las miles de copias que se van a producir el mes en curso desde el lanzamiento del juego.

$x_i$ = miles de copias a producir en el mes $i$ desde el lanzamiento del juego. $(i \in \{1, 2, 3\})$.

Función objetivo

Como se mencionó, el plan de producción tiene que minimizar los costos para la empresa, tanto los gastos de producción de sus videojuegos como el almacenamiento de estos.

El costo de producción es simplemente el número de copias producidas por cada mes, multiplicado por el costo de fabricación de cada copia ($\$20$). Esto es: $20(x_1 + x_2 + x_3)$.

Y luego consideramos el costo de almacenamiento de las copias que no fueron demandadas por la empresa en ese mes. Entonces, para el primer mes, $x_1 – 80$ son las miles de copias que la empresa tiene que cubrir en gastos de almacenamiento. Para el segundo mes, las copias demandadas al momento son las acumuladas del primer y segundo mes ($140000$) y los juegos producidos son solamente $x_1 + x_2$. Entonces, los miles de juegos por los que hay que cubrir el costo de almacenamiento son $x_1 + x_2 – 140$. Y para el tercer mes, las copias demandadas son las acumuladas de los primeros 3 meses ($180000$) y los juegos producidos serán $x_1 + x_2 + x_3$ en miles de copias, y así, los costos de almacenamiento para el tercer mes serán $x_1 + x_2 + x_3 – 180$.

Entonces, el número de miles de copias por las que hay que cubrir costos de almacenamiento para estos 3 meses será: $(x_1 – 80) + (x_1 + x_2 – 140) + (x_1 + x_2 + x_3 -180)$. Y esta cantidad la multiplicamos por el costo de almacenamiento mensual por millar de copias (\$2000).

Entonces, juntando las expresiones, el costo total que hay que minimizar sería:

$$Min \quad z = 20000(x_1 + x_2 + x_3) + 2000[(x_1 – 80) + (x_1 + x_2 – 140) + (x_1 + x_2 + x_3 – 180)]$$

O si lo queremos poner de la forma más resumida posible, esto es:

$$Min \quad z = 26000x_1 + 24000x_2 + 22000x_3 – 800000$$

Restricciones del problema de producción e inventario

Primero, vayamos con las restricciones de oferta:

\begin{align*}
x_1 \leq 110\\
x_2 \leq 50\\
x_3 \leq 30\\
\end{align*}

Después, vayamos con las restricciones de demanda:

\begin{align*}
x_1 \geq 80\\
x_2 + (x_1 – 80) \geq 60\\
x_3 + (x_1 + x_2 – 140) \geq 40\\
\end{align*}

Recordemos que la razón de la última restricción es para que la empresa productora no se quede ninguna copia más de las demandadas para que no haya cuota por almacenamiento en las tiendas para el cuarto mes.

Y naturalmente nuestras variables de decisión son no negativas ya que hablamos de la cantidad de unidades que tenemos de un producto.

Resumen de formulación del problema de producción e inventario

En resumen, nuestro problema de programación lineal quedaría planteado así:

\begin{align*}
Min \quad z = 20000(x_1 + x_2 + x_3) &+ 2000[(x_1 – 80) + (x_1 + x_2 – 140) + (x_1 + x_2 + x_3 – 180)]\\
&s.a\\
x_1 &\leq 110\\
x_2 &\leq 50\\
x_3 &\leq 30\\
x_1 &\geq 80\\
x_2 + (x_1 – 80) &\geq 60\\
x_3 + (x_1 + x_2 – 140) &\geq 40\\
x_i &\geq 0, i \in \{1, 2, 3\}\\
\end{align*}

Más adelante…

La siguiente entrada muestra nuestro último ejemplo introductorio: el problema de la ruta más corta. Como veremos, en este problema también es necesario aprovechar la situación del problema de manera creativa para poder llevarlo a un contexto lineal.

Tarea

El problema se vuelve mucho más sencillo si únicamente hay dos periodos. Plantea un problema que refleje esta situación en el caso particular de la entrada y resuélvelo. Es decir, determina en esos dos periodos (el primer y segundo mes) cuál es la cantidad correcta de unidades a producir por mes, para minimizar el costo total.
Cambia el planteamiento dado en la entrada por uno en el que el costo de almacenaje en las tiendas sea de \$0. En ese caso, ¿cuál sería el plan de producción e inventario óptimo?
En esta entrada dimos la formulación de un caso particular del problema de producción e inventario. Sin embargo, ya tienes todas las herramientas para plantear el problema de manera general. Realiza una formulación general en la que:
1. Se tengan n periodos con demanda de unidades$d_1, d_2, \ldots, d_n$ por cada periodo.
2. Se tengan capacidades de producción $o_1, o_2, \ldots, o_n$ unidades en cada periodo.
3. Se tengan costos $P$ y $A$, de producir y almacenar una unidad de producto respectivamente.
En un problema general de producción e inventario. ¿Por qué podría ser mala idea producir mucho más de lo necesario en las temporadas en las que se puede? Intenta justificar intuitivamente, y luego encuentra algunos casos particulares del problema que apoyen tus argumentos.

Respuestas

1.- Si eliminamos un mes del problema, tendríamos la siguiente tabla de productividad y demanda:

Meses transcurridos a partir del lanzamiento	0	1
Demanda en miles de copias del mes en curso	80	60
Productividad disponible del mes en curso	110	50

Tenemos las mismas variables de decisión: $x_i$ = miles de copias a producir el mes $i$ desde el lanzamiento del juego. $i \in \{1, 2\}$

Para la función objetivo, el costo de producción de las copias va a ser: $20000(x_1 + x_2)$. Los gastos de almacenamiento del primer y segundo mes serán: $2000[(x_1 – 80) + (x_1 + x_2 – 140)]$.

Entonces la función objetivo queda de la siguiente manera:

$$Min \quad z = 24000x_1 + 22000x_2 – 440000$$

Las restricciones de oferta y de demanda serían:

\begin{align*}
x_1 &\leq 110\\
x_2 &\leq 50\\
x_1 &\geq 80\\
x2 + (x_1 – 80) &\geq 60\\
\end{align*}

Entonces, el problema con dos periodos de tiempo quedaría planteado de la siguiente manera:

\begin{align*}
Min \quad z &= 24000x_1 + 22000x_2 – 440000\\
&s.a\\
x_1 &\leq 110\\
x_2 &\leq 50\\
x_1 &\geq 80\\
x_2 + (x_1 – 80) &\geq 60\\
x_i &\geq 0, i \in \{1, 2\}\\
\end{align*}

Ahora, una posible solución a este problema sea satisfacer la demanda del primer mes, con tal de que sobren solamente la menor cantidad de copias que al sumarlas con la producción del segundo mes, nos cumplan también la demanda exacta de ese mes. Es decir, producir en el primer mes 90000 copias, almacenar 10000 que sobrarían en tienda y producir hasta el límite de producción el segundo mes que son 50000 copias y juntos con las 10000 que había almacenadas, se cumplirá la demanda que tenemos para el segundo periodo que son 60000 copias. De esta manera no se incurre en gastos innecesarios de almacenamiento, ya que para el tercer mes no hay copias por almacenar que nos generen ese gasto.

2.- Si no hubiera costo por almacenamiento tenemos varias soluciones que podrían ser óptimas, pero en realidad lo sería cualquiera donde se cumplan los valores de demanda al mínimo, es decir, que se produzcan las unidades que nos piden por los tres meses y ni una más.

3.- Sea una empresa tiene que producir un producto y este producto se vende en n periodos de tiempo, con su respectiva demanda ($d_1, \ldots, d_n$) y oferta de productos ($o_1, \ldots, o_n$) en cada uno de ellos.

Se tiene un costo $P$ de fabricación por producto y un costo A de almacenamiento por producto de un periodo a otro.

Se quiere determinar el plan de producción e inventario que satisfaga la demanda y minimice los costos.

Variables de decisión: $x_i$ = número de unidades a producir en el periodo $i$. $i \in \{1, \ldots, n\}$

Función objetivo:

$$Min \quad z = P(x_1 + \ldots + x_n) + A[(x_1-d_1) + (x_1 + x_2 – d_1 – d_2) + \ldots + (\sum_{i=1}^n{x_i} – \sum_{i=1}^n{d_i})]$$

Y por último, las restricciones serían:

\begin{align*}
x_1 &\leq o_1\\
x_2 &\leq o_2\\
&\vdots\\
x_n &\leq o_n\\
x_1 &\geq d_1\\
x_1 + x_2 – d_1 &\geq d_2\\
\vdots\\
\end{align*}

$$(\sum_{i=1}^n{x_i} – \sum_{i=1}^{n-1}{d_i}) \geq \sum_{i=1}^n{d_i}$$

$$x_i \geq 0,\quad i \in \{1, \ldots, n\}$$

4.- Dependería del problema pero en general como se intenta minimizar los costos, esto también sería minimizar los costos que conlleva el almacenaje de productos y si se producen muchos cada periodo, esto incurrirá en el aumento de los gastos mencionados y no será lo optimo para el objetivo que tenemos.

Entradas relacionadas

Ir a Investigación de Operaciones
Entrada anterior del curso: El problema del transporte
Entrada siguiente del curso: El problema de la ruta más corta

Investigación de Operaciones: El problema del transporte (6)

Por Aldo Romero

Deja un comentario

Introducción

En esta entrada abordaremos otro de los problemas conocidos que se pueden plantear en términos de programación lineal: el problema del transporte. A grandes rasgos, el problema del transporte habla de cómo surtir a diferentes destinos de un cierto producto que parte de diferentes orígenes con disponibilidad limitada.

Siendo un poco más concretos, cada origen tiene una cierta cantidad de unidades de producto. Cada destino requiere de una cierta cantidad de unidades de producto. Además, para cada pareja origen-destino se tiene un costo de transporte unitario. El objetivo es determinar cuál es la manera más económica de cumplir con todos los requisitos de oferta y demanda.

Ejemplo del problema del transporte

Supongamos que una compañía que produce electrónicos tiene tres almacenes $A$, $B$ y $C$. La cantidad de computadoras portátiles disponibles en cada uno de los almacenes se encuentra registrada en la siguiente tabla.

Origen	A	B	C
Oferta en unidades	200	350	470

Pensemos que hay dos tiendas de electrónicos $X$ y $Y$ que desean vender computadoras portátiles de dicha compañía. La cantidad de computadoras portátiles que necesita cada tienda está dada en la siguiente tabla.

Destino	X	Y
Demanda en unidades	300	500

Además de esto sabemos que transportar cada una de las computadoras portátiles tiene un costo que depende del almacén origen y de la tienda destino. El costo unitario de transporte está dado por la siguiente tabla.

	A	B	C
X	35	40	42
Y	44	37	45

Así, por ejemplo, transportar una computadora portátil del almacén $B$ a la tienda $Y$ tiene un costo de \$37.

Queremos determinar cuántas computadoras portátiles se tienen que enviar de cada origen a cada destino de manera que no se exceda la cantidad disponible en cada origen, a cada tienda llegue la cantidad de computadoras que se deben enviar y se minimice el costo total de envío.

Variables de decisión

Lo que tenemos que decidir en nuestro problema es cuántas computadoras portátiles se envían de cada origen a cada destino. Por ejemplo, debemos decidir cuánto vale una variable $x_{AX}$ que nos dice cuántas computadoras portátiles enviar del almacén $A$ a la tienda $X$. Así, las variables se definen de la siguiente manera:

$x_{ij}$ = número de computadoras a transportar del almacén $i$ al destino $j$. $i \in \{A, B, C\}, j \in \{X, Y\}$.

En este ejemplo en concreto, la cantidad de unidades debe ser un número entero (no podemos enviar $1/2$ de computadora portátil de un almacén a una tienda).

Función objetivo

Debemos de establecer cuál es la función objetivo que queremos optimizar. Notemos que el costo total que involucrarán las computadoras portátiles enviadas del almacén $A$ a la tienda $X$ es $35x_{AX}$, pues de acuerdo a la tabla de costos de transporte, hay un costo de \$35 para enviar cada computadora portátil. Todas las computadoras que salgan del almacén $A$ tendrán entonces un costo de $35x_{AX}+44x_{AY}$. Si calculamos de manera similar el costo de las computadoras que se salen de los almacenes $B$ y $C$ obtenemos el total. Entonces la función objetivo será la siguiente expresión:

$$Min \quad z = 35x_{AX}+44x_{AY}+40x_{BX}+37x_{BY}+42x_{CX}+45x_{CY}.$$

Restricciones

Hay dos tipos de restricciones que debemos cuidar:

Que ninguno de los almacenes exceda la cantidad de computadoras portátiles que tiene disponible.
Que cada tienda reciba el número de computadoras portátiles que requiere.

En el caso de la primera restricción, lo que estamos haciendo es limitar a las sumas que involucren a un mismo almacén. Por ejemplo, para no exceder las $200$ unidades que se tienen disponibles en el almacén $A$, se debe cumplir que $x_{AX}+x_{AY}\leq 200$. De manera similar, con el almacén $B$ obtenemos que $x_{BX}+x_{BY}\leq 350$ y con el almacén $C$ obtenemos que $x_{CX}+x_{CY}\leq 470$.

En el caso de la segunda restricción, ahora la desigualdad es opuesta: es una condición que requiere que las computadoras portátiles que lleguen a cada tienda sean al menos un valor dado. Entonces, para la tienda $X$ se tiene que cumplir $x_{AX}+x_{BX}+x_{CX}\geq 300$ y para la tienda $Y$ se tiene que cumplir $x_{AY}+x_{BY}+x_{CY}\geq 500$.

Entonces, juntando todas las restricciones, tenemos:

\begin{align*}
x_{AX}+x_{AY} \leq 200\\
x_{BX}+x_{BY} \leq 350\\
x_{CX}+x_{CY} \leq 470\\
x_{AX}+x_{BX}+x_{CX} \geq 300\\
x_{AY}+x_{BY}+x_{CY} \geq 500\\
x_{ij} \in \mathbb N, i \in \{A, B, C\}, j \in \{X, Y\}\\
\end{align*}

Resumen de formulación del problema del transporte

En resumen, el ejemplo de problema de transporte queda resumido en el siguiente PPL.

\begin{align*}
Min \quad z = 35x_{AX}+44x_{AY}+40x_{BX}&+37x_{BY}+42x_{CX}+45x_{CY}&\\
s.a.&\\
x_{AX}+x_{AY}&\leq 200\\
x_{BX}+x_{BY}&\leq 350\\
x_{CX}+x_{CY}&\leq 470\\
x_{AX}+x_{BX}+x_{CX}&\geq 300\\
x_{AY}+x_{BY}+x_{CY}&\geq 500\\
x_{ij} \in \mathbb N, i \in \{A, B, C\}, j \in \{X, Y\}\\
\end{align*}

Formulación general del problema del transporte

De manera general, en el problema del transporte se requieren transportar ciertas unidades de un producto desde $m$ centros de oferta (también llamados orígenes), a $n$ centros de demanda, (también denominados destinos). Cada centro de oferta tiene una cierta cantidad de unidades disponibles, y cada centro de demanda tiene una cierta cantidad de unidades que desea recibir.

Llamemos $o_i$ a la oferta del origen $i$ en unidades del producto ($i=1, \ldots , m$) y $d_j$ la demanda del destino $j$ en unidades del producto ($j=1, \ldots, n$). Para cada origen $i$ y cada destino $j$ tiene cierto costo enviar una unidad de producto. Sea $c_{ij}$ el costo unitario de transporte del producto del origen $i$ al destino $j$ ($i = 1, \ldots , m;j=1, \ldots , n$).

Lo que buscamos es determinar para cada origen $i$ y cada destino $j$ cuántas unidades $x_{ij}$ se deben transportar de tal modo que no se exceda la producción de cada origen, se satisfaga la demanda en cada destino y se incurra en el mínimo costo de transporte.

Como lo hemos hecho en entradas anteriores, las condiciones anteriores pueden ser planteadas en términos lineales. Para no exceder la oferta del origen $i$, se debe cumplir que

$$\sum_{j=1}^nx_{ij} \leq o_i,$$

para cada $i=1,\ldots,m$. A estas desigualdades les llamamos las restricciones de oferta.

Para cumplir con la demanda en el destino $j$ se debe cumplir que

$$\sum_{i=1}^{m}x_{ij} \geq d_j,$$

para cada $j=1,\ldots,n$. A estas desigualdades les llamamos las restricciones de demanda.

Agregando las condiciones de positividad y estableciendo que queremos minimizar el costo total, obtenemos el problema planteado de la siguiente manera:

\begin{align*}
Min \quad z &= \sum_{i=1}^{m} \sum_{j=1}^{n} c_{ij}x_{ij}\\
s.a.&\\
\sum_{j=1}^nx_{ij} &\leq o_i, \quad i=1, \ldots , m \quad \quad (1)\\
\sum_{i=1}^{m}x_{ij} &\geq d_j, \quad j=1, \ldots , n \quad \quad (2)\\
x_{ij} &\geq 0; \quad i=1, \ldots , m; j=1, \ldots , n,\\
\end{align*}

donde $x_{ij}$ es el número de unidades del producto a transportar del origen $i$ al destino $j$, para cada $i=1, \ldots , m$ y cada $j = 1, \ldots , n$.

Las desigualdades en (1) se llaman restricciones de oferta y en (2) restricciones de demanda.

Más adelante…

Con este problema contamos ya con tres ejemplos de situaciones que se pueden plantear en términos de programación lineal: el problema de la dieta, el problema de la mochila y el problema del transporte. A continuación veremos dos más: el problema de producción e inventario, y el problema de la ruta más corta.

Tarea

Encuentra por lo menos una manera de realizar las asignaciones de variables en el problema de los almacenes de computadoras portátiles y las tiendas. No importa que el costo total que encuentres no sea óptimo, pero sí se deben cumplir las restricciones de oferta y de demanda.
¿Qué sucede en el problema del transporte si la cantidad total de demanda excede a la cantidad total de oferta? Plantea esta posibilidad en términos de los parámetros $o_i$ y $d_j$ de oferta y demanda, respectivamente.
Imagina que en el ejemplo que planteamos de computadoras portátiles, almacenes y tiendas sucede que el precio de transportar una computadora portátil es de \$30 sin importar el almacén origen o la tienda destino. En este caso, ¿cuál sería una manera óptima de realizar los envíos, y tal que se cumplan las restricciones de oferta y demanda?
Se presenta la siguiente situación:

Una empresa coreana fabrica y luego distribuye sus pantallas a diferentes vendedores. En este momentos tienen pantallas de 4 diferentes tamaños: 43″, 50″, 55″ y 65″. Los países a donde distribuyen sus productos son Japón, China y Estados Unidos. En la siguiente tabla se muestra el costo de exportación en miles de dólares por cada 1000 televisores de cada modelo.

	43″	50″	55″	65″	Demanda este año
Japón	\$50k	\$60k	\$65k	\$70k	100k
China	\$60k	\$70k	\$75k	\$80k	300k
Estados Unidos	\$80k	\$90k	\$95k	\$100k	350k
Disponibilidad	250k	220k	180k	150k	——

También se señaló en la tabla anterior cual es la demanda de cada país para este año y las pantallas que fueron fabricadas este año por cada modelo.

Plantea este problema como un problema del transporte como se hizo anteriormente.

Un posible caso particular del problema del transporte sucede cuando hay muchos orígenes y únicamente un destino. Plantea esta posibilidad de manera general. En este caso, ¿cuál sería una buena estrategia para decidir cuáles orígenes deben enviar unidades del producto al destino?

Respuestas

1.- (Respuesta a criterio del lector)

2.- Si la demanda supera a la oferta, por lo menos uno de los destinos del problema va a cumplir que $\sum_{i=1}^{m}x_{ij} < d_j$, por lo que no cumplirá una de las restricciones de nuestro problema y el problema ya no será factible.

3.- En este caso, sería indistinto de donde elijamos enviar nuestras computadoras con tal de que se satisfaga la demanda, y solamente se parará de enviar computadoras cuando se satisfaga esta demanda de 800 computadoras, que en cualquier caso nos dará un costo total de envío de $24000.

4.- Nuestra variable de decisión va a ser la siguiente: $x_{ij}$ = miles de televisores del tamaño $i$ que van a ser exportados al país $j$, $i \in \{1 (\textrm{43″}), 2 (\textrm{50″}), 3 (\textrm{55″}), 4 (\textrm{65″})\}$, $j \in \{1 (\textrm{Japón}), 2 (\textrm{China}), 3 (\textrm{Estados Unidos})\}$

Si seguimos los pasos como lo hemos venido haciendo, el problema debería quedar planteado de la siguiente manera:

\begin{align*}
Min \quad z = &50x_{11} + 60 x_{12} + 80x{13} + 60 x_{21} + 70 x_{22} + 90x_{23}\\
+ &65x_{31} + 75x_{32} + 95x_{33} + 70x_{41} + 80x_{42} + 100x_{43}\\
&s.a\\
&x_{11} + x_{21} + x_{31} + x_{41} \geq 100\\
&x_{12} + x_{22} + x_{32} + x_{42} \geq 300\\
&x_{13} + x_{23} + x_{33} + x_{43} \geq 350\\
&x_{11} + x_{12} + x_{13} \leq 250\\
&x_{21} + x_{22} + x_{23} \leq 220\\
&x_{31} + x_{32} + x_{33} \leq 180\\
&x_{41} + x_{42} + x_{43} \leq 150\\
&x_{ij} \in \mathbb{N}\\
\end{align*}

5.- Como solamente habría un destino, la variable de decisión sería la siguiente:
$x_i$ = unidades de producto que vamos a enviar del origen $i$ a nuestro destino, $i \in \{1, \ldots, m\}$

Sea $d$ la demanda de nuestro único destino.

El planteamiento general sería el siguiente:

\begin{align*}
Min \quad z &= \sum_{i=1}^{m} c_{i}x_{i}\\
s.a.&\\
x_i &\leq o_i, \quad i \in \{1, \ldots , m\}\\
\sum_{i=1}^{m}x_i &\geq d\\
x_i &\geq 0 \quad i \in \{1, \ldots , m\}\\
\end{align*}

Una buena estrategia para resolver el problema simplemente sería ir agotando las unidades que nos puede proporcionar cada origen empezando por los que nos dan el menor costo de transporte por unidad, y parar justo cuando se haya cumplido la demanda de este único destino.

Entradas relacionadas

Ir a Investigación de Operaciones
Entrada anterior del curso: El problema de la mochila
Entrada siguiente del curso: El problema de producción e inventario