Introducción
En esta entrada veremos una función muy particular: el valor absoluto. Ésta nos permitirá «medir la distancia» entre un par de números reales. Finalizaremos con la demostración de la Desigualdad del triángulo y algunas de sus consecuencias. Esta desigualdad es usada en las demostraciones de Límite y Continuidad que veremos más adelante.
Definición formal
Definición (Valor absoluto): Para todo $x\in \r$ definimos la función valor absoluto como sigue:
\begin{equation*}
|x|=
\begin{cases}
x &\text{si $x \geq 0$}\\
-x & \text{si $x< 0$}
\end{cases}
\end{equation*}
Recordando las propiedades de orden, la definición quedaría de la siguiente manera:
\begin{equation*}
|x|=
\begin{cases}
x &\text{si $x =0 \quad\text{o}\quad x\in P$}\\
-x & \text{si $-x\in P$}
\end{cases}
\end{equation*}
Esta última nos será de utilidad para la demostración de la desigualdad del triángulo que veremos más adelante.
Observación: De la definición anterior notamos que para toda $x \in \r$, su valor absoluto $|x|$ es mayor o igual a cero.
Midiendo distancias
Si observamos la definición del valor absoluto, notamos que asocia a cualquier número real con su distancia respecto al cero. Veámoslo en los ejemplos siguientes:
- $|-3|=3$
- $|14|= 14$
En consecuencia, si consideramos la distancia entre cualquier par de números reales tendríamos la siguiente definición.
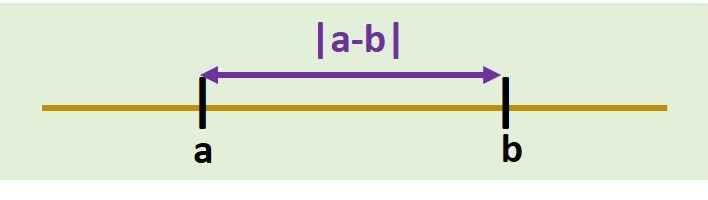
Definición: Para cualesquiera $a,b \in \r$ tenemos que están a distancia $|a-b|$.
Observemos que la distancia siempre será positiva o cero.
Desigualdad del triángulo
Teorema (Desigualdad del triángulo): Para todo $a,b \in \r$ se cumple la siguiente desigualdad:
$$|a+b| \leq |a|+|b|\text{.}$$
Demostración: Dada la definición del valor absoluto, debemos considerar casos sobre los signos de $a$ y $b$.
CASO 1: $a \geq 0$ y $b \geq 0$.
Recordemos que $P$ es cerrado bajo la suma, por lo que tenemos lo siguiente:
\begin{align*}
|a+b|&= a + b\\
&= |a|+|b|.
\end{align*}
La última igualdad se sigue de $a = |a|$ y $b = |b|$.
Para los siguientes casos haremos uso de los siguientes resultados que serán demostrados posteriormente:
Resultados: Para cualesquiera $a,b,c \in \r$ se cumplen:
- $-a-b=-(a+b)$.
- Si $b<0 \Rightarrow b<-b$.
- Si $a<b \Rightarrow a+c < b+c$.
CASO 2: $a < 0$ y $b < 0$.
Notemos que $-a \in P$ y $-b \in P$ por lo que $-a-b \in P$. Así se sigue que:
\begin{align*}
|a+b|&= -(a+b)\tag{por ser $a+b$ negativo}\\
&= -a – b\tag{por el resultado 1}\\
&= (-a)+(-b)\\
&= |a|+|b|,
\end{align*}
porque $|a|=-a$ y $|b|=-b$.
CASO 3: $a \geq 0$ y $b < 0$.
Para esta demostración debemos considerar dos subcasos.
SUBCASO 1: $a+b \geq 0$.
Dado lo anterior aplicando la definición de valor absoluto ocurre que:
\begin{align*}
|a+b|&=a+b\\
&< a-b. \tag{por los resultados 2 y3}\\
\end{align*}
Como tenemos que $a-b = |a|+|b|$, concluimos:
$$|a+b|<|a|+|b|.$$
SUBCASO 2: $a+b < 0$.
Procederemos análogamente al subcaso anterior:
\begin{align*}
|a+b|&=-(a+b)\\
&= -a-b\\
&< a-b. \tag{por resultados 2 y3}\\
\end{align*}
Ya que $a-b = |a|+|b|$, tenemos:
$$|a+b|<|a|+|b|.$$
CASO 4: $a < 0$ y $b \geq 0$.
Al igual que en el caso 3, para verificar la desigualdad se deberán considerar dos subcasos. La demostración de este caso se deja como parte de la Tarea moral.
$\square$
Para poder dar por terminada la prueba, debemos demostrar los siguientes resultados auxiliares que utilizamos:
Resultados: Para cualesquiera $a,b,c \in \r$ se cumplen:
- $-a-b=-(a+b)$.
- Si $b<0 \Rightarrow b<-b$.
- Si $a<b \Rightarrow a+c < b+c$.
Demostración:
1. Debemos verificar que $-a-b =(-a)+(-b)$ es inverso aditivo de $a+b$.
\begin{align*}
(a+b)+((-a)+(-b))&= (b+a)+((-a)+(-b))\\
&= ((b+a)+(-a))+(-b)\\
&= (b+(a+(-a))+(-b)\\
&= (b+0)+(-b)\\
&= b + (-b)\\
&=0.
\end{align*}
Concluimos que $(-a)+(-b) = -(a+b)$.
2. Ya que $b<0$ sabemos que $-b \in P$. Queremos probar que $-b-b > 0$.
Observemos que: $-b-b=(-b)+(-b)\in P$.
Por lo que concluimos que $b<-b$.
3. Bastaría ver que $(b+c)-(a+c) \in P$. Debido a que $b-a \in P$. Observamos lo siguiente.
\begin{align*}
b-a &= (b-a)+0\\
&= (b-a) + (c-c)\\
&= (b+c)-(a+c).
\end{align*}
$$\therefore\quad (b+c)-(a+c) \in P.$$
$$\therefore \quad b+c > a+c.$$
$\square$
Observemos que las demostraciones de estos resultados no utilizan la desigualdad del triángulo, más bien hacen uso de las propiedades vistas en las entradas anteriores.
Consecuencias de la desigualdad del triángulo
Proposición (Consecuencias de la desigualdad del triángulo): Sean $a,b \in \r$. Se cumplen las siguientes desigualdades:
- $|a-b| \leq |a|+|b|$
- $|a|-|b|\leq |a-b|$
- $|b|-|a|\leq |a-b|$
En esta ocasión sólo probaremos el punto 2.
Demostración:
2. Como $|a|= |a+0|$, al desarrollar esta igualdad obtenemos:
\begin{align*}
|a|&= |a+0|\\
&= |a+ (b+ (-b))|\\
&= |(a-b)+b|\\
&\leq |a-b| + |b| \tag{por la desigualdad del triángulo}\\
\end{align*}
$$\therefore |a| \leq |a-b| + |b|$$
$$\therefore |a|-|b| \leq |a-b|$$
$\square$
Más adelante
En la próxima entrada comenzaremos a resolver desigualdades donde el valor absoluto se encuentra involucrado.
Tarea moral
- Propiedades del valor absoluto.
Prueba los siguientes resultados:- $|a|=|-a|.$
- $|ab|=|a||b|$.
- $|\frac{1}{a}|=\frac{1}{|a|}$ con $a\neq 0$.
- $\frac{|a|}{|b|}=|\frac{a}{b}|$ con $b \neq 0$.
- Desigualdad del triángulo.
- Realiza la prueba del CASO 4 .
- Demuestra que para cualesquiera $a,b \in \r$:
- $|a-b| \leq |a|+|b|$.
- $|b|-|a|\leq |a-b|$.
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I:Intervalos y desigualdades en los números reales.
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Valor absoluto y desigualdades
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»