Introducción
En esta entrada nos dedicaremos a resolver desigualdades que involucran el valor absoluto. Para ello retomaremos la definición del valor absoluto de un número real y utilizaremos algunos resultados que probaremos a continuación.
Un par de resultados importantes
Lema: Para todo $a \in \r$. $a \leq |a|$ y $-a \leq |a|$.
Demostración: Procederemos a revisar los siguientes dos casos.
CASO 1: Si $a \geq 0$.
Por un lado tenemos por la definición de valor absoluto $|a|=a$.
$$\therefore |a|\geq a.$$
Y por otro que $a \geq 0 \geq -a$, así por transitividad se concluye que:
$$ |a| \geq -a.$$
CASO 2: Si $a \leq 0$.
Así se sigue por definición que $|a|=-a$ entonces tenemos que $|a|\geq -a$.
Y análogamente al caso anterior: $-a \geq 0 \geq a \Rightarrow |a|\geq a$.
$\square$
Teorema: Consideremos $a,x \in \r$ con $a\geq 0$.
- \begin{align*}
|x|\leq a &\Leftrightarrow -a \leq x\quad \text{y} \quad x \leq a\\
&\Leftrightarrow x\in [-a,a].
\end{align*} - \begin{align*}
|x|\geq a &\Leftrightarrow -a \geq x\quad \text{o} \quad x \geq a\\
&\Leftrightarrow x\in (-\infty,-a] \cup [a, \infty).
\end{align*}
NOTA.- «$\Leftrightarrow$» se lee como «si y sólo si». Y recordemos que $\Rightarrow$ significa «entonces».
Demostración:
1. $\Rightarrow$: Por hipótesis tenemos que $|x|\leq a$, aplicando el lema anterior:
$$x \leq |x|\quad \text{y} \quad -x \leq |x|$$
Por transitividad: $$x \leq a \quad \text{y} \quad -x \leq a$$
$$\therefore x \leq a\quad \text{y} \quad x \leq -a$$
Lo anterior nos indica lo siguiente: $x \in (-\infty, a]$ y $x \in [-a,\infty)$. Así al tomar la intersección de estos intervalos, obtenemos:
$$(-\infty, a] \cap [-a,\infty) = [-a,a]$$
$\Leftarrow$: Ahora consideremos $x \in [-a,a]$, así tenemos que:
$$x\in [-a,a]=(-\infty, a] \cap [-a,\infty)$$
Aplicando la respectiva definición de intervalo e intersección:
$$x \leq a\quad \text{y} \quad x \leq -a$$
Y por el lema:
$$x \leq |x|\quad \text{y} \quad -x \leq |x|$$
$$\therefore |x| \leq a$$
2. El punto 2 se quedará de ejercicio para la Tarea moral.
$\square$
Ahora continuaremos con ejercicios de desigualdades, en ellos deberemos encontrar todos los valores que las satisfagan.
Ejercicio 1
$$|x-3|=8$$
Recordemos que debido a la definición de valor absoluto, siempre deberemos considerar casos.
Para resolver este ejercicio deberemos considerar los siguientes:
CASO 1: $x-3 \geq 0$
Por lo que $|x-3|=x-3$ y sustituyendo tenemos:
\begin{align*}
x-3 =8 &\Leftrightarrow x=8+3\\
&\Leftrightarrow x = 11.
\end{align*}
CASO 2: $x-3 < 0$
Así $|x-3|= -x+3$, por lo que se sigue:
\begin{align*}
-x+3 =8 &\Leftrightarrow -x=8-3\\
&\Leftrightarrow -x =5\\
&\Leftrightarrow x= -5.
\end{align*}
De los casos anteriores obtenemos que los valores de $x$ que satisfacen la igualdad son
$x =11$ o $x=-5$
Ejercicio 2
$$|3x-3| \leq 2x+1$$
Para este ejercicio aplicando el teorema tendríamos:
$-2x-1 \leq 3x-3 \quad$ y $\quad 3x-3 \leq 2x+1$.
Comenzaremos desarrollando la primera desigualdad:
\begin{align*}
-2x-1 \leq 3x-3 &\Leftrightarrow -2x-3x \leq -3+1\\
&\Leftrightarrow -5x \leq -2\\
&\Leftrightarrow 5x \geq 2\\
&\Leftrightarrow x \geq \frac{2}{5}.
\end{align*}
$$\therefore \quad x \in \left[\frac{2}{5}, \infty \right)$$
Y de la segunda obtenemos:
\begin{align*}
3x-3 \leq 2x+1 &\Leftrightarrow 3x-2x \leq 1+3\\
&\Leftrightarrow x\leq 4.
\end{align*}
$$\therefore \quad x \in(-\infty,4]$$
Por lo que al tomar la intersección de ambos intervalos nos queda que los valores que satisfacen la desigualdad son:
$$ x \in (-\infty,4] \cap \left[\frac{2}{5}, \infty \right)= \left [\frac{2}{5}, 4 \right]$$
$$\therefore \quad x \in \left [\frac{2}{5}, 4 \right]$$
Ejercicio 3
$$|2x+1|-|3x+2|<1$$
Debido a que tenemos dos valores absolutos, para resolver este ejercicio necesitaremos considerar los siguientes casos:
- $2x+1 \geq 0 \quad$ y $\quad 3x+2 \geq 0$
- $2x+1 \leq 0 \quad$ y $\quad 3x+2 \leq 0$
- $2x+1 \geq 0 \quad$ y $\quad 3x+2 \leq 0$
- $2x+1 \leq 0 \quad$ y $\quad 3x+2 \geq 0$
Nuestra solución final será la unión de todas las soluciones obtenidas en los casos anteriores.
CASO 1: $2x+1 \geq 0$ y $3x+2 \geq 0$
Desarrollando las desigualdades:
\begin{align*}
2x+1 \geq 0\quad &\text{y} \quad 3x+2 \geq 0\\
\Leftrightarrow 2x \geq -1 \quad &\text{y} \quad 3x \geq -2\\
\Leftrightarrow x \geq -\frac{1}{2} \quad &\text{y} \quad x \geq -\frac{2}{3}\\
\end{align*}
$$\Leftrightarrow x \geq -\frac{1}{2}$$
Aplicando el valor absoluto obtenemos:
\begin{align*}
|2x+1|-|3x+2|<1 &\Leftrightarrow 2x+1-(3x+2) <1\\
&\Leftrightarrow 2x+1-3x-2-1<0\\
&\Leftrightarrow -x -2 <0\\
&\Leftrightarrow x+2>0\\
&\Leftrightarrow x> -2
\end{align*}
Por lo que al tomar la siguiente intersección tenemos que la solución de este caso es:
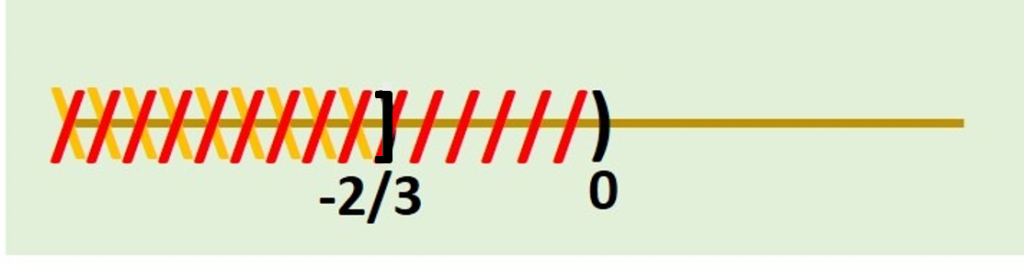
$$\left[-\frac{1}{2}, \infty \right) \cap (-2, \infty)= \left[-\frac{1}{2}, \infty \right)$$
CASO 2: $2x+1 \leq 0 \quad$ y $\quad 3x+2 \leq 0$
Tendríamos que:
\begin{align*}
2x+1 \leq 0\quad &\text{y} \quad 3x+2 \leq 0\\
\Leftrightarrow 2x \leq -1 \quad &\text{y} \quad 3x \leq -2\\
\Leftrightarrow x \leq -\frac{1}{2} \quad &\text{y} \quad x \leq -\frac{2}{3}\\
\end{align*}
$$\Leftrightarrow x \leq -\frac{2}{3}$$
Al sustituir tenemos:
\begin{align*}
|2x +1|-|3x+2|<1 &\Rightarrow -(2x+1)-(-(3x+2))<1\\
&\Rightarrow -2x-1+3x+2-1<0\\
&\Rightarrow x <0
\end{align*}
Así tenemos la solución:
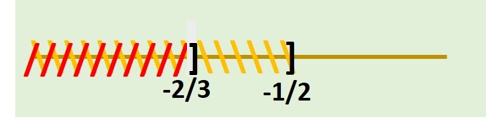
$$ (-\infty, 0) \cap \left(-\infty, -\frac{2}{3} \right] = \left(-\infty, -\frac{2}{3} \right] $$
CASO 3: $2x+1 \geq 0 \quad$ y $\quad 3x+2 \leq 0$
Ahora se sigue que:
\begin{align*}
2x+1 \geq 0\quad &y \quad 3x+2 \leq 0\\
\Leftrightarrow 2x \geq -1 \quad &y \quad 3x \leq -2\\
\Leftrightarrow x \geq -\frac{1}{2} \quad &y \quad x \leq -\frac{2}{3}\\
\end{align*}
Así observamos:
$$\left(-\infty, -\frac{2}{3} \right] \cap \left[-\frac{1}{2}, \infty \right) = \emptyset$$
CASO 4: $2x+1 \leq 0 \quad$ y $\quad 3x+2 \geq 0$
Desarrollando:
\begin{align*}
2x+1 \leq 0 \quad &\text{y} \quad 3x+2 \geq 0\\
\Leftrightarrow 2x \leq -1 \quad &\text{y} \quad 3x \geq -2\\
\Leftrightarrow x \leq -\frac{1}{2} \quad &\text{y} \quad x \geq -\frac{2}{3}\\
\end{align*}
$$\Leftrightarrow -\frac{2}{3} \leq x \leq -\frac{1}{2}$$
Aplicando la definición del valor absoluto:
\begin{align*}
|2x+1|-|3x+2|<1 &\Rightarrow -(2x+1) – (3x+2) < 1\\
&\Leftrightarrow -2x-1-3x-2-1< 0\\
&\Leftrightarrow -5x -4 < 0\\
&\Leftrightarrow 5x+4 > 0\\
&\Leftrightarrow 5x> -4\\
&\Leftrightarrow x > -\frac{4}{5}
\end{align*}
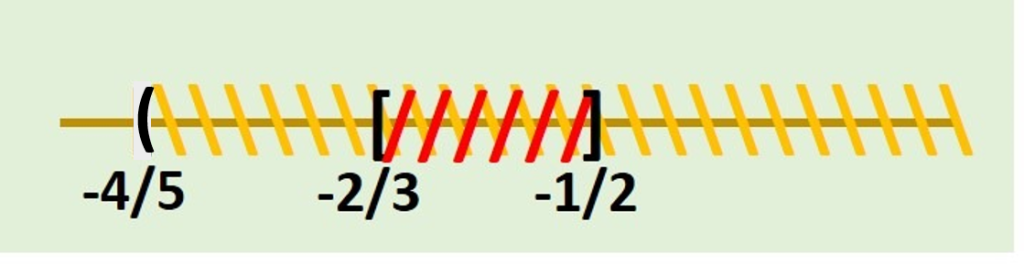
Concluimos que la solución a este caso es:
$$\left[-\frac{2}{3}, -\frac{1}{2} \right] \cap \left(-\frac{4}{5}, \infty \right)= \left[-\frac{2}{3}, -\frac{1}{2} \right]$$
Finalizamos considerando como solución total a la unión de los intervalos obtenidos en los cuatro casos:
$$\left(-\infty, -\frac{2}{3} \right] \cup\left[-\frac{2}{3}, -\frac{1}{2} \right] \cup \left[-\frac{1}{2}, \infty \right) = (-\infty, \infty)$$
Observemos que para la resolución de este tipo de desigualdades, siempre deberemos considerar los casos correspondientes a los signos del argumento de la función valor absoluto, es decir, cuando el argumento es positivo y cuando es negativo. En la sección de Tarea moral encontrarás ejercicios que te ayudarán a reforzar lo visto en esta entrada.
Más adelante
Ahora que ya hemos visto el procedimiento para encontrar los valores que satisfacen una desigualdad con valor absoluto, en la siguiente entrada lo utilizaremos para continuar resolviendo ejercicios que lo involucren adicionando el concepto de raíz cuadrada de un número real. Veremos que el valor absoluto está relacionado con la definición formal de raíz cuadrada y algunos resultados útiles.
Tarea moral
Demuestra el punto 2 del teorema:
\begin{align*}
|x|\geq a &\Leftrightarrow -a \geq x\quad o \quad x \geq a\\
&\Leftrightarrow x\in (-\infty,-a] \cup [a, \infty)
\end{align*}
Encuentra los valores que satisfacen las siguientes desigualdades:
- $|x-3|< 8$
- $|3x-3| > 2x+1$
- $|x-1||x+2|=3$
- $|x-1|+|x-2|> 1$
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Valor absoluto. Desigualdad del triángulo.
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Raíz cuadrada y desigualdades.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»