Introducción
Hasta ahora hemos visto que a diferencia de $\mathbb{R}^2$, el conjunto de los números complejos $\mathbb{C}$ es un campo dotado con las operaciones definidas en la entrada 2 de la primera unidad. Sin embargo, no es difícil convencerse de que como $\mathbb{R}$-espacios vectoriales estos son isomorfos.
Al estudiar matemáticas uno de los conceptos más importantes es el de función. De manera intuitiva podemos pensar a una función como una regla que asocia elementos entre dos conjuntos. A lo largo de nuestros cursos de Cálculo hemos estudiado a detalle funciones de una y varias variables reales, por lo que pensar en funciones de $\mathbb{R}^2$ a $\mathbb{R}^2$ no debe parecernos algo ajeno, de hecho en nuestros cursos de Geometría dedicamos un tiempo al estudio de algunas funciones de estas llamadas transformaciones lineales. Entonces, considerando que $\mathbb{R}^2$ y $\mathbb{C}$ son isomorfos como $\mathbb{R}$-espacios vectoriales podríamos pensar que al definir una función sobre $\mathbb{C}$ de variable compleja debería ser algo indistinguible de una función de dos variables reales. Sin embargo, es claro que si pensamos en una función $f(z)$, donde la variable $z$ es un número complejo, entonces estamos trabajando con una función de una única variable como en el caso real, por lo que de algún modo podemos pensar que las funciones complejas de variable compleja parecen estar entre las funciones reales de variable real y las funciones vectoriales de dos variables reales.
Funciones complejas
Definición 12.1. (Función compleja de variable compleja.)
Sea $S\subset\mathbb{C}$. Una función compleja de variable compleja $f(z)$, o simplemente una función compleja, definida en $S$ es una regla que para cada $z=x+iy\in S$ asigna un único número complejo $w=u+iv\in\mathbb{C}$ y se escribe como $f:S\to\mathbb{C}$. El número $w$ es llamado el valor de $f$ en $z$, lo cual denotamos como $f(z)$, es decir $w=f(z)$. Al conjunto $S$ se le llama el dominio de $f(z)$ y el conjunto $f(S) = \{f(z) \, : \, z\in S\} \subset \mathbb{C}$ es llamado el rango o la imagen de $f(z)$.
Observación 12.1.
De acuerdo con la definición podemos pensar que una función compleja transforma los valores de un plano $z$ en valores de un plano $w$. Esto lo analizaremos a detalle en la entrada 24, ya que nos será imposible visualizar la gráfica de una función compleja puesto que ésta tiene lugar en $\mathbb{R}^4$.
Observación 12.2.
Cuando una función está dada sólo por su regla de correspondencia sin especificar el dominio $S$, entonces se toma como dominio al mayor conjunto $S$ donde dicha función está definida, en dicho caso al conjunto $S$ se le suele llamar el dominio natural de la función.
Observación 12.3.
El término dominio se usa aquí en un sentido conjuntista y no topólogico, es decir el conjunto $S$ no tendría porque ser en principio un conjunto abierto y conexo (región), aunque a lo largo del curso estaremos trabajando comúnmente en dominios $S$ que son una región (definición 10.3).
Observación 12.4.
A lo largo de esta unidad estaremos trabajando con funciones complejas de variable compleja. Sin embargo, dado que $\mathbb{R}\subset\mathbb{C}$ es posible considerar al dominio $S$ de una función $f$ tal que $S\subset\mathbb{R}$, en cuyo caso tendríamos una función compleja de variable real. Más aún, podríamos tener que $f(S)\subset\mathbb{R}$, en dicho caso reduciríamos nuestro estudio al de funciones reales de variable real. Por lo que, nuestro objetivo en esta entrada será generalizar los resultados y propiedades ya conocidos de las funciones reales de variable real para las funciones complejas de variable compleja.
Funciones elementales
Definición 12.2. (Polinomios complejos.)
Sean $a_0, a_1, a_2, \ldots, a_n\in\mathbb{C}$ constantes. Un polinomio complejo es una función de la forma: \begin{equation*} f(z) = a_0 + a_1 z + a_2 z^2 + \cdots + a_{n-1} z^{n-1} + a_n z^n. \end{equation*} El mayor índice $n$ tal que $a_n \neq 0$ es el grado del polinomio.
Toda función polinómica tiene como dominio a todo $\mathbb{C}$.
Definición 12.3. (Funciones racionales.)
Sean $P(z)$ y $Q(z)$ dos polinomios complejos. Se denomina función racional a una función de la forma: \begin{equation*} f(z) = \frac{P(z)}{Q(z)}. \end{equation*} Toda función racional tiene como dominio natural a los números complejos sin el conjunto donde el polinomio $Q(z)$ se anule, es decir, sin el conjunto de raíces de $Q(z)$.
Ejemplo 12.1.
Las siguientes son funciones complejas cuyo dominio $S$ es todo $\mathbb{C}$:
a) $w_1 = f_1(z) = |z|^2$.
b) $w_2 = f_2(z) = 3z^2 + 7z$.
c) $w_3 = f_3(z) = \overline{z}$.
Mientras que:
d) $w_4 = f_4(z) = \dfrac{1}{z}$,
e) $w_5 = f_5(z) = \dfrac{1}{z^2-1}$,
son también funciones complejas, pero sus dominios naturales son $S_4 = \mathbb{C}\setminus\{0\}$ y $S_5 = \mathbb{C}\setminus\{-1,1\}$, respectivamente.
Ejemplo 12.2.
Sean $z_1, z_2\in\mathbb{C}$ tales que $z_1 \neq z_2$, entonces la función $L:[0,1]\to \mathbb{C}$ dada por: \begin{equation*} w = L(t) = (1-t)z_1 + tz_2, \end{equation*}
es una función compleja de variable real que nos determina al segmento de recta que va de $z_1$ a $z_2$, es decir al conjunto $[z_1, z_2]$.
Definición 12.4. (Operaciones de funciones.)
Denotemos al conjunto de todas las funciones definidas de $S\subset\mathbb{C}$ en $\mathbb{C}$ como $\mathcal{F}(S)$. Considerando la definición 12.1 tenemos que de manera natural las operaciones de suma y producto definidas en $\mathbb{C}$ se trasladan al conjunto $\mathcal{F}(S)$, es decir para $f,g\in\mathcal{F}(S)$ podemos definir su suma $f+g$ y su producto $f\cdot g$ como: \begin{equation*} (f+g)(z) = f(z)+g(z), \quad \forall z\in S. \end{equation*} \begin{equation*} (f\cdot g)(z) = f(z) \cdot g(z), \quad \forall z\in S. \end{equation*} Utilizaremos el símbolo «$\cdot$» para denotar el producto entre funciones solo cuando sea necesario, en general lo omitiremos.
Como caso particular del producto de funciones, si una de ellas es constante, entonces definimos el producto por escalares complejos como:
\begin{equation*} (c \, f)(z) = c \, f(z), \quad \forall z\in S, \end{equation*} donde $c\in\mathbb{C}$ es una constante.
Más aún, si $g(z)\neq0$ para toda $z\in S$, entonces definimos a la función cociente $\dfrac{f}{g}$ como: \begin{equation*} \left(\frac{f}{g}\right)(z) = \frac{f(z)}{g(z)}, \quad \forall z\in S. \end{equation*}
Definición 12.5. (Partes real e imaginaria, conjugado y módulo de una función compleja.)
Sean $S\subset\mathbb{C}$ y $f\in\mathcal{F}(S)$ una función. Entonces para todo $z\in S$ definimos las funciones:
- parte real de $f$: \begin{equation*} \left(\operatorname{Re} f\right)(z) = \operatorname{Re} f(z), \end{equation*}
- parte imaginaria de $f$: \begin{equation*} \left(\operatorname{Im} f\right)(z) = \operatorname{Im} f(z), \end{equation*}
- el conjugado de $f$: \begin{equation*} \overline{f}(z) = \overline{f(z)}, \end{equation*}
- el módulo de $f$: \begin{equation*} |\,f\,| (z) = |\,f(z)\,|. \end{equation*}
Al igual que cada número complejo $z$ es caracterizado por un par de números reales, digamos $x$ e $y$, una función compleja $f$ de variable $z$ puede ser especificada por dos funciones reales de las variables reales $x$ e $y$, digamos $u=u(x,y)$ y $v=v(x,y)$. Para justificar esto consideremos la siguiente:
Proposición 12.1.
Sean $S\subset\mathbb{C}$ y $f:S\to\mathbb{C}$ una función compleja.
- Si $z=x+iy\in S$, entonces $w=f(z)$ puede expresarse como: \begin{equation*} w = u(x,y) + iv(x,y), \end{equation*} donde $u (x,y)$ y $v(x,y)$ son funciones reales de las variables $x$ e $y$.
- Sean $u(x,y)$ y $v(x,y)$ dos funciones reales de las variables $x$ e $y$, definidas en $S$. Si $z = x+iy \in S$, entonces: \begin{equation*} w = u(x,y) + iv(x,y), \end{equation*} es una función compleja en $S$.
Demostración. Dadas las hipótesis, consideremos a $z=x+iy \in S$. Sabemos que: \begin{equation*} x = \frac{z+\overline{z}}{2}, \quad y = \frac{z-\overline{z}}{2i}. \tag{12.1} \end{equation*}
- Considerando (12.1) es claro que existe una relación estrecha entre los números reales $x$ e $y$ y el número complejo $z$, por lo que especificar los valores de $x$ e $y$ en $S$ equivale a especificar a un número complejo $z=x+iy\in S$. Entonces $f$ es una función compleja de las variables $x$ e $y$, por lo que definiendo: \begin{align*} u(x,y) = \frac{f(x+iy) + \overline{f}(x+iy)}{2},\\ v(x,y) = \frac{f(x+iy) – \overline{f}(x+iy)}{2i}, \end{align*} tenemos que: \begin{align*} u(x,y) + iv(x,y) & = \frac{f(x+iy) + \overline{f}(x+iy)}{2} + i \frac{f(x+iy) – \overline{f}(x+iy)}{2i}\\ & = f(x+iy)\\ & = f(z)\\ & = w. \end{align*} Notemos que: \begin{align*} \overline{u}(x,y) & = \overline{\frac{f(x+iy) + \overline{f}(x+iy)}{2}}\\ & = \frac{\overline{f}(x+iy) + f(x+iy)}{2}\\ & = u(x,y), \end{align*} \begin{align*} \overline{v}(x,y) & = \overline{\frac{f(x+iy) – \overline{f}(x+iy)}{2i}}\\ & = \frac{\overline{f}(x+iy) – f(x+iy)}{-2i}\\ & = v(x,y), \end{align*} por lo que, considerando la proposición 2.2(5), tenemos que $u(x,y)$ y $v(x,y)$ son funciones reales de las variables $x$ e $y$ para todo $z = x+iy \in S$.
- Sea $z=x+iy\in S$. Es claro que $g(z) = \overline{z}$ es una función compleja de $z$ definida en $S$. Entonces, de acuerdo con (12.1), tenemos que las funciones: \begin{align*} u(x,y) = u \left( \frac{z+\overline{z}}{2}, \frac{z-\overline{z}}{2i} \right),\\ v(x,y) = v \left( \frac{z+\overline{z}}{2}, \frac{z-\overline{z}}{2i} \right), \end{align*} son ambas funciones de $z$ para todo $z\in S$, por lo que su suma también es una función de $z$ para toda $z\in S$. Entonces para todo $z=x+iy \in S$: \begin{equation*} w = u(x,y) + iv(x,y), \end{equation*} es una función compleja definida en $S$.
$\blacksquare$
De acuerdo con el resultado anterior, tenemos que una función compleja $f:S\to\mathbb{C}$, tal que para cada $z=x+iy\in S$ cumple que $f(z)=w\in\mathbb{C}$, puede escribirse de la forma: \begin{equation*} w = f(z) = f(x+iy) = u(x,y) + iv(x,y), \end{equation*} donde las funciones $u$ y $v$ son llamadas la parte real e imaginaria respectivamente de la función $f$, es decir $\operatorname{Re} f = u$ e $\operatorname{Im} f=v$. Además dichas funciones $u$ y $v$ tienen como común dominio al dominio de la función $f$.
Observación 12.5.
Como hemos visto en la entrada 4 de la primera unidad, en ocasiones resulta más conveniente trabajar con un número complejo $z\in\mathbb{C}$, con $z = x+iy \neq 0$, en su forma polar, es decir: \begin{equation*} z = r\left[\operatorname{cos}(\theta) + i \operatorname{sen}(\theta)\right], \end{equation*} donde $r = |\,z\,|$ y $\theta = \operatorname{arg} z$. Tenemos entonces que $x = r \operatorname{cos}(\theta)$ e $y= r \operatorname{sen}(\theta)$, por lo que, considerando la proposición 12.1, es claro que una función compleja $f$, al trabajar con la variable $z$ en su forma polar, se puede escribir como: \begin{equation*} w = f(z) = u(r,\theta) + iv(r,\theta). \end{equation*}
Ejemplo 12.3.
Consideremos las primeras tres funciones del ejemplo 12.1 y sea $z=x+iy\in\mathbb{C}$, entonces:
a) \begin{align*} f_1(x+iy) & = |\,x+iy\,|^2\\
& = x^2 + y^2, \end{align*} de donde se sigue que $\operatorname{Re}f_1(z) = u_1(x,y)=x^2 + y^2$ e $\operatorname{Im}f_1(z) = v_1(x,y)=0$.
b) \begin{align*} f_2(x+iy) & = 3(x+iy)^2 + 7(x+iy)\\
& = (3x^2-3y^2+7x) + i(6xy+7y), \end{align*} de donde se sigue que $\operatorname{Re}f_2(z) = u_2(x,y)=3x^2-3y^2+7x$ e $\operatorname{Im} f_2(z)=v_2(x,y)=6xy+7y$.
c) \begin{align*} f_3(x+iy) & = \overline{x+iy}\\
& = x – iy, \end{align*} de donde se sigue que $\operatorname{Re}f_3(z) = u_3(x,y)=x$ e $\operatorname{Im}f_3(z)=v_3(x,y)=-y$.
Para el inciso d) del ejemplo 12.1 consideremos a $z=x+iy\in\mathbb{C}\setminus\{0\}$, de acuerdo con la observación 3.2 tenemos que: \begin{equation*} f_4(z) = \frac{1}{z} = \frac{\overline{z}}{|\,z\,|^2} = \frac{f_3(z)}{f_1(z)},\end{equation*} entonces:
d)\begin{align*} f_4(x+iy) & = \frac{x-iy}{x^2+y^2}\\
& = \frac{x}{x^2+y^2} – i\left(\frac{y}{x^2+y^2}\right),
\end{align*} de donde se sigue que $\operatorname{Re}f_4(z)=u_4(x,y)=\dfrac{x}{x^2+y^2}$ e $\operatorname{Im}f_4(z)=v_4(x,y)=\dfrac{-y}{x^2+y^2}$.
Ejemplo 12.4.
Considerando a $z$ en su forma polar expresemos a las funciones complejas $f(z) = z^5 + 4z^3$ y $g(z) = z^2$ en términos de las funciones reales $u(r,\theta)$ y $v(r,\theta)$.
Solución. Sea $z = r\operatorname{cis}(\theta) \neq 0$, con $r=|z|$ y $\theta=\operatorname{arg} z$. De acuerdo con la fórmula de De Moivre, proposición 4.1 de la primera unidad, tenemos que:
a) \begin{align*} f(z) & = z^5 + 4z^3\\ & = \left(r\operatorname{cis}(\theta) \right)^5 + 4\left(r\operatorname{cis}(\theta) \right)^3\\ & = r^5\operatorname{cis}(5\theta) + 4 r^3 \operatorname{cis}(3\theta)\\ & = \left( r^5\operatorname{cos}(5\theta) + 4 r^3 \operatorname{cos}(3\theta)\right) + i \left( r^5\operatorname{sen}(5\theta) + 4 r^3 \operatorname{sen}(3\theta)\right), \end{align*} de donde $u(r,\theta) = r^5\operatorname{cos}(5\theta) + 4 r^3 \operatorname{cos}(3\theta)$ y $v(r,\theta)=r^5\operatorname{sen}(5\theta) + 4 r^3 \operatorname{sen}(3\theta)$.
b) \begin{align*} g(z) = z^2 & = \left(r\operatorname{cis}(\theta) \right)^2\\
& = r^2 \operatorname{cos}(2\theta) + i \, r^2 \operatorname{sen}(2\theta), \end{align*} de donde $u(r,\theta) = r^2 \operatorname{cos}(2\theta)$ y $v(r,\theta)=r^2 \operatorname{sen}(2\theta)$.
Ejemplo 12.5.
Si $u(x,y) = -x$, $v(x,y) = -(1+5y)$ y $w = u(x,y) + iv(x,y)$, escribe a $w$ como función de la variable compleja $z=x+iy$.
Solución. Considerando las coordenadas complejas conjugadas (12.1) tenemos que: \begin{align*} w & = u(x,y) + iv(x,y)\\ & = -x -i(1+5y)\\ & = – \frac{z+\overline{z}}{2} – i\left[ 5\left(\frac{z – \overline{z}}{2i}\right) + 1 \right]\\ & = \frac{-z-\overline{z}}{2} – i\left[ \frac{5z – 5\overline{z} + 2i}{2i}\right]\\ & = \frac{-z-\overline{z} – 5z + 5\overline{z} – 2i}{2}\\ & = \frac{-z6 + 4\overline{z} – 2i}{2}\\ & = -3z + 2\overline{z} – i. \end{align*} Por lo que $w = f(z) = -3z + 2\overline{z} – i$.
Es claro que esta última expresión representa una función compleja, sin embargo podemos preguntarnos si esta función representa un polinomio complejo de acuerdo con la definición 12.2. Para responder esto consideremos la siguiente:
Observación 12.5.
Mediante la definición 12.2, se establece que un polinomio complejo en la variable $z$ es una función compleja que considera potencias de $z$ y coeficientes complejos, por ejemplo: \begin{equation*} i + (2+i)z + 3z^2. \end{equation*}
De acuerdo con la proposición 12.1, es claro que el polinomio anterior puede expresarse como un polinimio en dos variables reales, las cuales están dadas por su parte real e imaginaria, es decir, considerando a $z=x+iy\in\mathbb{C}$ tenemos que:
\begin{align*} i + (2+i)z + 3z^2 & = i + (2+i)(x+iy) + 3(x+iy)^2\\ & = i + 2x + ix + 2iy – y + 3x^2 + 6ixy – 3y^2\\ & = 3(x^2-y^2) + 2x – y + i(x + 2y + 6xy + 1). \end{align*}
Debe ser claro que esta última expresión sigue siendo una función compleja. Sin embargo, abordar el concepto de polinomio desde el sentido complejo requiere cierto cuidado. Podemos hablar de un polinomio en las variables $x$ e $y$, donde $(x,y)\in\mathbb{R}^2$, considerando coeficientes complejos, por ejemplo: \begin{equation*} (3+i)xy + 3ix^2 + 5y^2. \end{equation*}
Entonces dicho polinomio en las variables $x$ e $y$ nos determina una función de $\mathbb{R}^2$ en $\mathbb{C}$, la cual podemos pensar como una función compleja estableciendo $z=x+iy\in\mathbb{C}$.
Considerando lo anterior, debe ser claro que el ejemplo 12.5 no representa un polinomio complejo. En general, tenemos que existen polinomios en las variables $x$ e $y$, que son funciones complejas, pero que no son polinomios complejos, puesto que son funciones que no pueden ser escritas en términos de la variable $z=x+iy\in\mathbb{C}$, desde que aparecen expresiones en términos de $\overline{z}$.
Lo anterior es de suma importancia, ya que identificar a las funciones complejas, no solo polinomios, que dependan únicamente de la variable $z$ y no de $\overline{z}$ será la llave al análisis complejo. Como veremos en las siguientes entradas, este detalle tan sutil resultará de suma importancia pues nos permitirá caracterizar propiedades como la diferenciabilidad en el sentido complejo a través de este hecho.
Definición 12.6. (Composición de funciones.)
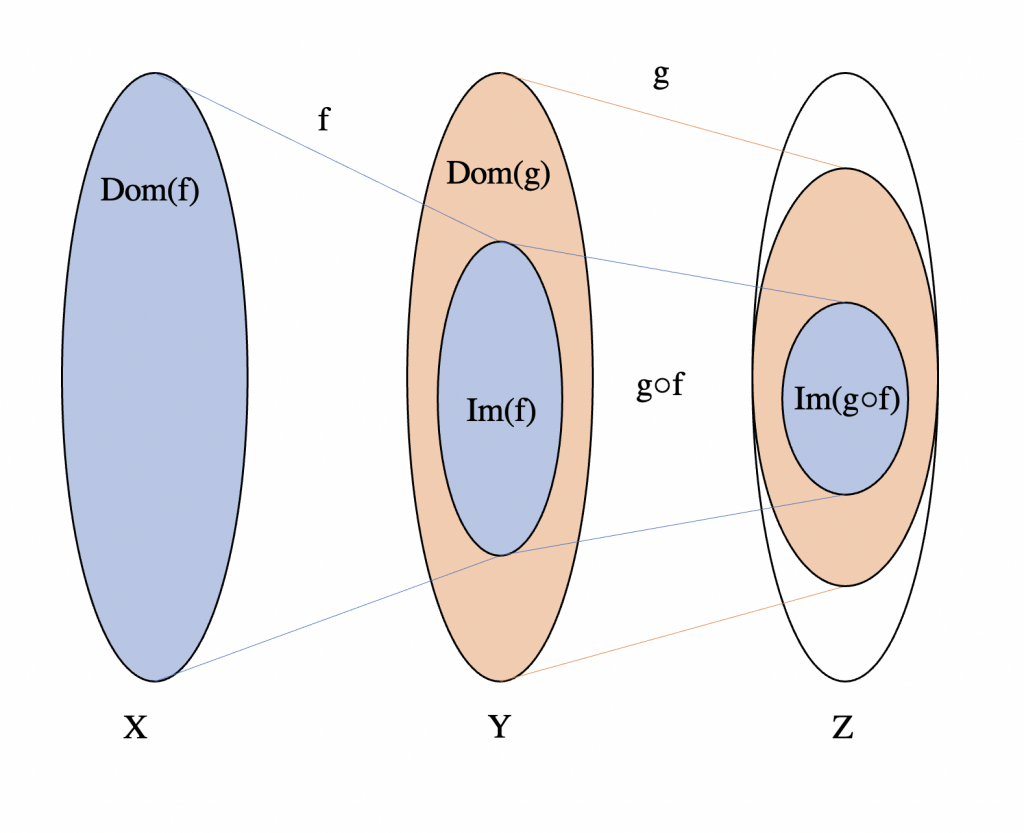
Sea $g\in\mathcal{F}(H)$. Sabemos que $g(H) = \{g(z) \,: \, z\in H\}$ es la imagen de $g$. Sea $f\in\mathcal{F}(S)$ y $g(H)\subset S$, entonces se define a la composición de $f$ con $g$ como la función $f\circ g: H \rightarrow \mathbb{C}$ tal que: \begin{equation*} (f\circ g)(z) = f(g(z)), \quad \forall z\in H. \end{equation*}
Definición 12.7. (Función inyectiva, suprayectiva, biyectiva e inversa.)
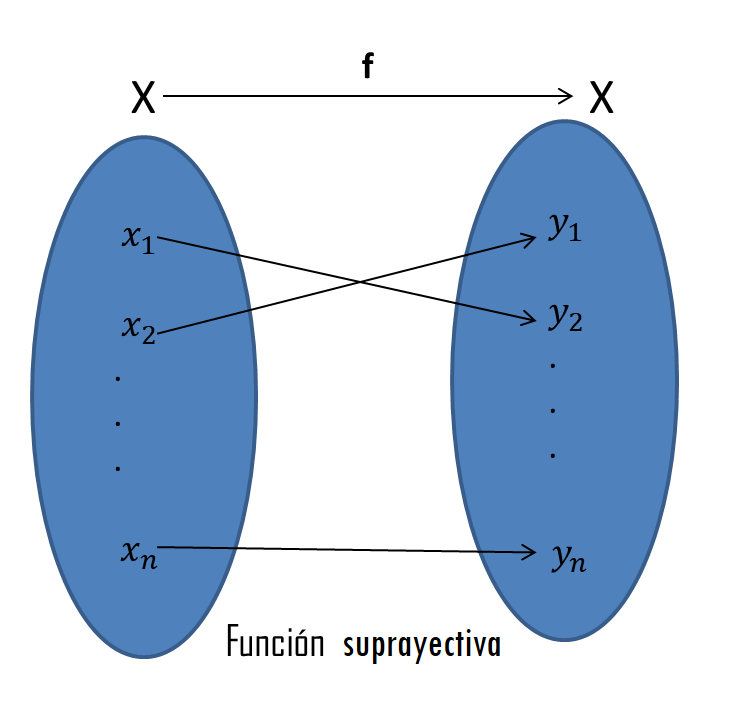
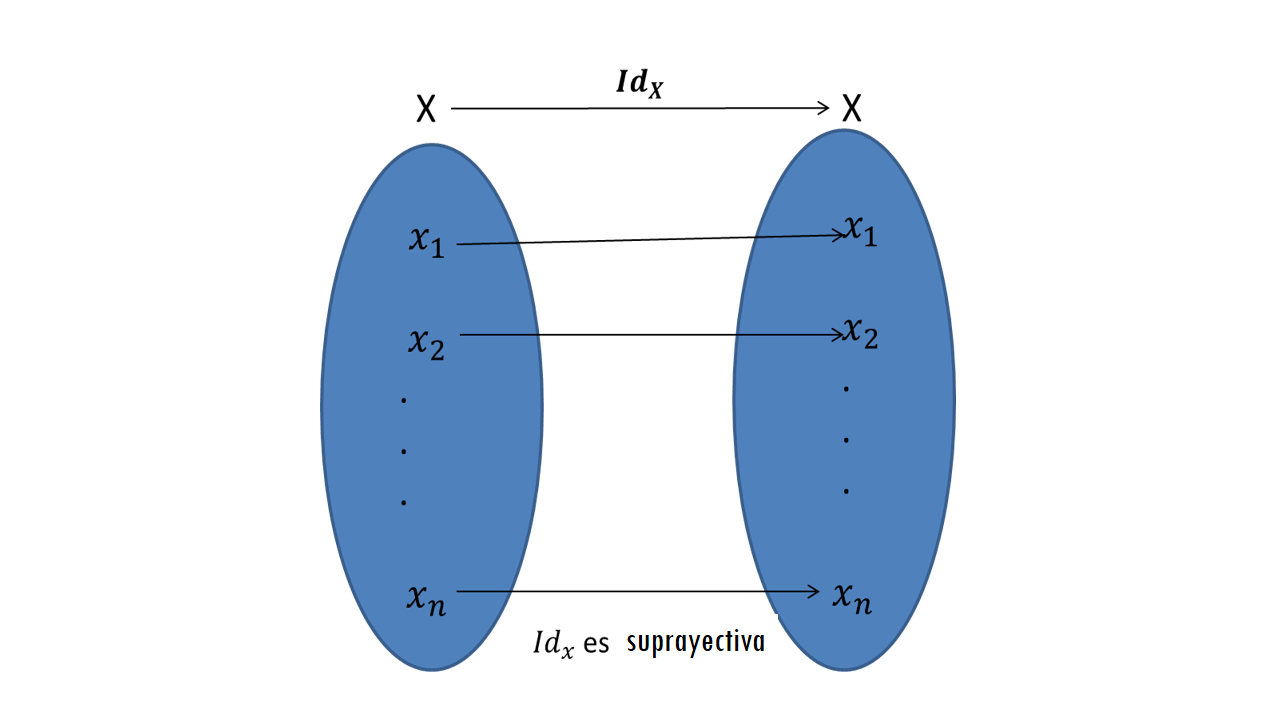
Sean $S,H\subset\mathbb{C}$ y sea $f:S \to H$ una función. Diremos que $f$ es inyectiva si para toda imagen $w\in H$ existe un único $z\in S$ tal que $f(z) = w$. Diremos que $f$ es suprayectiva si para todo $w\in H$ existe una preimagen $z\in S$, es decir si existe $z\in S$ tal que $f(z) = w$. Diremos que $f$ es una biyección si $f$ es una función inyectiva y suprayectiva.
Si $f:S \to H$ es una función biyectiva, entonces diremos que una función $g:H \to S$ es la inversa de $f$ si para todo $w\in H$ se cumple que $f(g(w)) = z$ y para todo $z\in S$ se cumple que $g(f(z)) = w$, es decir si las composiciones $f\circ g$ y $g\circ f$ son las funciones identidad en $H$ y en $S$ respectivamente.
Ejemplo 12.6.
a) La función $f(z) = z^2$ no es inyectiva.
Solución. Claramente $f(z)$ es una función de variable compleja con valores en $\mathbb{C}$. Desde que: \begin{equation*} f(i) = i^2 = -1 = (-i)^2 = f(-i), \end{equation*} entonces $f(z)$ no es inyectiva en $\mathbb{C}$.
b) La función $f:\mathbb{C} \to \mathbb{C}$ dada por $f(z) = 2z – 6i$ es biyectiva. Determina su función inversa.
Solución. Primero probemos que $f(z)$ es inyectiva. Sean $z_1, z_2 \in \mathbb{C}$ tales que $f(z_1) = f(z_2)$. Veamos que $z_1 = z_2$.
Notemos que: \begin{align*} f(z_1) = f(z_2) &\Longleftrightarrow 2z_1 – 6i = 2z_2 – 6i\\ &\Longleftrightarrow 2z_1 = 2z_2\\ &\Longleftrightarrow z_1 = z_2, \end{align*} por lo que $f(z)$ es inyectiva.
Procedemos ahora a verificar que $f(z)$ es suprayectiva. Sea $w \in \mathbb{C}$, entonces existe: \begin{equation*} z := \frac{w+6i}{2}\in\mathbb{C}, \end{equation*} tal que: \begin{align*} f(z) & = 2\left(\frac{w+6i}{2}\right) – 6i\\ & = w, \end{align*} por lo que $f(z)$ es suprayectiva. Por lo tanto $f(z)$ es una función biyectiva y su función inversa está dada por: \begin{equation*} f^{-1}(z) = \frac{z+6i}{2}, \end{equation*} desde que: \begin{align*} f\left(f^{-1}(z)\right) & = f\left(\frac{z+6i}{2}\right)\\ & = 2\left(\frac{z+6i}{2}\right) – 6i\\ & = z, \end{align*} \begin{align*} f^{-1}\left(f(z)\right) & = f^{-1}\left(2z-6i\right)\\ & = \frac{2z-6i+6i}{2}\\ & = z, \end{align*} para todo $z\in\mathbb{C}$.
Definición 12.8. (Función acotada.)
Sea $S\subset\mathbb{C}$. Diremos que una función $f:S\to\mathbb{C}$ es acotada si existe un número $M>0$ tal que para todo $z\in S$ se cumple que: \begin{equation*} |\,f(z)\,| \leq M. \end{equation*}
Ejemplo 12.7.
Si $|\,z\,|\leq 1$, entonces la función $f(z) = \operatorname{Re}(2+\overline{z} + z^3)$ es acotada.
Solución.
Tenemos que: \begin{align*} |\,f(z)\,| & = |\, \operatorname{Re}(2+\overline{z} + z^3) \,|\\ & \leq |\,2+\overline{z} + z^3\,|\\ & \leq |\,2 \,| + |\,\overline{z}\,| + |\,z^3\,|\\ & = 2 + |\,z\,| + |\,z\,|^3. \end{align*} Dado que $|\,z\,|\leq 1$, entonces: \begin{equation*} |f(z)| \leq 2 + |\,z\,| + |\,z\,|^3 = 4. \end{equation*}
Tarea moral
- Considera las siguientes funciones complejas. Escribelas en la forma $f(z) = u(x,y) + iv(x,y)$ identificando claramente a las funciones $u$ y $v$ y los dominios de definición de cada función.
a) $\dfrac{2}{z-1+i}$.
b) $2z^2 + z\overline{z}+3z$.
c) $\overline{z} + \dfrac{2}{z}$.
- Escribe las siguientes funciones complejas en la forma $f(z) = u(r,\theta) + iv(r,\theta)$ expresando a $z$ en su forma polar e identifica a las funciones $u$ y $v$.
a) $f(z)=z^6-\overline{z}^2$.
b) $f(z)= z + \dfrac{1}{z}$.
c) $f(z)=\dfrac{z+1}{z}$.
- Considera la siguiente forma de construir a los números complejos. Sea: \begin{equation*} K = \left\{ \begin{pmatrix} a & -b\\ b & a \end{pmatrix} \,:\, a,b\in\mathbb{R} \right\} \end{equation*} un subconjunto del anillo de matrices reales de $2\times2$ ($M_{2\times2}(\mathbb{R})$). Verifica que $K$ es cerrado bajo la suma y multiplicación de matrices, es decir es un subanillo de $M_{2\times2}(\mathbb{R})$. Además, muestra que: \begin{equation*} \begin{pmatrix} 0 & -1\\ 1 & 0 \end{pmatrix}^2 = – \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}. \end{equation*}
Por último prueba que la función $f:K \to \mathbb{C}$ tal que: \begin{equation*} f\left(\begin{pmatrix} a & -b\\ b & a \end{pmatrix}\right) = a + ib, \end{equation*} define un isomorfismo entre $K$ y el campo de los números complejos $\mathbb{C}$, es decir:
i) $f$ es biyectiva,
ii) $f(A+B) = f(A) + f(B)$, para todo $A,B\in K$,
iii) $f(AB) = f(A)f(B)$, para todo $A,B\in K$.
Observa que si se aplica dicha función $f$ sobre el subconjunto de matrices escalares de $K$, es decir el subconjunto de $K$ tal que $b=0$, entonces $f$ es un isomorfismo sobre el campo de los números reales $\mathbb{R}$.
- Considerando la parte real y la parte imaginaria, funciones $u(x,y)$ y $v(x,y)$ respectivamente, determina a la función compleja $w=u(x,y)+iv(x,y)$ como función de la variable compleja $z=x+iy$.
a) $u(x,y)=\dfrac{x^2 + x – y^2 }{(x+1)^2 + y^2}$ y $v(x,y)=\dfrac{y(1-2x)}{(x+1)^2 + y^2}$.
Hint: Recuerda que para todo $z\in\mathbb{C}$ se tiene que $z \overline{z} = |\,z\,|^2$.
b) $u(x,y) = 6x – 5$ y $v(x,y) = 6y+9$.
c) $u(x,y)=2(x^2 – y^2)$ y $v(x,y)=0$.
Hint: Observa que $v(x,y)=2ixy – 2ixy$.
- Determina la función inversa de las siguientes funciones.
a) $f(z) = \dfrac{1}{z}$, para $z\neq 0$.
b) $f(z) = \dfrac{z-1}{z+1}$, para $z\neq -1$.
c) $f(z) = -z$.
- Considera las siguientes funciones y prueba que son acotadas en su dominio.
a) $f(z) = \dfrac{1}{z^4 – 4z^2 + 3}$, entonces $|\,f(z)\,|\leq \dfrac{1}{3}$ si $|\,z\,| = 2$.
b) $f(z) = \dfrac{1}{z^2 + z + 1}$, entonces $|\,f(z)\,|\leq 4$ si $|\,z\,| \leq \dfrac{1}{2}$.
c) $f(z) = z^5 -4$, entonces $|\,f(z)\,|\leq 5$ si $|\,z\,| \leq 1$.
- Sea $z=x+iy\in\mathbb{C}$. Determina cuáles de las siguientes funciones complejas son polinomios complejos y cuáles no. Justifica tu respuesta.
a) $f(z) = 4x^2 – iy$.
b) $f(z) = xy + i(x+y)$.
c) $f(z) = x^2 + y^2$.
d) $f(z) = x^2 – y^2 + 2ixy$.
e) $f(z) = 5x^2 – 5y^2 + i + (3+i)x + (3i-1)y + 10ixy$.
Más adelante…
En esta entrada hemos abordado de manera formal la definición de una función compleja de variable compleja, además de dar las definiciones elementales de operaciones de funciones desde el enfoque de la variable compleja.
Como vimos en esta entrada, toda función de variable compleja puede describirse considerando a su parte real e imaginaria, las cuales resultaron ser funciones reales de dos variables. En las siguientes entrada veremos que a través de estas funciones podremos abordar diversos conceptos como el de límite, continuidad, diferenciabilidad, entre otros, utilizando los resultados que ya conocemos para funciones reales de dos variables, lo cual resultará de gran utilidad para el estudio de las funciones complejas.
La siguiente entrada hablaremos del concepto de función multivaluada, el cual resultará fundamental en el estudio de las funciones complejas, pues como veremos a lo largo de esta unidad muchas de las funciones complejas elementales, que extienden a las funciones reales, resultan ser funciones multivaluadas.
Entradas relacionadas