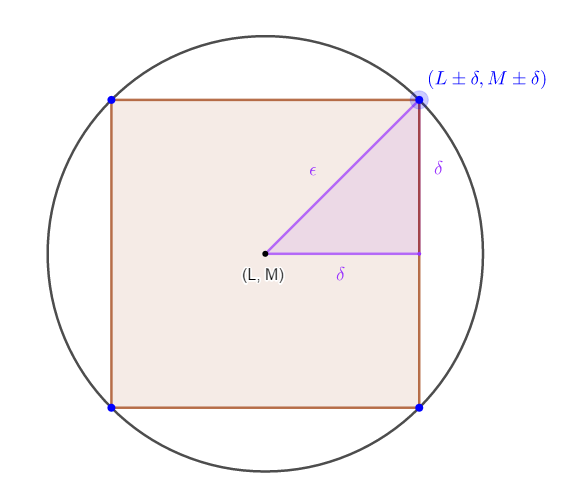
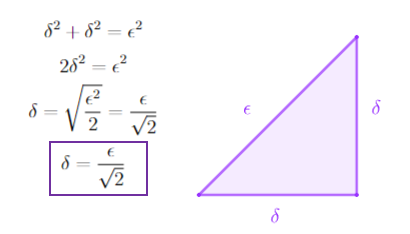Teorema: $F$ es cerrado $\iff \partial F \subseteq F$.
Teorema: $F$ es cerrado $\iff F = \overline{F \,}.$
Demostración:
[$\Leftarrow$] Supongamos que $F = \overline{F \,}$
[por demostrar: $F^c$ es abierto]
Sea $x \in F^c$. Sabemos que $\mathbb{R}^n =$ int $F \; \cup$ ext $F \cup \partial F$ y además sabemos que un punto no pude pertenecer a dos de estos conjuntos.
Entonces, tenemos que $x \notin F$ porque de estarlo $x \in F$. (CONTRADICCIÓN)
Además $x \notin \partial F$ porque si $x \in \partial F \Longrightarrow x \in \overline{F \,} = F$. (CONTRADICIÓN)
Por lo que la única posibilidad es que $x \in$ ext $F$.
Luego, existe una bola contenida en el $F^c$ entonces $x$ es punto interior de $F^c \Longrightarrow F^c$ es abierto.
[$\Rightarrow$] Supongamos que $F^c$ es abierto.
$\big[$ por demostrar: $F = \overline{F \,} \, \big]$
Sabemos que siempre ocurre que $F \subseteq \overline{F \,}$.
$\big[$por demostrar: $\overline{F \,} \subseteq F \big] $
Sea $x \in \overline{F \,} = F \cup \partial F.$
Caso 1) $x \in F$ $\checkmark$
Caso 2) $x \in \partial F$ $\big[ $por demostrar: $x \in F \big]$
Supongamos que $x \notin F$ entonces $x \in F^c$, como $F^c$ es abierto, existe una bola $B_r(x) \subseteq F^c$ entonces en esa bola no hay puntos de $F$. (CONTRADICCIÓN)
$\therefore x \in F$
$\therefore F = \overline{F \,}$ $_\blacksquare$
Proposición: Sea $\mathcal{A} \subseteq \mathbb{R}^n$ entonces $\partial \mathcal{A} = \partial \mathcal{A}^c$.
Demostración:
Sea $x \in \partial \mathcal{A}$ $$\iff \forall r > 0 \; B_r(x) \cap \mathcal{A} \neq \emptyset$$ y también $$B_r(x) \cap \mathcal{A}^c \neq \emptyset$$ $$\forall x \in \partial \mathcal{A}^c \; \; _{\blacksquare}$$
Observación:
1) int $\mathcal{A}$ es abierto.
Demostración:
int $\mathcal{A}$ es abierto $\iff$ int ( int $\mathcal{A}$) ) = int $\mathcal{A}$.
Sabemos que int ( int $\mathcal{A}$) ) $\subseteq$ int $\mathcal{A}$. $\checkmark$
$\big[$ por demostrar: int $\mathcal{A}$ $\subseteq$ int $\big($ int $\big($ $\mathcal{A} \big) \big) \big]$
Sea $\mathcal{B} =$ int $\mathcal{A}$
$\big[$ por demostrar: $\mathcal{B} \subseteq$ int $\mathcal{B} \big]$
Sea $b \in \mathcal{B} =$ int $\mathcal{A}$
entonces $\exists B_r (b) \subseteq \mathcal{A}$.
Sea $x \in B_r (b)$
entonces $\exists \, B_{{r }’} (x) \subseteq B_r (b) \subseteq \mathcal{A}$.
Luego $x$ es punto interior de $\mathcal{A}$, por lo que $x \in \mathcal{B}$. Entonces $b$ es punto interior de $\mathcal{B}$ $$\therefore \mathcal{B} \subseteq \text{int} \mathcal{B}.\; \; _\blacksquare$$
2) $\overline{F \,}$ es cerrado.
Demostración:
Sea $E = \overline{F \,}$
$\big[$ por demostrar: $E$ es cerrado $\big]$
$\big[$ por demostrar: $E = \overline{E \,}$ $\big]$
$\big[$ por demostrar: $\partial E \subseteq E$ $\big]$
Sea $x \in \partial E$
$\forall \; r > 0$ $B_r (x) \cap E \neq \emptyset $ y $B_r (x) \cap E^c \neq \emptyset $.
$\big[$ por demostrar: $x \in E$ $\big]$
Si no fuera así, $x \in E^c =$ ext $F$ ya que $\mathbb{R}^n =$ int $F \cup \partial F \cup$ ext $F$. Pero int $F \cup \partial F = \overline{F \,}$, por lo que $\mathbb{R}^n = \overline{F \,} \; \cup$ ext $F$, lo que es lo mismo que $\mathbb{R}^n = E \; \cup$ ext $F$.
Luego, $\exists \, B_r (x)$ en la cual todos los puntos están en $F^c$. Allí no hay ningún punto de $E$, ya que $E = F \cup \partial F$.
Si hubiera un $w \in \partial F$, $w \in B_r (x)$ entonces $\exists \; r’ > 0$ tal que $B_{{r}’} (w) \subset B_r (x) \subset F^c$.
Por lo que $w$ no puede ser punto frontera de $F$ pues tiene una vecindad contenida en $F^c$. Luego $B_r (x) \cap E = \emptyset$. (CONTRADICCIÓN)
Entonces para cualquier $\mathcal{A} \subseteq \mathbb{R}^n$ se tiene que int $\mathcal{A} \subseteq \mathcal{A} \subseteq \overline{\mathcal{A} \,}$. $_{\blacksquare}$
Proposición: $\emptyset$ es abierto y cerrado.
Demostración:
int $\emptyset \subseteq \emptyset \Longrightarrow$ int $\emptyset = \emptyset.$
$$\therefore \emptyset \text{ es abierto}$$
Además, $\partial \emptyset = \emptyset$ y también $\emptyset = \emptyset \; \cup \partial \emptyset = \overline{\emptyset}.$ $$\therefore \emptyset \text{ es cerrado. } \; _{\blacksquare}$$
Observación: $\mathbb{R}^n$ es abierto y cerrado.
Proposición: Sea $\mathcal{T}$ la familia de todos los abiertos de $\mathbb{R}^n$ tiene tres propiedades especiales:
1) $\emptyset \in \mathcal{T}$, $\mathbb{R}^n \in \mathcal{T},$
2) la unión arbitraria de abiertos es abierta,
3) la intersección finita de abiertos es abierta.
Luego, $(X, \mathcal{T})$ es un espacio topológico si $\mathcal{T}$ tiene estas tres propiedades.
$(\mathbb{R}^n, \mathcal{T})$ es un espacio topológico.
Esto pasa para cualquier espacio métrico $(X, d)$ y la que hemos definido sería la topología inducida por la métrica. $(X, \mathcal{T}_d )$
Demostración:
1) se cumple. $\checkmark$
2) Sea $\{\mathcal{A}_i \}_{i \in I} $ una familia de abiertos.
$\mathcal{A}_i \in \mathcal{T} \; \; \forall i \in I$. Además $\mathcal{A}_i \subseteq \mathbb{R}^n \; \; \forall i \in I.$
$\big[$ por demostrar: $\bigcup\limits_{i \in I}\mathcal{A}_i$ es abierta $\big]$
$\big[$ por demostrar: $\bigcup\limits_{i \in I}\mathcal{A}_i \in \mathcal{T} \big]$
Sea $x \in \bigcup\limits_{i \in I}\mathcal{A}_i \iff x \in \mathcal{A}_i$ para algún $i \in I$ pero como $\mathcal{A}_i$ es abierto, $\exists \, B_r (x) \subseteq \mathcal{A}_i \subseteq \bigcup\limits_{j \in I}\mathcal{A}_j$
3) Sean $\mathcal{A}_1, \; \mathcal{A}_2,\; \dotsc,\; \mathcal{A}_n \in \mathcal{T}$ abiertos.
$\big[$ por demostrar: $\bigcap\limits_{i=1}^{n} \mathcal{A}_i \in \mathcal{T}$ es abierta $\big]$
Sea $x \in \mathcal{A}_1\bigcap\limits \mathcal{A}_2 \bigcap\limits \dotsc \bigcap\limits \mathcal{A}_n$.
Dado que $x \in \mathcal{A}_1$ y como $\mathcal{A}_1$ es abierto, $\exists \; r_1\; >\; 0$ tal que $B_{r_1}(x) \subseteq \mathcal{A}_1.$
De igual manera $x \in \mathcal{A}_2$ y como $\mathcal{A}_2$ es abierto, $\exists \; r_2\; >\; 0$ tal que $B_{r_2}(x) \subseteq \mathcal{A}_2.$
Y así sucesivamente hasta el último conjunto, de modo que, como
$x \in \mathcal{A}_n$ y como $\mathcal{A}_n$ es abierto, $\exists \; r_n\; >\; 0$ tal que $B_{r_n}(x) \subseteq \mathcal{A}_n.$
Sea $\varepsilon = \text{mín} \{r_1, r_2, \dotsc, r_n\}$ tenemos que para $\varepsilon > 0, \; B_{\varepsilon} (x) \subseteq \mathcal{A}_i \; \; \forall \; i=1, 2, \dotsc , n$, por lo que $B_{\varepsilon} (x) \subseteq \bigcap\limits_{i=1}^{n} \mathcal{A}_i.$ $_{\blacksquare}$
$\mathcal{T}$ recibe el nombre de Topología.
Tarea moral
Usando las leyes de De Morgan, muestra que los cerrados tienen estas tres propiedades:
- 1) $\emptyset \in \mathcal{T}$, $\mathbb{R}^n \in \mathcal{T},$
- 2) la unión finita de cerrados es cerrada,
- 3) la intersección arbitraria de cerrados es cerrada.