Introducción
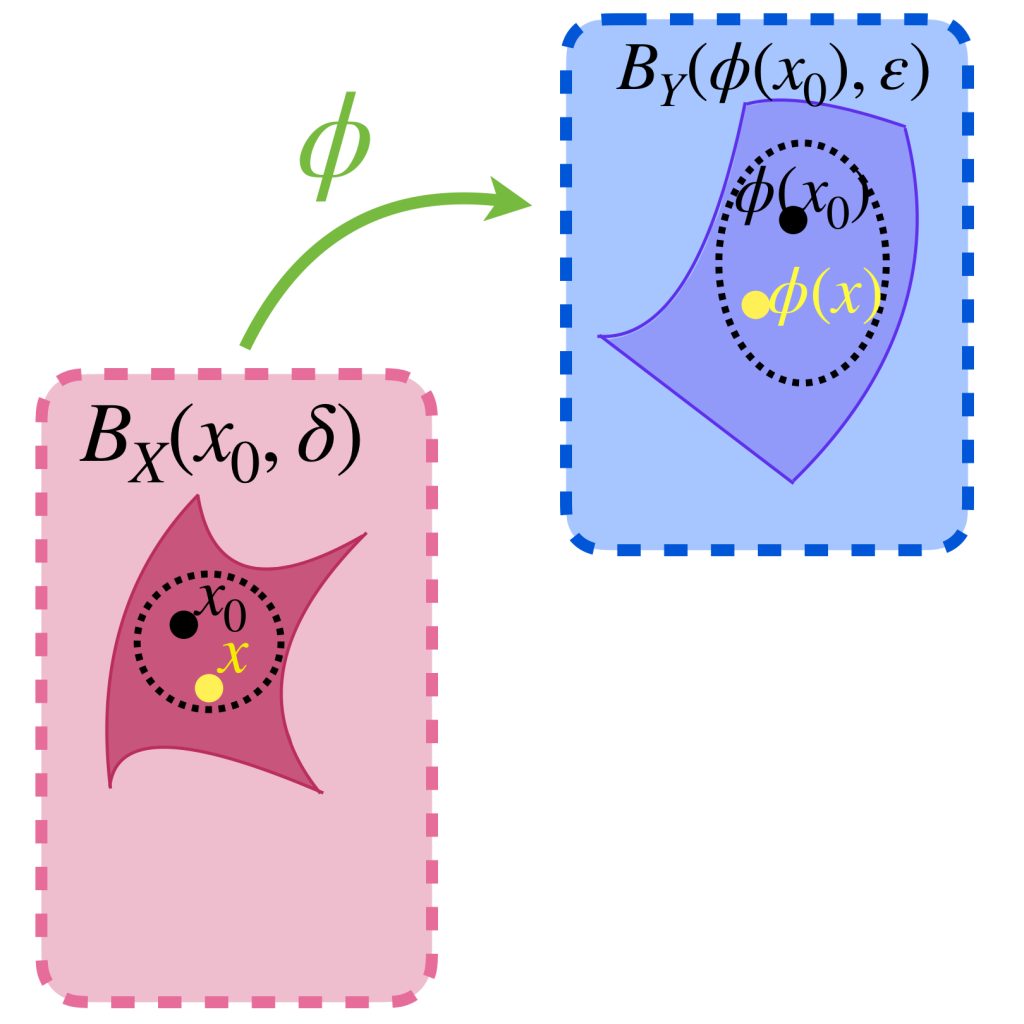
Hasta este punto, ya hemos visto varias propiedades que las funciones continuas tienen entre espacios métricos. De acuerdo a la definición, la continuidad en un punto se da cuando los puntos cercanos a él, son enviados a puntos cercanos en el otro espacio métrico.
Dado $\varepsilon >0$, incluso cuando la función $\phi :X \to Y$ es continua en todos los puntos $x_0$ de $X$, el valor de una $\delta_{x_0}$ que cumple que $\phi (B_X(x_0,\delta_{x_0})) \subset B_Y(\phi(x_0), \varepsilon)$ podría ser diferente para cada punto.
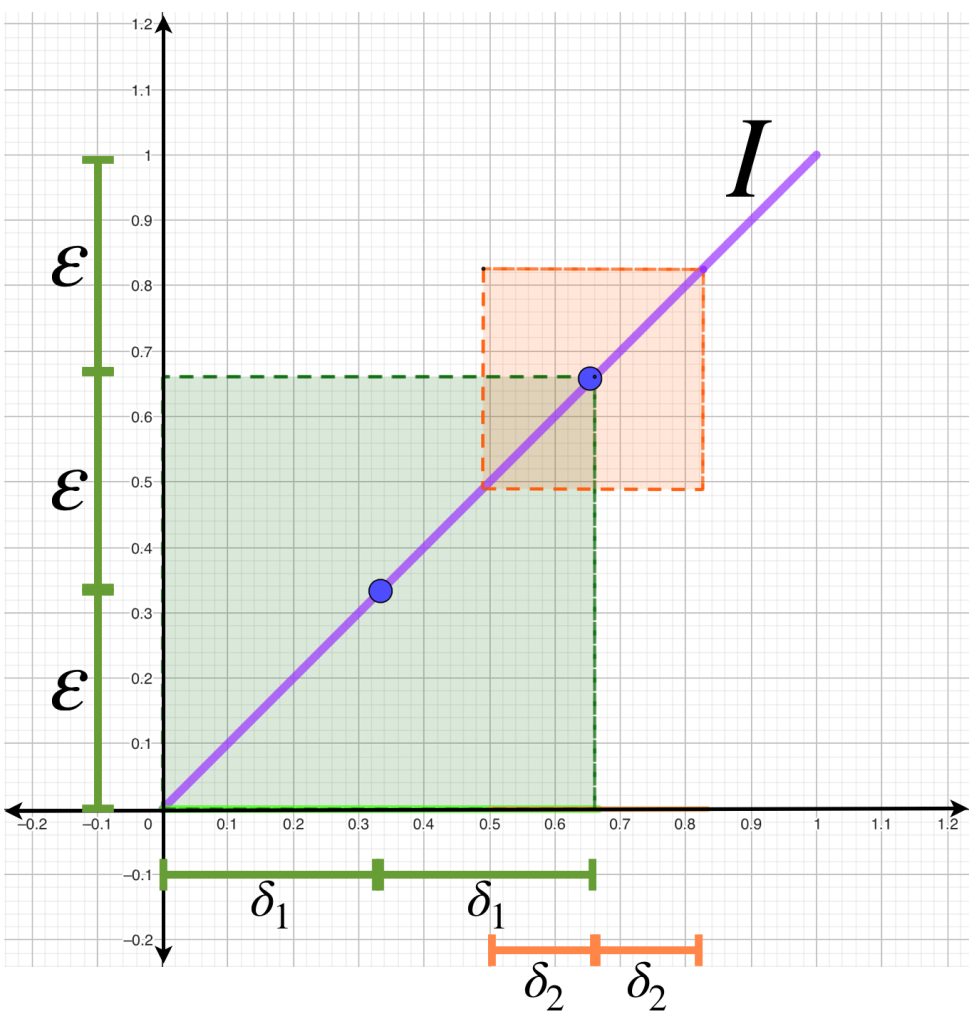
Por ejemplo, sabemos que la función identidad $I:[0,1] \to [0,1]$ es continua en $[0,1]$. Si suponemos $\varepsilon = \frac{1}{3}$ podemos hablar más explícitamente de la continuidad en los puntos $\frac{1}{3}$ y $\frac{2}{3}$ asignando $\delta_1 = \frac{1}{3}$ y $\delta_2 = \frac{1}{6}$, respectivamente.
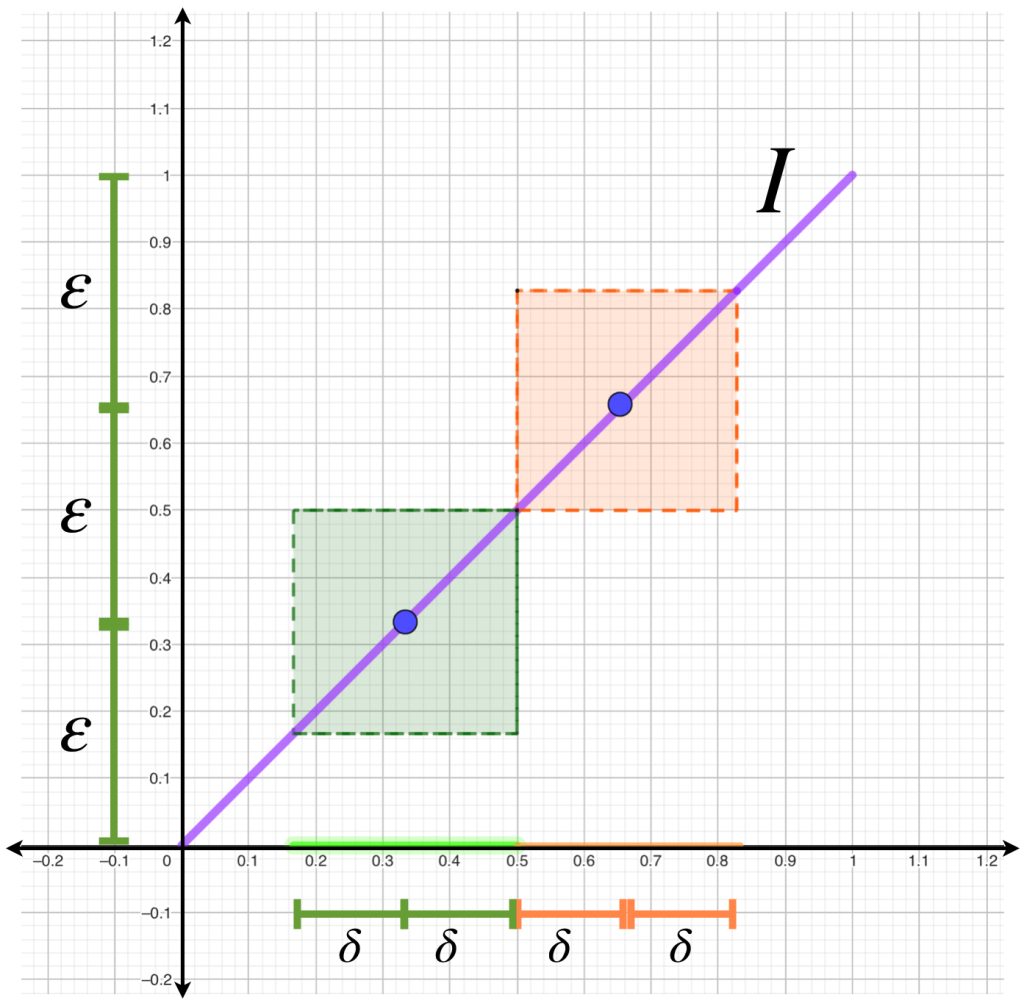
Podemos comprobar que ambas deltas satisfacen la definición de continuidad y sin embargo son diferentes. No obstante, eligiendo $\delta$ como la mínima entre las dos, podemos argumentar también la continuidad en ambos puntos con la misma $\delta.$
En general, en una cantidad finita de puntos donde la función es continua, también es posible elegir el valor de $\delta$ mínimo y este funciona para demostrar la continuidad en cada punto, pero si la continuidad es en un conjunto infinito no siempre existe una delta general .
En los ejemplos de continuidad que hemos visto, fijamos un punto en el espacio del dominio $X$ y observamos un conjunto en torno a él (la bola de radio $\delta$).
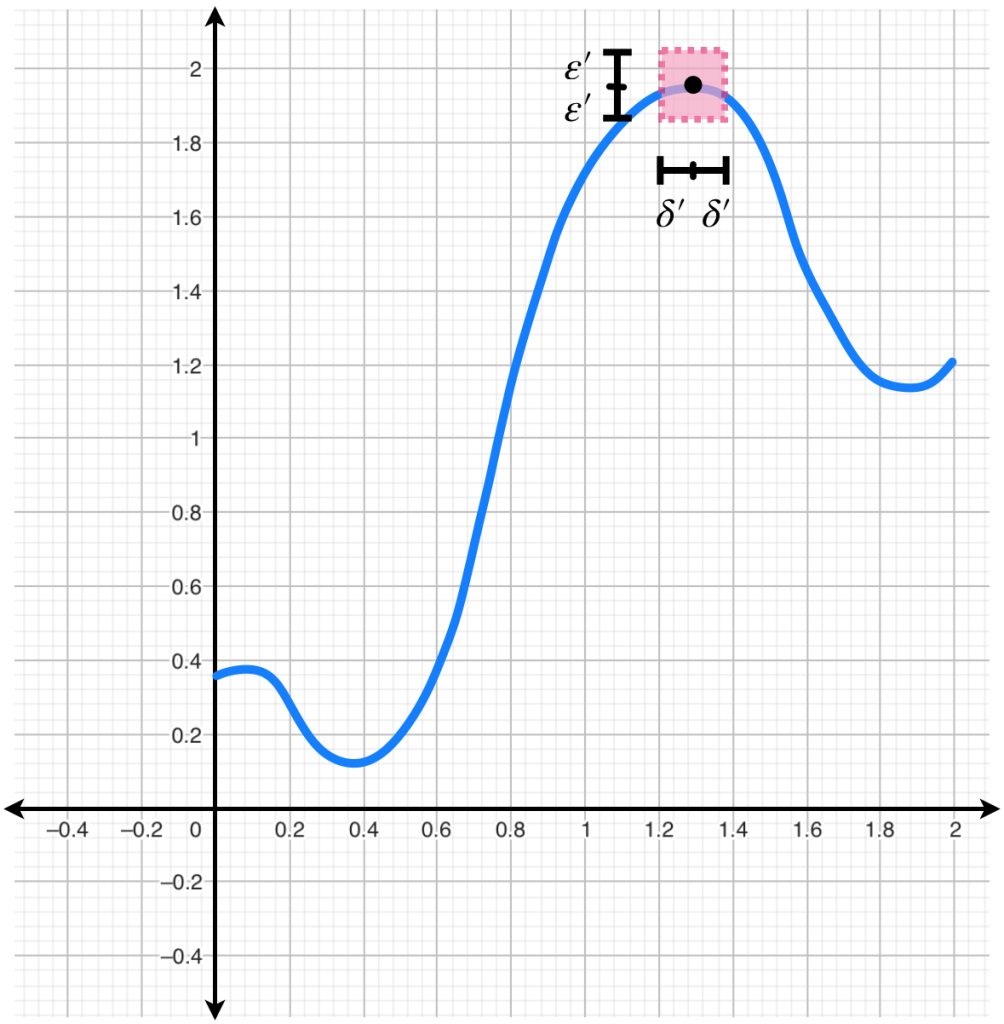
¿Qué pasa si nos fijamos en bolas de radio $\delta$ de manera arbitraria en el dominio? ¿Serán enviados a puntos cercanos en el espacio métrico $Y$?
Esta discusión incentiva la siguiente:
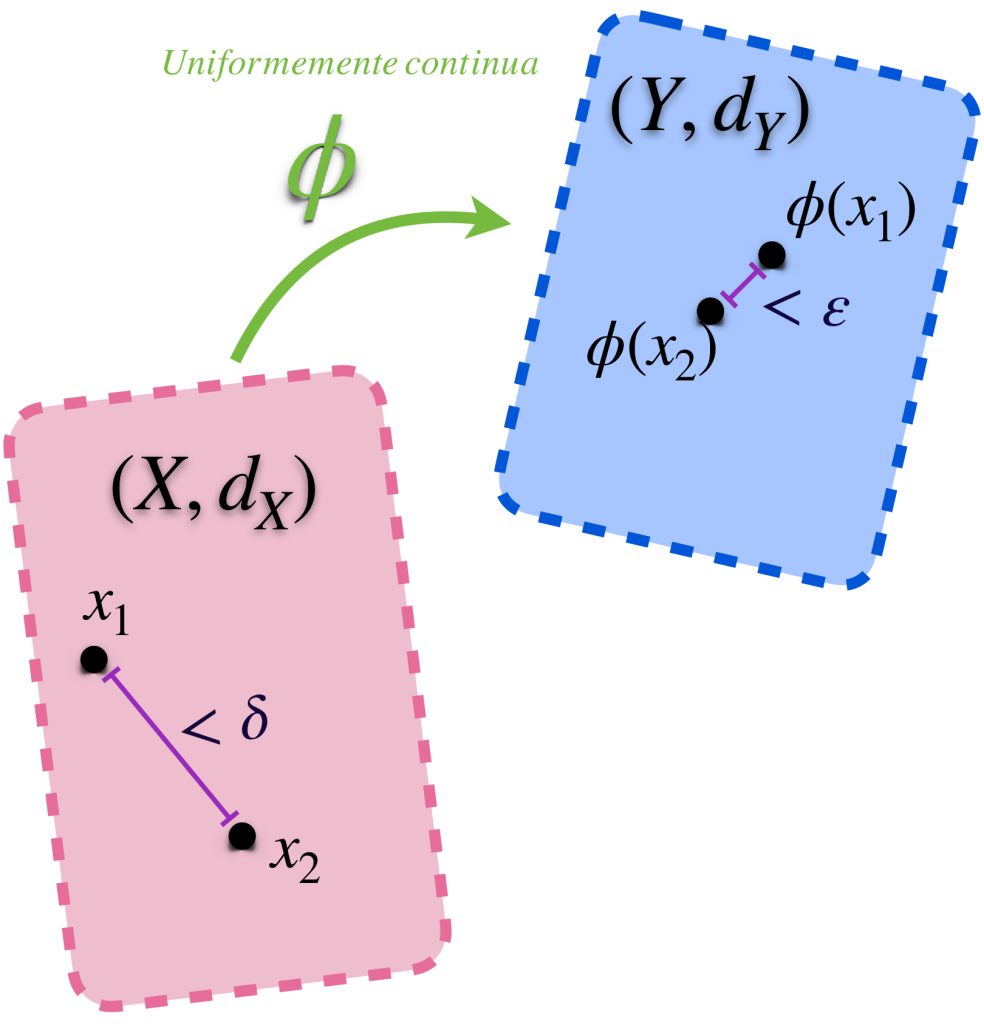
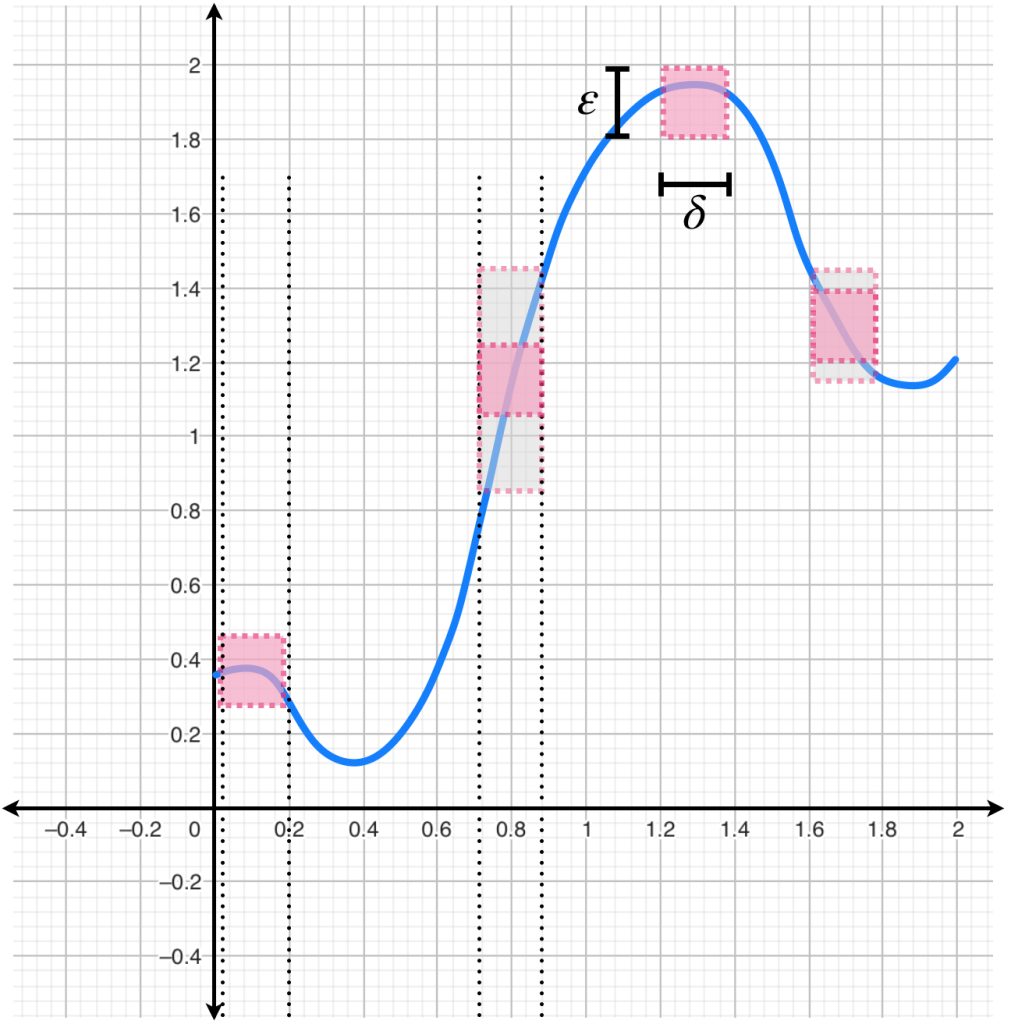
Definición. Función uniformemente continua: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. Decimos que una función $\phi :X \to Y$ es uniformemente continua en $X$ si dada $\varepsilon >0$ existe $\delta >0$ tal que para cualesquiera $x_1, x_2 \, \in \, X$, si satisfacen que $d_X(x_1,x_2)< \delta$, entonces $d_Y(\phi(x_1), \phi(x_2)) < \varepsilon$.
Al final de esta sección se propone demostrar que toda función uniformemente continua es continua. No obstante, hay funciones continuas que no son uniformemente continuas.
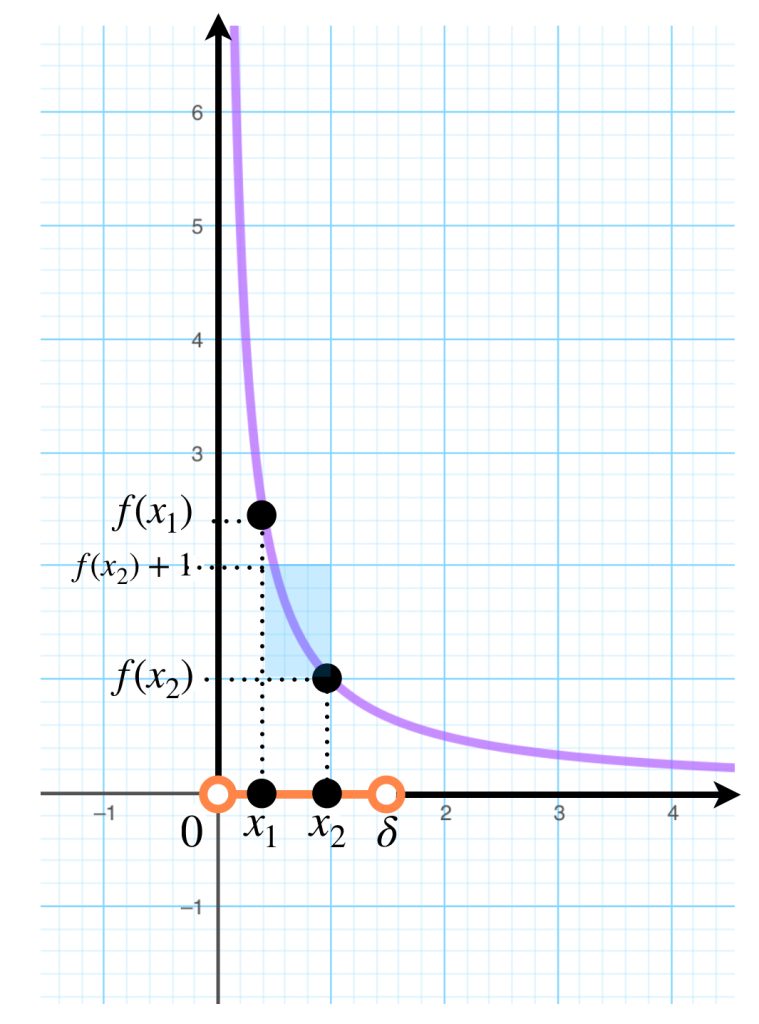
Ejemplo: La función $f:(0,\infty) \to \mathbb{R}, \, f(x)= \frac{1}{x}$ es continua en $(0,\infty)$ pero no es uniformemente continua, pues si consideramos $\varepsilon=1$ y cualquier $\delta>0$ todos los pares de puntos en el intervalo $(0,\delta)$ tienen distancia menor que $\delta.$ Sea $x_1 \in (0,\delta).$ Como $f$ es decreciente y tiende a $\infty$ en cero por la derecha entonces existe $x_2 < x_1$ tal que $f(x_2)>1+f(x_1)$ por lo tanto, aunque $|x_2-x_1|< \delta$ se tiene que $|f(x_2)-f(x_1)|>1= \varepsilon$ y en consecuencia, la función no es uniformemente continua.
Pero hay una propiedad que hace equivalentes ambos tipos de funciones:
Proposición: Sea $A$ un espacio métrico compacto. Si $\phi : A \to Y$ es una función continua, entonces $\phi$ es uniformemente continua.
Demostración:
Supón por el contrario que $\phi:A \to Y$ no es uniformemente continua. Entonces existe $\varepsilon >0$ tal que $\forall \, \delta>0$ existen $a_1,a_2$ con distancia menor que $\delta$ pero cuya distancia correspondiente en $Y$ para $\phi(a_1)$ y $\phi(a_2)$ es mayor igual que \varepsilon.
Particularmente, para cada $n \in \mathbb{N}$ existen $x_n,x’_n \in A$ tales que $d_A(x_n,x’_n)<\frac{1}{n}$ y $d_Y(\phi(x_n),\phi(x’_n)) \geq \varepsilon.$
Entonces la sucesión $(x_n)_{n \in \mathbb{N}}$ que está en $A$ compacto, tiene una subsuseción $(x_{k_j})$ que converge en algún $x \in A.$ La sucesión correspondiente $(x’_{k_j})$ también converge en $x,$ pues:
$$d_A(x,x’_{k_j}) \leq d_A(x,x_{k_j})+d_A(x_{k_j},x’_{k_j}) \to 0$$
Entonces, como $\phi$ es continua se cumple que $\phi(x_{k_j}) \to \phi(x)$ y $\phi(x’_{k_j}) \to \phi(x)$ de modo que existe $J \in \mathbb{N}$ tal que.
$d_Y(\phi(x_{k_j}),\phi(x’_{k_j})) \leq d_Y(\phi(x_{k_j}),\phi(x))+d_Y(\phi(x),\phi(x’_{k_j})) < \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon.$
Pero esto es una contradicción, pues al principio se seleccionaron términos que satisfacen que $d_Y(\phi(x_{k_j}),\phi(x’_{k_j})) \geq \varepsilon.$ Por lo tanto la función sí es uniformemente continua.
Más adelante…
Ya que conocemos algunos resultados de la compacidad en los conjuntos, mostraremos una herramienta para identificarla en espacios de funciones: el teorema de Arzelá-Azcoli. En la siguiente sección veremos las definiciones que nos llevarán a ella.
Tarea moral
- Demuestra que toda función uniformemente continua es continua.
- ¿Es cierto que toda función Lipschitz continua es uniformemente continua?
- ¿Es cierto que toda función uniformemente continua es Lipschitz continua?
- ¿Es la función $f:[a,\infty) \to \mathbb{R}, \, f(x)= \frac{1}{x}, \, a>0,$ uniformemente continua?