Introducción
En esta entrada vamos a ver una forma de definir distancias (sí, de nuevo) pero ahora no directamente entre los elementos de un conjunto, sino entre los subconjuntos de un espacio métrico. Entonces, los subconjuntos pasarán a ser vistos como elementos de un nuevo espacio con cierta métrica. Al final haremos sucesiones de conjuntos. Descubriremos bajo qué condiciones estas sucesiones de conjuntos convergen. Será emocionante descubrir que dos conjuntos están cerca uno de otro, cuando son muy parecidos entre sí (en forma y tamaño). Esta entrada está basada en el contenido del libro «A course in Metric Geometry», escrito por Dmitri Burago, Yuri Burago y Sergei Ivanov (páginas 252 y 253). Omitiremos las demostraciones de las proposiciones, pues no son parte de los objetivos del curso. El lector puede consultarlas en el libro mencionado si así lo desea.
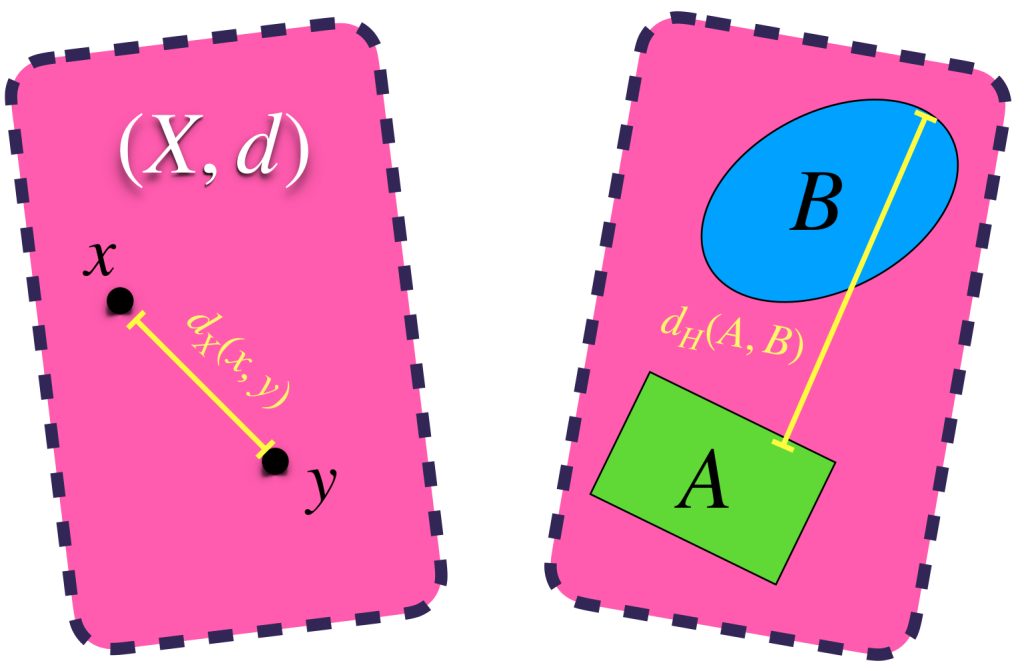
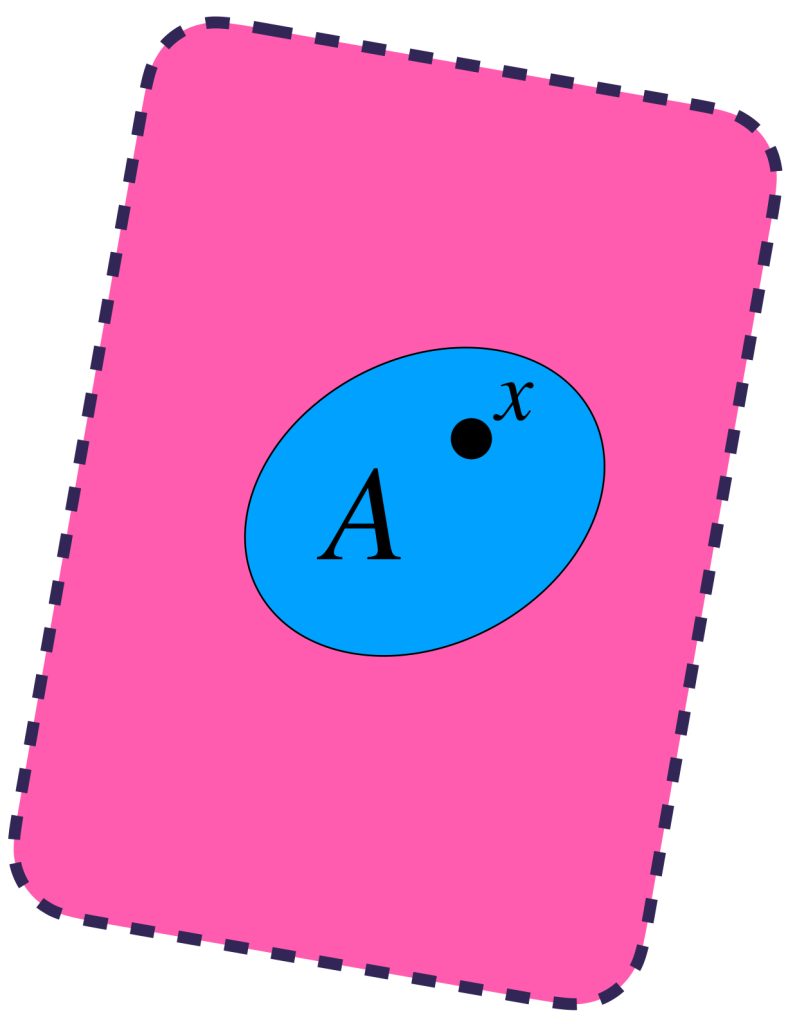
Sea $(X,d)$ un espacio métrico. Visualiza un conjunto $A \subset X$ y un punto arbitrario $x \in A$.
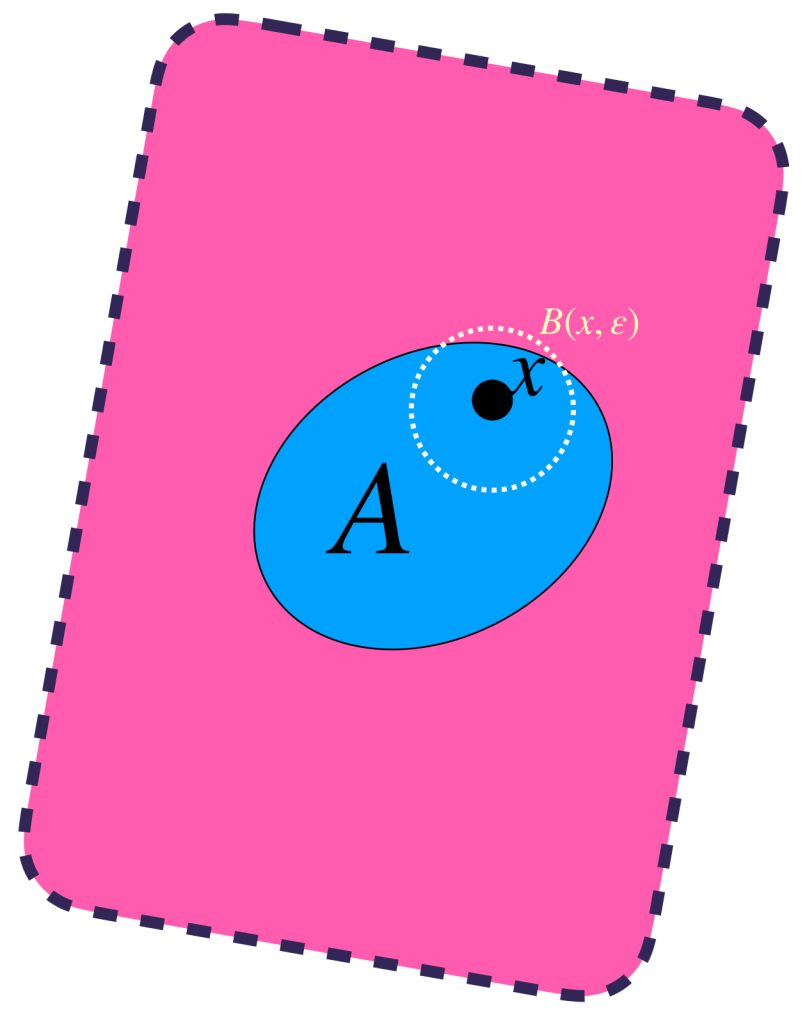
Sea $\varepsilon >0$. Este valor define a $B(x,\varepsilon)$.
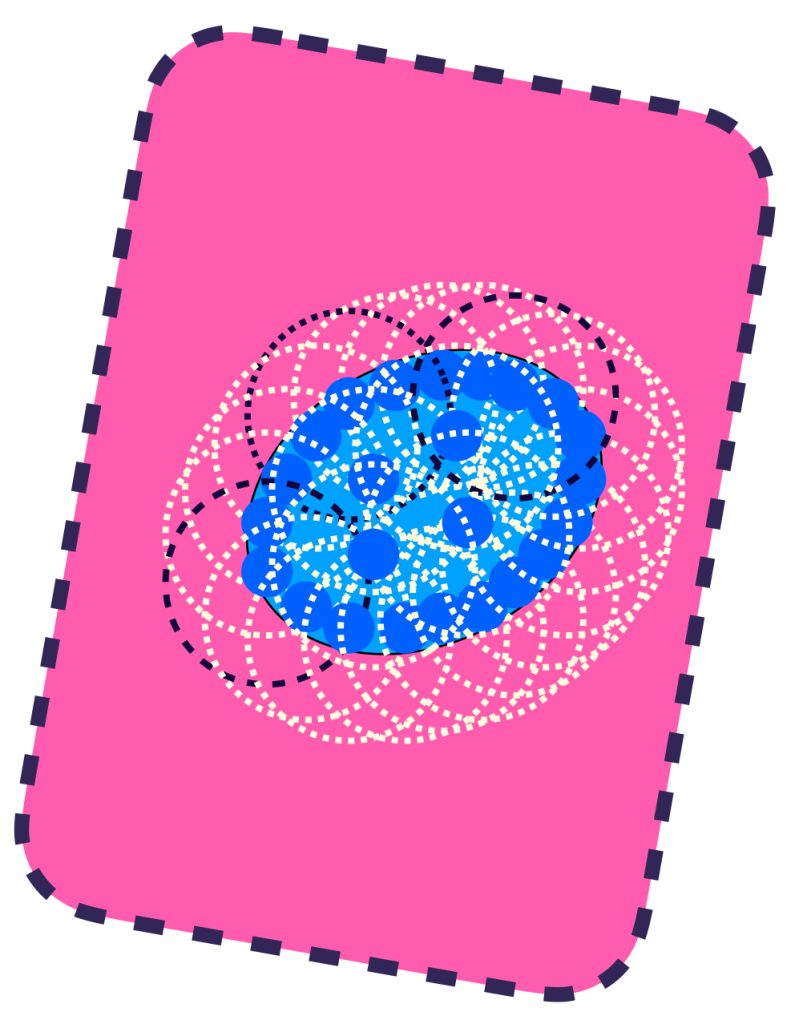
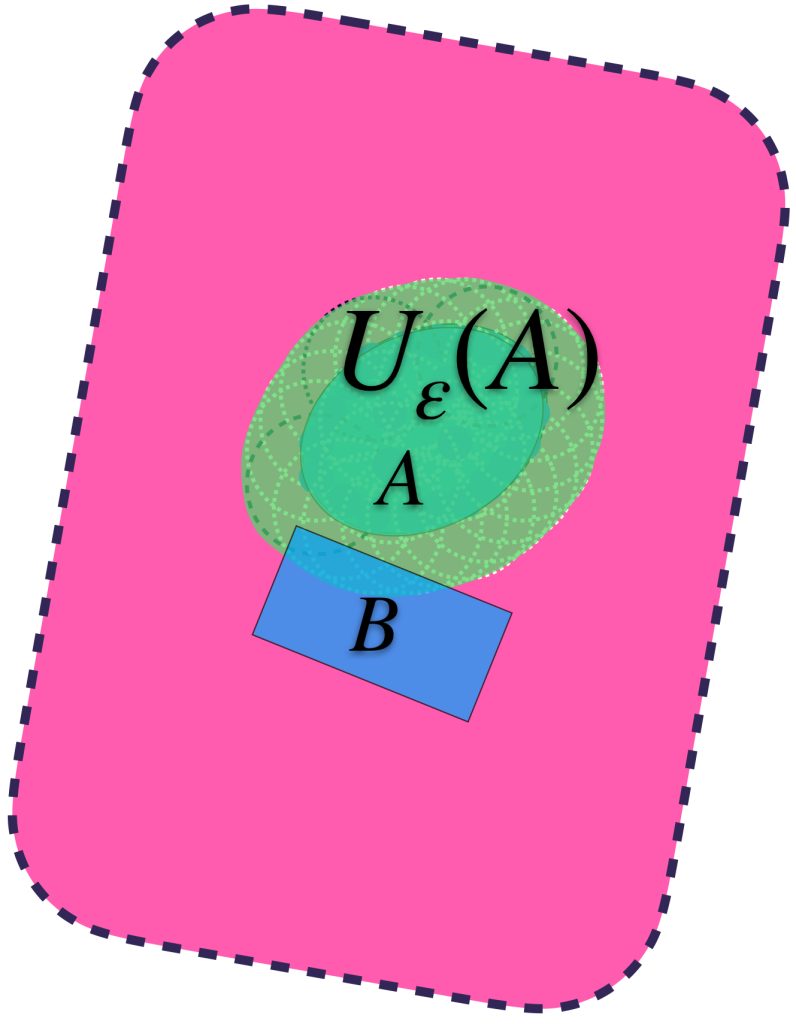
Visualiza la unión de todas las bolas de radio $\varepsilon$. Definimos el conjunto $U_\varepsilon(A) =: \underset{x\in A}{\cup}B(x,\varepsilon)$. Nota que este conjunto contiene al conjunto $A$.
Asímismo, todos los elementos de $U_\varepsilon(A)$ distan en menos que $\varepsilon$ a algún elemento de $A$, pues están en una de las bolas de radio $\varepsilon$.
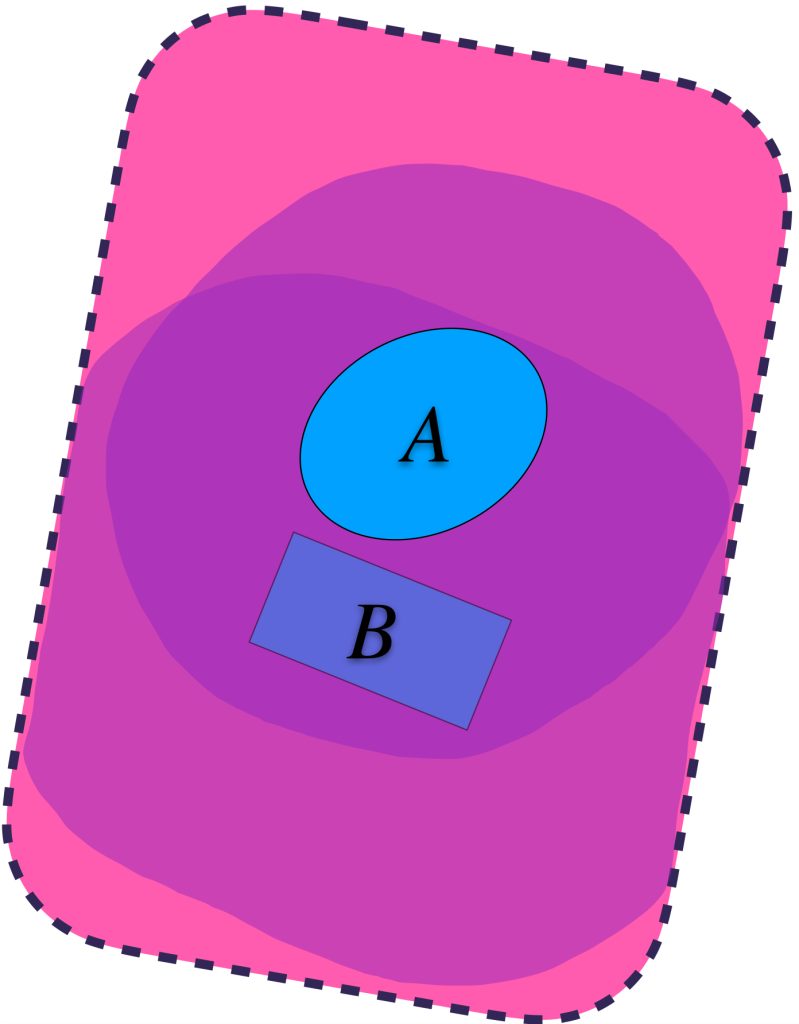
Pensemos ahora en los conjuntos definidos de esta forma en $A$ pero buscando que también contengan a un conjunto $B \subset X$
Se puede dar el caso en que aunque $U_\varepsilon(A)$ contiene a $A,$ no contiene al conjunto $B.$
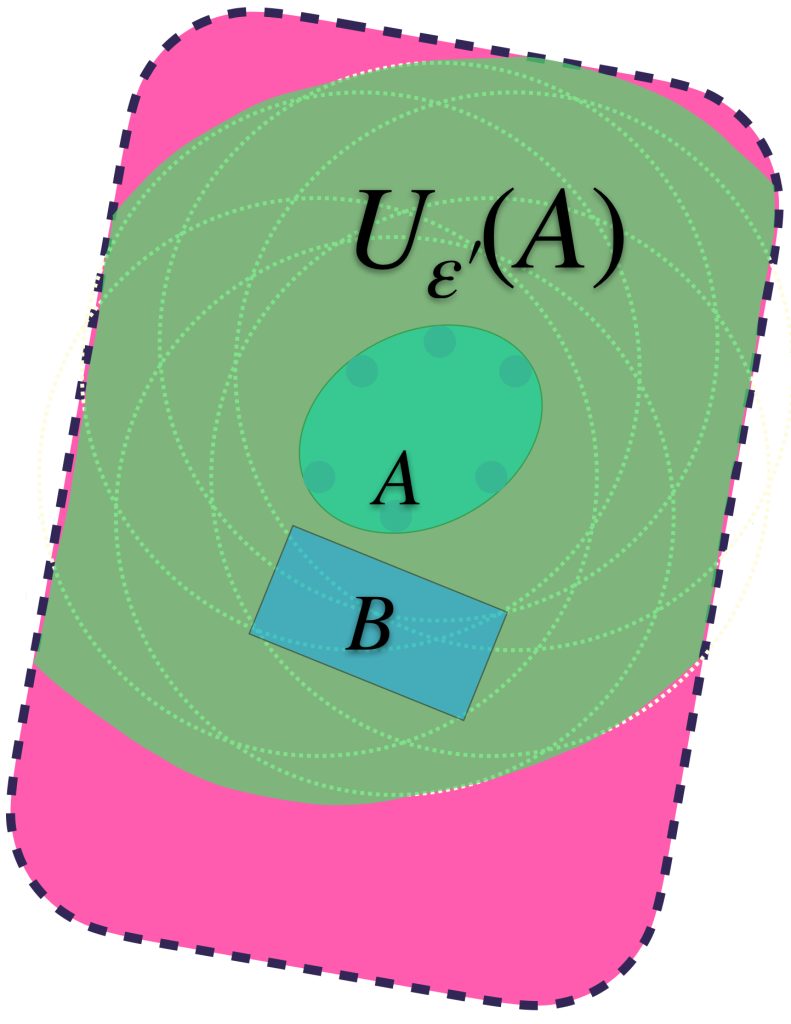
Identificando valores para $\varepsilon >0$ suficientemente grandes, se logra la contención deseada:
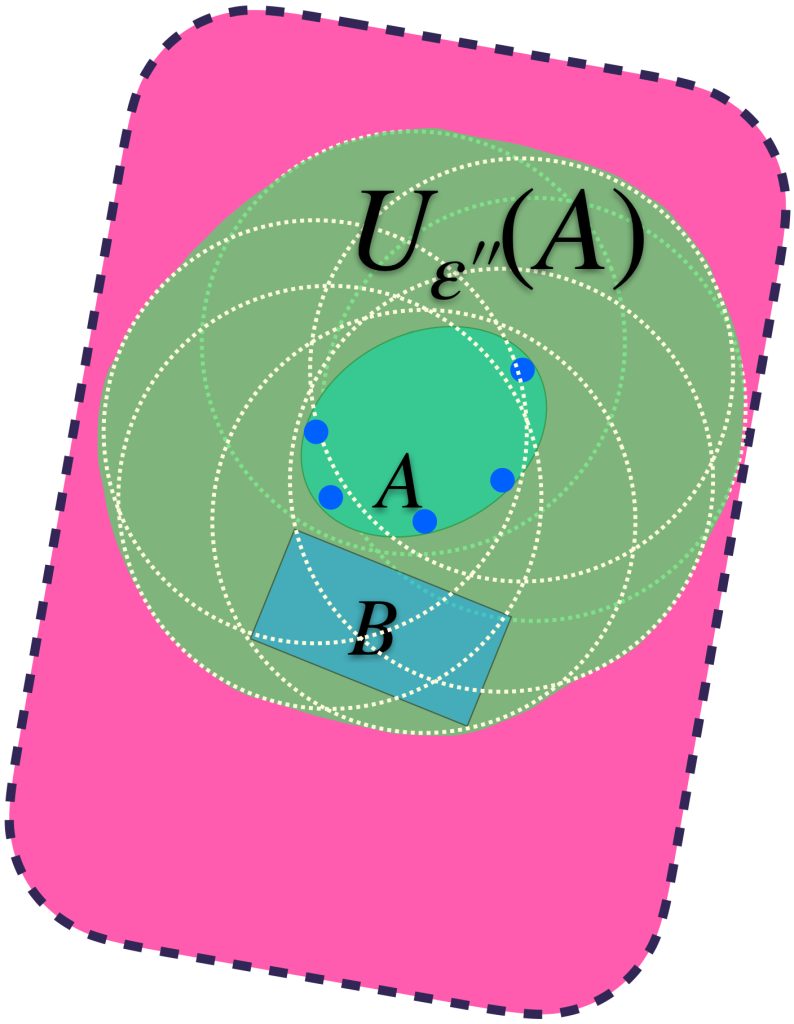
Podemos identificar al ínfimo de los $\varepsilon$´s $>0$ y encontrar así un conjunto $U_{\varepsilon´´}(A)$ más ajustado pero que sigue conteniendo a ambos conjuntos.
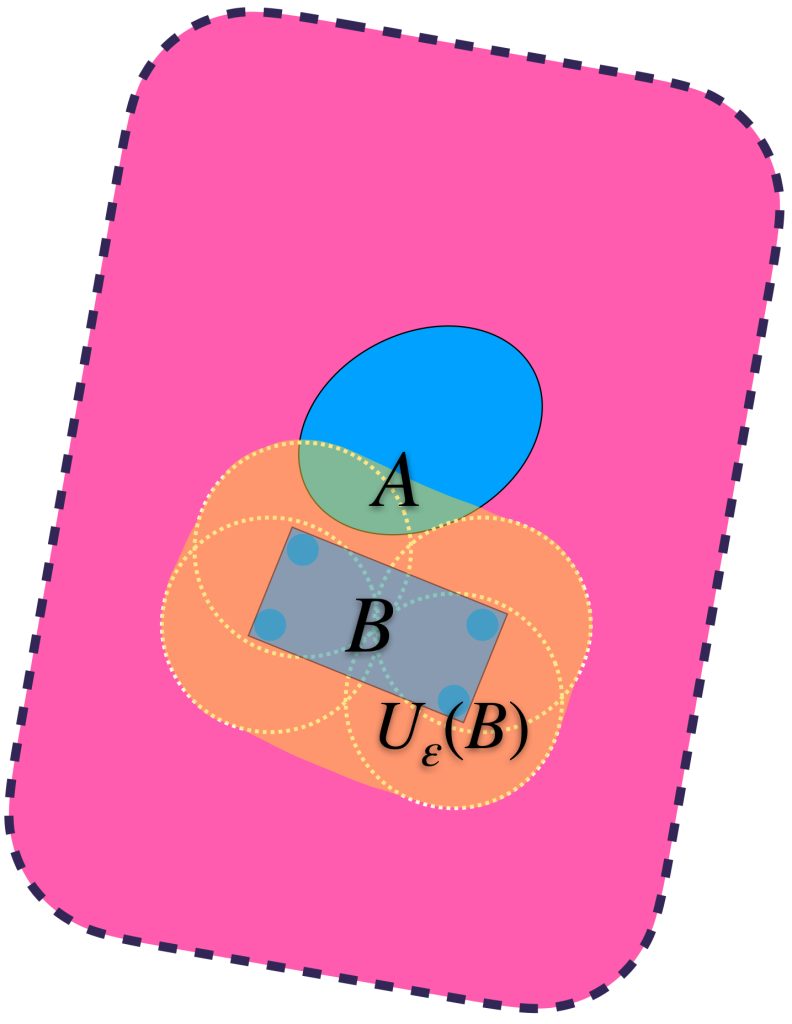
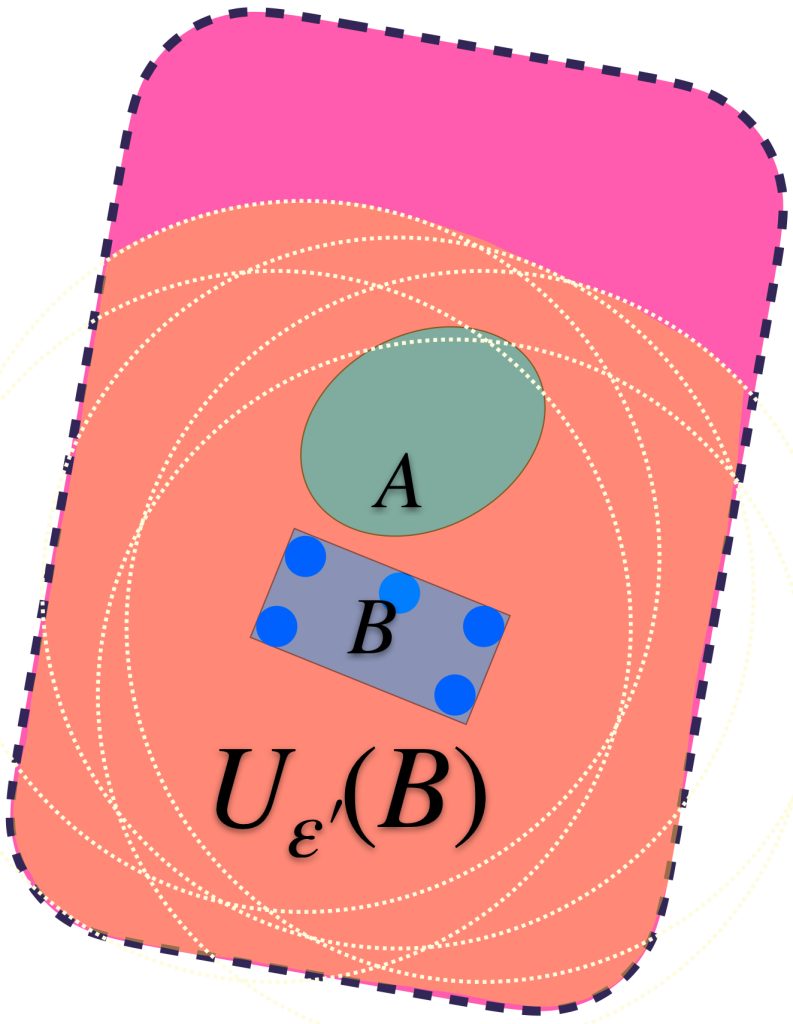
Análogamente, vamos a identificar los conjuntos $U_\varepsilon(B)$ que también contienen a $A$.
Se puede dar el caso en que aunque $U_\varepsilon(B)$ contiene a $B,$ no contiene al conjunto $A.$
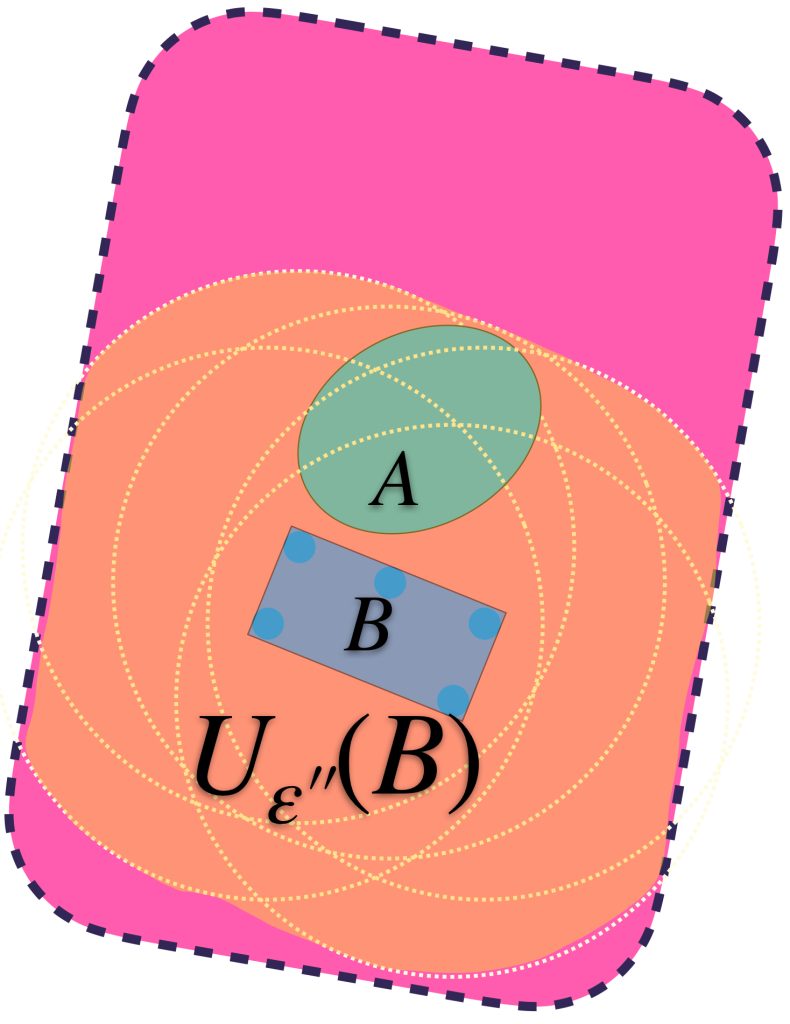
Identificando valores para $\varepsilon >0$ suficientemente grandes, se logra la contención deseada:
Podemos identificar al ínfimo de los $\varepsilon$´s $>0$ y encontrar así un conjunto $U_{\varepsilon´´}(B)$ más ajustado pero que sigue conteniendo a ambos conjuntos.
Si seleccionamos al ínfimo de los $\varepsilon$’s tales que ambos conjuntos quedan contenidos de la forma $A \subset U_\varepsilon(B)$ y $B \subset U_\varepsilon(A)$. Podemos definir la distancia de Hausdorff entre $A$ y $B$ como ese ínfimo. Formalmente:
$$d_H(A,B) =: inf \{\varepsilon>0: A \subset U_\varepsilon(B) \,y\, B \subset U_\varepsilon(A) \}$$
Sean $A\subset X$ y $B\subset X$ y $\varepsilon >0$. Si definimos $\text{dist}(a,B) =: \underset{b \in B}{inf} \, d(a,b)$ para cada $a \in A$ y análogamente $\text{dist}(b,A) =: \underset{a \in A}{inf} \, d(a,b)$ para $b \in B$ entonces las siguientes son propiedades de la distancia de Hausdorff.
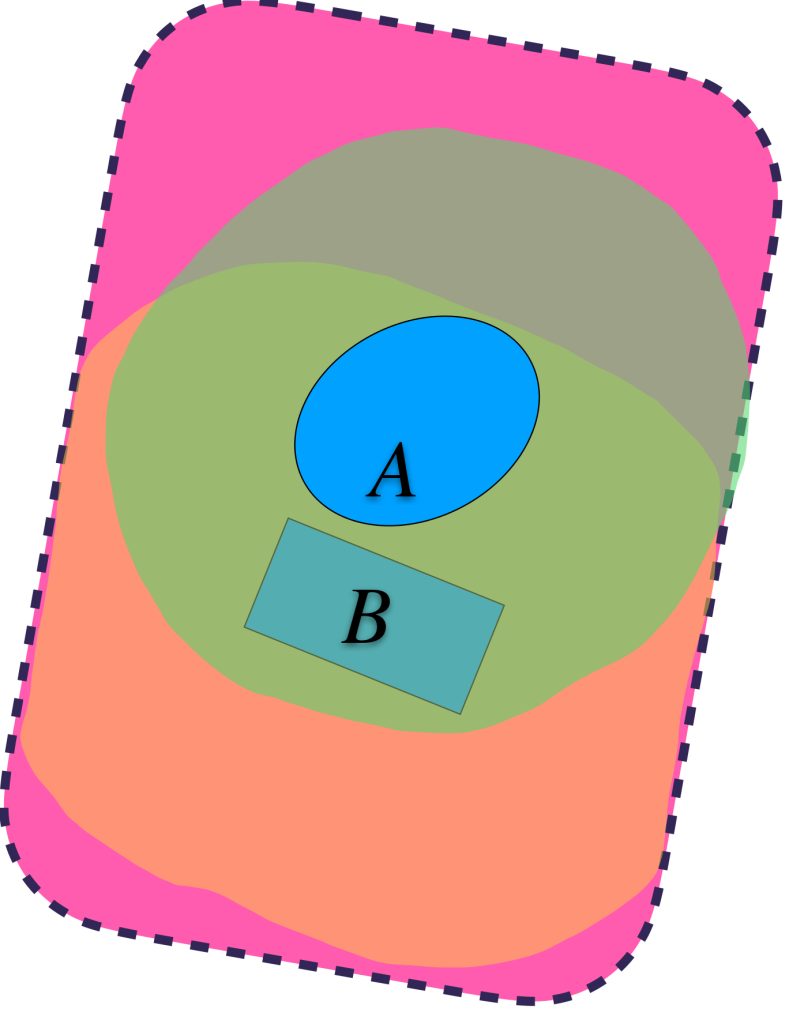
a) $d_H(A,B) = max\{\underset{a \in A}{sup} \, \text{dist}(a,B),\underset{b \in B}{sup} \, \text{dist}(b,A)\}.$
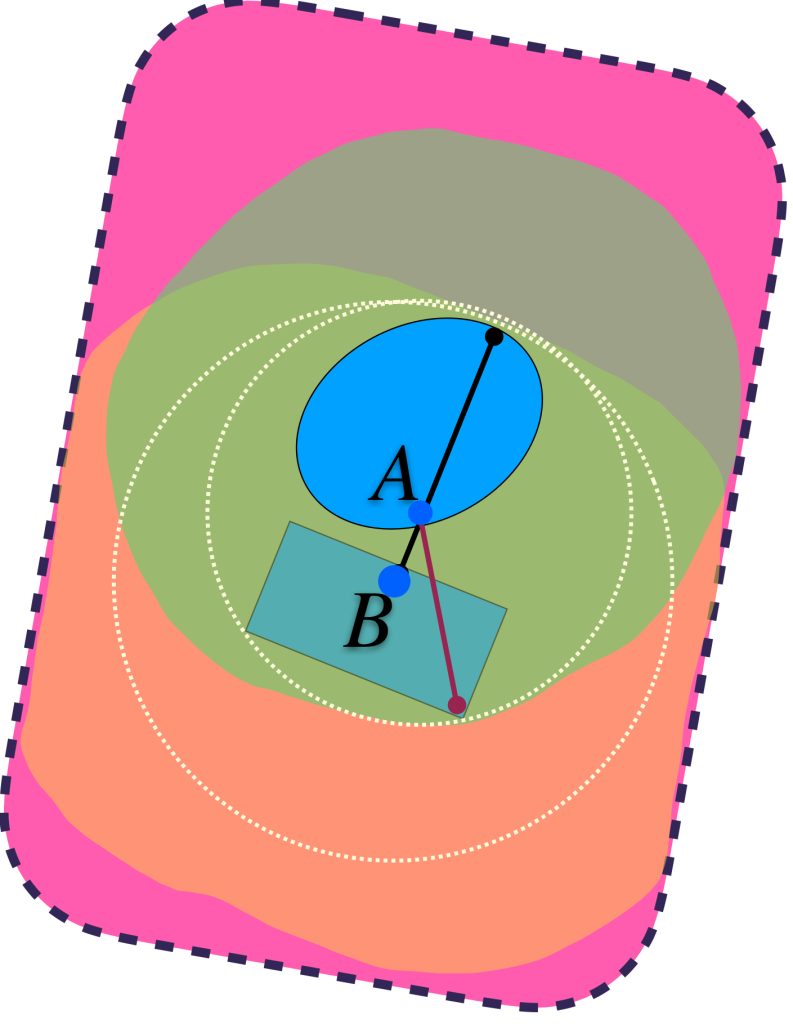
Las líneas señalan las distancias «más grandes» que hay de algún punto de $A$ al conjunto $B$ y de un punto de $B$ al conjunto $A$. Se garantiza que el máximo define el radio de las bolas que hace que los dos conjuntos $U_{\varepsilon}(A)$ y $U_{\varepsilon}(B)$ contengan tanto a $A$ como a $B$.
b) $d_H(A,B) \leq \varepsilon$ si y solo si para todo $a \in A,$ $\text{dist}(a,B) \leq \varepsilon$ y para todo $b \in B, \, \text{dist}(b,A) \leq \varepsilon.$ Esto puede no ocurrir si cambiamos «$\leq$» por «$<$».
Anteriormente hemos hablado de la definición de una función acotada (Espacios de funciones) y de una sucesión acotada (Convergencia), veamos esta definición de un modo más general:
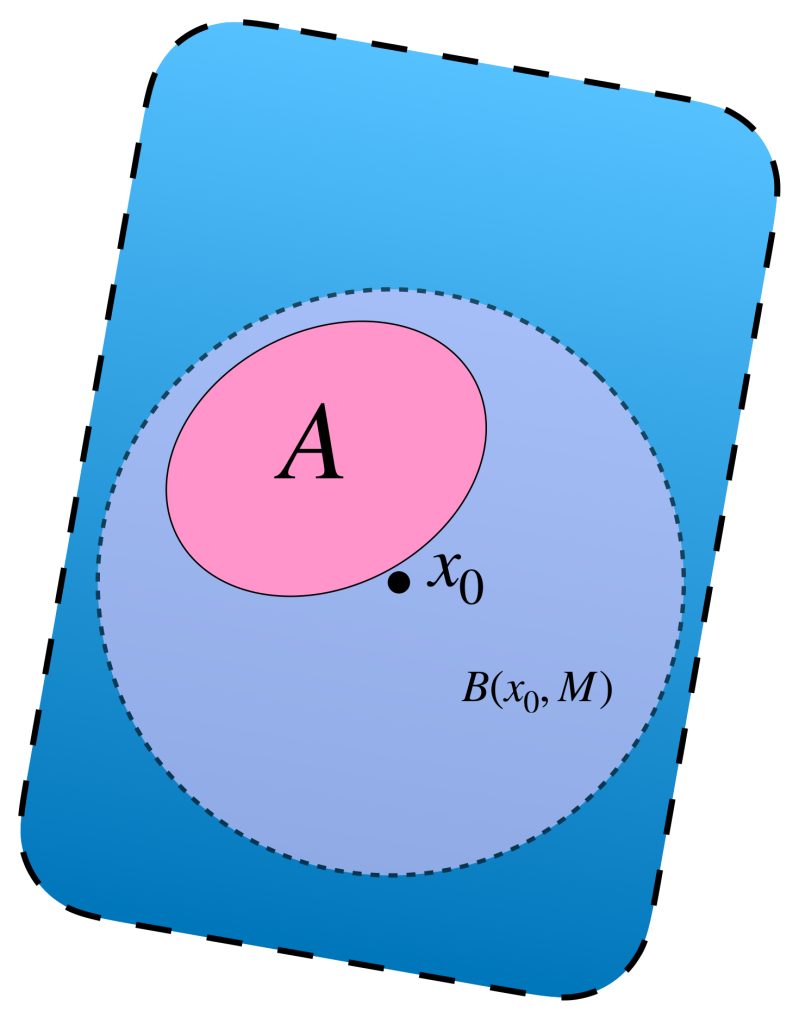
Definición conjunto acotado. Sea $A \subset X$ decimos que $A$ es un conjunto acotado en $X$ si existe un punto $x_0 \in X$ y $M >0$ tal que para toda $x \in A$ se cumple que $d(x,x_0)<M$. Nota que esto es equivalente a decir que $A \subset B(x_0,M)$.
Proposición: Si $(X,d)$ es un espacio métrico, entonces $d_H$ define una métrica en el conjunto de conjuntos cerrados y acotados $\mathcal{M}(X):=\{F \subset X: F \text{ es cerrado y acotado}\}$. (En el libro de Burago la métrica puede tomar el valor infinito, en ese sentido $d_H$ también sería una métrica en el conjunto de los subconjuntos cerrados de $X$, incluyendo los no acotados).
Eso significa que $A,B \in \mathcal{M}(X)$ cumplen:
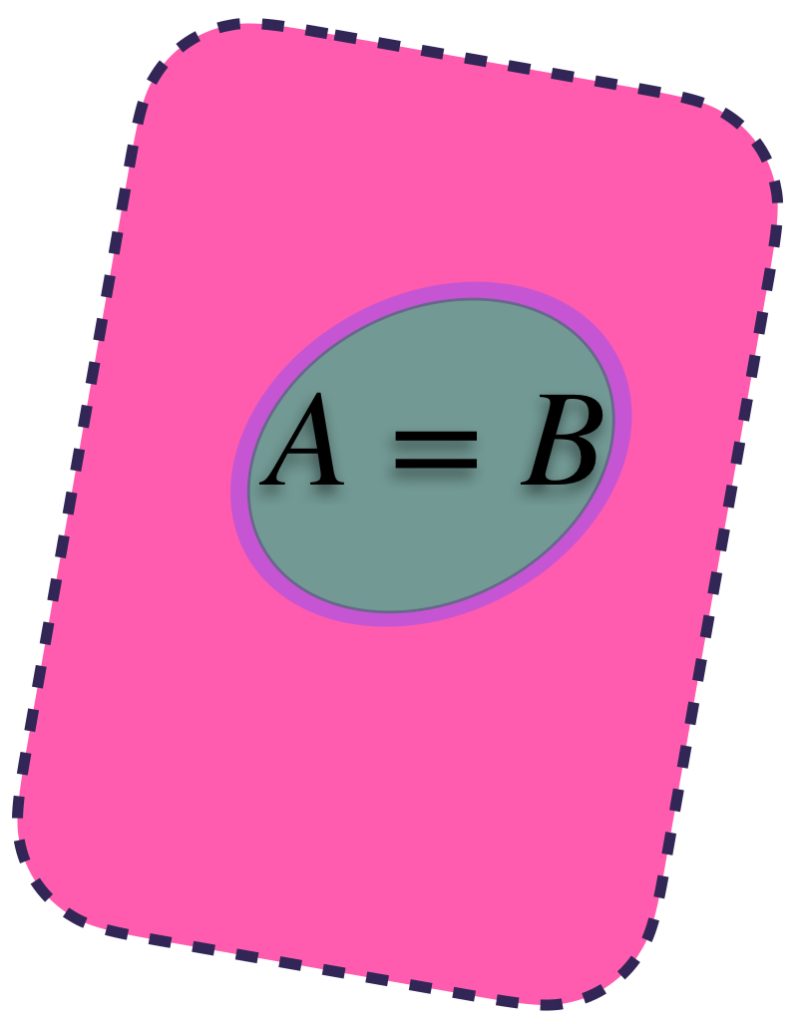
1) $d_H(A,B)=0$ si y solo si los conjuntos son iguales. En este caso tendremos que para todo $\varepsilon>0$ $A \subset U_\varepsilon(B)$ y $B \subset U_\varepsilon(A)$. Además $U_\varepsilon(B)=U_\varepsilon(A).$
2) La propiedad de simetría en espacios métricos dice que $d_H(A,B) = d_H(B,A)$
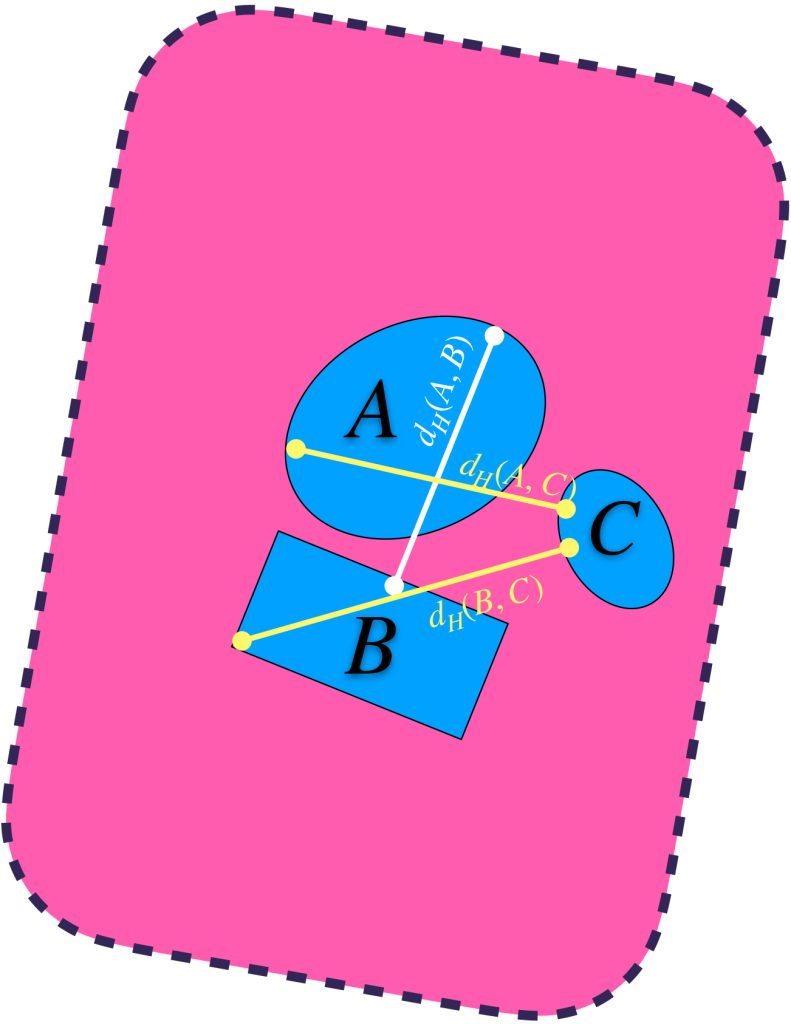
3) Se cumple la desigualdad del triángulo entre conjuntos: $$d_H(A,B) \leq d_H(A,C) + d_H(C,B)$$.
Para fines ilustrativos de esta propiedad recordemos que:
$d_H(A,B) = max\{\underset{a \in A}{sup} \, \text{dist}(a,B),\underset{b \in B}{sup} \, \text{dist}(b,A)\}.$
$d_H(A,C) = max\{\underset{a \in A}{sup} \, \text{dist}(a,C),\underset{c \in C}{sup} \, \text{dist}(c,A)\}.$
$d_H(B,C) = max\{\underset{b \in B}{sup} \, \text{dist}(b,C),\underset{c \in C}{sup} \, \text{dist}(c,B)\}.$
La imagen siguiente representa esas distancias.
A continuación, visualizaremos ejemplos de sucesiones en el espacio métrico de Hausdorff. Entonces los elementos de las sucesiones serán conjuntos cerrados y acotados.
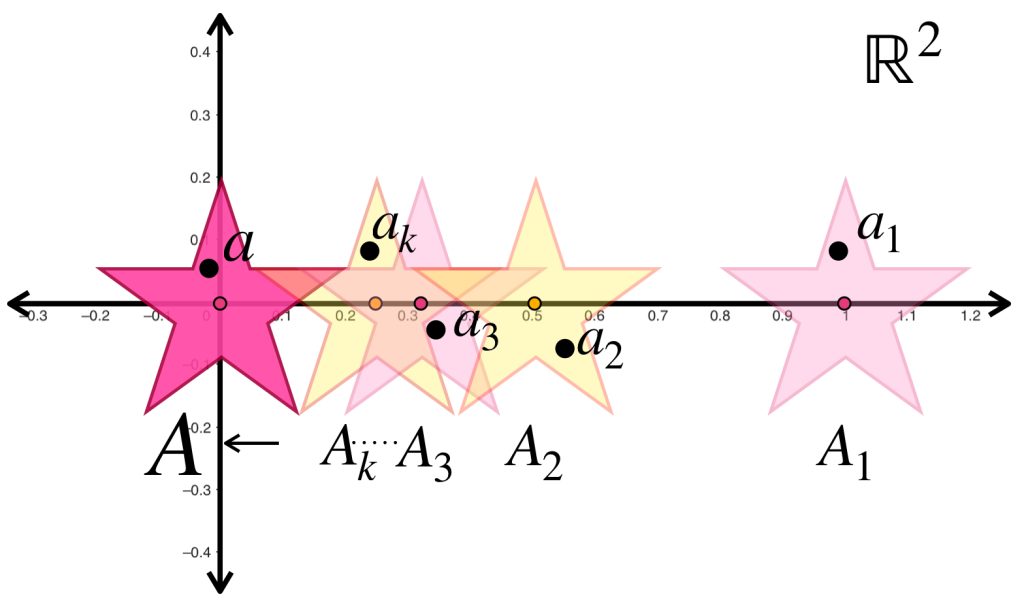
Si $(A_n)_{n \in \mathbb{N}}$ es una sucesión de conjuntos de un espacio métrico y $A_n \to A$ en la métrica de Hausdorff, entonces $d_H(A_n,A) \to 0$ en $\mathbb{R}.$ Eso significa que los conjuntos indicados por la sucesión no solo se van a acercar (en posición, si podemos pensarlo así) al conjunto $A$, sino que se van a ver como éste (pues cuando $d_H =0$ los conjuntos son iguales).
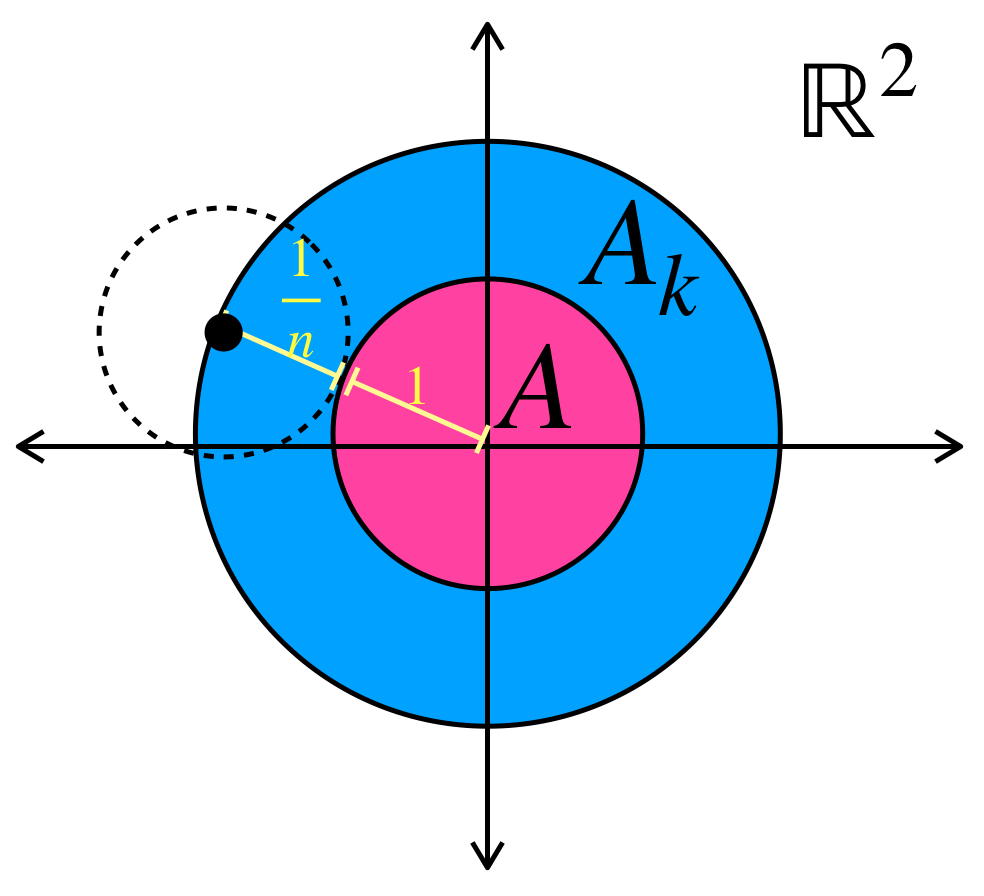
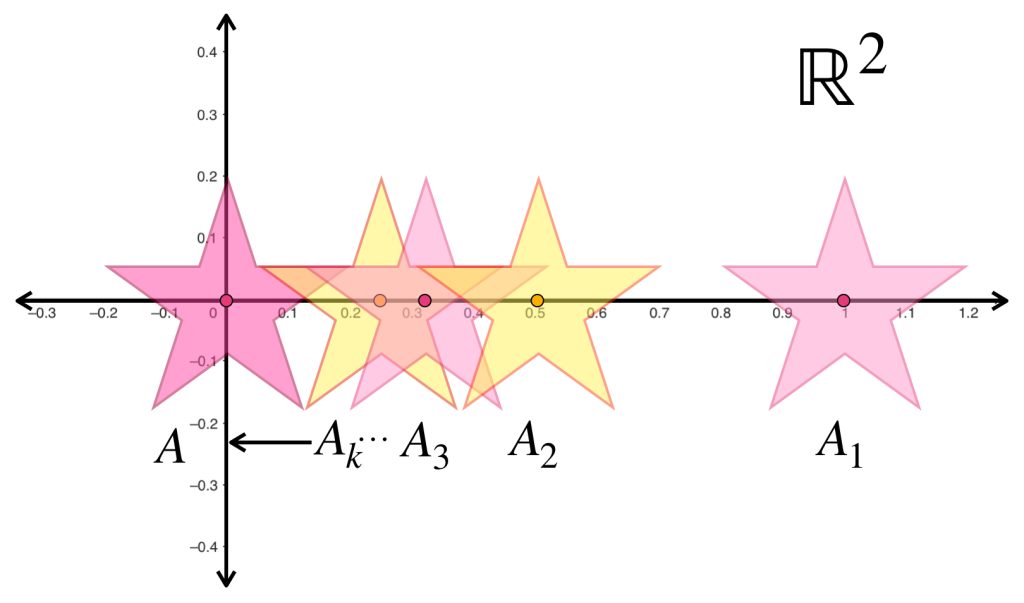
La sucesión presentada muestra estrellas de la misma forma y tamaño pero distinta posición en $\mathbb{R}^2$ cada vez más grandes pero proporcionales entre sí. Para cada $n \in \mathbb{N}$ la estrella $A_n$ tiene su centro en el punto $(\frac{1}{n},0)$. Entonces la sucesión $(A_n)_{n \in \mathbb{N}}\,$ converge a la estrella con centro en $(0,0)$.
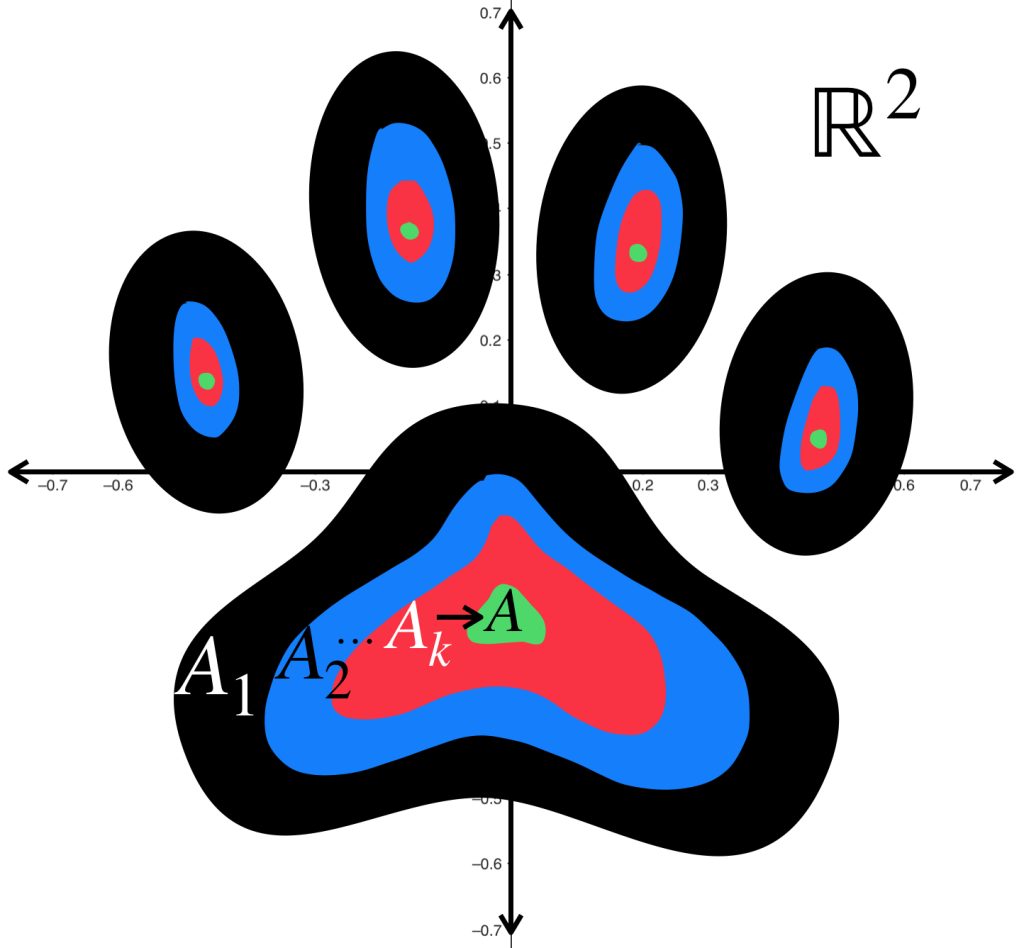
La sucesión de huellas de perrito muestra manchas cada vez más pequeñas que convergen a las manchas verdes.
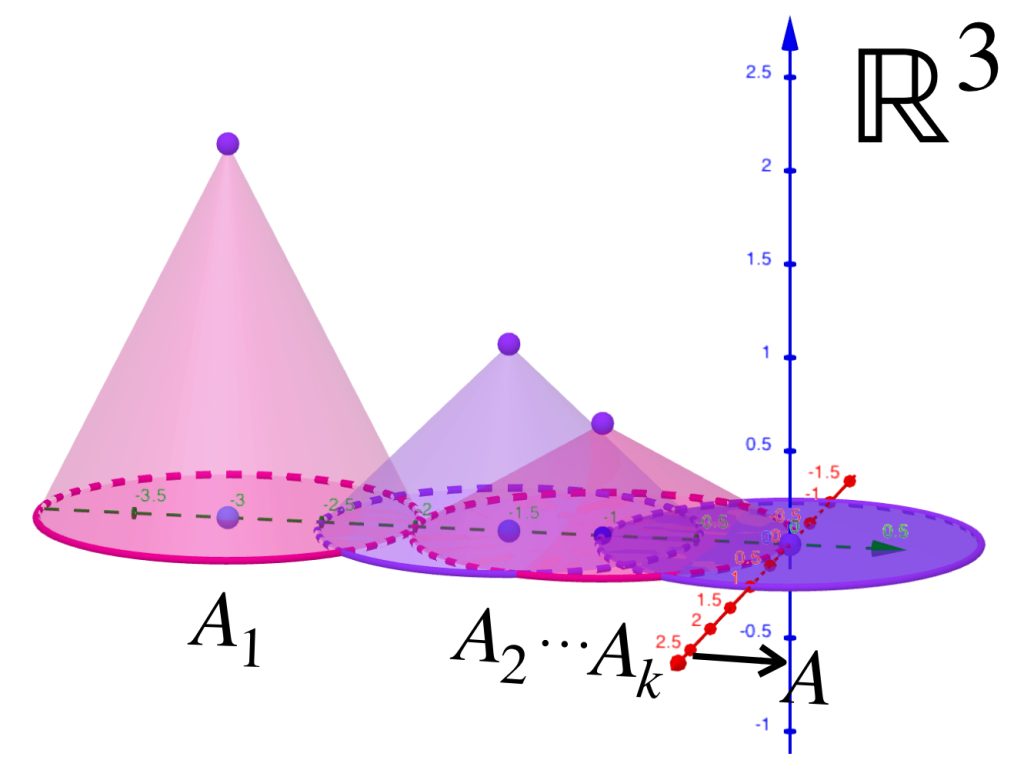
Tenemos una sucesión de conos $(A_n)_{n \in \mathbb{N}}\,$ definida como sigue: para cada $n \in \mathbb{N}$ el cono $A_n$ tiene su centro en $(0,\frac{-3}{n},0)$, altura $\frac{2}{n}$ y radio $1$. Entonces los conos ven disminuída su altura hasta llegar a $0$ mientras que el centro se desplaza al origen. Finalmente convergen al círculo unitario en el plano horizontal.
Formalmente, tenemos los siguientes:
Ejemplos de sucesiones de conjuntos en espacios euclidianos que convergen a un conjunto $A$ en el espacio de Hausdorff.
Para cada $n \in \mathbb{N}$ considera en el espacio euclidiano $\mathbb{R}^2$ el conjunto $A_n =: \overline{B}(0,1+\frac{1}{n})$. Entonces $(A_n)_{n \in \mathbb{N}}\,$ es una sucesión en el espacio de Hausdorff que converge al conjunto $A=:\overline{B}(0,1)$.
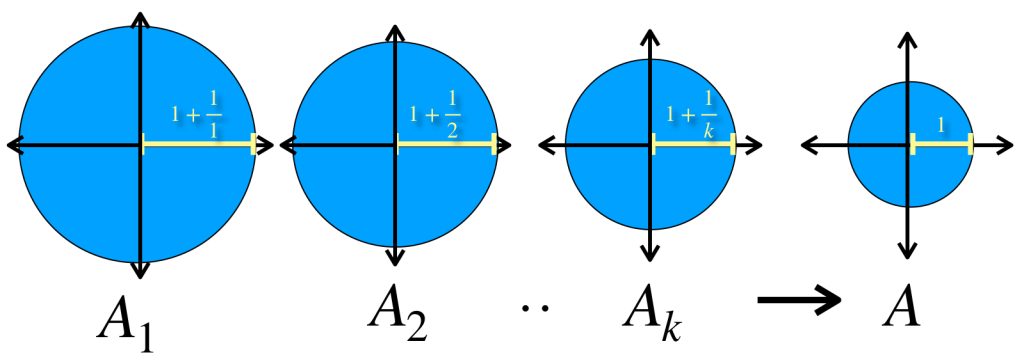
Basta con demostrar que $d_{H}(A_n,A) = max\{\underset{a \in A_n}{sup} \, \text{dist}(a,A),\underset{b \in A}{sup} \, \text{dist}(b,A_n)\} \to 0$ en $\mathbb{R}$. Es sencillo probar que para cada $n \in \mathbb{N}, \,d_{H}(A_n,A) = \frac{1}{n} \to 0 \in \mathbb{R}$ por lo tanto $A_n \to A$.
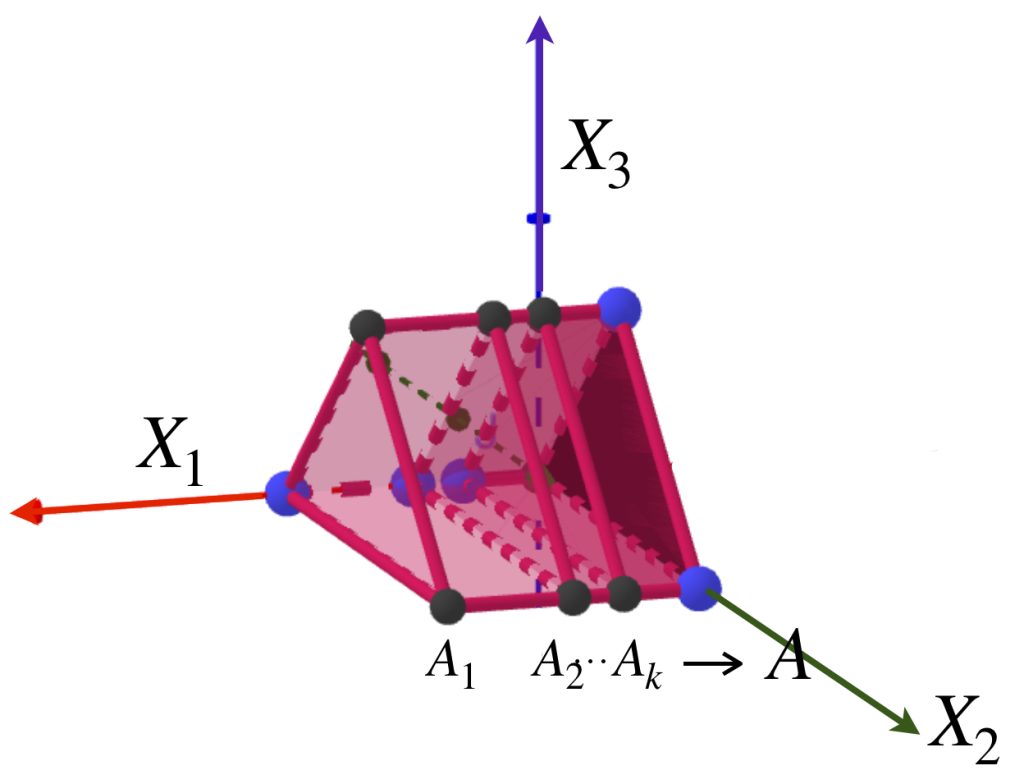
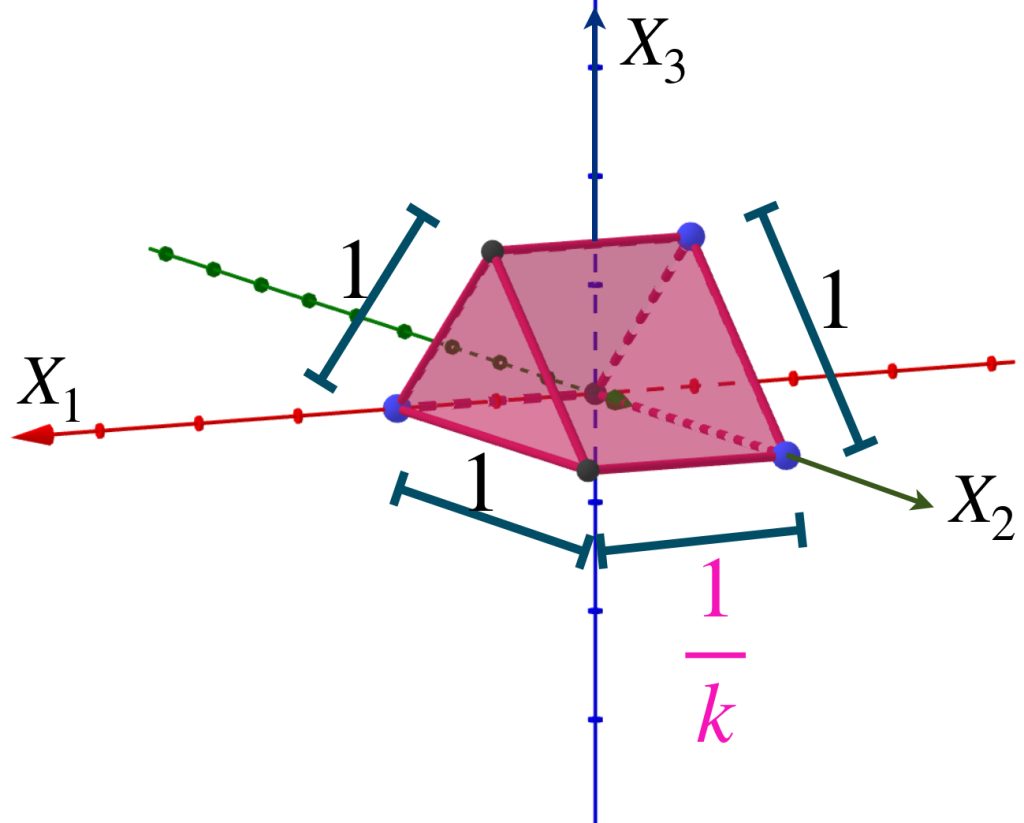
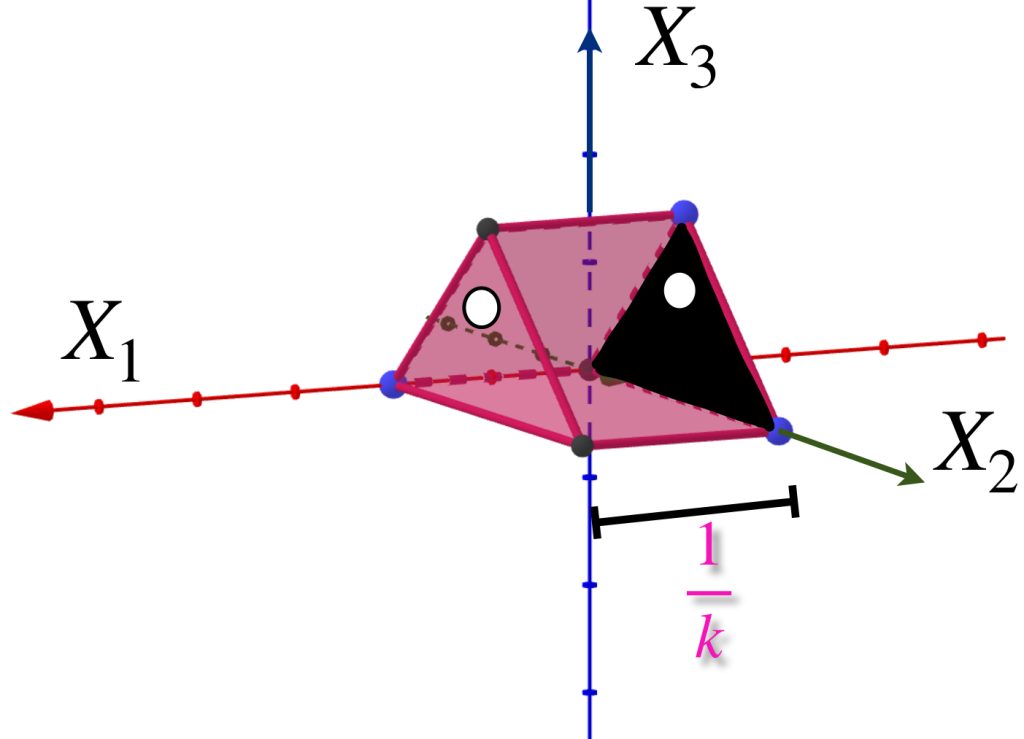
Presentamos una sucesión de prismas ubicadas en el espacio euclidiano $\mathbb{R}^3$ como muestra la imagen.
Sea $A$ el triángulo que es una cara del prisma y está en el plano $X_2, X_3$. Nota que para cada $k \in \mathbb{N}$, $d_{H}(A_k,A) = max\{\underset{a \in A_k}{sup} \, \text{dist}(a,A),\underset{b \in B}{sup} \, \text{dist}(b,A_k)\}= \frac{1}{k}$
Entonces $d_{H}(A_n,A) = \frac{1}{n} \to 0 \in \mathbb{R}$ por lo tanto $A_n \to A$.
La demostración de las siguientes dos sucesiones se dejará como ejercicio.
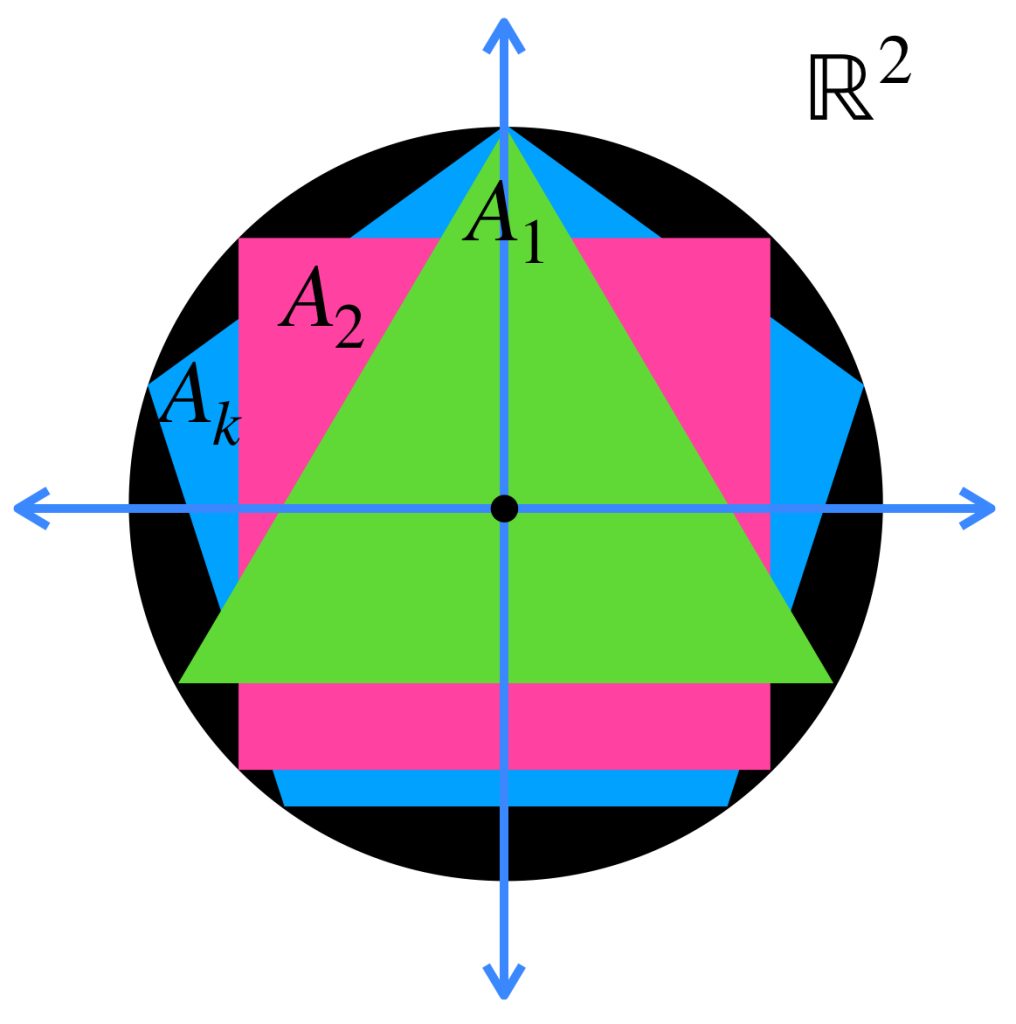
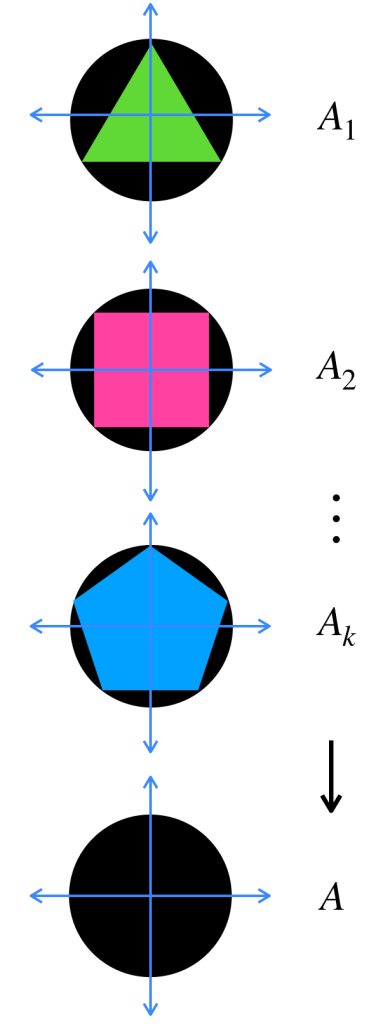
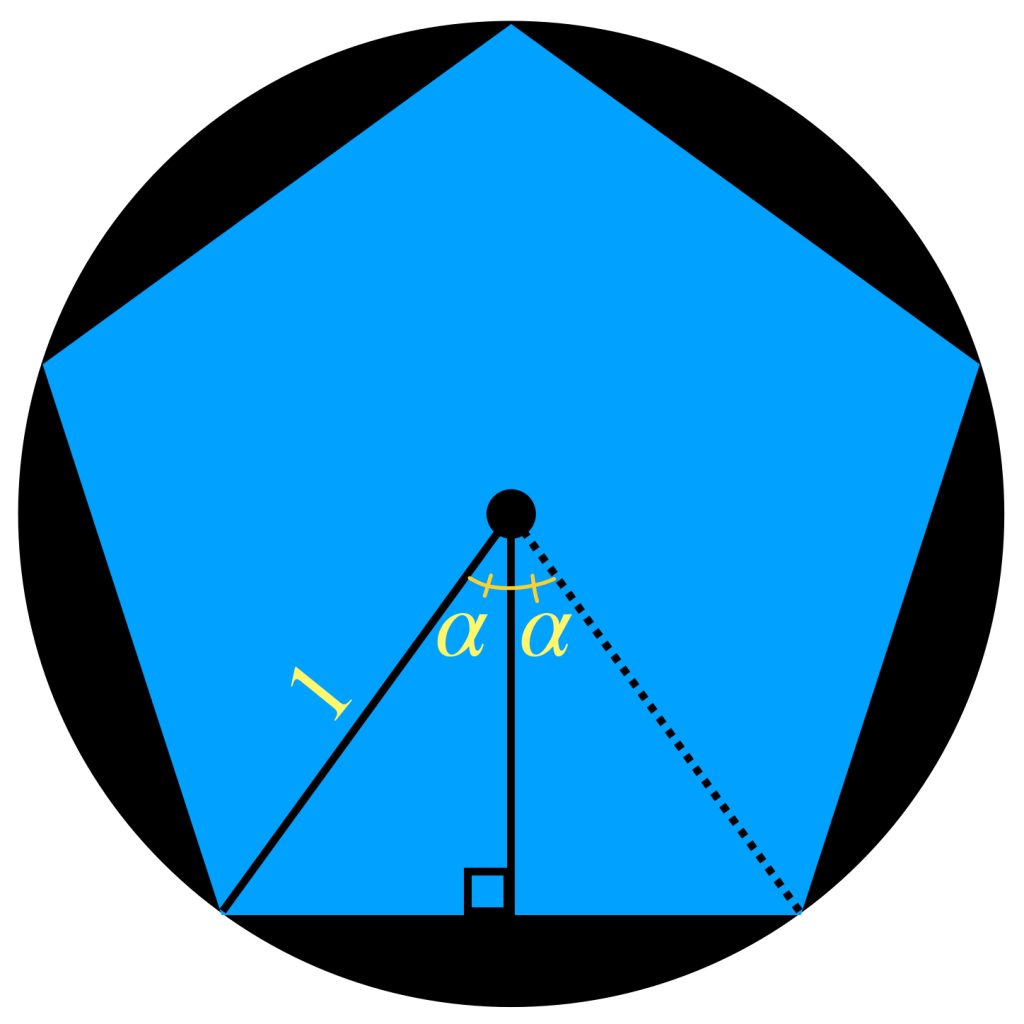
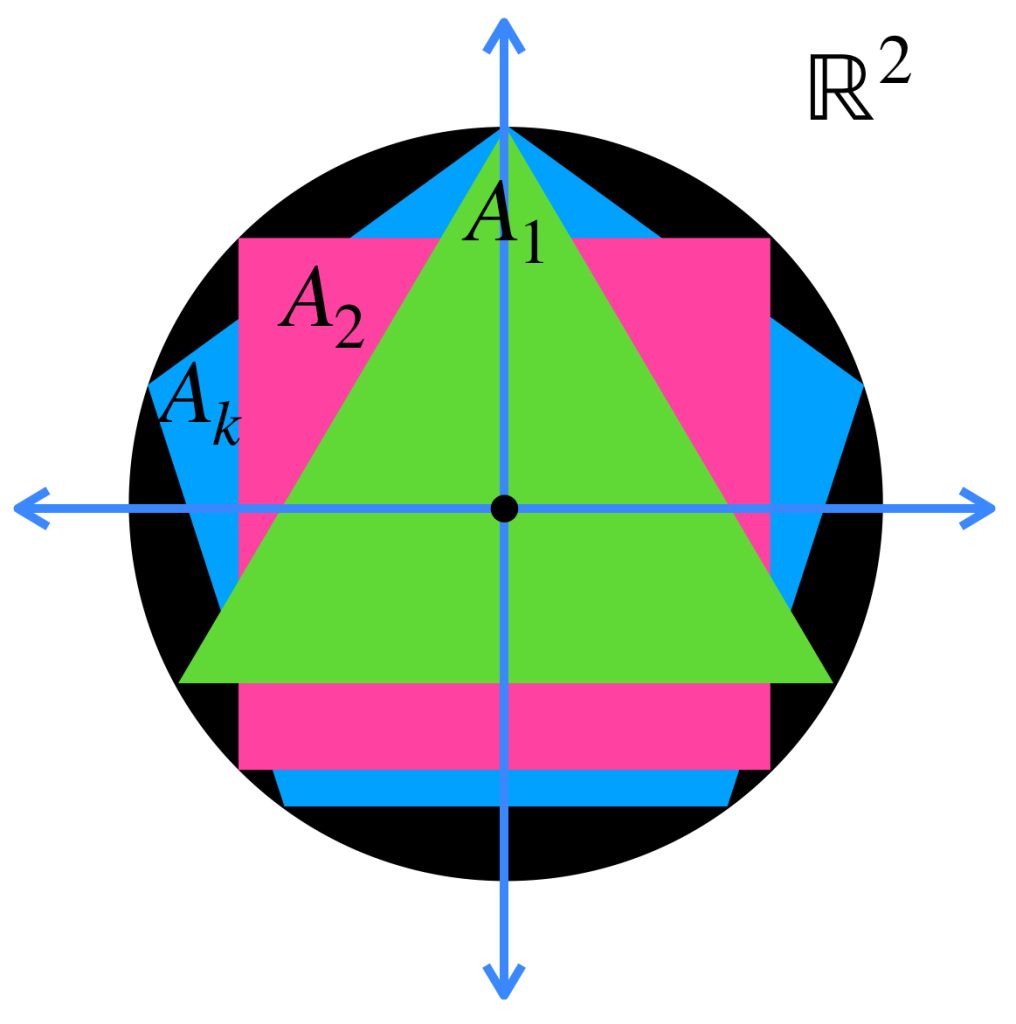
Tenemos una sucesión de polígonos regulares en $\mathbb{R}^2$ $(A_n)_{n \in \mathbb{N}} \,$ donde, para cada natural $n$, $ A_n$ es el polígono regular de $\, n \,$ lados con centro en $(0,0)$ y circunscrito en el círculo con centro en $(0,0)$ y radio $1$. Demuestra que $A_n \to \overline{B}(0,1)$ en el espacio de Hausdorff.
Como sugerencia, puedes demostrar que la medida del apotema vista como $\, cos \alpha \,$ tiende a $1$ en $\mathbb{R}$.
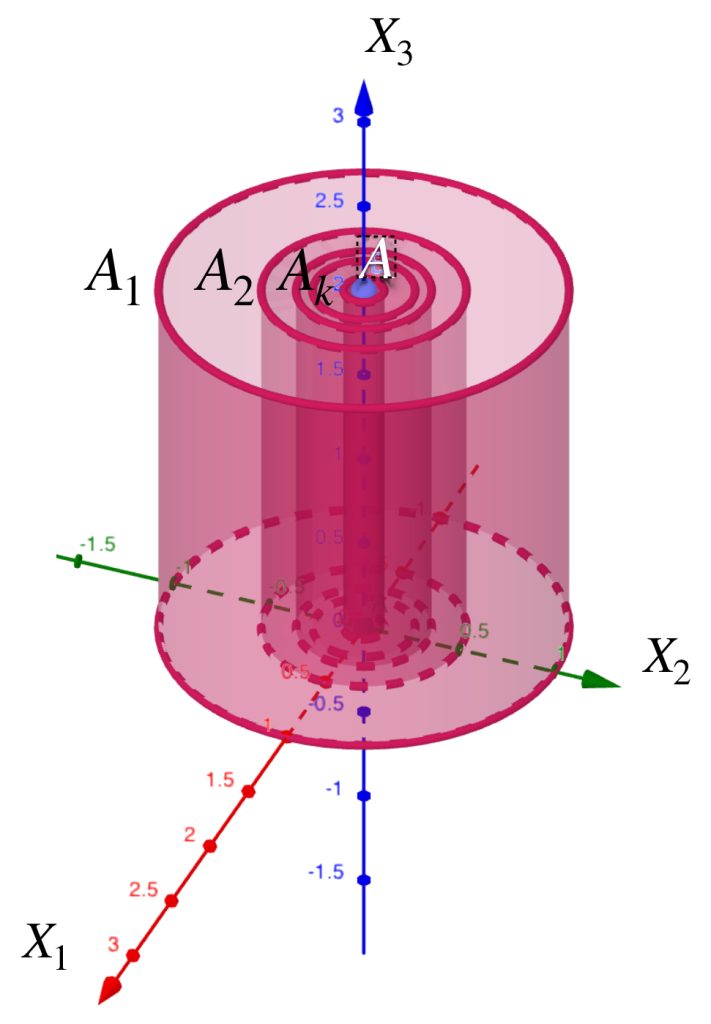
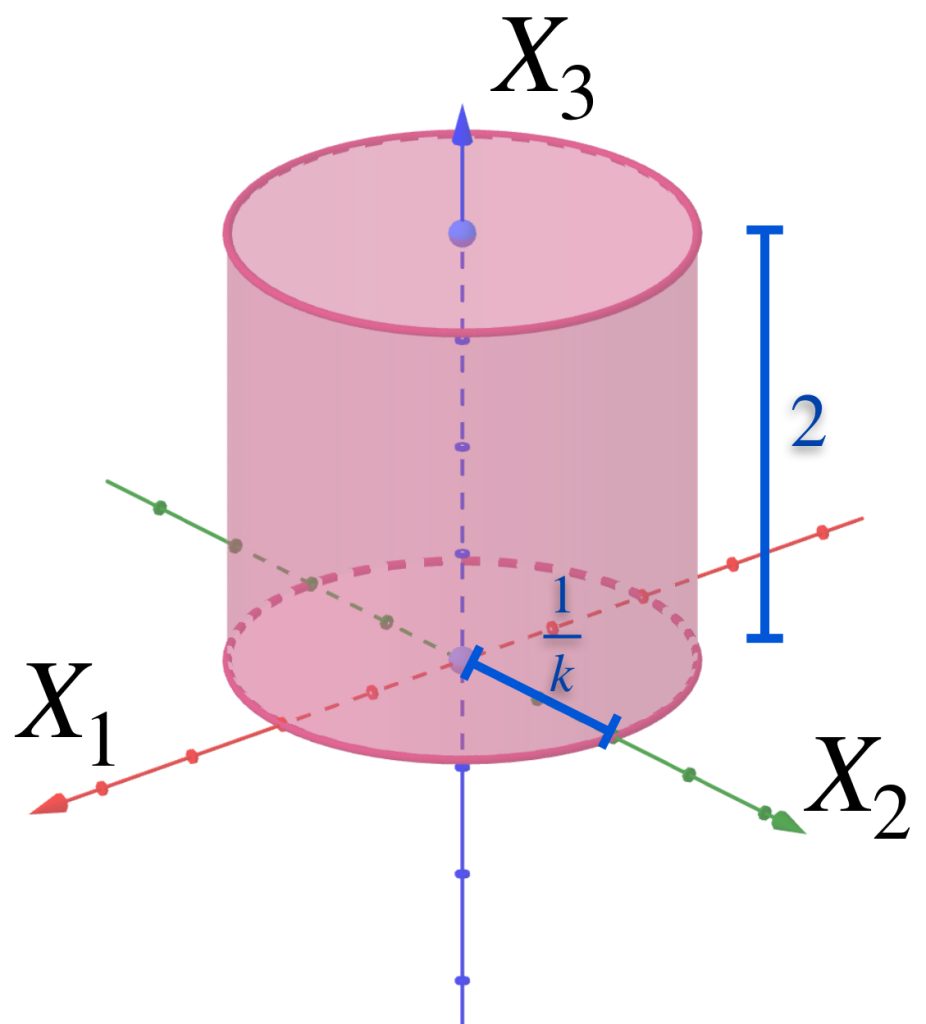
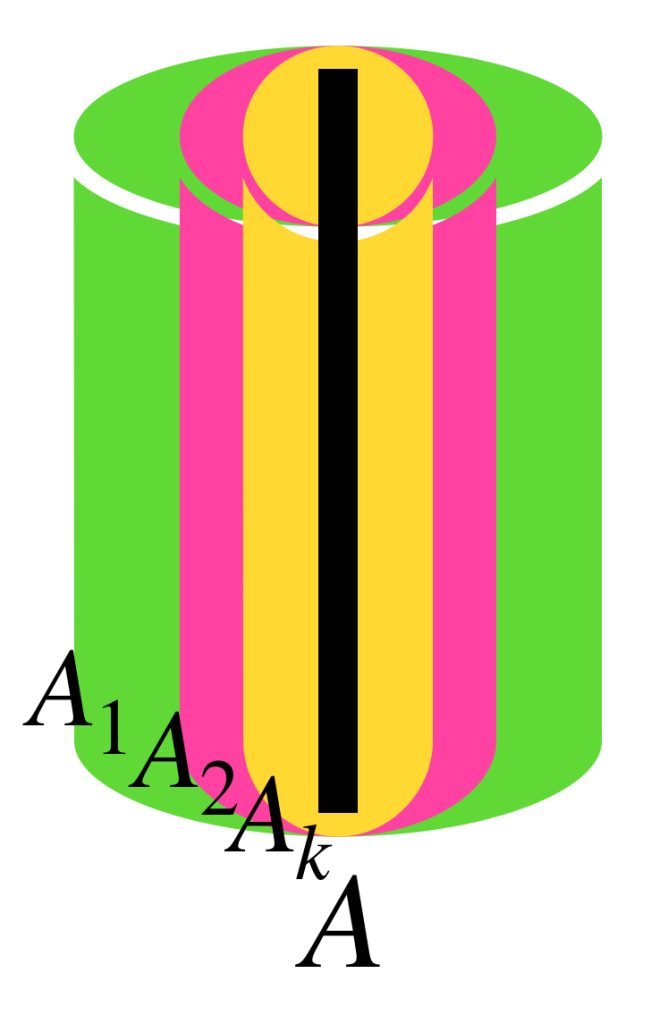
La siguiente sucesión muestra cilindros en $\mathbb{R}^3$.
Para cada $n \in \mathbb{N}$ considera $A_n$ como el cilindro que tiene de base al círculo con centro en el origen, radio $\frac{1}{n}$ y altura $2$. Demuestra que la sucesión $(A_n)_{n \in \mathbb{N}}\,$ converge al segmento $\{(0,0,x_3): x_3 \in [0,2]\}$.
Ahora presentaremos algunas condiciones que garantizan la convergencia en sucesiones de conjuntos. En la última se menciona la noción de compacidad, concepto del que se hablará en entradas próximas. Por el momento podemos imaginar el resultado en espacios euclidianos, donde los compactos son los conjuntos cerrados y acotados.
Proposición: Sea $(A_n)_{n \in \mathbb{N}}$ una sucesión en $\mathcal{M}(X)$ tal que $A_n \to A$ en $\mathcal{M}(X)$. Entonces:
a) $A$ es el conjunto de límites de todas las sucesiones convergentes $(x_n)_{n \in \mathbb{N}}$ en $X$ tales que para toda $n \in \mathbb{N}, \, a_n \in A_n$.
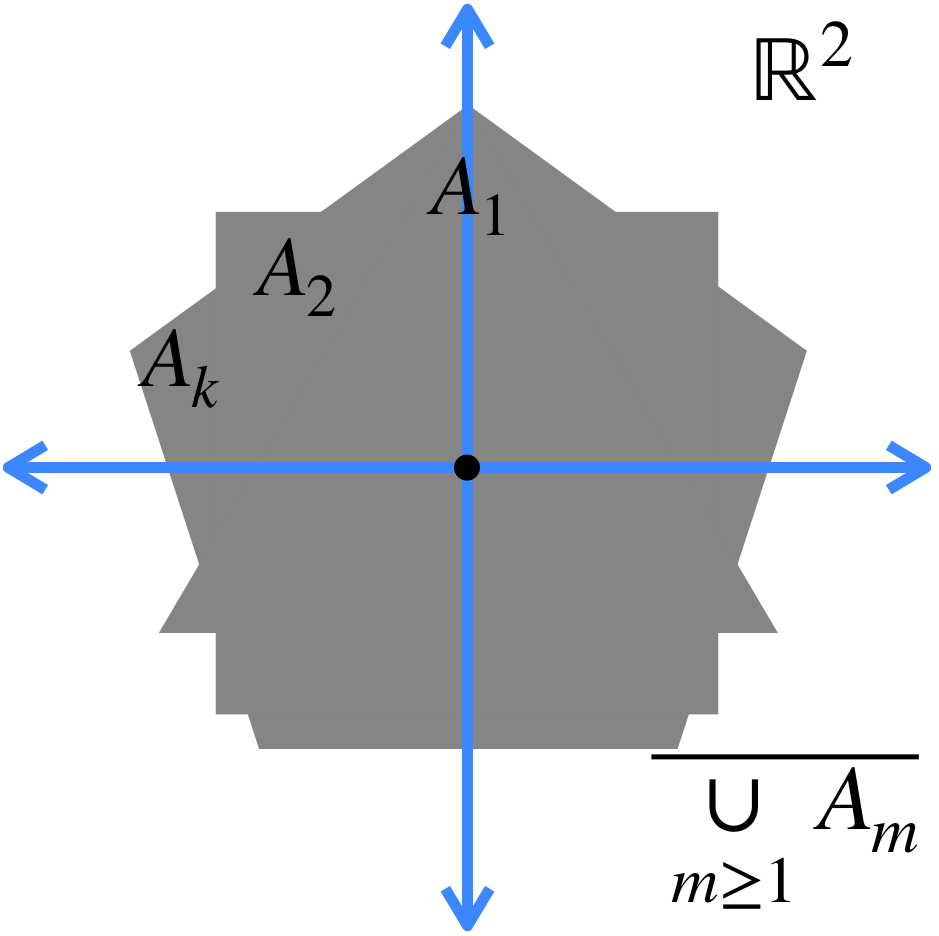
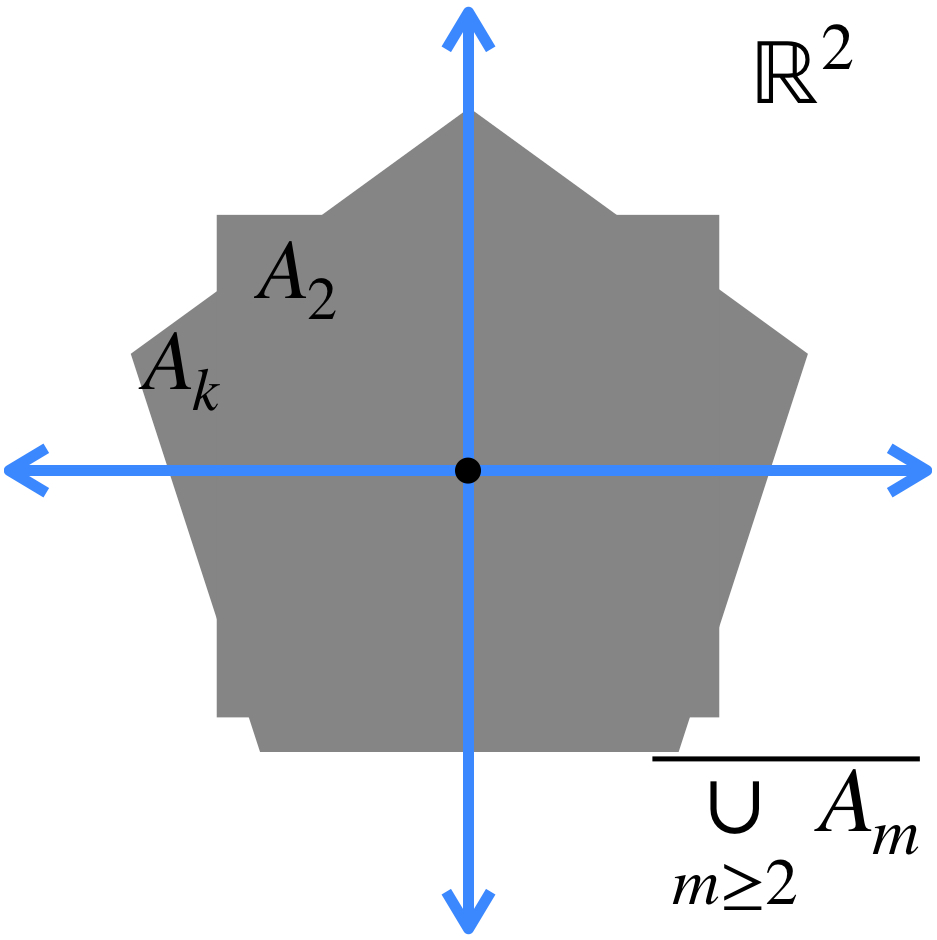
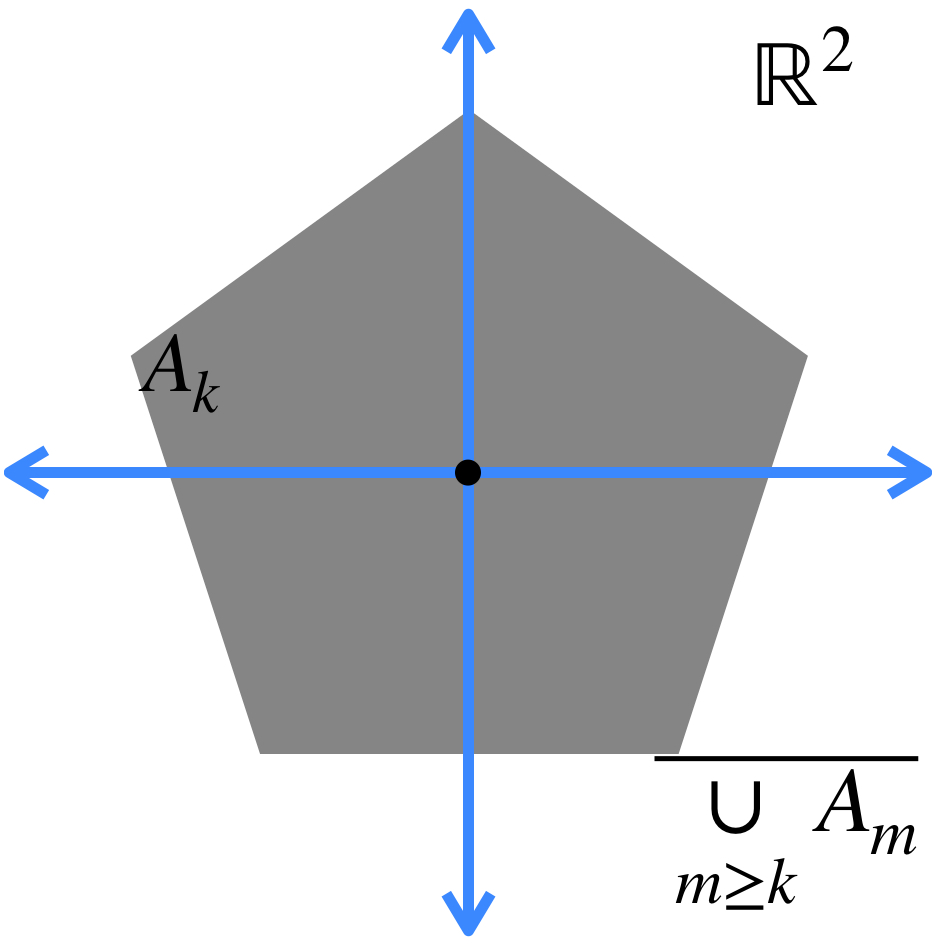
b) El conjunto al que converge la sucesión está dado por: $A = \underset{n \in \mathbb{N}}{\cap} (\overline{\underset{m \geq n}{\cup} A_m})$.
Esto significa que en cada iteración, vamos a considerar la cerradura de la unión de todos los conjuntos, exceptuando los de las primeras posiciones (según la iteración en la que vayamos). Esto define nuevos conjuntos, cuya intersección es el conjunto al que la sucesión converge.
La intersección de todos los conjuntos de este estilo es el conjunto al que la sucesión converge:
Proposición: Sea $(X,d)$ un espacio métrico compacto y $(A_n)_{n \in \mathbb{N}} \,$ una sucesión de subespacios compactos en él, entonces:
a) Si $A_{n+1} \subset A_n$, entonces $A_n \to \underset{n \in \mathbb{N}}{\cap}A_n$ en $\mathcal{M}(X)$.
Entonces cuando una sucesión es tal que cada término está contenido en el anterior, la sucesión converge a la intersección de todos los conjuntos.
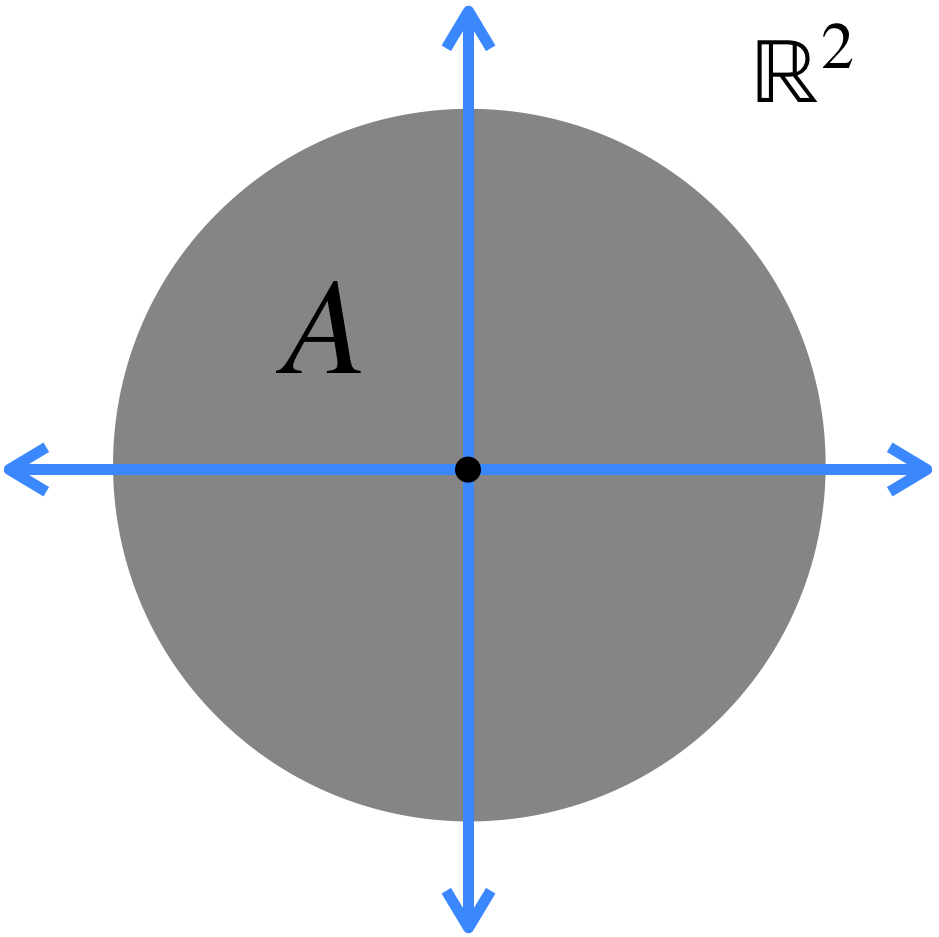
b) Si para todo $n \in \mathbb{N}, \, A_n \subset A_{n+1}$, entonces $A_n \to \overline{\underset{n \in \mathbb{N}}{\cup}A_n}$ en $\mathcal{M}(X)$.
Entonces cuando una sucesión es tal que cada término contiene al anterior, la sucesión converge a la cerradura de la unión de todos los conjuntos.
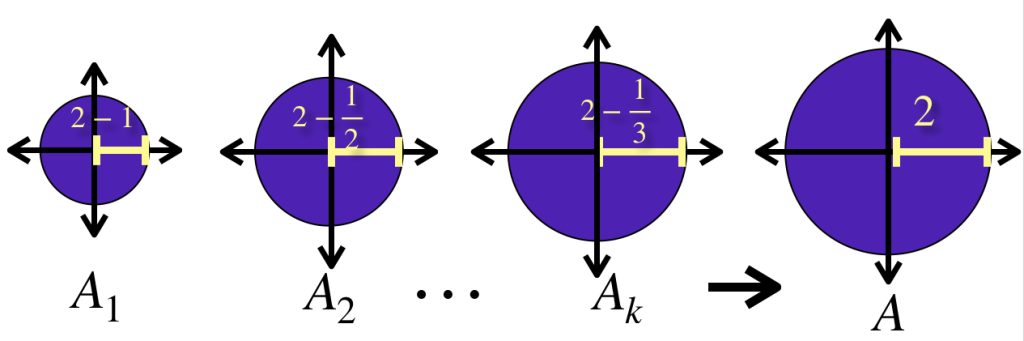
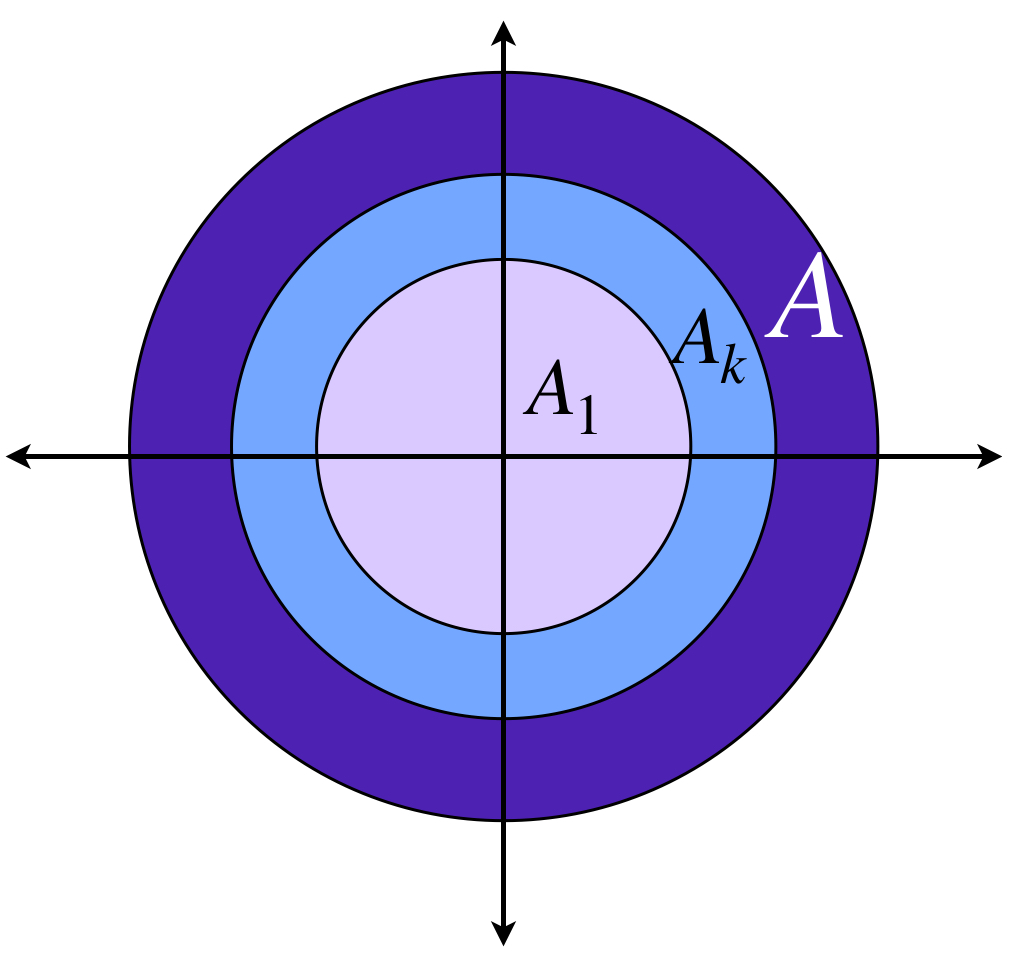
En el dibujo la sucesión $(A_n)_n \in \mathbb{N}$ tiene como conjunto $A_n = \overline{B}(0,2-\frac{1}{n})$ para cada $n \in \mathbb{N}$. Es sencillo demostrar que $A_n \to \overline{B}(0,2)$ en $\mathbb{R}^2.$
Más adelante…
Ya que hemos estudiado algunas propiedades en un espacio métrico, comenzaremos a relacionar un espacio con otros a través de funciones. Veremos bajo qué circunstancias es posible hablar de “cercanía” en puntos del contradominio cuando se parte de puntos cercanos en el espacio métrico del dominio.
Tarea moral
- Describe las características de las sucesión definida como:
$A_1=[0,1]$
$A_2=[0,1] \setminus (\frac{1}{3},\frac{2}{3})=[0,\frac{1}{3}] \cup [\frac{2}{3},1],$
$A_3=[0,\frac{1}{3}] \setminus (\frac{1}{9},\frac{2}{9}) \cup [\frac{2}{3},1]\setminus (\frac{7}{9},\frac{8}{9})=[0,\frac{1}{9}] \cup [\frac{2}{9},\frac{1}{3}] \cup [\frac{2}{3},\frac{7}{9}] \cup[\frac{8}{9},1]$
Y así, recursivamente, se va quitando la tercera parte central, de cada intervalo que quedaba. La intersección de estos conjuntos es conocido como el conjunto de Cantor. ¿Bajo qué resultados mencionados en esta entrada podemos concluir la convergencia de la sucesión? - El copo de nieve de Koch es la curva a la que converge una sucesión definida como sigue:
$A_1$ es un triángulo equilátero.
$A_2$ sustituye la tercera parte central de cada lado por dos aristas de la misma medida.
$A_3$ Hace lo mismo. Se repite el proceso recursivamente
¿Qué puedes decir del área encerrada por las curvas a medida que la sucesión aumenta? ¿Hay condiciones suficientes para concluir la convergencia de estos conjuntos? - Demuestra la convergencia en el espacio de Hausdorff de la sucesión de polígonos circunscritos descrita anteriormente.
- Demuestra la convergencia en el espacio de Hausdorff de la sucesión de cilindros expresada anteriormente.