Archivo de la etiqueta: teoría de los conjuntos

Teoría de los Conjuntos I: Conjuntos infinitos no numerables.

Por Gabriela Hernández Aguilar

Deja un comentario

Introducción

Al hablar de conjuntos infinitos, resulta natural pensar que entre cualesquiera dos de ellos debería existir una manera de «emparejar» sus elementos, es decir, establecer una biyección entre tales conjuntos, ya que, al fin y al cabo, ambos contienen infinitos elementos. Esta idea puede deberse a que, cuando uno piensa en conjuntos infinitos, lo primero que viene a la mente es el conjunto de los números naturales o el de los enteros, los cuales están ordenados de una manera bastante agradable y nos resulta «fácil» ubicarlos en una recta, como si fueran números colocados sobre una cinta métrica infinita.

Sin embargo, no todos los conjuntos infinitos poseen un orden tan agradable como el de estos dos conjuntos, y muchos de ellos presentan propiedades considerablemente diferentes. Por ejemplo, algunos conjuntos infinitos pueden no tener un buen orden como el de los naturales, o quizás exista tal orden pero nos resulte extremadamente difícil de identificar.

El teorema de Cantor demuestra que, efectivamente, la idea de que se pueden emparejar los elementos de cualesquiera dos conjuntos infinitos es incorrecta. Un ejemplo específico es el conjunto de los números naturales $\mathbb{N}$ y su conjunto potencia $\mathcal{P}(\mathbb{N})$; es imposible emparejar cada elemento de $\mathcal{P}(\mathbb{N})$ con uno y solo un elemento de $\mathbb{N}$. Este hecho muestra que existen conjunto infinitos más grandes que otros.

Esta entrada está dedicada precisamente a esta cuestión: exhibir conjuntos infinitos con «diferentes tamaños», específicamente, conjuntos que no sean numerables, es decir, que no sean equipotentes con $\mathbb{N}$. Como hemos venido haciendo, también emplearemos el muy importante teorema de Cantor-Schröder-Bernstein para probar ciertas equipotencias.

Conjuntos más grandes que $\mathbb{N}$

Por el teorema de Cantor sabemos que para cada conjunto $A$ se tiene $|A|<|\mathcal{P}(A)|$, es decir, que existe una función inyectiva de $A$ en $\mathcal{P}(A)$ pero no una función biyectiva. Así pues, por ejemplo, $\mathcal{P}(\mathbb{N})$ además de ser un conjunto infinito, tiene «más» elementos que $\mathbb{N}$, el cual es también infinito. Esto es una muestra de que existen conjuntos infinitos que no son equipotentes. En lo subsecuente exhibiremos algunos otros conjuntos infinitos que sí se pueden biyectar con $\mathcal{P}(\mathbb{N})$ y que por tanto no son numerables.

Comenzaremos proporcionando ejemplos que involucran conceptos que hemos visto en la entrada anterior.

Ejemplo.

El conjunto de sucesiones en $\mathbb{N}$, que denotaremos por $\mathbb{N}^{\mathbb{N}}$, es equipotente a $\mathcal{P}(\mathbb{N})$.

Demostración.

En la entrada anterior probamos que para cada $A\subseteq\mathbb{N}$ infinito, existe una única función biyectiva $F_A:\mathbb{N}\to A$ tal que $F_A(0)=\textnormal{min}(A)$ y que $F_A(n)<F_A(n+1)$ para cada $n\in\mathbb{N}$. Lo mismo mencionamos respecto a conjuntos finitos no vacíos, es decir, si $A\subseteq\mathbb{N}$ es un conjunto finito no vacío, digamos $|A|=n+1$ con $n\in\mathbb{N}$, existe una única función biyectiva $f_A:n+1\to A$ tal que $f_A(0)=\textnormal{min}(A)$ y que $f_A(m)<f_A(k)$ si y sólo si $m<k$ para cualesquiera $m,k\in n+1$.
Si $A\subseteq\mathbb{N}$ es finito, podemos extender la función $f_A$ a todo $\mathbb{N}$ de la siguiente manera: si $f_A:n+1\to A$ es la única función biyectiva que satisface $f_A(0)=\textnormal{min}(A)$ y $f_A(m)<f_A(k)$ si y sólo si $m<k$ para cualesquiera $m,k\in n+1$, definimos $F_A:\mathbb{N}\to A$ por medio de $$F_A(m)=\left\{\begin{array}{lcc}
f_A(m) & \textnormal{si}\ m\in n+1\\
\textnormal{min}(A) & \textnormal{si}\ m\notin n+1
\end{array}
\right.$$

Lo anterior nos permite asociar a cada elemento de $\mathcal{P}(\mathbb{N})\setminus\{\emptyset\}$ una única sucesión en $\mathbb{N}^{\mathbb{N}}$ por medio de la siguiente función: definamos $F:\mathcal{P}(\mathbb{N})\setminus\{\emptyset\}\to\mathbb{N}^{\mathbb{N}}$ como $F(A)=F_A$ para cada $A\in\mathcal{P}(\mathbb{N})$. Debido a la definición de las funciones $F_A$, en cualquier caso, ya sea que $A\subseteq\mathbb{N}$ es finito o infinito, se cumple que $F_A[\mathbb{N}]=A$; en consecuencia, si $A$ y $B$ son conjuntos no vacíos tales que $F(A)=F(B)$ tendríamos que para cada $k\in\mathbb{N}$, $F_A(k)=F_B(k)$ y, por ende, que $A=F_A[\mathbb{N}]=F_B[\mathbb{N}]=B$, lo cual muestra que $F$ es inyectiva.

Ahora bien, para cada $x\in\mathbb{N}^{\mathbb{N}}$ definamos $x+1:\mathbb{N}\to\mathbb{N}$ por medio de $(x+1)(n):=x(n)+1$ para cada $n\in\mathbb{N}$. La función $g:\mathbb{N}^{\mathbb{N}}\to\mathbb{N}^{\mathbb{N}}$ definida por medio de $g(x)=x+1$ es una función inyectiva, pues si $g(x)=g(y)$ para algunas $x,y\in\mathbb{N}^{\mathbb{N}}$, entonces, $x(n)+1=y(n)+1$ para cada $n\in\mathbb{N}$ y, por tanto, $x(n)=y(n)$ para cada $n\in\mathbb{N}$, es decir, $x=y$. Observemos además que $g(x)\not=x_0$ para cada $x\in\mathbb{N}^{\mathbb{N}}$, donde $x_0(n)=0$ para cada $n\in\mathbb{N}$; en efecto, si $x\in\mathbb{N}^{\mathbb{N}}$, entonces, $g(x)(n)=(x+1)(n)=x(n)+1\not=0$ para cada $n\in\mathbb{N}$ ya que $0$ no es sucesor de ningún número natural. Así, la función $g\circ F:\mathcal{P}(\mathbb{N})\setminus\set{\emptyset}\to\mathbb{N}^{\mathbb{N}}$ es inyectiva y $(g\circ F)(A)\not=x_0$ para cada $A\in\mathcal{P}(\mathbb{N})\setminus\{\emptyset\}$. Por tanto la función $h:\mathcal{P}(\mathbb{N})\to\mathbb{N}^{\mathbb{N}}$ definida como \[h(A)=\left\{\begin{array}{lcc}
(g\circ F)(A) & \textnormal{si}\ A\not=\emptyset\\
x_0 & \textnormal{si}\ A=\emptyset
\end{array}
\right.\] es inyectiva.

Para dar una función inyectiva de $\mathbb{N}^{\mathbb{N}}$ en $\mathcal{P}(\mathbb{N})$ retomaremos al conjunto de números primos $\mathbb{P}=\{p_n:n\in\mathbb{N}\}$ enumerado de tal forma que $p_n<p_{n+1}$ para cada $n\in\mathbb{N}$. Definamos ahora $T:\mathbb{N}^{\mathbb{N}}\to\mathcal{P}(\mathbb{N})$ por medio de $T(x)=\{p_n^{x(n)}:n\in\mathbb{N}\}$. Notemos que $T$ es una función inyectiva, pues si $T(x)=T(y)$, entonces, $\{p_n^{x(n)}:n\in\mathbb{N}\}=\{p_n^{y(n)}:n\in\mathbb{N}\}$ y así $p_n^{x(n)}=p_n^{y(n)}$ y $x(n)=y(n)$ para cada $n\in\mathbb{N}$, pues de otro modo se contradice al teorema fundamental de la aritmética. Por lo tanto, $x=y$ y $T$ es inyectiva.

Por el teorema de Cantor-Schröder-Bernstein concluimos que $|\mathcal{P}(\mathbb{N})|=|\mathbb{N}^{\mathbb{N}}|$.

$\square$

Al contrario de los conjuntos finitos, existen ejemplos de conjuntos infinitos que poseen subconjuntos propios equipotentes a ellos mismos, es decir, existe una biyección entre el subconjunto propio y el conjunto original. Un ejemplo de lo anterior es el conjunto de los números naturales, pues cualquier subconjunto propio de $\mathbb{N}$ que sea infinito resulta ser numerable. A continuación vamos a proporcionar otro de estos ejemplos, pero esta vez con un conjunto infinito no numerable.

Ejemplo.

El conjunto $2^{\mathbb{N}}:=\{f\in\mathbb{N}^{\mathbb{N}}:f(n)\in\{0,1\}\ \textnormal{para cada}\ n\in\mathbb{N}\}$ es equipotente a $\mathcal{P}(\mathbb{N})$.

Demostración.

Para demostrar la equipotencia de este ejemplo vamos a exhibir una biyección entre tales conjuntos. Para ello haremos lo siguiente, si $A\in\mathcal{P}(\mathbb{N})$ definimos $\chi_{A}:\mathbb{N}\to\mathbb{N}$ por medio de $\chi_{A}(n)=\left\{\begin{array}{lcc}
1 & \textnormal{si}\ n\in A\\
0 & \textnormal{si}\ n\in\mathbb{N}\setminus A
\end{array}
\right.$

Lo anterior nos permite establecer una función entre $\mathcal{P}(\mathbb{N})$ y $2^{\mathbb{N}}$, función que de hecho resulta ser biyectiva. Veamos primero la inyectividad. Si para $A,B\in\mathcal{P}(\mathbb{N})$ se cumple $\chi_A=\chi_B$, entonces $\chi_A(n)=\chi_B(n)$ para cada $n\in\mathbb{N}$. En consecuencia, si $n\in A$, $1=\chi_A(n)=\chi_B(n)$ y por ende $n\in B$; análogamente, si $n\in B$, $1=\chi_B(n)=\chi_A(n)$ y por tanto $n\in A$. Por consiguiente $A=B$, lo que demuestra la inyectividad de la función.
Resta probar la sobreyectividad. Consideremos $\chi\in 2^{\mathbb{N}}$ un elemento arbitrario. Definamos $A:=\{n\in\mathbb{N}:\chi(n)=1\}$ y veamos que $\chi_A=\chi$. Si $n\in A$, entonces $\chi(n)=1$ por definición del conjunto $A$ y, por otro lado, $\chi_A(n)=1$ por definición de la función $\chi_A$. Si ahora $n\in\mathbb{N}\setminus A$, $\chi(n)=0$ por definición del conjunto $A$ mientras que $\chi_A(n)=0$ por definición de la función $\chi_A$. Esto muestra que $\chi(n)=\chi_A(n)$ para cada $n\in\mathbb{N}$ y por ende que $\chi=\chi_A$. Así pues, la función $F:\mathcal{P}(\mathbb{N})\to2^{\mathbb{N}}$ definida por medio de $F(A)=\chi_A$ para cada $A\in\mathcal{P}(\mathbb{N})$ es una biyección y, por tanto, $|\mathcal{P}(\mathbb{N})|=|2^{\mathbb{N}}|$.

$\square$

Como lo mencionamos previamente, ahora contamos con un ejemplo de un conjunto infinito no numerable que posee un subconjunto propio equipotente a él, específicamente $\mathbb{N}^{\mathbb{N}}$ y $2^{\mathbb{N}}$ son equipotentes y $2^{\mathbb{N}}\subsetneq\mathbb{N}^{\mathbb{N}}$. Conjuntos de este tipo, es decir, conjuntos que poseen subconjuntos propios equipotentes a ellos, reciben un nombre particular que anotamos en la siguiente definición.

Definición. Un conjunto $X$ se llama infinito según Dedekind si existe una función inyectiva $f:X\to X$ tal que $f[X]\not=X$.

Que un conjunto sea infinito según Dedekind implica que dicho conjunto es infinito. Y ya que contamos con algunos ejemplos de conjuntos infinitos que también son infinitos según Dedekind, surge de manera natural la pregunta: ¿todo conjunto infinito es infinito según Dedekind? Dicha cuestión no la podemos responder con lo que hemos visto hasta ahora y es por eso que la dejaremos para más adelante.

Una consecuencia inmediata del último ejemplo es el siguiente corolario.

Corolario. Sean $a_0,a_1,\ldots,a_n\in\mathbb{N}$ naturales distintos con $n\geq1$. El conjunto $\{f\in\mathbb{N}^{\mathbb{N}}:f[\mathbb{N}]\subseteq\{a_0,a_1,\ldots,a_n\}\}$ es equipotente a $\mathbb{N}^{\mathbb{N}}$.

Demostración.

Dado que $j:\{f\in\mathbb{N}^{\mathbb{N}}:f[\mathbb{N}]\subseteq\{a_0,a_1,\ldots,a_n\}\}\to\mathbb{N}^{\mathbb{N}}$ definida por medio de $j(f)=f$ es una función inyectiva, basta exhibir una función inyectiva de $\mathbb{N}^{\mathbb{N}}$ en $\{f\in\mathbb{N}^{\mathbb{N}}:f[\mathbb{N}]\subseteq\{a_0,a_1,\ldots,a_n\}\}$.

Denotemos $A:=\{f\in\mathbb{N}^{\mathbb{N}}:f[\mathbb{N}]\subseteq\{a_0,a_1,\ldots,a_n\}\}$. Si denotamos $B:=\{f\in\mathbb{N}^{\mathbb{N}}:f[\mathbb{N}]\subseteq\{a_0,a_1\}\}$, entonces $B\subseteq A$. Para cada $\chi\in2^{\mathbb{N}}$ definamos $f_\chi:\mathbb{N}\to\mathbb{N}$ de la siguiente manera $f_\chi(n)=\left\{\begin{array}{lcc}
a_0 & \textnormal{si}\ \chi(n)=0\\
a_1 & \textnormal{si}\ \chi(n)=1
\end{array}
\right.$
A partir de la definición anterior tenemos que $f_{\chi}\in B$ para cada $\chi\in2^{\mathbb{N}}$, lo cual nos permite definir $F:2^{\mathbb{N}}\to B$ por medio de $F(\chi)=f_{\chi}$. Resulta que $F$ es una biyección. En efecto, por un lado es inyectiva ya que si $F(\chi)=F(\chi’)$, entonces $f_{\chi}(n)=f_{\chi’}(n)$ para cada $n\in\mathbb{N}$, de modo que si $\chi(n)=0$ se tiene que $a_0=f_{\chi}(n)=f_{\chi’}(n)$ y por tanto $\chi'(n)=0$; asimismo, si $\chi(n)=1$ se tiene que $a_1=f_{\chi}(n)=f_{\chi’}(n)$ por lo que $\chi'(n)=1$. Por tanto $\chi(n)=\chi'(n)$ para cada $n\in\mathbb{N}$ y así $\chi=\chi’$.
Ahora para mostrar que $F$ es sobreyectiva tomemos $f\in B$ elemento arbitrario y definamos $\chi:\mathbb{N}\to\mathbb{N}$ por medio de $\chi(n)=\left\{\begin{array}{lcc}
1 & \textnormal{si}\ f(n)=a_1\\
0 & \textnormal{si}\ f(n)=a_0
\end{array}
\right.$
Luego, $f_{\chi}=f$, pues si $n\in\mathbb{N}$ es tal que $f(n)=a_1$ se tiene que $\chi(n)=1$ por definición de $\chi$ y así $f_{\chi}(n)=a_1$; por otro lado, si $n\in\mathbb{N}$ es tal que $f(n)=a_0$ se tiene que $\chi(n)=0$ por definición de $\chi$ y por ende $f_{\chi}(n)=a_0$. Podemos concluir entonces que $F( \chi)=f_{\chi}=f$, lo que demuestra que $F$ es sobreyectiva. Por tanto $F$ es una biyección y $|2^{\mathbb{N}}|=|B|$.
Ahora, sean $h:\mathbb{N}^{\mathbb{N}}\to2^{\mathbb{N}}$ una función biyectiva (la cual sabemos que existe pues $|\mathbb{N}^{\mathbb{N}}|=|\mathcal{P}(\mathbb{N})|=|2^{\mathbb{N}}|$) y $\iota:B\to A$ la función inclusión, es decir, $\iota(f)=f$ para cada $f\in B$. Luego, $\iota\circ h:\mathbb{N}^{\mathbb{N}}\to A$ es una función inyectiva.
Por el teorema de Cantor-Schröder-Bernstein concluimos que $|\mathbb{N}^{\mathbb{N}}|=|A|$.

$\square$

Observemos que el corolario muestra que existen una infinidad de subcojuntos propios de $\mathbb{N}^{\mathbb{N}}$ equipotentes a él. Dado que $|\mathcal{P}(\mathbb{N})|=|\mathbb{N}^{\mathbb{N}}|$, entonces $\mathcal{P}(\mathbb{N})$ también posee una cantidad infinita de subconjuntos propios equipotentes a él. El siguiente ejemplo es uno de tales subconjuntos.

Ejemplo.

El conjunto $[\mathbb{N}]^{\mathbb{N}}:=\{A\subseteq\mathbb{N}:|A|=|\mathbb{N}|\}$ es equipotente a $\mathcal{P}(\mathbb{N})$.

Demostración.

Dado que $[\mathbb{N}]^{\mathbb{N}}\subseteq\mathcal{P}(\mathbb{N})$ lo único que hace falta es exhibir una función inyectiva de $\mathcal{P}(\mathbb{N})$ en $[\mathbb{N}]^{\mathbb{N}}$.

Consideremos al conjunto de números primos $\mathbb{P}=\{p_n:n\in\mathbb{N}\}$ donde $p_n<p_{n+1}$ para cada $n\in\mathbb{N}$. Definamos $g:\mathbb{N}^{\mathbb{N}}\to[\mathbb{N}]^{\mathbb{N}}$ como $g(x)=\{p_n^{x(n)+1}:n\in\mathbb{N}\}$. Dado que para cada $x\in\mathbb{N}^{\mathbb{N}}$, $x(n)+1\not=0$ para toda $n\in\mathbb{N}$, tenemos que $\{p_n^{x(n)+1}:n\in\mathbb{N}\}$ es un conjunto infinito, por lo que $g$ tiene el codominio adecuado. Por otro lado, $g$ es inyectiva ya que si $g(x)=g(y)$, entonces $p_n^{x(n)+1}=p_n^{y(n)+1}$ para cada $n\in\mathbb{N}$ por el teorema fundamental de la aritmética y, más aún, $x(n)+1=y(n)+1$ para cada $n\in\mathbb{N}$, lo que demuestra que $x=y$. Si $h:\mathcal{P}(\mathbb{N})\to\mathbb{N}^{\mathbb{N}}$ es una biyección se sigue que $g\circ h:\mathcal{P}(\mathbb{N})\to[\mathbb{N}]^{\mathbb{N}}$ es una función inyectiva. Por el teorema de Cantor-Schröder-Bernstein concluimos que $|\mathcal{P}(\mathbb{N})|=|[\mathbb{N}]^{\mathbb{N}}|$.

$\square$

Como un ejercicio para esta entrada dejaremos el siguiente ejemplo.

Ejemplo.

$\mathbb{N}^{\nearrow\mathbb{N}}:=\{f\in\mathbb{N}^{\mathbb{N}}:f(n)<f(n+1)\ \textnormal{para cada}\ n\in\mathbb{N}\}$ es equipotente a $[\mathbb{N}]^{\mathbb{N}}$, y por tanto equipotente a $\mathcal{P}(\mathbb{N})$.

Para finalizar con esta serie de ejemplos de conjuntos no numerables y equipotentes a $\mathcal{P}(\mathbb{N})$ hablaremos del conjunto de números reales.
Para lo que sigue vamos a suponer que ya conocemos todas las propiedades básicas del conjunto de números reales, y si no se conocen dichas propiedades o lo que es un número real, puedes consultar cualquier libro introductorio a la teoría de conjuntos como el de Hernández1, o también puedes consultarlo en un libro de cálculo como el de Spivak2.
Además de lo dicho en el párrafo precedente, estaremos haciendo un abuso de notación escribiendo las contenciones $\mathbb{N}\subseteq\mathbb{Z}\subseteq\mathbb{Q}\subseteq\mathbb{R}$.
Dicho lo anterior tenemos la siguiente proposición.

Proposición. El intervalo abierto $(0,1)=\{r\in\mathbb{R}:0<r<1\}$ es equipotente a $\mathbb{R}$.

Demostración.

Definamos $f:\mathbb{R}\to(0,1)$ por medio de $f(x)=\left\{\begin{array}{lcc}
\frac{4x+1}{4x+2} & \textnormal{si}\ x\geq0\\
\frac{1}{2(1-2x)} & \textnormal{si}\ x<0
\end{array}
\right.$
Lo primero que se debe observar es que la función $f$ tiene el codominio adecuado, es decir, $f(x)\in(0,1)$ para cada $x\in\mathbb{R}$. Si $x\geq0$, entonces, $0<4x+1<4x+2$ y por tanto $0<\frac{4x+1}{4x+2}<1$, es decir, $f(x)\in(0,1)$; por otro lado, si $x<0$, entonces $0<-2x$ y así $1<1-2x$, lo cual implica que $0<\frac{1}{1-2x}<1$ y que $0<\frac{1}{2(1-2x)}<\frac{1}{2}<1$, es decir, $f(x)\in(0,1)$. Por tanto, $f(x)\in(0,1)$ para cada $x\in\mathbb{R}$. Es importante notar que para $x<0$ vimos que no sólo se cumple $0<f(x)<1$, sino también que $0<f(x)<\frac{1}{2}$. Por otro lado, para $x\geq0$, tenemos que $0<1+2x\leq1+4x$ por lo que $1\leq\frac{4x+1}{2x+1}$ y por tanto $\frac{1}{2}\leq\frac{4x+1}{4x+2}$; de modo que para $x\geq0$ no sólo se cumple que $f(x)\in(0,1)$, sino también que $f(x)\in[\frac{1}{2},1)$.
Veamos ahora que $f$ es una función inyectiva. Sean $x,y\in\mathbb{R}$ con $x\not=y$. Debido a que $\mathbb{R}$ posee un orden lineal podemos suponer que $y<x$. Tenemos los siguientes casos.
Caso 1. $y<0\leq x$. En este caso se tiene que $f(y)\in(0,\frac{1}{2})$ mientras que $f(x)\in[\frac{1}{2},1)$, razón por la cual $f(x)\not=f(y)$.
Caso 2. $0\leq y<x$. En este caso se tiene que $f(y)=\frac{4y+1}{4y+2}$ y $f(x)=\frac{4x+1}{4x+2}$. Luego, si ocurriera que $\frac{4y+1}{4y+2}=\frac{4x+1}{4x+2}$, entonces $(4y+1)(4x+2)=(4x+1)(4y+2)$, lo cual implica $(4y+1)(2x+1)=(4x+1)(2y+1)$, es decir, $8xy+4y+2x+1=8xy+4x+2y+1$ y por ende $2y=2x$, lo cual contradice que $x\not=y$. Por tanto, $f(x)\not=f(y)$.
Caso 3. $y<x<0$. Si ocurriera que $f(x)=f(y)$, entonces $\frac{1}{2(1-2x)}=\frac{1}{2(1-2y)}$ y por ende, $1-2x=1-2y$, de donde $x=y$ y eso contradice la elección de $x$ y $y$. Por tanto $f$ es una función inyectiva.

Veamos ahora que $f$ es sobreyectiva. Sea $r\in(0,1)$. Si $r\in(0,\frac{1}{2})$, entonces $2<\frac{1}{r}$, lo cual implica $\frac{1}{2}<\frac{1}{4r}$ y así $x:=\frac{1}{2}-\frac{1}{4r}$ es un número real menor a $0$; luego, para tal $x$ tenemos que $f(x)=\frac{1}{2(1-2x)}=\frac{1}{2(1-(1-\frac{1}{2r}))}=\frac{1}{2\cdot\frac{1}{2r}}=r$. Si ahora $r\in[\frac{1}{2},1)$, entonces $2r-1\geq0$ y $1-r>0$, por lo que $x:=\frac{2r-1}{4(1-r)}$ es un número real mayor o igual a $0$ para el cual se cumple $f(x)=\frac{4x+1}{4x+2}=\frac{4(\frac{2r-1}{4(1-r)})+1}{4(\frac{2r-1}{4(1-r)})+2}=\frac{\frac{2r-1}{1-r}+1}{\frac{2r-1}{1-r}+2}=\frac{\frac{2r-1+1-r}{1-r}}{\frac{2r-1+2-2r}{1-r}}=\frac{r}{1}=r$. Lo anterior prueba que $f$ es sobreyectiva.

Por lo tanto $f$ es una biyección y $|\mathbb{R}|=|(0,1)|$.

$\square$

Una consecuencia de la proposición anterior es el siguiente corolario.

Corolario. El intervalo $[0,1]:=\{r\in\mathbb{R}:0\leq r\leq1\}$ es equipotente a $\mathbb{R}$.

Demostración.

Dado que $[0,1]\subseteq\mathbb{R}$, basta mostrar que existe una función inyectiva de $\mathbb{R}$ en $[0,1]$. Por la proposición anterior existe una función biyectiva $f:\mathbb{R}\to(0,1)$ y así la función $F:\mathbb{R}\to[0,1]$ definida como $F(x)=f(x)$ para cada $x\in\mathbb{R}$ es inyectiva. Por el teorema de Cantor-Schröder-Bernstein concluimos que $|\mathbb{R}|=|[0,1]|$.

$\square$

Si bien la demostración del corolario anterior fue muy rápida y utilizamos el importante teorema de Cantor-Schröder-Bernstein, siempre resulta interesante determinar una biyección explícita, y precisamente en el caso del corolario anterior lo podemos hacer.

Definamos $S:=\{\frac{1}{n}:n\in\mathbb{N}\setminus\set{0}\}\cup\{0\}$. Definamos $g:[0,1]\to(0,1)$ por medio de $g(x)=\left\{\begin{array}{lcc}
x & \textnormal{si}\ x\notin S\\
\frac{1}{n+2} & \textnormal{si}\ x=\frac{1}{n},\ n\in\mathbb{N}\setminus\{0\}\\
\frac{1}{2} & \textnormal{si}\ x=0
\end{array}
\right.$

La función anterior resulta ser una biyección entre $[0,1]$ y $(0,1)$. Primero veremos que $g$ es inyectiva. Sean $x,y\in[0,1]$ con $x\not=y$. Tenemos algunos casos.

Caso 1. $x,y\notin S$. En este caso $g(x)=x\not=y=g(y)$.
Caso 2. $x\in S$, $y\notin S$. Dado que para cada $z\in S$ se tiene $g(z)\in S$, entonces, $g(x)\in S$ mientras que $g(y)=y\notin S$. Por tanto $g(x)\not=g(y)$.
Caso 3. $x\notin S$, $y\in S$. Análogo al caso $2$.
Caso 4. $x,y\in S$. Si $x=0$ y $y=\frac{1}{n}$ con $n\in\mathbb{N}\setminus\{0\}$, entonces $g(x)=\frac{1}{2}$ y $g(y)=\frac{1}{n+2}$. Como $n\geq1$ se tiene que $n+2\geq3$ y por tanto $\frac{1}{2}\not=\frac{1}{n+2}$, es decir, $g(x)\not=g(y)$. Análogamente, si $y=0$ y $x=\frac{1}{n}$ con $n\in\mathbb{N}\setminus\{0\}$, $g(x)\not=g(y)$. Supongamos ahora que $x=\frac{1}{n}$ y $y=\frac{1}{m}$ con $n,m\in\mathbb{N}\setminus\{0\}$ con $n\not=m$.
Luego, $g(x)=\frac{1}{n+2}\not=\frac{1}{m+2}=g(y)$ pues de lo contrario tendríamos $n+2=m+2$ y $n=m$, lo cual contradice $n\not=m$.
Los cuatro casos anteriores muestran que $g$ es inyectiva.

Veamos ahora que $g$ es sobreyectiva. Sea $x\in(0,1)$. Si $x\in S$, entonces $x=\frac{1}{n}$ con $n\in\mathbb{N}$, $n\geq2$, por lo que existe $m\in\mathbb{N}$ tal que $m+2=n$; si $m=0$, entonces $x=\frac{1}{2}=g(0)$ y si $m>0$, entonces, $g(\frac{1}{m})=\frac{1}{m+2}=\frac{1}{n}=x$.
Si $x\notin S$, entonces $g(x)=x$. Por tanto, $g$ es sobreyectiva y en consecuencia una biyección. Esto muestra que $[0,1]$ y $(0,1)$ son equipotentes y, por tanto, $[0,1]$ y $\mathbb{R}$ son equipotentes. Más aún, contamos con una biyección explícita entre $[0,1]$ y $\mathbb{R}$.

Para exhibir la biyección entre $[0,1]$ y $(0,1)$ utilizamos el hecho de que $[0,1]$ contiene un conjunto numerable, específicamente el conjunto $S=\{\frac{1}{n}:n\in\mathbb{N}\setminus\{0\}\}\cup\{0\}$. Precisamente este hecho fue el que jugó un papel fundamental, pues como veremos en la siguiente proposición, si $X$ es un conjunto infinito que contiene un conjunto numerable, entonces, para cada $A\subseteq X$ conjunto finito, se cumple $|X\setminus A|=|X|$.

Proposición. Sea $X$ un conjunto infinito tal que existe una función inyectiva $f:\mathbb{N}\to X$. Entonces, para cada $A\subseteq X$ conjunto finito, $|X\setminus A|=|X|$.

Demostración.

Como lo mostrarás en los ejercicios de esta sección, basta mostrar que para cada $x\in X$, los conjuntos $X\setminus\{x\}$ y $X$ son equipotentes.

Sea pues $x\in X$. Sea $f:\mathbb{N}\to X$ una función inyectiva y denotemos por $N$ a la imagen de $f$, esto es $N:=im(f)=\{f(n):n\in\mathbb{N}\}$.

Si $x\notin N$, definamos $g:X\to X\setminus\{x\}$ por medio de $g(y)=\left\{\begin{array}{lcc}
y & \textnormal{si}\ y\notin N\cup\{x\}\\
f(0) & \textnormal{si}\ y=x\\
f(n+1) & \textnormal{si}\ y=f(n)
\end{array}
\right.$

Comprobar que esta función es biyectiva es análogo a como lo hicimos con la función biyectiva que exhibimos entre los intervalos $[0,1]$ y $(0,1)$, por lo que lo dejaremos como un ejercicio para esta entrada.

Supongamos ahora que $x\in N$ y sea $n\in\mathbb{N}$ tal que $x=f(n)$. Para este caso definamos $h:X\to X\setminus\{x\}$ por medio de $h(y)=\left\{\begin{array}{lcc}
y & \textnormal{si}\ y\notin N\setminus\{f(m):m<n\}\\
f(m+1) & \textnormal{si}\ y=f(m),\ m\geq n
\end{array}
\right.$

Nuevamente, comprobar que esta función es biyectiva es similar a lo que hemos hecho. Esto nos permite concluir que $|X\setminus\{x\}|=|X|$ para cada $x\in X$.

$\square$

Para culminar la entrada mostraremos que $(0,1)$ y $\mathcal{P}(\mathbb{N})$ son equipotentes y que por tanto $\mathbb{R}$ y $\mathcal{P}(\mathbb{N})$ lo son. Esto lo escribiremos como un teorema.

Teorema. $(0,1)$ y $\mathcal{P}(\mathbb{N})$ son equipotentes.

Demostración.

Primero vamos a mostrar la siguiente afirmación: para cada $r\in(0,1)$, existe una única función $\chi_r:\mathbb{N}\to\mathbb{N}$ que satisface $\chi_r(n)\in\{0,1,2,3,4,5,6,7,8,9\}$ para cada $n\in\mathbb{N}$ y tal que $0\leq x-\sum_{i=0}^{n}\frac{\chi_r(i)}{10^i}<\frac{1}{10^{n}}$.

Sea pues $r\in(0,1)$. Probaremos por inducción que para cada $n\in\mathbb{N}$ existe una única función $\chi^{(n)}_r:n+1\to\mathbb{N}$ tal que $\chi^{(n)}_{r}[n+1]\subseteq\{0,1,2,3,4,5,6,7,8,9\}$ y $0\leq x-\sum_{i=0}^{n}\frac{\chi^{(n)}_{r}(i)}{10^i}<\frac{1}{10^n}$.
Para $n=0$ definamos $\chi^{(0)}_r:1\to\mathbb{N}$ por medio de $\chi^{(0)}_r(0)=0$. Luego, $0\leq r=r-\frac{\chi^{(0)}_r(0)}{10^0}<1=\frac{1}{10^0}$. Si $y:1\to\mathbb{N}$ es otra función tal que $y(0)\in\{0,1,2,3,4,5,6,7,8,9\}$ y $0\leq r-\frac{y(0)}{10^0}<\frac{1}{10^0}$, entonces, $y(0)\leq r<1$ y por tanto $y(0)=0$, ya que el único natural menor a $1$ es $0$. Por tanto, $\chi^{(0)}_r=y$, lo que demuestra que para $n=0$ el enunciado es verdadero.
Supongamos que el resultado es válido para algún $n\geq0$. Sea $\chi^{(n)}_r:n+1\to\mathbb{N}$ la única función de la hipótesis. Primero vamos a demostrar la existencia de una función $\chi^{(n+1)}_r$ con las propiedades deseadas y luego probaremos su unicidad. Dado que $0\leq r-\sum_{i=0}^{n}\frac{\chi^{(n)}_r(i)}{10^i}<\frac{1}{10^{n}}$ se sigue que $0\leq10^n(r-\sum_{i=0}^{n}\frac{\chi^{(n)}_r(i)}{10^i})<1$. Si ocurriera que $ r-\sum_{i=0}^{n}\frac{\chi^{(n)}_r(i)}{10^i}=0$, definimos $\chi^{(n+1)}_r:n+2\to\mathbb{N}$ como $\chi^{(n+1)}_r(i)=\left\{\begin{array}{lcc}
\chi^{(n)}_r(i) & \textnormal{si}\ i\in n+1\\
0 & \textnormal{si}\ i=n+1
\end{array}
\right.$
Definida de esa manera la función $\chi^{(n+1)}_r$ se satisfacen las hipótesis deseadas. Supongamos ahora que $0<r-\sum_{i=0}^{n}\frac{\chi^{(n)}_r(i)}{10^i}$ y definamos $\hat{r}:=10^n(r-\sum_{i=0}^{n}\frac{\chi^{(n)}_r(i)}{10^i})$, número real que sabemos satisface $0<\hat{r}<1$. Consideremos el conjunto $A=\{m\in\mathbb{N}:m\leq 10\hat{r}\}$, el cual es no vacío ya que $0<\hat{r}$ y por tanto $0\leq 10\hat{r}$; además, $A$ es acotado superiormente ya que $\hat{r}<1$ y por tanto $10\hat{r}<10$, de modo que si $m\in A$, entonces $m<10$. Así, existe $a=\textnormal{max}(A)$, el cual es un natural dentro del conjunto $\{0,1,2,3,4,5,6,7,8,9\}$. Por la maximalidad de $a$ se tiene que $10\hat{r}<a+1$ y así $\frac{a}{10}\leq\hat{r}<\frac{a}{10}+\frac{1}{10}$, es decir, $0\leq\hat{r}-\frac{a}{10}<\frac{1}{10}$.
Luego, dado que $\hat{r}=10^n(r-\sum_{i=0}^{n}\frac{\chi^{(n)}_r(i)}{10^i})$ se sigue que $0\leq r-\sum_{i=0}^{n}\frac{\chi^{(n)}_r(i)}{10^i}-\frac{a}{10^{n+1}}<\frac{1}{10^{n+1}}$. Si definimos $\chi^{(n+1)}_r:n+2\to\mathbb{N}$ por medio de $\chi^{(n+1)}_r(i)=\left\{\begin{array}{lcc}
\chi^{(n)}_r(i) & \textnormal{si}\ i\in n+1\\
a & \textnormal{si}\ i=n+1
\end{array}
\right.$

entonces $\chi^{(n+1)}_r$ es una función que satisface las condiciones deseadas. Así, hemos demostrado la existencia de una función con las características requeridas. Veamos que ésta es única. Supongamos que $\eta:n+2\to\mathbb{N}$ es otra función que satisface las mismas propiedades que $\chi_r^{(n+1)}$.
Luego, en particular, $0\leq r-\sum_{i=0}^{n+1}\frac{\eta(i)}{10^i}<\frac{1}{10^{n+1}}$ y por tanto $0\leq r-\sum_{i=0}^{n}\frac{\eta(i)}{10^i}<\frac{1}{10^{n+1}}+\frac{\eta(n+1)}{10^{n+1}}\leq \frac{1}{10^{n+1}}+\frac{9}{10^{n+1}}=\frac{10}{10^{n+1}}=\frac{1}{10^n}$. De este modo, la función $\eta\upharpoonright_{n+1}:n+1\to\mathbb{N}$ satisface las mismas condiciones que la función $\chi^{(n)}_r$, y por la unicidad de esta última función se sigue que $\eta(i)=\chi^{(n)}_r(i)$ para cada $i\in n+1$. Así, la función $\eta$ coincide con la función $\chi^{(n+1)}_r$ en $n+1$, por lo que resta probar que $\eta(n+1)=\chi^{(n+1)}_r(n+1)=a$.
Sabemos que $0\leq r-\sum_{i=0}^{n}\frac{\chi^{(n+1)}_r(i)}{10^i}-\frac{\eta(n+1)}{10^{n+1}}<\frac{1}{10^{n+1}}$ y por tanto, $0\leq 10^{n+1}(r-\sum_{i=0}^{n}\frac{\chi^{(n+1)}(i)}{10^i})-\eta(n+1)<1$, es decir, $\eta(n+1)\leq10\hat{r}<\eta(n+1)+1$, de modo que $\eta(n+1)\in A$ y por tanto $\eta(n+1)\leq a=\chi^{(n+1)}_r(n+1)$. Podemos elegir $k\in\{0,1,2,3,4,5,6,7,8,9\}$ tal que $\eta(n+1)+k=a$ y tenemos $a=\eta(n+1)+k\leq10\hat{r}$, razón por la cual \[k\leq10\hat{r}-\eta(n+1)<(\eta(n+1)+1)-\eta(n+1)=1\] y en consecuencia, $k=0$. Por tanto, $\eta(n+1)=a=\chi^{(n+1)}_r(n+1)$. Esto demuestra la unicidad de $\chi^{(n+1)}_r$.

Por lo tanto, para cada $n\in\mathbb{N}$ existe una única función $\chi^{(n)}_r:n+1\to\mathbb{N}$ tal que $\chi^{(n)}_r[\mathbb{N}]\subseteq\{0,1,2,3,4,5,6,7,8,9\}$ y $0\leq r-\sum_{i=0}^{n}\frac{\chi^{(n)}_r(i)}{10^i}<\frac{1}{10^n}$. En el proceso de la demostración de la existencia y unicidad de tales funciones, mostramos además que si $\chi^{(n+1)}_r:n+2\to\mathbb{N}$ es la única función con tales propiedades, entonces, $\chi^{(n)}_r=\chi^{(n+1)}_r\upharpoonright_{n+1}$, lo que muestra que el conjunto de funciones $\mathcal{F}:=\{\chi^{(n)}_r:n\in\mathbb{N}\}$ es un sistema de funciones compatibles y, por tanto, $\chi_r=\bigcup\mathcal{F}:\mathbb{N}\to\mathbb{N}$ es la única función con las propieades que enunciamos en la afirmación.

Estamos entonces en condiciones de definir una función $F:(0,1)\to\{f\in\mathbb{N}^{\mathbb{N}}:f[\mathbb{N}]\subseteq\{0,1,2,3,4,5,6,7,8,9\}\}$ por medio de $F(r)=\chi_r$. Dicha función es inyectiva, ya que si $\chi_r=\chi_{r’}$, entonces, para cada $n\in\mathbb{N}$, \[|r-r’|=|r-\sum_{i=0}^{n}\frac{\chi_r(i)}{10^i}+\sum_{i=0}^{n}\frac{\chi_{r’}(i)}{10^i}-r’|\] \[\leq|r-\sum_{i=0}^{n}\frac{\chi_r(i)}{10^i}|+|\sum_{i=0}^{n}\frac{\chi_{r’}(i)}{10^i}-r’|\] \[<\frac{1}{10^n}+\frac{1}{10^n}=\frac{2}{10^n}\] lo cual muestra que $|r-r’|=0$, es decir, $r=r’$. Por tanto, existe una función inyectiva de $(0,1)$ en $\mathbb{N}^{\mathbb{N}}$, de modo que $|(0,1)|\leq|\mathbb{N}^{\mathbb{N}}|=|\mathcal{P}(\mathbb{N})|$.

Ahora vamos a definir una función inyectiva de $2^{\mathbb{N}}$ en $(0,1)$. Sea $f\in2^{\mathbb{N}}$ y veamos que la sucesión de números racionales $(\sum_{i=0}^{n}\frac{f(i)}{10^{i+1}})_{n\in\mathbb{N}}$ converge. Dado que $f(i)\in\{0,1\}$ para cada $i\in\mathbb{N}$, la sucesión $(\sum_{i=0}^{n}\frac{f(i)}{10^{i+1}})_{n\in\mathbb{N}}$ es no decreciente. Luego, para cada $n\in\mathbb{N}$, $0\leq\sum_{i=0}^{n}\frac{f(i)}{10^{i+1}}\leq\sum_{i=0}^{n}\frac{1}{10^{i+1}}=\sum_{i=1}^{n+1}\frac{1}{10^i}=\frac{1-\frac{1}{10^{n+2}}}{1-\frac{1}{10}}-1=\frac{1-\frac{1}{10^{n+2}}}{(\frac{9}{10})}-1<\frac{1}{(\frac{9}{10})}-1=\frac{10}{9}-1=\frac{1}{9}<1$, por lo que dicha sucesión está acotada inferiormente por $0$ y superiormente por $\frac{1}{9}$ y, por tanto, converge a algún número real en el intervalo $[0,\frac{1}{9}]$. Sea $r_f\in[0,\frac{1}{9}]$ el límite de dicha sucesión.
Si la función $f$ no es la constante cero, entonces, $r_f\in(0,\frac{1}{9}]$, ya que existe $N\in\mathbb{N}$ tal que $f(N)=1$ y por tanto, para cada $n\geq N$, $\frac{1}{10^{N+1}}\leq\sum_{i=0}^{n}\frac{f(i)}{10^{i+1}}\leq r_f$.
Dado que el número real $r_f$ es único para cada $f\in2^{\mathbb{N}}$, estamos en condiciones de definir la siguiente función: sea $G:2^{\mathbb{N}}\to[0,1)$ tal que $G(f)=\left\{\begin{array}{lcc}
r_f & \textnormal{si}\ f\not=0\\
0 & \textnormal{si}\ f=0
\end{array}
\right.$

Veamos que $G$ es inyectiva. Por la definición de $G$ sabemos que si $f\not=0$, entonces $G(f)\not=G(0)$. Ahora, sean $f,h\in2^{\mathbb{N}}$ funciones no cero tales que $r_f=G(f)=G(h)=r_h$. Veamos que $f(n)=h(n)$ para cada $n\in\mathbb{N}$.
Algo que será de utilidad para probar esto último es la desigualdad $\sum_{i=n+1}^{m}\frac{1}{10^i}<\frac{1}{2\cdot10^n}$, la cual es cierta para cualesquiera $n,m\in\mathbb{N}$ tales que $n<m$. En efecto, si $n,m\in\mathbb{N}$ con $n<m$, tenemos \[\sum_{i=n+1}^{m}\frac{1}{10^i}=\sum_{i=0}^{m}\frac{1}{10^i}-\sum_{i=0}^{n}\frac{1}{10^i}=\frac{1-\frac{1}{10^{m+1}}}{1-\frac{1}{10}}-\frac{1-\frac{1}{10^{n+1}}}{1-\frac{1}{10}}=\frac{\frac{1}{10^{n+1}}-\frac{1}{10^{m+1}}}{(\frac{9}{10})}=\frac{\frac{1}{10^n}-\frac{1}{10^m}}{9}\] y este número racional es menor que $\frac{1}{2\cdot10^n}$, pues $\frac{1}{10^n}-\frac{1}{10^m}<\frac{1}{10^n}<\frac{9}{2}\cdot\frac{1}{10^n}$, pues $1<\frac{9}{2}$. Por tanto, para cualesquiera $n,m\in\mathbb{N}$ con $n<m$, $\sum_{i=n+1}^{m}\frac{1}{10^i}<\frac{1}{2\cdot10^n}$.

Ahora sí, veamos que $f(n)=h(n)$ para cada $n\in\mathbb{N}$.
Dado que las sucesiones de números racionales $(\sum_{i=0}^{n}\frac{f(i)}{10^{i+1}})_{n\in\mathbb{N}}$ y $(\sum_{i=0}^{n}\frac{h(i)}{10^{i+1}})_{n\in\mathbb{N}}$ convergen al número real $r_f$, existe $m\in\mathbb{N}$ tal que para cada $n>m$, $0\leq r_f-\sum_{i=0}^{n}\frac{f(i)}{10^{i+1}}<\frac{1}{4\cdot10}$ y $0\leq r_f-\sum_{i=0}^{n}\frac{h(i)}{10^{i+1}}<\frac{1}{4\cdot10}$. Luego, $$|\sum_{i=0}^{m+1}\frac{f(i)}{10^{i+1}}-\sum_{i=0}^{m+1}\frac{h(i)}{10^{i+1}}|=|\sum_{i=0}^{m+1}\frac{f(i)}{10^{i+1}}-r_f+r_f-\sum_{i=0}^{m+1}\frac{h(i)}{10^{i+1}}|$$ $$\leq|\sum_{i=0}^{m+1}\frac{f(i)}{10^{i+1}}-r_f|+|r_f-\sum_{i=0}^{m+1}\frac{h(i)}{10^{i+1}}|<\frac{1}{4\cdot10}+\frac{1}{4\cdot10}=\frac{1}{2\cdot10}.$$ Por otro lado, $|\frac{f(0)-h(0)}{10}|-|\sum_{i=1}^{m+1}\frac{f(i)-h(i)}{10^{i+1}}|\leq|\sum_{i=0}^{m+1}\frac{f(i)-h(i)}{10^{i+1}}|<\frac{1}{2\cdot10}$ y así \[|\frac{f(0)-h(0)}{10}|<\frac{1}{2\cdot10}+|\sum_{i=1}^{m+1}\frac{f(i)-h(i)}{10^{i+1}}|\leq\frac{1}{2\cdot10}+\sum_{i=1}^{m+1}\frac{|f(i)-h(i)|}{10^{i+1}}.\] Dado que $|f(i)-h(i)|=\left\{\begin{array}{lcc}
1 & \textnormal{si}\ \{f(i),h(i)\}=\{0,1\}\\
0 & \textnormal{si}\ f(i)=h(i)=0\ \textnormal{o}\ f(i)=h(i)=1
\end{array}
\right.$ entonces, $|f(i)-h(i)|\leq1$ para cada $i\in\mathbb{N}$ y, como $\sum_{i=1}^{m+1}\frac{1}{10^{i+1}}=\sum_{i=2}^{m+2}\frac{1}{10^i}<\frac{1}{2\cdot10}$, se sigue que \[\frac{|f(0)-h(0)|}{10}\leq\frac{1}{2\cdot10}+\sum_{i=1}^{m+1}\frac{1}{10^{i+1}}<\frac{1}{10}\] lo cual implica que $|f(0)-h(0)|=0$, es decir, $f(0)=h(0)$. Supongamos que para algún $n\in\mathbb{N}$ hemos probado que $f(m)=h(m)$ para cada $m\leq n$ y veamos que $f(n+1)=h(n+1)$.
Sea $m\in\mathbb{N}$, $m\geq n+1$, tal que para cada $k>m$, $|r_f-\sum_{i=0}^{k}\frac{f(i)}{10^{i+1}}|<\frac{1}{4\cdot10^{n+2}}$ y $|r_f-\sum_{i=0}^{k}\frac{h(i)}{10^{i+1}}|<\frac{1}{4\cdot10^{n+2}}$.
Luego, $|\sum_{i=n+1}^{m+1}\frac{f(i)-h(i)}{10^{i+1}}|=|\sum_{i=0}^{m+1}\frac{f(i)-h(i)}{10^{i+1}}|\leq|r_f-\sum_{i=0}^{m+1}\frac{f(i)}{10^{i+1}}|+|r_f-\sum_{i=0}^{m+1}\frac{h(i)}{10^{i+1}}|<\frac{1}{2\cdot10^{n+2}}$. Por otro lado, \[\frac{|f(n+1)-h(n+1)|}{10^{n+2}}-|\sum_{i=n+2}^{m+1}\frac{f(i)-h(i)}{10^{i+1}}|\leq|\sum_{i=n+1}^{m+1}\frac{f(i)-h(i)}{10^{i+1}}|<\frac{1}{2\cdot10^{n+2}}\] por lo que $$\frac{|f(n+1)-h(n+1)|}{10^{n+2}}<\frac{1}{2\cdot10^{n+2}}+|\sum_{i=n+2}^{m+1}\frac{f(i)-h(i)}{10^{i+1}}|\leq\frac{1}{2\cdot10^{n+2}}+\sum_{i=n+2}^{m+1}\frac{|f(i)-h(i)|}{10^{i+1}}$$ \[\leq\frac{1}{2\cdot10^{n+2}}+\sum_{i=n+2}^{m+1}\frac{1}{10^{i+1}}=\frac{1}{2\cdot10^{n+2}}+\sum_{i=n+3}^{m+2}\frac{1}{10^i}<\frac{1}{2\cdot10^{n+2}}+\frac{1}{2\cdot10^{n+2}}=\frac{1}{10^{n+2}}\]
y en consecuencia, $|f(n+1)-h(n+1)|=0$, es decir, $f(n+1)=h(n+1)$. Por tanto, para cada $n\in\mathbb{N}$, $f(n)=h(n)$, lo que demuestra que $f=h$.
Así, la función $G$ es inyectiva y, por consiguiente, $|2^{\mathbb{N}}|\leq|[0,1)|$. Dado que $|[0,1)|=|(0,1)|$, se sigue que $|\mathcal{P}(\mathbb{N})|=|2^{\mathbb{N}}|\leq|(0,1)|$. Por el teorema de Cantor-Schröder-Bernstein concluimos que $|(0,1)|=|\mathcal{P}(\mathbb{N})|$.

$\square$

Concluimos la entrada con el siguiente corolario, cuya prueba es consecuencia del teorema anterior y el hecho que $|\mathbb{R}|=|(0,1)|$.

Corolario. $\mathbb{R}$ y $\mathcal{P}(\mathbb{N})$ son equipotentes.

$\square$

Tarea moral

  1. Demuestra que el conjunto $\mathbb{N}^{\nearrow\mathbb{N}}:=\{f\in\mathbb{N}^{\mathbb{N}}:f(n)<f(n+1)\ \textnormal{para cada}\ n\in\mathbb{N}\}$ es equipotente a $[\mathbb{N}]^{\mathbb{N}}$.
  2. Demuestra que para cualquier conjunto infinito $X$ que contenga un conjunto numerable se cumple que $|X\setminus A|=|X|$, para cada $A\subseteq X$ conjunto finito.
  3. Sean $a,b\in\mathbb{R}$ con $a<b$. Demuestra que $|(a,b)|=|(0,1)|$.
  4. Exhibe una biyección entre $\mathbb{R}$ y $[0,\infty):=\{r\in\mathbb{R}:r\geq0\}$.

Más adelante…

Entradas relacionadas

  1. Hernández, F., Teoría de Conjuntos, México: Aportaciones Matemáticas No.13,
    SMM, 1998 ↩︎
  2. Spivak, M., Cálculo Infinitesimal (2a ed). México: Reverté, 1998. ↩︎

Teoría de los Conjuntos I: Conjuntos numerables (parte II)

Por Gabriela Hernández Aguilar

Deja un comentario

Introducción

En la entrada anterior hemos mostrado algunos ejemplos de conjuntos equipotentes al conjunto de los números naturales. En algunos casos exhibimos funciones biyectivas del conjunto de los números naturales en cada uno de los respectivos conjuntos. Sin embargo, esta labor puede resultar complicada, en muchas ocasiones exhibir funciones biyectivas de un conjunto en otro presenta diversas dificultades. Debido a esto, en varias situaciones resulta muy útil aplicar el teorema de Cantor-Schröder-Bernstein para mostrar que dos conjuntos son equipotentes sin necesidad de proporcionar una biyección. En esta entrada añadiremos otro par de ejemplos de conjuntos equipotentes al conjunto de los números naturales, pero haremos uso del teorema de Cantor-Schröder-Bernstein para mostrar tal equipotencia.

Conjuntos numerables.

En el siguiente ejemplo aparece un conjunto que ya conocíamos y que de hecho se encuentra en la entrada anterior, se trata del conjunto de números racionales, para el cual dimos dos maneras de mostrar que es numerable.

Ejemplo.

$\mathbb{Q}$ es numerable, es decir, equipotente a $\mathbb{N}$.

Lo que haremos será mostrar que $\mathbb{Q}^{+}\cup\{0\}$ y $\mathbb{N}$ son equipotentes con ayuda del teorema de Cantor-Schröder-Bernstein. Luego, como $\mathbb{Q}^{-}$ y $\mathbb{Q}^{+}$ son equipotentes podremos concluir que $\mathbb{Q}$ es la unión de dos conjuntos ajenos numerables y, por tanto, que $\mathbb{Q}$ es numerable.

Ante un claro abuso de notación en lo que sigue, definamos $f:\mathbb{N}\to\mathbb{Q}^{+}\cup\{0\}$ por medio de $f(n)=\frac{n}{1}$. Luego, $f$ es una función ineyctiva de $\mathbb{N}$ en $\mathbb{Q}^{+}\cup\{0\}$, pues si $f(n)=f(m)$, entonces, $\frac{n}{1}=\frac{m}{1}$ lo cual implica que $n\cdot 1=m\cdot1$, es decir, $n=m$. Ahora, tenemos que exhibir una función inyectiva de $\mathbb{Q}^{+}\cup\{0\}$ en $\mathbb{N}$. Definamos $g:\mathbb{Q}^{+}\cup\{0\}\to\mathbb{N}\times\mathbb{N}$ por medio de $$g\left(\frac{p}{q}\right)=\left\{\begin{array}{lcc}
(p,q) & \textnormal{si}\ \frac{p}{q}\in\mathbb{Q}^{+}\ \textnormal{y}\ p\ \textnormal{y}\ q\ \textnormal{son primos relativos}\\
(0,0) & \textnormal{si}\ \frac{p}{q}=0
\end{array}
\right.$$

Debido a que cada racional en $\mathbb{Q}^{+}$ tiene una expresión única de la forma $\frac{p}{q}$ con $p$ y $q$ primos relativos, entonces, $g$ está bien definida. Veamos que $g$ es inyectiva. Supongamos que $\frac{p}{q},\frac{s}{t}\in\mathbb{Q}^{+}\cup\{0\}$ son tales que $g(\frac{p}{q})=g(\frac{s}{t})$. Si $\frac{p}{q}=0$, entonces, $g(\frac{p}{q})=(0,0)$ y así $g(\frac{s}{t})=(0,0)$; luego, $\frac{s}{t}=0$, pues en caso contrario, podríamos asumir que $s$ y $t$ son primos relativos y por tanto $g(\frac{s}{t})=(s,t)\not=(0,0)$ ya que $s\not=0$. Así pues, si $\frac{p}{q}=0$, entonces, $\frac{s}{t}=0$. Análogamente, si $\frac{s}{t}=0$, entonces, $\frac{p}{q}=0$. Supongamos ahora que $\frac{p}{q}\not=0\not=\frac{s}{t}$ y que tanto $p$ y $q$ como $s$ y $t$, son primos relativos. Así, $g(\frac{p}{q})=(p,q)$ y $g(\frac{s}{t})=(s,t)$ y por consiguiente, $(p,q)=(s,t)$, de modo que $s=p$ y $q=t$, lo que demuestra que $\frac{p}{q}=\frac{s}{t}$. Por tanto, $g$ es una función inyectiva. Finalmente, si consideramos la función inyectiva $h:\mathbb{N}\times\mathbb{N}\to\mathbb{N}$ definida por medio de $h(n,m)=2^n(2m+1)$, la cual aparece en los ejercicios de la sección anterior, tendremos que $h\circ g:\mathbb{Q}^{+}\cup\{0\}\to\mathbb{N}$ es una función inyectiva. Por el teorema de Cantor-Schröder-Bernstein concluimos que $\mathbb{Q}^{+}\cup\{0\}$ es numerable y, consecuentemente, $\mathbb{Q}$ es numerable.

$\square$

El siguiente ejemplo también aparece en la entrada anterior, pero ahora utilizaremos el teorema de Cantor-Schröder-Bernstein. Como bien lo vimos, dicho ejemplo nos proporciona una gran cantidad de conjuntos numerables y, al mismo tiempo, muestra una propiedad interesante del conjunto de números naturales.

Ejemplo.

Si $A\subseteq\mathbb{N}$ es un conjunto infinito, entonces, $A$ es numerable.

Demostración.

Sea $A\subseteq\mathbb{N}$ un conjunto infinito. La función $\iota:A\to\mathbb{N}$ definida por medio de $\iota(n)=n$ para cada $n\in\mathbb{N}$ es una función inyectiva. Ahora vamos a exhibir una función inyectiva de $\mathbb{N}$ en $A$.
Para cada $n\in A$ definamos $n^{\uparrow}:=\{m\in A:n<m\}$. Notemos que para cada $n\in A$, $n^{\uparrow}\not=\emptyset$, pues en caso contrario existiría $n\in A$ tal que para cada $m\in A$, $m\leq n$ y en consecuencia, $A\subseteq s(n)=n\cup\{n\}$, lo cual implicaría que $A$ es finito, contradiciendo la hipótesis sobre $A$. Así pues, por el buen orden de $\mathbb{N}$, para cada $n\in A$ existe $min(n^{\uparrow})$. Una vez hecho lo anterior elijamos $n_0=min(A)$ y definamos $g:A\to A$ por medio de $g(n)=min(n^{\uparrow})$. Por el teorema de recursión, existe una única función $f:\mathbb{N}\to A$ tal que $f(0)=n_0$ y $f(n+1)=g(f(n))$ para cada $n\in\mathbb{N}$. Veamos que $f$ es una función inyectiva. Para ello, veamos que $f(n)<f(n+1)$ para cada $n\in\mathbb{N}$. Sea $n\in\mathbb{N}$. Luego, $f(n+1)=g(f(n))=min(f(n)^{\uparrow})$ por lo que $f(n+1)\in f(n)^{\uparrow}$ y así $f(n)<f(n+1)$. Por lo tanto $f$ es una función inyectiva de $\mathbb{N}$ en $A$. Por el teorema de Cantor-Schröder-Bernstein podemos concluir que $\mathbb{N}$ y $A$ son equipotentes.

$\square$

Como probarás en los ejercicios de esta entrada, la función $f:\mathbb{N}\to A$ que aparece en el ejemplo precedente es de hecho biyectiva. Por otro lado, como lo habíamos mencionado previo al ejemplo, éste nos proporciona una gran cantidad de conjuntos numerables; por mencionar algunos tenemos los conjuntos $A_n:=\{m\in\mathbb{N}:n<m\}$ para cada $n\in\mathbb{N}$, o también algunos que ya conocíamos como el conjunto de números pares $\{2k:k\in\mathbb{N}\}$, el cual ya sabíamos que era equipotente a $\mathbb{N}$, y algunos otros más interesantes, como el conjunto de números primos pues dicho conjunto es infinito. Para conocer la definición de número primo puedes consultar el siguiente enlace Álgebra Superior II: Números primos y sus propiedades.
Otra consecuencia del ejemplo anterior es el siguiente corolario.

Corolario. Si $B$ es un conjunto numerable y $A\subseteq B$ es un conjunto inifinito, entonces, $A$ es un conjunto numerable.

Demostración.

Dado que $B$ es numerable, existe una función biyectiva $g:B\to\mathbb{N}$. Luego, la restricción de $g$ al conjunto $A$, $g\upharpoonright_{A}:A\to\mathbb{N}$, es una función inyectiva y, más aún, es una biyección entre $A$ y $g[A]\subseteq\mathbb{N}$. Dado que $A$ es infinito, también lo es $g[A]$, pero por el ejemplo anterior sabemos que $g[A]$ es numerable y, en consecuencia, $A$ es numerable.

$\square$

Hasta ahora, en los dos ejemplos que hemos visto, si bien hicimos uso del teorema de Cantor-Schröder-Bernstein y nos facilitó probar la equipotencia de tales conjuntos con $\mathbb{N}$, también es factible exhibir o mostrar directamente la existencia de una función biyectiva. En los ejemplos subsecuentes será más clara la utilidad e importancia del teorema de Cantro-Schröder-Bernstein, y además un tanto más interesantes, pues sin dicho teorema probar la equipotencia con $\mathbb{N}$ es bastante más complicado.

Para introducir el siguiente ejemplo es necesario mencionar un resultado importante del conjunto de números enteros, conocido como el teorema fundamental de la aritmética. Tal teorema asegura que dado cualquier número entero positivo mayor a 1, éste tiene una expresión única como producto de números primos, es decir, si $z\in\mathbb{Z}^{+}$ es cualquier entero positivo mayor a 1, existen únicos números primos $p_1,\ldots,p_n$ y únicos números naturales distintos de cero $\alpha_1,\ldots,\alpha_n$ tales que $z=p_1^{\alpha_1}\cdots p_n^{\alpha_n}=\Pi_{i=1}^{n}p_i^{\alpha_i}$. Puedes consultar el teorema fundamental de la aritmética y su prueba en el siguiente enlace Álgebra Superior II: Teorema fundamental de la aritmética e infinidad de números primos; más aún, en dicho enlace puedes encontrar la prueba de que el conjunto de números primos es inifinito y, de acuerdo al último ejemplo que enunciamos, éste conjunto es numerable.

Ejemplo.

$[\mathbb{N}]^{<\mathbb{N}}:=\{A\subseteq\mathbb{N}:A\ \textnormal{es finito}\}$ es numerable.

Demostración.

Notemos que la función $f:\mathbb{N}\to[\mathbb{N}]^{<\mathbb{N}}$ definida por medio de $f(n)=\{n\}$ es una función inyectiva, de modo que para aplicar el teorema de Cantor-Schröder-Bernstein hace falta exhibir una función inyectiva de $[\mathbb{N}]^{<\mathbb{N}}$ en $\mathbb{N}$.
Para construir tal función inyectiva, consideremos en primer lugar al conjunto de números primos $\mathbb{P}:=\{p\in\mathbb{Z}^{+}:p\ \textnormal{es primo}\}$. Dado que $\mathbb{P}$ puede ser visto como un subconjunto de $\mathbb{N}$, sabemos, por el ejemplo anterior, que existe una función (biyectiva) $f:\mathbb{N}\to \mathbb{P}$ tal que $f(0)=min(\mathbb{P})$ y tal que $f(n)<f(n+1)$ para cada $n\in\mathbb{N}$. Así, si denotamos como $p_n:=f(n)$ para cada $n\in\mathbb{N}$, podemos escribir $\mathbb{P}=\{p_n:n\in\mathbb{N}\}$ y se satisface que $p_n<p_{n+1}$ para cada $n\in\mathbb{N}$. Vamos a considerar para el resto de la prueba que $\mathbb{P}$ está enumerado de esta manera.
Ahora bien, si $A\subseteq\mathbb{N}$ es un conjunto finito y no vacío, digamos $|A|=n+1$ con $n\in\mathbb{N}$, entonces, $A$ puede ser enumerado de manera similar a como lo hicimos con $\mathbb{P}$; esto es, existe una función biyectiva (de hecho única) $f_A:n+1\to A$ tal que $f_A(0)=min(A)$ y $f_A(k)<f_A(m)$ si y sólo si $k<m$. Así, si denotamos como $a_k:=f_A(k)$ para cada $k\in n+1$, tenemos que $A=\{a_k:k\in n+1\}$ y que $a_k<a_m$ si y sólo si $k<m$. Para el resto de la prueba utilizaremos estas enumeraciones con cualquier subconjunto finito no vacío de $\mathbb{N}$, es decir, dado $A\subseteq\mathbb{N}$ no vacío, con $|A|=n+1$, escribiremos $A=\{a_k:k\in n+1\}$ y se entenderá que $a_k<a_m$ si y sólo si $k<m$.

Una vez mencionado lo anterior definamos $F:[\mathbb{N}]^{<\mathbb{N}}\setminus\{\emptyset\}\to\mathbb{Z}^{+}$ por medio de $F(A)=\Pi_{k=0}^{n}p_k^{a_k}$ si $A=\{a_k:k\in n+1\}$, para cada $A\in[\mathbb{N}]^{<\mathbb{N}}\setminus\{\emptyset\}$. Veamos que tal función es inyectiva. Supongamos que $A,B\in[\mathbb{N}]^{<\mathbb{N}}\setminus\{\emptyset\}$ son conjuntos tales que $F(A)=F(B)$. Si $|A|=n+1$ y $|B|=m+1$ con $n,m\in\mathbb{N}$, y además $A=\{a_k:k\in n+1\}$ y $B=\{b_k:k\in m+1\}$, entonces, $F(A)=\Pi_{k=0}^{n}p_k^{a_k}$ mientras que $F(B)=\Pi_{k=0}^{m}p_k^{b_k}$; luego, como $\Pi_{k=0}^{n}p_k^{a_k}=\Pi_{k=0}^{m}p_k^{b_k}$ se tiene $n=m$, pues si $n<m$, entonces, $m>0$ y $b_m>0$, ya que $b_m>b_0$ y $b_0\geq0$, por lo que $p_m^{b_m}$ es una potencia positiva del primo $p_m$ que no aparece en el producto $\Pi_{k=0}^{n}p_k^{a_k}$, pero que sí aparece en el producto $\Pi_{k=0}^{m}p_k^{b_k}$, lo cual contradice el teorema fundamental de la aritmética. Análogamente, no puede ocurrir que $m<n$. Por tanto, $n=m$ y, por consiguiente, $a_k=b_k$ para cada $k\in n+1$. En consecuencia, $A=B$. Por tanto, $F$ es una función inyectiva. Finalmente, como $\mathbb{Z}^{+}$ es numerable, existe $G:\mathbb{Z}^{+}\to\mathbb{N}\setminus\set{0}$ función biyectiva y así $G\circ F:[\mathbb{N}]^{<\mathbb{N}}\setminus\set{\emptyset}\to\mathbb{N}\setminus\set{0}$ es una función inyectiva. Por consiguiente, la función $\tilde{F}:[\mathbb{N}]^{<\mathbb{N}}\to\mathbb{N}$ definida por medio de $$\tilde{F}(A)=\left\{ \begin{array}{lcc}
0 & \textnormal{si}\ A=\emptyset \\
(G\circ F)(A) & \textnormal{si}\ A\not=\emptyset
\end{array}
\right.$$

es inyectiva. El teorema de Cantor-Schröder-Bernstein nos permite concluir que $[\mathbb{N}]^{<\mathbb{N}}$ es numerable.

$\square$

Para el último ejemplo que trataremos en esta entrada vamos a definir lo que es una sucesión.

Definición. Si $A$ es un conjunto y $f:\mathbb{N}\to A$ es una función, diremos que $f$ es una sucesión en $A$. Por otro lado, si $n\in\mathbb{N}$ y $g:n\to A$ es una función, diremos que $g$ es una sucesión finita de longitud $n$ en $A$.

Dado un conjunto $A$ vamos a denotar como $^nA$ al conjunto de todas las sucesiones finitas de longitud $n$ en $A$.

Ejemplo.

El conjunto $\mathbb{N}^{<\mathbb{N}}:=\cup_{n\in \mathbb{N}}\ ^n\mathbb{N}$ es numerable.

Demostración.

Primero vamos a dar una función inyectiva de $\mathbb{N}$ en $\mathbb{N}^{<\mathbb{N}}$. Para cada $n\in\mathbb{N}\setminus\{0\}$ definamos $x_n:1\to\mathbb{N}$ como $x_n(0)=n$. Si $n\in\mathbb{N}\setminus\{0\}$, $x_n$ es una sucesión finita de longitud $1$ en $\mathbb{N}$, es decir, $x_n\in{^1\mathbb{N}}$. Ahora, para $n=0$ definamos $x_0:=\emptyset:0\to\mathbb{N}$ la función vacía, es decir, la única sucesión finita de longitud $0$ en $\mathbb{N}$, de modo que $x_0\in{^0\mathbb{N}}$. Una vez definidas estas sucesiones finitas vamos a considerar la función $f:\mathbb{N}\to\mathbb{N}^{<\mathbb{N}}$ dada por $f(n)=x_n$ para cada $n\in\mathbb{N}$. Notemos que $f$ es inyectiva, pues si $n,m\in\mathbb{N}$ son naturales distintos podemos suponer que $n<m$; luego, si $n=0$, entonces $f(n)=f(0)=x_0=\emptyset$ mientras que $m>0$ y $f(m)=x_m=\{(0,m)\}$, de modo que $f(n)\not=f(m)$. Si ahora $0<n$, entonces también $0<m$ y $f(n)=x_n=\{(0,n)\}$ mientras que $f(m)=x_m=\{(0,m)\}$, pero dado que $(0,n)\not=(0,m)$ pues $n\not=m$, concluimos que $f(n)\not=f(m)$. Por tanto $f$ es inyectiva.

Ahora vamos a dar una función inyectiva de $\mathbb{N}^{<\mathbb{N}}$ en $\mathbb{N}$. En el penúltimo ejemplo consideramos al conjunto de números primos enumerado como $\mathbb{P}=\{p_n:n\in\mathbb{N}\}$ de tal manera que $p_n<p_{n+1}$ para cada $n\in\mathbb{N}$. Retomando dicha enumeración del conjunto de números primos definamos $g:\mathbb{N}^{<\mathbb{N}}\to\mathbb{N}\times\mathbb{Z}$ por medio de $$g(x)=\left\{\begin{array}{lcc}
(n+1,\Pi_{k=0}^{n}p_k^{x(k)}) & \textnormal{si}\ x\in{^{n+1}\mathbb{N}} \\
(0,0) & \textnormal{si}\ x=\emptyset
\end{array}
\right.
$$

Probar que la función $g$ es inyectiva requiere, esencialmente, del teorema fundamental de la aritmética; si $x\in{^{n+1}\mathbb{N}}$ y $y\in{^{m+1}\mathbb{N}}$ con $n\not=m$, entonces, $n+1\not=m+1$ y por ende $g(x)=(n+1,\Pi_{k=0}^{n}p_k^{x(k)})\not=(m+1,\Pi_{k=0}^{m}p_k^{y(k)})=g(y)$. Si $x=\emptyset$ y $y\in{^{n+1}\mathbb{N}}$ con $n\in\mathbb{N}$, entonces $g(y)=(n+1,\Pi_{k=0}^{n}p_k^{y(k)})\not=(0,0)=g(x)$. Por tanto, para concluir que $g$ es inyectiva, basta comprobar que si $n\in\mathbb{N}$ y $x,y\in{^{n+1}\mathbb{N}}$ son elementos distintos, entonces $g(x)\not=g(y)$, lo cual dejamos como un ejercicio al final de esta entrada.

Por el teorema de Cantor-Schröder-Bernstein, $\mathbb{N}^{<\mathbb{N}}$ es numerable.

$\square$

Tarea moral

  • Sea $A\subseteq\mathbb{N}$ conjunto inifinito. Para cada $n\in A$ definimos $n^{\uparrow}:=\{m\in A:n<m\}$. Definimos $g:A\to A$ por medio de $g(n)=\textnormal{min}(n^{\uparrow})$ y consideremos la única función $f:\mathbb{N}\to A$ tal que $f(0)=\textnormal{min}(A)$ y $f(n+1)=g(f(n))$ para cada $n\in\mathbb{N}$. Demuestra que $f$ es una biyección.
  • Prueba que la función $g:\mathbb{N}^{<\mathbb{N}}\to\mathbb{N}\times\mathbb{Z}$ definida por medio de $g(x)=\left\{\begin{array}{lcc} (n+1,\Pi_{k=0}^{n}p_k^{x(k)}) & \textnormal{si}\ x\in^{n+1}\mathbb{N} \\ (0,0) & \textnormal{si}\ x=\emptyset
    \end{array}
    \right.$ es inyectiva.
  • Demuestra lo siguiente:
    $(a)$ Si $A\subseteq\mathbb{N}$ es un conjunto finito no vacío con $|A|=n+1$, $n\in\mathbb{N}$, existe una única función biyectiva $f_A:n+1\to A$ tal que $f_A(0)=\textnormal{min}(A)$ y que $f_A(m)<f_A(k)$ si y sólo si $m<k$ para cualesquiera $m,k\in n+1$.
    $(b)$ Utilizando el hecho de que $\mathbb{N}^{<\mathbb{N}}$ es numerable muestra que $[\mathbb{N}]^{<\mathbb{N}}$ es numerable. Puede que te ayude de algo el inciso $(a)$.
  • Demuestra que si $B\subseteq A$ son conjuntos tales que $B$ es numerable pero $A$ no, entonces, $A\setminus B$ no es numerable.
  • Diremos que una sucesión $x$ en $\mathbb{N}$ es semiconstante si existe $n_0\in\mathbb{N}$ tal que para cada $n\geq n_0$, $x(n)=x(n_0)$. Demuestra que si $\mathcal{S}$ es el conjunto de todas las sucesiones semiconstantes en $\mathbb{N}$, entonces $\mathcal{S}$ es numerable.

Más adelante…

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Teoría de los Conjuntos I: El complemento de un conjunto

Por Gabriela Hernández Aguilar

Deja un comentario

Introducción

En esta entrada hablaremos acerca del complemento de un conjunto y algunos resultados que se dan a partir de esta definición. A su vez, veremos las leyes de De Morgan, las cuales nos dirán cuál es el complemento de la intersección y de la unión de dos o más conjuntos.

Complemento de un conjunto

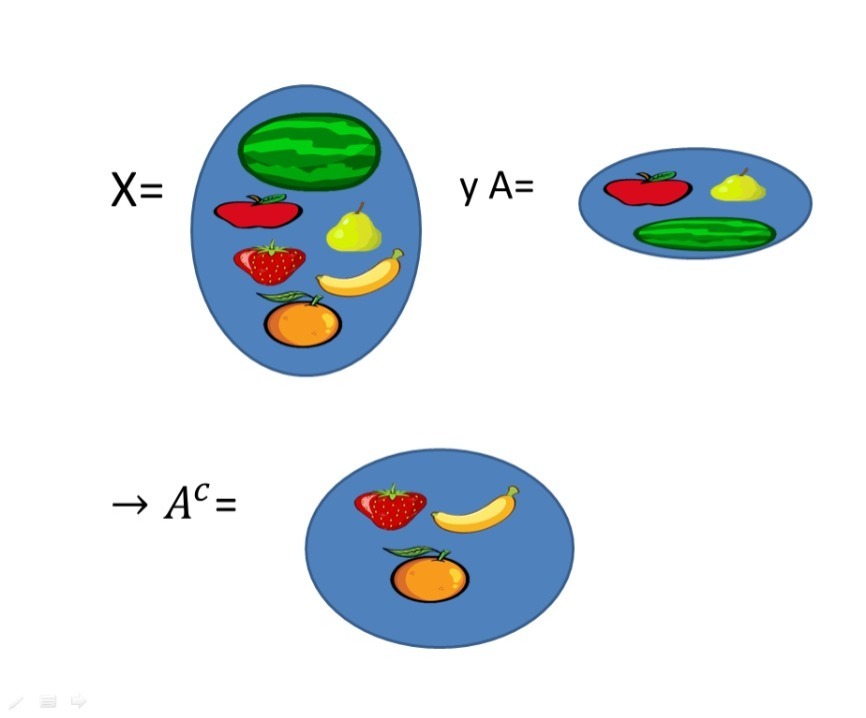
Definición. Sean $A$ y $X$ conjuntos, tales que $A\subseteq X$. Definimos al complemento de $A$ respecto del conjunto $X$, como la diferencia $X\setminus A$.

Ejemplo.

Sea $X=\set{\emptyset, \set{\emptyset}, \set{\set{\emptyset}}, \set{\emptyset, \set{\emptyset}}}$ y sea $A=\set{\emptyset, \set{\emptyset, \set{\emptyset}}}$. Tenemos que $X\setminus A=\set{x\in X: x\notin A}=\set{\set{\emptyset}, \set{\set{\emptyset}}}$.

En efecto, pues $\emptyset\in X$ y $\emptyset\in A$ por lo que $\emptyset\notin X\setminus A$ pues no cumple la propiedad para ser elemento del conjunto $X\setminus A$. Por su parte, $\set{\emptyset,\set{\emptyset}}$ tampoco es elemento de $X\setminus A$ pues $\set{ \emptyset,\set{\emptyset}}\in X$ y $\set{ \emptyset,\set{\emptyset}}\in A$. Finalmente, $\set{\emptyset}$, $\set{\set{\emptyset}}\in X$ y $\set{\emptyset}$, $\set{\set{\emptyset}}\notin A$, por lo que $\set{\emptyset}$, $\set{\set{\emptyset}}\in X\setminus A$.

$\square$

Resultados del conjunto complemento

Usaremos el siguiente resultado repetidamente para la demostración de propiedades posteriormente.

Proposición. Sean $A$, $B$, $X$ conjuntos, tales que $A$, $B\subseteq X$. Demuestra que $A\setminus B=A\cap (X\setminus B)$.

Demostración.

$\subseteq$] Sea $a\in A\setminus B$, entonces $a\in A$ y $a\notin B$. Como $a\in A\subseteq X$, entonces $a\in X$. Así, es cierto que $a\in A$ y ($a\in X$ y $a\notin B$), por lo que $a\in A$ y $a\in X\setminus B$ y por lo tanto, $a\in A\cap (X\setminus B)$.

Concluimos que $A\setminus B\subseteq A\cap (X\setminus B)$.

$\supseteq$] Sea $a\in A\cap(X\setminus B)$, entonces $a\in A$ y $a\in X \setminus B$. Entonces $a\in A$ y $a\in X$ y $a\notin B$, en particular, $a\in A$ y $a\notin B$. Así, $a\in A\setminus B$.

Por lo tanto, $A\cap (X\setminus B)= A\setminus B$.

$\square$

Veamos otras tres propiedades del complemento.

Proposición. Sean $A$ y $X$ conjuntos tales que $A\subseteq X$. Entonces se cumple lo siguiente:

a) $A\cap (X\setminus A)=\emptyset$,

b) $A\cup (X\setminus A)=X$,

c) $X\setminus(X\setminus A)= A$.

Demostración:

a) Supongamos que $A\cap(X\setminus A)\not=\emptyset$ en búsqueda de una contradicción. Entonces, existe $x\in A\cap(X\setminus A)$, de donde $x\in A$ y $x\in X\setminus A$.

Así, $x\in A$ y $x\in X$ y $x\notin A$. En particular, $x\in A$ y $x\notin A$ lo cual no puede ocurrir. Por lo tanto, $A\cap(X\setminus A)=\emptyset$.

b) Sea $x\in A\cup (X\setminus A)$, entonces $x\in A$ o $x\in X\setminus A$.

Caso 1: Si $x\in A$, entonces $x\in X$ pues $A\subseteq X$.

Caso 2: Si $x\in X\setminus A$, entonces $x\in X$ y $x\notin A$. En particular, $x\in X$.

En cualquier caso, $x\in X$. Por lo tanto, $A\cup (X\setminus A)\subseteq X$.

Por otro lado, supongamos que $x\in X$. Tenemos dos casos: $x\in A$ o $x\notin A$.

Caso 1: Si $x\in A$, entonces $x\in A\cup (X\setminus A)$.

Caso 2: Si $x\notin A$, entonces $x\in X$ y $x\notin A$ y así, $x\in X\setminus A$. Por lo tanto, $x\in A\cup(X\setminus A)$.

En cualquiera de los dos casos concluimos que $X\subseteq A\cup (X\setminus A)$.

Por lo tanto, $A\cup (X\setminus A)= X$.

c) Primero veamos que $A\subseteq X\setminus (X\setminus A)$. Sea $x\in A$, entonces $x\notin X\setminus A$. Por otro lado, $x\in X$ pues $A\subseteq X$.

Por lo que $x\in X$ y $x\notin X\setminus A$, es decir, $x\in X\setminus(X\setminus A)$. Esto concluye la prueba de que $A\subseteq X\setminus (X\setminus A)$.

Ahora, sea $x\in X\setminus (X\setminus A)$, entonces $x\in X$ y $x\notin X\setminus A$. Esto implica que $x\in X$ y ($x\notin X$ o $x\in A$). Como $x\in X$, entonces $x\notin X$ no es posible y así, $x\in A$. Por lo tanto, $X\setminus(X\setminus A)\subseteq A$.

Por lo tanto, $A=X\setminus (X\setminus A)$.

$\square$

Leyes de De Morgan

Las leyes de De Morgan nos dicen cómo se comportan los complementos de uniones e intersecciones. A continuación damos la versión para uniones e intersecciones de dos conjuntos. En los ejercicios tendrás que demostrar las versiones para uniones e intersecciones arbitrarias.

Teorema. Sean $A$, $B$ y $X$ conjuntos. Entonces

  1. $X\setminus (A\cap B)= (X\setminus A)\cup (X\setminus B)$,
  2. $X\setminus (A\cup B)= (X\setminus A)\cap (X\setminus B)$. 1

Demostración.

  1. Se tiene $x\in X\setminus (A\cap B)$,
    si y sólo si $x\in X$ y $x\notin A\cap B$ por definición de complemento,
    si y sólo si $x\in X$ y ($x\notin A$ o $x\notin B$),
    si y sólo si ($x\in X$ y $x\notin A$) o $(x\in X$ y $x\notin B$),
    si y sólo si $x\in X\setminus A$ o $x\in X\setminus B$,
    si y sólo si $x\in (X\setminus A)\cup (X\setminus B)$.
    Por lo tanto, $X\setminus(A\cap B)=(X\setminus A)\cup (X\setminus B)$.
  2. Se tiene $x\in X\setminus (A\cup B)$,
    si y sólo si $x\in X$ y $x\notin A\cup B$ por definición de complemento,
    si y sólo si $x\in X$ y ($x\notin A$ y $x\notin B$),
    si y sólo si ($x\in X$ y $x\notin A$) y $(x\in X$ y $x\notin B$),
    si y sólo si $x\in X\setminus A$ y $x\in X\setminus B$,
    si y sólo si $x\in (X\setminus A)\cap (X\setminus B)$.
    Por lo tanto, $X\setminus(A\cup B)=(X\setminus A)\cap (X\setminus B)$.

$\square$

Tarea moral

  • Demuestra que para $X$ un conjunto cualquiera se cumple que $X\setminus \emptyset= X$.
  • Prueba que si $X$ un conjunto arbitrario, entonces $X\setminus X=\emptyset$.
  • Sean $A$, $B\subseteq X$ conjuntos. Prueba que $A\subseteq B$ si y sólo si $X\setminus B\subseteq X\setminus A$.
  • Muestra que si $A$ es un conjunto no vacío, entonces $(A\cup A)\setminus A\not=A\cup (A\setminus A)$.
  • Sean $X$ y $F$ conjuntos:
    – Muestra que $X\setminus (\bigcup F) = \bigcap (X\setminus F)$.
    – Supongamos que $F\neq \emptyset$. Muestra que $X\setminus (\bigcap F) = \bigcup (X\setminus F)$.

Este último ejercicio son las leyes de De Morgan para intersecciones y uniones arbitrarias.

Más adelante…

En la siguiente entrada hablaremos acerca del álgebra de conjuntos, para ello retomaremos las operaciones entre conjuntos que definidas anteriormente. Así mismo, haremos uso de los resultados que probamos en esta sección acerca del complemento de un conjunto. Un poco después, definiremos una nueva operación entre conjuntos: la diferencia simétrica.

Entradas relacionadas

Entradas relacionadas:


Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

  1. También puedes consultar la demostración de este teorema en: Gómez L. C, Álgebra Superior Curso Completo. Publicaciones Fomento Editorial, 2014, p. 32-33. ↩︎