Introducción
Así como ya hicimos comparaciones de continuidad o diferenciabilidad del límite de una sucesión de funciones a partir de sus términos, en esta ocasión lo haremos con funciones integrables.
Partimos de una sucesión de funciones donde para cada $n \in \mathbb{N}, \, f_n:[a,b] \to \mathbb{R}, \, a,b \in \mathbb{R}.$ Supón además que $(f_n)_{n \in \mathbb{N}}$ converge puntualmente a una función $f$ en $[a,b].$
Si cada una de las funciones $f_n$ son integrables, ¿será $f$ también integrable?
¿La sucesión de integrales converge? ¿Su límite coincide con la integral del límite? Veamos el siguiente:
Ejemplo.
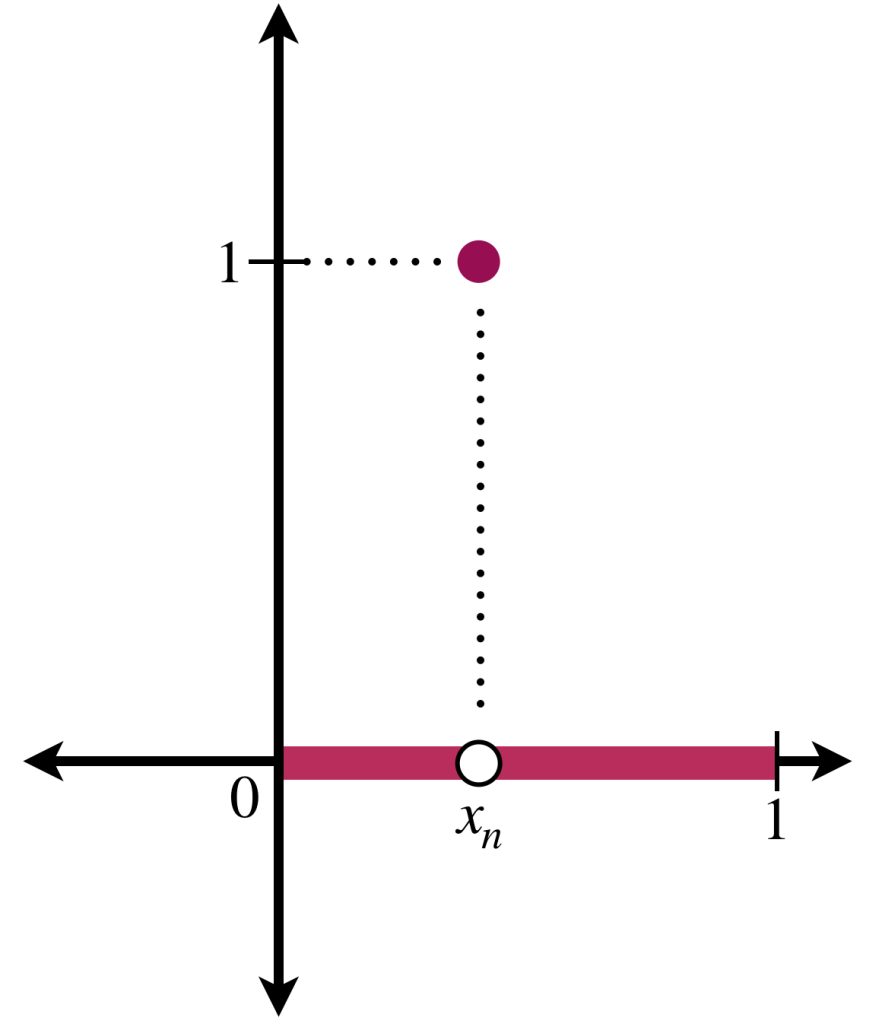
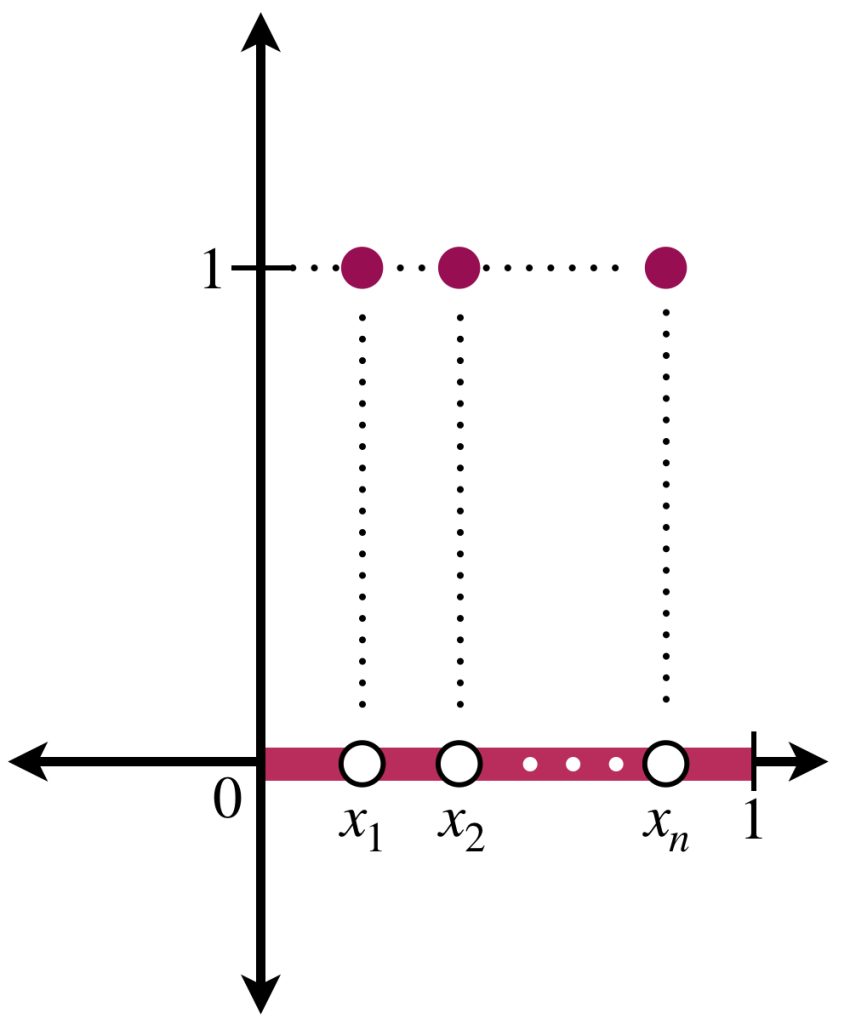
Considera el conjunto $\mathbb{Q} \cap [0,1].$ Como es numerable, podemos identificarlo como $\mathbb{Q} \cap [0,1] = \{ x_n: n \in \mathbb{N} \}.$ Para cada $n \in \mathbb{N}$ definimos $\mathcal{X}_{\{x_n\}}$ como la función característica dada por:
\begin{equation*}
\mathcal{X}_{\{x_n\}} = \begin{cases}
1 & \text{si $x = x_n$} \\
0 & \text{si $x \neq x_n$}
\end{cases}
\end{equation*}
Ahora, para cada $n \in \mathbb{N}$ definimos $f_n = \mathcal{X}_{\{x_1\}}+…+\mathcal{X}_{\{x_n\}}.$
Entonces la función $f_n$ es integrable en $[a,b]$ y la sucesión $(f_n)_{n \in \mathbb{N}}$ converge puntualmente a la función:
\begin{equation*}
\mathcal{X}_{ \, \mathbb{Q} \cap [0,1]} = \begin{cases}
1 & \text{si $x \in \mathbb{Q} \cap [0,1]$} \\
0 & \text{si $x \notin\mathbb{Q} \cap [0,1]$}
\end{cases}
\end{equation*}
Pero $\mathcal{X}_{ \, \mathbb{Q} \cap [0,1]}$ no es integrable en $[0,1].$ Por lo tanto la convergencia puntual podría no bastar para que el límite sea integrable. ¿Y si la convergencia es uniforme?
Proposición: Sea $(f_n)_{n \in \mathbb{N}}$ una sucesión de funciones integrables en $[a,b]$ que converge uniformemente a una función $f$ en $[a,b].$ Entonces $f$ es integrable y
$$\int_{a}^{b} f = \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n.$$
Demostración:
Para cada $n \in \mathbb{N}$ sea $\large{\varepsilon_n} := \underset{a \leq x \leq b}{sup}|f_n(x) – f(x)|.$
Entonces $f_n \, – \, \large{\varepsilon_n} \leq f \leq f_n + \varepsilon_n,$ de modo que las integrales superior e inferior de $f$ satisfacen:
$\int_{a}^{b} (f_n \, – \, \large{\varepsilon_n}) \, dx \leq \underline{\int} f \, dx\leq \overline{\int} f \, dx \leq \int_{a}^{b}(f_n + \large{\varepsilon_n}) \, dx$
Entonces $0 \leq \overline{\int} f \, dx – \underline{\int} f \, dx \leq \int_{a}^{b}(f_n + \large{\varepsilon_n}) \, dx – \int_{a}^{b} (f_n – \large{\varepsilon_n}) \, dx = 2\large{\varepsilon_n}[b-a].$
Dado que $\large{\varepsilon_n} \to 0$ porque $(f_n)_{n \in \mathbb{N}} \to f$ de manera uniforme, se sigue que $\overline{\int} f=\underline{\int} f.$ Por lo tanto $f$ es integrable.
Podemos ver también que
$\left| \int_{a}^{b} f \, dx \, – \, \int_{a}^{b} f_n \, dx \right| \leq \large{\varepsilon_n}[b-a] \to 0$ lo que demuestra que
$$\int_{a}^{b} f = \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n.$$
Es importante mencionar que la convergencia uniforme no es una condición necesaria para que se de esta igualdad. Veamos el siguiente:
Ejemplo.
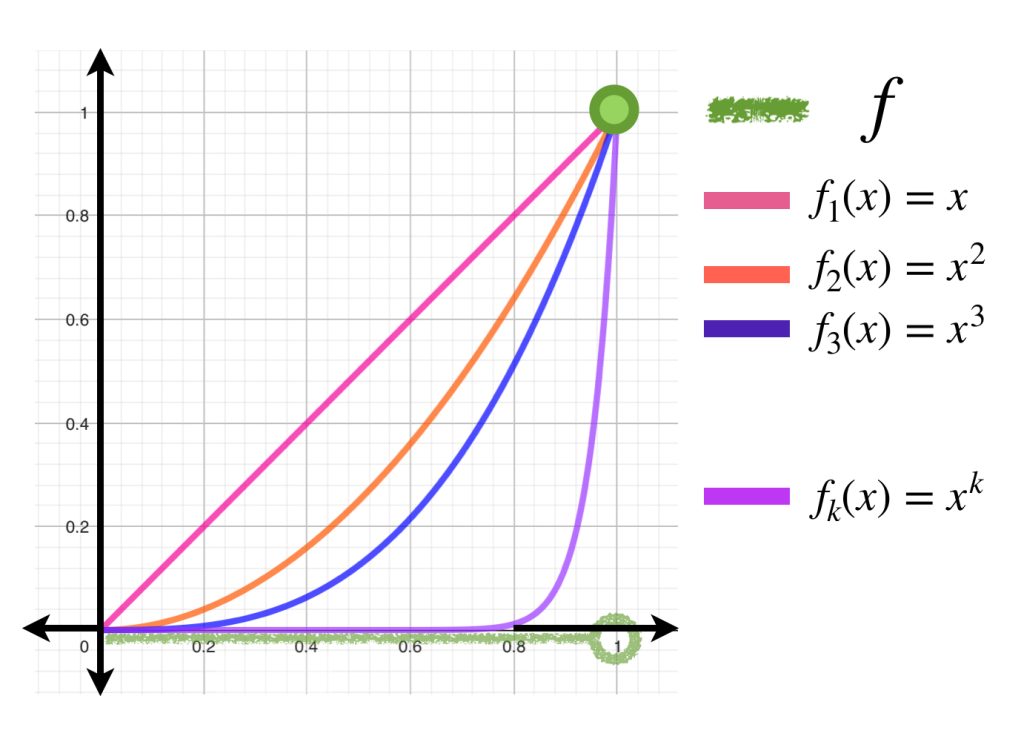
Para cada $n \in \mathbb{N}$ sea $f_n(x) = x^n$ con $x \in [0,1].$ En la entrada Convergencia uniforme y continuidad mostramos que la sucesión $(x^n)_{n \in \mathbb{N}} \, $ converge puntualmente a la función:
\begin{equation*}
f(x)= \begin{cases}
0 & \text{ si $0\leq x<1$}\\
1 & \text{ si $x=1$}
\end{cases}
\end{equation*}
Si calculamos las integrales tenemos que para cada $n \in \mathbb{N}:$
$\large{\int_{0}^{1}x^n} \, dx = \dfrac{1}{n+1} \to 0 = \large{\int_{0}^{1} f(x)} \, dx.$
Por lo tanto
$$ \int_{0}^{1}f(x) \, dx =\underset{n \to \infty}{lim} \, \int_{0}^{1}f_n(x) \, dx.$$
Las condiciones de este ejemplo pueden generalizarse. Antes conozcamos algunas definiciones:
Definición. Sucesión uniformemente acotada: Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión de funciones con $f_n: A \subset \mathbb{R} \to \mathbb{R}, \, n \in \mathbb{N}$. Diremos que es uniformemente acotada en $A$ si existe $M >0 \in \mathbb{R}$ tal que $|f_n(x)| \leq M$ para cualquier $x \in A$ y cualquier $n \in \mathbb{N}.$
Definición. Sucesión acotadamente convergente: Una sucesión de funciones $(f_n)_{n \in \mathbb{N}} \,$ con $f_n: A \subset \mathbb{R} \to \mathbb{R}, \, n \in \mathbb{N}$ es acotadamente convergente en $A$ si converge puntualmente y es uniformemente acotada en $A.$
Proposición: Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión acotadamente convergente en $[a,b]$ donde cada función es integrable en $[a,b],$ y que la función límite $f$ es integrable en $[a,b].$ Supongamos también que existe una partición $P$ de $[a,b],$ a saber, $P=\{x_0,x_1,…,x_m\},$ tal que la sucesión $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente convergente hacia $f$ en cada subintervalo $[c,d] \subset [a,b]$ que no contenga ninguno de los puntos $x_k \in P.$ Entonces:
$$ \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n(x) \, dx = \int_{a}^{b} f(x) \, dx.$$
Demostración:
Dado que $f$ es acotada y $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente acotada, existe $M >0$ tal que $|f(x)| \leq M$ para cada $x \in [a,b]$ y para cualquier $n \in \mathbb{N}.$
Sea $\varepsilon > 0$ tal que $2 \varepsilon < \norm{P},$
sea $h = \frac{\varepsilon}{2m},$ donde $m$ es el múmero de subintervalos de $P,$
considera una nueva partición $P’$ de $[a,b]$ dada por:
$P’=\{x_0, \, x_0+h,\, x_1-h,\, x_1+h, \, … \, ,x_{m-1}-h, \, x_{m-1}+h, \, x_m-h, \, x_m\}$
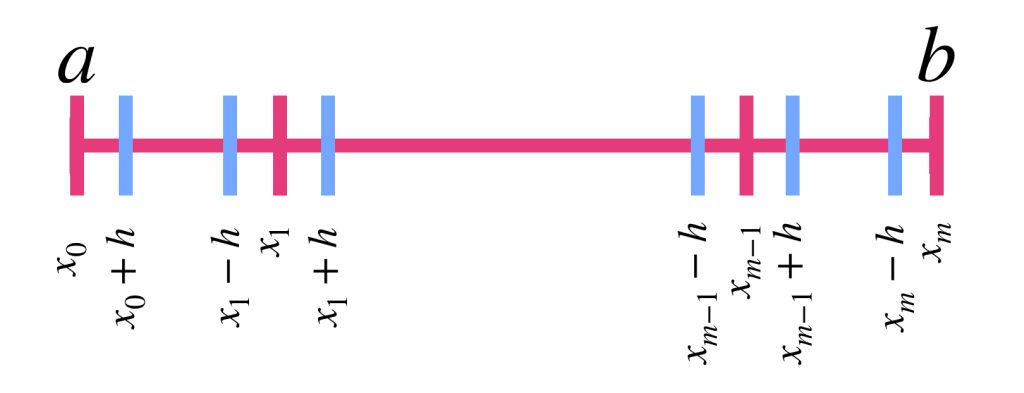
Nota que la función $|f-f_n|$ es integrable en $[a,b]$ y es acotada por $2M.$ Consideremos la integral de esta función en cada uno de los intervalos de la nueva partición $P’.$
Por un lado, consideremos la suma de las integrales de $|f-f_n|$ tomadas sobre los intervalos que sí tienen algún punto de $P,$ es decir los intervalos
$[x_0,x_0+h], \, [x_1-h,x_1+h],…,[x_{m-1}-h,x_{m-1}+h], \, [x_m-h,x_m].$
La suma está dada por:
\begin{align*}
&\int_{x_0}^{x_0+h} |f-f_n|(x)\, dx + \int_{x_1-h}^{x_1+h} |f-f_n|(x)\, dx +…+ \int_{x_{m-1}-h}^{x_{m-1}+h} |f-f_n|(x)\, dx + \int_{x_m-h}^{x_m} |f-f_n|(x)\, dx \\
\leq & 2M(x_0+h-x_0) + 2M(x_1+h-(x_1-h))+…+2M(x_{m-1}+h-(x_{m-1}-h))+2M(x_m-(x_m-h)) \\
=&2Mh+2M(2h)+…+2M(2h)+2Mh \\
=&2M(2hm) \\
=&2M \varepsilon
\end{align*}
El subconjunto restante de $[a,b]$ lo llamaremos $S.$ Está formado por un número finito de intervalos cerrados en los que $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente hacia $f$ (pues no tiene ningún punto de $P$). Por consiguiente, existe $N \in \mathbb{N}$ tal que para cada $x \in S,$ si $n \geq N \,$ se cumple que
$$|f(x)-f_n(x)| < \varepsilon$$
De modo que la suma de las integrales de $|f-f_n|$ sobre los intervalos de $S$ es a lo sumo $\large{\varepsilon} (b-a),$ luego para cada $n \geq N:$
$\int_{a}^{b}|f(x)-f_n(x)|dx \leq (2M + b-a) \large{\varepsilon} \, \to \, 0.$
Esto demuestra que $\int_{a}^{b}f_n(x)dx \to \int_{a}^{b}f(x)dx$ cuando $n \to \infty .$
En la última sección de Análisis Matemático I hablaremos de la integral de Riemann-Stieljes, que es un concepto que generaliza la integral de Riemann. La proposición vista aquí se puede expresar como sigue:
Proposición. Sucesión de funciones Riemann-Stieljes: Sea $\alpha$ monótona en $[a,b].$ Supón que para cada $n \in \mathbb{N}, \, f_n \in \mathcal{R}(\alpha)$ en $[a,b].$ Si $(f_n)_{n \in \mathbb{N}}$ converge uniformemente a $f$ en $[a,b]$ entonces $f \in \mathcal{R}(\alpha)$ en $[a,b]$ y:
$$\int_{a}^{b} f \, d \alpha = \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n \, d \alpha .$$
Más adelante…
Hablaremos de series de funciones y del límite de ellas. Así conoceremos el concepto de convergencia uniforme pero ahora en sumas infinitas.
Tarea moral
- Sea $f_n$ como en el primer ejemplo. Prueba que en efecto la sucesión $(f_n)_{n \in \mathbb{N}} \,$ no converge uniformemente a la función:
\begin{equation*}
\mathcal{X}_{ \, \mathbb{Q} \cap [0,1]} = \begin{cases}
1 & \text{si $x \in \mathbb{Q} \cap [0,1]$} \\
0 & \text{si $x \notin\mathbb{Q} \cap [0,1]$}
\end{cases}
\end{equation*} - Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión de funciones acotadas con $f_n: A \subset \mathbb{R} \to \mathbb{R}, \, n \in \mathbb{N}, \,$ tal que converge uniformemente a una función $f:A \to \mathbb{R}.$ Demuestra que $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente acotada en $A.$
- Regresa luego de ver la integral de Riemann-Stieljes y demuestra la última proposición de esta sección.