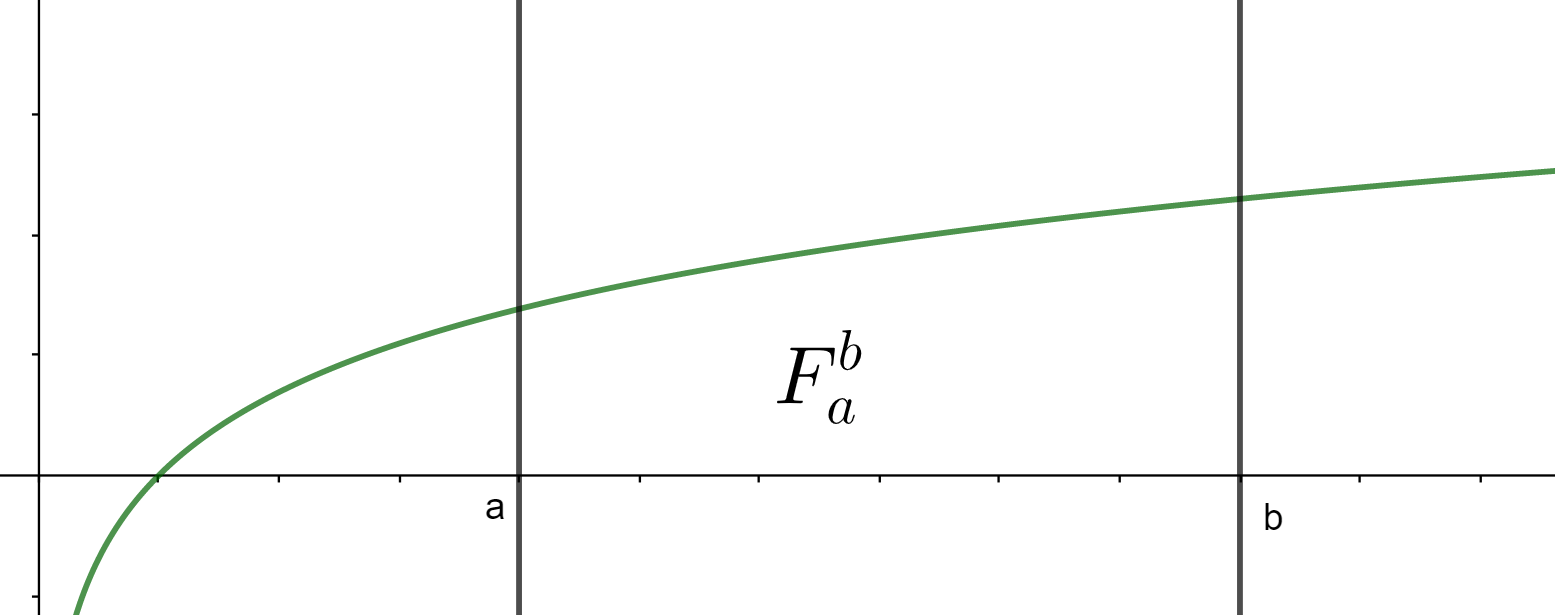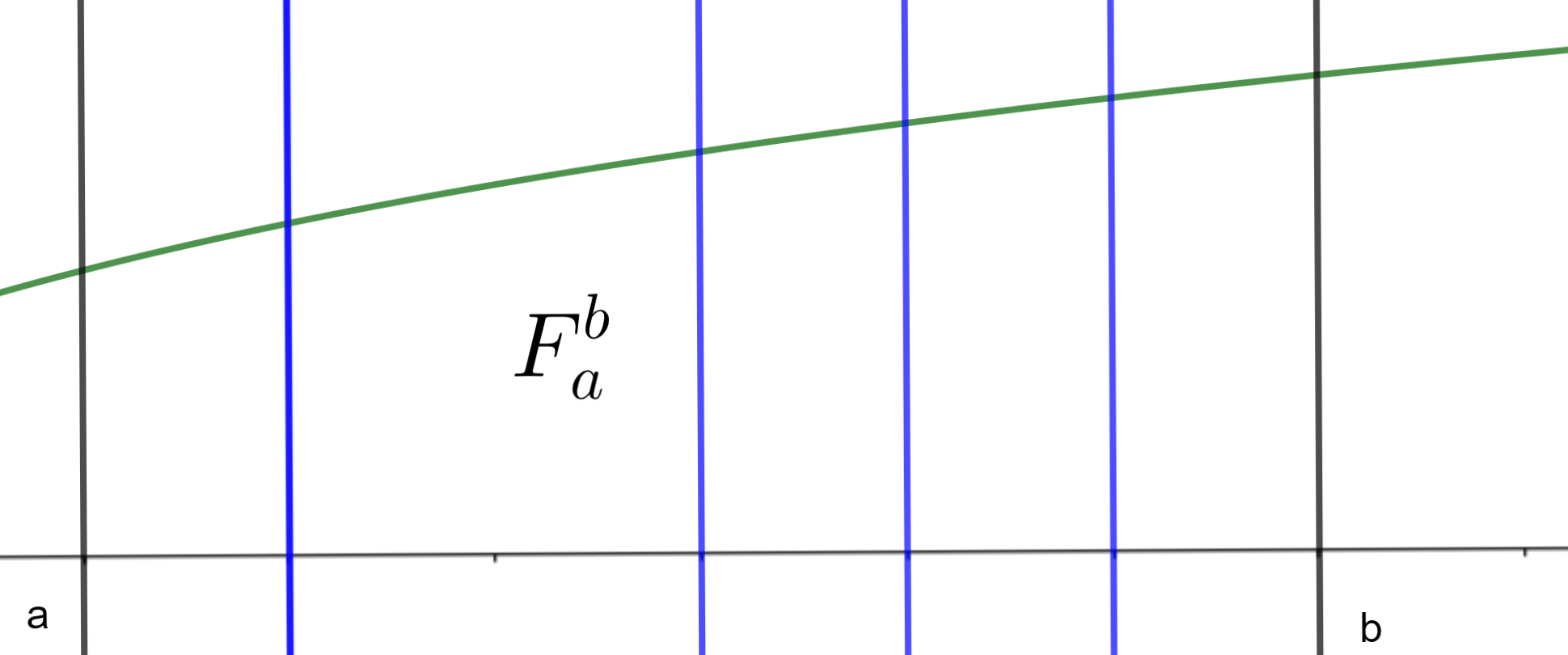Archivo de la etiqueta: ínfimo

Teoría de los Conjuntos I: Cotas inferiores e ínfimos

Por Gabriela Hernández Aguilar

Introducción

En esta entrada hablaremos acerca de cotas inferiores e ínfimos. Estos nuevos conceptos nos permitirán establecer intuitivamente qué quiere decir que un conjunto esté «limitado» una vez que hemos dado un orden.

Cotas inferiores

Para comenzar definiremos qué es una cota inferior. Notaremos que este concepto es muy parecido al de mínimo, sin embargo una cota inferior podría no ser elemento de $B$ un subconjunto de $A$ . Veamos la definición.

Definición. Sea $(A, \leq)$ un orden parcial y sea $B \subseteq A$ . Decimos que $a \in A$ es una cota inferior de $B$ si $a \leq x$ para toda $x \in B$ . Si $B$ tiene por lo menos una cota inferior, diremos que $B$ está acotado inferiormente.

Ejemplo.

Sea $A = {\emptyset, {\emptyset}, {\emptyset, {\emptyset}}}$ y consideremos al conjunto parcialmente ordenado $(A, \subseteq)$ . Sea $B = {{\emptyset}, {\emptyset, {\emptyset}}} \subseteq A$ , tenemos que $\emptyset \in A$ es una cota inferior de $B$ pues $\emptyset \subseteq x$ para todo $x \in B$ , como se muestra en el siguiente diagrama:

Sin embargo, podemos notar que $\emptyset \notin B$ , por lo que para ser cota inferior no es necesario ser elemento de $B$ , solo de $A$ . Por otro lado, ${\emptyset} \in B$ también es una cota inferior de $B$ pues para cada $x \in B$ , ${\emptyset} \subseteq x$ . Más aún, ${\emptyset}$ es el elemento mínimo de $B$ .

El ejemplo anterior sugiere que la propiedad de ser mínimo implica ser cota inferior, pero no es válido el recíproco.

En este último ejemplo es posible notar que la cota inferior en un conjunto puede no ser única, y entonces podemos pensar en el conjunto que tenga a todas las cotas inferiores. Esta idea junto con el concepto de máximo motiva el concepto de ínfimo.

Ínfimos

Definición. Sea $(A, \leq)$ un orden parcial y sea $B \subseteq A$ . Decimos que $a \in A$ es ínfimo de $B$ si es el elemento máximo del conjunto de todas las cotas inferiores de $B$ . Lo denotaremos por $inf (B)$ .

Ejemplo.

Retomando el ejemplo anterior, si consideramos al conjunto de todas las cotas inferiores de $B$ , es decir, ${\emptyset, {\emptyset}}$ tenemos que el ínfimo es ${\emptyset}$ pues respecto al orden de $A$ , $\emptyset \subseteq {\emptyset}$ y por lo tanto, ${\emptyset}$ es el máximo de las cotas inferiores de $B$ .

Teorema. Sea $(A, \leq)$ un orden parcial y $B \subseteq A$ un conjunto no vacío. Si $B$ tiene ínfimo en el orden $\leq$ , entonces es único.

Demostración.

Sea $(A, \leq)$ un orden parcial y $B \subseteq A$ no vacío. Supongamos que $B$ tiene ínfimo, es decir, que existe $a \in A$ de tal forma que $a \leq x$ para toda $x \in B$ y, si $b \in A$ es tal que $b \leq x$ para toda $x \in B$ , entonces, $b \leq a$ .

Supongamos que $a_{1}, a_{2} \in A$ son ínfimos de $B$ . Veamos que $a_{1} = a_{2}$ .

Como $a_{1}$ es ínfimo $B$ , en particular se tiene que $a_{1} \leq x$ para toda $x \in B$ . Luego, como $a_{2}$ es ínfimo de $B$ se sigue por definición que $a_{1} \leq a_{2}$ . De manera análoga, como $a_{2}$ es ínfimo de $B$ , en particular se tiene que $a_{2} \leq x$ para toda $x \in B$ y así, como $a_{1}$ es ínfimo de $B$ se sigue por definición que $a_{2} \leq a_{1}$ .

Tenemos entonces que $a_{1} \leq a_{2}$ y $a_{2} \leq a_{1}$ , de donde se sigue que $a_{1} = a_{2}$ , lo cual demuestra la unicidad del ínfimo.

Teorema. Sea $(A, \leq)$ un orden parcial y $B \subseteq A$ un conjunto no vacío. Si $B$ tiene un elemento mínimo $b$ , entonces $b$ es el ínfimo de $B$ .

Demostración.

Sea $(A, \leq)$ un orden parcial y $B \subseteq A$ un conjunto no vacío. Luego, si $b \in B$ es el elemento mínimo de $B$ , entonces para cualquier $x \in B$ , $b \leq x$ .

Sea $C$ el conjunto de todas las cotas inferiores de $B$ . Veamos que $b \in C$ y que $b = max (C)$ . Dado que $b \leq x$ para todo $x \in B$ , $b$ es cota inferior de $B$ y, por tanto, $b \in C$ . Luego, si $c \in C$ es cualquier elemento, entonces $c$ es cota inferior de $B$ , es decir, $c \leq x$ para cualquier $x \in B$ . En particular, como $b \in B$ se tiene que $c \leq b$ . Esto muestra que $b = max (C)$ .

Por lo tanto, $b = inf (B)$ .

Aún cuando ser mínimo implica ser ínfimo, no siempre va a ocurrir que el ínfimo de un conjunto sea mínimo, como ocurre en el siguiente ejemplo.

Ejemplo.

Sea $A = {\emptyset, {\emptyset}, {{\emptyset}}, {\emptyset, {\emptyset}}}$ y consideremos al conjunto parcialmente ordenado $(A, \subseteq)$ . Sea $B = {{\emptyset}, {{\emptyset}}, {\emptyset, {\emptyset}}} \subseteq A$ . Tenemos que $\emptyset \in A$ es una cota inferior de $B$ pues $\emptyset \leq x$ para todo $x \in B$ , como se muestra en el siguiente diagrama:

Sin embargo, $B$ no tiene mínimo pues no existe $x \in B$ tal que $x \leq y$ para todo $y \in B$ . En efecto, si existiera tal $x$ tendría que ser simultáneamente subconjunto de ${\emptyset}$ y de ${{\emptyset}}$ . Pero el único subconjunto que comparten estos conjuntos es $\emptyset$ , que no está en $B$ .

Tarea moral

La siguiente lista de ejercicios te ayudará a reforzar el contenido de esta entrada y de la entrada anterior.

Sean $(A, \leq)$ un orden parcial y $B \subseteq A$ un conjunto no vacío. Demuestra que si $b$ es ínfimo y $b \in B$ , entonces $b$ es mínimo de $B$ .
Sean $(A, \leq)$ un orden parcial y $B, C \subseteq A$ no vacíos. Si $B$ y $C$ tienen ínfimo y $C \subseteq B$ , demuestra que $i n f (B) \leq i n f (C)$ .
Exhibe un conjunto que esté acotado inferiormente pero que no tenga ínfimo.
Da un ejemplo de un conjunto parcialmente ordenado $(A, \leq)$ en el cual se cumpla que el conjunto $\emptyset$ tiene ínfimo.
Escribe las definiciones de cota inferior e ínfimo para un orden parcial estricto.

Más adelante…

La siguiente entrada estará dedicada a cotas superiores y supremos. Con esto concluiremos la sección de acotar conjuntos ordenados.

Entradas relacionadas

Ir a Teoría de los Conjuntos I
Entrada anterior: Teoría de los Conjuntos I: Mínimos, máximos, minimales y maximales
Siguiente entrada: Teoría de los Conjuntos I: Cotas superiores y supremos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Cálculo Diferencial e Integral II: Propiedades de la integral definida

Por Moisés Morales Déciga

Deja un comentario

Introducción

En las entradas anteriores se dio la motivación de la construcción de la integral y la definición de la integral de Riemann. Para que cierta integral exista, necesitamos que el ínfimo de ciertas sumas superiores coincida con el supremo de ciertas sumas inferiores. Vimos algunas condiciones que garantizan que esto suceda, por ejemplo, que exista el límite de las sumas superiores e inferiores para las particiones homogéneas, y que dicho límite sea el mismo en ambos casos. Lo que haremos ahora es estudiar más propiedades de la integral.

Las propiedades que veremos nos permitirán concluir la existencia de ciertas integrales de manera sencilla y, a la vez, nos permitirán manipular algebraicamente a las integrales. En caso de necesitar un recordatorio de la definición de integral, te recomendamos consultar la entrada anterior.

Integrabilidad de familias de funciones especiales

Hay algunas propiedades de funciones que se estudian desde Cálculo I que implican la integrabilidad. A continuación presentamos un par de ejemplos.

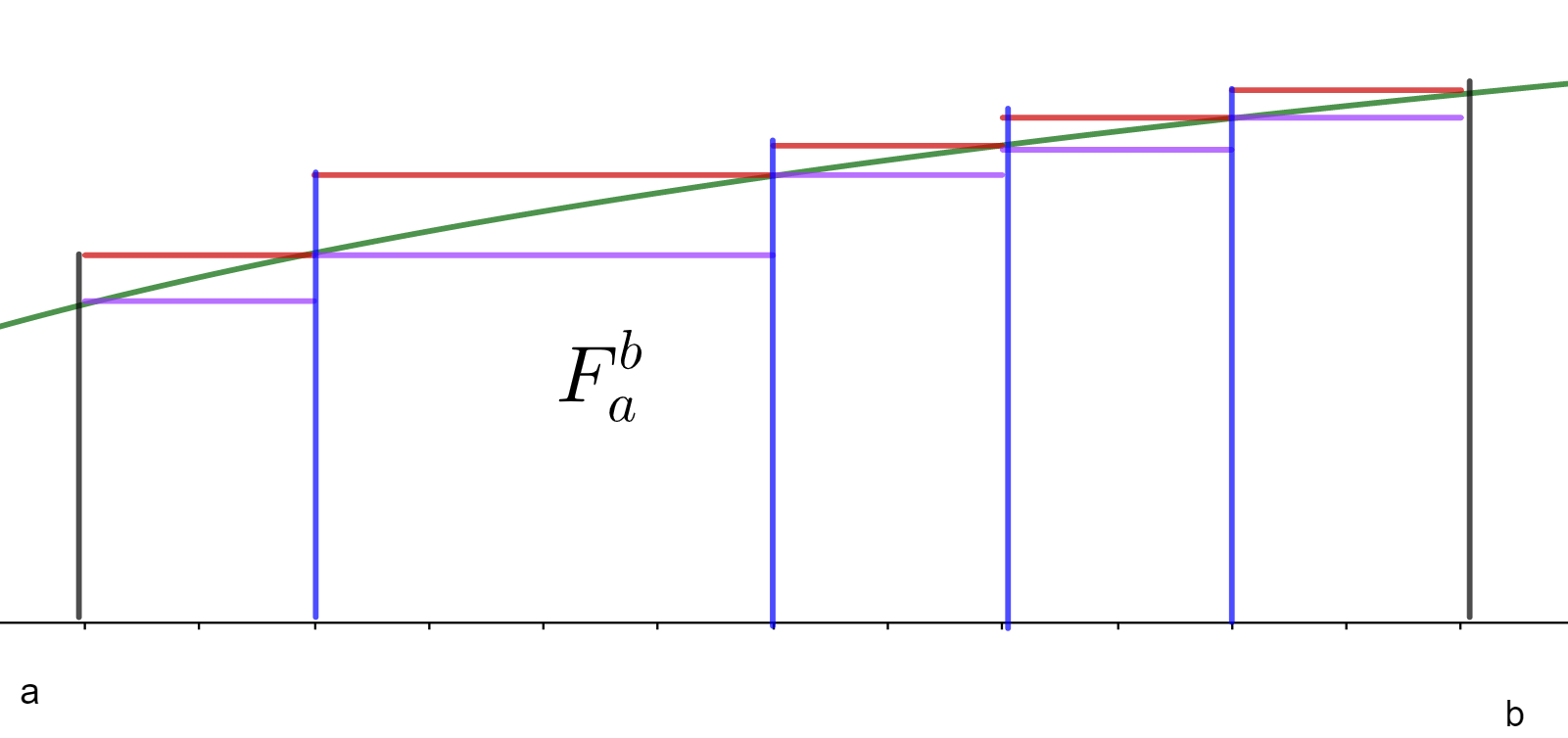
Proposición. Si $f : R \to R$ es acotada y monótona en $[a, b]$ , entonces es Riemann integrable en $[a, b]$ .

Demostración. Supondremos que $f$ es estrictamente creciente. Otras variantes de monotonía (no decreciente, no creciente, estrictamente decreciente) tienen una demostración similar, que puedes hacer por tu cuenta.

Tomemos la partición homogénea $P_{n}$ del intervalo $[a, b]$ . Definiendo $x_{j} = a + j \frac{b - a}{n}$ para $j = 0, \dots, n$ , se tiene que las celdas son $[x_{0}, x_{1}], [x_{1}, x_{2}], \dots, [x_{n - 1}, x_{n}] .$

Las celdas tienen todas longitud $\frac{b - a}{n}$ y como la función es estrictamente creciente, el mínimo se alcanza al inicio de cada celda. De esta manera, la suma inferior para esta partición es:

$\begin{array}{r} \underset{―}{S} (f, P_{n}) = \frac{b - a}{n} (f (x_{0}) + \dots + f (x_{n - 1})) . \end{array}$

Similarmente, el máximo se alcanza al final de cada celda. Por ello, la suma superior para esta partición es

$\begin{array}{r} \overset{―}{S} (f, P_{n}) = \frac{b - a}{n} (f (x_{1}) + \dots + f (x_{n})) . \end{array}$

Restando la suma inferior a la superior, obtenemos

$\begin{aligned} \overset{―}{S} (f, P_{n}) - \underset{―}{S} (f, P_{n}) & = (\frac{b - a}{n} (f (x_{1}) + \dots + f (x_{n}))) - (\frac{b - a}{n} (f (x_{0}) + \dots + f (x_{n - 1}))) \\ = \frac{b - a}{n} (f (x_{n}) - f (x_{0})) \\ = \frac{(b - a) (f (b) - f (a))}{n} . \end{aligned}$

De acuerdo a la condición de Riemann (enunciada en la entrada anterior), la función será integrable si logramos que esta diferencia sea tan pequeña como queramos. Tomemos entonces cualquier $ϵ > 0$ y $n$ un entero tan grande como para que $n > \frac{1}{ϵ} (b - a) (f (b) - f (a))$ . Para este $n$ , se cumple que

$\begin{aligned} \overset{―}{S} (f, P_{n}) - \underset{―}{S} (f, P_{n}) & = \frac{(b - a) (f (b) - f (a))}{n} < ϵ, \end{aligned}$

y por ello la función es integrable.

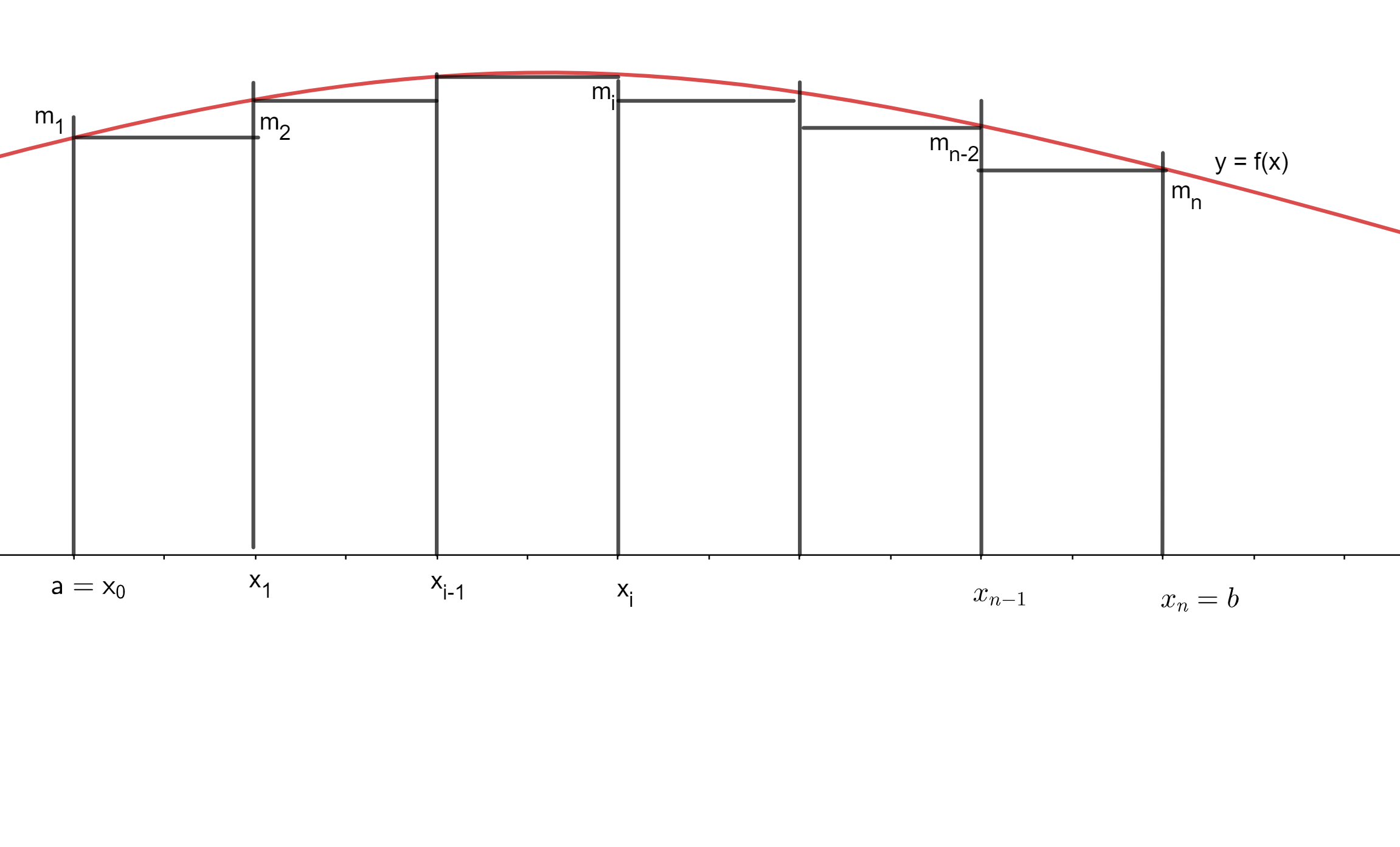
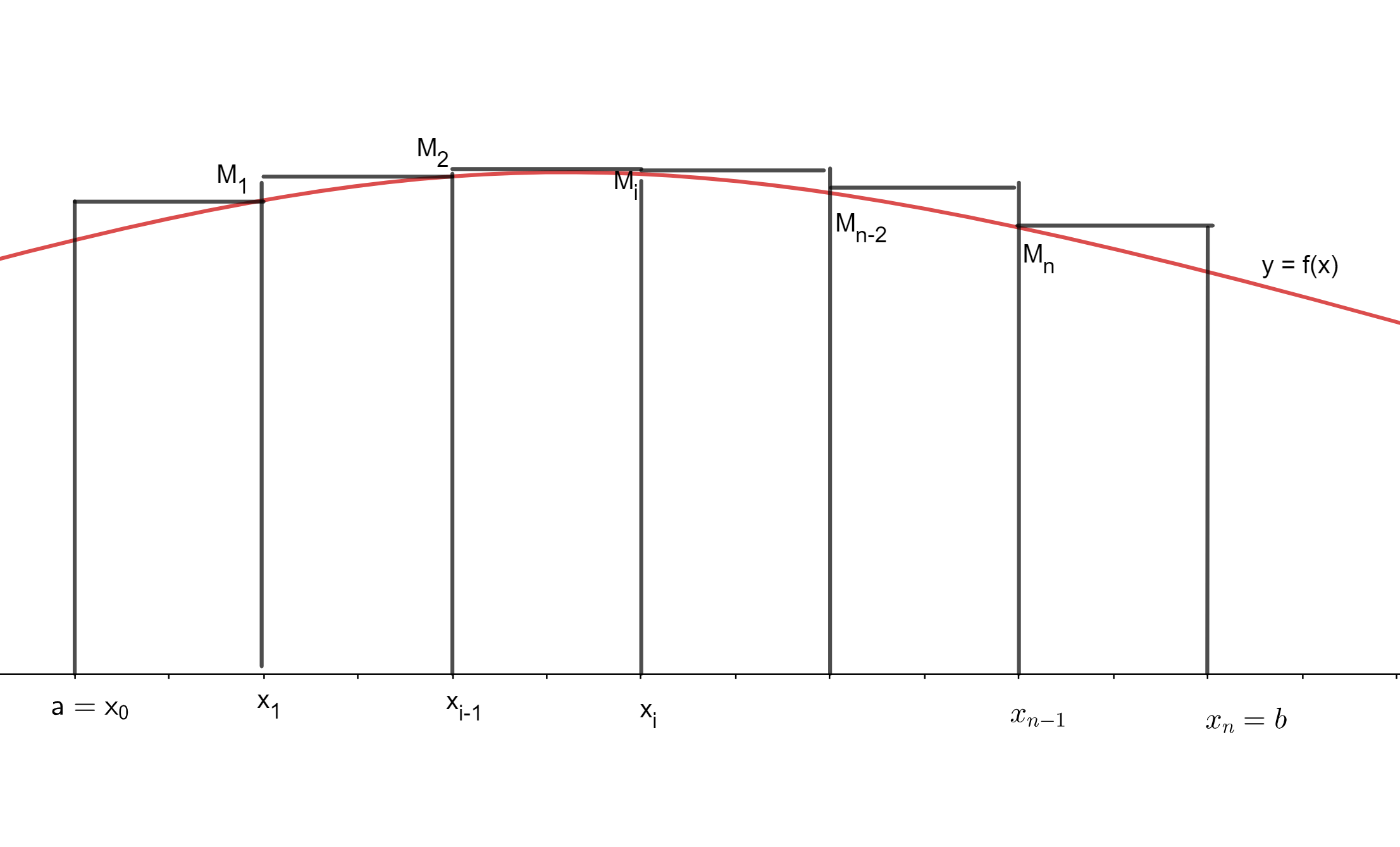
Proposición. Si $f : R \to R$ es continua en $[a, b]$ , entonces es Riemann integrable en $[a, b]$ .

Demostración. Como primera observación, como $f$ es continua en el intervalo cerrado y acotado $[a, b]$ , entonces es acotada, de modo que sí podemos hablar de sus sumas superiores e inferiores.

La estrategia que usaremos para ver que es integrable será verificar nuevamente la condición de Riemann, es decir, que para cualquier $ϵ > 0$ , existe una suma superior y una inferior cuya diferencia es menor que $ϵ$ . La intuición es que con una partición suficientemente fina, el máximo y mínimo de $f$ son muy cercanos porque los puntos que los alcanzan están en una celda muy chiquita (y entonces son muy cercanos). Para poder hacer esto «globalmente» en todas las celdas, necesitaremos una propiedad un poco más fuerte que continuidad: continuidad uniforme (puedes seguir el enlace para recordar este contenido aquí en el blog). Pero ésta se tiene pues las funciones continuas en intervalos cerrados y acotados son uniformemente continuas.

Tomemos entonces $ϵ > 0$ . Como mencionamos, $f$ es uniformemente continua y el intervalo $[a, b]$ es cerrado y acotado, entonces $f$ es uniformememente continua. Así, existe una $δ > 0$ tal que si $| x - y | < δ$ , entonces $| f (x) - f (y) | < \frac{ϵ}{b - a}$ . Tomemos $n$ tan grande como para que $\frac{b - a}{n} < δ$ . Tras hacer esto, en cada celda $i$ de la partición homogénea $P_{n}$ los valores $m_{i}$ y $M_{i}$ donde $f$ alcanza el mínimo y máximo respectivamente cumplen que $| M_{i} - m_{i} | \leq \frac{b - a}{n} < δ$ y por lo tanto para cada $i$ se tiene $f (M_{i}) - f (m_{i}) = | f (M_{i}) - f (m_{i}) | < \frac{ϵ}{b - a}$ .

Ya tenemos los ingredientes para realizar la cuenta de sumas superiores e inferiores.

Por un lado,

$\overset{―}{S} (f, P_{n}) = \frac{b - a}{n} (f (M_{1}) + \dots + f (M_{n})) .$

Por otro,

$\underset{―}{S} (f, P_{n}) = \frac{b - a}{n} (f (m_{1}) + \dots + f (m_{n})),$

así que

$\begin{aligned} \overset{―}{S} (f, P_{n}) - \underset{―}{S} (f, P_{n}) & = \frac{b - a}{n} \sum_{i = 1}^{n} (f (M_{i}) - f (m_{i})) \\ < \frac{b - a}{n} \sum_{i = 1}^{n} \frac{ϵ}{b - a} \\ = \frac{b - a}{n} (n \frac{ϵ}{b - a}) \\ = ϵ . \end{aligned}$

Esto muestra que podemos acercar una partición superior tanto como queramos a una inferior. Por el criterio de la entrada anterior, la función $f$ es integrable en $[a, b]$ .

Separación de la integral en intervalos

Enunciemos una propiedad importante de la integral: puede partirse en intervalos.

Proposición. Sea $f : R \to R$ una función acotada. Sea $c$ cualquier valor entre $[a, b]$ . Si la integral

$\int_{a}^{b} f (x) d x$

existe, entonces las dos integrales

$\int_{a}^{c} f (x) d x, \int_{c}^{b} f (x) d x$

también existen. Y viceversa, si estas dos integrales existen, entonces la primera también.

Cuando las tres integrales existen, se cumple además la siguiente igualdad:

$\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x .$

Demostración. Veamos primero que si la integral en todo $[a, b]$ existe, entonces las otras dos también. Trabajaremos usando la condición de Riemann. Sea $ϵ > 0$ . Como $f$ es integrable en $[a, b]$ , entonces existe una partición $P$ de $[a, b]$ tal que

$\overset{―}{S} (f, P) - \underset{―}{S} (f, P) < ϵ .$

Podemos suponer que uno de los puntos de $P$ es el punto $c$ , pues de no serlo, refinamos a $P$ incluyendo a $c$ . Esto no aumenta la suma superior, ni disminuye la inferior, así que sigue cumpliendo la desigualdad anterior. Si $P = {x_{0}, \dots, x_{n}}$ , podemos entonces pensar que para alguna $k$ en ${0 \dots, n}$ se cumple que $x_{k} = c$ , y entonces de esta partición de $[a, b]$ salen las particiones:

$P_{1} = {a = x_{0}, x_{1}, \dots, x_{k} = c}$ de $[a, c]$ y
$P_{2} = {c = x_{k}, x_{k + 1}, \dots, x_{n} = b}$ de $[c, b]$ .

Como las celdas de $P$ son celdas de $P_{1}$ ó $P_{2}$ , entonces las sumas superiores e inferiores cumplen:

$\begin{aligned} \overset{―}{S} (f, P_{1}) + \overset{―}{S} (f, P_{2}) & = \overset{―}{S} (f, P), \\ \underset{―}{S} (f, P_{1}) + \underset{―}{S} (f, P_{2}) & = \underset{―}{S} (f, P) . \end{aligned}$

Si se restan ambas sumas, se obtiene lo siguiente:

$\begin{array}{r} (\overset{―}{S} (f, P_{1}) - \underset{―}{S} (f, P_{1})) + (\overset{―}{S} (f, P_{2}) - \underset{―}{S} (f, P_{2})) = \overset{―}{S} (f, P) - \underset{―}{S} (f, P) < ϵ . \end{array}$

Ambos términos de la izquierda son positivos y su suma es menor que $ϵ$ , así que concluimos:

$\begin{aligned} \overset{―}{S} (f, P_{1}) - \underset{―}{S} (f, P_{1}) & < ϵ, \\ \overset{―}{S} (f, P_{2}) - \underset{―}{S} (f, P_{2}) & < ϵ . \end{aligned}$

De este modo, por el criterio de Riemann se tiene que $f$ es integrable en $[a, c]$ y en $[c, b]$ .

Si la integrales en $[a, c]$ y $[c, b]$ existen, entonces puede hacerse una prueba similar: para cualquier $ϵ$ habrá una partición $P$ de $[a, c]$ con diferencia de suma superior e inferior menor a $ϵ / 2$ , y lo mismo para una partición $P^{'}$ de $[c, b]$ . Un argumento similar al de arriba ayudará a ver que $P \cup P^{'}$ es una partición de $[a, b]$ que hace que la diferencia de la suma superior e inferior sea menor a $ϵ$ . Los detalles quedan para que los verifiques por tu cuenta.

Veamos ahora que cuando las integrales existen, entonces se cumple la igualdad

$\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x .$

Tomemos cualquier partición $P^{'}$ de $[a, b]$ . Tomemos el refinamiento $P = P^{'} \cup {c}$ y escribamos $P = P_{1} \cup P_{2}$ como arriba. Usando que las integrales son ínfimos de sumas superiores (y por lo tanto son cotas inferiores), tenemos que:

$\begin{aligned} \overset{―}{S} (f, P^{'}) & \geq \overset{―}{S} (f, P) \\ = \overset{―}{S} (f, P_{1}) + \overset{―}{S} (f, P_{2}) \\ \geq \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x . \end{aligned}$

Por definición, $\int_{a}^{b} f (x) d x$ es el ínfimo de las sumas superiores sobre todas las particiones $P^{'}$ de $[a, b]$ y entonces es la mayor de las cotas inferiores. Como arriba tenemos que $\int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x$ es cota inferior para todas estas sumas superiores, entonces:

$\int_{a}^{b} f (x) d x \geq \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x .$

Así mismo, para cualesquiera particiones $P_{1}$ y $P_{2}$ de $[a, c]$ y $[c, b]$ respectivamente, tenemos que $P_{1} \cup P_{2}$ es partición de $[a, b]$ y entonces

$\overset{―}{S} (f, P_{1}) + \overset{―}{S} (f, P_{2}) = \overset{―}{S} (f, P_{1} \cup P_{2}) \geq \int_{a}^{b} f (x) d x,$

de donde

$\overset{―}{S} (f, P_{1}) \geq \int_{a}^{b} f (x) d x - \overset{―}{S} (f, P_{2}) .$

Así, para cualquier partición $P_{2}$ fija, hemos encontrado que $\int_{a}^{b} f (x) d x - \overset{―}{S} (f, P_{2})$ es cota inferior para todas las sumas superiores de particiones $P_{1}$ de $[a, c]$ . De este modo, por ser la integral en $[a, c]$ la mayor de estas cotas inferiores, se tiene

$\int_{a}^{c} f (x) d x \geq \int_{a}^{b} f (x) d x - \overset{―}{S} (f, P_{2})$

para cualquier partición $P_{2}$ de $[c, b]$ . Pero entonces

$\overset{―}{S} (f, P_{2}) \geq \int_{a}^{b} f (x) d x - \int_{a}^{c} f (x) d x,$

se cumple para toda partición $P_{2}$ de $[b, c]$ , de donde concluimos

$\int_{b}^{c} f (x) d x \geq \int_{a}^{b} f (x) d x - \int_{a}^{c} f (x) d x .$

Despejando, obtenemos la desigualdad

$\int_{a}^{b} f (x) d x + \int_{b}^{c} f (x) d x \geq \int_{a}^{b} f (x) .$

Junto con la desigualdad que mostramos arriba, se obtiene la desigualdad deseada.

Límites reales arbitrarios

Hasta ahora siempre hemos hablado de la existencia de la integral de una función en un intervalo $[a, b]$ con $a \leq b$ . Cuando $a = b$ , la integral que buscamos es en el intervalo $[a, a]$ y se puede mostrar que en este caso la integral siempre existe y es igual a cero, es decir, que $\int_{a}^{a} f (x) d x = 0.$

La siguiente definición nos dice qué hacer cuando en los límites de integración vamos de un número mayor a uno menor.

Definición. Sea $f : R \to R$ una función acotada. Sean $a < b$ reales. Si la integral de $f$ en el intervalo $[a, b]$ existe, entonces definimos la integral de $f$ de $b$ a $a$ como sigue: $\int_{b}^{a} f (x) d x = - \int_{a}^{b} f (x) d x .$

Esta definición es compatible con todo lo que hemos platicado, y nos permite extender la identidad $\int_{a}^{c} f (x) d x, \int_{c}^{b} f (x) d x$ de la proposición de la sección anterior a valores arbitrarios de $a, b, c$ , sin importar en qué orden estén en la recta real (siempre y cuando las integrales existan, por supuesto). Por ejemplo, si $a > b > c$ , entonces podemos proceder como sigue mediante lo que ya hemos demostrado y definido:

$\begin{aligned} \int_{a}^{b} f (x) d x & = - \int_{b}^{a} f (x) d x Def. int. para a > b . \\ = - (\int_{c}^{a} f (x) d x - \int_{c}^{b} f (x) d x) Por prop. anterior pues c < b < a . \\ = - \int_{c}^{a} f (x) d x + \int_{c}^{b} f (x) d x Distribuir el - \\ = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x Def. int. para a > c . \end{aligned}$

Aquí se ve como con un orden específico de $a, b, c$ se sigue cumpliendo la identidad buscada, aunque $c$ no quede entre $a$ y $b$ y no se cumpla que $a \leq b$ . Siempre es posible hacer esto y te recomendamos pensar en cómo argumentar todos los casos posibles de $a, b, c$ .

La intuición en áreas de que la integral $\int_{b}^{a} f (x) d x$ cambia de signo con respecto a $\int_{a}^{b} f (x) d x$ es que en una recorremos el área de izquierda a derecha y en la otra de derecha a izquierda. Entonces, «recorremos el área al revés» porque «graficamos hacia atrás». Por ejemplo, se tiene el intervalo $[5, 1]$ , la forma en que se recorrerá al momento de graficar sería del $5$ al $1$ y, si la función es positiva, la integral será negativa.

Linealidad de la integral

Tomemos dos funciones acotadas $f : R \to R$ y $g : R \to R$ y supongamos que son integrables en el intervalo $[a, b]$ . Tomemos cualquier real arbitrario $α$ . A partir de esto, podemos construir la función $f + α g$ , que recordemos que su definición es que es una función de $[a, b]$ a $R$ con regla de asignación $(f + α g) (x) = f (x) + α g (x) .$

Si tomamos una partición $P$ de $[a, b]$ , se puede verificar fácilmente que

$\begin{aligned} \overset{―}{S} (f + α g, P) & = \overset{―}{S} (f, P) + α \overset{―}{S} (g, P), \\ \underset{―}{S} (f + α g, P) & = \underset{―}{S} (f, P) + α \underset{―}{S} (g, P) . \end{aligned}$

Restando ambas expresiones,

$\overset{―}{S} (f + α g, P) - \underset{―}{S} (f + α g, P) = (\overset{―}{S} (f, P) - \underset{―}{S} (f, P)) + α (\overset{―}{S} (g, P) - \underset{―}{S} (g, P)) .$

Intuitivamente (respaldados por el criterio de Riemann), el lado derecho puede ser tan pequeño como queramos pues $f$ y $g$ son integrables. Así que el lado izquierdo también. Esto muestra que $f + α g$ también es integrable en $[a, b]$ . Te recomendamos hacer una demostración formal.

Además, si $P_{n}$ es una sucesión de particiones en donde los tamaños de celda convergen a cero (y por lo tanto para las cuales las sumas superiores convergen a la integral para cada función de arriba), entonces:

$\begin{aligned} \int_{a}^{b} (f + α g) (x) d x & = lim_{n \to \infty} \overset{―}{S} (f + α g, P_{n}) \\ = lim_{n \to \infty} (\overset{―}{S} (f, P_{n}) + α \overset{―}{S} (g, P_{n})) \\ = lim_{n \to \infty} \overset{―}{S} (f, P_{n}) + α lim_{n \to \infty} \overset{―}{S} (g, P_{n}) \\ = \int_{a}^{b} f (x) d x + α \int_{a}^{b} g (x) d x . \end{aligned}$

En resumen, hemos demostrado lo siguiente:

Teorema. La integral es lineal. Es decir, si $f : R \to R$ y $g : R \to R$ son funciones acotadas e integrables en $[a, b]$ , entonces para cualquier real $α$ también $f + α g$ es integrable en $[a, b]$ y además se cumple $\int_{a}^{b} (f + α g) (x) d x = \int_{a}^{b} f (x) d x + α \int_{a}^{b} g (x) d x .$

Dos casos particulares de interés son los siguientes:

Si en el teorema anterior tomamos $α = 1$ , entonces obtenemos que $\int_{a}^{b} (f + g) (x) = \int_{a}^{b} f (x) d x + \int_{a}^{b} g (x) d x$ , es decir, la integral abre sumas.
Si en el teorema anterior tomamos $f$ como la función constante cero, entonces obtenemos que $\int_{a}^{b} α g (x) d x = α \int_{a}^{b} g (x) d x$ , es decir la integral saca escalares.

La integral respeta desigualdades

Veamos que la integral, en cierto sentido, respeta desigualdades. Un primer paso que es muy sencillo de verificar es lo que sucede con la integral de funciones no negativas.

Proposición. Si $f : R \to R$ es una función integrable en el intervalo $[a, b]$ y se cumple $f (x) \geq 0$ para todo $x \in [a, b]$ , entonces $\int_{a}^{b} f (x) d x \geq 0.$

Demostración. Como $f (x) \geq 0$ , entonces claramente para cualquier partición $P$ se cumple que $\overset{―}{S} (f, P) \geq 0$ , pues aparecen puros términos positivos en la suma superior. Así, $0$ es una cota inferior para las sumas superiores. Como la integral es la máxima de dichas cotas superiores, entonces $\int_{a}^{b} f (x) d x \geq 0,$ como queríamos.

De este resultado y las propiedades que hemos mostrado, podemos deducir algo mucho más general.

Teorema. Sean $f : R \to R$ y $g : R \to R$ funciones integrables en un intervalo $[a, b]$ , dentro del cual también se cumple que $f (x) \leq g (x)$ . Entonces, $\int_{a}^{b} f (x) d x \leq \int_{a}^{b} g (x) d x .$

Demostración. Como $f$ y $g$ son integrables en $[a, b]$ , entonces la combinación lineal $g - f$ también lo es, y además $(g - f) (x) = g (x) - f (x) \geq 0$ . Por la proposición anterior y la linealidad de la integral, tenemos entonces que: $\int_{a}^{b} g (x) d x - \int_{a}^{b} f (x) d x = \int_{a}^{b} (g - f) (x) d x \geq 0.$

De aquí, $\int_{a}^{b} f (x) d x \leq \int_{a}^{b} g (x) d x,$ como queríamos.

Más adelante…

Todas las propiedades que hemos enunciado se utilizarán de aquí en adelante. Es importante que las tengas presentes. Son propiedades que nos permiten factorizar funciones para que al momento de integrar o que nos permiten partir una integral complicada en otras más sencillas con integración inmediata o ya conocida.

En la siguiente entrada enunciaremos y demostraremos el teorema del valor medio para la integral. Es un teorema muy relevante, pues será uno de los ingredientes en la demostración de otros teoremas importantes para el cálculo integral.

Tarea moral

Utilizando las propiedades anteriores, resuelve las siguientes integrales.
- $\int_{0}^{1} 7 (4 + 3 x^{2}) d x .$
- $\int_{2}^{0} \frac{1}{4} (32 x - 3 x^{2} + 6) d x .$
Termina con detalle todas las demostraciones de la entrada que hayan quedado pendientes.
Usndo las propiedades de esta entrada, demuestra que la integral $\int_{- 10}^{10} x^{7} - x^{5} + 3 x^{3} + 27 x d x$ existe y determina su valor. Sugerencia. Muestra que la función dentro de la integral es continua y cumple $f (x) = - f (x)$ . Usa varias de las propiedades de esta entrada.
Demuestra la siguiente igualdad:
$\int_{a}^{b} α f (x) d x + \int_{a}^{b} β g (x) d x = \int_{a}^{b} α f (x) + β g (x) d x .$
Sean $a \leq b \leq c \leq d$ números reales. Sea $f : R \to R$ una función integrable en $[a, d]$ . Demuestra que todas las integrales $\int_{a}^{c} f (x) d x, \int_{b}^{d} f (x) d x, \int_{a}^{d} f (x) d x, \int_{b}^{c} f (x) d x$
existen y muestra que satisfacen la siguiente identidad:
$\int_{a}^{c} f (x) d x + \int_{b}^{d} f (x) d x = \int_{a}^{d} f (x) d x + \int_{b}^{c} f (x) d x .$
Sean $a < b$ reales. Demuestra que si la función $f : R \to R$ es continua en $[a, b]$ , se cumple que $f (x) \geq 0$ para $x \in [a, b]$ y además existe por lo menos un punto $c$ tal que $f (c) > 0$ , entonces $\int_{a}^{b} f (x) d x > 0$ . Como sugerencia, demuestra que existe todo un intervalo (aunque sea muy chiquito) donde la función es positiva, y usa otras propiedades que hemos mostrado. Luego, encuentra un contraejemplo para esta afirmación en donde $f$ no sea continua.

Entradas relacionadas

Página del curso: Cálculo Diferencial e Integral II
Entrada anterior: Definición de la integral definida
Entrada siguiente: Teorema del valor medio para la integral

Cálculo Diferencial e Integral II: Definición de la integral definida

Por Moisés Morales Déciga

Deja un comentario

Introducción

En la entrada anterior se introdujo el problema de calcular el área que se encuentra en una región delimitada por ciertas líneas verticales, el eje $x$ y la gráfica de una función. Hablamos de cómo aproximar esta área cuando la función es «bien portada», pero aún no hemos dicho a qué se refiere esto. En esta entrada haremos una formalización de este concepto mediante la definición de integral definida.

La intuición que puedes tener a lo largo de la entrada es que para poder hablar de que una función sea integrable en cierto intervalo, intuitivamente necesitamos que las sumas de Riemann convergan a un valor conforme hacemos las celdas tender a cero en longitud. Esto diría que sin importar cómo hagamos la partición, las sumas de Riemann deben converger a un mismo valor conforme la partición se hace más y más fina. En particular, necesitaremos que las sumas superiores e inferiores cumplan esto. Como en ellas entendemos bien qué pasa con los refinamientos, entonces nos conviene más dar la definición en términos de ellas. Es lo más conveniente y, en particular, implica lo anterior.

Integral definida de Riemann

La definición clave que estudiaremos es la siguiente.

Definición. Sean $f : R \to R$ una funcion acotada y $a \leq b$ reales. Sea $P$ el conjunto de las particiones de $[a, b]$ . Definimos

$\begin{aligned} \underset{―}{S} (f) & = sup {\underset{―}{S (f, P)} | P \in P} \\ \overset{―}{S} (f) & = inf {\overset{―}{S (f, P)} | P \in P}, \end{aligned}$

es decir al supremo de las sumas inferiores y al ínfimo de las sumas superiores sobre todas las particiones posibles de $[a, b]$ . Diremos que existe la integral definida de Riemann para $f$ en el intervalo $[a, b]$ si

$\underset{―}{S (f)} = \overset{―}{S (f)} .$

En este caso, a este valor en común lo denotamos por $\int_{a}^{b} f (x) d x .$

En otras palabras, para que $f$ sea integrable, necesitamos que el ínfimo de las sumas superiores sea igual al supremo de las sumas inferiores. A veces también decimos que $f$ es Riemann integrable en $[a, b]$ o, si el contexto es claro, simplemente que es integrable.

No todas las funciones son Riemann integrables. Hacia el final de esta unidad daremos ejemplos de funciones que no lo son. Sin embargo, por ahora nos enfocaremos en ver algunos ejemplos que sí son Riemann integrables y probar propiedades de la integral definida en los casos en los que sí exista.

Ejemplo de integral definida

Veamos un ejemplo sencillo de cómo se verifica la definición de integral definida.

Ejemplo. Tomemos la función $f : [0, 1] \to R$ dada por $f (x) = x$ . Veamos que dicha función es integrable en el intervalo $[0, 1]$ . Para ello, demos la partición $P_{n}$ homogénea del intervalo $[0, 1]$ en celdas de longitud $1 / n$ , con $n$ un entero positivo. Si hacemos esto, las celdas de la partición son

$[0, 1 / n], [1 / n, 2 / n], \dots [(n - 1) / n, 1] .$

Los supremos de los valores de $f$ en dicho intervalo son

$1 / n, 2 / n, \dots, 1,$

y los ínfimos son

$0, 1 / n, \dots, (n - 1) / n .$

De este modo, para esta partición la suma superior sería

$\begin{aligned} \overset{―}{S} (f, P_{n}) & = \frac{1}{n} (\frac{1}{n} + \frac{2}{n} + \dots + \frac{n}{n}) \\ = \frac{1}{n^{2}} (1 + 2 + \dots + n) \\ = \frac{n (n + 1)}{2 n^{2}} \\ = \frac{1}{2} + \frac{1}{2 n} . \end{aligned}$

y la suma inferior sería

$\begin{aligned} \underset{―}{S} (f, P_{n}) & = \frac{1}{n} (\frac{0}{n} + \frac{2}{n} + \dots + \frac{n - 1}{n}) \\ = \frac{1}{n^{2}} (0 + 1 + 2 + \dots + (n - 1)) \\ = \frac{(n - 1) n}{2 n^{2}} \\ = \frac{1}{2} - \frac{1}{2 n} . \end{aligned}$

La sucesión de números $\frac{1}{2} + \frac{1}{2 n}$ se acerca tanto como queramos a $\frac{1}{2}$ por arriba. Como el ínfimo $\overset{―}{S} (f)$ que estamos buscando es cota inferior de todas las sumas inferiores, en particular es de estas que vienen de particiones homogéneas. Así, $\overset{―}{S} (f) \leq \frac{1}{2}$ . Pero además, por una proposición de la entrada anterior sabemos que cualquier suma inferior es cota inferior de todas las sumas inferiores. Como $\overset{―}{S} (f)$ es la mayor cota inferior, tenemos que $\overset{―}{S} (f) \geq \frac{1}{2} - \frac{1}{2 n}$ para todo $n$ , y entonces $\overset{―}{S} (f) \geq \frac{1}{2}$ . Todo esto nos permite concluir que $\overset{―}{S} (f) = \frac{1}{2}$ .

De manera totalmente análoga (que te sugerimos argumentar cuidadosamente), se tiene que $\underset{―}{S} (f) = \frac{1}{2}$ . Concluimos entonces que $f$ es integrable en $[0, 1]$ y que $\int_{0}^{1} f (x) d x = \frac{1}{2} .$

$△$

Aunque este ejemplo tuvo un intervalo y una función muy sencillas, se volvió algo elaborado justificar la parte de los ínfimos y supremos. Es por ello que nos conviene enunciar y demostrar algunos resultados sobre funciones integrables que nos permitirán determinar la integrabilidad con más comodidad.

Integral definida mediante particiones homogéneas y la condición de Riemann

Lo primero que haremos es demostrar que para que una función sea integrable, nos basta estudiar a las particiones homogéneas.

Teorema. Sean $f : R \to R$ una funcion acotada y $a \leq b$ reales. Sea $P_{n}$ la partición homogéneas del intervalo $[a, b]$ en $n$ partes. Supongamos que se da la siguiente igualdad de límites:

$lim_{n \to \infty} \overset{―}{S} (f, P_{n}) = lim_{n \to \infty} \underset{―}{S} (f, P_{n}) .$

Entonces, la integral existe y es igual a ese límite en común.

Demostración. $\Leftarrow)$ La demostración sigue argumentos muy parecidos al ejercicio que presentamos como ejemplo arriba. Supongamos que los límites para las particiones homogéneas existen y son iguales a $L$ . Estudiemos $\overset{―}{S} (f)$ . Por ser ínfimo de todas las sumas superiores, tendríamos en particular para las particiones homogéneas que $\overset{―}{S} (f) \leq \overset{―}{S} (f, P_{n}),$

para todo entero positivo $n$ . Haciendo tender $n$ a infinito, obtenemos $\overset{―}{S} (f) \leq L$ . Por otro lado, sabemos que cualquier suma inferior es cota inferior de cualquier suma superior, en particular, cada $\underset{―}{S} (f, P_{n})$ es una de estas cotas inferiores. Como $\overset{―}{S} (f)$ es la mayor de las cotas inferiores, tendríamos que $\overset{―}{S} (f) \geq \underset{―}{S} (f, P_{n}) .$

Haciendo tender $n$ a infinito, obtenemos $\overset{―}{S} (f) \geq L$ . Así, $\overset{―}{S} (f) = L$ . Un argumento análogo demuestra que $\underset{―}{S} (f) = L$ , y por lo tanto la función es integrable en $[a, b]$ .

Un siguiente resultado importante es la condición de Riemann, que nos dice que para que una función sea integrable, nos basta encontrar una partición en donde la suma superior y la inferior estén tan cerca como querramos. A esto se le conoce como la condición de Riemann.

Teorema. Sean $f : R \to R$ una funcion acotada y $a \leq b$ reales. Se tiene que $f$ es integrable en $[a, b]$ si y sólo si para todo $ϵ > 0$ existe una partición $P_{ϵ}$ tal que:

$\overset{―}{S} (f, P_{ϵ}) - \underset{―}{S} (f, P_{ϵ}) < ϵ .$

Demostración. $\Rightarrow)$ Sea $f$ integrable. Debemos mostrar que para cada $ϵ > 0$ existe una partición $P_{ϵ}$ tal que $\overset{―}{S} (f, P_{ϵ}) - \underset{―}{S} (f, P_{ϵ}) < ϵ .$

Para ello, tomemos $ϵ^{*} = ϵ / 2$ . Como $\overset{―}{S} (f)$ es ínfimo de las sumas superiores, entonces $\overset{―}{S} (f) + ϵ^{*}$ ya no es cota inferior para dichas sumas superiores, por lo que existe una partición $P$ tal que $\overset{―}{S} (f, P) < \overset{―}{S} (f) + ϵ^{*}$ . Así mismo, existe una partición $P^{'}$ tal que $\underset{―}{S} (f, P^{'}) > \underset{―}{S} - ϵ^{*}$ . Si $P_{ϵ}$ es un refinamiento mutuo de $P$ y $P^{'}$ , tendríamos entonces que

$\begin{aligned} \overset{―}{S} (f, P_{ϵ}) & < \overset{―}{S} (f, P) < \overset{―}{S} (f) + ϵ^{*} \\ \underset{―}{S} (f, P_{ϵ}) & > \underset{―}{S} (f, Q) > \underset{―}{S} (f) - ϵ^{*} . \end{aligned}$

Multiplicando la segunda igualdad por $- 1$ y sumando ambas, obtenemos entonces que

$\begin{aligned} \overset{―}{S} (f, P_{ϵ}) - \underset{―}{S} (f, P_{ϵ}) & < \overset{―}{S} (f) + ϵ^{*} - \underset{―}{S} (f) + ϵ^{*} \\ = 2 ϵ^{*} \\ = ϵ . \end{aligned}$

Aquí usamos que $\overset{―}{S} (f) = \underset{―}{S} (f)$ por ser $f$ integrable.

$\Leftarrow)$ Supongamos ahora que para todo $ϵ$ se puede encontrar la partición $P_{ϵ}$ que satisface $\overset{―}{S} (f, P_{ϵ}) - \underset{―}{S} (f, P_{ϵ}) < ϵ$ . Veremos que a partir de esto se puede probar que $\overset{―}{S} (f) = \underset{―}{S} (f) .$

Por ser $\overset{―}{S} (f)$ el ínfimo de todas las sumas superiores, se tiene que

$\overset{―}{S} (f, P_{ϵ}) > \overset{―}{S} (f) .$

$\underset{―}{S} (f, P_{ϵ}) < \underset{―}{S} (f) ⟹ - \underset{―}{S} (f, P_{ϵ}) > - \underset{―}{S} (f) .$

$⟹ ϵ > \overset{―}{S} (f, P_{ϵ}) - \underset{―}{S} (f, P_{ϵ}) > \overset{―}{S} (f) - \underset{―}{S} (f) .$

Y $ϵ$ es tan pequeño como lo queramos, por lo tanto.

$\overset{―}{S} (f) = \underset{―}{S} (f) .$

Ejemplos de integral definida con los resultados que probamos

Veamos algunos ejemplos de cómo utilizar los resultados que acabamos de mostrar para demostrar que ciertas integrales definidas existen, y para encontrar su valor.

Ejemplo. Calculemos la integral de la función $f (x) = x$ en el intervalo $[3, 4]$

Usaremos la técnica de los límites de las particiones homogéneas. Estudiaremos con detalle el caso de las sumas superiores y dejaremos el de las inferiores como ejercicio. Si la partición $P_{n}$ del intervalo $[a, b]$ es homogénea y en $n$ partes, las celdas tienen longitud $\frac{b - a}{n}$ y entonces son:

$[a, a + \frac{b - a}{n}], [a + \frac{b - a}{n}, a + 2 \frac{b - a}{n}], \dots, [a + (n - 1) \frac{b - a}{n}, b] .$

La función $f (x) = x$ es creciente, y entonces los máximos se alcanzan al final de cada intervalo. Así, para el intervalo $[3, 4]$ tenemos:

$\begin{aligned} \overset{―}{S} (f, P_{n}) & = \sum_{i = 1}^{n} f (3 + i \cdot \frac{4 - 1}{n}) \frac{4 - 3}{n} \\ = \sum_{i = 1}^{n} (3 + \frac{i}{n}) \frac{1}{n} \\ = \sum_{i = 1}^{n} (\frac{3}{n} + \frac{i}{n^{2}}) \\ = \sum_{i = 1}^{n} (\frac{3}{n}) + \sum_{i = 1}^{n} (\frac{i}{n^{2}}) \\ = \frac{3}{n} \cdot n + \frac{1}{n^{2}} \sum_{i = 1}^{n} i \\ = 3 + \frac{n (n + 1)}{2 n^{2}} \\ = 3 + \frac{1}{2} + \frac{1}{2 n} \\ = \frac{7}{2} + \frac{1}{2 n} . \end{aligned}$

De este modo,

$lim_{n \to \infty} \overset{―}{S} (f, P_{n}) = lim_{n \to \infty} (\frac{7}{2} + \frac{1}{2 n}) = \frac{7}{2} .$

Por tu cuenta, revisa que que también se cumple lo siguiente

$lim_{n \to \infty} \underset{―}{S} (f, P_{n}) = \frac{7}{2} .$

Así, por la proposición que mostarmos arriba, tenemos que la integral en el intervalo $[3, 4]$ existe y por lo tanto:

$\int_{3}^{4} x d x = \frac{7}{2} .$

$△$

Ejemplo. Ahora calculemos la integral de la función $f (x) = - x^{2} + 3$ en el intervalo $[1, 3]$ . Al hacer una figura, obtenemos la siguiente gráfica.

Observa que en este caso tenemos 2 áreas: del eje $x$ y otra por debajo del eje $x$ . Todo lo que hemos hecho funciona tanto para funciones positivas, como negativas. Pero obtendremos algo interesante de la conclusión de este problema.

Para ver que la integral existe, usaremos nuevamente la técnica de las particiones homogéneas. Ahora haremos las sumas inferiores. Como la función es decreciente, los valores más chicos aparecen al final de cada intervalo. Tenemos entonces que:

$\begin{aligned} \underset{―}{S} (f, P) & = \sum_{i = 1}^{n} (- {(1 + i \cdot (\frac{3 - 1}{n}))}^{2} + 3) (\frac{3 - 1}{n}) \\ = \sum_{i = 1}^{n} (- {(1 + i \cdot (\frac{2}{n}))}^{2} + 3) (\frac{2}{n}) \\ = \sum_{i = 1}^{n} (- (1 + \frac{4 i}{n} + \frac{4 i^{2}}{n^{2}}) + 3) (\frac{2}{n}) \\ = \sum_{i = 1}^{n} (\frac{4}{n} - \frac{8 i}{n^{2}} - \frac{8 i^{2}}{n^{3}}) \\ = \frac{4}{n} \sum_{i = 1}^{n} - \frac{8}{n^{2}} \sum_{i = 1}^{n} i - \frac{8}{n^{3}} \sum_{i = 1}^{n} i^{2} \\ = \frac{4}{n} \cdot n - \frac{8}{n^{2}} \frac{n (n + 1)}{2} - \frac{8}{n^{3}} \frac{n (n + 1) (2 n + 1)}{6} \\ = 4 - \frac{8 n^{2}}{2 n^{2}} - \frac{8 n}{2 n^{2}} - \frac{8 \cdot 2 n^{3}}{6 n^{3}} - \frac{8 \cdot 3 n^{2}}{6 n^{3}} - \frac{8 n}{6 n^{3}} \\ = - \frac{8}{3} - \frac{8 n}{2 n^{2}} - \frac{8 \cdot 3 n^{2}}{6 n^{3}} - \frac{8 n}{6 n^{3}} . \end{aligned}$

Así, $lim_{n \to \infty} \underset{―}{S} (f, P) = - \frac{8}{3} .$

Se puede mostrar que el límite de las sumas superiores para las particiones homogéneas también es $- \frac{8}{3}$ (verifícalo), así que la integral buscada tiene este valor. De esta forma,

$\int_{1}^{3} - x^{2} + 3 d x = - 8 / 3 .$

$△$

¿Áreas negativas?

Se comentó que la integral se utiliza para el cálculo de áreas bajo la curva, entonces, ¿Por qué el resultado del ejemplo anterior es negativo? ¿Hay áreas negativas? Intuitivamente, no debería haber áreas negativas. Sin embargo, el procedimiento que usamos para definir a la integral definida sí nos puede dar números negativos. Puedes pensarlo como sigue: el área que estamos calculando va del eje $x$ a la gráfica de la función $f$ . Si esa gráfica está por debajo, entonces estámos yendo en dirección negativa. En el último ejemplo hay tanto una región por encima del eje $x$ , como una por debajo. El número que nos salió es la diferencia de ambas áreas: el área por arriba del eje $x$ , menos el área por debajo del eje $x$ . Como el resultado que obtuvimos fue negativo, entonces el área por debajo del eje $x$ era mayor en magnitud.

Esta es una propiedad un poco antintuitiva, pero es importante preservarla. El cálculo de áreas es sólo una de las aplicaciones que tiene la integral. En otras aplicaciones, es importante que la integral mida qué tanto estuvimos por encima del eje $x$ y qué tanto estuvimos por debajo.

¿Y si queremos realmente entender la suma de las dos áreas de la figura y no la resta? En ese caso, tendremos que hacer una figura para entender cómo hacer las cuentas. Si hay área que está por debajo del eje $x$ , deberemos agregar un signo $-$ para contarla correctamente como área positiva. Pero entonces tendremos que partir nuestro intervalo de integración en varios intervalos de acuerdo a cuándo la gráfica de $f$ cruza al eje $x$ .

Con esto en mente, retomemos el ejemplo anterior.

Ejemplo. Encontremos el área en valor absoluto que genera la función $f (x) = - x^{2} + 3$ en el intervalo $[1, 3]$ .

Lo primeo que haremos es obtener el punto donde la función cruza al eje $x$ . Para ello, se requiere que $- x^{2} + 3 = 0$ , que en dicho intervalo sucede en $x = \sqrt{3}$ .

Una vez encontrado el punto raíz o la raíz de la función, ahora podemos partir el área absoluta que nos interesa en dos intervalos: el $[1, \sqrt{3}]$ y el $[\sqrt{3}, 3]$ .

Pensando en que queremos calcular el área absoluta, necesitamos dividir la formula que se planteó anteriormente en los intervalos correspondientes, y en el intervalo $[\sqrt{3}, 3]$ será necesario agregar un signo menos para que el área que se calcula como negativa, ahora se cuente de manera positiva. De esta manera, tendríamos:

$F_{1}^{3} = \int_{1}^{\sqrt{3}} - x^{2} + 3 d x - \int_{\sqrt{3}}^{3} - x^{2} + 3 d x .$

Ahora queda replicar el proceso que vimos en la suma anterior con estos 2 nuevos intervalos y juntarlos considerando el cambio de signo. Desarrollando los cálculos, se encuentra que el área generada por la función es de:

$F_{1}^{3} = 4 \sqrt{3} - \frac{8}{3} .$

$△$

Nota. En este ejemplo partimos el intervalo en dos subintervalos, pero el intervalo puede quedar partido tantas veces como la función $f$ lo requiera, de acuerdo a la cantidad de veces que se cruza el eje $x$ .

Más adelante…

En esta entrada dimos la definición formal de que una función sea integrable en cierto intervalo. O mejor dicho, que sea Riemann integrable. En cursos más avanzados de matemáticas se definen y estudian otras nociones de integrabilidad, pero por ahora esta es la que nos interesa. Para que la integral de Riemann exista, necesitamos que coindidan el ínfimo de las sumas superiores y el supremo de las sumas inferiores de la función dada. En ese caso, el valor de la integral es ese valor en común.

Ya dada la definición, dimos algunos resultados que nos ayudarán a determinar cuándo una función es integrable. En siguientes entradas daremos más propiedades que nos ayudarán entender mejor la integrabilidad y la integral. Varias entradas despuésse hablará de las integrales indefinidas y del teorema fundamental del cálculo, que daran pie a numerosas técnicas de integración.

Lo último que hicimos en esta entrada es notar que hay casos en donde el valor de la integral que se encuentra es negativo. Esto contradice un poco nuestra intuición de que la integral es un área. Sin embargo, ya platicamos qué hacer en este caso si queremos realmente el «área positiva». Seguiremos explorando esta idea de integrales negativas un poco más adelante. Por ahora, lo que puedes hacer es identificar los intervalos en los que la función tiene determinado signo.

Tarea moral

Completa las cuentas que quedaron pendientes en cada uno de los ejercicios.
Expresa la siguiente expresión como una integral en el intervalo $[0, π]$ . $lim_{n \to \infty} \sum_{i = 1}^{n} (x_{i}^{3} + x_{i} s i n (x_{i})) △ x .$
Encuentra el área delimitada por la curva $f (x) = x^{2} + 2$ y el eje $x$ en el intervalo $[1, 4]$ .

4. Encuentra el valor del área delimitada por la gráfica de la función $f (x) = x^{3} - 6 x$ en el intervalo $[0, 3]$ , que es la zona sombreada. Realiza las cuentas tanto con áreas absolutas, tanto con áreas con signo.

5. Encuentra el área de la función $f (x) = \sqrt{1 - x^{2}}$ en el intervalo $[0, 1]$ .

Entradas relacionadas

Página del curso: Cálculo Diferencial e Integral II
Entrada anterior: Motivación de integral, sumas superiores e inferiores
Entrada siguiente: Propiedades de la integral definida

Cálculo Diferencial e Integral II: Motivación de la integral y sumas de Riemann

Por Moisés Morales Déciga

Deja un comentario

Introducción

La principal motivación y aplicación de la integral es el cálculo de áreas. En esta entrada hablaremos de cómo aproximar áreas mediante sumas de Riemann. Para introducir este concepto, recordemos que en la entrada pasada se ilustró el método de exhaución. Vimos que es un acercamiento geométrico al cálculo del área del círculo mediante polígonos inscritos o circunscritos. Intuitivamente, conforme aumentamos el número de lados de estos polígonos, el área generada por ellos se aproximaba cada vez mejor al área del círculo.

Sin embargo, en las aplicaciones no sólo queremos calcular el área de círculos, sino de muchos tipos diferentes de figuras. Idealmente, nos gustaría poder calcular el área de muchas figuras u objetos, siempre y cuando éstos se puedan describir.

La forma de describirlos en este curso será mediante funciones. Por lo tanto, buscaremos encontrar una función cuya gráfica se parezca al contorno del objeto (o bien cuyo contorno pueda ser descrito por más de una función). Esta gráfica será una curva que define una región. Hablaremos de cómo definir el área de esta región de manera que coincida con nuestra intuición.

En esta entrada empezaremos con algunas definiciones generales e ideas de aproximación basadas en el método exhaustivo.

Área bajo la curva

El origen analítico de la integral se origina al asociar áreas con funciones.

Tomemos dos reales $a$ y $b$ con $a < b$ . Tomemos una función $f : R \to R$ que, para fijar las ideas correctamente por ahora, supondremos que es positiva en todo el intervalo $[a, b]$ . Supongamos que delimitamos una región en el plano cartesiano de la siguiente manera.

Por la izquierda con la línea vertical $x = a$ .
Por la derecha con la línea vertical $x = b$ .
Por abajo con el eje $x$ .
Por arriba con la gráfica de cierta función $f (x)$ .

Entonces, la magnitud del espacio que se encuentra acotado por estas curvas se le conoce como el «área bajo la curva» o más específicamente, el «área bajo la curva de $f (x)$ en el intervalo $[a, b]$ .» Usaremos la notación $F_{a}^{b}$ para referirnos a esta magnitud. En el transcurso de toda esta entrada supondremos que tenemos un ejemplo «bien portado» en el que sí tiene sentido hablar de dicha área $F_{a}^{b}$ (recuerda que las funciones pueden tener comportamientos muy raros). Será importante definir qué quiere decir exactamente «bien portado», pero eso lo haremos un poco más adelante.

Ejemplo. En la siguiente figura, la curva verde es la gráfica de la función $f (x)$ . La región que nos interesa está bajo esta gráfica, entre las verticales en $a$ y $b$ , y sobre el eje $x$ . Su magnitud $F_{a}^{b}$ es el área bajo la curva que nos interesa.

$△$

Particiones, celdas y rectángulos

Una vez definida la región a la que se le va a calcular el área, buscaremos hacer una aproximación a esa área mediante la suma de áreas de rectángulos. Estos pueden ser inscritos (que quedan por dentro o por debajo de la función) o circunscritos (que quedan por afuera o por encima de la función). La razón por la cual usamos rectángulos es que son figuras cuya área se calcula de manera muy sencilla: el área $A$ es su base $b$ por su altura $a$ .

Para definir los rectángulos que usaremos para aproximar el área, será necesario hacer una partición $P$ del intervalo $[a, b]$ del eje $x$ en una cierta cantidad de partes (que llamaremos celdas), no necesariamente todas ellas de la misma longitud. Estas partes serán las bases de los rectángulos que usaremos. Comencemos a formalizar estos conceptos.

Definición. Sean $a$ y $b$ números reales con $a \leq b$ . Sea $f : R \to R$ una función. Sea $n \geq 0$ un entero. Una partición (en $n$ partes) del intervalo $[a, b]$ será una elección de números reales $x_{0} \leq x_{1} \leq \dots \leq x_{n}$ con $x_{0} = a$ y $x_{n} = b$ . A cada subintervalo de la forma $[x_{i - 1}, x_{i}]$ para $1 \leq i \leq n$ le llamaremos una celda de la partición.

A una partición la escribiremos usualmente poniendo sus elementos en orden, de la siguiente manera:

$P = {x_{0}, x_{1}, x_{2}, \dots, x_{n - 1}, x_{n}} .$

Definición. Dada la celda $[x_{i - 1}, x_{i}]$ para $1 \leq i \leq n$ de una partición, su longitud será $x_{i} - x_{i - 1}$ y la denotaremos por $Δ x_{i}$ . Así,

$Δ x_{i} = x_{i} - x_{i - 1}, (i = 1, 2, \dots, n) .$

Definición. Si las celdas de una partición tienen todas la misma longitud, diremos que es una partición homogénea. Si no, es decir, si hay celdas de longitudes distintas, diremos que es una partición no homogénea.

Al tomar una partición del intervalo $[a, b]$ , podemos dibujar líneas verticales en cada punto de la partición. El área $F_{a}^{b}$ que nos interesa queda dividida en regiones o franjas como en la siguiente figura.

La función es en verde, la partición está en azul.

Intuición de las sumas superiores e inferiores

El área de cada una de las franjas que hicimos la podemos aproximar (al estilo del método exhaustivo) mediante rectángulos. Sin embargo, dado que la gráfica de la función no es exactamente horizontal, la suma de ciertos rectángulos que usemos para aproximar el área podría no ser exactamente el área bajo la curva. ¿Qué podríamos hacer para tener un poco más de control sobre cómo es el área de cada rectángulo con respecto al área de cada franja? Podemos usar como base las longitudes de las celdas y como altura podemos usar el máximo o mínimo de la función $f (x)$ en cada intervalo. Esto es un caso particular de lo que más adelante llamaremos sumas de Riemann.

La siguiente figura muestra rectángulos desde el eje $x$ hasta la altura morada (que es el mínimo de la función en cada celda) y rectángulos desde el eje $x$ hasta la altura roja (que es el máximo de la función en cada celda).

Cuando tomamos los mínimos en cada celda y consideramos el área de los rectángulos morados, la suma de cada rectángulo será menor que cada franja, y por lo tanto la suma total de áreas de estos rectángulos será menor que el área bajo la curva que queremos.

Por otro lado, si tomamos los máximos de cada celda, tenemos los rectángulos rojos, que análogamente a lo dicho arriba, tienen suma de área total mayor al área bajo la curva buscada. Intuitivamente, hemos acotado el área buscada entre dos áreas que sí sabemos calcular.

Formalización de sumas superiores e inferiores

Introduciremos un poco de notación para hablar de sumas superiores e inferiores. Primero, le queremos dar un símbolo al ínfimo y al supremo de las evaluaciones de la función que nos interesa en cada celda.

Definición. Dada una partición $P = {x_{0}, \dots, x_{n}}$ del intervalo $[a, b]$ y una función acotada $f : R \to R$ :

Al ínfimo de los valores de $f$ en la parte $[x_{i - 1}, x_{i}]$ le llamaremos $m_{i}$ . En símbolos: $m_{i} = inf {f (x) | x_{i - 1} \leq x \leq x_{i}}, i = 1, \dots, n .$
Al supremo de los valores de $f$ en la parte $[x_{i - 1}, x_{i}]$ le llamaremos $M_{i}$ . En símbolos: $M_{i} = sup {f (x) | x_{i - 1} \leq x \leq x_{i}}, i = 1, \dots, n .$

Te recomendamos recordar la teoría de ínfimos y supremos de Cálculo I, que puedes consultar en el siguiente enlace: Supremo e ínfimo. Como nota, observa que en este punto estamos suponiendo muy poco de $f$ , simplemente que es acotada.

La siguiente definición formaliza la idea de «aproximar el área por abajo».

Definición. Sean $f : R \to R$ una funcion acotada y $a \leq b$ reales. Sea $P = {x_{0}, \dots, x_{n}}$ una partición de $[a, b]$ . Diremos que la suma inferior $\underset{―}{S}$ correspondiente a la función $f$ en la partición $P$ del intervalo $[a, b]$ es el número:

$\begin{aligned} \underset{―}{S} (f, P) & = \sum_{i = 1}^{n} m_{i} Δ x_{i}, \end{aligned}$

donde $m_{i}$ es el ínfimo de los valores de $f$ la celda $[x_{i - 1}, x_{i}]$ y $Δ x_{i}$ es la longitud de dicha celda. La expresión anterior se desarrolla explícitamente entonces como

$m_{1} (x_{1} - x_{0}) + m_{2} (x_{2} - x_{1}) + . . . + m_{n} (x_{n} - x_{n - 1}) .$

Esto es precisamente la suma de áreas de varios rectángulos que, por tomar la altura como el ínfimo en cada celda, quedan todos ellos por debajo de la gráfica de la función, como en la siguiente figura.

La siguiente definición formaliza la idea de «aproximar el área por arriba».

Definición. Sean $f : R \to R$ una funcion acotada y $a \leq b$ reales. Sea $P = {x_{0}, \dots, x_{n}}$ una partición de $[a, b]$ . Diremos que la suma superior $\overset{―}{S}$ correspondiente a la función $f$ en la partición $P$ del intervalo $[a, b]$ es el número:

$\begin{aligned} \overset{―}{S} (f, P) & = \sum_{i = 1}^{n} m_{i} Δ x_{i}, \end{aligned}$

donde $M_{i}$ es el supremo de los valores de $f$ la celda $[x_{i - 1}, x_{i}]$ y $Δ x_{i}$ es la longitud de dicha celda. La expresión anterior se desarrolla explícitamente entonces como

$M_{1} (x_{1} - x_{0}) + M_{2} (x_{2} - x_{1}) + . . . + M_{n} (x_{n} - x_{n - 1}) .$

Ahora tenemos la suma de áreas de varios rectángulos que quedan por encima de la gráfica de la función, como se muestra a continuación:

Si regresamos a pensar que la función $f$ es «bien portada» como para que el área $F_{a}^{b}$ tenga sentido, entonces las sumas superiores e inferiores nos ayudan a acotar dicha área. En efecto, notemos que para cualquier $i = 1, \dots, n$ , tenemos que

$m_{i} \leq f (x) \leq M_{,} para x \in [x_{i - 1}, x_{i}] .$

De aquí, el área en cada franja queda acotada entre el área de dos rectángulos y sumando en todas las celdas tendríamos que

$\underset{―}{S} \leq F_{a}^{b} \leq \overset{―}{S} .$

Es decir, la suma inferior es menor o igual que el valor de la integral y la suma superior es mayor o igual que la integral. Un poco más adelante formalizaremos esto, cuándo hablemos apropiadamente de las funciones «bien portadas».

Refinamientos de una partición

Si hacemos una partición con más puntos, habrá más celdas dentro del intervalo y por lo tanto, la cantidad de rectángulos aumenta. Intuitivamente, nuestras aproximaciones deberían acercarse más al área buscada. En efecto, más adelante veremos que esto es así. Por ello, es importante introducir la siguiente definición formal.

Definición. Sea $P$ una partición del intervalo $[a, b]$ . Un refinamiento de $P$ es otra partición $Q$ de $[a, b]$ tal que $P \subseteq Q$ .

Al momento de pedir que la partición $P$ esté contenida en $Q$ , aseguramos que todos los puntos de la partición generados en $P$ se encuentran en $Q$ , y por lo tanto que cada celdas de $Q$ sean subconjunto de alguna celda de $P$ .

Intuitivamente, las aproximaciones que hagamos con la partición $Q$ deben de ser entonces mejores que las que hagamos con la partición $P$ . Si cierta suma de áreas de rectángulos hechas con $Q$ es $S_{Q}$ y esa suma de áres hechas con $P$ es $S_{P}$ suena razonable que:

$| F_{a}^{b} - S_{Q} | \leq | F_{a}^{b} - S_{P} | .$

Sin embargo, nos estamos adelantando un poco. Lo que sí podemos mostrar formalmente por ahora es el siguiente resultado auxiliar.

Lema. Sean $f : R \to R$ una funcion acotada y $a \leq b$ reales. Si $P$ y $Q$ son particiones de $[a, b]$ y $Q$ es refinamiento de $P$ , entonces $\underset{―}{S} (f, P) \leq \underset{―}{S} (f, Q) y \overset{―}{S} (f, Q) \leq \overset{―}{S} (f, P)$

Demostración. Por definición, $P$ y $Q$ son subconjuntos finitos de $[a, b]$ , y $P \subseteq Q$ , así que se puede llegar de $P$ a $Q$ agregando elementos de $[a, b]$ uno por uno. Bastará entonces ver que las desigualdades de arriba se cumplen cuando $Q$ tiene exactamente un elemento más que $P$ , digamos $Q = P \cup {y}$ . Tomemos $P = {x_{0}, \dots, x_{n}}$ . El real $y$ cae dentro de alguna celda de $P$ , digamos en la celda $[x_{j - 1}, x_{j}]$ .

Estudiemos qué suecede con las sumas inferiores. La suma inferior con respecto a $P$ es $\begin{aligned} {\underset{―}{S}}_{P} & = \sum_{i = 1}^{n} m_{i} Δ x_{i}, \end{aligned}$

Para la suma inferior con respecto a $Q$ , la celda $[x_{j - 1}, x_{j}]$ queda partida en dos celdas $[x_{j - 1}, y]$ y $[y, x_{j}]$ . Los ínfimos respectivos $r$ y $s$ de la función $f$ en estas dos celdas cumplen $r \geq m_{j}$ y $s \geq m_{j}$ , pues estamos tomando el ínfimo sobre conjuntos más chicos. Así, la suma inferior con respecto a $Q$ cumple:

$\begin{aligned} \underset{―}{S} (f, Q) & = \sum_{i = 1}^{j - 1} m_{i} Δ x_{i} + r (y - x_{j - 1}) + s (x_{j} - y) + \sum_{i = j + 1}^{n} m_{i} Δ x_{i} \\ \leq \sum_{i = 1}^{j - 1} m_{i} Δ x_{i} + m_{j} (y - x_{j - 1}) + m_{j} (x_{j} - y) + \sum_{i = j + 1}^{n} m_{i} Δ x_{i} \\ = \sum_{i = 1}^{j - 1} m_{i} Δ x_{i} + m_{j} (x_{j} - x_{j - 1}) + \sum_{i = j + 1}^{n} m_{i} Δ x_{i} \\ = \sum_{i = 1}^{n} m_{i} Δ x_{i} \\ = \underset{―}{S} (f, P) . \end{aligned}$

Esto termina la demostración para las sumas inferiores. El caso de las sumas superiores es análogo.

En palabras, el lema anterior dice que la suma inferior con la partición $P$ es menor que la suma inferior con la partición $Q$ y la suma superior con la partición $P$ es mayor que la suma superior con la partición $Q$ .

Otra aplicación muy importante de los refinamientos es que nos ayudan a demostrar que cualquier suma superior siempre es mayor que cualquier suma inferior, sin importar la partición que tomemos en una y en otra.

Proposición. Sean $f : R \to R$ una funcion acotada y $a \leq b$ reales. Sean $P$ y $Q$ particiones de $[a, b]$ . Entonces,

$\underset{―}{S} (f, P) \leq \overset{―}{S} (f, Q) .$

La idea de la demostración es sencilla. Para cualesquiera dos particiones $P$ y $Q$ podemos encontrar una partición $R$ que es un refinamiento de ambas (¿cómo la encontrarías?). Ya teniendo dicha partición, tenemos la cadena de desigualdades:

$\underset{―}{S} (f, P) \leq \underset{―}{S} (f, R) \leq \overset{―}{S} (f, R) \leq \overset{―}{S} (f, Q) .$

Dar la partición $R$ de manera explícita y los detalles de cómo justificar la cadena de desigualdades anterior queda como parte de los ejercicios de esta entrada.

Sumas de Riemann y regla del punto medio

Ya vimos cómo hacer aproximaciones con rectángulos inferiores y cómo hacer aproximaciones con rectángulos superiores. Pero, como te imaginarás, los rectángulos podríamos tomarlos bajo otro criterio. Por ejemplo, podemos hacer rectángulos tomando un punto cualquiera $ξ_{i}$ dentro de cada celda $[x_{i - 1}, x_{i}]$ de una partición.

Ahora la aproximación quedaría de la siguiente manera:

$\begin{aligned} F_{n} & = \sum_{i = 1}^{n} f (ξ_{i}) Δ x_{i} \\ = \sum_{i = 1}^{n} f (ξ_{i}) (x_{i} - x_{i - 1}) \\ = f (ξ_{1}) (x_{1} - x_{0}) + f (ξ_{2}) (x_{2} - x_{1}) + . . . + f (ξ_{n}) (x_{n} - x_{n - 1}) \end{aligned}$

A las expresiones de este estilo se les conoce como sumas de Riemann.

Una manera de dar de manera explícita algunos valores $ξ_{i}$ es tomando los puntos medios en cada celda, como en la siguiente figura.

Este método nos dará otra manera de aproximar el área que buscamos. Si de nuevo refinamos la partición y usamos los puntos medios, tendremos otro procedimiento exhaustivo para aproximar el área. Pero igual podríamos tomar otra, y otra, y otra manera de aproximar el área. ¿Será que todas estas aproximaciones nos llevan a la misma área? Es parte de lo que tendremos que entender formalmente más adelante. Sin embargo, por ahora haremos algunos ejemplos concretos de las ideas que hemos discutido hasta ahora.

Ejemplo de sumas de Riemann superiores, inferiores y de punto medio

Ejemplo. Tomamos la función $f : [2, 8] \to R$ dada por $f (x) = x + 2$ . Tomemos la partición homogénea $P = {2, 3, 4, 5, 6, 7, 8}$ , en donde cada celda tiene longitud $1$ . Encontremos la suma superior, la inferior y la que se obtiene mediante la regla del punto medio.

Para la suma inferior, tenemos el siguiente conjunto de ínfimos (en este caso, mínimos) de las celdas generadas:

$m = {4, 5, 6, 7, 8, 9} .$

De este modo, la suma inferior es

$\underset{―}{S} (f, P) = 4 \cdot (3 - 2) + 5 \cdot (4 - 3) + 6 \cdot (5 - 4) + 7 \cdot (6 - 5) + 8 \cdot (7 - 6) + 9 \cdot (8 - 7) = 39.$

En el caso de la suma superior, los supremos (en este caso, máximos) son

$M = {5, 6, 7, 8, 9, 10} .$

Desarrollemos la suma superior:

$\overset{―}{S} (f, P) = 5 \cdot (3 - 2) + 6 \cdot (4 - 3) + 7 \cdot (5 - 4) + 8 \cdot (6 - 5) + 9 \cdot (7 - 6) + 10 \cdot (8 - 7) = 45.$

Finalmente, para la regla del punto medio, tenemos que los valores de la función evaluada en el punto medio de cada intervalo son:

$ξ = {4.5, 5.5, 6.5, 7.5, 8.5, 9.5} .$

Desarrollando la suma, obtenemos

$S = 4.5 \cdot (3 - 2) + 5.5 \cdot (4 - 3) + 6.5 \cdot (5 - 4) + 7.5 \cdot (6 - 5) + 8.5 \cdot (7 - 6) + 9.5 \cdot (8 - 7) = 42.$

$△$

Más adelante…

En esta entrada empezamos a motivar cómo el área bajo una curva puede ser aproximada mediante rectángulos. Sin embargo, supusimos que nuestra curva estaba dada por una función «bien portada» la cuál sí hace un área apropiada. Esto no necesariamente pasará siempre, pues si la función tiene una gráfica muy complicada, entonces no podremos hablar apropiadamente del área debajo de ella.

De hecho, lo que hicimos en esta entrada nos ayudará a dar formalidad a exactamente qué quiere decir que la función sea «bien portada». La idea de particiones nos servirá para definir el área justo cuando cualquier proceso de aproximar «suficientemente bien» nos lleve al mismo límite. Tomaremos entonces la intuición desarrollada de las sumas inferiores, superiores e incluso las de la regla del punto medio, para introducir la definición de integral definida de la siguiente entrada.

Tarea moral

Aproxima el área bajo la curva de las siguientes funciones en el intervalo dado, usando una partición homogénea con cinco celdas en el intervalo dado. En cada caso, realiza la cuenta con las sumas inferiores, las sumas superiores y con la regla del punto medio.
- $f (x) = x^{2}$ en el intervalo $[0, 1]$ .
- $f (x) = 2 x - 3$ en el intervalo $[0, 2]$ .
- $f (x) = x e^{x}$ en el intervalo $[2, 3]$ (puedes usar calculadora para aproximar las respuestas)
En esta entrada sólo hemos hablado de cómo encontrar el área entre la gráfica de una función positiva y el eje $x$ (dados dos límites verticales). ¿Qué tendríamos que hacer si la función es negativa?
Ahora imaginemos que queremos encontrar el área que se encuentra entre la gráfica de dos funciones. Por ejemplo, imagina que queremos aproximar con las ideas de esta entrada el área entre las gráficas de las siguientes dos funciones, desde la línea vertical $x = 0$ hasta el primer punto de intersección que tienen.

$f (x) = s i n (x^{3}) + 2 x$

$g (x) = c o s (x^{2}) + 3 x^{2} - 2$

Puedes ver estas funciones en la figura. Para realizar la aproximación, haz lo siguiente.

Encuntra el punto $c$ tal que $f (c) = g (c)$ , es decir, en qué ubicación horizontal se cruzan las gráficas.
Haz una partición homogénea en 10 partes del intervalo $[0, c]$ . ¿Qué longitud tiene cada celda?
Crea rectángulos usando como altura la distancia máxima entre las curvas en cada celda. ¿Cuánto queda la suma de áreas de rectángulos? ¿Y si usas la distancia mínima entre las curvas en cada celda?

En el texto se da la demostración de que en un refinamiento, la suma inferior se vuelve más grande. Completa los detalles para ver el resultado análogo de que en un refinamiento la suma superior se vuelve más pequeña. ¿Qué propiedades del supremo estás utilizando?
Completa los detalles de la proposición de que cualquier suma superior es mayor a cualquier suma inferior, aunque estemos hablando de particiones diferentes.
La gráfica de la función $f (x) = \sqrt{1 - x^{2}}$ es un semicírculo que va de $- 1$ a $1$ . Usa una partición homogénea en $10$ celdas del intervalo $[- 1, 1]$ y la regla del punto medio para dar una aproximación al área de este semicírculo. Entonces, ¿cuál sería una aproximación al área del círculo de radio $1$ ? De aquí, ¿cuál sería una aproximación para $π$ ?

Entradas relacionadas

Página del curso: Cálculo Diferencial e Integral II
Entrada anterior: Introducción al curso
Entrada siguiente: Definición de la integral definida

Cálculo Diferencial e Integral I: Supremo e ínfimo

Por Karen González Cárdenas

Deja un comentario

Introducción

Ya hemos visto los conceptos de máximo, mínimo, cota superior e inferior de un conjunto en $R$ . En esta entrada definiremos formalmente el concepto de supremo e ínfimo de un conjunto, veremos que los revisados previamente se encuentran relacionados. Adicionalmente, demostraremos algunas proposiciones útiles y algunos ejemplos en los cuales aplicaremos las definiciones respectivas.

Supremo e ínfimo, primera definición

Definición: Sea $A \subseteq R$ con $A \neq \emptyset$ . Decimos que $α \in R$ es:

El supremo de $A \Leftrightarrow$
- $α$ es cota superior de $A$
- $α$ es la mínima cota superior, es decir, si $β$ es cota superior de $A \Rightarrow α \leq β$ .
  
  En otras palabras, la mínima cota superior de un conjunto es el menor número real que es una cota superior de ese conjunto.

El ínfimo de $A \Leftrightarrow$
- $α$ es cota inferior de $A$
- $α$ es la máxima cota inferior, es decir, si $β$ es cota inferior de $A \Rightarrow β \leq α$ .
  
  De esta manera, la máxima cota inferior de un conjunto es el número real más grande que sirve como cota inferior para dicho conjunto.

Retomemos el último ejemplo visto en la entrada pasada:

$A = {\frac{1}{n} : n \in N ∖ {0}}$

El conjunto de cotas superiores de $A$ está dado por:
$[1, \infty)$
tiene elemento mínimo y es 1. Esto nos indica que existe una mínima cota superior, ya que el $1$ es el menor número real que sirve como cota superior para dicho conjunto.
El conjunto de cotas inferiores de $A$ está dado por:
$(- \infty, 0]$
tiene elemento máximo y es 0. Esto nos indica que existe una máxima cota inferior, debido a que el $0$ es el mayor número real que sirve como cota inferior para $(- \infty, 0]$ .

Dadas las observaciones anteriores ahora podemos decir que:

El supremo de $A$ es $1$ : $s u p (A) = 1$
El ínfimo de $A$ es $0$ : $i n f (A) = 0$

Observación: El supremo o el ínfimo de un conjunto puede o no pertenecer al conjunto.

Pasemos a revisar la existencia y la unicidad de supremos e ínfimos.

Existencia del supremo y del ínfimo

En general, no tendremos que preocuparnos por la existencia del supremo ni del ínfimo cuando hablemos de un conjunto no vacío y acotado de números reales; en cambio, consideraremos como axioma que siempre existen.

En la siguiente entrada motivaremos y hablaremos con más detalle del siguiente axioma.

Axioma del Supremo: Si $A \subseteq R$ es no vacío y $A$ es acotado superiormente entonces existe $α \in R$ tal que:
$α = s u p (A)$

En esa entrada, también demostraremos a partir de este axioma que los conjuntos no vacíos y acotados inferiormente siempre tienen ínfimo. Igualmente, hablaremos de otras propiedades de los números reales relacionadas con este axioma, como que el conjunto de los números reales no está acotado y la propiedad arquimediana. Por ahora, sólo lo enunciamos, pues en las siguientes secciones demostraremos varias propiedades del supremo y del ínfimo para las que necesitaremos su existencia.

Unicidad del supremo y del ínfimo

El Axioma del Supremo nos garantiza la existencia del supremo e implica la del ínfimo pero, ¿habrá más de un supremo o un ínfimo para un mismo conjunto?

Teorema: Sea $A \subseteq R$ con $A \neq \emptyset$ y acotado. El supremo y el ínfimo de $A$ son únicos.

Demostración (Unicidad del supremo): Supongamos que existen $α_{1}, α_{2}$ tales que:
$α_{1} = s u p (A)$ y $α_{2} = s u p (A)$ .

Para $α_{1}$ tenemos que para toda $a \in A, a \leq α_{1}$ . Y como $α_{1}$ es mínima cota superior entonces $\forall M$ cota superior de $A, α_{1} \leq M$ . Así en particular ocurre que: $α_{1} \leq α_{2}$ es cota superior.

Análogamente para $α_{2}$ tenemos que: $α_{2} \leq M$ donde $M$ es cota superior de $A$ .
$\Rightarrow α_{2} \leq α_{1}$ es cota superior.

Debido a que $α_{1} \leq α_{2}$ y $α_{2} \leq α_{1}$ concluimos:
$α_{1} = α_{2} .$
$∴$ El supremo de $A$ es único.

Relaciones entre supremos e ínfimos

Proposición: Sean $A, B \subseteq R$ distintos del vacío. Si se cumple que para toda $a \in A$ y para toda $b \in B$ $a \leq b \Rightarrow s u p (A) \leq i n f (B) .$

Demostración:
Primero observamos que $A$ tiene supremo, ya que como $A \neq \emptyset$ y $B \neq \emptyset$ :
$\Rightarrow \exists b_{0} \in B, \forall a \in A$ se cumple que $a \leq b_{0}$
$\Rightarrow b_{0}$ es cota superior de $A$
$\Rightarrow A \neq \emptyset$ y acotado superiormente
$∴ \exists α = s u p (A) \in R .$

Ahora vemos que $B$ tiene ínfimo, esto se sigue de $B \neq \emptyset$ y $A \neq \emptyset$ :
$\Rightarrow \exists a_{0} \in A, \forall b \in B$ ocurre que $a_{0} \leq b$
$\Rightarrow a_{0}$ es cota inferior de $B$
$\Rightarrow B \neq \emptyset$ y acotado inferiormente
$∴ \exists β = i n f (B) \in R .$

Por lo que sólo nos falta verificar que $α \leq β$ . Cómo por hipótesis tenemos que $\forall a \in A, \forall b \in B (a \leq b)$ obtenemos:
$\Rightarrow \forall a \in A$ ( $a$ es cota inferior de $B$ )
$\Rightarrow \forall a \in A$ ( $a \leq β$ )
$\Rightarrow β$ cota superior de $A$
$\Rightarrow α \leq β$

Proposición: Sean $C \subseteq A \subseteq R$ donde $C$ es no vacío y $A$ acotado.
$\Rightarrow i n f (A) \leq i n f (C) \leq s u p (C) \leq s u p (A)$ .
Demostración:

Sea $C \neq \emptyset$ subconjunto de $A$ , como $C \subseteq A \Rightarrow A \neq \emptyset$ .
Ya que $A$ es acotado para toda $a \in A$ ocurre que: $m \leq a \leq M$ donde $m$ es cota inferior y $M$ es cota superior de $A$ . Así si tomamos $c \in C$ tenemos:
$c \in A \Rightarrow m \leq c \leq M \Rightarrow C$ es acotado.
Por lo que afirmamos que existen:
$s u p (A), s u p (C), i n f (A), i n f (C) .$
Observemos que $s u p (A)$ al ser cota superior de $A$ y $C \subseteq A \Rightarrow sup (A)$ es cota superior de $C$ , por lo que podemos concluir:
$s u p (C) \leq s u p (A) .$
Análogamente para los ínfimos se sigue que:
$i n f (A) \leq i n f (C) .$
Y como $i n f (C) < s u p (C)$ obtenemos:
$i n f (A) \leq i n f (C) \leq s u p (C) \leq s u p (A) .$

Proposición: Sean $A^{'} \subseteq A \subseteq R$ y $B^{'} \subseteq B \subseteq R$ donde $A^{'}, B^{'}$ son distintos del vacío. Si se cumple que:

$\forall a \in A, \forall b \in B (a \leq b)$
$s u p (A^{'}) = i n f (B^{'})$

$\Rightarrow s u p (A) = i n f (B)$
Demostración:

Primero observemos que $A$ y $B$ son no vacíos ya que:

$A^{'} \neq \emptyset$ y $A^{'} \subseteq A$
$B^{'} \neq \emptyset$ y $B^{'} \subseteq B$

Por lo que afirmamos que existen en $R$ :
$s u p (A) i n f (B)$
Por hipótesis aplicando el resultado anterior y la primera proposición de esta sección tenemos:
$s u p (A^{'}) \leq s u p (A) \leq i n f (B) \leq i n f (B^{'})$
$∴ s u p (A) \leq i n f (B)$
Además vemos que:
$i n f (B) \leq i n f (B^{'}) = s u p (A^{'}) \leq s u p (A)$
$∴ i n f (B) \leq s u p (A)$
Por lo que obtenemos la igualdad:
$i n f (B) = s u p (A)$

Ahora continuaremos con una definición de supremo e ínfimo equivalente a la primera.

Supremo e ínfimo segunda definición

Definición: Sea $A \subseteq R$ con $A \neq \emptyset$ . Decimos que $α \in R$ es:

El supremo de $A \Leftrightarrow$
- $α$ es cota superior de $A$
- $\forall ε > 0, \exists x_{ε} \in A$ tal que $α - ε < x_{ε}$ .
El ínfimo de $A \Leftrightarrow$
- $α$ es cota inferior de $A$
- $\forall ε > 0, \exists x_{ε} \in A$ tal que $x_{ε} < α + ε$ .

Ejemplos

Veamos para
$B = {2 - \frac{1}{n} : n \in N ∖ {0}}$
consideramos como candidatos $i n f (B) = 1$ y $s u p (B) = 2$ .

Comenzaremos probando $i n f (B) = 1$ haciendo uso de la segunda definición:

Tenemos que probar que $1$ es cota inferior de $B$ , es decir, $1 \leq x$ para toda $x \in B$ .
Sea $x \in B \Rightarrow x = 2 - \frac{1}{n}$ para algún $n \in N ∖ {0}$ .
$\begin{aligned} 1 \leq 2 - \frac{1}{n} & \Leftrightarrow 1 - 2 \leq - \frac{1}{n} \\ \Leftrightarrow - 1 \leq - \frac{1}{n} \\ \Leftrightarrow 1 \geq \frac{1}{n} \\ \Leftrightarrow n \geq 1 \end{aligned}$
$∴ 1$ es cota inferior
Ahora probamos que $\forall ε > 0, \exists x_{ε} \in B$ tal que $x_{ε} < 1 + ε$ .
Sea $ε > 0$ . Tomemos $x_{ε} = 1 \in B$ entonces $1 < 1 + ε$
$∴ 1$ es ínfimo de $B$ .

Ahora procedamos a demostrar que $s u p (B) = 2$ :

$2$ es cota superior de $B$ , es decir, $2 \geq x$ para toda $x \in B$ .
Tomemos $x \in B \Rightarrow x = 2 - \frac{1}{n}$ para algún $n \in N ∖ {0}$ .
$\begin{aligned} 2 \geq 2 - \frac{1}{n} & \Leftrightarrow 2 - 2 \geq - \frac{1}{n} \\ \Leftrightarrow 0 \geq - \frac{1}{n} \\ \Leftrightarrow 0 \leq \frac{1}{n} \end{aligned}$
$∴ 2$ es cota superior
Demostremos que $\forall ε > 0, \exists x_{ε} \in B$ tal que
$2 - ε < x_{ε}$ .
Sea $ε > 0$ . Tomemos $x_{ε} = 2 - \frac{1}{n}$ para algún $n \in N ∖ {0}$ .
$\begin{aligned} 2 - ε < 2 - \frac{1}{n} & \Leftrightarrow - ε < - \frac{1}{n} \\ \Leftrightarrow ε > \frac{1}{n} \\ \Leftrightarrow (ε) n > 1 \\ \Leftrightarrow n > \frac{1}{ε} \end{aligned}$
$∴ 2$ es supremo de $B$

Hallar el supremo y el ínfimo del siguiente conjunto:
$C = {x : x^{2} + x + 1 \geq 0}$

Solución:
Notemos que:
$\begin{aligned} x^{2} + x + 1 \geq 0 & \Leftrightarrow x^{2} + x + \frac{1}{4} + 1 - \frac{1}{4} \geq 0 \\ \Leftrightarrow {(x + \frac{1}{2})}^{2} + \frac{3}{4} \geq 0 \end{aligned}$
Vemos que la última desigualdad la cumple cualquier número real. Por lo tanto, tenemos que $C = R$ .
$∴$ no existe ni $s u p (C)$ ni $i n f (C)$

Más adelante…

Ahora que ya hemos visto el concepto de supremo, en la siguiente entrada veremos una propiedad más que cumple el conjunto de números reales: el Axioma del Supremo. Veremos su enunciado y varias de sus aplicaciones, algunas de ellas se demostrarán en las próximas unidades.

Tarea moral

Prueba que la primera y segunda definición de supremo e ínfimo son equivalentes.
Demuestra que el ínfimo de un conjunto es único.
Sugerencia: La prueba es análoga a la dada para el supremo.
Para $A = {\frac{1}{n} : n \in N ∖ {0}}$ prueba usando la definición que prefieras que $s u p (A) = 1$ e $i n f (A) = 0$ .
Encontrar el supremo y el ínfimo del conjunto
$D = {x : x^{2} + x - 1 < 0}$

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I:Cota superior e inferior de un conjunto.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Axioma del supremo y sus aplicaciones.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»