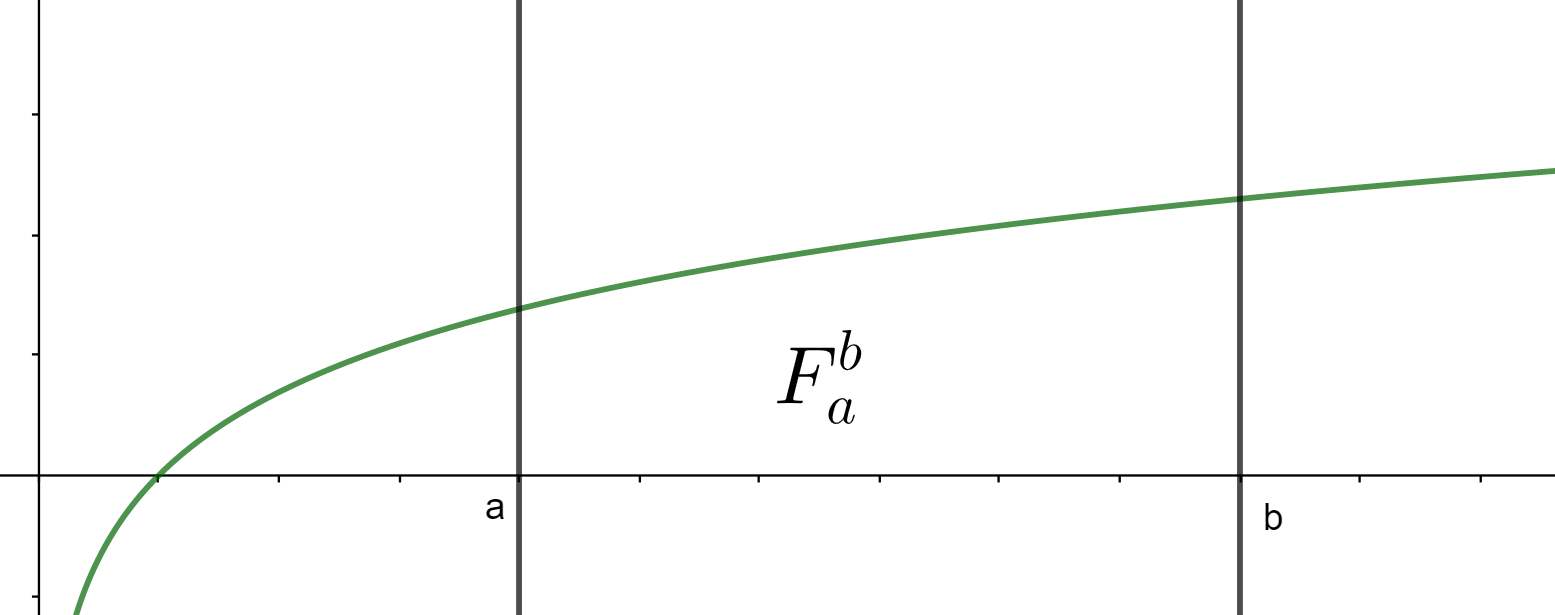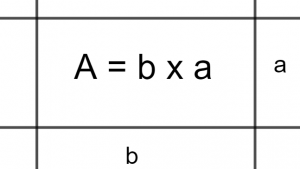Introducción
La principal motivación y aplicación de la integral es el cálculo de áreas. En esta entrada hablaremos de cómo aproximar áreas mediante sumas de Riemann. Para introducir este concepto, recordemos que en la entrada pasada se ilustró el método de exhaución. Vimos que es un acercamiento geométrico al cálculo del área del círculo mediante polígonos inscritos o circunscritos. Intuitivamente, conforme aumentamos el número de lados de estos polígonos, el área generada por ellos se aproximaba cada vez mejor al área del círculo.
Sin embargo, en las aplicaciones no sólo queremos calcular el área de círculos, sino de muchos tipos diferentes de figuras. Idealmente, nos gustaría poder calcular el área de muchas figuras u objetos, siempre y cuando éstos se puedan describir.
La forma de describirlos en este curso será mediante funciones. Por lo tanto, buscaremos encontrar una función cuya gráfica se parezca al contorno del objeto (o bien cuyo contorno pueda ser descrito por más de una función). Esta gráfica será una curva que define una región. Hablaremos de cómo definir el área de esta región de manera que coincida con nuestra intuición.
En esta entrada empezaremos con algunas definiciones generales e ideas de aproximación basadas en el método exhaustivo.
Área bajo la curva
El origen analítico de la integral se origina al asociar áreas con funciones.
Tomemos dos reales $a$ y $b$ con $a<b$. Tomemos una función $f:\mathbb{R}\to \mathbb{R}$ que, para fijar las ideas correctamente por ahora, supondremos que es positiva en todo el intervalo $[a,b]$. Supongamos que delimitamos una región en el plano cartesiano de la siguiente manera.
- Por la izquierda con la línea vertical $x = a$.
- Por la derecha con la línea vertical $x=b$.
- Por abajo con el eje $x$.
- Por arriba con la gráfica de cierta función $f(x)$.
Entonces, la magnitud del espacio que se encuentra acotado por estas curvas se le conoce como el «área bajo la curva» o más específicamente, el «área bajo la curva de $f(x)$ en el intervalo $[a,b]$.» Usaremos la notación $F_a^b$ para referirnos a esta magnitud. En el transcurso de toda esta entrada supondremos que tenemos un ejemplo «bien portado» en el que sí tiene sentido hablar de dicha área $F_a^b$ (recuerda que las funciones pueden tener comportamientos muy raros). Será importante definir qué quiere decir exactamente «bien portado», pero eso lo haremos un poco más adelante.
Ejemplo. En la siguiente figura, la curva verde es la gráfica de la función $f(x)$. La región que nos interesa está bajo esta gráfica, entre las verticales en $a$ y $b$, y sobre el eje $x$. Su magnitud $F_{a}^b$ es el área bajo la curva que nos interesa.
$\triangle$
Particiones, celdas y rectángulos
Una vez definida la región a la que se le va a calcular el área, buscaremos hacer una aproximación a esa área mediante la suma de áreas de rectángulos. Estos pueden ser inscritos (que quedan por dentro o por debajo de la función) o circunscritos (que quedan por afuera o por encima de la función). La razón por la cual usamos rectángulos es que son figuras cuya área se calcula de manera muy sencilla: el área $A$ es su base $b$ por su altura $a$.
Para definir los rectángulos que usaremos para aproximar el área, será necesario hacer una partición $P$ del intervalo $[a,b]$ del eje $x$ en una cierta cantidad de partes (que llamaremos celdas), no necesariamente todas ellas de la misma longitud. Estas partes serán las bases de los rectángulos que usaremos. Comencemos a formalizar estos conceptos.
Definición. Sean $a$ y $b$ números reales con $a\leq b$. Sea $f:\mathbb{R}\to \mathbb{R}$ una función. Sea $n\geq 0$ un entero. Una partición (en $n$ partes) del intervalo $[a,b]$ será una elección de números reales $x_0\leq x_1 \leq \ldots\leq x_n$ con $x_0=a$ y $x_n=b$. A cada subintervalo de la forma $[x_{i-1},x_i]$ para $1\leq i\leq n$ le llamaremos una celda de la partición.
A una partición la escribiremos usualmente poniendo sus elementos en orden, de la siguiente manera:
$$P =\lbrace{x_0, x_1, x_2,…, x_{n-1}, x_n}\rbrace.$$
Definición. Dada la celda $[x_{i-1},x_i]$ para $1\leq i\leq n$ de una partición, su longitud será $x_i-x_{i-1}$ y la denotaremos por $\Delta x_i$. Así,
$$\Delta x_i= x_i \ – \ x_{i-1}, \quad (i=1,2,…,n).$$
Definición. Si las celdas de una partición tienen todas la misma longitud, diremos que es una partición homogénea. Si no, es decir, si hay celdas de longitudes distintas, diremos que es una partición no homogénea.
Al tomar una partición del intervalo $[a,b]$, podemos dibujar líneas verticales en cada punto de la partición. El área $F_a^b$ que nos interesa queda dividida en regiones o franjas como en la siguiente figura.
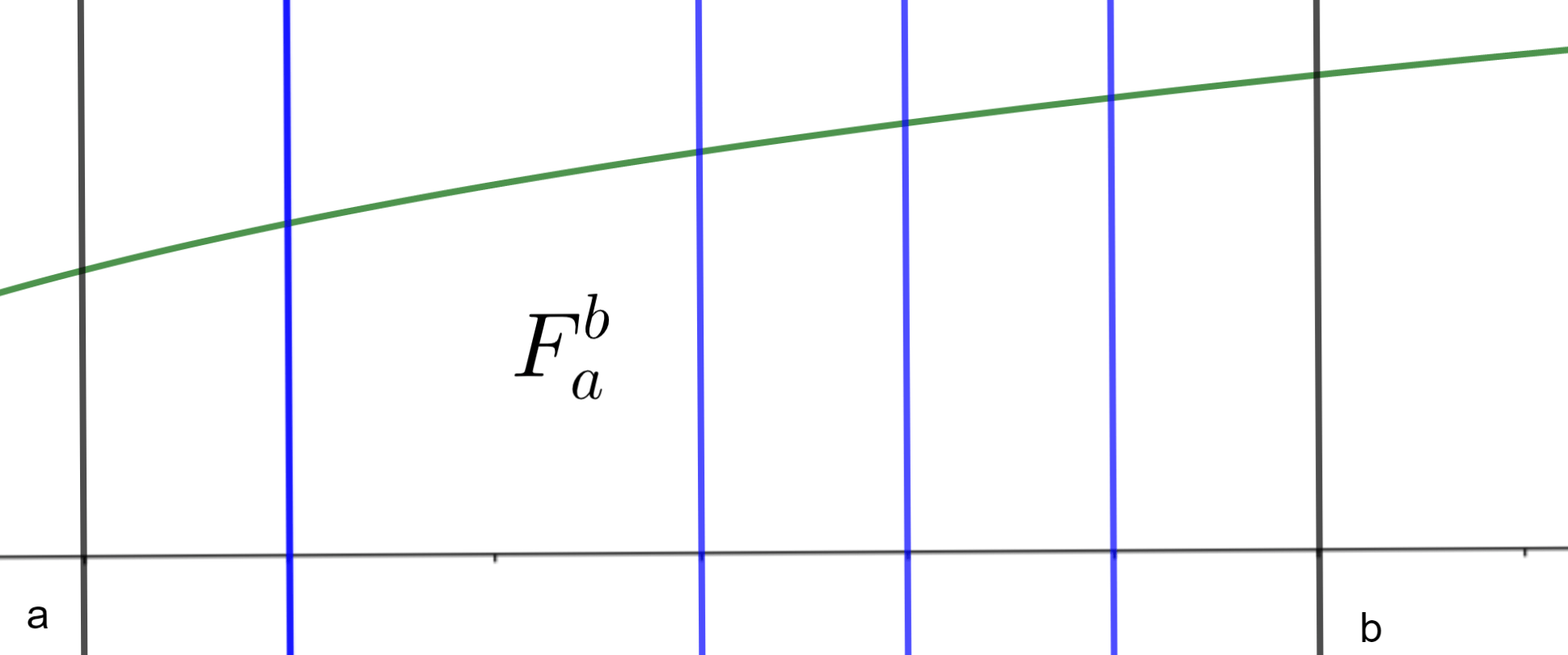
Intuición de las sumas superiores e inferiores
El área de cada una de las franjas que hicimos la podemos aproximar (al estilo del método exhaustivo) mediante rectángulos. Sin embargo, dado que la gráfica de la función no es exactamente horizontal, la suma de ciertos rectángulos que usemos para aproximar el área podría no ser exactamente el área bajo la curva. ¿Qué podríamos hacer para tener un poco más de control sobre cómo es el área de cada rectángulo con respecto al área de cada franja? Podemos usar como base las longitudes de las celdas y como altura podemos usar el máximo o mínimo de la función $f(x)$ en cada intervalo. Esto es un caso particular de lo que más adelante llamaremos sumas de Riemann.
La siguiente figura muestra rectángulos desde el eje $x$ hasta la altura morada (que es el mínimo de la función en cada celda) y rectángulos desde el eje $x$ hasta la altura roja (que es el máximo de la función en cada celda).
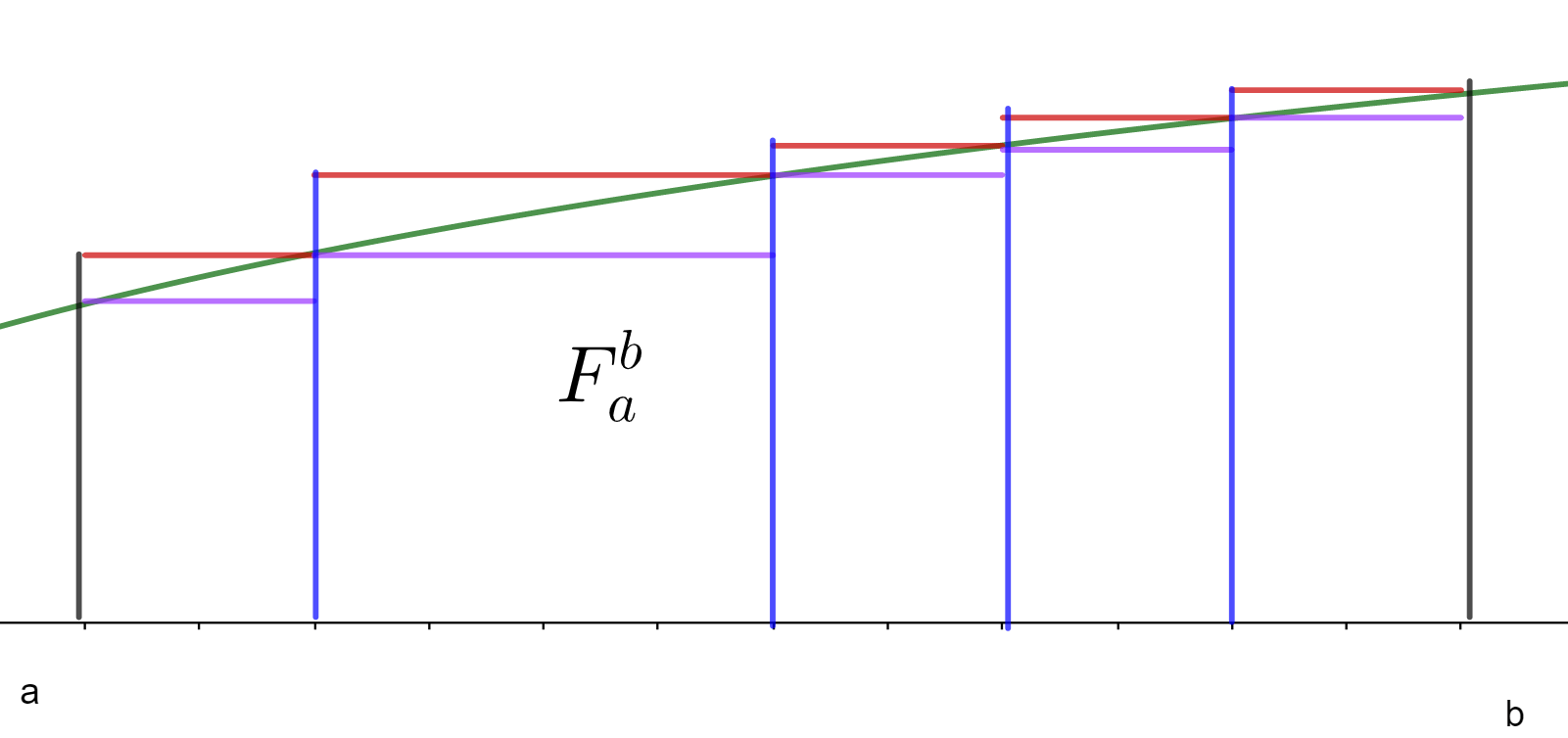
Cuando tomamos los mínimos en cada celda y consideramos el área de los rectángulos morados, la suma de cada rectángulo será menor que cada franja, y por lo tanto la suma total de áreas de estos rectángulos será menor que el área bajo la curva que queremos.
Por otro lado, si tomamos los máximos de cada celda, tenemos los rectángulos rojos, que análogamente a lo dicho arriba, tienen suma de área total mayor al área bajo la curva buscada. Intuitivamente, hemos acotado el área buscada entre dos áreas que sí sabemos calcular.
Formalización de sumas superiores e inferiores
Introduciremos un poco de notación para hablar de sumas superiores e inferiores. Primero, le queremos dar un símbolo al ínfimo y al supremo de las evaluaciones de la función que nos interesa en cada celda.
Definición. Dada una partición $P=\{x_0,\ldots,x_n\}$ del intervalo $[a,b]$ y una función acotada $f:\mathbb{R}\to \mathbb{R}$:
- Al ínfimo de los valores de $f$ en la parte $[x_{i-1},x_i]$ le llamaremos $m_i$. En símbolos: $$m_i = \inf \lbrace {f(x) | x_{i-1} \leq x \leq x_i} \rbrace, \quad i = 1,…,n .$$
- Al supremo de los valores de $f$ en la parte $[x_{i-1},x_i]$ le llamaremos $M_i$. En símbolos: $$M_i = \sup \lbrace {f(x) | x_{i-1} \leq x \leq x_i} \rbrace, \quad i = 1,…,n .$$
Te recomendamos recordar la teoría de ínfimos y supremos de Cálculo I, que puedes consultar en el siguiente enlace: Supremo e ínfimo. Como nota, observa que en este punto estamos suponiendo muy poco de $f$, simplemente que es acotada.
La siguiente definición formaliza la idea de «aproximar el área por abajo».
Definición. Sean $f:\mathbb{R}\to \mathbb{R}$ una funcion acotada y $a\leq b$ reales. Sea $P=\{x_0,\ldots,x_n\}$ una partición de $[a,b]$. Diremos que la suma inferior $\underline{S}$ correspondiente a la función $f$ en la partición $P$ del intervalo $[a,b]$ es el número:
\begin{align*}
\underline{S}(f,P) &= \sum_{i=1}^{n} m_i\Delta x_i,
\end{align*}
donde $m_i$ es el ínfimo de los valores de $f$ la celda $[x_{i-1},x_i]$ y $\Delta x_i $ es la longitud de dicha celda. La expresión anterior se desarrolla explícitamente entonces como
$$m_1(x_1 – x_0) + m_2(x_2 – x_1) + . . . + m_n(x_n – x_{n-1}).$$
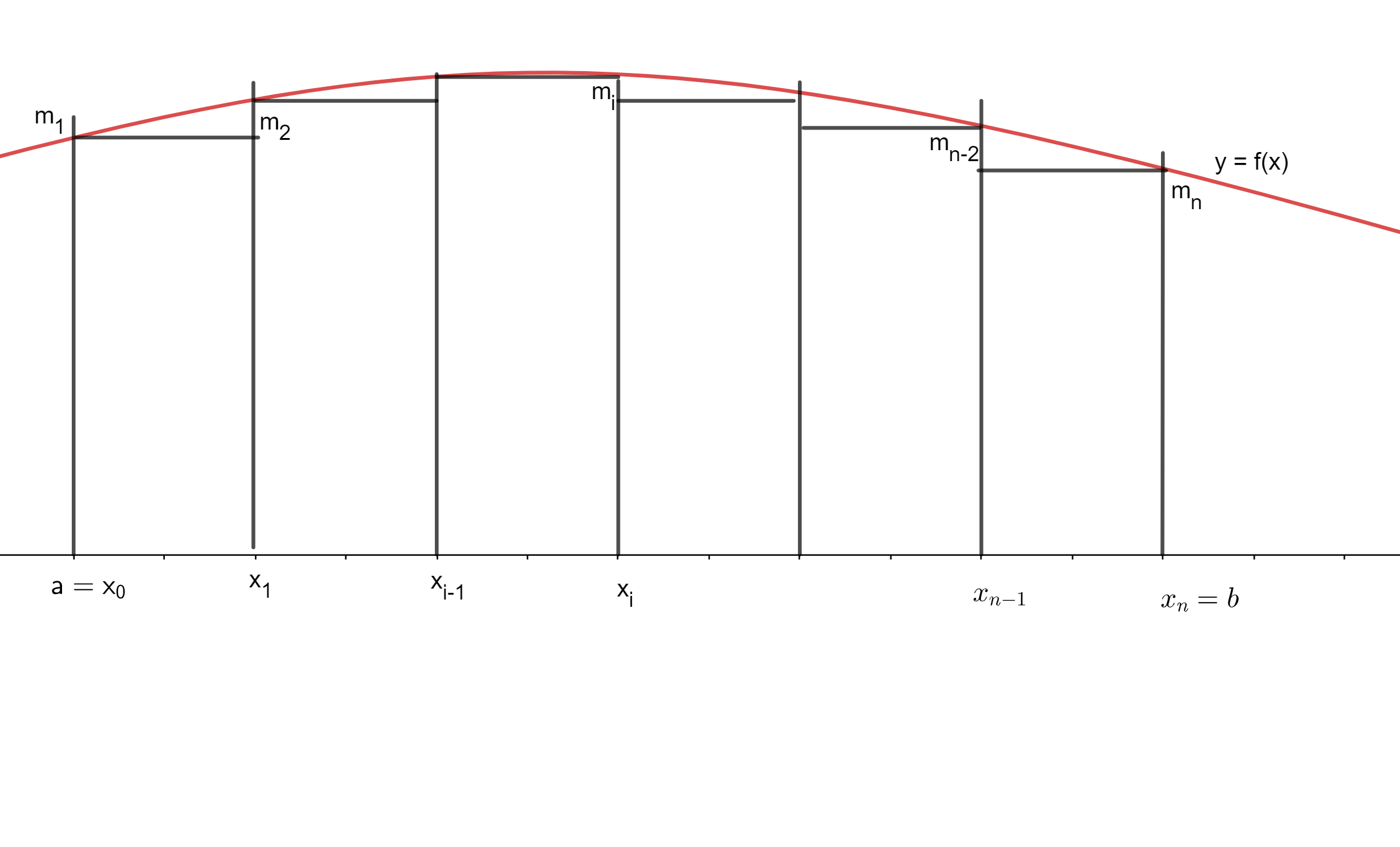
Esto es precisamente la suma de áreas de varios rectángulos que, por tomar la altura como el ínfimo en cada celda, quedan todos ellos por debajo de la gráfica de la función, como en la siguiente figura.
La siguiente definición formaliza la idea de «aproximar el área por arriba».
Definición. Sean $f:\mathbb{R}\to \mathbb{R}$ una funcion acotada y $a\leq b$ reales. Sea $P=\{x_0,\ldots,x_n\}$ una partición de $[a,b]$. Diremos que la suma superior $\overline{S}$ correspondiente a la función $f$ en la partición $P$ del intervalo $[a,b]$ es el número:
\begin{align*}
\overline{S}(f,P) &= \sum_{i=1}^{n} m_i\Delta x_i,
\end{align*}
donde $M_i$ es el supremo de los valores de $f$ la celda $[x_{i-1},x_i]$ y $\Delta x_i $ es la longitud de dicha celda. La expresión anterior se desarrolla explícitamente entonces como
$$M_1(x_1 – x_0) + M_2(x_2 – x_1) + . . . + M_n(x_n – x_{n-1}).$$
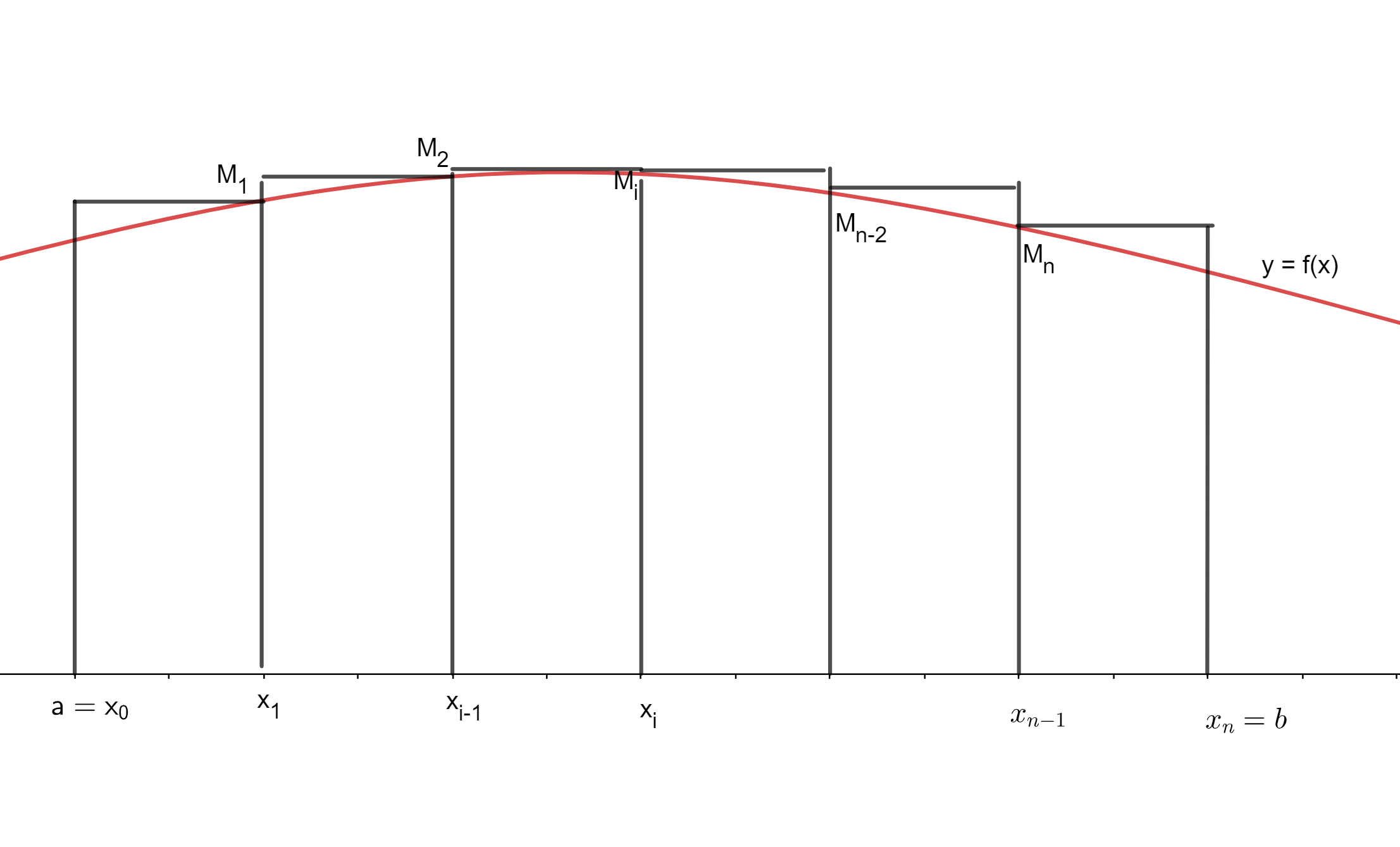
Ahora tenemos la suma de áreas de varios rectángulos que quedan por encima de la gráfica de la función, como se muestra a continuación:
Si regresamos a pensar que la función $f$ es «bien portada» como para que el área $F_a^b$ tenga sentido, entonces las sumas superiores e inferiores nos ayudan a acotar dicha área. En efecto, notemos que para cualquier $i=1,\ldots,n$, tenemos que
$$m_i \leq f(x) \leq M_, \quad \text{para } x\in [x_{i-1},x_i].$$
De aquí, el área en cada franja queda acotada entre el área de dos rectángulos y sumando en todas las celdas tendríamos que
$$ \underline{S} \leq F_a^b \leq \overline{S} \quad .$$
Es decir, la suma inferior es menor o igual que el valor de la integral y la suma superior es mayor o igual que la integral. Un poco más adelante formalizaremos esto, cuándo hablemos apropiadamente de las funciones «bien portadas».
Refinamientos de una partición
Si hacemos una partición con más puntos, habrá más celdas dentro del intervalo y por lo tanto, la cantidad de rectángulos aumenta. Intuitivamente, nuestras aproximaciones deberían acercarse más al área buscada. En efecto, más adelante veremos que esto es así. Por ello, es importante introducir la siguiente definición formal.
Definición. Sea $P$ una partición del intervalo $[a,b]$. Un refinamiento de $P$ es otra partición $Q$ de $[a,b]$ tal que $P \subseteq Q$.
Al momento de pedir que la partición $P$ esté contenida en $Q$, aseguramos que todos los puntos de la partición generados en $P$ se encuentran en $Q$, y por lo tanto que cada celdas de $Q$ sean subconjunto de alguna celda de $P$.
Intuitivamente, las aproximaciones que hagamos con la partición $Q$ deben de ser entonces mejores que las que hagamos con la partición $P$. Si cierta suma de áreas de rectángulos hechas con $Q$ es $S_Q$ y esa suma de áres hechas con $P$ es $S_P$ suena razonable que:
$$ \left|F_a^b – S_Q\right| \leq \left|F_a^b – S_P \right|.$$
Sin embargo, nos estamos adelantando un poco. Lo que sí podemos mostrar formalmente por ahora es el siguiente resultado auxiliar.
Lema. Sean $f:\mathbb{R}\to \mathbb{R}$ una funcion acotada y $a\leq b$ reales. Si $P$ y $Q$ son particiones de $[a,b]$ y $Q$ es refinamiento de $P$, entonces $$\underline{S} (f,P) \leq \underline{S} (f,Q) \quad \text{y} \quad \overline{S} (f,Q) \leq \overline{S} (f,P)$$
Demostración. Por definición, $P$ y $Q$ son subconjuntos finitos de $[a,b]$, y $P\subseteq Q$, así que se puede llegar de $P$ a $Q$ agregando elementos de $[a,b]$ uno por uno. Bastará entonces ver que las desigualdades de arriba se cumplen cuando $Q$ tiene exactamente un elemento más que $P$, digamos $Q=P\cup \{y\}$. Tomemos $P=\{x_0,\ldots,x_n\}$. El real $y$ cae dentro de alguna celda de $P$, digamos en la celda $[x_{j-1},x_j]$.
Estudiemos qué suecede con las sumas inferiores. La suma inferior con respecto a $P$ es \begin{align*}
\underline{S}_P &= \sum_{i=1}^{n} m_i\Delta x_i,
\end{align*}
Para la suma inferior con respecto a $Q$, la celda $[x_{j-1},x_j]$ queda partida en dos celdas $[x_{j-1},y]$ y $[y,x_j]$. Los ínfimos respectivos $r$ y $s$ de la función $f$ en estas dos celdas cumplen $r\geq m_j$ y $s\geq m_j$, pues estamos tomando el ínfimo sobre conjuntos más chicos. Así, la suma inferior con respecto a $Q$ cumple:
\begin{align*}
\underline{S}(f,Q) &= \sum_{i=1}^{j-1} m_i\Delta x_i + r (y-x_{j-1}) + s (x_j-y)+ \sum_{i=j+1}^{n} m_i\Delta x_i\\
&\leq \sum_{i=1}^{j-1} m_i\Delta x_i + m_j (y-x_{j-1}) + m_j (x_j-y)+ \sum_{i=j+1}^{n} m_i\Delta x_i\\
&=\sum_{i=1}^{j-1} m_i\Delta x_i + m_j (x_j-x_{j-1})+ \sum_{i=j+1}^{n} m_i\Delta x_i\\
&= \sum_{i=1}^{n} m_i\Delta x_i\\
&= \underline{S}(f,P).
\end{align*}
Esto termina la demostración para las sumas inferiores. El caso de las sumas superiores es análogo.
$\square$
En palabras, el lema anterior dice que la suma inferior con la partición $P$ es menor que la suma inferior con la partición $Q$ y la suma superior con la partición $P$ es mayor que la suma superior con la partición $Q$.
Otra aplicación muy importante de los refinamientos es que nos ayudan a demostrar que cualquier suma superior siempre es mayor que cualquier suma inferior, sin importar la partición que tomemos en una y en otra.
Proposición. Sean $f:\mathbb{R}\to \mathbb{R}$ una funcion acotada y $a\leq b$ reales. Sean $P$ y $Q$ particiones de $[a,b]$. Entonces,
$$\underline{S}(f,P) \leq \overline{S}(f,Q).$$
La idea de la demostración es sencilla. Para cualesquiera dos particiones $P$ y $Q$ podemos encontrar una partición $R$ que es un refinamiento de ambas (¿cómo la encontrarías?). Ya teniendo dicha partición, tenemos la cadena de desigualdades:
$$\underline{S} (f,P) \leq \underline{S} (f,R) \leq \overline{S} (f,R) \leq \overline{S} (f,Q).$$
Dar la partición $R$ de manera explícita y los detalles de cómo justificar la cadena de desigualdades anterior queda como parte de los ejercicios de esta entrada.
Sumas de Riemann y regla del punto medio
Ya vimos cómo hacer aproximaciones con rectángulos inferiores y cómo hacer aproximaciones con rectángulos superiores. Pero, como te imaginarás, los rectángulos podríamos tomarlos bajo otro criterio. Por ejemplo, podemos hacer rectángulos tomando un punto cualquiera $\xi_i$ dentro de cada celda $[x_{i-1},x_i]$ de una partición.
Ahora la aproximación quedaría de la siguiente manera:
\begin{align*}
F_n &= \sum_{i=1}^n f(\xi_i) \Delta x_i\\
&= \sum_{i=1}^n f(\xi_i) (x_i-x_{i-1})\\
&=f(\xi_1)(x_1 \ – \ x_0) + f(\xi_2)(x_2 \ – \ x_1) + . . . + f(\xi_n)(x_n \ – \ x_{n-1})
\end{align*}
A las expresiones de este estilo se les conoce como sumas de Riemann.
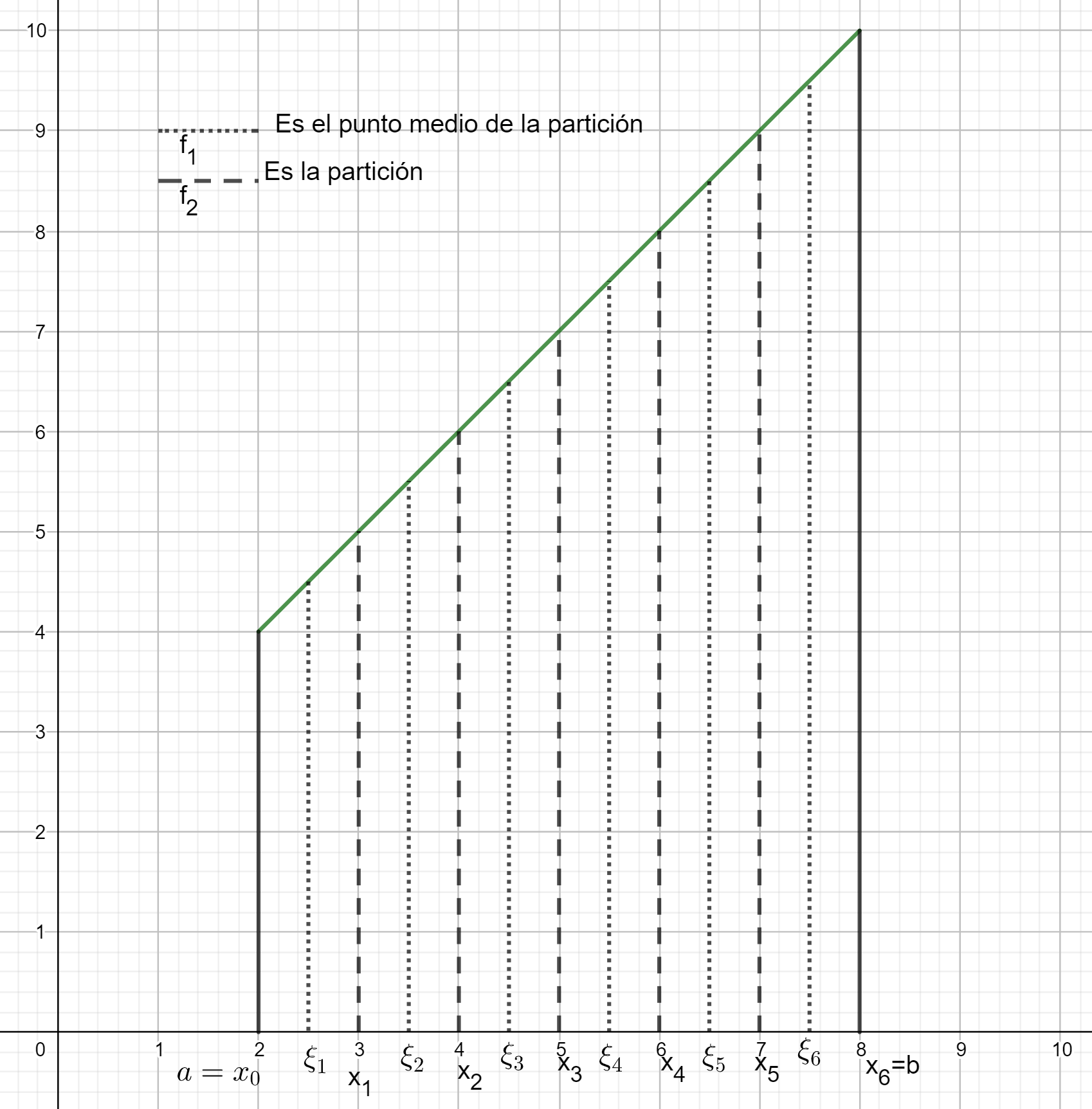
Una manera de dar de manera explícita algunos valores $\xi_i$ es tomando los puntos medios en cada celda, como en la siguiente figura.

Este método nos dará otra manera de aproximar el área que buscamos. Si de nuevo refinamos la partición y usamos los puntos medios, tendremos otro procedimiento exhaustivo para aproximar el área. Pero igual podríamos tomar otra, y otra, y otra manera de aproximar el área. ¿Será que todas estas aproximaciones nos llevan a la misma área? Es parte de lo que tendremos que entender formalmente más adelante. Sin embargo, por ahora haremos algunos ejemplos concretos de las ideas que hemos discutido hasta ahora.
Ejemplo de sumas de Riemann superiores, inferiores y de punto medio
Ejemplo. Tomamos la función $f:[2,8]\to \mathbb{R}$ dada por $f(x)=x+2$. Tomemos la partición homogénea $P=\{2,3,4,5,6,7,8\}$, en donde cada celda tiene longitud $1$. Encontremos la suma superior, la inferior y la que se obtiene mediante la regla del punto medio.
Para la suma inferior, tenemos el siguiente conjunto de ínfimos (en este caso, mínimos) de las celdas generadas:
$$m= \lbrace {4, 5, 6, 7, 8, 9}\rbrace .$$
De este modo, la suma inferior es
$$\underline{S}(f,P) = 4\cdot(3-2) + 5 \cdot (4-3) + 6 \cdot (5-4) + 7 \cdot (6-5) + 8 \cdot (7-6) + 9 \cdot (8-7) = 39.$$
En el caso de la suma superior, los supremos (en este caso, máximos) son
$$M= \lbrace {5, 6, 7, 8, 9, 10}\rbrace.$$
Desarrollemos la suma superior:
$$\overline{S}(f,P) = 5 \cdot (3-2) + 6 \cdot (4-3) + 7 \cdot (5-4) + 8 \cdot (6-5) + 9 \cdot (7-6) + 10 \cdot (8-7) = 45.$$
Finalmente, para la regla del punto medio, tenemos que los valores de la función evaluada en el punto medio de cada intervalo son:
$$\xi= \lbrace {4.5, 5.5, 6.5, 7.5, 8.5, 9.5}\rbrace .$$
Desarrollando la suma, obtenemos
$$S= 4.5 \cdot (3-2) + 5.5 \cdot (4-3) + 6.5 \cdot (5-4) + 7.5 \cdot (6-5) + 8.5 \cdot (7-6) + 9.5 \cdot (8-7) = 42.$$
$\triangle$
Más adelante…
En esta entrada empezamos a motivar cómo el área bajo una curva puede ser aproximada mediante rectángulos. Sin embargo, supusimos que nuestra curva estaba dada por una función «bien portada» la cuál sí hace un área apropiada. Esto no necesariamente pasará siempre, pues si la función tiene una gráfica muy complicada, entonces no podremos hablar apropiadamente del área debajo de ella.
De hecho, lo que hicimos en esta entrada nos ayudará a dar formalidad a exactamente qué quiere decir que la función sea «bien portada». La idea de particiones nos servirá para definir el área justo cuando cualquier proceso de aproximar «suficientemente bien» nos lleve al mismo límite. Tomaremos entonces la intuición desarrollada de las sumas inferiores, superiores e incluso las de la regla del punto medio, para introducir la definición de integral definida de la siguiente entrada.
Tarea moral
- Aproxima el área bajo la curva de las siguientes funciones en el intervalo dado, usando una partición homogénea con cinco celdas en el intervalo dado. En cada caso, realiza la cuenta con las sumas inferiores, las sumas superiores y con la regla del punto medio.
- $f(x) = x^2$ en el intervalo $[0,1]$.
- $f(x)=2x-3$ en el intervalo $[0,2]$.
- $f(x)=x e^x$ en el intervalo $[2,3]$ (puedes usar calculadora para aproximar las respuestas)
- En esta entrada sólo hemos hablado de cómo encontrar el área entre la gráfica de una función positiva y el eje $x$ (dados dos límites verticales). ¿Qué tendríamos que hacer si la función es negativa?
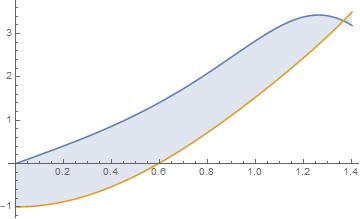
- Ahora imaginemos que queremos encontrar el área que se encuentra entre la gráfica de dos funciones. Por ejemplo, imagina que queremos aproximar con las ideas de esta entrada el área entre las gráficas de las siguientes dos funciones, desde la línea vertical $x=0$ hasta el primer punto de intersección que tienen.
$f(x)= sin(x^3) + 2x$
$g(x)=cos(x^2)+3x^2-2$
Puedes ver estas funciones en la figura. Para realizar la aproximación, haz lo siguiente.
- Encuntra el punto $c$ tal que $f(c)=g(c)$, es decir, en qué ubicación horizontal se cruzan las gráficas.
- Haz una partición homogénea en 10 partes del intervalo $[0,c]$. ¿Qué longitud tiene cada celda?
- Crea rectángulos usando como altura la distancia máxima entre las curvas en cada celda. ¿Cuánto queda la suma de áreas de rectángulos? ¿Y si usas la distancia mínima entre las curvas en cada celda?
- En el texto se da la demostración de que en un refinamiento, la suma inferior se vuelve más grande. Completa los detalles para ver el resultado análogo de que en un refinamiento la suma superior se vuelve más pequeña. ¿Qué propiedades del supremo estás utilizando?
- Completa los detalles de la proposición de que cualquier suma superior es mayor a cualquier suma inferior, aunque estemos hablando de particiones diferentes.
- La gráfica de la función $f(x)=\sqrt{1-x^2}$ es un semicírculo que va de $-1$ a $1$. Usa una partición homogénea en $10$ celdas del intervalo $[-1,1]$ y la regla del punto medio para dar una aproximación al área de este semicírculo. Entonces, ¿cuál sería una aproximación al área del círculo de radio $1$? De aquí, ¿cuál sería una aproximación para $\pi$?
Entradas relacionadas
- Página del curso: Cálculo Diferencial e Integral II
- Entrada anterior: Introducción al curso
- Entrada siguiente: Definición de la integral definida