Introducción

Este curso es la continuación de la materia Cálculo Diferencial e Integral I. En el primer curso de cálculo hablamos del cálculo diferencial. Nuestro principal objeto matemático fue la derivada y cómo se puede interpretar como la razón de cambio del objeto de análisis: la tangente de una curva, la velocidad y aceleración de una partícula, la variación de un objeto en su trayectoria, etc.

En este siguiente curso hablaremos de temas relacionados con el cálculo integral. Hablaremos un poco de sus orígenes, de los principales objetos matemáticos que estudia, de varios aspectos fundamentales de su teoría y de sus aplicaciones. El objetivo principal de esta rama matemática es el estudio de las integrales y las anti-derivadas. Una motivación importante es que ellas son una herramienta para la solución de problemas de cálculo de áreas y de volúmenes.

Así, el objeto matemático estelar del curso será la integral y la motivaremos mediante su gran utilidad para el cálculo de áreas. Sin embargo, esto no será lo único que haremos. La definiremos formalmente, probaremos las muchas propiedades matemáticas que tiene y veremos numerosas aplicaciones no sólo al cálculo de integrales, sino también a la construcción de otros objetos matemáticos fundamentales como la función exponencial.

Es muy probable que ya cuentes con una buena noción de área. En cursos de primaria, secundaria y bachillerato se explica un poco de esto y se dan fórmulas para calcular áreas. Sin embargo, estas fórmulas no salen de la nada. Pueden ser construidas a partir de nociones más básicas y por distintos métodos. Uno de ellos es la integración. Hasta que hagamos más precisiones formales, puedes aprovechar la intuición que ya tienes sobre las áreas y pensar en ellas intuitivamente como una magnitud que «mide» qué tan grande es una región contenida dentro de ciertos límites y cuyas unidades están «al cuadrado». Esto te ayudará a tener en qué cimentar tu intuición para cuando demos una definición más formal.

Algunas notas históricas

Históricamente, se han encontrado casos de utilización de de herramientas de cálculo diferencial en trabajos antiguos, por ejemplo, los trabajos de Arquímedes. Pero fue hasta los siglos XVI y XVII donde se tuvo un desarrollo sistemático, atribuido a Isaac Newton y Gottfried Leibniz, quienes son considerados como los dos grandes pioneros y más grandes representantes del Cálculo. Sin embargo, no fueron los únicos aportadores a éste.

Otra persona importante, Isaac Barrow, quién sería el profesor de Newton, tenía una comprensión sobre la reciprocidad entre la derivación e integración. Este concepto es el punto de partida del cálculo desarrollado por Newton y Leibnitz. Es primordial pues da pie a la introducción y demostración de los dos teoremas fundamentales del cálculo.

Método exhaustivo

A modo de introducción, platicaremos en esta entrada sobre el método exhaustivo. Es un método matemático que utiliza la geometría para aproximar algún resultado o aproximar a la solución un problema que tengamos. La característica que tiene el método es que, a la vez que aumenta el cálculo o las repeticiones, aumenta el grado de precisión de nuestra aproximación con respecto al resultado que queremos.

Arquímides desarrolló una de las aplicaciones de este método para el cálculo de áreas planas. Eudoxo también trabajó con este método, sólo que su objetivo era calcular el volumen de las pirámides de Egipto. En cierto sentido, también ya usamos este método cuando hablamos de la derivada de una función. Para pensar en la tangente en un punto $P$ a la gráfica de una función, la intuición (y de hecho, en cierto sentido la definición formal) consistió en tomar rectas secantes que pasaran por $P$ y otro punto $Q$ en la gráfica. Conforme $Q$ se acercaba a $P$ nos aproximábamos más y más a la tangente y, si cierto límite existía, justo esa era la definición de tangente.

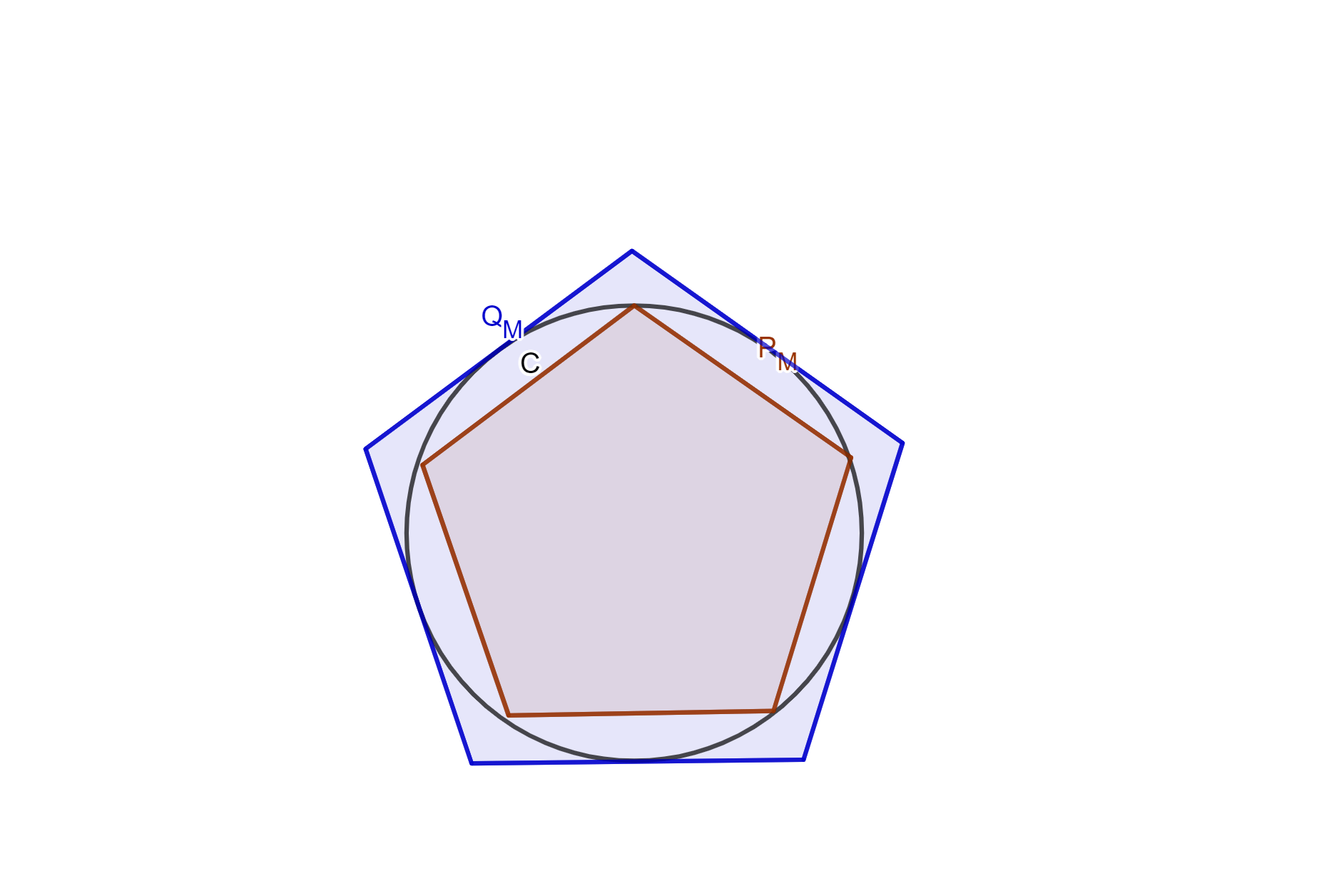
Para ejemplificar nuevamente el método exhaustivo, veremos cómo encontrar de manera un poco informal el el área de un círculo. Sea $C$ un círculo y sea $M\geq 3$ un número natural. Tomemos $P_M$ un polígono regular de $M$ lados inscrito al círculo $C$ y $Q_M$ un polígono de $M$ lados circunscrito al círculo $C$. Para que dichos polígonos queden bien definidos, podemos pedir además que su lado inferior sea horizontal. Por ejemplo, en la figura a continuación se muestra el caso $M = 5$.

Notemos que los polígonos que definimos tienen dos áreas: una que incluye al área del círculo y otra que está incluida en el círculo.

Para cada valor de $M$ tenemos dos polígonos. De este modo, estamos generando dos sucesiones de polígonos: la de polígonos inscritos $\{P_M\}_{M\geq 3}$ y la de polígonos circunscritos $\{Q_M\}_{M\geq 3}$. Notemos que el área cada uno de los polígonos inscritos $P_M$ queda acotada superiormente por el área de cada uno de los polígonos $Q_M$; a su vez, el área de cada uno de los polígonos circunscritos $Q_M$ queda acotada inferiormente por el área de cada uno de los polígonos $P_M$. Además, no es muy difícil convencerse de que el área de los polígonos inscritos crece conforme $M$ aumenta y, en contraparte, el área de los circunscritos decrece conforme $M$ aumenta. Recordando del primer curso de cálculo lo que sabemos sobre supremos, ínfimos y sobre sucesiones monótonas y acotadas, tendríamos entonces que los siguientes dos límites existen:

\begin{align*}
p&=\lim_{M\to \infty} \text{área}(P_M)=\sup_{M\geq 3} \text{área}(P_M)\\
q&=\lim_{M\to \infty} \text{área}(Q_M)=\inf_{M\geq 3} \text{área}(Q_M).
\end{align*}

Además, $p\leq q$. De hecho, si el área del círculo $C$ que nos interesa es $c$, entonces por lo que mencionamos arriba tendríamos que $p \leq c \leq q$. Nuestra intuición nos dice que cuando la $M$ aumenta, generamos un polígono con más lados que van acercándose a la circunferencia, y que en el límite debemos obtener el área de la circunferencia. Por lo tanto, esperaríamos que $p=c=q$.

¿Qué sería suficiente para respaldar esta intuición? ¿Bastaría que calculáramos explícitamente $\lim_{M\to \infty} \text{área}(P_M)$ y $\lim_{M\to \infty} \text{área}(Q_M)$ (por ejemplo, dividiendo los polígonos en triángulos para encontrar una fórmula explícita) y que viéramos que son iguales? Esto seguro aumentaría mucho la confianza en nuestro procedimiento. Pero, ¿qué tal que aproximamos al círculo con otros polígonos que no son regulares? ¿nos dará lo mismo? Nuestra definición formal de área ayudará a resolver estas dudas.

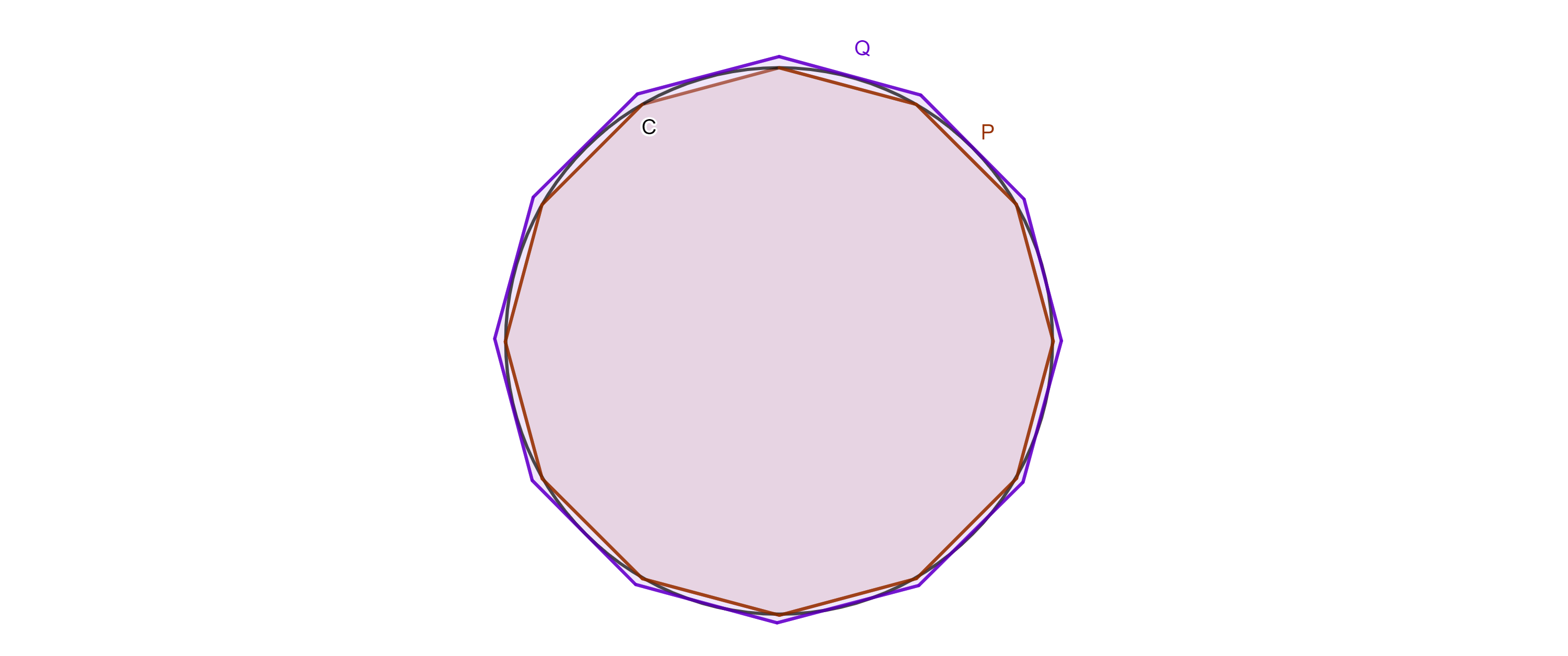
En resumen, el método iterativo nos permite aproximar el área del círculo, encerrándolo entre 2 polígonos, de los cuales sabemos calcular el área mediante triángulos. Intuitivamente, mientras más fraccionemos los polígonos, la aproximación del área del círculo será mejor. Esta idea de «encerrar» el área que nos interesa entre dos áreas que sepamos (o acordemos) cómo calcular será clave cuando definamos la integral definida.

Más adelante…

En esta entrada hablamos brevemente sobre la conexión de este curso de cálculo con el anterior. Dimos unas pocas notas históricas e introducimos la idea del método exhaustivo. En la siguiente entrada comenzaremos a formalizar estas ideas para el cálculo de áreas entre la gráfica de una función y el eje $x$.

Tarea moral

1. Con las herramientas de geometría que has adquirido en la educación básica, intenta completar el ejemplo que comenzamos sobre el método exhaustivo. No te preocupes mucho por la formalización de límites, funciones trigonométricas, fórmulas de áreas de triángulos, etc. Es parte de lo que haremos en este curso. Entre otras cosas, tendrás que:
   • Calcular explícitamente la distancia del centro de un círculo $C$ de radio $r$ a un vértice (y a un lado) del polígono inscrito (y circunscrito) en $C$ que es regular y de $n$ lados.
   • Encontrar el área de $P_n$ y $Q_n$.
   • Encontrar los límites de estas áreas conforme $n$ tiende a infinito.
2. Investiga más sobre los orígenes del cálculo integral.
3. Averigua sobre el método exhaustivo y otros usos históricos que se le ha dado.
4. El método exhaustivo puede ser algo peligroso si se usa apresuradamente. Por ejemplo, toma un cuadrado de lado $1$ y divídelo en cuadrados pequeños para formar un tablero de $n\times n$. Mediante un camino $C_n$ que sube y va a la derecha alternadamente, se puede comenzar en el vértice inferior izquierdo y llegar al vértice superior derecho. Intuitivamente, cuando $n$ tiende a infinito, este camino pareciera converger a la diagonal del cuadrado, la cual tiene longitud $\sqrt{2}$. Sin embargo, la longitud de cada camino $C_n$ siempre es $2$ pues en total avanza una unidad a la derecha y una hacia arriba. ¿Por qué la longitud de $C_n$ no tiende a $\sqrt{2}$ si aparentemente $C_n$ tiende a la diagonal del cuadrado?
5. Realiza un repaso de los teoremas principales de Cálculo Diferencial e Integral I. ¡Te serán sumamente útiles para este curso! En particular, sería bueno que revises los siguientes temas:
   • Definición y propiedades de límites.
   • Definición y propiedades de funciones contínuas.
   • Definición y propiedades de derivadas.
   • Reglas de derivación.
   • El teorema del valor intermedio.
   • El teorema del valor medio.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral II
• Siguiente entrada del curso: Motivación de la integral y sumas de Riemann