Archivo de la etiqueta: funciones continuas

Cálculo Diferencial e Integral I: Continuidad y monotonía

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

En esta entrada estableceremos la relación existente entre la monotonía y la continuidad. Para lo cual haremos un repaso rápido de algunos conceptos revisados previamente.

Definición. Sea $A \subset \mathbb{R}$ y $f: A \to \mathbb{R}$.

  • Se dice que $f$ es creciente si para cada $x_1$, $x_2 \in A$ tales que $x_1 < x_2$, entonces se tiene que $f(x_1) \leq f(x_2)$. Decimos que es estrictamente creciente si se da la desigualdad estricta, es decir, $f(x_1) < f(x_2)$.
  • Análogamente, decimos que $f$ es decreciente si para cada $x_1$, $x_2 \in A$ tales que $x_1 < x_2$, entonces se tiene que $f(x_1) \geq f(x_2)$. Decimos que es estrictamente decreciente si se da la desigualdad estricta, es decir, $f(x_1) > f(x_2)$.
  • Si una función es creciente o decreciente decimos que es monótona. Si la función es estrictamente creciente o estrictamente decreciente, decimos que es estrictamente monótona.

Tras haber retomado las definiciones anteriores, vale la pena mencionar que el hecho de que una función sea monótona en un intervalo no implica que sea continua. Podemos considerar como ejemplo:
$$f(x) = \begin{cases}
-1 & \text{ si } x < 0 \\
1 & \text{ si } x \geq 0.
\end{cases}$$

Se tiene que $f$ es monótona en $\mathbb{R}$, pero no es continua en $x=1$.

Funciones continuas que son monótonas

Estamos listos para ver la relación que existe entre la monotonía y la continuidad. Iniciaremos de viendo un resultado que va de continuidad a monotonía.

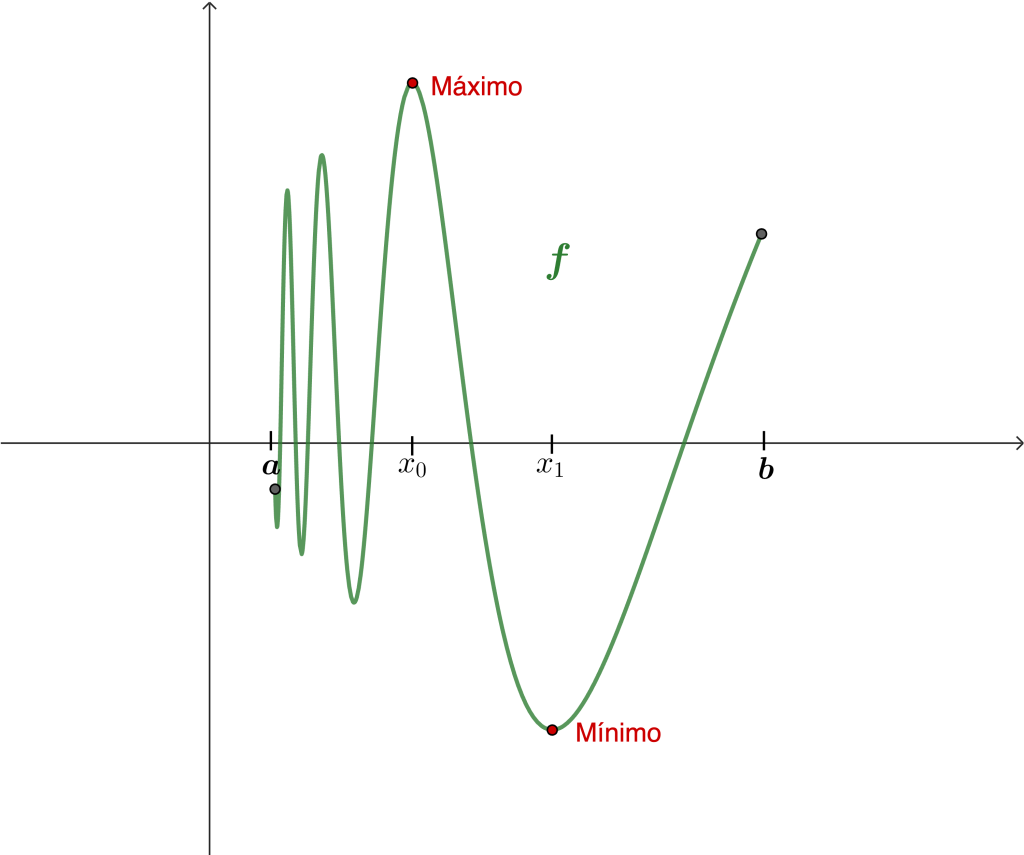
Teorema. Sea $A = [a, b]$ un intervalo y $f : A \to \mathbb{R}$ una función continua e inyectiva. Entonces $f$ es estrictamente monótona.

Demostración.

Dado que la función es inyectiva, se tiene que $f(a) \neq f(b)$. Así, tenemos dos casos.

  • Caso 1: $f(a) < f(b)$.
    Primero veamos que si $x \in [a,b]$, entonces se tiene que
    $$f(a) \leq f(x) \leq f(b) \tag{1}.$$
    Sea $x \in [a,b]$ y supongamos que $f(x) < f(a)$. Por el teorema del valor intermedio, sabemos que existe $y \in [x, b]$ tal que $f(y) = f(a)$, pero esto contradice la inyectividad. Por tanto, se concluye que $f(a) \leq f(x)$.

    Análogamente, si $x \in [a,b]$ y supongamos que $f(b) < f(x)$. Por el teorema del valor intermedio, existe $y \in [a,x]$ tal que $f(y) = f(b)$, pero esto contradice la inyectividad. Por tanto, se concluye que $f(x) \leq f(b)$.

    Ahora probaremos que $f$ es estrictamente creciente. Sean $x$, $y \in [a,b]$ tal que $x<y$. Por $(1)$, se tiene que $f(x) \leq f(b)$, más aún, se tiene la desigualdad estricta $f(x) < f(b)$ dado que la función es inyectiva y $x< y \leq b$. Tomemos el intervalo $[x,b]$ donde $f$ sigue siendo continua e inyectiva y se cumple que $f(x) < f(b)$, aplicando nuevamente $(1)$, se tiene que $f(x) \leq f(y)$ y por ser $f$ inyectiva se tiene la desigualdad estricta, es decir, $f(x) < f(y)$ y por tanto $f$ es estrictamente creciente.

  • Caso 2: $f(b) > f(a)$.
    Definimos $g: [a,b] \to \mathbb{R}$ tal que $g(x) = -f(x)$ para todo $x \in \mathbb{R}$. De esta forma $g$ también es continua e inyectiva en $[a,b]$. Notemos que $g(a) = -f(a) < -f(b) = g(b)$, es decir, $g(a) < g(b)$; y por el Caso 1, se tiene que si $x$, $y \in [a,b]$ tales que $x <y$, entonces $g(x) < g(y)$, esto implica que $-f(x) < -f(y)$ por lo que se concluye que $f(y) > f(x)$. Es decir, se tiene que $f$ es estrictamente decreciente.

De ambos casos, se concluye que si $f$ es continua e inyectiva en el intervalo $[a,b]$ entonces $f$ es estrictamente monótona.

$\square$

En el teorema anterior, nos limitamos a intervalos de la forma $[a, b]$. Sin embargo, podemos extender aún más este resultado para cualquier tipo de intervalo.

Teorema. Sea $A \subset \mathbb{R}$ un intervalo y $f : A \to \mathbb{R}$ una función continua e inyectiva. Entonces $f$ es estrictamente monótona.

Demostración.

Procederemos a realizar esta demostración por contradicción.

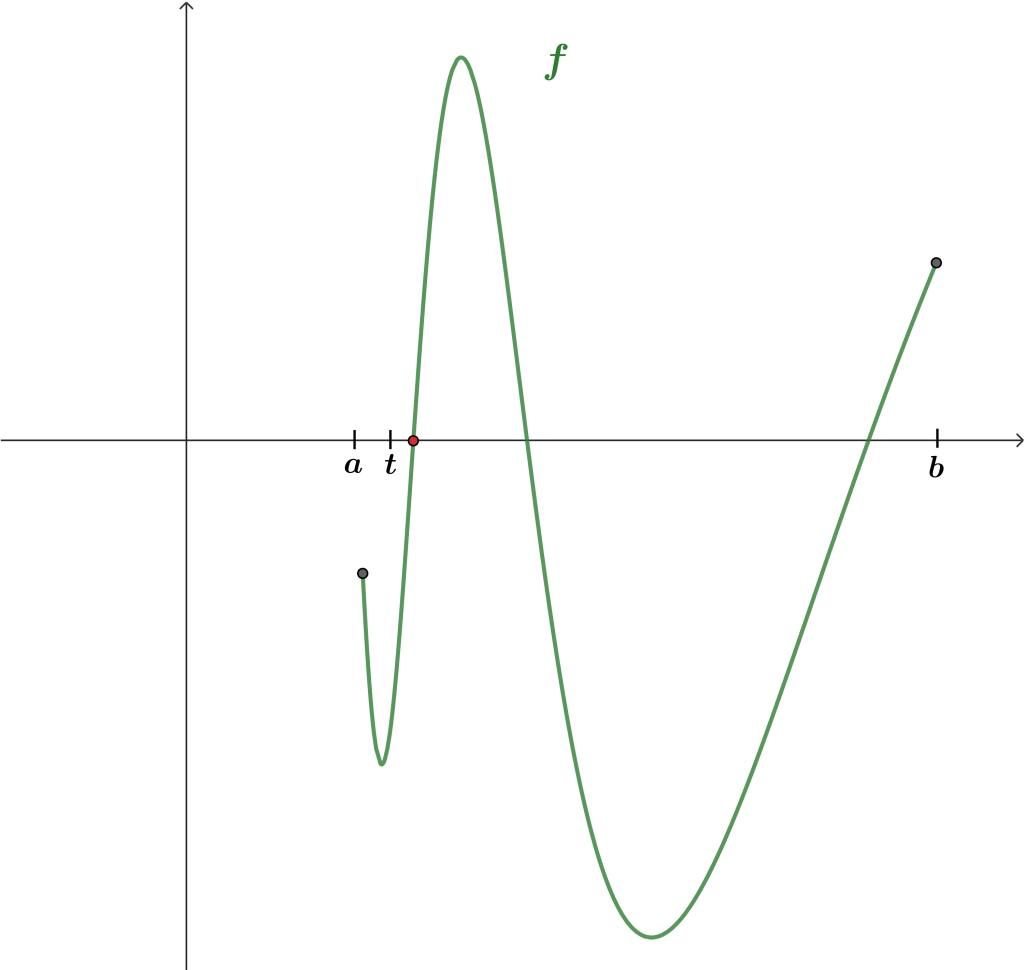
Supongamos que $f : A \to \mathbb{R}$ es una función continua e inyectiva, pero no es monótona. Es decir, existen $x_1,$ $x_2,$ $y_1,$ $y_2 \in A$ tales que

$$ x_1 < y_1, \quad x_2 < y_2 \quad \text{ y } \quad f(x_1) > f(y_1), \quad f(x_2) < f(y_2) \tag{1}.$$

Sea $a = min\{x_1, x_2 \}$ y $b = max \{y_1, y_2\}$.

Haremos uso de un resultado que se probará en la siguiente entrada: Si $A$ es un intervalo, entonces para cualesquiera $x$, $y \in A$, $x < y$, se tiene que $[x,y] \subset A$.

Aplicando lo anterior, tenemos que $[a,b] \subset A$ y así $f$ es continua e inyectiva en el intervalo $[a,b]$. Dado que $x_1$, $x_2$, $y_1$, $y_2 \in [a,b]$ y por $(1)$ se sigue que $f$ no es monótona en el intervalo lo cual es una contradicción al teorema anterior. Por tanto, $f$ sí es monótona en $A$.

$\square$

Funciones monótonas que son continuas

Para finalizar, veremos un teorema que relaciona funciones monótonas con la continuidad.

Teorema. Si $f : A \to \mathbb{R}$ es una función creciente y $f(A)$ es un intervalo, entonces $f$ es continua en $A$.

Demostración.

Supongamos que $f$ es creciente. Sea $x \in A$. Para probar que $f$ es continua en $x$ haremos uso de la relación existente entre el límite de una función y el de una sucesión. Tomaremos una sucesión monótona arbitraria $\{a_n\}$ tal que $a_n \to x$ y probaremos que $\{f(a_n)\} \to f(x)$.

Sea $\{a_n\}$ una sucesión creciente que converge a $x$. Entonces para todo $n \in \mathbb{N}$ se cumple que $a_n \leq a_{n+1} \leq x$ y debido a que $f$ es creciente se tiene que $f(a_n) \leq f(a_{n+1}) \leq f(x)$. Por lo anterior, se tiene que $\{f(a_n)\}$ es una sucesión creciente y acotada superiormente por lo que también es convergente.

Sea $L = \lim\limits_{n \to \infty} f(a_n)$, se cumple que $L \leq f(x)$.

Supongamos que $L < f(x)$ y consideremos $y \in \mathbb{R}$ tal que $L < y < f(x)$. Como $\{f(a_n)\}$ es creciente, se sigue que $f(a_1) < y < f(x)$. Dado que $f(A)$ es un intervalo, entonces existe $z \in A$ tal que $f(z) = y$. Se tienen dos casos.

  • Caso 1: $z \geq x$.
    Esto genera una contradicción al hecho de que $f$ es creciente, pues $y = f(z) < f(x)$.

  • Caso 2: $z < x$.
    Como $\{a_n\} \to x$, existe $n_0 \in \mathbb{N}$ tal que $z < a_{n_0} < x$ lo que implica que $y = f(z) \leq f(a_{n_0}) \leq f(x)$, lo cual es una contradicción pues estamos suponiendo que $L < y < f(x)$.

De ambos casos, se concluye que $L = f(x)$. Es decir, $\{f(a_n)\} \to f(x)$ y dado que $x$ es un punto arbitrario se $A$, se concluye que $f$ es continua en $A$.

$\square$

Más adelante…

En la siguiente entrada veremos qué sucede con la inversa de una función continua para lo cual será fundamental tener presentes los conceptos y teoremas revisados en esta entrada respecto a funciones monótonas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista

  • Da un ejemplo de una función que sea creciente y continua y un ejemplo de una función que sea decreciente y discontinua.
  • Demuestra que si $f$ y $g$ son funciones crecientes y positivas en un intervalo $A$, entonces su producto es creciente en $A$.
  • Prueba que si $f : A \to \mathbb{R}$ es una función decreciente y $f(A)$ es un intervalo, entonces $f$ es continua en $A$.
  • Sea $f: \mathbb{R} \to \mathbb{R}$ una función continua. Prueba que si $f|_{\mathbb{Q}}$ es monótona, entonces $f$ es monótona.
  • Sea $A=[a,b]$ un intervalo y $f: A \to \mathbb{R}$ una función creciente. Entonces el punto $a$ se tiene un mínimo de $f$ y en $b$ un máximo.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Funciones acotadas y teorema del máximo-mínimo

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

En esta entrada revisaremos el teorema del máximo-mínimo que nos indica que para una función continua en un intervalo $[a, b]$, existe un punto $x_0$ tal que $f(x_0) \geq f(x)$ para todo valor de $x$ en el intervalo. Para llegar a la prueba de tal teorema, revisaremos antes la definición de función acotada y probaremos que toda función continua en un intervalo está acotada en tal intervalo.

Funciones acotadas

Comenzaremos dando la definición de función acotada.

Definición. Decimos que $f$ está acotada superiormente en $A$ si existe $M \in \mathbb{R}$ tal que para todo $x \in A$ se cumple que $f(x) \leq M$. De manera similar, decimos que $f$ está acotada inferiormente en $A$ si existe $m \in \mathbb{R}$ tal que para todo $x \in A$ se tiene que $m \leq f(x)$. Finalmente, diremos que $f$ está acotada si existen $m$, $M \in \mathbb{R}$ tales que para todo $x \in A$ se tiene que $m \leq f(x) \leq M$.

Revisaremos el siguiente ejemplo para aplicar esta nueva definición.

Ejemplo 1. Sea $f: \mathbb{R} \setminus \{0\} \to \mathbb{R}$ definida como $f(x) = \frac{1}{x}.$

Afirmación. $f$ está acotada en el intervalo $A = [1, \infty)$.

Demostración.

Sea $x \in [1, \infty)$. Como $1 \leq x$, entonces $\frac{1}{x} \leq 1$. Se sigue que
\begin{gather*}
& 0 < \frac{1}{x} \leq 1 \quad \forall x \in [1, \infty). \\ \\
& \therefore 0 \leq f(x) \leq 1 \quad \forall x \in [1, \infty).
\end{gather*}

Por tanto, $f$ está acotada en el intervalo $A = [1, \infty)$.

$\square$

Afirmación. $f$ no está acotada superiormente en $B = (0, 1].$

Demostración.

Supongamos que la función $f$ sí está acotada superiormente en $B$, entonces existe $M \in \mathbb{R}$ tal que para todo $x \in B$ se tiene que $f(x) = \frac{1}{x} \leq M$.

Para todo $n \in \mathbb{N}$, se tiene que $n \geq 1$, entonces $0 < \frac{1}{n} \leq 1$ y, por tanto, $\frac{1}{n} \in B$.

\begin{gather*}
& f \left( \frac{1}{n} \right) = \frac{1}{\frac{1}{n}} \leq M. \\ \\
\therefore & n \leq M \quad \forall n \in \mathbb{N}.
\end{gather*}

Lo cual es una contradicción pues el conjunto de los números naturales no está acotado superiormente, por lo tanto $f$ no está acotada superiormente.

De forma análoga, se puede probar que $f$ está acotada en el intervalo $(-\infty, 1]$ y que no está acotada inferiormente en $[-1,0)$.

$\square$

Ahora veremos dos proposiciones respecto a las funciones acotadas. La primera nos indica que si $f$ es una función acotada en $A$ y se tiene un subconjunto $B$ de $A$, entonces $f$ también está acotada en $B$; mientras que la segunda nos indica que si $B$ y $C$ son subconjuntos de $A$, entonces $f$ también estará acotada en la unión de $B$ y $C.$

Proposición. Si $f$ está acotada en $A$ y $B \subset A$, entonces también está acotada en $B.$

Demostración.

Dado que $f$ está acotada en $A$, existen $m$, $M \in \mathbb{R}$ tal que para todo $x \in A$ se tiene que $m \leq f(x) \leq M$. Como $B \subset A$, entonces para todo $x \in B$ se tiene que $x \in A$, así $f$ también está acotada en $B.$

$\square$

Proposición. Si $B \subset A$, $C \subset A$. Si $f$ está acotada en $B$ y en $C$, entonces $f$ está acotada en $B \cup C.$

El razonamiento detrás de la prueba de esta proposición es similar al anterior, por lo que se dejará como tarea moral.

Continuaremos revisando una equivalencia de la definición de función acotada donde, en lugar de tener dos reales $m$, $M$ que acoten inferior y superiormente, solo se considerará un real $T$ que cumpla que $|f(x)| \leq T.$

Proposición. Existen $m$, $M \in \mathbb{R}$ tales que para todo $x \in A$, $m \leq f(x) \leq M$ si y solo si existe $T \in \mathbb{R}$ tal que para todo $x \in A$, $|f(x)| \leq T.$

Demostración.

$\Rightarrow]$ Sabemos que existen $m$, $M$ en $\mathbb{R}$ tales que para todo $x \in A$, $m \leq f(x) \leq M.$

Consideremos $T = max\{ |m|, |M| \}.$

Sea $x \in A$, entonces

\begin{gather*}
& f(x) \leq M \leq |M| \leq T. \\
\Rightarrow & f(x) \leq T. \tag{1}
\end{gather*}

Por otro lado

\begin{gather*}
& m \leq f(x). \\
\Leftrightarrow & – m \geq -f(x).
\end{gather*}

De esta forma, se sigue que
\begin{gather*}
-f(x) \leq -m \leq |m| \leq T.
\end{gather*}

Es decir,
\begin{gather*}
& -f(x) \leq T. \\
\therefore & -T \leq f(x). \tag{2}
\end{gather*}

De $(1)$ y $(2)$ podemos concluir que $|f(x)| \leq T.$

$\Leftarrow]$ Supongamos que existe $T$ tal que para todo $x \in A$, $|f(x)| \leq T.$

Consideremos $m = -T$ y $M = T$, entonces $ m \leq f(x) \leq M.$

$\square$

Teorema de acotabilidad

La siguiente propiedad nos indica que si $f$ es continua en un punto, entonces existe un intervalo alrededor de dicho punto donde la función está acotada. Esta propiedad será ampliamente usada para probar el teorema del máximo-mínimo.

Proposición. Sea $a \in A$, si $f$ es continua en $a$, entonces existe $\delta > 0$ tal que $f$ está acotada en el intervalo $(a-\delta, a+\delta) \cap A.$

Demostración.

Como $f$ es continua en $a$, considerando particularmente $\varepsilon = 1$, existe $\delta > 0$ tal que si $|x-a| < \delta$, $x \in A$, entonces

$$|f(x)-f(a)|<1.$$

Es decir, si $x \in (a – \delta, a + \delta) \cap A$, entonces

\begin{gather*}
& |f(x)|- |f(a)| < |f(x)- f(a)| < 1. \\
\Rightarrow & |f(x)| < 1 + |f(a)|.
\end{gather*}

Por tanto, $f$ está acotada en el intervalo $(a – \delta, a + \delta) \cap A.$

$\square$

El último teorema que veremos antes del máximo-mínimo nos indica que toda función continua en un intervalo cerrado está acotada en tal intervalo. De forma ilustrativa, podemos observarlo en la siguiente gráfica.

Teorema de acotabilidad. Sea $f: [a,b] \to \mathbb{R}$ tal que $f$ es continua en $[a,b]$. Entonces $f$ está acotada en $[a,b].$

Demostración.

Sea $A = \{ t \in [a, b] \quad | \quad f \text{ sí está acotada en } [a, t] \}$.

Veamos que $A \neq \varnothing$.
Consideremos $a \in [a,b]$. Como $f$ es continua en $[a,b]$ y por la proposición anterior, existe $\delta_1 > 0$ tal que para todo $x \in (a-\delta_1, a+\delta_1) \cap [a, b]$ se tiene que $f$ está acotada.
Por lo tanto, para todo $x \in [a, a+\delta_1)$, $f$ sí está acotada.

Notemos que tenemos dos casos derivados de si $a+ \delta_1$ está o no en el intervalo $[a,b].$

  • Si $b > a + \delta_1$, entonces $a+\delta_1 \in A$.
  • Si $b \leq a + \delta_1$, entonces $b \in A$.

$$\therefore A \neq \varnothing.$$

Además, $A$ está acotado superiormente pues si $t \in A$, por definición del conjunto, $t \leq b$.

Como $A$ es no vacío y está acotado superiormente, entonces tiene supremo. Sea $\alpha = supA$, notemos que $\alpha \leq b$, pues $\alpha$ es el supremo y $b$ es una cota superior.

Probaremos que $\alpha = b$, es decir, veremos que el supremo del conjunto $A$ es justamente $b$ y, en consecuencia, $f$ está acotada en $[a,b].$

Supongamos que $\alpha \neq b$. Entonces $a < \alpha < b$. Como $f$ es continua en $[a,b]$, entonces $f$ es continua en $\alpha$. Por la proposición anterior, existe $\delta_2$ tal que $f$ está acotada en $(\alpha-\delta_2, \alpha + \delta_2) \cap [a, b].$

Como $\alpha – \delta_2 < \alpha$, existe $t \in A$ tal que $\alpha – \delta_2 \leq t \leq \alpha$. Tomemos $s$ tal que $\alpha < s < \alpha + \delta_2$ y $s < b$. De esta forma se tiene que $[t,s] \subset (a- \delta_2, a + \delta_2) \cap [a, b]$ y $f$ está acotada en $[a, t]$ pues $t \in A$. Por lo tanto $f$ está acotada en $[a,s] = [a,t] \cup [t,s].$

Así $s \in A$ y $\alpha < s$, lo cual es una contradicción al hecho de que $\alpha$ es el supremo del conjunto $A.$

Por tanto, concluimos que $\alpha = b$. Ahora solo falta probar que $b \in A$ y, en consecuencia, $f$ está acotada en $[a,b].$

Dado que $b \in [a, b]$, f es continua en b, entonces existe $\delta_3 > 0$ tal que $f$ está acotada en $(b- \delta_3, b + \delta_3) \cap [a,b] = (b- \delta_3, b]$. Como $b = supA$ y $b-\delta_3 < b$, entonces existe $t \in A$ tal que $b-\delta_3 < t \leq b$, entonces $f$ está acotada en $[a,t]$. Como $[t, b] \subset (b – \delta_3, b]$ entonces $f$ está acotada en $[a,b] = [a,t] \cup [t, b].$

$\square$

Teorema del máximo-mínimo

Estamos listos para demostrar que para toda función continua en un intervalo $[a,b]$ existen $x_0, x_1 \in [a,b]$ donde la función alcanza su máximo y su mínimo respectivamente.

Teorema. Sea $f: [a,b] \to \mathbb{R}$ y continua en $[a,b]$, entonces existe $x_0 \in [a,b]$ tal que para todo $x \in [a,b]$ se tiene que $f(x) \leq f(x_0).$

Demostración.

Sea $B = \{ y = f(x) | x \in [a,b] \}.$

Por el teorema anterior, sabemos que existe $M \in \mathbb{R}$ tal que para todo $x \in [a,b]$ se tiene que $y = f(x) \leq M$. Por lo tanto $B$ está acotado.

Además $a \in [a,b]$, entonces $f(a) \in B$, así $B \neq \varnothing$. Por tanto, sabemos que existe $\alpha \in \mathbb{R}$ tal que $\alpha = supB$. Notemos que para todo $y \in B$, $y \leq \alpha$. Es decir, para todo $x \in [a,b]$, se tiene que $f(x) \leq \alpha.$

Ahora probaremos que existe $x_0 \in [a,b]$ tal que $f(x_0) = \alpha$ y, por tanto, para todo $x \in [a,b]$, $f(x) \leq f(x_0).$

Supongamos que para todo $x \in [a, b]$, $f(x) \neq \alpha.$
Entonces para todo $x \in [a,b]$, se tiene que $f(x) < \alpha.$ Es decir,

$$0 < \alpha – f(x).$$

Consideremos la siguiente función auxiliar $g(x) = \frac{1}{\alpha – f(x)}$. Se tiene que

$$g(x) = \frac{1}{\alpha – f(x)} > 0 \quad \forall x \in [a,b]. \tag{1}$$

Además, $g$ es la división de dos funciones continuas y el denominador no se hace cero en $[a,b]$, entonces $g$ es continua en $[a,b]$, por lo tanto $g$ está acotada en $[a,b]$. Es decir, existe $T \in \mathbb{R}$ tal que para todo $x \in [a,b]$ se tiene

\begin{gather*}
&|g(x)|\leq T. \\
\Rightarrow & 0 < \frac{1}{\alpha – f(x)} \leq T \text{, por }(1).
\end{gather*}

Se sigue que
\begin{gather*}
& \alpha – f(x) \geq \frac{1}{T} \quad \forall x \in [a,b]. \\
\therefore & \alpha – \frac{1}{T} \geq f(x) \quad \forall x \in [a,b]. \\
\end{gather*}

Entonces se tiene que $\alpha – \frac{1}{T}$ es cota superior de $B$, pero como $\frac{1}{T} > 0$, entonces $\alpha – \frac{1}{T} < \alpha$ y esto es una contradicción al hecho de que $\alpha$ es el supremo.

Por lo tanto, podemos concluir que sí existe $x_0 \in [a,b]$ tal que $f(x_0) = \alpha.$
$$\therefore f(x) \leq f(x_0) \quad \forall x \in [a,b].$$

$\square$

Corolario. Sea $f: [a,b] \to \mathbb{R}$ continua en $[a,b]$. Entonces existe $x_1 \in [a,b]$ tal que para todo $x \in [a,b]$ se tiene que $f(x_1) \leq f(x)$.

Demostración.

Consideremos la función $g: [a,b] \to \mathbb{R}$, $g(x) = -f(x)$ continua en $[a,b]$.

Por el teorema anterior existe $x_1 \in [a,b]$ tal que

\begin{gather*}
& g(x) \leq g(x_1) \quad \forall x \in [a,b]. \\
\Rightarrow & -f(x) \leq -f(x_1) \quad \forall x \in [a,b]. \\
\end{gather*}

$$\therefore f(x_1) \leq f(x) \quad \forall x \in [a,b].$$

$\square$

Más adelante…

En la siguiente entrada estudiaremos resultados derivados del teorema del valor intermedio y del teorema del máximo-mínimo, razón por la cual será fundamental tenerlos presentes.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Sean $f$, $g: \mathbb{R} \to \mathbb{R}$. Prueba que si $f$ y $g$ están acotadas en $\mathbb{R}$, entonces la suma $f+g$ también está acotada en $\mathbb{R}$.
  • Si $B \subset A$, $C \subset A$. Si $f$ está acotada en $B$ y en $C$, entonces $f$ está acotada en $B \cup C$.
  • Prueba que si $f : \mathbb{R} \to \mathbb{R}$ está acotada en $\mathbb{R}$ y definimos $g: \mathbb{R} \to \mathbb{R}$ tal que $g(x)=xf(x)$, entonces $g$ es continua en $x_0=0.$
  • Si $f$ es una función continua en $[0,1]$, sea $||f||$ el valor máximo de $|f|$ en $[0,1]$. Prueba que $||c \cdot f|| = |c|\cdot||f||$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Teorema del valor intermedio

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

En la entrada anterior se revisó el concepto de continuidad en un punto, así como algunas de sus propiedades. Además, se definió la continuidad en un intervalo, concepto que se empleará en esta entrada para probar uno de los resultados más relevantes para las funciones continuas: el teorema del valor intermedio.

Idea intuitiva

Este teorema nos dice que para una función continua en determinado intervalo $[a,b]$, si el valor de $f$ al evaluarla en $a$ cambia de signo con respecto al valor que se obtiene al evaluarla en $b$, entonces existe algún punto $x$ tal que al evaluar la función en dicho punto, toma el valor de cero.

Recordemos la idea intuitiva de continuidad, una función es continua si puedes dibujarla sin soltar el lápiz; pensemos en el caso particular que $f(a)  < 0$ y $f(b) > 0$. En la siguiente imagen se muestra una función continua que pasa por ambos.

¿Podrías dibujar una función continua que pase por ambos puntos sin pasar por $0$ en el eje horizontal? Probaremos que esto no es posible en el siguiente teorema; pero antes desarrollemos la intuición de lo que debe suceder. Para ello, recordemos el último teorema revisado en la entrada anterior.

Teorema. Supongamos que $f$ es continua en $x_0$ y $f(x_0)>0$. Entonces $f(x) >0$ para todo $x$ en un intervalo que contiene a $x_0$, es decir, existe $\delta > 0$ tal que $f(x) >0$ para todo $x$ tal que $|x-x_0|< \delta$.

De forma análoga, si $f(x_0) <0$, entonces existe $\delta > 0$ tal que $f(x) < 0$ para todo $x$ tal que $|x-x_0|< \delta$.

Es decir, si una función continua toma un valor positivo en un punto $x_0$, entonces debe suceder que es positiva en todo un intervalo: $(x_0-\delta, x_0+\delta)$. Análogamente, si la función es negativa en determinado punto, entonces debe suceder que es negativa en todo un intervalo. Así, podemos pensar en el intervalo más grande que captura el comportamiento negativo (o positivo), ¿en qué punto se termina? Para responder esta pregunta, haremos uso de un concepto revisado anteriormente, el supremo.

Teorema del valor intermedio

Teorema del valor intermedio. Sea $f:[a,b] \to \mathbb{R}$ continua en todo el intervalo $[a,b]$. Si $f(a) < 0$ y $f(b) > 0,$ entonces existe $c$, $a<c<b,$ tal que $f(c) = 0$.

Demostración.

Como $f(a) < 0$, sabemos que existe $\delta_1$ tal que para todo $x \in (a – \delta_1, a + \delta_1) \cap [a,b]$ se tiene que $f(x) < 0$. Es decir,

$$\forall x \in [a, a+\delta_1), \quad f(x) <0. \tag{1}$$

Como $f(b) > 0$, sabemos que existe $\delta_2$ tal que para todo $x \in (b – \delta_2, b + \delta_2) \cap [a,b]$ se tiene que $f(x) > 0$. Es decir,

$$\forall x \in (b-\delta_2,b], \quad f(x) > 0. \tag{2}$$

Definamos ahora el siguiente conjunto:

$$A = \{ t \in [a,b] \quad | \quad \forall x \in [a, t], f(x) < 0 \}.$$


Es decir, el conjunto $A$ está formado por todos los números reales que forman un intervalo $[a, t]$ donde $f$ toma valores negativos. Utilizando la ilustración del inicio, se puede ejemplificar cómo se ve $t$, que estará en el eje $x$ entre $a$ y el punto rojo marcado.

Primero veamos que $A \neq \varnothing$.

Consideremos $t_0 = a + \frac{\delta_1}{2}$. Es inmediato que $a< a + \frac{\delta_1}{2} < a +\delta_1 $ y como $[a, a + \frac{\delta_1}{2}] \subset [a, a+\delta_1)$, por $(1)$ se tiene que, para todo $x \in [a, a + \frac{\delta_1}{2}]$, $f(x) < 0$.

$$\therefore t_0 \in A \Rightarrow A \neq \emptyset.$$

Notemos que el conjunto $A$ está acotado. Por definición si $t \in A$, entonces $t \in [a,b]$, es decir, $t \leq b$. Ahora, como nuestro conjunto $A$ es no vacío y está acotado, sí tiene supremo. Sea $\alpha = supA$.

Adicionalmente, notemos que

  1. $t_0 = a+\frac{\delta_1}{2} \in A$ y $a+\frac{\delta_1}{2} \leq \alpha \leq b$.
  2. Por $(2)$, para todo $x \in (b-\delta_2, b]$ se tiene que $f(x) >0$, entonces $\alpha \leq b-\delta_2$.

Por lo anterior, se tiene
\begin{gather*}
& a< a+\frac{\delta_1}{2} \leq \alpha \leq b-\delta_2 < b.
\end{gather*}
Se sigue que $a<\alpha<b.$

Para finalizar con la prueba, demostraremos que $f(\alpha) = 0$.

Para demostrarlo procederemos por contracción, es decir, supongamos que $f(\alpha) \neq 0$, entonces existen dos casos, $f(\alpha) > 0$ ó $f(\alpha) < 0$.

  • Caso 1: $f(\alpha) < 0$.

    Se tiene que $f(\alpha) < 0$, entonces existe $\delta_3$ tal que para todo $x \in (\alpha – \delta_3, \alpha + \delta_3) \cap [a,b]$ se cumple que $f(x) < 0$.

    Dado que $\alpha = supA \quad$ y $\quad \alpha – \delta_3 < \alpha$, entonces existe $t \in A$ tal que $\alpha-\delta_3 < t \leq \alpha$. Adicionalmente, consideremos $s$ tal que $\alpha < s < \alpha + \delta_3$ y $s <b$.

    Como $[t, s] \subset (\alpha – \delta_3, \alpha + \delta_3)$, entonces

    $$\forall x \in [a,s], \quad f(x) < 0.$$

    Además, por definición del conjunto A, para todo $x \in [a,t]$ se tiene $f(x) < 0$. Entonces

    $$\forall x \in [a,s] = [a,t] \cup [t,s], \quad f(x) < 0.$$

    Entonces $s \in A$ y $\alpha < s$, lo cual es una contradicción pues $\alpha$ es el supremo de $A$.

    $$\therefore f(\alpha) \geq 0.$$
  • Caso 2: $f(\alpha) > 0$.

    Dado que $f$ es continua en $\alpha$, entonces existe $\delta_4 > 0$ tal que para todo $x \in (\alpha – \delta_4, \alpha + \delta_4)$, $f(x) > 0$.

    Como $\alpha – \delta_4 < \alpha$, entonces existe $t \in A$ tal que $\alpha – \delta_4 < t \leq \alpha$. Como $t \in A$, entonces $f(t) < 0$ y como $\alpha – \delta_4<t \leq \alpha < \alpha + \delta$, $f(t) >0$, lo cual es una contradicción.

    Por tanto, $f(\alpha) = 0$.

Así, consideremos $c = \alpha$, $a<c<b$ y $f(c) = 0.$

$\square$

Podemos notar que el teorema no solo vale cuando la función va de negativo ($f(a) < 0$) a positivo ($f(b) > 0$), sino también en el caso inverso ($f(a) > 0$ y $f(b) < 0$) y lo probaremos en el siguiente corolario.

Corolario. Sea $f: [a, b] \to \mathbb{R}$, continua en $[a, b]$. Si $f(a) > 0$ y $f(b) < 0$, entonces existe $c$, $a<c<b$, tal que $f(x) = c$.

Demostración.

Consideremos la función $h: [a, b] \to \mathbb{R}$, $h(x) = -f(x).$

Notemos que $h$ es continua pues $f$ lo es. Además $h(a) = -f(a) <0$ y $h(b) = -f(b) >0$. Aplicando el teorema del valor intermedio, existe $c$ que cumple $a<c<b$ tal que

\begin{gather*}
h(c) = 0.
\end{gather*}

Se sigue que
\begin{gather*}
& -f(c) = 0. \\
\therefore & f(c) = 0.
\end{gather*}

$\square$

Más aún, si en un intervalo $[a, b]$ se cumple que $f(a) < M$ y $f(b) > M$, entonces también existe un punto $c$ tal que $f(c) = M$.

Corolario. Sea $M \in \mathbb{R}$, si $f(a) < M$ y $f(b) > M$. Entonces existe $c$, $a<c<b$, tal que $f(c) = M$.

Demostración.

Consideremos la función $h:[a,b] \to \mathbb{R}$, con $h(x) = f(x)-M$.

Notemos que $h$ es continua. Además $h(a) = f(a)-M < 0$ y $h(b) = f(b)-M > 0$. Por el teorema del valor intermedio, existe $c$, $a<c<b$, tal que $h(c) = 0$. Entonces $f(c)-M = 0$.

$$\therefore f(c) = M.$$

$\square$

Análogamente, tenemos el siguiente resultado.

Corolario. Sea $M \in \mathbb{R}$, si $f(a) >M$ y $f(b) < M$. Entonces existe $c$, $a<c<b$, tal que $f(c) = M$.

Más adelante…

En la siguiente entrada demostraremos otra propiedad fuerte respecto a las funciones continuas: si una función es continua en un intervalo, entonces está acotada. Más aún, existe un valor $x_0$ en el intervalo tal que la función alcanza su máximo en dicho punto. De forma análoga, existe un punto en el que la función alcanza su mínimo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Sea $f$ continua en el intervalo $[0,1]$ y tal que $f(0) = f(1)$. Demostrar que existe un punto $c \in [0, \frac{1}{2}]$ tal que $f(c) = f(c + \frac{1}{2}).$
  • Sea $M \in \mathbb{R}$, si $f(a) >M$ y $f(b) < M$. Prueba que existe $c$, $a<c<b$ tal que $f(c) = M.$
  • Dado $f(x) = x^2 + 2x – 7$, demuestra que existe $c$ tal que $f(c) = 50.$
  • Para la ecuación $2x^7= x-1$, encuentra una solución en $[0,1].$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Definición de continuidad y sus propiedades

Por Juan Manuel Naranjo Jurado

3 respuestas

Introducción

En esta entrada definiremos la continuidad de una función, es probable que hayas estudiado antes tal concepto y la manera en que se suele definir de forma intuitiva es mediante la siguiente sentencia: «Si puedes dibujar la función sin levantar el lápiz, entonces es una función continua». Nosotros revisaremos el tema con mayor formalidad, pero notarás que tal enunciado será de ayuda para interpretar la definición.

Definición de continuidad

En palabras sencillas, una función es continua en un punto $x_0$ si el límite en tal punto es igual a evaluar la función en $x_0$.

Definición. Sean $f: A \to \mathbb{R}$ con $A \subset \mathbb{R}$ y $x_0 \in A$. La función $f$ es continua en $x_0$ si para todo $\varepsilon > 0$, existe $\delta > 0$ tal que para todo $x \in A$ que satisface que $0<|x-x_0|< \delta$, entonces se cumple que $|f(x)-f(x_0)|< \varepsilon$.

Observación. Si además $x_0$ es un punto de acumulación de $A$, entonces se dice que $f$ es continua en $x_0$ si $$ \lim_{x \to x_0} f(x) = f(x_0).$$

En la entrada de definición formal de límite se vieron algunos ejemplos de funciones continuas; específicamente se dejaron dos ejercicios como tarea moral que procederemos a probar en esta entrada.

Ejemplo 1. La función $f(x) = c$, es continua en $x_0$ para todo $x_0 \in \mathbb{R}$.

Demostración.

Sea $\varepsilon > 0$. Dado que la función es constante, cualquier valor de delta nos funciona, así consideremos $\delta = 1$.

Si $0<|x-x_0|< \delta$, entonces

\begin{align*}
|f(x)-f(x_0)| & = |c-c|\\
& = 0 \\
& < \varepsilon.
\end{align*}

$$\therefore \lim_{x \to x_0} f(x) = f(x_0).$$

$\square$

Ejemplo 2. La función $f(x) = x$ es continua en $x_0$ para todo $x_0 \in \mathbb{R}$.

Demostración.

Sea $\varepsilon > 0$. Consideremos $\delta = \varepsilon$.

Si $0<|x-x_0|<\delta$, entonces
\begin{align*}
|f(x)-f(x_0)| & = |x-x_0|\\
& < \delta \\
& = \varepsilon.
\end{align*}

$$\therefore \lim_{x \to x_0} f(x) = f(x_0).$$

Antes de revisar el siguiente ejemplo, demostraremos un resultado que nos será muy útil al momento de calcular límites.

Proposición. Sea $f: A \to \mathbb{R}$, entonces

$$\lim_{x \to x_0} f(x) = L \Leftrightarrow \lim_{h \to 0} f(x_0+h) = L.$$

Demostración.

$\Rightarrow]$ Supongamos que $$\lim_{x \to x_0} f(x) = L.$$

Sea $\varepsilon > 0$. Existe $\delta > 0 $ tal que si $0 < |x-x_0| < \delta$, entonces $|f(x)-L| < \varepsilon.$

Notemos que si $0 < |h| < \delta$, entonces $0 < |(h+x_0)-x_0| < \delta$. Por lo tanto, $|f(x_0+h)-L| < \varepsilon.$

$$\therefore \lim_{h \to 0} f(x_0+h) = L.$$

$\Leftarrow]$ Supongamos que $$\lim_{h \to 0} f(x_0+h) = L.$$

Sea $\varepsilon>0$. Existe $\delta >0$ tal que si $0<|h|<\delta$, entonces $|f(x_0+h)-L|< \varepsilon.$

Notemos que si $0<|x−x_0|<\delta$, entonces $|f(x_0+(x−x_0))−L|=|f(x)−L|<\varepsilon$.

$$\therefore \lim_{x \to x_0} f(x) = L.$$

$\square$

Ejemplo 3. La función $f(x) = sen(x)$ es continua en $x_0$ para todo $x_0 \in \mathbb{R}.$

Demostración.

Para probar la continuidad de esta función, procederemos a calcular sus límites laterales y emplearemos el hecho de que las funciones seno y coseno son continuas en $x = 0$, lo cual se demostró en esta entrada. Además, usaremos las siguientes identidades trigonométricas:

  1. $$sen(a+b) = sen(a)cos(b) + cos(a)sen(b).$$
  2. $$sen(a-b) = sen(a)cos(b) – cos(a)sen(b).$$

Calculando el límite por la derecha, usando la primera identidad y empleando la proposición anterior, tenemos

\begin{align*}
\lim_{x \to x_0^+} sen(x) & = \lim_{h \to 0^+} sen(x_0+h) \\
& = \lim_{h \to 0^+} sen(x_0)cos(h) + cos(x_0)sen(h) \text{, pues $h > 0$} \\
& = sen(x_0)cos(0) + cos(x_0)sen(0) \\
& = sen(x_0).
\end{align*}

Calculando el límite por la izquierda, usando la segunda identidad y empleando la proposición anterior, tenemos

\begin{align*}
\lim_{x \to x_0^-} sen(x) & = \lim_{h \to 0^-} sen(x_0+h) \\
& = \lim_{h \to 0^-} sen(x_0)cos(h) – cos(x_0)sen(h) \text{, pues $h < 0$} \\
& = sen(x_0)cos(0) + cos(x_0)sen(0)\\
& = sen(x_0).
\end{align*}

Como los límites laterales existen y coinciden, se concluye que

$$\lim_{x \to x_0} sen(x) = sen(x_0).$$

Por lo tanto, la función es continua.

$\square$

Propiedades básicas de la continuidad

A continuación revisaremos tres propiedades aritméticas de las funciones continuas.

Teorema. Si $f$ y $g$ son funciones continuas en $x_0$, entonces

  1. $f+g$ es continua en $x_0$.
  2. $f \cdot g$ es continua en $x_0$.
  3. Si además $g(x_0) \neq 0$, entonces $\frac{1}{g}$ es continua en $x_0$.

Demostración.

Como $f$ y $g$ son continuas en $x_0$, entonces
$$\lim_{x \to x_0} f(x) = f(x_0) \quad \text{ y } \quad \lim_{x \to x_0} g(x) = g(x_0).$$
Por las propiedades del límite, tenemos lo siguiente
\begin{align*}
\lim_{x \to x_0} (f + g)(x) & = \lim_{x \to x_0} [f(x) + g(x)] \\
& = \lim_{x \to x_0} f(x) + \lim_{x \to x_0} g(x) \\
& = f(x_0) + g(x_0) \\
& = (f+g)(x_0).
\end{align*}

$$\therefore \lim_{x \to x_0} (f + g)(x) = (f+g)(x_0).$$

Por lo tanto, $f+g$ es continua en $x_0$.

Podemos notar que los incisos siguientes tienen demostraciones análogas ocupando las propiedades demostradas para el límite de una función, por lo cual su prueba se omitirá.

$\square$

Gracias al teorema anterior y los ejemplos vistos, tenemos una gama de funciones continuas, las funciones polinomiales: $p(x) = \alpha_n x^n + \alpha_{n-1} x^{n-1} + \ldots + \alpha_1 x +\alpha_0$.

La siguiente propiedad que veremos hace referencia a la composición de funciones continuas.

Teorema. Si $g$ es continua en $x_0$ y $f$ es continua en $g(x_0)$, entonces la composición de funciones $f \circ g$ es continua en $x_0.$

Demostración.

Queremos probar que $$\lim_{x \to x_0} (f \circ g)(x) = (f \circ g)(x_0)$$
y para demostrarlo procederemos mediante la definición épsilon-delta.

Sea $\varepsilon > 0$.

Como $f$ es continua en $g(x_0)$, existe $\delta’ > 0$ tal que para todo $y$ que cumpla $|y-g(x_0)|< \delta’$, entonces $|f(y)-f(g(x_0))|< \varepsilon$.

Dado que estamos viendo la composición, podemos considerar particularmente $y = g(x)$, de esta manera se tiene que si $|g(x)-g(x_0)|< \delta’$, entonces
\begin{align*}|f(g(x))-f(g(x_0))| <\varepsilon. \tag{1} \end{align*}

Como $g$ es continua en $x_0$, para cualquier valor positivo arbitrario, en este caso consideraremos $\delta’>0$, existe $\delta > 0$ tal que si $0<|x-x_0|<\delta$, entonces
\begin{align*} |g(x)-g(x_0)| < \delta’. \tag{2} \end{align*}

De (1) y (2), se sigue que $$\text{si } 0<|x-x_0|<\delta \Rightarrow |g(x)-g(x_0)| < \delta’ \Rightarrow |f(g(x))-f(g(x_0))| <\varepsilon.$$

Es decir, si $0<|x-x_0|<\delta$, entonces $|f(g(x))-f(g(x_0))| <\varepsilon$.

$\square$

El teorema anterior nos permite extender aún más el almacén de funciones continuas. Por ejemplo, sabemos que $g(x) = x^2+x-10$ es continua en $x_0$ para todo $x_0 \in \mathbb{R}$ y la función $f(x) = sen(x)$ es continua en cualquier punto, particularmente en $g(x_0)$, entonces la composición $(f \circ g) (x) = sen(x^2+x-10)$ también es continua en $x_0$.

Existen cierto tipo de funciones que no están definidas en algún punto en particular. Por ejemplo $f(x) = xsen(\frac{1}{x})$, no está definida en $x_0=0$ y, por tanto, no puede ser continua en tal punto, pero a partir de ella podemos construir una nueva función que sí sea continua en $x_0=0$. En una entrada anterior, vimos que $$\lim_{x \to 0} xsen \left( \frac{1}{x} \right) = 0.$$

De esta forma, podemos definir una nueva función:

$$f(x) = \begin{cases} xsen(\frac{1}{x}) & \text{si } x \neq 0 \\
0 & \text{si } x = 0. \end{cases}$$

Esta nueva función $f$ es continua en $x_0 = 0$. A este tipo de funciones que podemos convertirlas en funciones continuas en $x_0$ redefiniéndolas en tal punto, se dice que tienen una discontinuidad removible o evitable.


Por otro lado, también hay funciones cuya discontinuidad es no removible. Consideremos la función $f(x) = sen\left( \frac{1}{x} \right)$, revisamos anteriormente que el límite de tal función no existe. Por lo cual, aunque la definiéramos en $x_0$, seguiría siendo discontinua en dicho punto.

Hasta ahora estuvimos empleando la definición de continuidad en un punto, sin embargo, para la mayoría de los ejemplos revisados probamos la continuidad para todo $\mathbb{R}$, puesto que consideramos un $x_0$ arbitrario. Es conveniente tener una definición para la continuidad en un intervalo. Y, como podrás imaginarlo, para que una función sea continua en un intervalo $(a,b)$, se requiere que la función sea continua en cada punto del intervalo (con una pequeña particularidad para intervalos cerrados).

Definición (Continuidad en un intervalo abierto). Si $f$ es continua en todo $x$ con $x \in (a,b)$, se dice que $f$ es continua en el intervalo $(a,b)$.

Definición (Continuidad en un intervalo cerrado). Si $f$ es continua en todo $x$ con $x \in (a,b)$ y se cumple que

$$\lim_{x \to a^+} f(x) = f(a) \quad \text{ y } \quad \lim_{x \to b^-} f(x) = f(b).$$

Entonces se dice que $f$ es continua en el intervalo $[a,b]$.

Terminaremos esta entrada probando un teorema que nos dice que si $f$ es continua en $x_0$ y $f(x_0)$ es mayor a cero (o menor a cero), entonces existe todo un intervalo en el que es mayor a cero (o menor a cero).

Teorema. Supongamos que $f$ es continua en $x_0$ y $f(x_0)>0$. Entonces $f(x) >0$ para todo $x$ en un intervalo que contiene a $x_0$, es decir, existe $\delta > 0$ tal que $f(x) >0$ para todo $x$ tal que $|x-x_0|< \delta$.

De forma análoga, si $f(x_0) <0$, entonces existe $\delta > 0$ tal que $f(x) < 0$ para todo $x$ tal que $|x-x_0|< \delta$.

Demostración.

Supongamos que $f$ es continua en $x_0$ y $f(x_0)>0$, entonces para $\varepsilon = \frac{1}{2}f(x_0) > 0$, existe $\delta>0$ tal que si $|x-x_0|< \delta$, entonces
\begin{gather*}
& |f(x)-f(x_0)|< \frac{1}{2}f(x_0). \\
\Leftrightarrow & -\frac{1}{2}f(x_0) < f(x)-f(x_0) < \frac{1}{2}f(x_0). \\
\Leftrightarrow & -\frac{1}{2}f(x_0) + f(x_0) < f(x) < \frac{1}{2}f(x_0) + f(x_0). \\
\Leftrightarrow & f(x) > \frac{1}{2}f(x_0) > 0.
\end{gather*}

La demostración para cuando $f(x_0)< 0$ es análoga usando $\varepsilon = – \frac{1}{2}f(x_0) > 0.$

$\square$

Más adelante…

Tras revisar las propiedades básicas de las funciones continuas, estamos listos para revisar resultados muy interesantes derivados de la continuidad. En la siguiente entrada revisaremos el popular teorema del valor intermedio, que nos indica que si una función continua en un intervalo $[a,b]$ y que al evaluarla en $a$ toma un valor negativo, $f(a) < 0$, y al evaluarla en $b$ toma un valor positivo, $f(b) > 0$, entonces dicha función necesariamente toma el valor cero, es decir, existe un $x_0$ en el intervalo $[a,b]$ tal que $f(x_0) = 0$. Para probar este resultado, se hará uso del último teorema revisado en esta entrada.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Prueba que la función $f(x) = cos(x)$ es continua en cualquier punto $x_0 \in \mathbb{R}$.
  • Sea $f: A \to \mathbb{R}$. Prueba que si $f$ es continua en un punto $x_0 \in A$, entonces la función $|f|(x):= |f(x)|$ también es continua en $x_0$. ¿Se cumple el regreso? Es decir, ¿si $|f|$ es continua en $x_0$ entonces $f$ también es continua en tal punto?
  • Se dice que una función $f$ es aditiva si $f(x+y) = f(x)+f(y)$ para todo $x$, $y$ en $\mathbb{R}$. Prueba que para una función aditiva $f$ tal que es continua en algún punto $x_0$, entonces es continua en todo su dominio.
  • Da un ejemplo de dos funciones $f$ y $g$ discontinuas en $x_0$ tales que la suma $f+g$ sea continua en $x_0.$
  • Da un ejemplo de dos funciones $f$ y $g$ discontinuas en $x_0$ tales que el producto $f \cdot g$ sea continuo en $x_0.$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Lineal I: Aplicaciones de bases ortogonales y descomposición de Fourier

Por Leonardo Ignacio Martínez Sandoval

3 respuestas

Introducción

En esta entrada continuamos hablando de bases ortogonales. Como recordatorio, para poder hablar de esto, necesitamos un espacio vectorial sobre $\mathbb{R}$ equipado con un producto interior, y por lo tanto podemos hablar de normas. Una base ortogonal de $V$ es una base en la cual cada par de vectores tiene producto interior $0$. Es ortonormal si además cada elemento es de norma $1$. Ahora veremos que dada una base ortonormal, podemos hacer una descomposición de Fourier de los vectores de $V$, que nos permite conocer varias de sus propiedades fácilmente.

La teoría que discutiremos está basada en el contenido de la Sección 10.5 del libro Essential Lineal Algebra with Applications de Titu Andreescu. Las últimas dos secciones de esta entrada son un poco abstractas, pero son la puerta a ideas matemáticas interesantes con muchas aplicaciones dentro de la matemática misma y en el mundo real.

Descomposición de Fourier

Es fácil conocer las coordenadas de un vector en términos de una base ortonormal.

Teorema. Si $V$ es un espacio Euclideano de dimensión $n$ con producto interior $\langle\cdot, \cdot\rangle$ y $B=\{e_1,\ldots,e_n\}$ es una base ortonormal con este producto interior, entonces para cualquier vector $v$, la coordenada de $v$ con respecto a $e_i$ es $\langle v, e_i \rangle$.

Demostración. Expresemos a $v$ en la base $B$ como $$v=\alpha_1e_1+\ldots+\alpha_n e_n.$$

Tomemos $j$ en $1,2,\ldots,n$. Usando la linealidad del producto interior, tenemos que
\begin{align*}
\langle v, e_j \rangle &= \left \langle \sum_{i=1}^n \alpha_i e_i, e_j \right \rangle\\
&=\sum_{i=1}^n \alpha_i \langle e_i,e_j \rangle.
\end{align*}

Como $B$ es base ortonormal, tenemos que en el lado derecho $\langle e_j,e_j\rangle = 1$ y que si $i\neq j$ entonces $\langle e_i, e_j\rangle=0$. De esta forma, el lado derecho de la expresión es $\alpha_j$, de donde concluimos que $$\langle v, e_j \rangle = \alpha_j,$$ como queríamos.

$\square$

Definición. Si $V$ es un espacio Euclideano de dimensión $n$ con producto interior $\langle\cdot, \cdot\rangle$ y $B=\{e_1,\ldots,e_n\}$ es una base ortonormal, a $$v=\sum_{i=1}^n \langle v, e_i \rangle e_i$$ le llamamos la descomposición de Fourier de $v$ con respecto a $B$.

Ejemplo. Trabajemos en el espacio vectorial $V=\mathbb{R}_2[x]$ de polinomios reales de grado a lo más $2$. Ya mostramos anteriormente (con más generalidad) que $$\langle p,q \rangle = p(-1)q(-1)+p(0)q(0)+p(1)q(1)$$ es un producto interior en $V$.

Los polinomios $\frac{1}{\sqrt{3}}$, $\frac{x}{\sqrt{2}}$ y $\frac{3x^2-2}{\sqrt{6}}$ forman una base ortonormal, lo cual se puede verificar haciendo las operaciones y queda de tarea moral. ¿Cómo expresaríamos a la base canónica $\{1,x,x^2\}$ en términos de esta base ortonormal? Los primeros dos son sencillos:
\begin{align}
1&=\sqrt{3}\cdot \frac{1}{\sqrt{3}}\\
x&=\sqrt{2}\cdot \frac{x}{\sqrt{2}}.
\end{align}

Para encontrar el tercero, usamos el teorema de descomposición de Fourier. Para ello, calculamos los siguientes productos interiores:

\begin{align*}
\left\langle x^2, \frac{1}{\sqrt{3}}\right\rangle &= \frac{2}{\sqrt{3}},\\
\left \langle x^2, \frac{x}{\sqrt{2}}\right\rangle &=0,\\
\left\langle x^2, \frac{3x^2-2}{\sqrt{6}} \right\rangle &=\frac{2}{\sqrt{6}}.
\end{align*}

De este modo, $$x^2= \frac{2}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}} + \frac{2}{\sqrt{6}}\cdot \frac{3x^2-2}{\sqrt{6}}.$$

$\triangle$

Norma usando la descomposición de Fourier

Cuando tenemos bases ortogonales u ortonormales, también podemos calcular la norma de un vector fácilmente.

Teorema. Si $V$ es un espacio Euclideano de dimensión $n$ con producto interior $\langle\cdot, \cdot\rangle$ y $B=\{e_1,\ldots,e_n\}$ es una base ortogonal con este producto interior, entonces para cualquier vector $$v=\alpha_1e_1+\ldots+\alpha_ne_n,$$ tenemos que $$\norm{v}^2 = \sum_{i=1}^n \alpha_i^2 \norm{e_i}^2.$$

En particular, si $B$ es una base ortonormal, entonces $$\norm{v}^2 = \sum_{i=1}^n \langle v, e_i \rangle^2.$$

Demostración. Usando la definición de norma y la bilinealidad del producto interior, tenemos que
\begin{align*}
\norm{v}^2 &= \langle v,v \rangle\\
&=\sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j \langle e_i, e_j\rangle.
\end{align*}

Como $B$ es base ortogonal, los únicos sumandos que quedan a la derecha son aquellos en los que $i=j$, es decir,
\begin{align*}
\norm{v}^2&=\sum_{i=1}^n \alpha_i^2 \langle e_i, e_i\rangle\\
&=\sum_{i=1}^n \alpha_i^2 \norm{e_i}^2\\
\end{align*}

como queríamos mostrar.

Si $B$ es base ortonormal, cada $\norm{e_i}^2$ es $1$, y por el teorema anterior, $\alpha_i=\langle v, e_i\rangle$. Esto prueba la última afirmación.

$\square$

Ejemplo. Continuando con el ejemplo anterior, como ya escribimos a $x^2$ en términos de la base ortogonal, podemos encontrar fácilmente su norma. Tendríamos que
\begin{align*}
\norm{x^2}^2&=\left(\frac{2}{\sqrt{3}}\right)^2+\left(\frac{2}{\sqrt{6}}\right)^2\\
&=\frac{4}{3}+\frac{4}{6}\\
&=2.
\end{align*}

De esta forma, $\norm{x^2}=\sqrt{2}$. En efecto, esto es lo que obtendríamos si hubiéramos calculado la norma de $x^2$ con la definición.

$\triangle$

Aplicación de descomposición de Fourier a polinomios

Vamos a continuar con un ejemplo que vimos en la entrada anterior. Recordemos que estábamos trabajando en $V=\mathbb{R}_n[x]$, que habíamos elegido $n+1$ reales distintos $x_0,\ldots,x_n$, y que a partir de ellos definimos $$\langle P, Q\rangle = \sum_{i=0}^n P(x_i)Q(x_i).$$ Mostramos que $\langle \cdot , \cdot \rangle$ es un producto interior y que para $j=0,\ldots,n$ los polinomios $$L_i=\prod_{0\leq j \leq n, j\neq i} \frac{x-x_j}{x_i-x_j}$$ forman una base ortonormal de $V$.

Por el teorema de descomposición de Fourier, tenemos que cualquier polinomio $P$ de grado a lo más $n+1$ con coeficientes reales satisface que $$P=\sum_{i=0}^n \langle P, L_i \rangle L_i,$$ lo cual en otras palabras podemos escribir como sigue.

Teorema (de interpolación de Lagrange). Para $P$ un polinomio con coeficientes en los reales de grado a lo más $n$ y $x_0,x_1,\ldots,x_n$ reales distintos, tenemos que $$P(x)=\sum_{i=0}^n P(x_i) \left(\prod_{0\leq j \leq n, j\neq i} \frac{x-x_j}{x_i-x_j}\right).$$

El teorema de interpolación de Lagrange nos permite decir cuánto vale un polinomio de grado $n$ en cualquier real $x$ conociendo sus valores en $n+1$ reales distintos. Ya habíamos mostrado este teorema antes con teoría de dualidad. Esta es una demostración alternativa con teoría de bases ortogonales y descomposición de Fourier.

Aplicación de ideas de Fourier en funciones periódicas

También ya habíamos visto que $$\langle f,g \rangle = \int_{-\pi}^\pi f(x)g(x)\, dx$$ define un producto interior en el espacio vectorial $V$ de funciones $f:\mathbb{R}\to \mathbb{R}$ continuas y periódicas de periodo $2\pi$.

En ese ejemplo, definimos \begin{align*}
C_n(x)&=\frac{\cos(nx)}{\sqrt{\pi}}\\
S_n(x)&=\frac{\sin(nx)}{\sqrt{\pi}}.
\end{align*} y $C_0(x)=\frac{1}{\sqrt{2\pi}}$, y mostramos que $$\mathcal{F}:=\{C_n:n\geq 0\}\cup \{S_n:n\geq 1\}$$ era un conjunto ortonormal.

No se puede mostrar que $\mathcal{F}$ sea una base ortonormal, pues el espacio $V$ es de dimensión infinita, y es bastante más complicado que los espacios de dimensión finita. Sin embargo, la teoría de Fourier se dedica a ver que, por ejemplo, la familia $\mathcal{F}$ es buena aproximando a elementos de $V$, es decir a funciones continuas y periódicas de periodo $2\pi$. No profundizaremos mucho en esto, pero daremos algunos resultados como invitación al área.

Para empezar, restringimos a la familia $\mathcal{F}$ a una familia más pequeña:

$$\mathcal{F}_n:=\{C_m:0\leq m \leq n\}\cup \{S_m:1\leq m \leq n\}$$

Motivados en la descomposición de Fourier para espacios Euclideanos, definimos a la $n$-ésima serie parcial de Fourier de una función $f$ en $V$ a la expresión $$S_n(f)=\sum_{g\in \mathcal{F}_n} \langle f, g \rangle g.$$ Haciendo las cuentas, se puede mostrar que $$S_n(f)=\frac{a_0(f)}{2}+\sum_{k=1}^n \left(a_k(f)\cos(kx)+b_k(f)\sin(kx)\right),$$ en donde para $k\geq 1$ tenemos $$a_k=\frac{1}{\pi}\int_{-\pi}^\pi f(x)\cos(kx)\, dx$$ y $$b_k=\frac{1}{\pi}\int_{-\pi}^\pi f(x)\sin(kx)\, dx.$$

A los números $a_k$ y $b_k$ se les conoce como los $k$-ésimos coeficientes de Fourier. Aunque $\mathcal{F}$ no sea una base para $V$, sí es buena «aproximando» a elementos de $V$. Por ejemplo, un resultado lindo de Dirichlet dice que si $f$ y su derivada son continuas, entonces $$\lim_{n\to \infty} S_n(f)(x) = f(x).$$ Este tipo de teoremas de aproximación se estudian con más a detalle en un curso de análisis matemático avanzado o de análisis de Fourier.

Considera ahora $W_n$ el subespacio de $V$ generado por $\mathcal{F}_n$. Tomemos una función $f$ cualquiera en $V$. La $n$-ésima serie de Fourier de $f$ es un elemento de $W_n$. De hecho, es precisamente la proyección de $f$ en $W_n$. Por esta razón, $$\norm{f_n}^2\leq \norm{f}^2<\infty$$

Podemos calcular la norma de $f_n$, usando el resultado para espacios Euclideanos en el espacio (de dimensión finita) $W_n$. Haciendo esto, podemos reescribir la desigualdad anterior como sigue:

$$\frac{a_0(f)^2}{2}+\sum_{k=1}^n(a_k(f)^2+b_k(f)^2)\leq \frac{1}{\pi} \norm{f}^2.$$

El lado derecho es constante, y en el lado izquierdo tenemos una suma parcial de la serie $$\sum_{k\geq 1}(a_k(f)^2+b_k(f)^2).$$ Los términos son positivos y la sucesión de sumas parciales es acotada, así que la serie converge. Entonces, necesariamente la sucesión de términos debe converger a cero. Acabamos de esbozar la demostración del siguiente teorema.

Teorema (de Riemann-Lebesgue). Sea $f$ una función continua y de periodo $2\pi$. Si $a_n(f)$ y $b_n(f)$ son los coeficientes de Fourier de $f$, entonces $$\lim_{n\to \infty} a_n(f) = \lim_{n\to \infty} b_n(f) = 0.$$

De hecho, se puede mostrar que la desigualdad que mostramos se convierte en igualdad cuando $n\to \infty$. Este es un resultado bello, profundo y cuya demostración queda fuera del alcance de estas notas.

Teorema (de Plancherel). Sea $f$ una función continua y de periodo $2\pi$. Si $a_n(f)$ y $b_n(f)$ son los coeficientes de Fourier de $f$, entonces $$\frac{a_0(f)^2}{2}+\sum_{k=1}^\infty(a_k(f)^2+b_k(f)^2)= \frac{1}{\pi} \int_{-\pi}^\pi f(x)^2\, dx.$$

Aunque no daremos la demostración de este resultado, en una entrada posterior veremos cómo podemos aplicarlo.

Más adelante…

En esta entrada seguimos estudiando las bases ortogonales. Usamos este concepto para hacer una descomposición de Fourier, para conocer propiedades de V y obtener otra manera de calcular la norma de un vector. Así mismo, vimos aplicaciones de la descomposición a polinomios, viendo el teorema de la interpolación de Lagrange ya previamente demostrado mediante teoría de dualidad.

Hasta ahora solo hemos hablado de cómo ver si una base es ortonomal y algunas propiedades de estas bases y conjuntos, en la siguiente entrada hablaremos de un método pata encontrar estas bases ortonormales usando el proceso de Gram-Schmidt.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Verifica que los tres polinomios del ejemplo de descomposición de Fourier en efecto forman una base ortogonal.
  • Calcula la norma de $x^2$ con el producto interior del ejemplo de descomposición de Fourier usando la definición, y verifica que en efecto es $\sqrt{2}$.
  • Con la misma base ortonormal $B$ de ese ejemplo, calcula las coordenadas y la norma del polinomio $1+x+x^2$.
  • Verifica que todo lo que mencionamos se cumple con el producto punto en $\mathbb{R}^n$ y con la base canónica.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»