Introducción

En esta entrada abordaremos de manera formal el concepto de continuidad en el sentido complejo. El concepto de continuidad en el ámbito matemático se remonta hace cientos de años atrás, aunque fue hasta mediados del siglo XIX cuando matemáticos como Augustin Louis Cauchy comienzan a dar una formulación precisa de dicho concepto. Desde entonces el concepto de continuidad ha sido refinado, abstraído y generalizado para muchas de las ramas de las matemáticas, en particular en el Cálculo y el Análisis.

En el caso real, solíamos asociar la idea intuitiva de que una función real continua era aquella cuya gráfica no tenía «huecos» o «saltos». Sin embargo, como hemos mencionado antes, en el caso complejo nos será imposible visualizar la gráfica de una función compleja, por lo que resulta interesante cuestionarnos sobre cómo podríamos pensar de forma intuitiva dicho concepto en el caso complejo.

Aunque tendremos definiciones similares a las del caso real, no debemos dar por hecho que el comportamiento de las funciones complejas será necesariamente el mismo que el de las funciones reales, de hecho veremos que las funciones complejas extienden ciertas propiedades de las funciones reales de dos variables continuas, pero veremos que en general las funciones complejas se comportan distinto a las funciones vectoriales de $\mathbb{R}^2$ a $\mathbb{R}^2$, pues resultan ser más restrictivas en ciertas propiedades.

Continuidad de funciones complejas

Definición 15.1. (Continuidad de una función compleja.)
Sean $S\subset\mathbb{C}$ y $f\in\mathcal{F}(S)$ una función. Diremos que $f$ es continua en un punto $z_0\in S$ si para todo $\varepsilon>0$ existe $\delta>0$ tal que si $z\in S$ y $|\,z-z_0\,|<\delta$, entonces $|\,f(z)-f(z_0)\,|<\varepsilon$. Si $f$ es continua en todo punto $z_0 \in S$, entonces diremos que $f$ es continua en $S$. Si $f$ no es continua en $z_0\in S$, entonces diremos que es discontinua en $z_0$.

Ejemplo 15.1
a) Veamos que las funciones $f(z) = \operatorname{Re}(z)$ y $g(z) = \operatorname{Im}(z)$ son continuas para todo $z_0\in\mathbb{C}$.
Solución. Sea $z_0 \in \mathbb{C}$. De acuerdo con la observación 3.1 tenemos que: \begin{equation*} |\,\operatorname{Re}(z) – \operatorname{Re}(z_0)\,| \leq |\,z – z_0\,|,\end{equation*} \begin{equation*}|\,\operatorname{Im}(z) – \operatorname{Im}(z_0)\,| \leq |\,z – z_0\,|. \end{equation*} Por lo que para todo $\varepsilon>0$ existe $\delta = \varepsilon >0$ tal que si $z\in\mathbb{C}$ y $|\,z – z_0\,| < \delta$, entonces:
\begin{equation*}|\,f(z) – f(z_0)\,| = |\,\operatorname{Re}(z) – \operatorname{Re}(z_0)\,| < \varepsilon, \end{equation*} \begin{equation*}|\,g(z) – g(z_0)\,| = |\,\operatorname{Im}(z) – \operatorname{Im}(z_0)\,| < \varepsilon. \end{equation*} De donde se sigue el resultado.

b) Veamos que la función $h(z)=|\,z\,|$ es continua para todo $z_0 \in\mathbb{C}$.
Solución. Sean $z, z_0\in\mathbb{C}$, con $z_0$ fijo. Por la proposición 3.3 sabemos que: \begin{equation*}|\,|\,z\,| – |\,z_0\,| \,| \leq |\,z – z_0\,|. \end{equation*} Entonces, para todo $\varepsilon>0$ existe $\delta = \varepsilon>0$ tal que si $z\in\mathbb{C}$ y $|\,z-z_0\,|<\delta$, entonces: \begin{equation*} |\,h(z) – h(z_0)\,| = |\,|\,z\,| – |\,z_0\,| \,| < \varepsilon. \end{equation*} Por lo que $f$ es continua para todo $z_0\in\mathbb{C}$.

Observación 15.1.
Al igual que con el límite, podemos ver que la continuidad de una función compleja $f(z) = u(x,y) + i v(x,y)$, se puede garantizar a través de la continuidad de las funciones reales $u(x,y)$ y $v(x,y)$, correspondientes con la parte real y la parte imaginaria de $f$. Para ello recordemos la definición de continuidad para una función real de dos variables, vista en nuestros cursos de Cálculo.

Definición 15.2. (Continuidad de una función real de dos variables.)
Sean $U\subset\mathbb{R}^2$ y $u:U\to\mathbb{R}$ una función real de dos variables, digamos $x$ e $y$. Para $(x_0, y_0)\in U$ diremos que $u$ es contninua en $(x_0, y_0)$ si para todo $\varepsilon>0$ existe $\delta>0$ tal que si $(x,y)\in U$ y $\sqrt{(x-x_0)^2 + (y-y_0)^2} < \delta$, entonces: \begin{equation*} |u(x,y) – u(x_0,y_0)| < \varepsilon. \end{equation*}

Proposición 15.1.
Toda función compleja es continua si y solo si su parte real y su parte imaginaria son continuas.

Demostración. Sean $S \subset \mathbb{C}$ y $f: S \to \mathbb{C}$ una función compleja arbitraria y sea $z = x+iy \in S$.

De acuerdo con la proposición 12.1 sabemos que toda función compleja $f$ puede escribirse de la forma:\begin{equation*} f(z) = u(x,y) + i v(x,y), \end{equation*} donde las funciones reales $u(x,y)$ y $v(x,y)$ son su parte real y su parte imaginaria, respectivamente.

Para $z_0 = x_0 + iy_0\in S$ fijo tenemos por la observación 3.1 que: \begin{equation*} |\,u(x,y) – u(x_0, y_0)\,| \leq |\,f(z) – f(z_0)\,| \leq |\,u(x,y) – u(x_0, y_0)\,| + |\,v(x,y) – v(x_0, y_0)\,|, \end{equation*} \begin{equation*} |\,v(x,y) – v(x_0, y_0)\,| \leq |\,f(z) – f(z_0)\,| \leq |\,u(x,y) – u(x_0, y_0)\,| + |\,v(x,y) – v(x_0, y_0)\,|, \end{equation*} por lo que considerando las definiciones 15.1, 15.2 y las desigualdades anteriores se sigue el resultado.

$\blacksquare$

Observación 15.2.
Notemos que en la definición 15.1 se tiene implícita la condición de que:

1. existe $f(z_0)$.

De acuerdo con la proposición 9.4 de la entrada 9, sabemos que para $z_0 \in S\subset\mathbb{C}$ pueden suceder dos casos:

• $z_0$ es un punto aislado de $S$, es decir que $z_0 \in S \setminus S’$,
• $z_0$ es un punto de acumulación de $S$, es decir que $z_0 \in S \cap S’$.

Debe ser claro que si $z_0$ es un punto aislado, entonces existe alguna $\delta$-vecindad de $z_0$, digamos $B(z_0,\delta)$, tal que no contiene otros puntos de $S$ aparte de $z_0$, es decir para todo $z\in S$: \begin{equation*} |\,z-z_0\,|<\delta \quad \Longrightarrow \quad z=z_0, \end{equation*} por lo que $|\,f(z) – f(z_0)\,|=0<\varepsilon$. Entonces, de acuerdo con la definición 15.1, una función compleja $f$ es siempre continua en un punto aislado.

Mientras que si $z_0 \in S\cap S’$ también debe cumplirse que:

2. existe $\lim\limits_{z \to z_0} f(z)$,
3. y $\lim\limits_{z \to z_0} f(z) = f(z_0)$.

Por lo que basta con que no se cumpla alguna de estas tres condiciones para que una función $f\in\mathcal{F}(S)$ sea discontinua en $z_0\in S\subset\mathbb{C}$.

Ejemplo 15.2.
Sea $c\in\mathbb{C}$ una constante y $n\in\mathbb{N}^+$. Consideremos a la función $f(z) = c z^n$. Veamos que $f$ es continua en $\mathbb{C}$.

Solución. De acuerdo con la observación 14.5 de la entrada anterior, para toda $n\in\mathbb{N}^+$ tenemos que: \begin{equation*} \lim_{z \to z_0} f(z) = c z_0^n. \end{equation*} Por otra parte, tenemos que $f(z_0) = cz_0^n$ para todo $n\in\mathbb{N}^+$, por lo que $f$ es una función continua en $\mathbb{C}$.

Ejemplo 15.3.
a) Verificar si la función $f(z) = z^2 – iz + 2$ es continua en $z_0 = 1 – i \in \mathbb{C}$.
Solución. De acuerdo con la observación 15.2 para ver si la función $f$ es continua en el punto $z_0 \in \mathbb{C}$ basta con ver que se cumplan las tres condiciones establecidas en dicha observación.

1. Es claro que $f$ está definida en $z_0$, y es tal que: \begin{equation*} f(z_0) = (1-i)^2 – i(1-i) + 2 = 1 – 3i. \end{equation*}
2. Considerando la observación 14.6 tenemos que: \begin{align*} \lim_{z \to z_0} f(z) &= \left(\lim_{z \to z_0} z\right)^2 – i \left( \lim_{z \to z_0} z\right) + 2\\ & = \left(1-i\right)^2 – i \left(1-i\right) + 2\\ & = 1-3i. \end{align*}
3. Tenemos que: \begin{equation*} \lim_{z \to z_0} f(z) = f(z_0). \end{equation*}

Por lo tanto $f$ es continua en $z_0 = 1-i \in \mathbb{C}$.

b) Consideremos a la siguiente función: \begin{equation*} f(z)= \left\{ \begin{array}{lcc} z^2 & \text{si} & z \neq i, \\ 0 & si & z = i. \end{array} \right. \end{equation*} Probar que $f$ no es continua en $z_0 = i$.
Solución. Notemos que:

1. $f$ está definida en $z_0$, y es tal que: \begin{equation*} f(z_0) = 0. \end{equation*}
2. De acuerdo con la observación 14.6 tenemos que: \begin{align*} \lim_{z \to z_0} f(z) &= \left(\lim_{z \to i} z\right)^2\ & = (i)^2 = -1. \end{align*}
3. Es claro que: \begin{equation*} \lim_{z \to z_0} f(z) = -1 \neq 0 = f(z_0). \end{equation*}

Por lo tanto, tenemos que $f$ no es continua en $z_0 = i$.

Observación 15.3.
Dado que $\mathbb{C}$ dotado con el módulo es un espacio métrico, entonces son válidas las propiedades de continuidad para espacios métricos probadas en la entrada 9, en particular establecemos la siguiente caracterización.

Proposición 15.2.
Sean $S\subset \mathbb{C}$, $z_0 \in S$ y $f\in\mathcal{F}(S)$ una función. Las siguientes condiciones son equivalentes:

1. $f$ es continua en $z_0$ de acuerdo con la definición 15.1,
2. para todo $\varepsilon>0$ existe $\delta>0$ tal que: \begin{equation*} B(z_0,\delta) \cap S \subset f^{-1}\left[ B(f(z_0),\varepsilon)\right]. \end{equation*}
3. $\lim\limits_{n\to\infty} f(z_n) = f(z_0)$, para toda sucesión $\{z_n\}_{n\geq 1} \subset S$ que converge a $z_0$.

$\blacksquare$

Proposición 15.3.
Sean $S\subset \mathbb{C}$ y $f\in\mathcal{F}(S)$ una función. Las siguientes condiciones son equivalentes:

1. $f$ es continua en $S$ de acuerdo con la definición 15.1,
2. si $U\subset \mathbb{C}$ es abierto en $\mathbb{C}$, entonces $f^{-1}(U)$ es también abierto en $S$,
3. si $F\subset \mathbb{C}$ es cerrado en $\mathbb{C}$, entonces $f^{-1}(F)$ es también cerrado en $S$.

$\blacksquare$

Proposición 15.4.
Sea $H\subset \mathbb{C}$, $g\in\mathcal{F}(H)$ una función tal que $g(H) \subset S \subset\mathbb{C}$ y sea $f\in\mathcal{F}(S)$. Supongamos que $z_0$ es un punto de acumulación de $H$, que $\lim\limits_{z \to z_0} g(z) = w_0 \in S$ y que $f$ es continua en $w_0$. Entonces $\lim\limits_{z \to z_0} f(g(z)) = f(w_0)$, es decir: \begin{equation*} \lim_{z \to z_0} f(g(z)) = f\left(\lim_{z \to z_0} g(z) \right). \end{equation*}

Demostración. Dadas las hipótesis, tenemos que dado $\varepsilon>0$ existe $\eta>0$ tal que si $w\in S$ y $|\,w – w_0\,| < \eta $ entonces: \begin{equation*} |\,f(w) – f(w_0)\,| < \varepsilon. \end{equation*} Más aún, tenemos que para dicha $\eta>0$ existe un $\delta>0$ tal que si $z\in H$ y $0<|\,z-z_0\,|<\delta$ entonces: \begin{equation*} |\,g(z) – w_0\,| < \eta. \end{equation*} Por lo que considerando estas dos implicaciones se sigue que si $z\in H$ y $0<|\,z-z_0\,|<\delta$ entonces: \begin{equation*} |\,f(g(z)) – f(w_0)\,| < \varepsilon. \end{equation*} Por lo tanto $\lim\limits_{z \to z_0} f(g(z)) = f(w_0)$.

$\blacksquare$

Proposición 15.5.
Sean $S\subset \mathbb{C}$ y $f,g\in\mathcal{F}(S)$ dos funciones continuas en $S$, entonces:

1. $f \pm g$ es continua en $S$.
2. $fg$ es continua en $S$. Si $g$ es constante, es decir si $g(z) = c\in\mathbb{C}$ para todo $z\in S$, entonces $cf$ es continua en $S$.
3. Si $g(z) \neq 0$ para todo $z\in S$, entonces $\dfrac{f}{g}$ es continua en $S$.
4. Si $z_0 \in S$ y $h$ es una función definida en un conjunto $U \subset f(S)$ tal que $h$ es continua en $f(z_0)$, entonces la composición $h\circ f$ es continua en $z_0$.

Demostración. Utilizando la definición 15.1 y la proposición 14.3 de la entrada anterior es fácil probar el resultado, por lo que se deja como ejercicio al lector.

$\blacksquare$

Corolario 15.1.
Los polinomios son continuos en $\mathbb{C}$. Las funciones racionales son continuas en su dominio de definición.

Demostración. Sea $p(z) = c_0 + c_1 z + c_2 z^2 + \cdots + c_n z^n$, con $z\in\mathbb{C}$, un polinomio de coeficientes complejos, es decir $c_i \in\mathbb{C}$ para toda $i\in{0,1,\ldots, n}$, con $c_n\neq 0$.

Procedemos a realizar la prueba por inducción sobre $n$. Notemos que para $n=0$ se tiene que $p(z) = c_0\neq 0$ es una función constante, entonces considerando el ejemplo 14.1(c) de la entrada anterior, tenemos que: \begin{equation*} \lim_{z\to z_0} p(z) = \lim_{z\to z_0} c_0= c_0 = p(z_0), \end{equation*} por lo que en dicho caso $p(z)$ es continuo para todo $z_0\in\mathbb{C}$.

Para $n=1$, tenemos que $p(z) = c_0 + c_1 z$, por lo que considerando la proposición 15.5(1), al ser $c_0$ y $c_1 z$ funciones continuas en $\mathbb{C}$, entonces $p(z) = c_0 + c_1 z$ es continuo para todo $z\in\mathbb{C}$. Supongamos que el polinomio $q(z) = c_0 + \sum_{i = 1}^{k}c_i z^i$, para algún $k\in\mathbb{N}$ fijo, es continuo para todo $z\in\mathbb{C}$.

Para $n=k+1$ tenemos que: \begin{align*} p(z) & = c_0 + \sum_{i = 1}^{k+1}c_i z^i\\ & = c_0 + \sum_{i = 1}^{k}c_i z^i + c_{k+1} z^{k+1}\\ & = q(z) + c_{k+1} z^{k+1}, \end{align*} por hipótesis de inducción tenemos que $q(z)$ es un polinomio continuo y al ser $c_{k+1} z^{k+1}$ una función continua, entonces por la proposición 15.5(1), es claro que para $n=k+1$ el polinomio $p(z)$ es continuo para todo $z\in\mathbb{C}$, por lo que el resultado es válido para todo $n\in\mathbb{N}$.

Por otra parte, consideremos a $f(z) = \dfrac{p(z)}{q(z)}$, la cual es una función racional definida como el cociente de dos polinomios. De acuerdo con la proposición 15.5(3), considerando que todo polinomio es continuo en $\mathbb{C}$ se sigue que $f$ es continua en todo su dominio de definición, es decir en $S =\{z\in\mathbb{C} \, : \, q(z)\neq 0\}$.

$\blacksquare$

Ejemplo 15.4.
Considera la siguiente función y determina dónde es continua. \begin{equation*} f(z) = \frac{z-i}{z^2 + 1}. \end{equation*}

Solución. Tenemos que $z^2 + 1 = 0$ si y solo si $z=i$ o $z=-i$, por lo que el dominio natural de $f$ es el conjunto $S = \mathbb{C}\setminus\{i, -i\}$. De acuerdo con el corolario 15.1, dado que $f$ es una función racional entonces $f$ es continua en $S$.

Una pregunta que podemos hacernos es ¿se puede asignar un valor a la función $f$ de tal modo que sea continua en $z=i$?

Notemos que: \begin{equation*} f(z) = \frac{z-i}{z^2 + 1} = \frac{z-i}{(z-i)(z+i)}. \end{equation*} Para $z\neq i$ tenemos que: \begin{align*} \lim_{z \to i} f(z) & = \lim_{z \to i} \frac{z-i}{z^2 + 1}\\ & = \lim_{z \to i} \frac{z-i}{(z-i)(z+i)}\\ & = \lim_{z \to i} \frac{1}{z+i}\\ & = \frac{1}{2i} = -\frac{i}{2}. \end{align*} Por lo que podemos definir a la función:
\begin{equation*} g(z)= \left\{ \begin{array}{lcc} \dfrac{z-i}{z^2 + 1} & \text{si} & z \neq -i, \\ -\dfrac{i}{2} & si & z = i, \end{array} \right. \end{equation*} la cual claramente es una función continua en $z=i$, por lo que la discontinuidad de la función $f(z)$ en el punto $z=i$ pudo removerse.

Definición. 15.3. (Discontinuidad removible.)
Sean $S\subset\mathbb{C}$ y $f\in\mathcal{F}(S)$ una función discontinua en un punto $z_0\in S$. Se dice que $f(z)$ tiene una {\bf discontinuidad removible} en $z_0$ si existe el límite de $f(z)$ en dicho punto y la función no está definida en $z_0$ o tiene asignado un valor distinto al del límite, en tal caso la función $f(z)$ puede hacerse continua definiendo el valor de la función en $z_0$ como el valor del límite.

Si un punto $z_0 \in S$ no es una discontinuidad removible, diremos que es una discontinuidad irremovible.

Ejemplo 15.5.
Veamos que la función $f(z) = \dfrac{\operatorname{Re}(z)}{z}$ tiene una discontinuidad irremovible en $z=0$.

Solución. De acuerdo con el corolario 15.1, es claro que la función $f(z)$ no es continua en $z=0$. Veamos que el límite de la función $f(z)$ cuando $z$ tiende a $0$ no existe.

Sea $z=x+iy \neq 0$. Si nos aproximamos a $0$ a lo largo del eje real, es decir si $y=0$ y $z=x$, entonces: \begin{align*} \lim_{z\to 0 } f(z) & = \lim_{z\to 0 } \frac{\operatorname{Re}(z)}{z}\\ & = \lim_{x\to 0 } \frac{x}{x}\\ & = \lim_{x\to 0 } 1\\ & = 1. \end{align*} Por otra parte, si nos aproximamos a $0$ a lo largo del eje imaginario, es decir si $x=0$ y $z=iy$, entonces: \begin{align*} \lim_{z\to 0 } f(z) & = \lim_{z\to 0 } \frac{\operatorname{Re}(z)}{z}\\ & = \lim_{x\to 0 } \frac{0}{iy}\\ & = \lim_{x\to 0 } 0\\ & = 0. \end{align*} Por lo que el $\lim\limits_{z \to 0} f(z)$ no existe. Entonces la función tiene una discontinuidad irremovible en $z=0$.

Ejemplo 15.6.
Veamos que la función $f(z) =\operatorname{Arg}(z)$ tiene una discontinuidad irremovible en $z=0$. Más aún, veamos que todo $z$ en el eje real negativo es una discontinuidad irremovible y por tanto que $f$ solo es continua en el dominio $\mathbb{C} \setminus (-\infty, 0]$.

Solución. Sabemos que para $z=0$ la función argumento principal no está definida, por lo que en $z=0$ dicha función no es continua. Veamos que dicho valor es una discontinuidad irremovible mostrando que el límite en dicho punto no existe.

Sabemos que:

1. si $z=x>0$, entonces $\operatorname{Arg}(z) = 0$,
2. si $z=x<0$, entonces $\operatorname{Arg}(z) = \pi$.

Por lo que:

1. para $x>0$ se tiene que $\lim\limits_{z \to 0} \operatorname{Arg}(z) = \lim\limits_{x \to 0^+} \operatorname{Arg}(z) = 0$,
2. mientras que para $x<0$ se tiene que $\lim\limits_{z \to 0} \operatorname{Arg}(z) = \lim\limits_{x \to 0^-} \operatorname{Arg}(z) = \pi$.

Por la unicidad del límite concluimos que no existe $\lim\limits_{z \to 0} \operatorname{Arg}(z)$, por lo que $z=0$ es una discontinuidad irremovible.

Sea $z_0\in \mathbb{C}\setminus\{0\}$, tal que $z_0 = x_0 < 0$, fijo, entonces $\operatorname{Arg}(z_0) = \pi$. De acuerdo con la definición de la función $\operatorname{Arg}(z)$ dada en la entrada 13, es claro que para $z=x+iy\in\mathbb{C}\setminus\{0\}$, se tiene que:

1. si $x<0$ y $y\geq0$, entonces $\operatorname{Arg}(z) = \operatorname{arc\,tan}\left( \frac{y}{x} \right) + \pi$,
2. si $x<0$ y $y <0$, entonces $\operatorname{Arg}(z) = \operatorname{arc \,tan}\left( \frac{y}{x} \right) – \pi$.

Por lo que, si nos aproximamos a $z_0$ mediante $z = z_0 + iy$ tenemos:
\begin{align*} \lim\limits_{z \to z_0} \operatorname{Arg}(z) = \lim\limits_{y \to 0^+} \operatorname{Arg}(z) = \pi,\\ \lim\limits_{z \to z_0} \operatorname{Arg}(z) = \lim\limits_{y \to 0^-} \operatorname{Arg}(z) = -\pi. \end{align*}

Entonces la función $\operatorname{Arg}(z)$ es discontinua en $z_0 = x_0<0$ y desde que no existe $ \lim\limits_{z \to z_0} \operatorname{Arg}(z)$ tenemos que $z_0$ es una discontinuidad irremovible. Como $z_0 = x_0<0$ era arbitrario, entonces todo $z_0 \in (-\infty, 0)$ es una discontinuidad irremovible.

Procedemos a verificar que $f$ es continua en el dominio $\mathbb{C} \setminus (-\infty, 0]$.

Por la proposición 13.1, entrada 13, sabemos que para $z\neq 0$ si $z \in \mathbb{C} \setminus (-\infty, 0)$ entonces: \begin{equation*} \operatorname{Arg}(z) = 2 \operatorname{arc tan}\left(\dfrac{y}{|\,z\,| + x}\right), \end{equation*} de donde $u(x,y) = 2 \operatorname{arc tan}\left(\dfrac{y}{|\,z\,| + x}\right)$ y $v(x,y) =0$, las cuales son funciones reales continuas, entonces de la proposición 15.1 se sigue que la función $\operatorname{Arg}(z)$ es continua en $\mathbb{C} \setminus (-\infty, 0]$.

Observación 15.4.
Debe ser claro que la función $f(z) = \operatorname{Arg}(z) = \operatorname{Arg}_{(-\pi, \pi]}(z)$ corresponde con una rama de la función multivaluada $G(z) = \operatorname{arg}(z)$ desde que $f$ es continua en $\mathbb{C} \setminus (-\infty, 0] = \left\{ z\in\mathbb{C} : |\,z\,|>0, -\pi < \operatorname{arg} z < \pi \right\}$, dicha rama es llamada la rama principal del argumento.

Más aún, para $\alpha \in \mathbb{R}$ fijo e $I=(\alpha, \alpha+2\pi]$, tenemos por la proposición 13.3 que la función $g(z) = \operatorname{Arg}_I(z)$ está dada por: \begin{equation*} \operatorname{Arg}_I(z) = \operatorname{Arg}\left(-z\operatorname{cis}(-\alpha)\right) + \alpha + \pi, \end{equation*} por lo que podemos verificar que $g$ será continua dónde lo sea $f$.

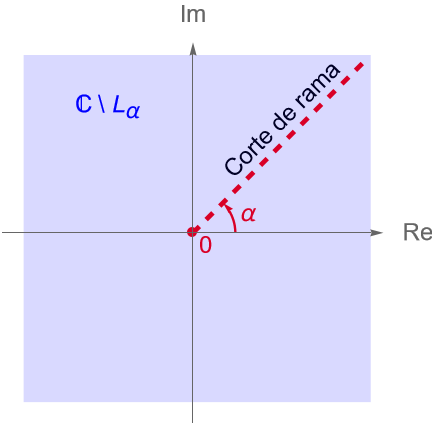
Veamos entonces que $g$ es continua en $\mathbb{C}\setminus L_\alpha$, donde $L_\alpha = \left\{ r\operatorname{cis}(\alpha) : r \geq 0 \right\}$, figura 69.

Notemos que si $z \in L_\alpha$, entonces $z = r\operatorname{cis}(\alpha)$, con $r = |\,z\,|$ y $\alpha = \operatorname{arg} z$. Claramente $r>0$ pues en $z=0$ la función $f$ no está definida. Entonces, por la prueba de la proposición 13.3 tenemos que: \begin{equation*} -z \operatorname{cis}(-\alpha) = -r\operatorname{cis}(\alpha)\operatorname{cis}(-\alpha) = -r\operatorname{cis}(\alpha – \alpha) = -r(1) = -r, \end{equation*} de donde $-r < 0$, por lo que $-r \in (-\infty, 0)$, pero en dicho conjunto $f$ no es continua, por lo que para $z \in L_\alpha$ la función $g(z) = \operatorname{Arg}_I(z) $ no es continua.

Por otra parte, si $z \in \mathbb{C}\setminus L_\alpha$ tenemos que $z = \rho \operatorname{cis}(\theta)$, con $\rho = |\,z\,|>0$ y $\theta = \operatorname{Arg}_I(z)$, entonces: \begin{equation*} \alpha < \theta < \alpha + 2\pi \quad \Longleftrightarrow \quad -\pi < \theta – \alpha – \pi < \pi, \end{equation*} pues $\operatorname{cis}(\alpha + 2\pi) = \operatorname{cis}(\alpha) \operatorname{cis}(2\pi) = \operatorname{cis}(\alpha)$.

Tenemos que:
\begin{equation*} -z \operatorname{cis}(-\alpha) = \operatorname{cis}(-\pi) \, \rho \operatorname{cis}(\theta)\operatorname{cis}(-\alpha) = \rho \operatorname{cis}(\theta – \alpha – \pi ), \end{equation*} por lo que $ -z \operatorname{cis}(-\alpha) \in \mathbb{C}\setminus(-\infty, 0]$, donde $f$ es continua.

Entonces la función $g(z) = \operatorname{Arg}_I(z)$ solo es continua en $\mathbb{C}\setminus L_\alpha$. Por lo tanto, la función $g$ determina una rama de la función multivaluada $G(z) = \operatorname{arg}(z)$, siempre que se defina en el dominio, figura 69: \begin{equation*} D = \mathbb{C}\setminus L_\alpha = \left\{ z\in\mathbb{C} : |\,z\,|>0, \alpha < \operatorname{arg} z < \alpha + 2\pi \right\}. \end{equation*}

Ejemplo 15.7.
Veamos que la función $f(z) = z^{1/2}$, correspondiente con la raíz cuadrada principal, definición 13.5, tiene una discontinuidad irremovible en $z=-1$. Más aún, veamos que todo $z$ en el eje real negativo es una discontinuidad irremovible, aún cuando esta función solo asigna una única raíz. Concluyamos que la raíz cuadrada principal es una rama, la rama principal de la función multivaluada $F(z) = z^{1/2}$, solo si se restringe al dominio $\mathbb{C} \setminus (-\infty, 0]$.

Solución. Sea $z =r\operatorname{cis}(\theta)\neq 0$. De acuerdo con la definición 13.5, la raíz cuadrada principal está dada por: \begin{equation*} f(z) = z^{1/2} = \sqrt{r} \operatorname{cis}\left(\frac{\theta}{2}\right), \end{equation*} donde $r=|\,z\,|$ y $\theta =\operatorname{Arg}(z)$.

Sea $z_0 = -1$, veamos que no existe $\lim\limits_{z\to z_0} f(z) = \lim\limits_{z\to -1} z^{1/2}$. Para ello consideremos a la circunferencia unitaria $C(0,1)$, es decir la circunferencia centrada en $z=0$ y de radio $1$, figura 70.

Si $z \in C(0,1)$, entonces podemos aproximarnos a $z_0 = -1$ mediante la trayectoria dada por el cuarto de circunferencia en el segundo cuadrante, es decir $\pi/2 < \operatorname{Arg}(z) < \pi$, con $\operatorname{Arg}(z) \to \pi$, entonces: \begin{align*} \lim_{z\to -1} z^{1/2} & = \lim_{z\to -1} \sqrt{|\,z\,|}\operatorname{cis}\left(\frac{\operatorname{Arg}(z)}{2}\right)\\ & = \lim_{\operatorname{Arg}(z) \to \pi} \sqrt{1}\operatorname{cis}\left(\frac{\operatorname{Arg}(z)}{2}\right)\\ & = \lim_{\operatorname{Arg}(z) \to \pi} \left[ \operatorname{cos}\left(\frac{\operatorname{Arg}(z)}{2}\right) + i \operatorname{sen}\left(\frac{\operatorname{Arg}(z)}{2}\right)\right]\\ & = \operatorname{cos}\left(\frac{\pi}{2}\right) + i \operatorname{sen}\left(\frac{\pi}{2}\right)\\ & = 0 + i(1)\\ & = i. \end{align*}

Si ahora nos aproximamos a $z_0=-1$ con $z\in C(0,1)$ a través de la trayectoria dada por el cuarto de circunferencia en el tercer cuadrante, es decir $-\pi < \operatorname{Arg}(z) < -\pi/$, con $\operatorname{Arg}(z) \to -\pi$, entonces: \begin{align*} \lim_{z\to -1} z^{1/2} & = \lim_{z\to -1} \sqrt{|\,z\,|}\operatorname{cis}\left(\frac{\operatorname{Arg}(z)}{2}\right)\\ & = \lim_{\operatorname{Arg}(z) \to -\pi} \sqrt{1}\operatorname{cis}\left(\frac{\operatorname{Arg}(z)}{2}\right)\\ & = \lim_{\operatorname{Arg}(z) \to -\pi} \left[ \operatorname{cos}\left(\frac{\operatorname{Arg}(z)}{2}\right) + i \operatorname{sen}\left(\frac{\operatorname{Arg}(z)}{2}\right)\right]\\ & = \operatorname{cos}\left(-\frac{\pi}{2}\right) + i \operatorname{sen}\left(-\frac{\pi}{2}\right)\\ & = 0 + i(-1)\\ & = -i. \end{align*}

Dado que estos dos límites son distintos, concluimos que $\lim\limits_{z\to -1} z^{1/2}$ no existe, por tanto $z_0 = -1$ es una discontinuidad irremovible.

De manera similar podemos probar que cualquier punto en el eje real negativo es una discontinuidad irremovible. Sin embargo, desde que la función $\operatorname{Arg}(z)$ es discontinua en $(-\infty, 0]$ y la función $f$ está dada en términos de dicha función, debe ser claro que $f$ será discontinua en el mismo conjunto.

Procedemos a verificar que $f$ es continua en el dominio $\mathbb{C} \setminus (-\infty, 0]$, es decir que bajo esa restricción obtenemos una rama de la función multivaluada $F(z) = z^{1/2}$, a la cual llamamos la rama principal $f_0$, es decir: \begin{equation*} f_0(z) = z^{1/2} = \sqrt{r} \operatorname{cis}\left(\frac{\theta}{2}\right), \end{equation*} donde $r=|\,z\,|$ y $\theta =\operatorname{Arg}(z)$ y $z \in \mathbb{C} \setminus(-\infty,0] = \left\{ w\in\mathbb{C} : |\,w\,|>0, -\pi < \operatorname{Arg}(w) <\pi \right\}$.

Sea $z = x+iy \in \mathbb{C} \setminus (-\infty, 0]$. Por la proposición 13.1 tenemos que: \begin{equation*} \operatorname{Arg}(z) = 2 \operatorname{arc tan}\left(\dfrac{y}{|\,z\,| + x}\right). \end{equation*}

Entonces, para $r=|\,z\,|$ y $\theta =\operatorname{Arg}(z)$ tenemos que: \begin{align*} f_0(z) & = \sqrt{|\,z\,|} \operatorname{cis}\left(\frac{\operatorname{Arg}(z)}{2}\right)\\ & = \sqrt[4]{x^2+y^2} \operatorname{cis}\left(\frac{2 \operatorname{arc tan}\left(\dfrac{y}{\sqrt{x^2+y^2} + x}\right)}{2}\right)\\ & = \sqrt[4]{x^2+y^2} \operatorname{cos}\left(\operatorname{arc tan}\left(\dfrac{y}{\sqrt{x^2+y^2} + x}\right)\right) + i \sqrt[4]{x^2+y^2} \operatorname{sen}\left(\operatorname{arc tan}\left(\dfrac{y}{\sqrt{x^2+y^2} + x}\right)\right)\\ & := u(x,y) + iv(x,y). \end{align*}

Como las funciones $u(x,y)$ y $v(x,y)$ son funciones reales continuas, entonces por la proposición 15.1 concluimos que la función $f_0$ es continua en $\mathbb{C} \setminus (-\infty, 0]$ y por tanto que es una rama de la función multivaluada $F(z) = z^{1/2}$.

Observación 15.5.
Considerando la definición 14.2 y la proposición 14.4 de la entrada anterior, notemos que podemos extender el concepto de continuidad para funciones definidas sobre el plano complejo extendido, es decir, diremos que una función $f: \mathbb{C}_\infty \to \mathbb{C}_\infty$ es continua en $\infty$ si \begin{equation*} f(\infty) = \lim_{z\to \infty} f(z) \end{equation*} y si $f(a) = \infty$, entonces $f$ es continua en $a$ si \begin{equation*} f(a) = \infty =\lim_{z\to a} f(z). \end{equation*}

Ejemplo 15.8.
Consideremos a la siguiente función:
\begin{equation*} f(z) = \frac{z+i}{z-i}. \end{equation*} Es claro que dicha función no está definida en $z=i$. Sin embargo, dado que: \begin{equation*} f(i) = \infty = \lim_{z\to i} f(z) \end{equation*} y \begin{equation*} f(\infty) = 1 = \lim_{z\to \infty} f(z), \end{equation*} entonces definiendo: \begin{equation*} g(z)= \left\{ \begin{array}{lcc}
\dfrac{z+i}{z-i} & \text{si} & z \neq i, \\ 1 & \text{si} & z = \infty, \\ \infty & \text{si} & z = i, \end{array} \right. \end{equation*} es claro que $g$ es una función continua de $\mathbb{C}_\infty$ en $\mathbb{C}_\infty$.

De acuerdo con los resultados de la entrada 10 para funciones continuas entre espacios métricos, tenemos que son válidas las siguientes afirmaciones para funciones complejas continuas.

Proposición 15.6. (Funciones continuas sobre conjuntos conexos y compactos.)
Sean $S\subset\mathbb{C}$ y $f\in\mathcal{F}(S)$ una función continua en $S$.

1. Si $S$ es un conjunto conexo, entonces $f(S)$ es también conexo.
2. Si $S$ es un conjunto compacto, entonces $f(S)$ es también compacto.

$\blacksquare$

Cerraremos esta entrada con el siguiente concepto.

Definición 15.4. (Continuidad uniforme.)
Sean $S\subset\mathbb{C}$ y $f\in\mathcal{F}(S)$ una función. Diremos que $f$ es uniformemente continua en $S$, si para todo $\varepsilon>0$ existe $\delta>0$ (que depende solo de $\varepsilon$) tal que si $z, w \in S$ y $|\,z-w\,|<\delta$ entonces $|\,f(z) – f(w)\,|<\varepsilon$.

Ejemplo 15.9.
Sea $f(z) = \overline{z}$ definida en $\mathbb{C}$. Veamos que $f$ es uniformemente continua en $\mathbb{C}$.

Solución. Para $z,w\in\mathbb{C}$ tenemos que: \begin{equation*} |\,f(z) – f(w)\,| = |\,\overline{z} – \overline{w}\,| = |\,\overline{\overline{z} – \overline{w}}\,| = |\,z-w\,| < \varepsilon, \end{equation*} por lo que tomando $\delta=\varepsilon>0$ se cumple la definición.

Observación 15.6.
De acuerdo con la definición 15.4, notamos que el concepto de continuidad uniforme es más restrictivo que el de continuidad de una función, por lo que la continuidad uniforme estará sujeta al conjunto $S$ en el que la función esté definida, para ver esto consideremos el siguiente:

Ejemplo 15.10.
a) Sea $f(z) = z^2$ definida en $S = B(0,1)$. Veamos que $f$ es uniformemente continua en $S$.

Solución. Notemos que para $z,w\in S$ se tiene que $|\,z\,|<1$ y $|\,w\,|<1$. Entonces: \begin{align*} |\,f(z) – f(w)\,| & = |\,z^2 – w^2\,|\\ & = |\,z – w\,| |\,z + w\,|\\ & < \left( |\,z\,| + |\,w\,|\right) \delta\\ & < 2\delta <\varepsilon, \end{align*} por lo que basta con tomar $\delta = \frac{\varepsilon}{2}>0$ para que se cumpla la definición.

b) Sea $f(z) = z^2$ definida en $\mathbb{C}$. Veamos que $f$ no es uniformemente continua en $\mathbb{C}$.

Solución. Sea $\varepsilon=1$, entonces dado $\delta>0$, por la propiedad arquimediana existe $n\in\mathbb{N}^+$ tal que $n\delta >1$. Sean $z = n$ y $w=n+\frac{\delta}{2}$, entonces se tiene que $|\,z-w\,|=\frac{\delta}{2} < \delta$, pero:
\begin{align*} |\,f(z) – f(w)\,| & = |\,z^2 – w^2\,|\\ & = n^2 + n\delta +\frac{\delta^2}{4} – n^2\\ & = n\delta +\frac{\delta^2}{4} > n\delta > 1 = \varepsilon, \end{align*} por lo que $f$ no es uniformemente continua en $\mathbb{C}$.

Proposición 15.7.
Sean $S\subset\mathbb{C}$ y $f\in\mathcal{F}(S)$ una función. Las siguientes afirmaciones son equivalentes.

1. $f$ es uniformemente continua en $S$,
2. $\operatorname{Re} f$ e $\operatorname{Im} f$ son uniformemente continuas en $S$,
3. para cualesquiera sucesiones $\{z_n\}_{n\geq 1}$ y $\{w_n\}_{n\geq 1}$ en $S$ tales que $\lim\limits_{n\to\infty} |\,z_n – w_n\,| = 0$, se cumple que $\lim\limits_{n\to\infty} |\,f(z_n) – f(w_n)\,| = 0$.

Dadas las hipótesis, tenemos que:
$1. \Leftrightarrow 2.$ Su prueba es análoga a la de la proposición 15.1, por lo que se deja como ejercicio al lector.

$1. \Rightarrow 3. $
Sean $\{z_n\}_{n\geq 1}$ y $\{w_n\}_{n\geq 1}$ dos sucesiones en $S$ tales que $\lim\limits_{n\to\infty} |\,z_n – w_n\,| = 0$ y supongamos que $f$ es uniformemente continua en $S$.

Sea $\varepsilon>0$, entonces existe $\delta>0$ tal que si $z,w\in S$ y $|\,z-w\,|<\delta$, entonces $|\,f(z) – f(w)\,|<\varepsilon$. Como $\lim\limits_{n\to\infty} |\,z_n – w_n\,| = 0$, entonces para el $\delta>0$ se tiene que existe $N\in\mathbb{N}^+$ tal que: \begin{equation*} |\,|\,z_n – w_n\,| – 0 \,| = |\,z_n – w_n\,| < \delta, \quad \forall n\geq N, \end{equation*} por lo que para toda $n\geq N$ se cumple que: \begin{equation*} |\,|\,f(z_n) – f(w_n)\,| – 0 \,| = |\,f(z_n) – f(w_n)\,| < \varepsilon, \end{equation*} es decir que $\lim\limits_{n\to\infty} |\,f(z_n) – f(w_n)\,| = 0$.

$3. \Rightarrow 1.$
Sean $\{z_n\}_{n\geq 1}$ y $\{w_n\}_{n\geq 1}$ dos sucesiones en $S$ tales que si $\lim\limits_{n\to\infty} |\,z_n – w_n\,| = 0$, entonces $\lim\limits_{n\to\infty} |\,f(z_n) – f(w_n)\,| = 0$.

Por reducción al absurdo, supongamos que $f$ no es uniformemente continua en $S$, entonces existe $\varepsilon>0$ tal que para todo $\delta>0$ existen $z,w\in S$ tales que $|\,z-w\,|<\delta$ y $|\,f(z) – f(w)\,|\geq \varepsilon$.

Tenemos que para todo $n\in\mathbb{N}^+$ se tiene que $z_n, w_n \in S$ y $\frac{1}{n}>0$, por lo que: \begin{equation*} |\,z_n – w_n\,|<\frac{1}{n} \quad \text{y} \quad |\,f(z_n) – f(w_n)\,|\geq \varepsilon, \end{equation*} lo cual contradice nuestra hipótesis, por lo que $f$ es uniformemente convergente.

Tarea moral

1. Sean $S\subset\mathbb{C}$ y $f\in\mathcal{F}(S)$ una función. Prueba que $f$ es continua en $z_0 \in S$ si y solo si $\overline{f}$ es continua en $z_0 \in S$.
2. Sea $S = [a,b] = \{ x\in\mathbb{R} \, : \, a\leq x \leq b\}$. Considera a $S\subset \mathbb{C}$ y sea $f: S \to \mathbb{C}$ una función compleja de variable real. Tomando $z=x+i0$ podemos escribir $f(z) = u(x) + i v(x)$. Prueba que $f$ es continua si y solo si $u$ y $v$ son continuas.
3. Analiza la continuidad de la función: \begin{equation*} f(z)= \left\{ \begin{array}{lcc} \dfrac{z^3 – 1}{z-1} & \text{si} & |\,z\,| \neq 1, \\ 3 & \text{si} & |\,z\,| = 1, \end{array} \right. \end{equation*} en los puntos $z_0 = 1$, $z_1 = -1$, $z_2 = i$ y $z_3 = -i$.
4. Analiza la continuidad de las siguientes funciones y determina el valor de $f(z)$ en el punto $z_0$ de tal forma que la función sea continua en dicho punto.
   a) $f(z) = \dfrac{z^3 – z_0}{z – z_0}$.
   b) $f(z) = \left(\dfrac{1}{z – z_0}\right)\left( \dfrac{1}{z} – \dfrac{1}{z_0}\right)$.
   c) $f(z) = \dfrac{\operatorname{Re}(z) \operatorname{Im}(z)}{|\,z\,|^2}$.
   d) $f(z) = \dfrac{\left(\operatorname{Re}(z)\right)^2 – \left(\operatorname{Im}(z)\right)^2}{|\,z\,|^2}$.
5. Sean $S\subset\mathbb{C}$ y $f\in\mathcal{F}(S)$ una función. Prueba que si $f$ es continua en $z_0 \in S$, entonces $|\,f\,|$ es continua en $z_0 \in S$. ¿Es cierto el recíproco?
6. Considera la siguiente función definida en $\mathbb{C}_\infty$: \begin{equation*} f(z)= \left\{ \begin{array}{lcc} \dfrac{z+1}{4z+3} & \text{si} & z \neq \frac{-3}{4}, \\ \infty & \text{si} & z = \frac{-3}{4}. \end{array} \right. \end{equation*} Analiza la continuidad de $f$ en $z = -\frac{3}{4}$.
7. Sean $S\subset\mathbb{C}$ y $f\in\mathcal{F}(S)$ una función. Prueba que si $f$ es uniformemente continua en $S$, entonces $f$ es continua en $S$. ¿Es cierto el recíproco?
8. Sea $f(z)=\dfrac{1}{z^2}$, prueba que:
   a) $f$ es uniformemente continua en $S = \left\{z\in\mathbb{C} : \frac{1}{2} \leq |\,z\,| \leq 1\right\}$,
   b) $f$ no es uniformemente continua en $S = \{z\in\mathbb{C} : |\,z\,| \leq 1\}$.

Más adelante…

En esta entrada hemos abordado de manera formal el concepto de continuidad y continuidad uniforme para funciones complejas. Caracterizamos la continuidad (y la continuidad uniforme) de las funciones complejas a través de la continuidad (y la continuidad uniforme) de su parte real e imaginaria, en particular vimos que toda función compleja continua es de la forma $f(z) = u(x,y) + i v(x,y)$.

Aunque las definiciones que hemos dado en esta entrada son muy similares a las de las funciones reales, veremos en la siguiente entrada que al trabajar con funciones complejas algunos conceptos se vuelven más restrictivos para estas funciones, el cual es el caso de la diferenciabilidad compleja.

La siguiente entrada abordaremos la diferenciabilidad en el sentido complejo y veremos que la diferenciabilidad para $\mathbb{R}^2$, que hemos estudiado en nuestros cursos de Cálculo, no bastará para garantizar la diferenciabilidad en el sentido complejo.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: Límites en $\mathbb{C}$.
• Siguiente entrada del curso: Diferenciabilidad en el sentido complejo.