Introducción

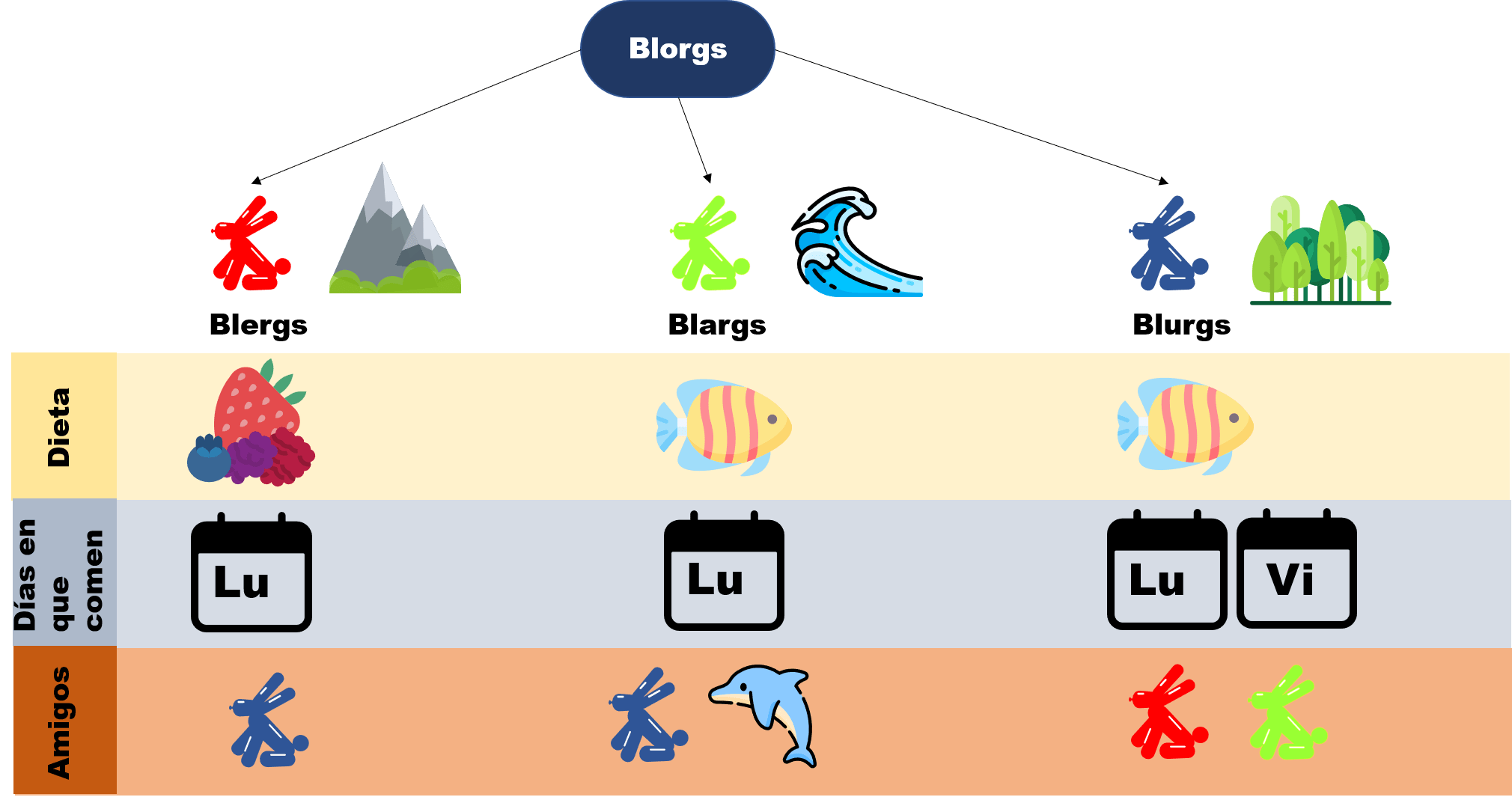
Esta entrada es parte de una serie de notas introductorias sobre técnicas de demostración. En esta entrada se habla sobre demostraciones por contradicción. Cada entrada está ligeramente relacionada con las otras. Para entenderlas bien, usamos el siguiente diagrama que recopila cómo se comporta un mundo fantástico llamado Axios, en donde habitan creaturas llamadas Blorgs. Para leer más sobre ello, haz click aquí.

Ya hemos empezado a ver algunas estrategias para empezar a demostrar cosas. Ahora veremos una siguiente que es muy común de encontrar: las demostraciones por contradicción. Comenzando con una proposición que queremos demostrar, supondremos que no es cierta. Puede sonarte que es un poco extraño, pero en esta entrada revisaremos de qué forma esta suposición nos ayudará.

La contradicción

Puede que en tu vida hayas escuchado la palabra contradicción usada en alguno u otro contexto. Podemos decir por ejemplo que una persona se contradice a sí misma cuando dice que es alérgica al camarón después de haberse comido un coctél de camarón. Esto suena poco convincente, ¿no? Pues al decir que alguien es alérgico al camarón sabemos que no puede comer camarón, al mismo tiempo que vemos a la persona haciéndolo. Esta idea va a ser similar en las matemáticas. Pero recuerda que aquí estamos en el lenguaje de las proposiciones.

Definición. Una contradicción es una fórmula proposicional en la cual sin importar la asignación de verdad de las variables proposicionales, siempre se obtiene algo falso.

Un ejemplo muy sencillo es la fórmula proposicional $(P \land \neg P)$. Si $P$ es falso, entonces la conjunción es falsa. Y si $P$ es verdadero, entonces $\neg P$ es falso y entonces también la conjunción es falsa.

Ahora observa la siguiente regla de inferencia:

\begin{array}{rl}
P \\
\neg P \\
\hline
\therefore Q.
\end{array}

Se puede probar que esta es una inferencia válida (es uno de los ejercicios al final de la entrada). Analiza un poco la regla y piensa: ¿esto qué significa? Observa que en ningún momento aparece el término $Q$ en las premisas y sin embargo es una conclusión. La parte de las premisas de la regla de inferencia sería $P\land \neg P$. En pocas palabras, esto nos quiere decir que «de una contradicción se puede deducir lo que sea». Es decir, si en algún momento llegamos a una contradicción, ya nada tiene sentido, pues cualquier cosa sería cierta. Si cambiamos $Q$ por «La luna es de queso», podemos concluirlo de una contradicción, y esto no tiene sentido. Es por eso que si en algún momento en las matemáticas llegamos a una contradicción, es que algo está raro. Bajo esta idea funcionarán las demostraciones por contradicción.

Demostraciones por contradicción

Hablemos ahora sí de la estrategia de hacer demostraciones por contradicción. Como platicamos en la sección anterior, de una contradicción podemos concluir cualquier cosa. En particular, podemos concluir lo que queremos demostrar. Esto, ¿cómo se ve en pasos específicos que tenemos que hacer? La estrategia general es la siguiente.

1. Pensemos que de ciertas premisas $Q_1, Q_2, \ldots, Q_n$ queremos llegar a la conclusión $P$.
2. Supongamos que además de dichas premisas, también tenemos a $\neg P$ como premisa.
3. A partir de $Q_1,\ldots,Q_n,\neg P$, obtengamos todas las cosas ciertas que podamos, con el objetivo de simultáneamente probar que tanto cierta proposición $R$ como cierta proposición $\neg R$ son ciertas.
4. Como ya tendremos $R$ y $\neg R$ en nuestras premisas, podremos concluir lo que sea, en particular, $P$.
5. Otra manera de pensarlo es que en el momento en que hemos encontrado tanto $R$ como $\neg R$. En matemáticas las contradicciones nos dicen que hay algo raro, pues sabemos que una proposición no puede ser verdadera y falsa a la vez (recuerda que esto es una contradicción). Así, habremos encontrado un problema lógico. Entonces nuestra suposición de que $\neg P$ es verdadera es imposible. Por lo tanto, $P$ es verdadera.

Otra manera en la que en que te puedas imaginar la reducción al absurdo es mediante la validez de la siguiente regla de inferencia (también tendrás que justificarla como uno de los ejercicios):

$$ \begin{array}{rl} & \neg P \Rightarrow (R \land \neg R) \\ \hline \therefore & P \end{array}.$$

Esto nos dice que si $P$ es falso (es decir, que $\neg P$ es verdad) implica tanto cierta proposición $Q$, como su negación $\neg Q$, entonces en realidad $P$ no puede ser falso, y por lo tanto es verdadero. Piénsalo como mejor te acomodes.

Ejemplo de demostración por contradicción

Hagamos una prueba en el mundo Axios.

Proposición. Para todo Blurg $x$, si $x$ come un cierto día, entonces pasan como mínimo tres días antes de que $x$ vuelva a comer.

Demostración. Vamos a hacer esta prueba por contradicción. Como dijimos antes, las pruebas por contradicción se basan en que para demostrar una proposición $P$, se empieza suponiendo $\neg P$, y a partir de ahí se ven las consecuencias y se intenta llegar a una contradicción. Ahora veamos la traducción de esto a nuestra proposición.

$P$ = Para todo Blurg $x$, si $x$ come un cierto día, entonces pasan como mínimo tres días antes de que $x$ vuelva a comer.

La negación es (recuerda que la negación de $\forall x: A(x)\Rightarrow B(x)$ es $\exists x: A\land \neg B$):

$\neg P$ = Existe un Blurg $x$ que comió cierto día, y no pasaron como mínimo tres días antes que de $x$ volviera a comer.

Otra manera de escribir esto es

$\neg P$ = Existe un Blurg $x$ que comió cierto día, y pasaron máximo dos días antes que de $x$ volviera a comer.

Entonces empecemos con $ \neg P$ y veamos qué obtenemos. Tomemos dicho Blurg $x$ que existe. Uno de nuestros axiomas dice que $Q =\text {Para todo Blurg $x$, se tiene que $x$ come exactamente los lunes y los viernes}$. Así, la primera vez que $x$ comió fue o lunes, o viernes.

• Si comió el lunes, entonces como estamos suponiendo $\neg P$, tenemos que $x$ comió máximo el martes o el jueves. Pero esto es $\neg Q$, pues existió un Blurg que no comió exactamente los lunes o viernes. Así, tendríamos $Q$ y $\neg Q$, una contradicción.
• Si comió el viernes, entonces como estamos suponiendo $\neg P$, tenemos que $x$ comió máximo el sábado, o el domingo. Pero esto es $\neg Q$ también, pues existió un Blurg que no comió exactamente los lunes o viernes. Una vez más tenemos $Q$ y $\neg Q$, una contradicción.

En cualquiera de los casos, llegamos a una contradicción. Nuestro error fue suponer que $P$ no era cierta, por lo tanto tiene que ser cierta $P$.

$\square$

Algunos ejemplos famosos de demostraciones por contradicción.

Ahorita estamos en Axios y seguiremos en él. Pero para acercárte un poco más a cómo se usa esta estrategia en matemáticas, aquí te compartimos unos ejemplos de demostraciones por contradicción. Para fines de este curso no necesitas saber demostrar estas proposiciones, únicamente son ejemplos que podrías checar para entender mejor cómo se utiliza esta estrategia.

• La demostración de que el $0$ es el único neutro aditivo en los números reales (es el único número que al sumarlo a otro número resulta el mismo otro número) utiliza esta estrategia, pues al suponer que no es único, se llega a una contradicción. Puedes checar la demostración aquí.
• En geometría euclideana, existen criterios para decir si dos triángulos son congruentes (son el «mismo» triángulo salvo quizá la reflexión y rotación, es decir hay una forma de rotarlo o reflejarlo para notar que se trata del «mismo» triángulo). Uno de estos se llama el criterio LAL que nos dice que si dos triángulos tienen dos lados que miden lo mismo y comparten el ángulo entre esos lados, entonces son congruentes. Una técnica para demostrar esto es con reducción a lo absurdo y supone que dos lados y el ángulo entre ellos son iguales, pero que el lado restante es distinto. De ahí se puede llegar a una contradicción. Puedes checar la demostración aquí.
• En el estudio de los tipos de números, se usa una prueba por contradicción para mostrar que el número $\sqrt{2}$ es irracional. Si fuera racional, se podría escribir como $\sqrt{2}=\frac{a}{b}$ con $a$ y $b$ enteros positivos que no comparten factores en común. Pero de esa igualdad se llega a $2b^2=a^2$, de donde se puede justificar con algunos pasos que tanto $a$ como $b$ son pares. Así, ¡simultáneamente $a$ y $b$ deberían y no deberían tener factores en común! Esa contradicción muestra la irracionalidad de $\sqrt{2}$.
• También puedes ver una colección de videos con pruebas por contradicción en el siguiente enlace: Busca una contradicción.

Más adelante…

En las siguientes entradas seguiremos hablando de cómo hacer demostraciones. Más que estrategias generales, serán una guía sobre cómo demostrar proposiciones que involucran conectores lógicos o cuantificadores. Ya hemos visto algunos de estos ejemplos y ahora profundizaremos un poco más en su estructura.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Usa tablas de verdad para ver que $(P\Rightarrow Q) \land (Q\Rightarrow P) \land P \land \neg Q$ es una contradicción.
2. Prueba que $$ \begin{array}{rl} & P \Rightarrow (R \land \neg R) \\ \hline \therefore & \neg P \end{array}$$ es una regla de inferencia válida.
3. Prueba que
   \begin{array}{rl}
   P \\
   \neg P \\
   \hline
   \therefore R
   \end{array}
   es una regla de inferencia válida.
   
4. Prueba por contradicción que «Para todo Blorg $x$, si $x$ no come fresas, ni come los viernes, entonces $x$ es un Blarg». Como ayuda, la negación es «Existe un Blorg $x$ tal que ni come fresas, ni come los viernes, ni es Blarg». Si no es Blarg, ¿qué casos hay y cómo llegas a una contradicción en cada uno de ellos?
5. El viernes pasado iba caminando y encontré un Blorg $A$ que estaba platicando con un amigo suyo, un Blorg $B$ el cual estaba comiendo. Luego, el Blorg $B$ se encontró a un amigo suyo que estaba comiendo lo mismo. ¿Tiene sentido mi historia? ¿Qué sucedería si toda mi historia es verdadera?

Entradas relacionadas

• Ir a Álgebra Superior I
• Entrada anterior del curso: Demostraciones directas e indirectas
• Siguiente entrada del curso: Problemas introductorios a demostraciones

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»