Archivo de la etiqueta: diámetro

Geometría Moderna I: Definiciones

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

Esta es la primera entrada del curso de Geometría Moderna I el cual está basado en el temario oficial de la Facultad de Ciencias de la UNAM. Aquí presentaremos algunos conceptos básicos que nos serán de ayuda para empezar el curso.

El termino Geometría Moderna se refiere a aquella geometría deductiva, que fue desarrollada después de Euclides y hasta el desarrollo de las geometrías no euclidianas, este periodo está comprendido entre los siglos III AC y XIX DC, es decir, la geometría griega hecha con regla y compás, pero después de los griegos.

La geometría euclidiana estudia propiedades básicas de los objetos geométrico tales como punto, recta, triángulo o circunferencia, a partir de un conjunto de axiomas y de manera sintética, es decir, sin el uso de un eje de coordenadas o métodos algebraicos muy complejos, aunque si se hace uso de nociones básicas de Teoría de Conjuntos, como las de pertenencia o intersección de conjuntos.

Muchas de estas propiedades son de carácter métrico, es decir, sobre la medición de magnitudes de ángulos, longitudes de segmentos, distancias entre puntos o áreas de figuras geométricas, pero también nos hablan sobre la concurrencia de rectas (rectas diferentes que pasan por un mismo punto), colinealidad de puntos (puntos distintos que están sobre una misma recta) o puntos cíclicos (puntos distintos que están en una misma circunferencia).

Punto, recta y circunferencia

Definición 1. Un punto es la representación de un lugar específico en el plano, no tiene longitud, altura ni ninguna otra dimensión, en nuestro cuaderno o el pizarrón podemos representar este lugar con la marca más pequeña y visible que nuestro lápiz o gis puedan hacer, la cual en realidad si tiene dimensiones, pero lo que solo nos interesa es la abstracción de ese lugar marcado.

La mayoría del tiempo para referirnos a puntos emplearemos letras mayúsculas.

Definición 2. Una línea recta es un objeto de una sola dimensión, solo tiene longitud y se extiende de manera infinita en ambos sentidos, todos sus puntos se encuentran en una misma dirección de manera que dos puntos distintos determinan a una línea recta.

Nos referiremos a una línea recta simplemente como recta. Si no conocemos dos puntos por donde pasa una recta la denotaremos con la letra $l$.

Cuando la intersección de dos rectas $l_{1}$, $l_{2}$ es vacía, es decir, no tienen ningún punto en común $l_{1} \cap l_{2} = \varnothing$, decimos que son rectas paralelas y lo denotamos como $l_{1} \parallel l_{2}$.

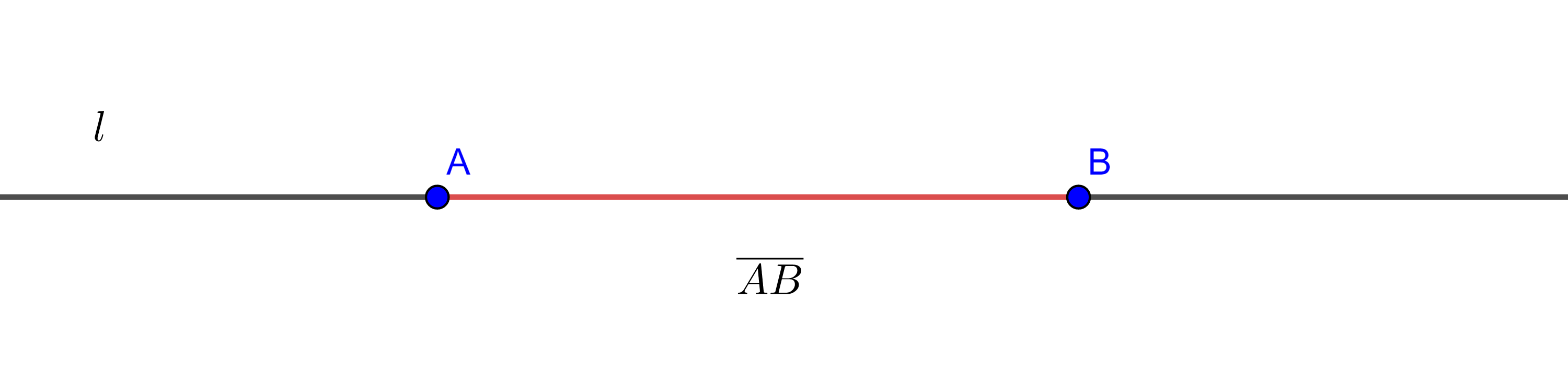
A la porción de línea recta que une dos puntos distintos en el plano (incluyendo a los puntos) y que no se extiende más allá de ellos le llamamos segmento de recta o simplemente segmento.

La distancia entre dos puntos es la magnitud del segmento de recta que los une.

Si conocemos dos puntos distintos $P$, $Q$ de una recta nos referiremos al segmento que une dichos puntos como $PQ$, en ocasiones también nos podremos referir a la recta completa con la misma notación de acuerdo al contexto del problema.

Figura 1

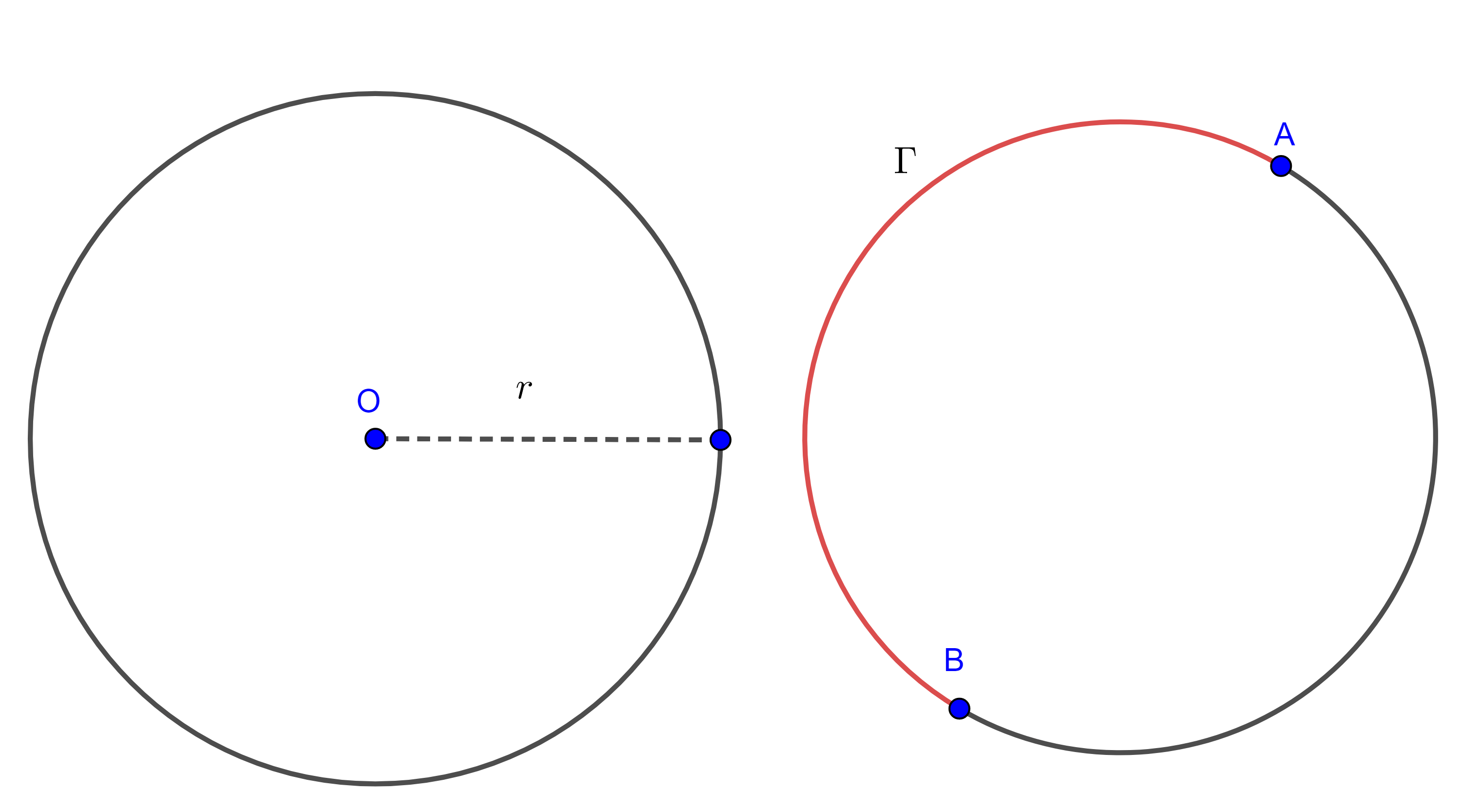
Definición 3. Dados un punto $O$ del plano y una magnitud $r \geq 0$, definimos a la circunferencia con centro en $O$ y radio $r$ $(O, r)$ como el conjunto de puntos en el plano cuya distancia al punto $O$ es $r$.

Algunas veces no nos importará o no conoceremos el centro o el radio de una circunferencia, en tal caso nos referiremos a ella con cualquier otra letra como $\Gamma$.

Al segmento que une dos puntos distintos de una circunferencia y que pasa por su centro le llamamos diámetro.

Si conocemos dos puntos $A$ y $B$ diametralmente opuestos de una circunferencia podemos denotarla como $\Gamma(AB)$.

A la porción de una circunferencia que une dos puntos distintos en ella le llamamos arco de circunferencia, para dos puntos distintos en una circunferencia $A$ y $B$, denotamos al arco recorrido de $A$ a $B$ en el sentido contrario de las manecillas del reloj como $\overset{\LARGE{\frown}}{AB}$.

Figura 2

Ángulo

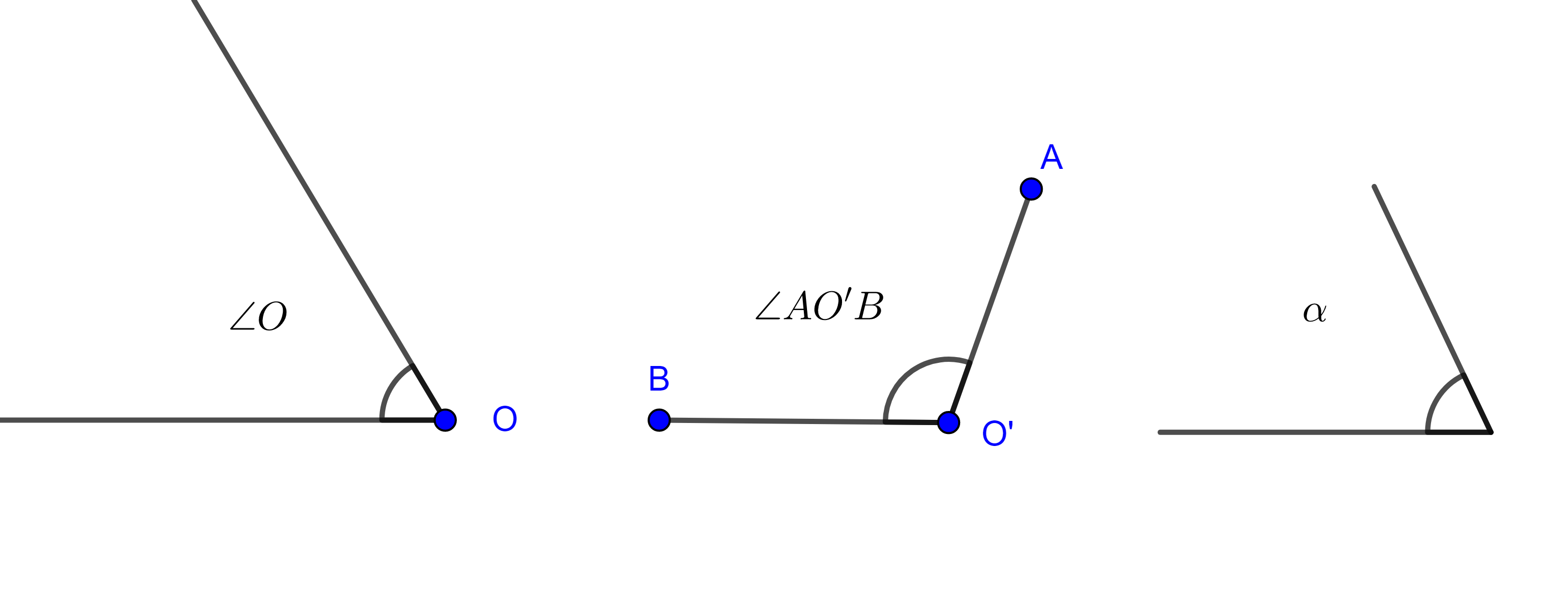
Definición 4. Un ángulo es un objeto formado cuando dos rectas o segmentos se intersecan. Al punto en común le llamamos vértice y los segmentos o semirectas que concurren en el vértice son los lados del ángulo.

Cuando es claro cuáles son los lados de un ángulo con vértice en $O$ lo denotamos como $\angle O$.

Cuando queremos hacer énfasis en los segmentos que forman un ángulo con vértice $O’$, escribimos $\angle AO’B$ si nos referimos al desplazamiento del segmento $AO$ hacia $BO$ en contra del movimiento de las manecillas del reloj.

También podemos etiquetar a un ángulo con letras griegas minúsculas.

Figura 3

Cuando dos rectas o segmentos distintos se intersecan se forman cuatro ángulos, en este caso a los ángulos que comparten un lado en común les llamamos adyacentes y a los que no tienen un lado en común, opuestos por el vértice.

Decimos que un ángulo es recto si es aquel que se obtiene cuando dos rectas $l_{1}$, $l_{2}$ se intersecan formando cuatro ángulos iguales y en este caso decimos que las rectas son perpendiculares $l_{1} \perp l_{2}$. Denotamos a la suma de dos ángulos rectos como $\pi$.

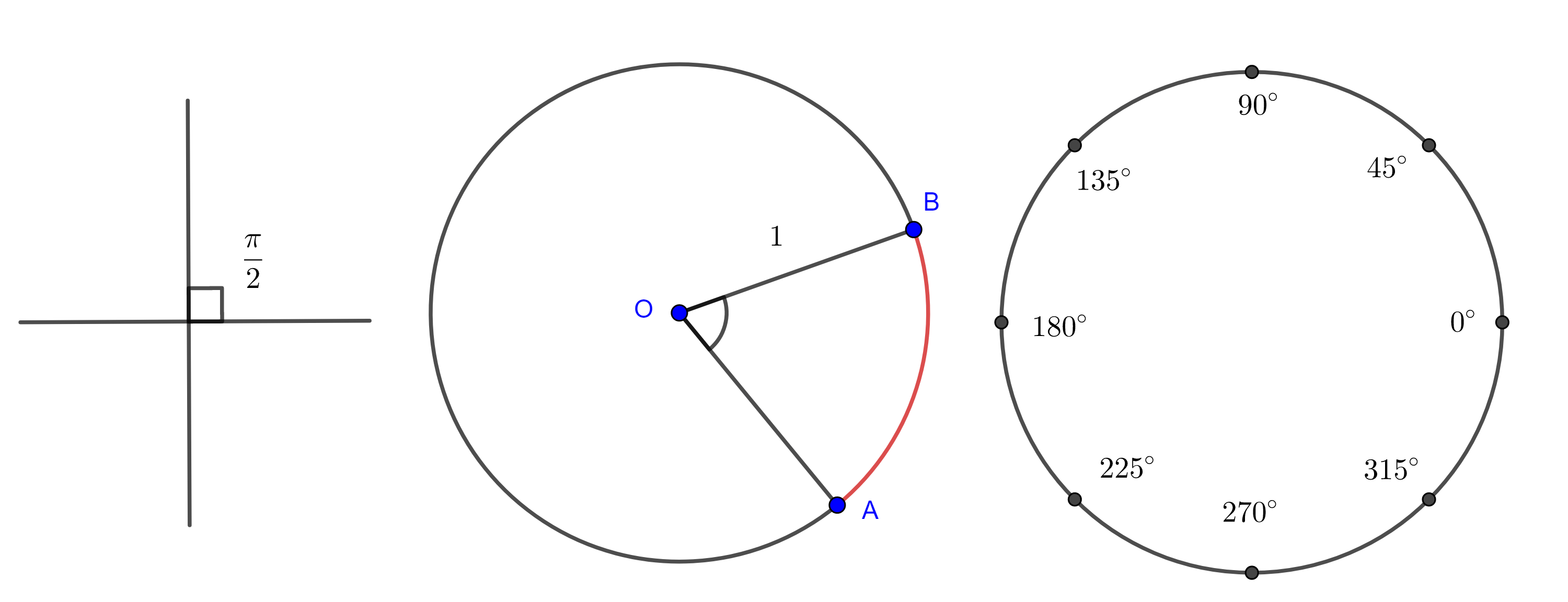
Para medir la magnitud de un ángulo $\angle O$ trazamos una circunferencia de radio $1$ con centro en el vértice del ángulo y ubicamos las intersecciones de los lados del ángulo con la circunferencia digamos $A$ y $B$, entonces la medida de $\angle AOB$ será la magnitud del arco $\overset{\LARGE{\frown}}{AB}$.

En calculo se muestra que $\pi = 3.14159…$, es un numero irracional, esto es, su representación decimal es infinita y no periódica.

Otra forma de medir los ángulos es dividir a la circunferencia en $360$ partes iguales o grados, de esto se sigue que $\dfrac{\pi}{2} = 90^{\circ}$, $\pi = 180^{\circ}$, $2\pi = 360^{\circ}$.

Figura 4

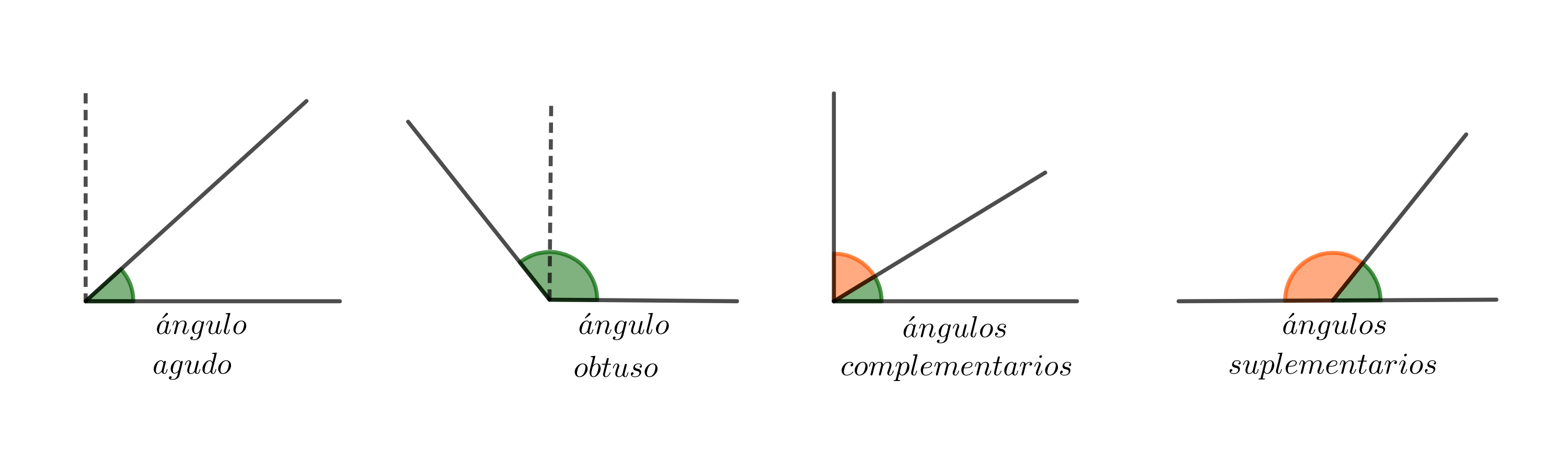
Un ángulo que es menor que uno recto es un ángulo agudo y uno que es mayor a uno recto se llama ángulo obtuso.

Dos ángulos que suman $\dfrac{\pi}{2}$ son complementarios y dos ángulos cuya suma es igual a $\pi$ se llaman suplementarios.

Figura 5

Triángulo

Definición 5. Un triángulo es una figura en el plano que consiste de tres puntos distintos, llamados vértices, que no son colineales, y por los segmentos que unen dichos vértices a los que llamamos lados del triángulo.

Si los vértices de un triangulo son $A$, $B$ y $C$, denotamos al triángulo como $\triangle ABC$ recorriendo los vértices en el sentido contrario de las manecillas del reloj.

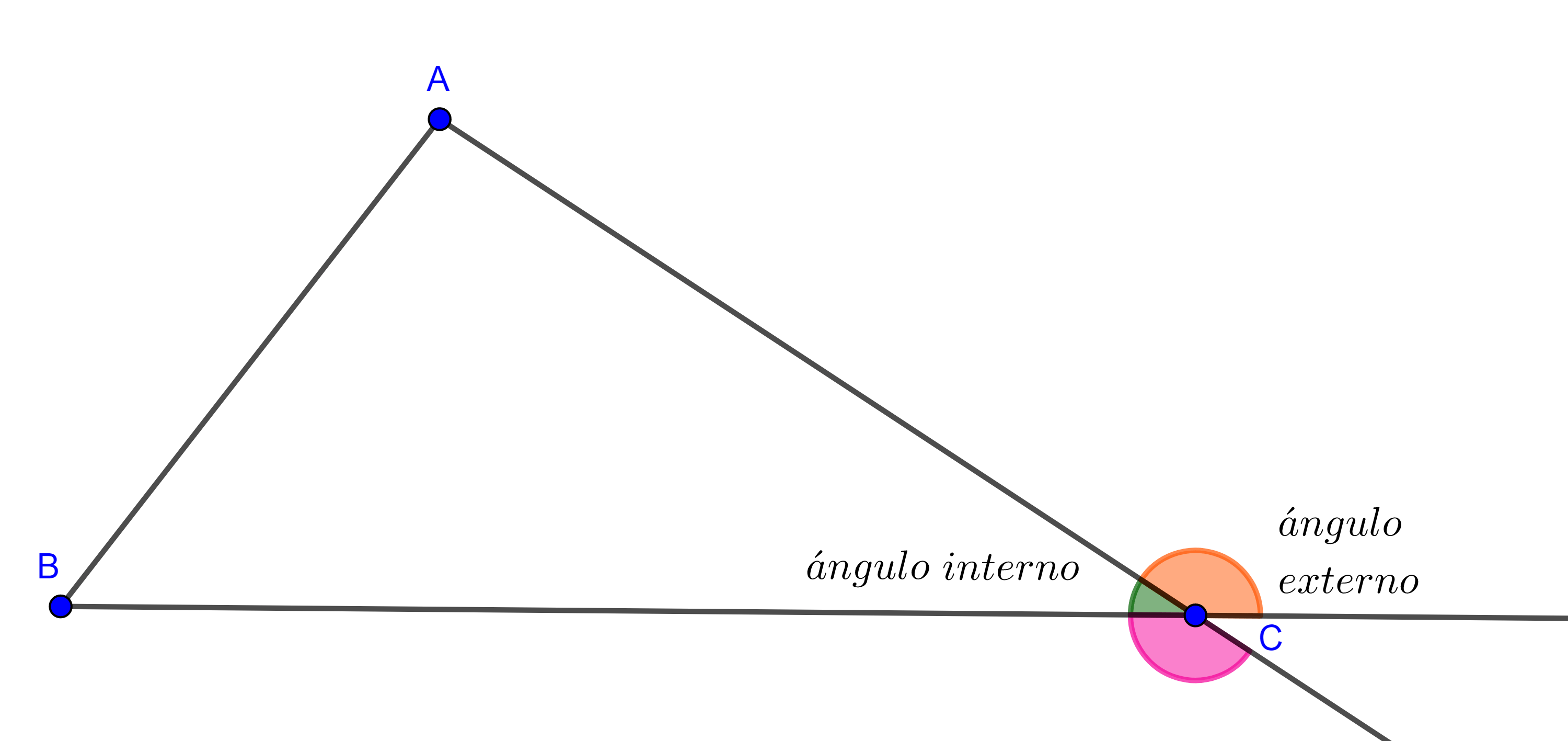
Recordemos leer los ángulos en el sentido contrario al de las manecillas del reloj. A $\angle BAC$, $\angle CBA$ y $\angle ACB$ les llamamos ángulos internos o interiores.

Si extendemos los lados del triángulo, a los ángulos que son suplementarios a los ángulos interiores les llamamos ángulos exteriores o externos, notemos que por cada ángulo interno hay dos externos.

Figura 6

Clasificamos a los triángulos de acuerdo a la magnitud de sus lados y de sus ángulos internos.

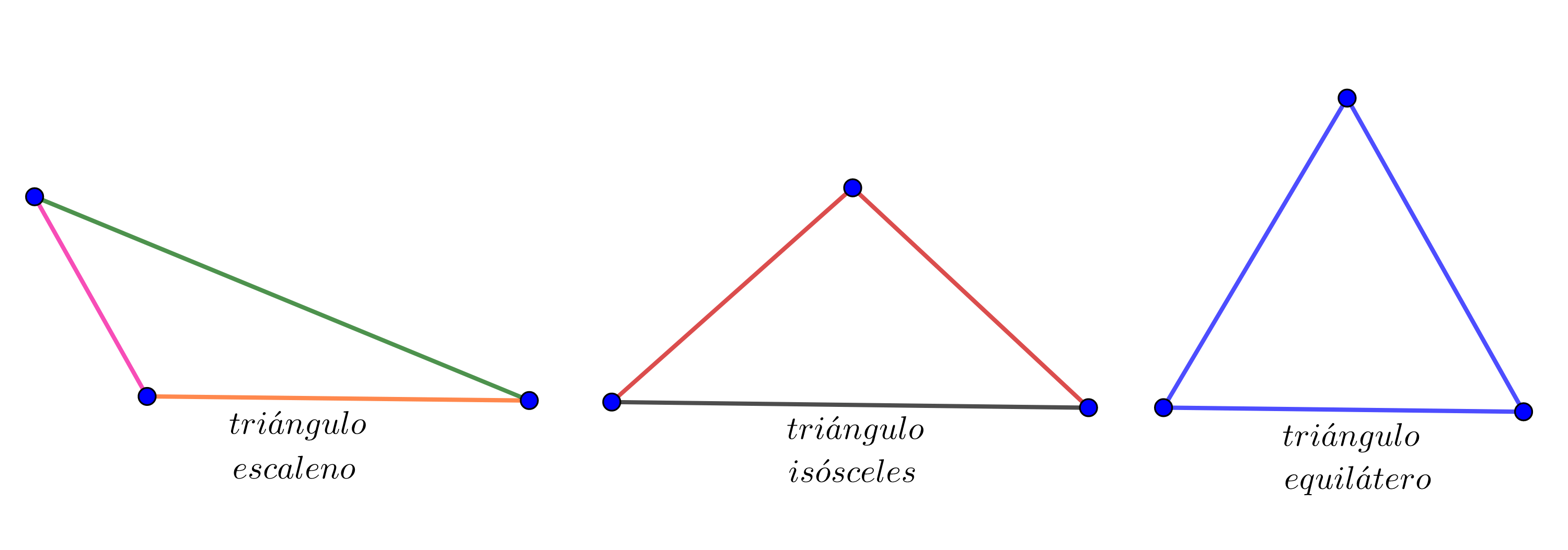
De acuerdo a sus lados:
escaleno, si ningún par de lados es igual,
isósceles, si tienen dos lados iguales,
equilátero, si todos sus lados son iguales.

Figura 7

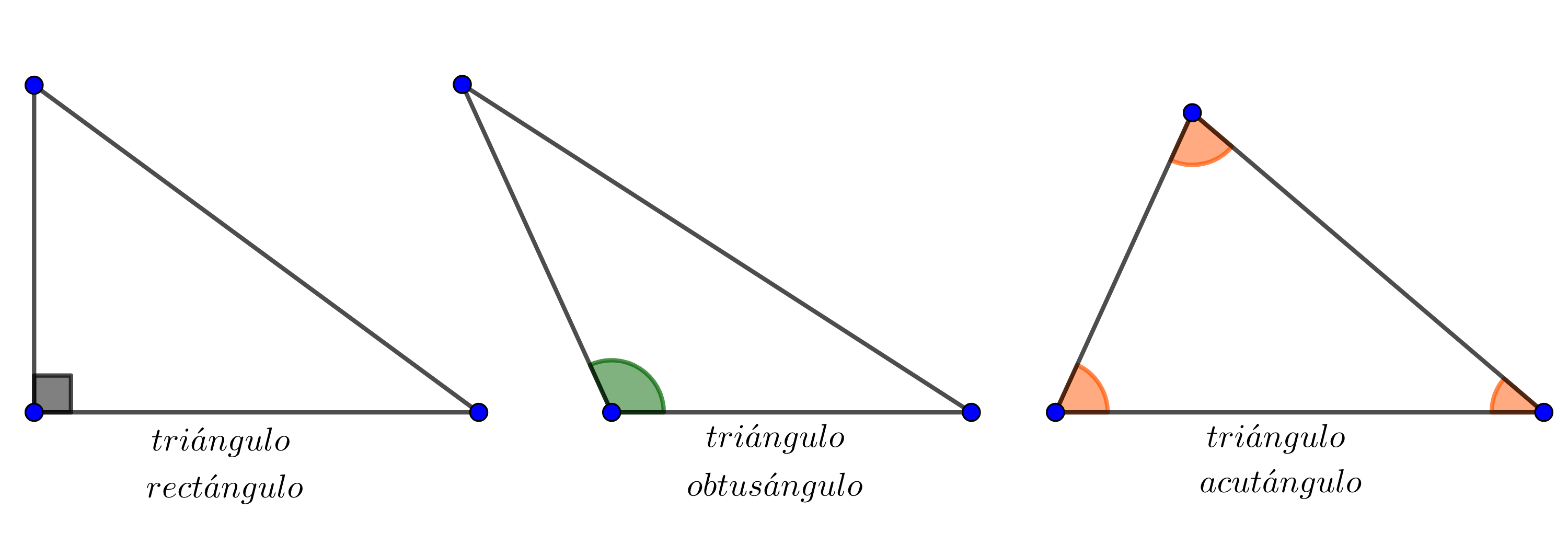
De acuerdo a sus ángulos internos:
rectángulo, si un ángulo interno es recto,
acutángulo, si todos sus ángulos internos son agudos,
obtusángulo, si uno de sus ángulos internos es obtuso.

Figura 8

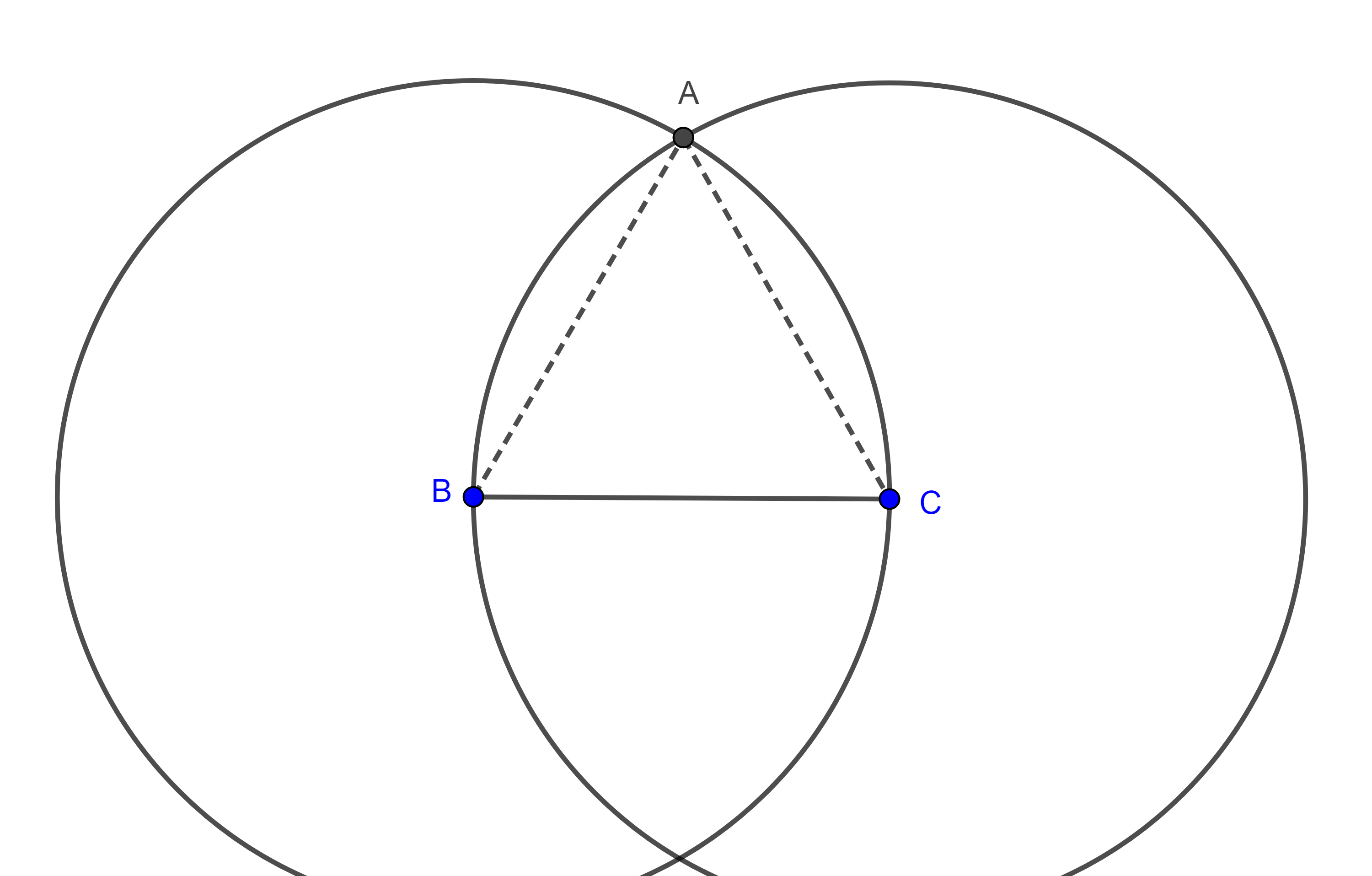
Problema. Dado un segmento construir sobre él un triángulo equilátero.

Solución. Para hacer una construcción geométrica usamos una regla sin graduar y un compás. La regla nos permite trazar la recta que une cualesquiera dos puntos distintos y con el compás podemos trazar circunferencias conociendo su centro y radio.

Sea $BC$ el segmento dado, trazamos dos circunferencias de radio $BC$, una con centro en $B$ y otra con centro en $C$.

Figura 9

Sea $A$ la intersección de $(B, BC)$ con $(C, BC)$, trazamos $AB$ y $AC$, entonces $AB = BC$, por ser radios de $(B, BC)$ y $AC = BC$, por ser radios de $(C, BC)$.

Por lo tanto, $AB = BC = AC$ y así $\triangle ABC$ es equilátero.

$\blacksquare$

El triángulo es uno de los objetos más estudiados en geometría euclidiana. En las próximas entradas abordaremos teoremas fundamentales acerca del triángulo como los de congruencia, semejanza o el teorema de Pitágoras.

Más adelante…

En la siguiente entrada presentaremos los postulados de Euclides que son el punto de partida para poder establecer relaciones entre los objetos que hemos definido.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que los ángulos opuestos por el vértice son iguales.
  2. Convierte a grados los siguientes ángulos: $\dfrac{\pi}{3}$, $\dfrac{\pi}{4}$, $\dfrac{3\pi}{4}$.
  3. Calcula la longitud de arco de los siguientes ángulos: $225^{\circ}$, $270^{\circ}$, $315^{\circ}$.
  4. Dados dos segmentos de distinta longitud, construir sobre el mayor un segmento de igual magnitud al menor.
  5. GeoGebra es un software libre de matemáticas muy útil, con él te puedes apoyar para hacer tus demostraciones durante este curso, aquí esta la versión online.

Entradas relacionadas

Fuentes

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Analítica I: Propiedades de elipses

Por Héctor Morales

3 respuestas

Introducción

En la entrada anterior definimos qué es una elipse, hablamos de una técnica para trazar una y cómo esta técnica, nos conduce naturalmente a su definición analítica: una elipse es la curva que define al conjunto de puntos que cumplen que la suma a dos puntos distintos llamados focos es constante. Finalmente vimos cómo escribir la ecuación canónica de la elipse; a partir de esta ecuación canónica podemos leer toda su información geométrica.

Ahora, para finalizar nuestro estudio de las elipses, vamos a hablar de sus elementos, propiedades focales y sus propiedades métricas. Verás cómo algunos problemas de aplicación motivan el estudio formal de estas propiedades y extenderemos algunas de ellas para el estudio de las cónicas que nos faltan. Sin más preámbulo, abordaremos el tema.

Elementos de una elipse

En la entrada anterior hicimos mención a algunos de los elementos que componen una elipse. Como mencionamos, a partir de la ecuación canónica puedes leer directamente información como el eje menor y el eje mayor; conociendo estos dos ejes, puedes deducir cuáles son sus vértices y sus focos. Haciendo más cuentas puedes deducir cuál es su lado recto y directrices.

En la siguiente figura puedes observar un diagrama que muestra todos los elementos de la elipse y en la siguiente tabla puedes ver qué relación guardan unos con otros. Es importante que sepamos extraer toda la información geométrica que nos sea posible cuando se nos presente una ecuación en su forma canónica.

Breve resumen de los elementos de una elipse. Estos elementos tienen análogos cuando tratamos con otras secciones cónicas.
Elemento dentro de la elipse canónicaExpresión analítica
Longitud del eje mayor$$2a$$
Coordenadas de los vértices$$(\pm a,0)$$
Longitud del eje menor$$2b$$
Coordenadas de los co-vértices$$(0,\pm b)$$
Coordenadas de los focos$(\pm c,0) \quad \text{donde} \quad c^{2}=a^{2}+b^{2}$
Excentricidad$$\varepsilon=\sqrt{\frac{a^{2}-b^{2}}{a^{2}}}=\sqrt{1-\frac{b^{2}}{a^{2}}}$$

Como puedes notar, la última fila se refiere a una propiedad de la elipse que no hemos discutido: la excentricidad. La excentricidad normalmente denotada como $\epsilon$ es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia. Pronto veremos que a partir de la excentricidad, podemos definir a las tres secciones cónicas como el lugar geométrico de los puntos $\mathbf{X}$ cuya razón de sus distancias a un foco $\mathbf{p}$ y a una recta $\ell$ es una constante fija. Profundizaremos en el estudio de la excentricidad a lo largo de esta unidad, por el momento fijemos la idea de que las elipses necesariamente deben tener una excentricidad menor que uno; es decir $\epsilon < 1$.

Otra observación importante: estas reglas se refieren a una elipse centrada en el origen que tiene una ecuación canónica $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$. No es el objetivo de esta unidad hablar de traslaciones y rotaciones; pero debes saber que si la elipse tiene el centro fuera del origen en un punto $(h,k)$, su ecuación se ve así: $\frac{x^{2}-h}{a^{2}}+\frac{y^{2}-k}{b^{2}}=1$. El estudio de elipses rotadas se aborda comúnmente en un segundo curso de geometría analítica.

Propiedad focal de la elipse

La propiedad focal de la elipse es es que cualquier fotón que sale de uno de los focos, se refleja dentro de la elipse para llegar al otro foco. Si no estás familiarizado con el fotón, imagina la siguiente situación: estás en un cuarto con paredes reflejantes y con forma elíptica; si tu te paras en uno de los focos del cuarto y apuntas con una linterna hacia algún punto en las paredes, el rayo de luz de tu linterna impactará directamente en el otro foco.

Existen dos formas de formalizar la propiedad que describimos en el párrafo anterior; la primera consiste en tomar el círculo de radio $2\mathbf{a}$ centrado en el foco $\mathbf{p}$ (este círculo contiene el otro foco $\mathbf{q}$, puesto que ahora $2 a>d(p, q)$) y luego ver que para los puntos de este círculo, su mediatriz con $\mathbf{q}$ es tangente a la elipse $\mathcal{E}$. La segunda forma de resolver este problema nos va a permitir abordar el clásico «problema del bombero», entonces dejaremos el primero como tarea moral.

Para hablar del problema del bombero observa la siguiente figura, supongamos que un bombero está para en el punto $\mathbf{p}$ y hay un incendio en el punto $\mathbf{q}$. Pero tiene su cubeta vacía, y entonces tiene que pasar primero a llenarla a un río cuyo borde es la recta $\mathcal{l}$. El problema consiste en saber cuál es la trayectoria óptima que debe seguir el bombero. Es decir, ¿para cuál punto $x \in \mathcal{l}$? se tiene que $\mathrm{d}(\mathbf{p}, \boldsymbol{x})+\mathrm{d}(\boldsymbol{x}, \mathbf{q})$ es mínima.

Nota cómo no hemos específicado de qué lado del río está el fuego; si estuviera del otro lado que el bombero, cualquier trayectoria al fuego tiene que pasar por $\mathcal{l}$ y entonces debe irse por la línea recta de $\mathbf{p}$ a $\mathbf{q}$ y tomar agua en $\boldsymbol{x}_{0}=\ell \cap \overline{\mathbf{p q}}$ (ver la siguiente figura). Entonces, si fuego y bombero están del mismo lado del río $\mathcal{l}$ podemos pensar en un «fuego virtual», que es el reflejado de $\mathbf{q}$ en $\mathcal{l}$, llamémosle $\mathbf{q}_{0}$, que cumple que $\mathrm{d}(\mathbf{x}, \mathbf{q})=\mathrm{d}\left(\mathbf{x}, \mathbf{q}_{0}\right)$ para todo $\mathbf{x} \in \mathcal{l}$, (para $\mathbf{q}$ y $\mathbf{q}_{0}$, \mathcal{l} es su mediatriz). La solución es, por el caso anterior, $\mathbf{x}_{0}=\ell \cap \overline{\mathbf{p q}_{0}}$.

Pero observa cómo además de que el ángulo $\alpha$ con el que llega el bombero a $\mathcal{l}$ es igual al ángulo de «de reflexión» con el que sale corriendo al fuego (ya con la cubeta llena), e igual al ángulo con el que seguiría su trayecto al fuego virtual; y que esta propiedad determina el punto de mínimo recorrido $\mathbf{x}_{0}$; es fácil convencerse de que para cualquier otro punto de $\mathcal{l}$ los ángulos de llegada y de salida son distintos. Si los bomberos fueran fotones que salen de $\mathbf{p}$ y $\mathcal{l}$ es un espejo, el único que llega a $\mathbf{q}$ es el fotón de recorrido mínimo.

Para aterrizar nuestro problema del bombero al caso de las elipses, considera ahora que $\mathbf{p}$ y $\mathbf{q}$ son los focos de una elipse y $\mathbf{x}_{0}$ un punto en ella. Sea $\mathcal{l}$ la recta que pasa por $\mathbf{x}_{0}$ y bisecta (por fuera) los segmentos de $\mathbf{p}$ y $\mathbf{q}$ a $\mathbf{x}_{0}$. Por construcción, y considerando la solución al problema del bombero, cualquier otro punto $\mathbf{x} \in \mathcal{l}$ tiene mayor suma de distancias a los focos y por tanto está fuera de la elipse. Esto demuestra que $\mathcal{l}$ es la tangente a la elipse en el punto $\mathbf{x}_{0}$, y por lo tanto, queda demostrada la propiedad focal de la elipse.

Antes de dar por terminada esta sección, te invito a que experimentes con el siguiente recuadro interactivo de GeoGebra: en él podrás ver cómo funciona esta propiedad focal de las elipses para elipses de diferentes tamaños y posiciones. ¿Puedes ver qué pasa con esta propiedad para el caso degenerado de la elipse? ¿Qué pasa si los focos son el mismo punto?

Propiedades métricas de la elipse

Tocaremos brevemente el tema de las propiedades métricas de la elipse; lo haremos sólo superficialmente pues una demostración formal se escapa de lo que planeamos cubrir en este curso. Si no estás familiarizado con los términos que aparecen en esta sección, no te preocupes, enfócate en entender cómo se llegó a los resultados y tenlos como referencia por si los ocupas en algún otro curso un poco más enfocado a las aplicaciones de las elipses.

La primera de sus propiedades métricas que vamos a abordar es el área de la elipse: considera que esta propiedad se refiere a la elipse con ecuación:

\begin{equation}
\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1
\end{equation}

La ecuación anterior, puede ser reescrita como

\begin{equation}
y(x)=b \sqrt{1-x^{2} / a^{2}}.
\end{equation}

Para toda $x \in[-a, a]$, esta curva es la mitad superior de la elipse. Entonces, el doble de la integral $y(x)$ sobre le intervalo $[-a, a]$ será el área de la elipse:

\begin{equation}
\begin{aligned}
A_{\text {ellipse }} &=\int_{-a}^{a} 2 b \sqrt{1-\frac{x^{2}}{a^{2}}} d x \
&=\frac{b}{a} \int_{-a}^{a} 2 \sqrt{a^{2}-x^{2}} d x .
\end{aligned}
\end{equation}

La segunda integral es el área del círculo con radio $a$, la cual vale $\pi a^{2}$. Entonces,

\begin{equation}
A_{\text {ellipse }}=\frac{b}{a} \pi a^{2}=\pi a b.
\end{equation}

La circunferencia de una elipse, es decir, el análogo del perímetro para las circunferencias presenta un problema: ¡es bastante difícil de obtener! pues hay que calcular una integral que no puede ser evaluada en términos de funciones elementales. De momento, pondremos sólo la fórmula, pues es un resultado bastante útil. Si te interesa ver cómo se llegó a este resultado, puedes revisar la siguiente fuente.

\begin{equation}
C \approx \pi[3(a+b)-\sqrt{(3 a+b)(a+3 b)}]=\pi\left[3(a+b)-\sqrt{10 a b+3\left(a^{2}+b^{2}\right)}\right]
\end{equation}

La última de estas propiedades métricas que veremos superficialmente será la curvatura; esto te podría resultar especialmente útil si por ejemplo quisieras calcular la curvatura de la trayectoria para una partícula que se mueve trazando una parábola. La curvatura para una elipse con ecuación canónica $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ será:

\begin{equation}
\kappa=\frac{1}{a^{2} b^{2}}\left(\frac{x^{2}}{a^{4}}+\frac{y^{2}}{b^{4}}\right)^{-\frac{3}{2}}.
\end{equation}

Más adelante…

En esta entrada y en la anterior profundizamos en las propiedades de la elipse. Seguiremos nuestro estudio de las secciones cónicas definiendo a las hipérbolas, veremos que a pesar de ser figuras muy distintas, guardan una relación estrecha con los círculos y las elipses. Al igual que para las figuras que hemos visto hasta el momento, entenderemos cómo llegar a una expresión analítica y aprenderemos a leer toda la información geométrica que contiene.

Tarea moral

  • Demuestra la propiedad focal de la elipse sin resolver el problema del bombero. Sugerencia. toma el círculo de radio $2\mathbf{a}$ centrado en un foco $\mathbf{p}$ y luego ve que para los puntos de este círculo, su mediatriz con $\mathbf{q}$ es tangente a una elipse.
  • Halle la ecuación de la elipse con centro en el origen que satisface las condiciones dadas; construya la curva:
  1. La longitud del eje mayor es $10$ y l del eje menor $8$; los focos están sobre el eje $y$.
  2. El eje menor mide $10$ y un vértice es $(6,0)$.
  3. El lado recto mide $\frac{32}{7}$ y uno de los extremos del eje menor está en $(4,0)$.
  • Obten el área de la elipse que tiene la siguiente ecuación:

$$
\frac{x^{2}}{16}+\frac{y^{2}}{25}=1
$$

  • Obtenga una aproximación del perímetro de la siguiente elipse:

$$
\frac{x^{2}}{25}+\frac{y^{2}}{225}=1
$$

  • Obtenga la curvatura de la siguiente elipse en el punto $(3,2)$:

$$
\frac{x^{2}}{16}+\frac{y^{2}}{9}=1
$$

Entradas relacionadas