Archivo de la etiqueta: secciones cónicas

Geometría Analítica I: Parábolas

Por Héctor Morales

Deja un comentario

Introducción

La última de las secciones cónicas que abordaremos en esta unidad es la parábola. De las tres cónicas que hemos revisado, probablemente es la que conoces mejor de forma intuitiva: ya sea que hayas escuchado sobre «las antenas parabólicas», «los espejos parabólicos» o «el tiro parabólico», estamos tan familiarizados con las propiedades de las parábolas que en esta unidad, más allá de introducir la figura como algo nuevo, nos encargaremos de formalizar sus propiedades .

¿Qué hace que la imagen mental que tenemos de las parábolas corresponda tan bien a la figura que podemos obtener a partir de una definición formal? Podrás recordar de tus clases de mecánica de la preparatoria que la Tierra ejerce una fuerza sobre cada uno de los objetos sobre su superficie que les da una aceleración constante, usualmente denotada por la letra $g$. Entonces, la trayectoria de un objeto, asumiendo condiciones ideales, que se mueve con velocidad constante en el eje horizontal y con movimiento acelerado en el eje vertical está descrita por:

\begin{equation}
\begin{aligned}
&x(t)=v_{0} t \cos (\theta) \
&y(t)=v_{0} t \sin (\theta)-\frac{1}{2} g t^{2}
\end{aligned}
\end{equation}

No es necesario que en este momento entiendas totalmente de dónde vienen estas dos ecuaciones; por el momento quédate con la idea de que es un buen modelo matemático de un proyectil en la Tierra que se mueve sobre un plano; es decir, estas dos ecuaciones describen bastante bien el movimiento de una bala de cañón al ser disparada, una pelota de fútbol después de ser pateada, etc. Resulta que estas dos ecuaciones son la parametrización de una parábola, de modo que una parábola es una descripción bastante buena de la trayectoria de un objeto cuando «lo lanzamos». Entonces, aunque estemos por abordar por primera vez el estudio formal de la parábola, verás que tanto sus elementos, como sus propiedades te resultarán bastante familiares.

240
La trayectoria de un objeto que tiene un movimiento rectilineo y uniforme en $x$ y un movimiento acelerado en $y$ describe una parábola.

Sin más preámbulo, pasaremos a la definición de una parábola: además de la definición como conjunto de puntos, obtendremos una ecuación canónica al igual que como lo hicimos para la elipse y la hipérbola y nos familiarizaremos con sus elementos más importantes. Dejaremos la descripción detallada de todos sus elementos y la exposición de sus propiedades para la siguiente entrada.

Definición de Parábola

Una parábola es el lugar geométrico de los puntos que equidistan de un punto $\mathbf{p}$ (llamado su foco) y una recta $\ell$, llamada su directriz, donde $\mathbf{p} \notin \ell$. Es decir, está definida por la ecuación

\begin{equation}
\mathrm{d}(\boldsymbol{x}, \boldsymbol{p})=\mathrm{d}(\boldsymbol{x}, \ell).
\end{equation}

En el siguiente recuadro interactivo de GeoGebra juega un poco con esta definición. Observa cómo una parábola, a primera vista, podría parecerte una elipse «cortada», pero date cuenta que es una curva que se dibuja a partir de una condición muy específica que se impone a una distancia entre la recta directriz y el foco ¿Puedes encontrar los casos degenerados de la parábola?¿Qué pasa si haces $p=0$?

Tomando un ejemplo sencillo con el foco en el eje $\mathbf{y}$, la directriz paralela al eje $\mathbf{x}$, y que además pase por el origen. Tenemos entonces $\mathbf{p}=(0, \mathrm{c})$, donde $\mathrm{c}>0$ digamos, y $\ell: \mathrm{y}=-\mathrm{c}$; de tal manera que la parábola queda determinada por la ecuación

\begin{equation}
\sqrt{x^{2}+(y-c)^{2}}=|y+c|.
\end{equation}

Como te puedes dar cuenta, lo único que hicimos fue aplicar la definición de norma en $\mathbb{R}^{2}$ tal como la estudiamos en la primera unidad. Como ambos lados de la ecuación son positivos, ésta es equivalente a la igualdad de sus cuadrados que da

\begin{equation}
\begin{aligned}
x^{2}+y^{2}-2 c y+c^{2} &=y^{2}+2 c y+c^{2} \
x^{2} &=4 c y.
\end{aligned}
\end{equation}

De tal manera que la gráfica de la función $x^{2}$ ($y=x^{2}$) es una parábola con foco $(0,\frac{1}{4})$ y directriz $y=-\frac{1}{4}$. Veremos ahora que cualquier parábola cumple la propiedad de «ser gráfica de una función» respecto de su directriz.

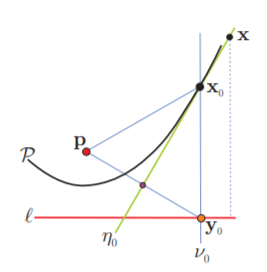
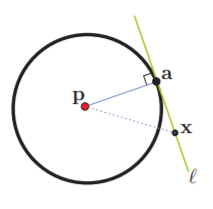
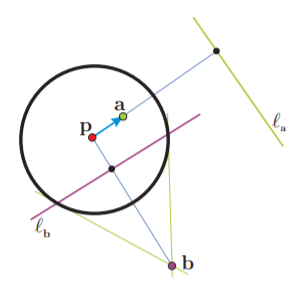
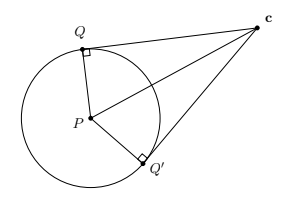
Sea $\mathcal{P}$ la parábola con foco p y directriz $\ell$ (donde $\mathbf{p} \notin \ell)$. Dado un punto $\mathbf{y}_{0} \in \ell$, es claro que los puntos del plano cuya distancia a $\ell$ coincide con (o se mide por) su distancia a $\mathbf{y}_{0}$ son precisamente los de la normal a $\ell$ que pasa por $\mathbf{y}_{0}$, llamémosla $v_{0} .$ Ver la figura.

Cualquier parábola cumple la propiedad de ser gráfica de una función respecto a su directriz.

Por otro lado, la mediatriz entre $\mathbf{y}_{0}$ y $\mathbf{p}$, llamémosla $\eta_{0}$, consta de los puntos cuyas distancias a $\mathbf{p}$ y $\mathbf{y}_{0}$ coinciden. Por lo tanto, la intersección de $\eta_{0}$ y $v_{0}$ está en la parábola $\mathcal{P}$, es decir $\boldsymbol{x}_{0}=v_{0} \cap \eta_{0} \in \mathcal{P}$ pues $\mathrm{d}\left(\boldsymbol{x}_{0}, \ell\right)=\mathrm{d}\left(\boldsymbol{x}_{0}, \mathbf{y}_{0}\right)=\mathrm{d}\left(\boldsymbol{x}_{0}, \boldsymbol{p}\right)$. Pero además $\mathbf{x}_{0}$ es el único punto en la normal $v_{0}$ que está en $\mathcal{P}$. Ésta es «la propiedad de la gráfica» a la que nos referíamos.

Podemos concluir aún más: que la mediatriz $\eta_{0}$ es la tangente a $\mathcal{P}$ en $\mathbf{x}_{0}$. Pues para cualquier otro punto $x \in \eta_{0}$ se tiene que su distancia a $\ell$ es menor que su distancia a $\mathbf{y}_{0}$ que es su distancia a $\mathbf{p}\left(\mathrm{d}(\mathbf{x}, \ell)<\mathrm{d}\left(\mathbf{x}, \mathbf{y}_{0}\right)=\mathrm{d}(\mathbf{x}, \mathbf{p})\right)$, y entonces $x \notin \mathcal{P}$. De hecho, la parábola $\mathcal{P}$ parte el plano en dos pedazos, los puntos más cerca de $\mathbf{p}$ que de $\ell$ (lo de adentro, digamos, definidos por la desigualdad $d(\mathbf{x}, \mathbf{p}) \leq d(\mathbf{x}, \ell)$) y los que están más cerca de $\ell$ que de $\mathbb{p}$ (lo de afuera, dado por $d(\mathbf{x}, \ell) \leq d(\mathbf{x}, \mathbf{p})$ en donde está $\eta_{0}$), que comparten la frontera donde estas distancias coinciden (la parábola $\mathcal{P}$). Así que $\eta_{0}$ pasa tangente a $\mathcal{P}$ en $\mathbf{x}_{0}$, pues $\mathbf{x}_{0} \in \eta_{0} \cap \mathcal{P}$ y además $\eta_{0}$ se queda de un lado de $\mathcal{P}$.

En el siguiente recuadro interactivo de GeoGebra familiarizate con la expresión analítica de la parábola y nota una cosa muy importante: ¿qué pasa cuando, contrario al caso «sencillo» que vimos en esta entrada, el vértice de la parábola está fuera del origen? Nota cómo una traslación de nuestro caso sencillo introduce un término lineal en la ecuación de la parábola y date cuenta qué papel juega cada uno de los coeficientes modificando la forma de la parábola.

Más adelante…

En esta entrada iniciamos nuestro estudio de las parábolas: a partir de su definición como el conjunto de puntos que equidistan de una recta y un punto construimos la curva y nos familiarizamos con su expresión analítica. Así como lo hicimos para las cónicas anteriores, le dedicaremos la siguiente sección a estudiar sus propiedades y a nombrar cada uno de sus elementos; posteriormente, haremos algunos ejercicios para tener práctica leyendo la información geométrica que contiene la ecuación de la parábola.

Tarea moral

  • Construye la curva y da el dominio y codominio de las siguientes curvas: $y^{2}=16x$, $x^{2}=-16y$, $x^{2}=10y$, $y^{2}=7x$, $3x^{2}+5y=0$, $5x^{2}-2y=0$, $y^{2}+6x=0$, $x^{2}=11y$.
  • A partir de la definición de parábola, encuentre la ecuación de la parábola de foco $(0,-5)$ y directriz $y=3$.
  • Cuáles son los puntos de intersección de la línea que tiene la ecuación $2x+3y=7$ y la parábola con ecuación $y=-2x^{2}+2x+5$

Entradas relacionadas

  • Ir a Geometría Analítica I
  • Entrada anterior del curso: Problemas con hipérbolas
  • Siguiente entrada del curso: Propiedades de parábolas

Geometría Analítica I: Hipérbolas

Por Héctor Morales

2 respuestas

Introducción

En las entradas anteriores definimos un círculo y establecimos algunas de sus propiedades; esto nos llevó naturalmente a estudiar las elipses: una de las tres figuras geométricas que podemos observar al hacer «cortes» en diferentes secciones de un cono. Al igual que para las circunferencias, discutimos detalladamente los elementos que componen a una elipse, estudiamos sus propiedades y hablamos, de manera general, sobre las aplicaciones que pueden tener en diferentes campos como en física o ingeniería.

La segunda de las secciones cónicas que vamos a estudiar en esta unidad son las hipérbolas. Decimos que será la segunda, pues recordemos que una circunferencia es una elipse; una en la cual el eje mayor y el eje menor tienen el mismo tamaño. Al igual que para las elipses, la motivación para estudiar analíticamente las hipérbolas, nace de observar fenómenos naturales. Probablemente ya has visto antes una hipérbola, y tal vez tengas dificultades pensando en qué momento de tu vida cotidiana has visto la misma figura; para motivarnos a estudiar la hipérbola hablaremos de una de sus aplicaciones: sistemas de navegación.

En el sistema de navegación LORAN se utiliza la propiedad de la definición de la hipérbola que nos dice que «la diferencia de las distancias de los puntos de la hipérbola a los focos es constante»; es este tipo de sistema de navegación, una estación radioemisora maestra y otra estación radioemisora secundaria emiten señales que pueden ser recibidas por un barco en altamar (ver figura). Puesto que un barco que monitoreé las dos señales estará probablemente más cerca de una de las estaciones, habrá una diferencia entra las distancias recorridas por las dos señales, lo cual se registrará como una pequeña diferencia de tiempo entre las señales. En tanto la diferencia de tiempo permanezca constante, la diferencia entre las dos distancias también será constante. Si el barco sigue la trayectoria correspondiente a una diferencia fija de tiempo, esta trayectoria será una hipérbola cuyos focos están localizados en las posiciones de las dos estaciones.

Esquema del sistema de navegación LORAN: una de las aplicaciones de la hipérbola a la ingeniería.

Como pudimos ver, las hipérbolas son extensamente usadas para resolver problemas importantes; entonces es importante encontrar una expresión analítica que nos permita extraer toda su información geométrica. Esta expresión analítica, saldrá naturalmente cuando veamos cómo podemos definir una hipérbola.

Definición de Hipérbola

Ya que hemos discutido brevemente por qué queremos tener una expresión analítica de la hipérbola, pasemos a definirla de una forma más formal. La hipérbola está definida como el lugar geométrico de los puntos cuya diferencia (em valor absoluto) de sus distancias a dos puntos fijos $\mathbf{p}$ y $\mathbf{q}$, llamados focos, es constante. Entonces, una hipérbola $\mathcal{H}$ está definida por la ecuación

\begin{equation}
|d(\mathbf{x}, \mathbf{p})-d(\mathbf{x}, \mathbf{q})|=2 a.
\end{equation}

donde $a>0$, y además $2 a<d(\mathbf{p}, \mathbf{q})=: 2 c$. A continuación puedes ver la figura que define a este conjunto de puntos, sometidos a la condición de la definición. Como ya te habrás dado cuenta, la definición de la hipérbola es muy parecida a la definición de la elipse. A lo largo de esta entrada y de la siguiente veremos que a pesar de ser figuras muy distintas comparten varios elementos y características.

Hipérbola como conjunto de puntos que cumplen la ecuación 1.

Así como hicimos para la elipse, queremos llegar a una ecuación canónica que sea «sencilla» y que nos permite leer toda la información geométrica de la figura. Si tomamos como focos a $\mathbf{p}=(c, 0)$ y a $\mathbf{q}=(-c, 0)$; ver la siguiente figura, esta ecuación toma la forma

\begin{equation}
\left|\sqrt{(x-c)^{2}+y^{2}}-\sqrt{(x+c)^{2}+y^{2}}\right|=2 a.
\end{equation}

y veremos a continuación que es equivalente a

\begin{equation}
\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1
\end{equation}

donde $b>0$ está definida por $a^{2}+b^{2}=c^{2}$. A esta última ecuación se le llama la ecuación canónica de la hipérbola.

Hipérbola vertical centrada en el orgien

Como las ecuaciones anteriores involucraban un valor absoluto, entonces se tienen dos posibilidad que corresponden a las dos ramas de la hipérbola. En una de ellas la distancia a uno de los focos es mayor y en la otra se invierten los papeles. De la ecuación $2$ se tienen dos posibilidades:

\begin{equation}
\sqrt{(x-c)^{2}+y^{2}}=2 a+\sqrt{(x+c)^{2}+y^{2}}
\end{equation}

\begin{equation}
\sqrt{(x+c)^{2}+y^{2}}=2 a+\sqrt{(x-c)^{2}+y^{2}}
\end{equation}

la primera corresponde a la rama donde $x<0$ y la segunda a $x>0$. Como hicimos en el caso de la elipse vamos a llegar a la ecuación canónica desarrollando todos los pasos. Partiendo de la definición y de la fórmula de distancia:

$$
d_{2}-d_{1}=\sqrt{(x-(-c))^{2}+(y-0)^{2}}-\sqrt{(x-c)^{2}+(y-0)^{2}}=2 a.
$$

Ahora, simplificando la expresión:

$$
\sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}=2 a.
$$

Si movemos uno de los radicales al lado opuesto:

$$
\sqrt{(x+c)^{2}+y^{2}}=2 a+\sqrt{(x-c)^{2}+y^{2}}.
$$

Luego, elevando al cuadrado ambos lados:

$$
(x+c)^{2}+y^{2}=\left(2 a+\sqrt{(x-c)^{2}+y^{2}}\right)^{2}.
$$

Después, expandimos los cuadrados:

$$
x^{2}+2 c x+c^{2}+y^{2}=4 a^{2}+4 a \sqrt{(x-c)^{2}+y^{2}}+(x-c)^{2}+y^{2}.
$$

Ahora, si expandimos el cuadrado restante:

$$
x^{2}+2 c x+c^{2}+y^{2}=4 a^{2}+4 a \sqrt{(x-c)^{2}+y^{2}}+x^{2}-2 c x+c^{2}+y^{2}.
$$

En la ecuación anterior combinamos los términos y separamos al radical:

$$
2 c x=4 a^{2}+4 a \sqrt{(x-c)^{2}+y^{2}}-2 c x
$$

$$
4 c x-4 a^{2}=4 a \sqrt{(x-c)^{2}+y^{2}}
$$

Dividiendo entre $4$ y elevando al cuadrado ambos lados:

$$
c x-a^{2}=a \sqrt{(x-c)^{2}+y^{2}}
$$

$$
\left(c x-a^{2}\right)^{2}=a^{2}\left[\sqrt{(x-c)^{2}+y^{2}}\right]^{2}
$$

Finalmente, expandiendo de nuevo el cuadrado y agrupando términos semejantes llegamos a que,

$$
c^{2} x^{2}-2 a^{2} c x+a^{4}=a^{2}\left(x^{2}-2 c x+c^{2}+y^{2}\right)
$$

$$
c^{2} x^{2}-2 a^{2} c x+a^{4}=a^{2} x^{2}-2 a^{2} c x+a^{2} c^{2}+a^{2} y^{2}
$$

$$
a^{4}+c^{2} x^{2}=a^{2} x^{2}+a^{2} c^{2}+a^{2} y^{2}
$$

$$
c^{2} x^{2}-a^{2} x^{2}-a^{2} y^{2}=a^{2} c^{2}-a^{4}
$$

$$
x^{2}\left(c^{2}-a^{2}\right)-a^{2} y^{2}=a^{2}\left(c^{2}-a^{2}\right)
$$

$$
x^{2} b^{2}-a^{2} y^{2}=a^{2} b^{2}
$$

$$
\frac{x^{2} b^{2}}{a^{2} b^{2}}-\frac{a^{2} y^{2}}{a^{2} b^{2}}=\frac{a^{2} b^{2}}{a^{2} b^{2}}
$$

$$
\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1
$$

Como ya mencionamos, esta última ecuación es la ecuación canónica de la hipérbola.

Como conclusión de este primer acercamiento a las hipérbolas, prueba el siguiente recuadro interactivo de GeoGebra. Identifica los elementos básicos de la hipérbola y dibuja algunas variando parámetros. Observa cómo variando los diferentes elementos de la ecuación cambia la forma de la hipérbola.

Más adelante…

En esta entrada nos familiarizamos con la idea elemental de la hipérbola. Todavía nos queda mucho que estudiar acerca de esta sección cónica. En la siguiente entrada nombraremos cada uno de sus elementos, presentaremos algunas propiedades métricas y discutiremos su propiedad focal. Al igual que como hicimos para las elipses, tocaremos brevemente el tema de excentricidad y luego realizaremos algunos ejercicios sobre hipérbolas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • A partir de la definición de hipérbola, determine la ecuación de la que tiene sus focos en $(6,0)$ y $(-6,0)$ si $2a=8$.
  • A partir de su definición, muestre que la ecuación de una hipérbola cuyos focos están en $F_{1}(a,a)$ y $F_{2}(-a,a)$ y para la cual se cumple que $$|\mathbf{PF}_{1}| – |\mathbf{PF}_{2}| = \pm 2a$$ para todo punto $P(x,y)$ de la curva es $xy=\frac{1}{2}a^{2}$.
  • Dada la siguiente ecuación, determina si se trata de una hipérbola. En caso de que sí, escríbela en su forma canónica:

$$
25 x^{2}-16 y^{2}=400
$$

Entradas relacionadas

Geometría Analítica I: Elipses

Por Héctor Morales

Deja un comentario

Introducción

Probablemente recuerdas un ejercicio muy común que se hace en las primarias en México: cuando se enseña a los niños sobre el Sistema Solar, comúnmente se les pide hacer una maqueta con esferas de unicel. Si alguna vez hiciste este ejercicio, tal vez recuerdas que las supuestas trayectorias de estos planetas en nuestra maqueta se distribuían como una serie de círculos concéntricos que iban aumentando en tamaño, con el «Sol» en su centro.

Por otro lado, si te interesa la astronomía, seguramente estás familiarizado con las Leyes de Kepler, una de ellas nos dice «Todos los planetas se mueven alrededor del Sol siguiendo órbitas elípticas. El Sol está en uno de los focos de la elipse.» Entonces, resulta que las trayectorias de los planetas no son círculos, si no «elipses», y todo este tiempo nuestra maqueta estuvo mal (¿o no tanto?). Si las elipses son tan importantes como para permitirnos visualizar el movimiento de un planeta, podrás darte cuenta de la importancia de tener una descripción analítica de esta figura; y por qué nos interesa estudiarla a fondo.

En esta entrada haremos justo eso: discutiremos desde cómo trazar una elipse en papel, pasando por su definición formal hasta obtener una expresión analítica que nos permitirá leer toda la información geométrica de la figura.

Dibujando y definiendo una elipse

Si alguna vez has visto un arbusto con forma elíptica (algo así como un círculo achatado), tal vez te has preguntado ¿cómo obtuvo esa forma? El método más sencillo para dibujar una elipse consiste en fijar dos tachuelas a una superficie de papel, amarrar holgadamente un hilo entre ellas y luego, manteniendo la tensión del hilo, girar el lápiz. Si intentas por tu cuenta este procedimiento, podrás ver que obtuviste una figura como la siguiente:

Elipse dibujada con el «Método del
Jardinero»

Esta figura es una de las secciones cónicas que estudiaremos durante el curso; como ya lo sugiere el método que usamos para dibujarla («Método del jardinero»), su definición tiene tres elementos importantes: dos puntos fijos y un tercer punto que se mueve manteniendo una suma de distancias totales constante. Sin más preámbulos, abordemos la definición de elipse con la que trabajaremos.

Definición. Las elipses son el lugar geométrico de los puntos cuya suma de distancias a dos puntos fijos llamados focos es constante. De tal manera que una elipse $\mathcal{E}$ queda totalmente determinada por la ecuación:

\begin{equation}
d(\mathbf{x}, \mathbf{p})+d(\mathbf{x}, \mathbf{q})=2 a
\end{equation}

donde $\mathbf{p}$ y $\mathbf{q}$ son los focos y $a$ es una constante positiva, llamada semieje mayor, tal que 2 a>d(\mathbf{p}, \mathbf{q}).

Un pregunta natural que te puede surgir al considerar esta definición es el por qué incluir el coeficiente $2$. La respuesta es que se incluye para que quede claro que si los focos coinciden, $\mathbf{p}=\mathbf{q}$, entonces se obtiene un círculo de radio $a$ y centro en el foco; dicho de una forma más explícita ¡Resulta que los círculos son un tipo especial de elipse!

Antes de continuar te invito a que manipules el siguiente recuadro interactivo de GeoGebra para familiarizarte con las elipses. Observa cómo cambiar el eje mayor y el eje menor la redefine totalmente; además cómo la figura es totalmente dependiente de la posición de sus focos.

Ahora, debes considerar que esta ecuación, poniéndole coordenadas a los focos, incluye raíces cuadradas por las distancias, lo cual la hace ver un poco intimidante. Veamos un caso especial que nos permitirá escribir a la ecuación de la elipse de una forma más agradable. Con este desarrollo, queremos llegar a la ecuación canónica de la elipse.

Supongamos que el centro de la elípse $\mathcal{E}$, i.e., el punto medio entre los focos, está en el origen y que además los focos están en el eje $x .$ Entonces tenemos que $\mathbf{p}=(c, 0)$ y $\mathbf{q}=(-c, 0)$ para alguna $c$ tal que $0<c<a$ (donde ya suponemos que la elipse no es un círculo al pedir $0<c$ ). Es fácil ver que entonces la intersección de $\mathcal{E}$ con el eje $x$ consiste de los puntos $(a, 0) \mathrm{y}$ $(-a, 0)$, pues la ecuación $(2.8)$ para puntos $(x, 0)$ es

\begin{equation}
|x-c|+|x+c|=2 a
\end{equation}

que sólo tiene las soluciones $x=a$ y $x=-a$, y de aquí el nombre de «semieje mayor» para la constante $a$. Como el eje $y$ es ahora la mediatriz de los focos, en él, es decir en los puntos $(0, y)$, la ecuación se vuelve:

\begin{equation}
\sqrt{c^{2}+y^{2}}=a
\end{equation}

que tiene soluciones $y=\pm b$, donde $b>0$, llamado el semieje menor de la elipse $\mathcal{E}$. es tal que:

\begin{equation}
b^{2}=a^{2}-c^{2} .
\end{equation}

Puedes guiarte con la siguiente figura para entender el desarrollo que acabamos de hacer:

Semieje mayor y semieje menor de una elipse.

Ahora sí, consideremos la ecuación $(2.8)$, que $\operatorname{con} \mathrm{x}=(x, y) \mathrm{y}$ la definición de nuestros focos se expresa:

$$
\sqrt{(x-c)^{2}+y^{2}}+\sqrt{(x+c)^{2}+y^{2}}=2 a
$$

Si elevamos al cuadrado directamente a esta ecuación, en el lado izquierdo nos quedaría un incomodo término con raíces. Así que conviene pasar a una de las dos raíces al otro lado, para obtener

$$
\sqrt{(x-c)^{2}+y^{2}}=2 a-\sqrt{(x+c)^{2}+y^{2}}
$$

Elevando al cuadrado se tiene

$$
(x-c)^{2}+y^{2}=4 a^{2}-4 a \sqrt{(x+c)^{2}+y^{2}}+(x+c)^{2}+y^{2}
$$

$$
x^{2}-2 c x+c^{2}=4 a^{2}-4 a \sqrt{(x+c)^{2}+y^{2}}+x^{2}+2 c x+c^{2}
$$

$$
4 a \sqrt{(x+c)^{2}+y^{2}}=4 a^{2}+4 c x
$$

$$
a \sqrt{(x+c)^{2}+y^{2}}=a^{2}+c x
$$

Elevando de nuevo al cuadrado, nos deshacemos de la raíz, y después, agrupando términos, obtenemos

$$
a^{2}\left((x+c)^{2}+y^{2}\right)=a^{4}+2 a^{2} c x+c^{2} x^{2}
$$

$$
a^{2} x^{2}+2 a^{2} c x+a^{2} c^{2}+a^{2} y^{2}=a^{4}+2 a^{2} c x+c^{2} x^{2}
$$

$$
\left(a^{2}-c^{2}\right) x^{2}+a^{2} y^{2}=a^{2}\left(a^{2}-c^{2}\right)
$$

$$
b^{2} x^{2}+a^{2} y^{2}=a^{2} b^{2}
$$

que, dividiendo entre $a^{2} b^{2}$, se escribe finalmente como

\begin{equation}
\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1
\end{equation}

llamada la ecuación canónica de la elipse centrada en el origen.

Después de este largo desarrollo pudimos llegar a una ecuación sencilla que nos permite leer toda la información geométrica de la elipse: su centro y la magnitud de su semieje mayor y semieje menor. Observa cómo ahora podemos demostrar sencillamente una de las afirmaciones que hicimos en esta entrada: si en la ecuación canónica de la elipse centrada en el origen hacemos $a=b$, es decir, forzamos a que la figura tenga el semieje mayor y el semieje menor iguales obtenemos la ecuación $x^2+y^2=a^2$ que es la expresión analítica de una circunferencia centrada en el origen.

Con estas herramientas estamos listos para realizar algunos ejercicios. En el primero obtendremos la ecuación de la elipse a partir de la definición, y en el segundo veremos cómo podemos extraer toda la información geométrica de la elipse a partir de su ecuación.

Ejercicio. Encuentra la ecuación de la elipse con fonoces en $(0,3)$ y $(0,-3)$ para la cual la suma de las distancias del foco a cada uno de sus puntos es $6\sqrt{3}$.

Utilizando la definición propuesta al inicio de esta entrada, nuestra elipse será el conjunto de puntos que cumplen la condición:

$$
d(\mathbf{x}, \mathbf{p})+d(\mathbf{x}, \mathbf{q})=2 a
$$

Aplicando la fórmula de la distancia que utilizando en la primera unidad del curso y considerando el valor de la constante $2a$ tenemos que

$$
\sqrt{x^{2}+(y-3)^{2}}+\sqrt{x^{2}+(y+3)^{2}}=6 \sqrt{3}
$$

Esto, lo podemos reescribir como

$$
\sqrt{x^{2}+(y-3)^{2}}=6 \sqrt{3}-\sqrt{x^{2}+(y+3)^{2}}
$$

Si elevamos ambos lados al cuadrado, llegamos a que

$$
x^{2}+(y-3)^{2}=108-12 \sqrt{3} \sqrt{x^{2}+(y+3)^{2}}+x^{2}+(y+3)^{2}
$$

Si te das cuenta, podemos cancelar algunos términos; y en nuestro caso nos conviene dividir ambos lados de la ecuación anterior entre $12$.Si reducimos la expresión anterior, tenemos que

$$
\sqrt{3} \sqrt{x^{2}+(y+3)^{2}}=9+y
$$

Una vez más elevamos ambos lados al cuadrado y llegamos a que

$$
3 x^{2}+2 y^{2}=54
$$

Lo cual es lo mismo a

$$
\frac{x^{2}}{27}+\frac{y^{2}}{18}=1
$$

que es la ecuación de la elipse en su forma canónica.

Ejercicio. ¿Cuál es la ecuación canónica de la elipse que tiene como vértices a los puntos $(\pm 8,0)$ y como focos a $(\pm 5,0)$?

Los focos están en el eje $x$, entonces el eje mayor estará también sobre el eje $x$. Así, la ecuación tendrá esta forma

$$
\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1
$$

Como los vértices son $(\pm 8,0)$, entonces $a=8$ y $a^{2} = 64$. Y puesto que los focos son $(\pm 5,0)$, entonces $c=5$ y $c^2 = 25$. Ahora, sabemos que los focos y los vértices están relacionados por la siguiente ecuación $c^{2}=a^{2}-b^{2}$. Si resolvemos para $b^2$ tenemos que $b^2=39$. Por lo tanto, la ecuación canónica de esta elipse será:

$$
\frac{x^{2}}{64}+\frac{y^{2}}{39}=1
$$

Más adelante…

En esta entrada aprendimos lo básico sobre una elipse: su definición, sus elementos y la ecuación canónica que la representa. Nos falta hablar de sus propiedades focales y del concepto de excentricidad, estos términos serán el tema de la siguiente entrada. Una vez que hayamos concluido nuestro estudio de las elipses, empezaremos a hablar de hipérbolas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Dibuja la elipse $\frac{x^{2}}{36}+\frac{y^{2}}{4}=1$ en algún programa de computadora e identifica sus elementos. Sugerencia: puedes utilizar GeoGebra, Mathematica, Matlab, Python o GNU plot.
  • Considera la siguiente ecuación de elipse $9 x^{2}+4 y^{2}=36$; encuentra sus focos, su semieje mayor, su semieje menor y dibújala.
  • Encuentra el área de una elipse con semieje mayor $a$ y semieje menor $b$. Sugerencia: Considera la ecuación canónica de una elipse centrada en el origen, despeja para $x$ e integra sobre $x$ sólo un cuadrante; eligiendo correctamente los límites de integración. El resultado de la integral multiplícalo por $4$. Cuidado, la integral es trigonométrica.

Entradas relacionadas

Geometría Analítica I: Forma vectorial de círculos, tangentes y polares

Por Héctor Morales

Deja un comentario

Introducción

En la entrada anterior construimos un puente entre la intuición que tenemos de las circunferencias y el estudio formal que podemos hacer de ellas utilizando las herramientas de la geometría analítica. Ahora queremos ir más allá de las propiedades básicas del círculo, como lo son su centro y su radio, para abordar propiedades un poco más avanzadas; sus rectas tangentes y polares.

Veremos a lo largo de esta entrada cómo la ecuación vectorial de la circunferencia nos prueba su utilidad al abordar problemas geométricos tales como encontrar puntos de tangencia sobre una circunferencia, hacer demostraciones que involucren las secantes de un círculo, entre otros.

Líneas tangentes a un círculo

Antes de abordar el tema de las líneas tangentes a un círculo, mencionaremos brevemente un problema físico que nos puede motivar a estudiarlo. El problema de la polea consiste en encontrar la longitud de un cable que conecta a dos circunferencias de radio $r_1$ y $r_2$ que no se cruzan; cuyos centros están separados por una distancia $P$. Aunque sea un problema en apariencia sencillo su solución requiere de herramientas como líneas bitangentes, ángulos verticales y congruencia. Pese a que la su solución no es trivial, es un problema de ingeniería bastante importante, pues se usa en el diseño de aeroplanos, bicicletas, autos, etc. No escribiremos explícitamente la solución a este problema, por el momento sólo diremos que para resolverlo es fundamental utilizar el concepto de línea tangente.

Problema de la polea

Ahora que comentamos una motivación, empezaremos a discutir el concepto de línea tangente. Intuitivamente podemos pensar que las líneas tangentes son las que tocan a una circunferencia en uno solo de sus puntos. Esto tiene varias implicaciones; la primera de ellas es que podemos pensar en las tangentes como las normales a los radios (los segmentos del centro a sus puntos). Empezaremos proponiendo la definición de las líneas tangentes y haremos una discusión detallada de cada uno de los elementos de esta definición.

Definición. Si $\mathbf{a}$ es un punto del círculo $\mathcal{C}$ dado por la ecuación vectorial

\begin{equation}
(\boldsymbol{x}-\mathbf{p}) \cdot(\boldsymbol{x}-\mathbf{p})=\mathrm{r}^{2}
\end{equation}

entonces su línea tangente es la recta $\ell$ normal a $(\mathbf{a} – \mathbf{p})$ y que pasa por $\mathbf{a}$.

Esta definición tiene algunas implicaciones interesantes que para los elementos que la constituyen que vale la pena observar con detalle. La primera es que, puesto que $\mathbf{a}$ es el punto más cercano a $\mathbf{p}$ en esta recta, para cualquier otro punto $x \in \ell$ se tiene que $\mathrm{d}(\boldsymbol{x}, \mathbf{p})>\mathrm{r}$. Dicho de una forma más sencilla: cualquier otro punto que no sea el punto de tangencia estará alejado del centro del círculo una distancia mayor que el radio. Puedes observar la figura para convencerte de este hecho.

Línea tangete del círculo y punto de tangencia.

Continuando nuestra exploración de los elementos de la definición que acabamos de presentar, observa que el círculo $\mathcal{C}$ parte el plano en dos pedazos; el interior donde $\mathrm{d}(\boldsymbol{x}, \mathbf{p})<\mathrm{r}$, y el exterior donde $\mathrm{d}(\boldsymbol{x}, \mathbf{p})>\mathrm{r}$, de esta forma $\ell$ está contenida en el exterior salvo por el punto $a \in \mathcal{C}$.

Para obtener una expresión analítica de las líneas tangentes conviene recordar las herramientas vectoriales que fueron presentadas durante la primera unidad, te podrás dar cuenta que si utilizamos la forma de la ecuación normal de recta con los elementos de nuestra definición, podemos ver que la recta $\ell$ está dada por la ecuación

\begin{equation}
\boldsymbol{x} \cdot(\boldsymbol{a}-\mathbf{p})=\boldsymbol{a} \cdot(\boldsymbol{a}-\mathbf{p}),
\end{equation}

esta ecuación tiene una manera más interesante de escribirse; si restamos $\mathbf{p} \cdot(\mathbf{a}-\mathbf{p})$ a ambos lados, se obtiene:

$$
\mathbf{x} \cdot(\mathbf{a}-\mathbf{p})-\mathbf{p} \cdot(\mathbf{a}-\mathbf{p})=\mathbf{a} \cdot(\mathbf{a}-\mathbf{p})-\mathbf{p} \cdot(\mathbf{a}-\mathbf{p})
$$

$$
(\mathbf{x}-\mathbf{p}) \cdot(\mathbf{a}-\mathbf{p})=(\mathbf{a}-\mathbf{p}) \cdot(\mathbf{a}-\mathbf{p})
$$

$$
(\mathbf{x}-\mathbf{p}) \cdot(\mathbf{a}-\mathbf{p})=r^{2}
$$

Esta forma de escribir la ecuación será importante en la siguiente sección cuando abordemos las rectas polares, sin embargo, antes de pasar a la siguiente sección hagamos un ejemplo sobre cómo encontrar la tangente de una circunferencia.

Ejemplo. Supongamos que tenemos un círculo con centro en $(4,-3)$ y radio $5$. Encuentre la línea de tangencia que pasa por el punto $(4,2)$.

Primero tenemos que verificar que el punto está dentro de la circunferencia. Si escribimos la ecuación cartesiana de nuestro círculo

\begin{equation}
(x-4)^{2} + (x+3)^{2}=25
\end{equation}

y sustituimos el punto $(4,2)$. Podemos darnos cuenta que el punto sí está en la circunferencia. Como ya vimos que está sobre el círculo, sólo tenemos que sustituir en la expresión analítica de la línea tangente

\begin{equation}
\boldsymbol{x} \cdot(\boldsymbol{a}-\mathbf{p})=\boldsymbol{a} \cdot(\boldsymbol{a}-\mathbf{p})
\end{equation}

los valores del punto de tangencia y el centro de la circunferencia. Haciendo esto tenemos que:

\begin{equation}
\boldsymbol{x} \cdot ((4,2)-(4,-3)) =\boldsymbol{a} \cdot ((4,2)-(4,-3))
\end{equation}

Por lo tanto, la ecuación de la línea tangente será:

\begin{equation}
\boldsymbol{x} \cdot (0,5) =\boldsymbol{a} \cdot (0,5)
\end{equation}

Escrito en forma cartesiana, tenemos que la recta tangente a nuestra circunferencia a través de ese punto es $y=2$.

Como vimos en nuestro ejemplo, obtener la expresión analítica de la línea tangente a través de un punto es muy fácil si recordamos la definición vectorial. Para terminar esta sección utiliza el siguiente recuadro interactivo para explorar diferentes líneas tangentes de una circunferencia. Nota cómo el punto de tangencia siempre se encuentra en los «bordes» del círculo. ¿Podríamos generalizar vectorialmente el concepto de tangencia para puntos que no se encuentran sobre la circunferencia?

Líneas polares de un círculo

Para empezar nuestro estudio de las líneas polares de un círculo, recuerda el último desarrollo algebraico que hicimos en la sección anterior: ese en el cual sustituimos $\mathbf{a}$ en una de las instancias de $\mathbf{x}$ en la ecuación vectorial. Recuerda cómo en el caso de la línea tangente, consideramos que el punto $\mathbf{a}$ estaba sobre la circunferencia. Con esto en mente, estamos listos para dar una definición de línea polar.

Definición. Consideremos un punto $\mathbf{a}$ en el plano, diferente del centro $(\mathbf{a} \neq \mathbf{p})$, diremos que $\ell_{a}$ es la recta polar de $\mathbf{a}$ respecto al círculo $\mathcal{C}$ y definiremos $\ell_{a}$ como

\begin{equation}
\ell_{\mathbf{a}}: \quad(\boldsymbol{x}-\mathbf{p}) \cdot(\boldsymbol{a}-\mathbf{p})=\mathrm{r}^{2}
\end{equation}

De la definición, se sigue que cuando $\boldsymbol{a} \in \mathcal{C}$ su polar $\ell_{\mathbf{a}}$ es su tangente. Como te puedes dar cuenta, las líneas polares son algo así como una generalización de las líneas tangentes; estamos repitiendo los desarrollos algebraicos que utilizamos en la primera sección sin restringirnos a los puntos que están sobre la circunferencia. Nuestra definición de líneas polares tiene varias consecuencias interesantes; una de ellas es que si el punto $\mathbf{a}$ está en el interior del círculo, entonces $\ell_{a}$ no lo intersecta (está totalmente contenida en el exterior), y que si está en el exterior (el punto $\mathbf{b}$ en la siguiente figura), entonces lo corta, y además lo corta en los dos puntos de $\mathcal{C}$ a los cuales se pueden trazar tangentes.

Existen tres posibles casos, que el punto polar esté dentro de la circunferencia, fuera o que esté sobre ella. El último caso se exploró a detalle en la primera parte de esta entrada.

Vamos a demostrar los enunciados que presentamos en el párrafo anterior. Para esto, expresemos las ecuación $\ell_{a}$ en su forma normal; desarrollando [numero de ecuación de la definición] se obtiene:

\begin{equation}
\boldsymbol{x} \cdot(\boldsymbol{a}-\mathbf{p})=\mathrm{r}^{2}+\mathbf{p} \cdot(\boldsymbol{a}-\mathbf{p})
\end{equation}

Esto indica que $\ell_{a}$ es perpendicular al vector que va de $\mathbf{p}$ a $\mathbf{a}$. Ahora veamos cuál es su punto de intersección con la recta que pasa por $\mathbf{p}$ y $\mathbf{a}$. Parametricemos esta última recta con $\mathbf{p}$ de cero y $\mathbf{a}$ de uno (es decir como $\mathbf{p}+\mathbf{t}(\mathbf{a}-\mathbf{p})$) y podemos despejar $t$ al sustituir en la variable $\mathbf{x}$ de la ecuación anterior (o bien, esto se ve más directo al sustituir en la [numero de ecuación de la definición] ), para obtener

\begin{equation}
t=\frac{r^{2}}{(\mathbf{a}-\mathbf{p}) \cdot(\mathbf{a}-\mathbf{p})}=\frac{r^{2}}{d(\mathbf{p}, \mathbf{a})^{2}} .
\end{equation}

Entonces la distancia de $\mathbf{p}$ a $\ell_{a}$ es

\begin{equation}
\mathrm{d}\left(\mathbf{p}, \ell_{a}\right)=\mathrm{t} \mathrm{d}(\mathbf{p}, \mathbf{a})=\frac{\mathrm{r}^{2}}{\mathrm{~d}(\mathbf{p}, \mathbf{a})}=\left(\frac{\mathrm{r}}{\mathrm{d}(\mathbf{p}, \mathbf{a})}\right) \mathrm{r}
\end{equation}

y tenemos lo primero que queríamos probar: si $\mathrm{d}(\mathbf{p}, \boldsymbol{a})<\mathrm{r}$ entonces $\mathrm{d}\left(\mathbf{p}, \ell_{\mathbf{a}}\right)>\mathrm{r}$; y al revés, si $\mathrm{d}(\mathbf{p}, \mathbf{a})>\mathrm{r}$ entonces $\mathrm{d}\left(\mathbf{p}, \ell_{\mathbf{a}}\right)<\mathrm{r}$. Dicho de otra manera, si el punto $\mathbf{a}$ está muy cerca de $\mathbf{p}$, su polar está muy lejos, y al revés, sus distancias al centro $\mathbf{p}$ se comportan como inversos «alrededor de r».

Para demostrar la segunda de nuestras afirmaciones, supongamos ahora que $\mathrm{d}(\mathbf{p}, \mathbf{a})>\mathrm{r}$, y sea $\mathbf{c}$ un punto en $\ell_{a} \cap \mathcal{C}$ (que sabemos que existe pues $\ell_{a}$ pasa por el interior de $\mathcal{C}$). Puesto que $\mathbf{c} \in \ell_{\mathrm{a}}$, se cumple la ecuación

\begin{equation}
(\mathbf{c}-\mathbf{p}) \cdot(\mathbf{a}-\mathbf{p})=\mathbf{r}^{2}
\end{equation}

Pero entonces $\mathbf{a}$ cumple la ecuación de $\ell_{c}$ que es la tangente a $\mathcal{C}$ en $\mathbf{c}$; es decir, la línea de $\mathbf{a}$ a $\mathbf{c}$ es tangente al círculo. Este argumento, visto de una forma todavía más general nos dice que para cualesquiera dos puntos $\mathbf{a}$ y $\mathbf{b}$ (distintos de $\mathbf{p}$) se tiene que

\begin{equation}
a \in \ell_{b} \Leftrightarrow \mathbf{b} \in \ell_{a}
\end{equation}

Y los puntos del círculo son los únicos para los cuales se cumple que $\mathbf{a} \in \ell_{a}$. Puedes apoyarte en la siguiente figura para seguir el desarrollo anterior.

Date cuenta cómo a lo largo de este procedimiento sin querer aprendimos a calcular los puntos de tangencia a un círculo desde un punto exterior $\mathbf{a}$. A saber, de la ecuación lineal de su polar, $\ell_{a}$, se despeja alguna de las dos variables y se sustituye en la ecuación del círculo. Esto nos da una ecuación de segundo grado en la otra variable que se puede resolver, y nos da dos raíces. Sustituyéndolas de nuevo en la ecuación de la polar se obtiene el otro par de coordenadas.

Para dejar bien claro este procedimiento, hagamos un ejercicio sobre cómo encontrar los puntos de tangencia desde un punto fuera de la circunferencia.

Ejemplo. Supongamos que tenemos un círculo con centro en $(3,-1)$ y radio $2$, encontraremos los puntos de tangencia desde el punto $\mathbf{a}=(1,3)$.

Podemos iniciar de dos maneras diferentes: la primera es utilizando lo que aprendimos en la entrada anterior, escribiendo directamente la ecuación vectorial de la circunferencia. Si hacemos esto, encontraremos que la circunferencia tiene la siguiente expresión vectorial

\begin{equation}
((x, y)-(3,-1)) \cdot((x, y)-(3,-1))=4 .
\end{equation}

Otra alternativa sería primero escribir la ecuación cartesiana y luego desarrollarla para pasarla a su forma vectorial; de ambas maneras, lo importante es escribir a la circunferencia en su forma vectorial. Ahora, para conocer los puntos de tangencia desde $\mathbf{a}=(1,3)$ sustituimos en la forma alternativa de la ecuación de la tangente:

$$((x, y)-(3,-1)) \cdot((1,3)-(3,-1))=4$$
$$(x-3, y+1) \cdot(-2,4)=4$$
$$-2 x+4 y+10=4$$
$$x-2 y=3 .$$

De aquí, para encontrar $\ell_{a} \cap \mathcal{C}$, conviene sustituir $x=3+2 y$ en la ecuación original del círculo para obtener

\begin{equation}
\begin{aligned}
(3+2 y)^{2}+y^{2}-6(3+2 y)+2 y &=-6 \
5 y^{2}+2 y-3 &=0
\end{aligned}
\end{equation}

Las raíces de esta ecuación cuadrática se pueden obtener utilizando la fórmula general:

\begin{equation}
y=\frac{-2 \pm \sqrt{4+60}}{10}=\frac{-2 \pm 8}{10}
\end{equation}

que nos da los valores $y_{0}=-1$ y $y_{1}=\frac{3}{5}$. Y estos, al sustituir de nuevo la ecuación de la polar nos dan los puntos de tangencia de $\mathbf{a}$; que son $(1,-1)$ y $\frac{1}{5}(21,3)$. Puedes verificar que satisfacen la ecuación del círculo sustituyendo en la ecuación lineal de la polar, y que efectivamente sus tangentes pasan por $\mathbf{a}$.

Para finalizar esta entrada te invito a que experimentes un momento con el recuadro interactivo. Nota cómo las líneas polares se convierten en las líneas tangentes cuando haces que el punto $\mathbf{a}$ esté sobre la circunferencia.

Más adelante…

En esta entrada finalizamos nuestra discusión de las circunferencias; la primera de las secciones cónicas que abordamos en nuestro curso. En la siguiente entrada podrás ver una serie de ejercicios para familiarizarte con la manipulación algébrica o vectorial de los conceptos que hemos introducido hasta ahora. En las siguientes entradas continuaremos nuestro estudio de las secciones cónicas hablando de parábolas, hipérbolas y elipses. Veremos cómo no es tan fácil dar una ecuación vectorial para el resto de las secciones cónicas; esto lo entenderemos tan pronto como empecemos a hablar de parábolas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Encuentra los puntos de tangencia: al círculo $x^{2}-2 x+y^{2}-4 y=-3$ desde el punto $(-1,2)$. Sugerencia: puedes consultar el segundo ejercicio realizado en esta entrada.
  • Demuestra que si $\mathbf{c}$ es un punto exterior (al círculo $\mathcal{C}$ con centro $P$ ) entonces su recta a $P$ biseca sus dos tangentes a $\mathcal{C}$. Y además que las distancias a sus pies en $\mathcal{C}$ (es decir, a los puntos de tangencia) son iguales. Sugerencia: Puedes utilizar la siguiente figura para tu demostración y pensar en el teorema de Pitágoras y en el criterio de congruencia LLL.

Entradas relacionadas

Geometría Analítica I: Círculos

Por Héctor Morales

Deja un comentario

Introducción

En nuestra vida cotidiana podemos encontrar muchos ejemplos de circunferencias. Desde la forma de una rueda, hasta el contorno de una taza y por supuesto en muchos fenómenos físicos como la trayectoria de una partícula en un campo magnético o el movimiento de un satélite alrededor de un planeta. Esta familiaridad que tenemos con las circunferencias, hacen que ésta sea la sección cónica más fácil de reconocer, pues incluso sin estudios formales en geometría estamos familiarizados con sus propiedades.

En esta entrada del blog propondremos una definición formal para la circunferencia; partiendo de la definición de la circunferencia como lugar geométrico, llegaremos a la ecuación cartesiana con la que probablemente ya estés familiarizado. Abordaremos la ecuación vectorial del círculo y vamos a ver qué ventajas tiene sobre la ecuación cartesiana.

Ecuación cartesiana de circunferencia

Probablemente en algún curso previo de álgebra o de geometría te hayas encontrado con el círculo unitario $\mathbb{S}^{1}$, definido por la ecuación

\begin{equation}
x^{2}+y^{2}=1
\end{equation}

Para generalizar las nociones que tenemos del círculo unitario a una circunferencia arbitraria, consideremos ahora a cualquier otro círculo $\mathcal{C}$. Tiene un centro $\mathbf{p}=(h, k)$, un radio $r>0$ y es el lugar geométrico de los puntos cuya distancia a $\mathbf{p}$ es $r$. Es decir, $\mathcal{C}=\left\lbrace\mathbf{x} \in \mathbb{R}^{2} \mid d(\mathbf{x}, \mathbf{p})=r\right\rbrace$; o bien, $\mathcal{C}$ está definido por la ecuación

\begin{equation}
d(\mathbf{x}, \mathbf{p})=r.
\end{equation}

La información geométrica clave de una circunferencia son su centro y su radio. Ambos se pueden pensar en términos de sus coordenadas cartesianas, o bien como vectores.

Puesto que ambos lados de esta ecuación son positivos, es equivalente a la igualdad de sus cuadrados que en coordenadas cartesianas toma la forma

\begin{equation}
(x-h)^{2}+(y-k)^{2}=r^{2}
\end{equation}

Así, todos los círculos de $\mathbb{R}^{2}$ están determinados por una ecuación cuadrática en las variables $x$ y $y$. Cuando la ecuación tiene la forma anterior, podemos leer inmediatamente toda la información geométrica (el centro y el radio). Lamentable, la mayoría de las veces que nos encontremos con ecuaciones de circunferencias las encontraremos «disfrazadas» como

\begin{equation}
x^{2}+y^{2}-2 h x-2 k y=\left(r^{2}-h^{2}-k^{2}\right)
\end{equation}

Es fácil ver que esta forma de escribir la circunferencia se obtiene al desarrollar la primera expresión. Veamos un ejemplo de cómo pasar una ecuación de circunferencia a su forma reducida.

Ejemplo. Consideremos la ecuación

\begin{equation}
x^{2}+y^{2}-6 x+2 y=-6 \text { . }
\end{equation}

Tenemos que determinar si la ecuación anterior define un círculo, y en caso de que así sea, qué características tiene. Lo primero que tenemos que hacer es completar los cuadrados, sumando en ambos lados las constantes que faltan

\begin{equation}
(x^{2}-6 x+9)+(y^{2}+2 y+1) =-6+9+1 \rightarrow (x-3)^{2}+(y+1)^{2} =4
\end{equation}

Claramente si desarrollamos esta última ecuación obtenemos la original. Así, podemos concluir que la ecuación define al círculo con centro en $(3,-1)$ y radio $2$.

Para terminar esta sección, puedes utilizar la ventana interactiva de GeoGebra para familiarizarte con la ecuación cartesiana de la circunferencia. Varía el radio y el centro del círculo y observa cómo cambia la ecuación. Intenta hacer una circunferencia por cada uno de los cuadrantes del plano poniendo mucha atención cómo cambian los signos dentro de los sumandos. Prueba casos límite ¿qué pasa si el radio el cero? ¿Un punto es una circunferencia?

Ecuación vectorial de circunferencia

Si nuestra ecuación cartesiana de circunferencia ya nos permitía «leer» toda la información geométrica de un círculo completando cuadrados, te puede parecer superfluo proponer una definición vectorial de la circunferencia. La motivación que tenemos para hacer esto es que una definición vectorial, al no hacer referencia a las coordenadas, tiene sentido en cualquier dimensión. Esto quiere decir que a diferencia de la ecuación cartesiana que sólo nos sirve para $\mathbb{R}^{2}$, una ecuación vectorial nos permitirá definir esferas en $\mathbb{R}^{3}$ y en dimensiones mayores.

Sin más preámbulo, diremos que el círculo $C$ con centro $\mathbf{p}$ y radio $r$ está definido por la ecuación

\begin{equation}
(\mathbf{x}-\mathbf{p}) \cdot(\mathbf{x}-\mathbf{p})=r^{2}
\end{equation}

Si tienes dificultades entendiendo por qué se utilizó el producto punto, te ayudará recordar que en la primera unidad de nuestro curso definimos la distancia euclidiana entre dos vectores (o norma) como el producto punto (o producto interior) del vector consigo mismo. En nuestro caso, sólo partimos de la definición de circunferencia como el lugar geométrico de todos los puntos que equidistan de un mismo punto y aplicamos la definición vectorial de distancia.

La ecuación, que llamaremos ecuación vectorial del círculo, se puede también reescribir como

\begin{equation}
\mathbf{x} \cdot \mathbf{x}-2 \mathbf{p} \cdot \mathbf{x}+\mathbf{p} \cdot \mathbf{p}=r^{2}
\end{equation}

Veamos un ejemplo de la ecuación vectorial del círculo para familiarizarnos con ella.

Ejemplo. Considere la circunferencia con centro en $(3,1)$ y radio $2$. Encuentre su ecuación vectorial y su ecuación cartesiana. Demuestre que ambas ecuaciones son equivalentes.

Lo primero que tenemos que hacer es obtener la ecuación vectorial de la circunferencia. Utilizando la definición que acabamos de escribir en esta entrada, podemos ver que la ecuación que buscamos es

\begin{equation}
(\mathbf{x}-(3,1)) \cdot(\mathbf{x}-(3,1))= 4
\end{equation}

También utilizando la definición para la ecuación cartesiana

\begin{equation}
(x-3)^{2}+(y-1)^{2}=4
\end{equation}

Estas dos expresiones, son las ecuaciones que buscamos. Sólo nos falta demostrar su equivalencia. Recordando las propiedades del producto punto que introducimos en la unidad anterior

\begin{equation}
\begin{array}{l}
(\mathbf{x}-(3,1)) \cdot (\mathbf{x}-(3,1)) = 4 \\
((x,y)-(3,1)) \cdot ((x,y)-(3,1)) = 4 \\
(x-3,y-1) \cdot (x-3,y-1) = 4 \\
(x-3)^{2}+(y-1)^{2}=4
\end{array}
\end{equation}

¡Listo! Ya nos convencimos que la ecuación cartesiana y la ecuación vectorial son equivalentes cuando estamos trabajando en $\mathbb{R}^{2}$. Por el momento, conservemos la idea de que la ecuación vectorial es un poco más general y de ella se puede extraer mucha información geométrica interesante.

Para finalizar esta sección, utiliza el siguiente recuadro interactivo para familiarizarte con la ecuación vectorial del círculo. Manipula el centro y el radio para ver cómo se reescribe la ecuación y entiende muy bien cómo el producto punto es la operación clave de la definición. ¿Puedes encontrar los parámetros adecuados para hacer que en ambos interactivos tengamos círculos equivalentes con diferentes formas de escribir la ecuación?

Más adelante…

En esta entrada discutimos detalladamente las definiciones cartesianas y vectorial de la circunferencia, propusimos algunos ejemplos para familiarizarnos con estas expresiones y aprendimos a «leer» la información geométrica que guardan. Sin embargo, no hemos acabado nuestro estudio de las circunferencias. En las siguientes entradas abordaremos el tema de las rectas tangentes y polares y resolveremos algunos ejercicios relacionados a estas secciones cónicas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • ¿Cuáles de las siguientes ecuaciones son ecuaciones de un círculo? Y en su caso, ¿de cuál?

\begin{equation}
\begin{array}{l}
x^{2}-6 x+y^{2}-4 y=12 \\
x^{2}+4 x+y^{2}+2 y=11 \\
2 x^{2}+8 x+2 y^{2}-4 y=-8 \\
x^{2}-4 x+y^{2}-2 y=-6 \\
4 x^{2}+4 x+y^{2}-2 y=4
\end{array}
\end{equation}

  • ¿Cuál es el lugar geométrico de los centros de los círculos que pasan por dos puntos (distintos) $a$ y $b$? Sugerencia: considera la definición geométrica de la circunferencia como el conjunto de puntos que equidistan de un centro y ten en cuenta la definición vectorial de la mediatriz.
  • Sean $p$ y $q$ dos puntos distintos en el plano. ¿Para cuáles números reales $c$, se tiene que la siguiente ecuación define un círculo? En su caso, ¿cuál es el radio y dónde está su centro?

\begin{equation}
(\mathbf{x}-\mathbf{p}) \cdot(\mathbf{x}-\mathbf{q})=c
\end{equation}

  • Determinar la ecuación, centro y radio de la circunferencia que pasa por los tres puntos $A(-1,1)$, $B(3,5)$ y $C(5,-3)$. Sugerencia: considera que la ecuación buscada tiene la forma $x^2 + y^2 + Dx+ Ey + F= 0$, luego sustituye la información que te ofrece el problema para llegar a un sistema de ecuaciones y resuelvelo.

Entradas relacionadas