Introducción
Probablemente recuerdas un ejercicio muy común que se hace en las primarias en México: cuando se enseña a los niños sobre el Sistema Solar, comúnmente se les pide hacer una maqueta con esferas de unicel. Si alguna vez hiciste este ejercicio, tal vez recuerdas que las supuestas trayectorias de estos planetas en nuestra maqueta se distribuían como una serie de círculos concéntricos que iban aumentando en tamaño, con el «Sol» en su centro.
Por otro lado, si te interesa la astronomía, seguramente estás familiarizado con las Leyes de Kepler, una de ellas nos dice «Todos los planetas se mueven alrededor del Sol siguiendo órbitas elípticas. El Sol está en uno de los focos de la elipse.» Entonces, resulta que las trayectorias de los planetas no son círculos, si no «elipses», y todo este tiempo nuestra maqueta estuvo mal (¿o no tanto?). Si las elipses son tan importantes como para permitirnos visualizar el movimiento de un planeta, podrás darte cuenta de la importancia de tener una descripción analítica de esta figura; y por qué nos interesa estudiarla a fondo.
En esta entrada haremos justo eso: discutiremos desde cómo trazar una elipse en papel, pasando por su definición formal hasta obtener una expresión analítica que nos permitirá leer toda la información geométrica de la figura.
Dibujando y definiendo una elipse
Si alguna vez has visto un arbusto con forma elíptica (algo así como un círculo achatado), tal vez te has preguntado ¿cómo obtuvo esa forma? El método más sencillo para dibujar una elipse consiste en fijar dos tachuelas a una superficie de papel, amarrar holgadamente un hilo entre ellas y luego, manteniendo la tensión del hilo, girar el lápiz. Si intentas por tu cuenta este procedimiento, podrás ver que obtuviste una figura como la siguiente:
Esta figura es una de las secciones cónicas que estudiaremos durante el curso; como ya lo sugiere el método que usamos para dibujarla («Método del jardinero»), su definición tiene tres elementos importantes: dos puntos fijos y un tercer punto que se mueve manteniendo una suma de distancias totales constante. Sin más preámbulos, abordemos la definición de elipse con la que trabajaremos.
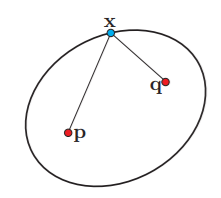
Definición. Las elipses son el lugar geométrico de los puntos cuya suma de distancias a dos puntos fijos llamados focos es constante. De tal manera que una elipse $\mathcal{E}$ queda totalmente determinada por la ecuación:
\begin{equation}
d(\mathbf{x}, \mathbf{p})+d(\mathbf{x}, \mathbf{q})=2 a
\end{equation}
donde $\mathbf{p}$ y $\mathbf{q}$ son los focos y $a$ es una constante positiva, llamada semieje mayor, tal que 2 a>d(\mathbf{p}, \mathbf{q}).
Un pregunta natural que te puede surgir al considerar esta definición es el por qué incluir el coeficiente $2$. La respuesta es que se incluye para que quede claro que si los focos coinciden, $\mathbf{p}=\mathbf{q}$, entonces se obtiene un círculo de radio $a$ y centro en el foco; dicho de una forma más explícita ¡Resulta que los círculos son un tipo especial de elipse!
Antes de continuar te invito a que manipules el siguiente recuadro interactivo de GeoGebra para familiarizarte con las elipses. Observa cómo cambiar el eje mayor y el eje menor la redefine totalmente; además cómo la figura es totalmente dependiente de la posición de sus focos.
Ahora, debes considerar que esta ecuación, poniéndole coordenadas a los focos, incluye raíces cuadradas por las distancias, lo cual la hace ver un poco intimidante. Veamos un caso especial que nos permitirá escribir a la ecuación de la elipse de una forma más agradable. Con este desarrollo, queremos llegar a la ecuación canónica de la elipse.
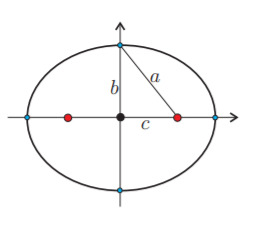
Supongamos que el centro de la elípse $\mathcal{E}$, i.e., el punto medio entre los focos, está en el origen y que además los focos están en el eje $x .$ Entonces tenemos que $\mathbf{p}=(c, 0)$ y $\mathbf{q}=(-c, 0)$ para alguna $c$ tal que $0<c<a$ (donde ya suponemos que la elipse no es un círculo al pedir $0<c$ ). Es fácil ver que entonces la intersección de $\mathcal{E}$ con el eje $x$ consiste de los puntos $(a, 0) \mathrm{y}$ $(-a, 0)$, pues la ecuación $(2.8)$ para puntos $(x, 0)$ es
\begin{equation}
|x-c|+|x+c|=2 a
\end{equation}
que sólo tiene las soluciones $x=a$ y $x=-a$, y de aquí el nombre de «semieje mayor» para la constante $a$. Como el eje $y$ es ahora la mediatriz de los focos, en él, es decir en los puntos $(0, y)$, la ecuación se vuelve:
\begin{equation}
\sqrt{c^{2}+y^{2}}=a
\end{equation}
que tiene soluciones $y=\pm b$, donde $b>0$, llamado el semieje menor de la elipse $\mathcal{E}$. es tal que:
\begin{equation}
b^{2}=a^{2}-c^{2} .
\end{equation}
Puedes guiarte con la siguiente figura para entender el desarrollo que acabamos de hacer:
Ahora sí, consideremos la ecuación $(2.8)$, que $\operatorname{con} \mathrm{x}=(x, y) \mathrm{y}$ la definición de nuestros focos se expresa:
$$
\sqrt{(x-c)^{2}+y^{2}}+\sqrt{(x+c)^{2}+y^{2}}=2 a
$$
Si elevamos al cuadrado directamente a esta ecuación, en el lado izquierdo nos quedaría un incomodo término con raíces. Así que conviene pasar a una de las dos raíces al otro lado, para obtener
$$
\sqrt{(x-c)^{2}+y^{2}}=2 a-\sqrt{(x+c)^{2}+y^{2}}
$$
Elevando al cuadrado se tiene
$$
(x-c)^{2}+y^{2}=4 a^{2}-4 a \sqrt{(x+c)^{2}+y^{2}}+(x+c)^{2}+y^{2}
$$
$$
x^{2}-2 c x+c^{2}=4 a^{2}-4 a \sqrt{(x+c)^{2}+y^{2}}+x^{2}+2 c x+c^{2}
$$
$$
4 a \sqrt{(x+c)^{2}+y^{2}}=4 a^{2}+4 c x
$$
$$
a \sqrt{(x+c)^{2}+y^{2}}=a^{2}+c x
$$
Elevando de nuevo al cuadrado, nos deshacemos de la raíz, y después, agrupando términos, obtenemos
$$
a^{2}\left((x+c)^{2}+y^{2}\right)=a^{4}+2 a^{2} c x+c^{2} x^{2}
$$
$$
a^{2} x^{2}+2 a^{2} c x+a^{2} c^{2}+a^{2} y^{2}=a^{4}+2 a^{2} c x+c^{2} x^{2}
$$
$$
\left(a^{2}-c^{2}\right) x^{2}+a^{2} y^{2}=a^{2}\left(a^{2}-c^{2}\right)
$$
$$
b^{2} x^{2}+a^{2} y^{2}=a^{2} b^{2}
$$
que, dividiendo entre $a^{2} b^{2}$, se escribe finalmente como
\begin{equation}
\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1
\end{equation}
llamada la ecuación canónica de la elipse centrada en el origen.
Después de este largo desarrollo pudimos llegar a una ecuación sencilla que nos permite leer toda la información geométrica de la elipse: su centro y la magnitud de su semieje mayor y semieje menor. Observa cómo ahora podemos demostrar sencillamente una de las afirmaciones que hicimos en esta entrada: si en la ecuación canónica de la elipse centrada en el origen hacemos $a=b$, es decir, forzamos a que la figura tenga el semieje mayor y el semieje menor iguales obtenemos la ecuación $x^2+y^2=a^2$ que es la expresión analítica de una circunferencia centrada en el origen.
Con estas herramientas estamos listos para realizar algunos ejercicios. En el primero obtendremos la ecuación de la elipse a partir de la definición, y en el segundo veremos cómo podemos extraer toda la información geométrica de la elipse a partir de su ecuación.
Ejercicio. Encuentra la ecuación de la elipse con fonoces en $(0,3)$ y $(0,-3)$ para la cual la suma de las distancias del foco a cada uno de sus puntos es $6\sqrt{3}$.
Utilizando la definición propuesta al inicio de esta entrada, nuestra elipse será el conjunto de puntos que cumplen la condición:
$$
d(\mathbf{x}, \mathbf{p})+d(\mathbf{x}, \mathbf{q})=2 a
$$
Aplicando la fórmula de la distancia que utilizando en la primera unidad del curso y considerando el valor de la constante $2a$ tenemos que
$$
\sqrt{x^{2}+(y-3)^{2}}+\sqrt{x^{2}+(y+3)^{2}}=6 \sqrt{3}
$$
Esto, lo podemos reescribir como
$$
\sqrt{x^{2}+(y-3)^{2}}=6 \sqrt{3}-\sqrt{x^{2}+(y+3)^{2}}
$$
Si elevamos ambos lados al cuadrado, llegamos a que
$$
x^{2}+(y-3)^{2}=108-12 \sqrt{3} \sqrt{x^{2}+(y+3)^{2}}+x^{2}+(y+3)^{2}
$$
Si te das cuenta, podemos cancelar algunos términos; y en nuestro caso nos conviene dividir ambos lados de la ecuación anterior entre $12$.Si reducimos la expresión anterior, tenemos que
$$
\sqrt{3} \sqrt{x^{2}+(y+3)^{2}}=9+y
$$
Una vez más elevamos ambos lados al cuadrado y llegamos a que
$$
3 x^{2}+2 y^{2}=54
$$
Lo cual es lo mismo a
$$
\frac{x^{2}}{27}+\frac{y^{2}}{18}=1
$$
que es la ecuación de la elipse en su forma canónica.
Ejercicio. ¿Cuál es la ecuación canónica de la elipse que tiene como vértices a los puntos $(\pm 8,0)$ y como focos a $(\pm 5,0)$?
Los focos están en el eje $x$, entonces el eje mayor estará también sobre el eje $x$. Así, la ecuación tendrá esta forma
$$
\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1
$$
Como los vértices son $(\pm 8,0)$, entonces $a=8$ y $a^{2} = 64$. Y puesto que los focos son $(\pm 5,0)$, entonces $c=5$ y $c^2 = 25$. Ahora, sabemos que los focos y los vértices están relacionados por la siguiente ecuación $c^{2}=a^{2}-b^{2}$. Si resolvemos para $b^2$ tenemos que $b^2=39$. Por lo tanto, la ecuación canónica de esta elipse será:
$$
\frac{x^{2}}{64}+\frac{y^{2}}{39}=1
$$
Más adelante…
En esta entrada aprendimos lo básico sobre una elipse: su definición, sus elementos y la ecuación canónica que la representa. Nos falta hablar de sus propiedades focales y del concepto de excentricidad, estos términos serán el tema de la siguiente entrada. Una vez que hayamos concluido nuestro estudio de las elipses, empezaremos a hablar de hipérbolas.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Dibuja la elipse $\frac{x^{2}}{36}+\frac{y^{2}}{4}=1$ en algún programa de computadora e identifica sus elementos. Sugerencia: puedes utilizar GeoGebra, Mathematica, Matlab, Python o GNU plot.
- Considera la siguiente ecuación de elipse $9 x^{2}+4 y^{2}=36$; encuentra sus focos, su semieje mayor, su semieje menor y dibújala.
- Encuentra el área de una elipse con semieje mayor $a$ y semieje menor $b$. Sugerencia: Considera la ecuación canónica de una elipse centrada en el origen, despeja para $x$ e integra sobre $x$ sólo un cuadrante; eligiendo correctamente los límites de integración. El resultado de la integral multiplícalo por $4$. Cuidado, la integral es trigonométrica.
Entradas relacionadas
- Ir a Geometría Analítica I
- Entrada anterior del curso: Problemas con círculos
- Siguiente entrada del curso: Propiedades de elipses