Archivo de la etiqueta: centroide

Geometría Moderna I: Punto simediano

Por Rubén Alexander Ocampo Arellano

2 respuestas

Introducción

El punto simediano es el punto en el que concurren las simedianas de un triángulo, es otro punto notable del triángulo, en esta entrada veremos algunas de sus propiedades.

Punto simediano

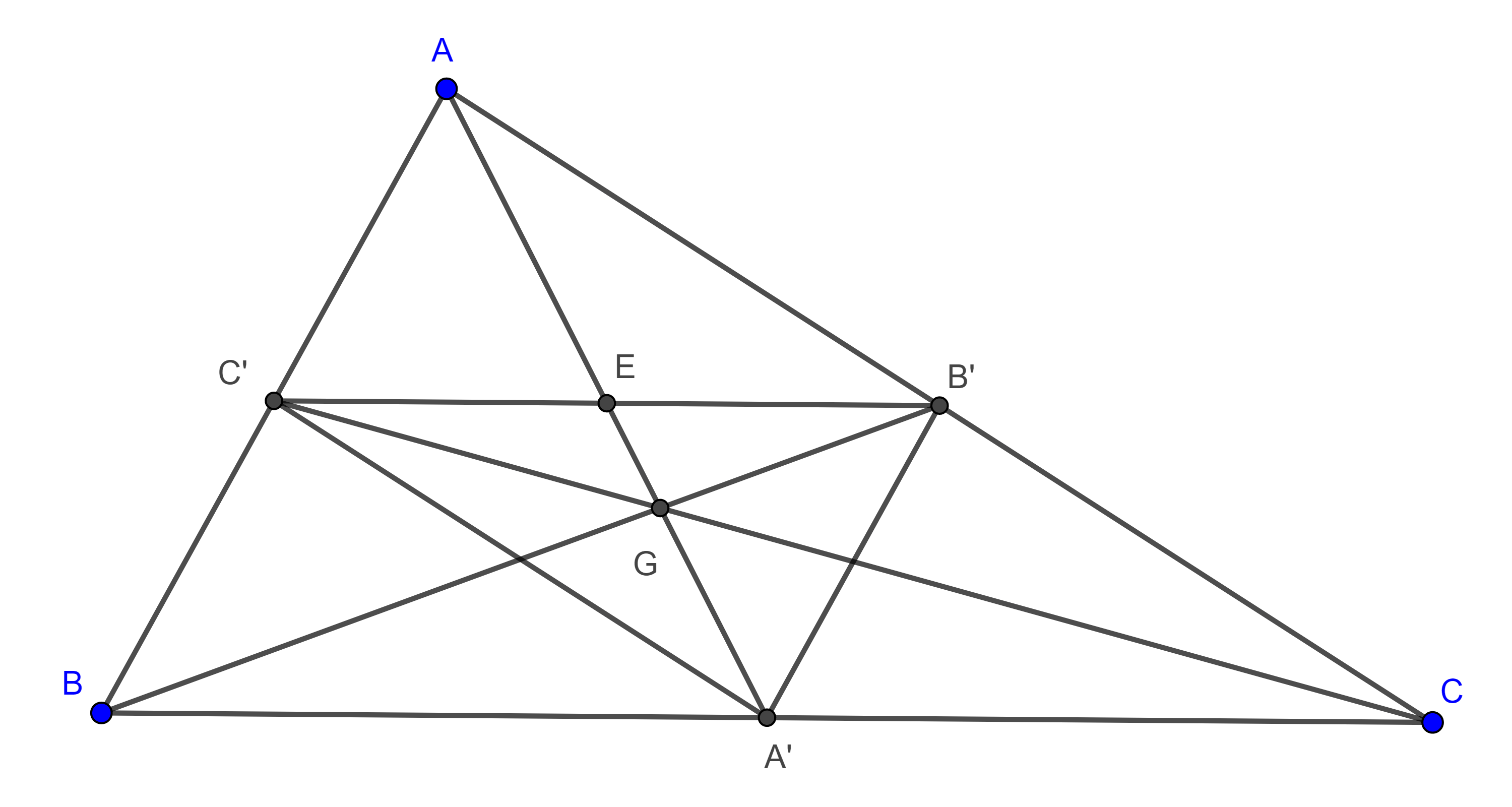
Teorema 1. Las tres simedianas de un triángulo son concurrentes, al punto de concurrencia se le conoce como punto simediano o punto de Lemoine a menudo denotado con la letra $K$.

Demostración. En la entrada teorema de Menelao mostramos que un triángulo $\triangle ABC$ y su triangulo tangencial $\triangle K_aK_bK_c$, están en perspectiva desde una recta, conocida como eje de Lemoine.

Por el teorema de Desargues, $\triangle ABC$ y $\triangle K_aK_bK_c$ están en perspectiva desde un punto, es decir, $AK_a$, $BK_b$ y $CK_c$ concurren en un punto $K$.

Figura 1

Por el teorema 2 de la entrada anterior, dos exsimedianas (los lados del triángulo tangencial $\triangle K_aK_bK_c$) y una simediana, que pasan por vértices distintos de $\triangle ABC$ concurren en un punto exsimediano, es decir, $AK_a$, $BK_b$, $CK_c$ son las simedianas de $\triangle ABC$.

$\blacksquare$

Observación. Como el eje de Lemoine de $\triangle ABC$ es el eje de Gergonne de $\triangle K_aK_bK_c$, entonces el punto de Lemoine de $\triangle ABC$ es el punto de Gergonne de $\triangle K_aK_bK_c$, su triángulo tangencial.

Corolario 1. Sea $S = AK \cap BC$ entonces $AKSK_a$ es una hilera armónica de puntos.

Demostración. Por el corolario de la entrada anterior $B(AK_bCK_a)$ es un haz armónico de rectas y como $AD$ es transversal entonces sus intersecciones con el haz forman una hilera armónica.

$\blacksquare$

Triángulo pedal del punto simediano

Definición. Dados un triángulo $\triangle ABC$ y un punto $P$, el triángulo pedal de $P$ respecto de $\triangle ABC$, es aquel cuyos vértices son las proyecciones de $P$ en los lados de $\triangle ABC$. Por ejemplo, el triángulo órtico es el triángulo pedal del ortocentro.

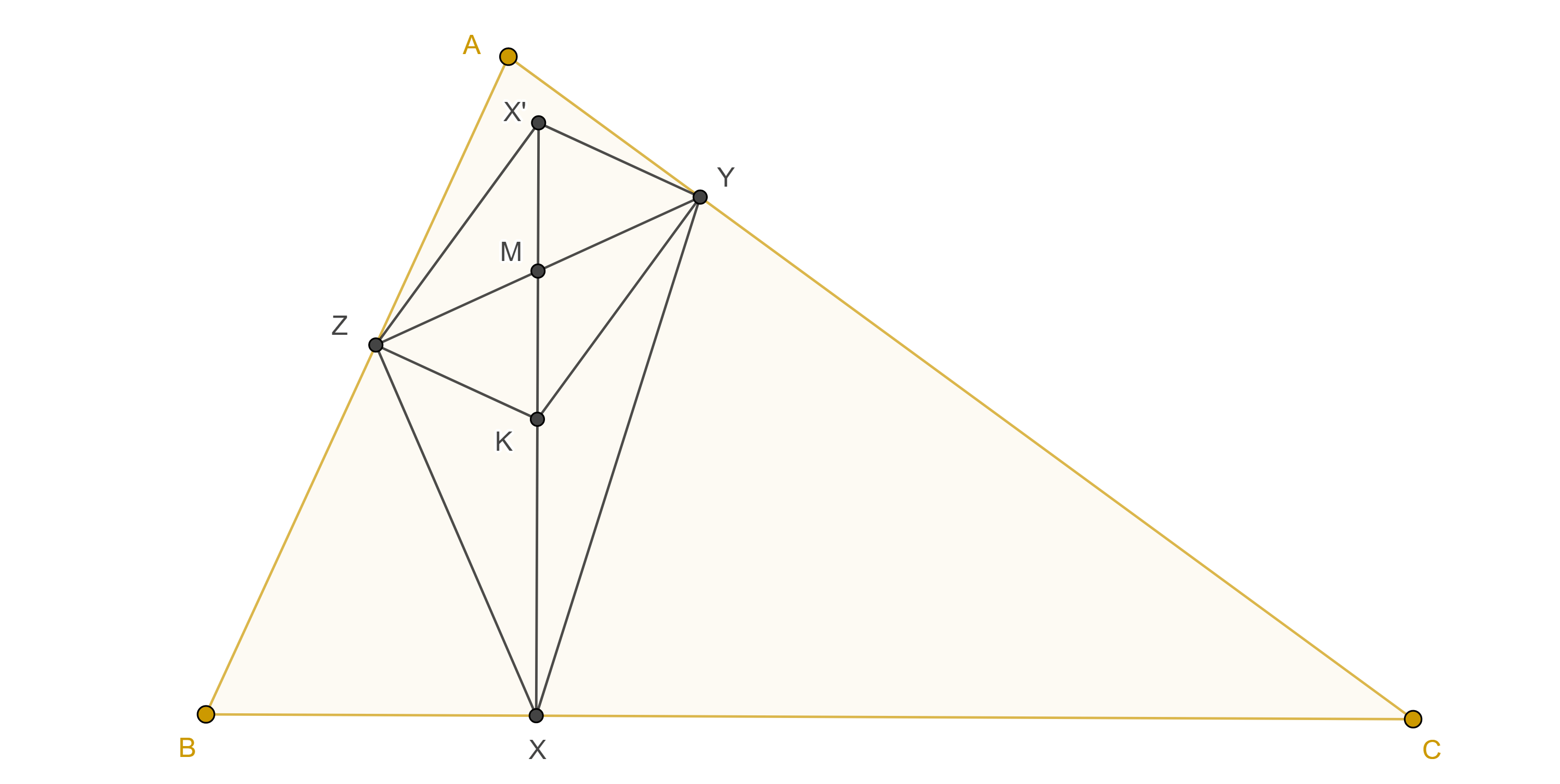
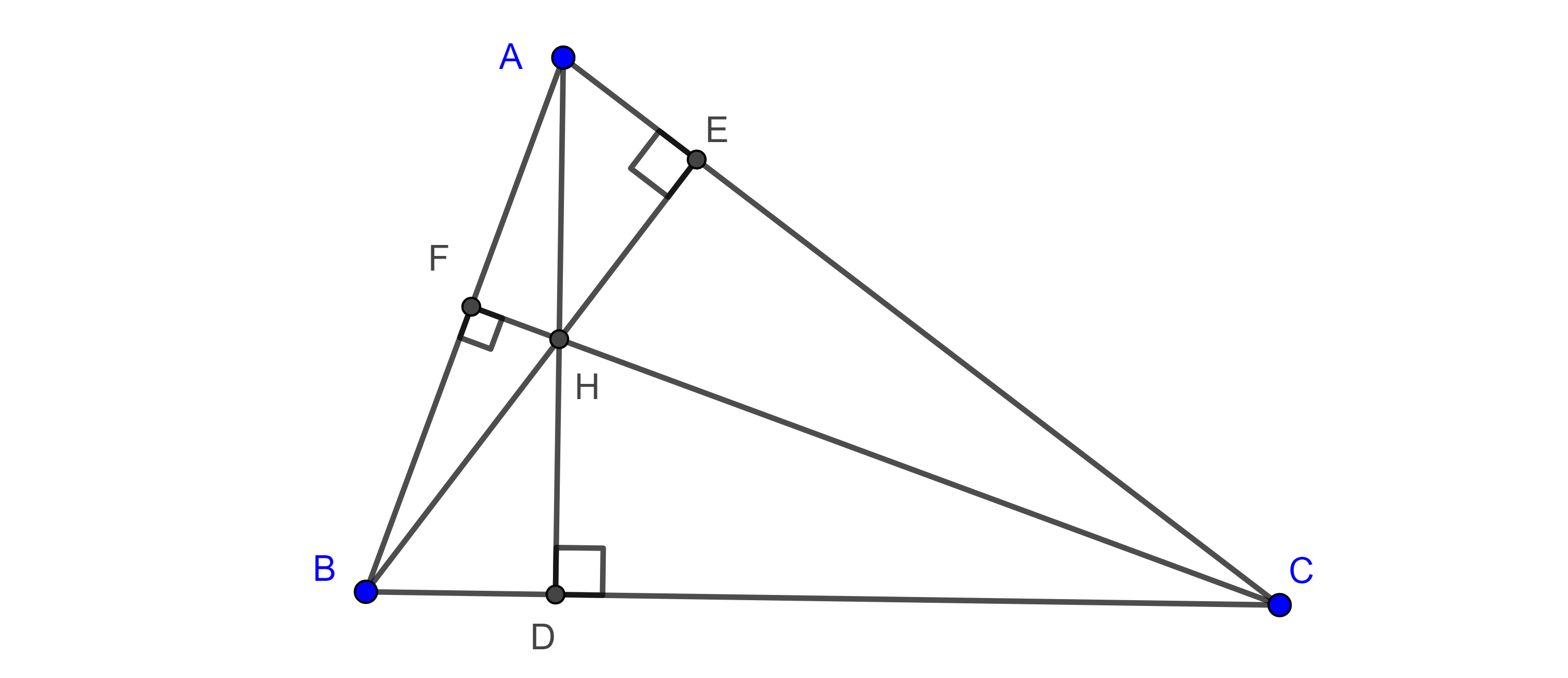
Teorema 2, de Lemoine. El punto simediano es el único punto del plano que es el centroide de su propio triángulo pedal.

Demostración. Sean $\triangle ABC$ y $K$ su punto simediano, considera $X$, $Y$ y $Z$ las proyecciones de $K$ en $BC$, $CA$ y $AB$ respectivamente, sea $X’ \in KX$ tal que $YX’ \parallel KZ$.

Figura 2

Entonces $\triangle ABC \sim \triangle YX’K$, pues sus respectivos lados son perpendiculares, esto es
$\dfrac{AB}{AC} = \dfrac{YX’}{YK}$.

Pero $\dfrac{AB}{AC} = \dfrac{KZ}{KY}$ pues $K$ esta en la $A$-simediana, por lo tanto $KZ = YX’$.

En consecuencia, $\square X’ZKY$ es un paralelogramo y por lo tanto $KX’$ biseca a $YZ$.

Como resultado tenemos que $XK$ es mediana de $\triangle XYZ$.

De manera análoga vemos que $YK$, $ZK$ son medianas de $\triangle XYZ$, por lo tanto, $K$ es el centroide de su triangulo pedal.

$\blacksquare$

Recíprocamente, supongamos que $K$ es el centroide de su triángulo pedal $\triangle XYZ$ respecto a $\triangle ABC$, con $X \in BC$, $Y \in CA$, $Z \in AB$, sea $M$ el punto medio de $YZ$, extendemos $KM$ hasta un punto $X’$ tal que $KM = MX’$.

Como $YZ$ y $KX’$ se bisecan entonces $\square X’ZKY$ es un paralelogramo, entonces $YX’ = KZ$ y $YX’ \parallel KZ$.

Ya que los lados de $\triangle YX’K$ son perpendiculares a los lados de $\triangle ABC$, entonces son semejantes, esto es
$\dfrac{AB}{AC} = \dfrac{YX’}{YK} = \dfrac{KZ}{KY}$.

Por lo tanto, $K$ está en la $A$-simediana, igualmente vemos que $K$ pertenece a las $B$ y $C$-simedianas.

En consecuencia, $K$ es el punto simediano de $\triangle ABC$.

$\blacksquare$

Conjugado isotómico del punto simediano

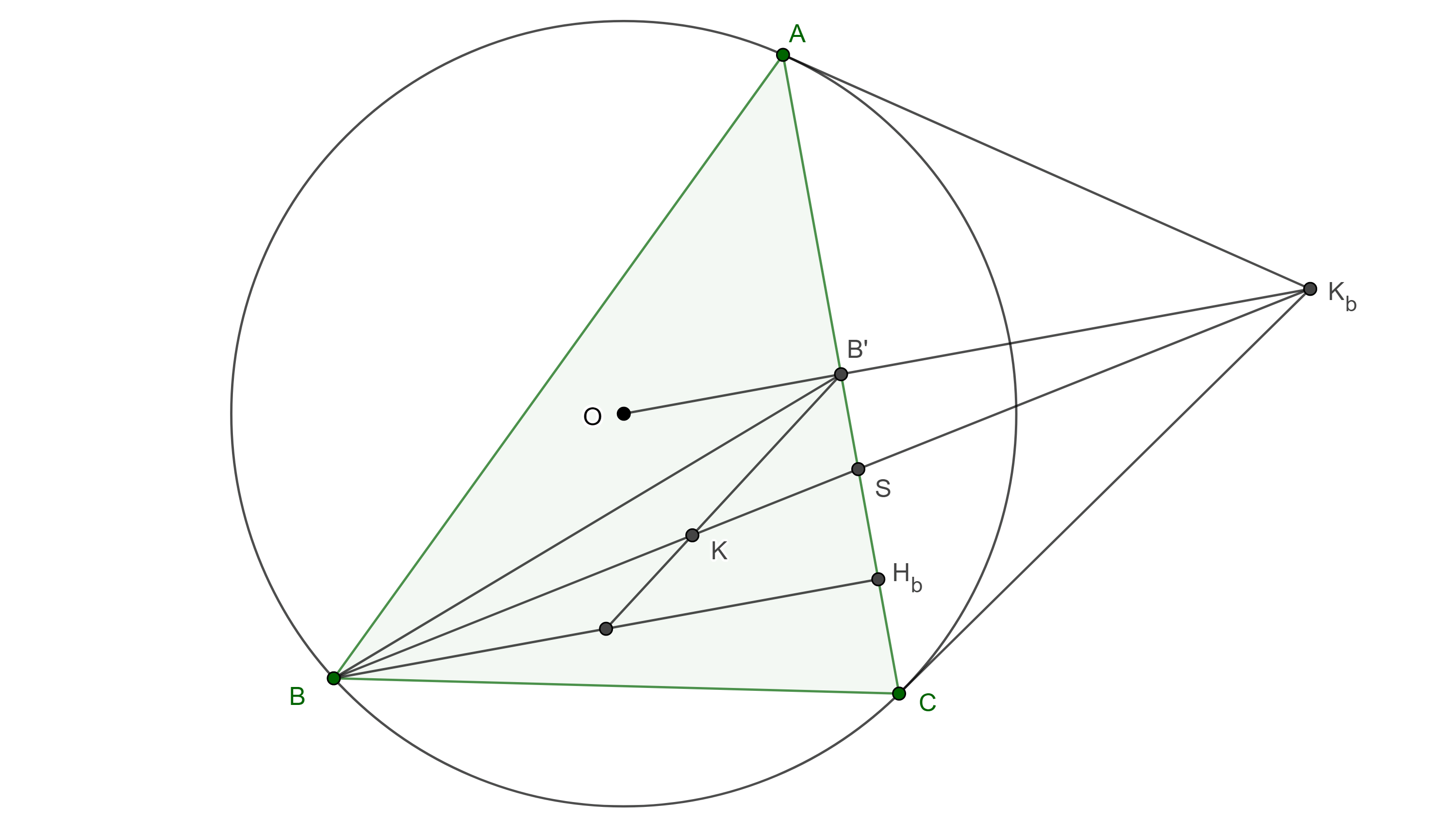
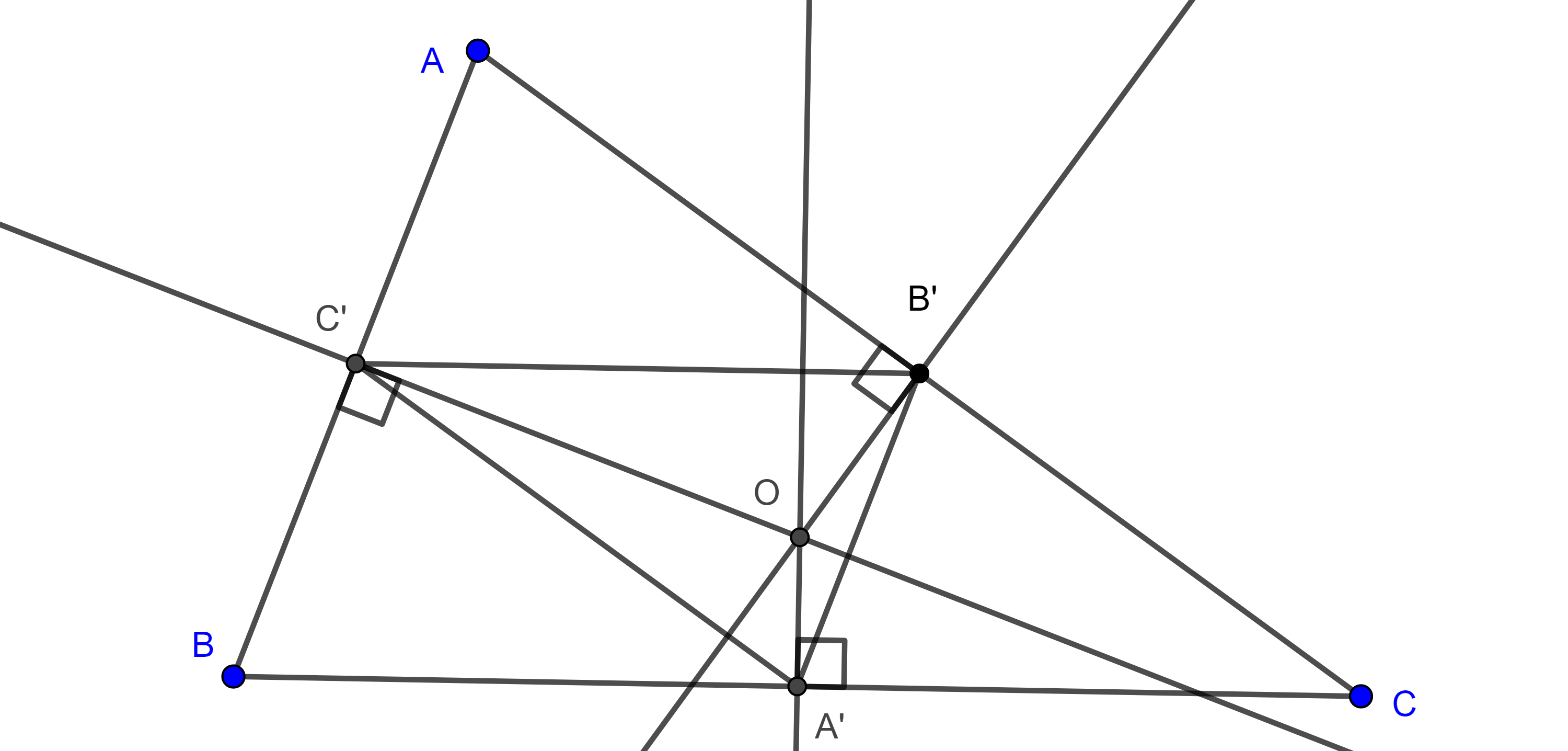
Teorema 3. Las rectas que unen el punto medio del lado de un triángulo con el punto medio de la altura perpendicular a ese lado concurren en el punto simediano del triángulo.

Demostración. Sean $\triangle ABC$, $K$ el punto simediano, $K_b$ el punto exsimediano opuesto al vértice $B$, $S = BK_b  \cap CA$.

Figura 3

Por el corolario 1, $BKSK_b$ es una hilera armónica, por lo tanto, $B’(BKSK_b)$ es un haz armónico, donde $B’$ es el punto medio de $CA$.

Considera $O$ el circuncentro de $\triangle ABC$ y $H_b$ el pie de la altura por $B$, notemos que $O$, $B’$ y $K_b$ son colineales, por lo tanto, $B’K_b$ es perpendicular a $CA$ y así $BH_b \parallel B’K_b$.

Como $BH_b$ es paralela a una de las rectas del haz armónico, entonces las otras tres rectas del haz dividen a $BH_b$ en dos segmentos iguales, es decir $B’K$ biseca a $BH_b$.

Igualmente vemos que $A’K$ y $C’K$ bisecan a $AH_a$ y $CH_c$ respectivamente, y de esto concluimos la concurrencia de las rectas mencionadas.

$\blacksquare$

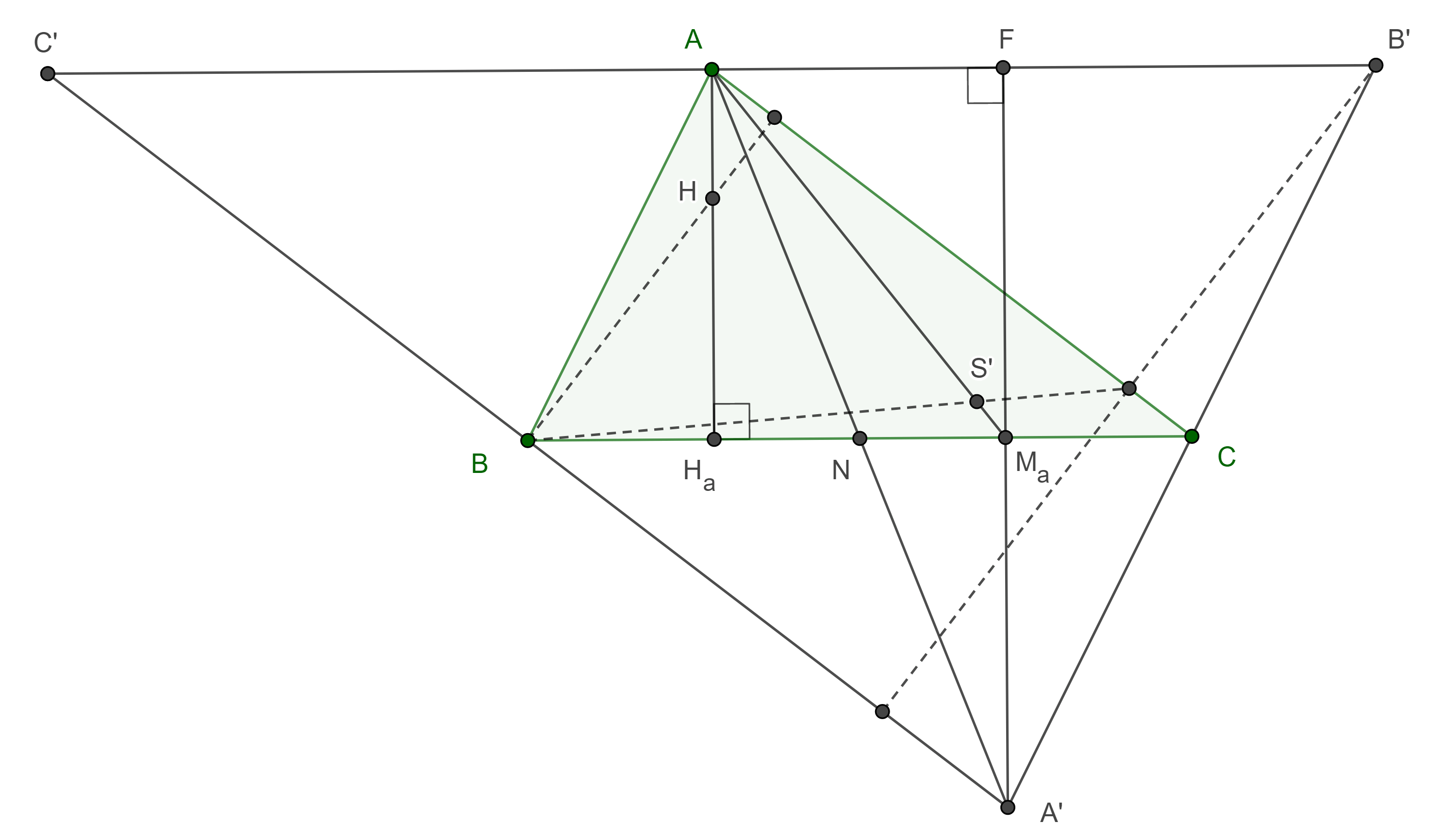
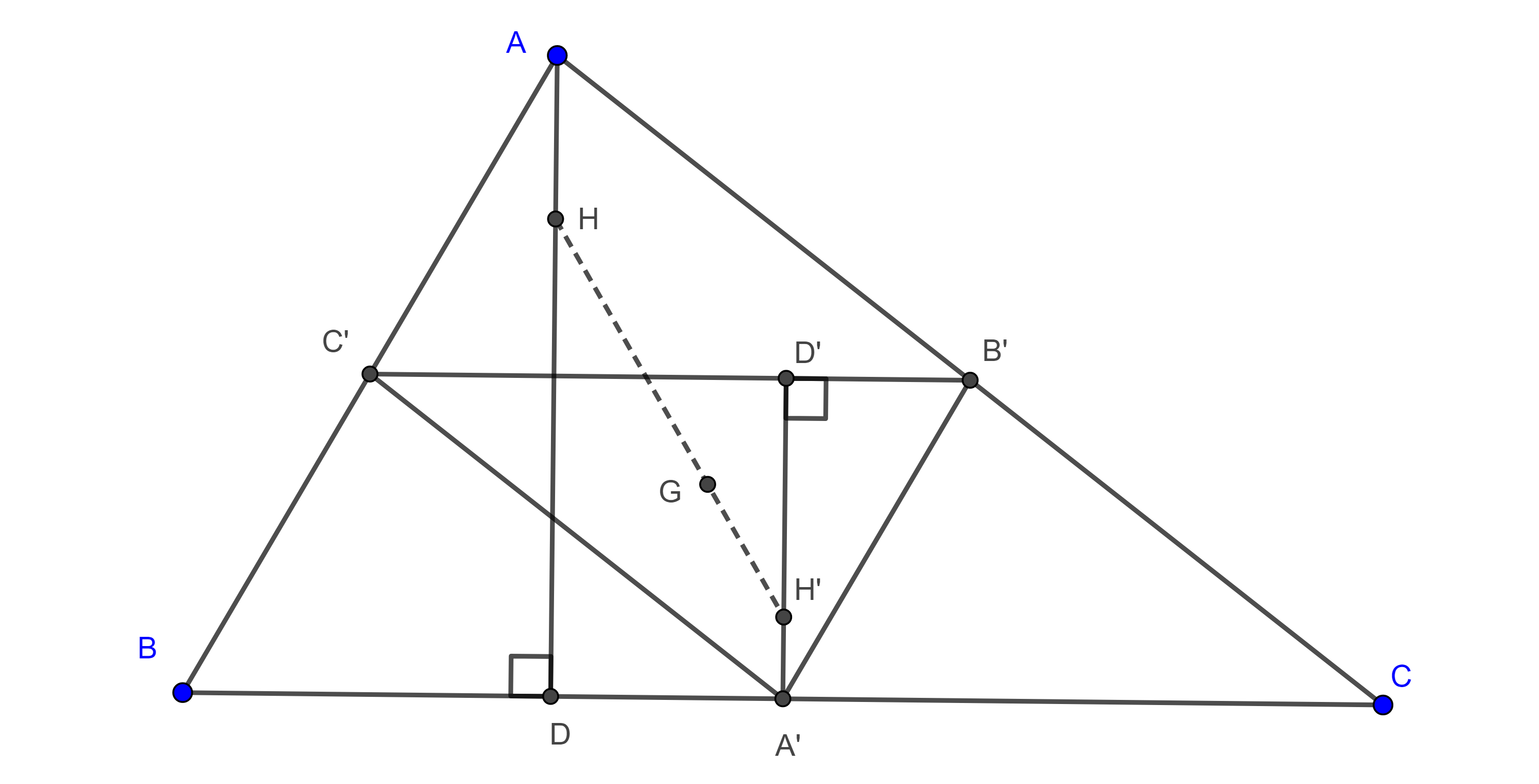
Proposición 1. El ortocentro de un triángulo y el punto simediano de su triángulo anticomplementario son conjugados isotómicos respecto del triángulo original.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo anticomplementario.

Como $AB$ y $AC$ son segmentos medios de $\triangle A’B’C’$, entonces $\square ABA’C$ es un paralelogramo, por lo tanto, $\triangle ABC$ y $\triangle A’CB$ son congruentes, además $AA’$ y $BC$ se intersecan en su punto medio $N$.

Figura 4

Sean $H_a$, $M_a$ los pies de las alturas desde $A$ y $A’$ respectivamente en $BC$, como $\triangle ABC \cong \triangle A’CB$, entonces $AH_a = M_aA’$.

Por criterio de congruencia ALA, $\triangle AH_aN \cong \triangle A’M_aN$, por lo que $H_aN = NM_a$, es decir, el punto medio de $H_a$ y $M_a$ coincide con el punto medio de $BC$,

Por lo tanto, $H_a$ y $M_a$ son puntos isotómicos respecto de $\triangle ABC$.

Sea $F$ el pie de la altura por $A’$ en $\triangle A’B’C’$, como $\square AH_aM_aF$ es un rectángulo entonces $M_aA’ = AH_a = FM_a$, y así $M_a$ es el punto medio de la altura $A’F$.

Por lo tanto, el segmento $AM_a$ une los puntos medios de un lado y una altura de $\triangle A’B’C’$.

De manera análoga vemos que los pies de las alturas en $\triangle ABC$, $H_b$, $H_c$ son isotómicos a los puntos medios de las alturas en $\triangle A’B’C’$, $M_b$, $M_c$, respectivamente.

Como las alturas de $\triangle ABC$ concurren en el ortocentro $H$ y, por el teorema 3, los segmentos $AM_a$, $BM_b$, $CM_c$ concurren en el punto simediano $S’$ de $\triangle A’B’C’$, entonces estos puntos son conjugados isotómicos respecto de $\triangle ABC$.

$\blacksquare$

Construcción de un triángulo dado su punto simediano

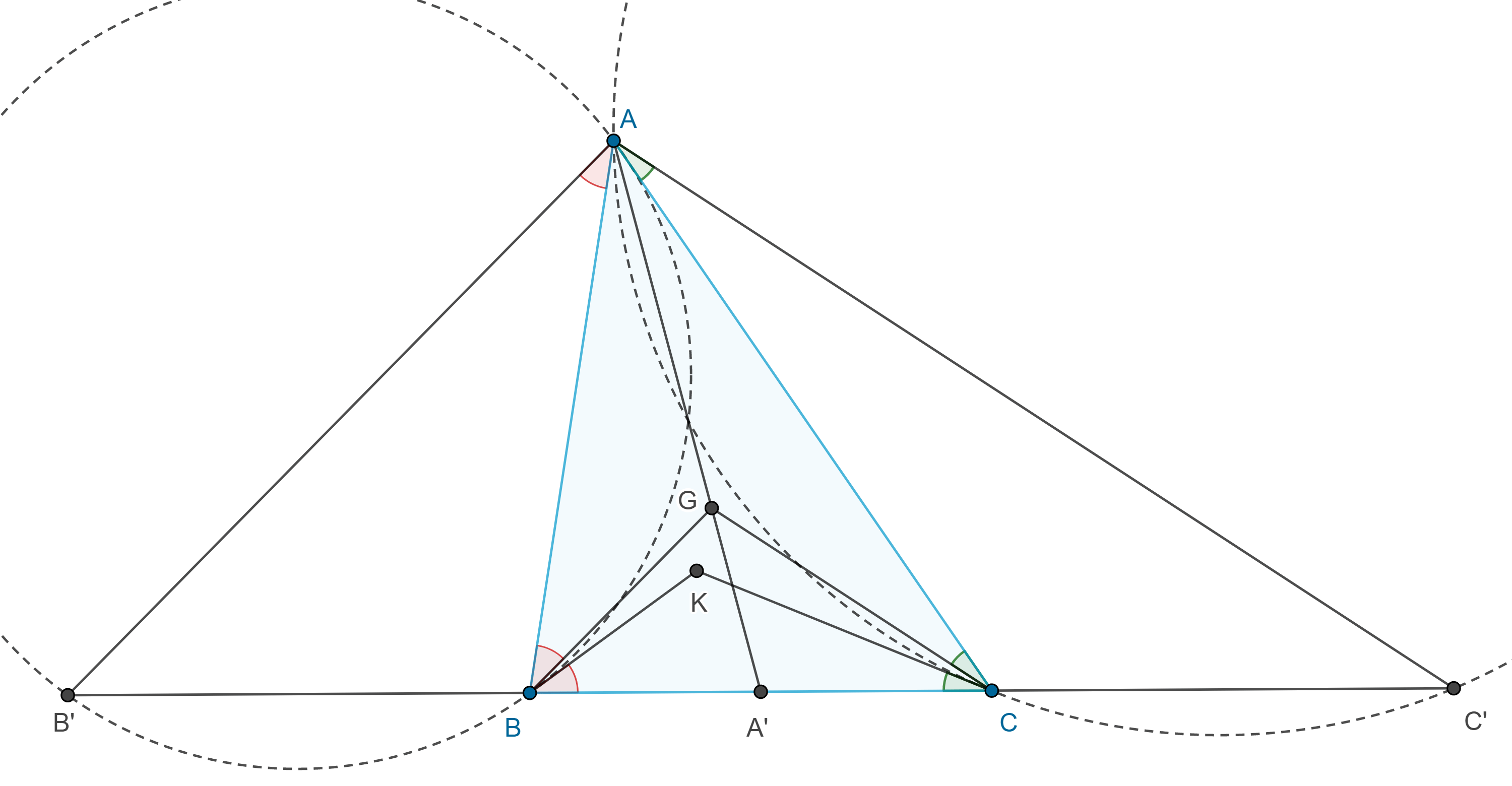
Problema. Construye un triángulo dados dos vértices $B$, $C$, y su punto simediano $K$.

Solución. Supongamos que $\triangle ABC$ es el triángulo requerido y consideremos $G$ y $A’$ el centroide y el punto medio de $BC$ respectivamente.

Sean $B’$, $C’ \in BC$, tales que $B’A \parallel BG$ y $AC’ \parallel GC$.

Figura 5

Por el teorema de Tales tenemos
$\dfrac{1}{2} = \dfrac{A’G}{GA} = \dfrac{A’B}{BB’} = \dfrac{A’C}{CC’}$.

Por lo tanto, $BB’ = CC’ = 2A’B = BC$, así que $B’$ y $C’$ pueden ser construidos teniendo $B$ y $C$.

Por otro lado, como $B’A \parallel BG$ y $AC’ \parallel GC$ y tomando en cuenta que $K$ esta en las reflexiones de $BG$ y $CG$ respecto de las bisectrices de $\angle B$ y $\angle C$ respectivamente, tenemos lo siguiente:

$\angle B’AB = \angle GBA = \angle KBC$ y $\angle CAC’ = \angle ACG = \angle KCB$.

Y estos ángulos son conocidos.

Entonces $B’B$ y $CC’$ subtienden ángulos conocidos en $A$, por lo que podemos trazar los arcos de circunferencia que son el lugar geométrico de los puntos que subtienden estos ángulos.

Así que de la intersección de estos dos arcos resultara en el vértice faltante.

Notemos que los arcos pueden tener dos intersecciones, ser tangentes o no intersecarse, por lo tanto, existen dos, una o cero soluciones.

$\blacksquare$

Distancia del punto simediano a los lados del triángulo

Proposición 2. El punto simediano de un triángulo es el único punto dentro del triángulo cuyas distancias a los lados del triángulo son proporcionales a los respectivos lados.

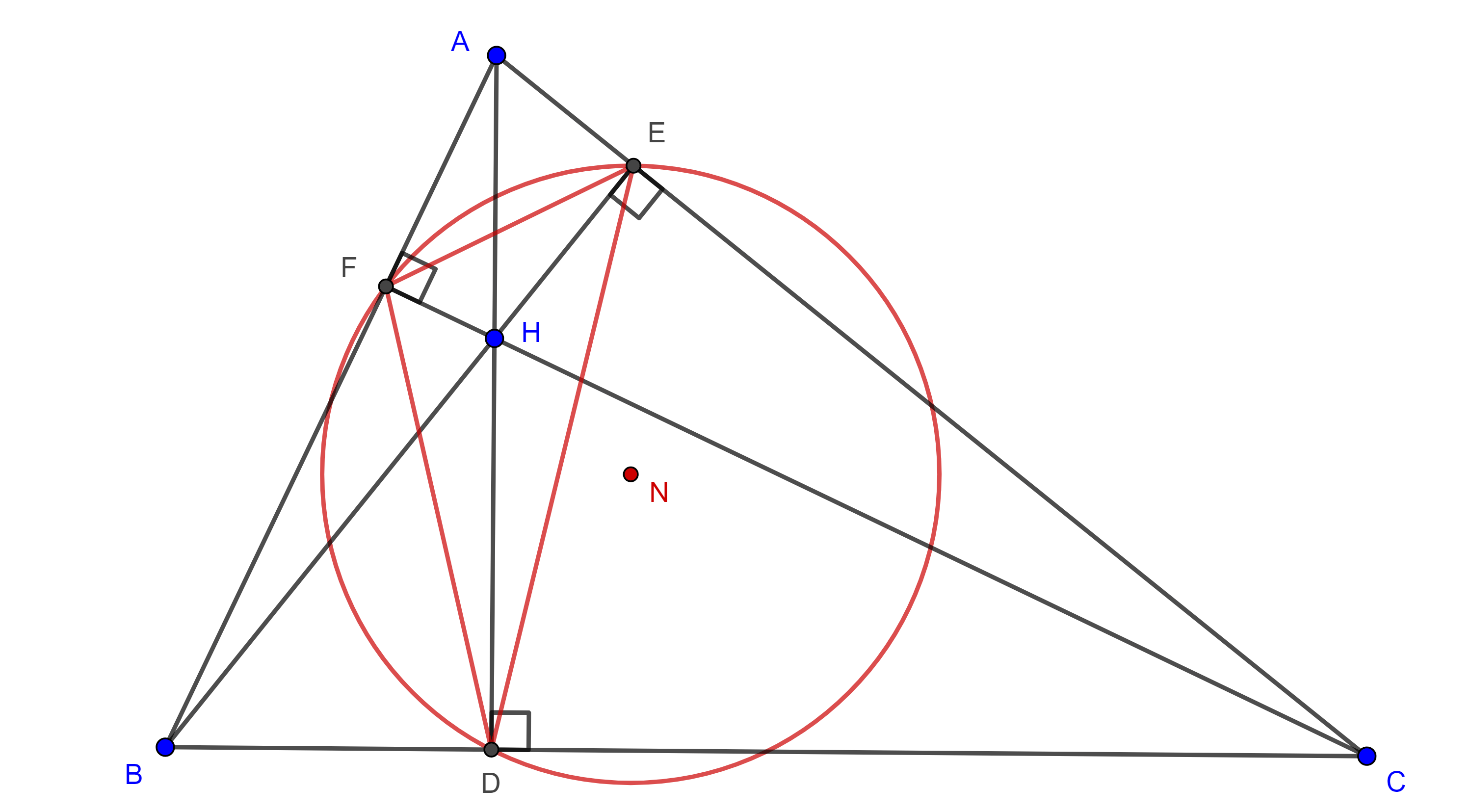
Demostración. Sean $\triangle ABC$ y $K$ su punto simediano, considera $X$, $Y$ y $Z$ las proyecciones de $K$ en $BC$, $CA$ y $AB$ respectivamente, denotemos $BC = a$, $CA = b$, $AB = c$.

Figura 6

Dado que $K$ está en las tres simedianas del triángulo, por el teorema 4 de la entrada anterior, las razones de sus distancias a los lados del triángulo son proporcionales a estos:

$\begin{equation} \dfrac{KZ}{KY} = \dfrac{c}{b}, \end{equation}$
$\begin{equation} \dfrac{KY}{KX} = \dfrac{b}{a}, \end{equation}$
$ \begin{equation} \dfrac{KX}{KZ} = \dfrac{a}{c}. \end{equation}$

Por $(1)$, $(2)$ y $(3)$
$\dfrac{KX}{a} = \dfrac{KY}{b} = \dfrac{KZ}{c} = q$.

Por lo tanto,
$KZ = \dfrac{cKY}{b} = cq$,
$KY = \dfrac{b KX}{a} = bq$,
$KX = \dfrac{a KZ}{c} = aq$.

La unicidad se da por que solo los puntos en las simedianas cumplen esa propiedad y solo $K$ se encuentra en las tres simedianas.

$\blacksquare$

Corolario. 2 $KX = a \dfrac{2(ABC)}{a^2 + b^2 + c^2}$.

Demostración. Calculamos el área de $\triangle ABC$ en función de áreas menores (figura 6).

$(\triangle ABC) = (\triangle KBC) + (\triangle KCA) + (\triangle KAB) $
$= \dfrac{1}{2}(aKX + bKY + cKZ)$
$= \dfrac{q}{2}(a^2 + b^2 + c^2)$.

Por lo tanto, $KX = aq = a \dfrac{2(ABC)}{a^2 + b^2 + c^2}$.

$\blacksquare$

Teorema 4. La suma de los cuadrados de las distancias de un punto a los lados de un triángulo dado, es mínima si el punto es el punto simediano del triángulo.

Demostración. Sean $a$, $b$, $c$, $x$, $y$, $z$ seis números reales entonces la siguiente igualdad es cierta:

 $(a^2 + b^2 + c^2)(x^2 + y^2 + z^2) = (ax + by + cz)^2 + (ay – bx)^2 + (az – cx)^2 + (bz – cy)^2$.

Para comprobarlo solo hace falta realizar los productos.

Podemos pensar estas cantidades como los lados de un triángulo $\triangle ABC$, $BC = a$, $CA = b$, $AB = c$, y $x$, $y$, $z$, las distancias de un punto $K$, a los lados de $\triangle ABC$.

Notemos $ax + by + cz$ representa al menos dos veces el área del triángulo $\triangle ABC$, $2(\triangle ABC)$, que junto con $(a^2 + b^2 + c^2)$ son constantes.

Como las cantidades $(ay – bx)^2$, $(az – cx)^2$, $(bz – cy)^2$ son mayores o iguales a cero, entonces el mínimo se alcanza si se satisfacen las siguientes igualdades:
$\begin{equation} (ay – bx)^2 = (az – cx)^2 = (bz – cy)^2 = 0, \end{equation}$
$\begin{equation} ax + by + cz = 2(\triangle ABC). \end{equation}$

Por otra parte, por las ecuaciones $(1)$, $(2)$ y $(3)$ sabemos que el punto simediano cumple $(4)$ y por el corolario 2 cumple $(5)$, también podemos calcular directamente,

$KX^2 + KY^2 + KZ^2 = \dfrac{(2(\triangle ABC))^2}{a^2 + b^2 + c^2}$.

Por lo tanto, si $K$ es el punto simediano de $\triangle ABC$, se alcanza el mínimo.

$\blacksquare$

Más adelante…

En la próxima entrada veremos otra propiedad del punto simediano, o punto de Lemoine, que amerita su propia entrada, se trata de un conjunto de circunferencias asociadas a este punto.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Si $K$ es el punto simediano de $\triangle ABC$, sea $X$ la proyección de $K$ en $BC$, muestra que la reflexión de $X$ respecto de $K$ esta en la mediana que pasa por $A$.
  2.  Encuentra el punto simediano de un triángulo rectángulo.
  3. Sobre los lados de un triángulo $\triangle ABC$ construye cuadrados externamente, muestra que los lados (de los cuadrados) opuestos a los lados de $\triangle ABC$ se intersecan formando un triángulo homotético a $\triangle ABC$, con centro de homotecia el punto simediano de $\triangle ABC$.
  4. Si las simedianas de $\triangle ABC$ intersecan a su circuncírculo en $D$, $E$ y $F$ muestra que $\triangle ABC$ y $\triangle DEF$ tienen el mismo punto simediano.
  5. $i)$ Muestra que las distancias a los lados de un triángulo desde sus puntos exsimedianos son proporcionales a las longitudes de los lados del triángulo,
    $ii)$ calcula dichas distancias.
  6. Prueba que de entre todos los triángulos inscritos en un triángulo dado, el triángulo pedal del punto simediano, es el que tiene la propiedad de que la suma de los cuadrados de sus lados es mínima.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 252-257.
  • Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 129-145.
  • Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 215-218.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral II: Centro de masa y momentos

Por Miguel Ángel Rodríguez García

1 respuesta

Introducción

En la sección anterior vimos el teorema de Pappus-Guldin el cual nos permite calcular el centroide, área y volumen de un sólido de revolución, en esta sección veremos una aplicación en el área de la física como aplicación de la integración para el cálculo de centro de masas y momentos. Cabe destacar que estudiaremos objetos unidimensionales y bidimensionales, ya que para objetos en el espacio se necesitan integrales múltiples, lo cual, no estudiaremos en este curso.

Centro de masas y momentos (unidimensional)

Figura 1: Varilla con dos pesas en sus extremos.

Comencemos con el caso de una varilla balanceada en un punto sobre el eje $x$ y en sus extremos una masa $m_{1}$ en $x_{1}$ y $m_{2}$ en $x_{2}$ como se muestra en la figura $(1)$. Sea $\bar{x}$ el centro de masa, la varilla se balanceara si:

$$m_{1}d_{1}=m_{2}d_{2}$$

Donde $d_{1}=\bar{x}-x_{1}$ y $d_{2}=x_{2}-\bar{x}$, sustituyendo esto en la ecuación anterior, tenemos que:

$$m_{1}(\bar{x}-x_{1})=m_{2}(x_{2}-\bar{x})$$

$$\Rightarrow m_{1}\bar{x}-m_{1}x_{1}=m_{2}x_{2}-m_{2}\bar{x}$$

$$\Rightarrow \bar{x}=\frac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$$

Por lo que, podemos calcular el centro de masa $\bar{x}$ del sistema con la relación anterior.

Se define a $m_{i}x_{i}$ el momento de la masa $m_{i}$, en este caso, tenemos dos momentos $m_{1}$ y $m_{2}$ con respecto al origen.

En general, si tenemos un sistema de $n$ partículas con sus respectivas masas $m_{1},\space m_{2}, \space …., \space m_{n}$ respectivamente localizadas en los puntos $x_{1},\space x_{2}, \space …., \space x_{n}$ sobre el eje $x$ y análogamente al estudio anterior, se puede demostrar que el centro de masa se puede calcular como:

$$\bar{x}=\frac{\sum_{i=1}^{n}m_{i}x_{i}}{\sum_{i=1}^{n}m_{i}}=\frac{M}{m}$$

Donde $m$ es la suma de las $n$ masas y $M$ es la suma de los $n$ momentos.

Centro de masas y momentos (bidimensional)

Consideremos ahora un sistema de $n$ partículas con masas $m_{1},\space m_{2}, \space …., \space m_{n}$ localizadas en los puntos $(x_{1},\space y_{1}),\space (x_{2},\space y_{2}), \space …., \space (x_{n},\space y_{n})$ en el plano $xy$ como se muestra en la figura $(2)$.

Figura 2: Sistema de $4$ partículas con masa $m$.

Análogamente al caso unidimensional, se define el momento del sistema respecto del eje $y$ como:

$$M_{y}=\sum_{i=1}^{n}m_{i}x_{i} \tag{1}$$

Y el momento del sistema respecto del eje $x$ como:

$$M_{x}=\sum_{i=1}^{n}m_{i}y_{i} \tag{2}$$

Por lo que el centro de masa $(\bar{x}, \bar{y})$ está dado como:

$$\bar{x}=\frac{M_{y}}{m} \space \space \space \space \space \space \bar{y}=\frac{M_{x}}{m}$$

Consideremos una placa con densidad uniforme $\rho$, se desea localizar su centro de masa, para esto, supongamos que esta región está en el intervalo $[a, b]$, dividimos este intervalo en $n$ subintervalos con puntos extremos $x_{0}, \space x_{1}, \space…., \space x_{n}$ e igual amplitud $\Delta x$. Sea $\bar{x_{i}}$ el punto medio del intervalo $[x_{i-1}, \space x_{i}]$, por lo que $\bar{x_{i}}=(x_{i-1}+x_{i})/2$, así, tendremos $n$ polígonos o $R_{i}$ rectángulos, aproximando a la placa como se muestra en la figura $(3)$.

Figura 3: Placa de densidad $\rho$.

El área del i-esimo rectángulo es:

$$A_{i}=f(\bar{x_{i}}) \Delta x_{i}$$

Como estamos en el caso bidimensional, recordemos que la densidad es una densidad superficial dada como:

$$\rho = \frac{M}{A}$$

Por lo que, para la masa:

$$M=\rho f(\bar{x_{i}}) \Delta x_{i}$$

El momento del rectángulo $R_{i}$ respecto del eje $y$ es el producto de su masa y la distancia del centroide del i-esimo rectángulo $R_{i}$ que es $C_{i}(\bar{x_{i}}, \frac{1}{2}f(\bar{x_{i}}))$ como se muestra en la figura $(3)$, por la definición de $M_{y}$ $(1)$, se tiene que:

$$M_{y}(R_{i})=(\rho f(\bar{x_{i}}) \Delta x_{i})\bar{x_{i}}$$

Al sumar estos momentos y tender $n \to \infty$ tenemos que:

$$M_{y}=\lim_{n \to \infty}\sum_{i=1}^{n}(\rho f(\bar{x_{i}}) \Delta x_{i})\bar{x_{i}}=\rho \int_{a}^{b}xf(x)dx $$

Del modo similar, el momento del rectángulo $R_{i}$ respecto del eje $x$ está dado como el producto de su masa por la distancia $C_{i} (\bar{x_{i}}, \frac{1}{2}f(\bar{x_{i}})) $ al eje $x$, por la definición de $M_{x}$ $(2)$, se tiene que:

$$M_{x}(R_{i})=(\rho f(\bar{x_{i}}) \Delta x_{i})\frac{1}{2}f(\bar{x_{i}})=\rho \frac{1}{2}[f(\bar{x_{i}}]^{2} \Delta x$$

Tomando el límite:

$$M_{x}=\lim_{n \to \infty}\sum_{i=1}^{n}\rho \frac{1}{2}[f(\bar{x_{i}}]^{2} \Delta x= \int_{a}^{b} \rho \frac{1}{2}[f(\bar{x_{i}}]^{2} dx $$

El centro de masa de la placa se define análogamente al sistema de $n$ partículas como:

$$\bar{x}=\frac{M_{y}}{m}$$

$$\bar{y}=\frac{M_{x}}{m}$$

Pero la masa de la placa es el producto de su densidad y su área, la cual podemos calcularla por medio de una integral:

$$m=\rho A=\rho \int_{a}^{b}f(x)dx$$

Por tanto, para calcular el centroide $(\bar{x},\bar{y})$ de esta placa se tiene que:

$$\bar{x}=\frac{M_{y}}{m}=\frac{\rho \int_{a}^{b}xf(x)dx}{\rho \int_{a}^{b}f(x)dx}=\frac{\int_{a}^{b}xf(x)dx}{\int_{a}^{b}f(x)dx}=\frac{1}{A}\int_{a}^{b}xf(x)dx \tag{3}$$

$$\bar{y}=\frac{M_{x}}{m}=\frac{\rho \int_{a}^{b}\frac{1}{2}[f(x)]^{2}dx}{\rho \int_{a}^{b}f(x)dx}=\frac{\int_{a}^{b}\frac{1}{2}[f(x)]^{2}dx}{\int_{a}^{b}f(x)dx}=\frac{1}{A}\int_{a}^{b}\frac{1}{2}[f(x)]^{2}dx \tag{4}$$

Si la región se encuentra entre dos curvas $y=f(x)$ y $y=g(x)$ donde $f(x)\geq g(x)$ podemos utilizar el mismo método anterior para encontrar el centroide $(\bar{x},\bar{y})$ como:

$$\bar{x}=\frac{\int_{a}^{b}x[f(x)-g(x)]dx}{\int_{a}^{b}(f(x)-g(x))dx}$$

$$\bar{y}=\frac{\int_{a}^{b}[f^{2}(x)-g^{2}(x)]dx}{2\int_{a}^{b}(f(x)-g(x))dx}$$

Veamos los siguientes ejemplos.

Ejemplos

  • Suponga que se colocan tres masas puntuales en el plano $xy$ de la siguiente manera: $m_{1}=2 kg$ en la coordenada $(-1,3)$, $m_{2}= 6 kg$ en la coordenada $(1,1)$ y $m_{3}=4kg$ en la coordenada $(2,-2)$. Encuentre el centro de masa del sistema.

Calculamos la masa total como:

$$m=\sum_{i=1}^{3}m_{i}=2+6+4=12 kg$$

Ahora, encontrando los momentos respectivos en el eje $x$ y $y$:

$$M_{y}=\sum_{i=1}^{3}m_{i}x_{i}=-2+6+8=12$$

$$M_{x}=\sum_{i=1}^{3}m_{i}y_{i}=6+6-8=4$$

Calculando el centro de masas:

$$\bar{x}=\frac{M_{y}}{m}=\frac{12}{12}=1$$

$$\bar{y}=\frac{M_{x}}{m}=\frac{4}{12}=\frac{1}{3}$$

Por lo que el centro de masas de este sistema es:

$$(\bar{x},\bar{y})=(1, \frac{1}{3})$$

  • Encuentre el centroide de la región acotada por las curvas $y=\cos(x)$,$y=0$, $x=0$ y $x=\pi/2$.

El área de la región es:

$$A=\int_{0}^{\pi /2}\cos(x)dx=\sin(x) \bigg|_{0}^{\pi /2}=1$$

Así, calculando el centroide se tiene que, para $\bar{x}$ $(3)$:

$$\bar{x}=\frac{1}{A}\int_{0}^{\pi /2}xf(x)dx=\int_{0}^{\pi /2}x\cos(x)dx=x\sin(x)\bigg|_{0}^{\pi /2}-\int_{0}^{\pi /2}\sin(x)dx$$

$$=\frac{\pi}{2}-1$$

Para $\bar{y}$ $(4)$:

$$\bar{y}=\frac{1}{A}\int_{0}^{\pi /2}\frac{1}{2}(f(x))^{2}dx=\frac{1}{2}\int_{0}^{\pi /2}\cos^{2}(x)dx$$

$$=\frac{1}{4}\int_{0}^{\pi /2}(1+\cos(2x))dx=\frac{1}{4}\left [ x+\frac{1}{2}\sin(2x) \right ]\bigg|_{0}^{\pi /2}=\frac{\pi}{8}$$

Por tanto, el centroide es: $$(\bar{x},\bar{y})=(\frac{\pi}{2}-1,\frac{\pi}{8})$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Encuentre los momentos del centro de masas cuyas masas son 3, 4 y 8 con coordenadas $(-1, 1)$, $(2, -1)$ y $(3, 2)$ respectivamente.
  2. Demuestre que el centro de masas de una varilla o de una franja recta y delgada de densidad constante se encuentra en su punto medio.
  3. Una varilla de longitud de 10cm. aumenta su grosor de izquierda a derecha en función de $f(x)=1+(x/10) kg/m$. Determinar el centro de masas de la varilla.
  4. Encuentre el centro de masas de una placa semicircular de radio $r$.
  5. Encuentre el centroide de la región acotada por la recta $y=x$ y la parábola $y=x^{2}$.

Más adelante…

En esta sección vimos como calcular el centro de masas y el momento de un sistema, en la siguiente sección veremos otra la aplicación de la integral en el área de la física, y es la aplicación de la integración al concepto de trabajo.

Entradas relacionadas

Cálculo Diferencial e Integral II: Teorema de Pappus-Guldinus

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En las secciones anteriores vimos como calcular tanto el volumen como el área de un sólido de revolución, en esta entrada veremos un teorema en el que podemos calcular áreas y volúmenes de sólidos de revolución con sus respectivos centroides, es decir, su centro de simetría, a este teorema se le conoce como teorema del centroide de Pappus que se divide a su vez en dos teoremas y aunque no es una aplicación directa de las integrales, podemos calcular el volumen o el área de estos sólidos de una manera más sencilla, veamos el primer teorema.

Teorema de Pappus (Volúmenes)

El volumen $V$ de un sólido de revolución generado mediante la rotación de una curva plana $C$ alrededor de un eje externo, de manera que, esta última no corte el interior de la región, es igual al producto del área $A$ por la distancia $2\pi d$ recorrida por su centroide en una rotación completa alrededor del eje:

$$V=2\pi A d$$

Demostración:

Sea un área $A$ generada mediante la rotación de una curva plana $C$ alrededor del eje $x$, consideremos un elemento $dA$ de dicha área, el volumen $dV$ generado por el elemento $dA$ es igual a:

$$dV=2 \pi ydA$$

Donde $y$ es la distancia entre el eje $x$ y el elemento $dA$, por tanto:

$$V=\int 2 \pi y dA=2 \pi \bar{y} A$$

Con $\bar{y}=d$ y $2\pi \bar{y}$ es la distancia recorrida por el centroide de $A$.

$\square$

Teorema 2 de Pappus (Áreas)

El área $A$ de una superficie de revolución generada mediante la rotación de una curva plana $C$ alrededor de un eje externo, es igual a su longitud $L$, multiplicada por la distancia $2\pi d$ recorrida por su centroide en una rotación completa alrededor del eje, entonces:

$$A=2\pi L d$$

Demostración:

Sea $L$ la longitud de una curva plana $C$ que rota alrededor del eje $x$ y consideremos un elemento $dL$ de dicha longitud. El área $dA$ generada por el elemento $dL$ es igual a:

$$dA= 2 \pi y dL$$

Donde $y$ es la distancia del elemento $dL$ al eje $x$, por tanto:

$$A=\int 2 \pi y dL=2 \pi \bar{y} L$$

Con $\bar{y}=d$ y $2\pi \bar{y}$ es la distancia recorrida por el centroide $L$.

$\square$

Veamos unos ejemplos de como aplicar el teorema de Pappus-Guldinus.

Ejemplos

  • Un toroide se forma al hacer girar un círculo de radio $r$ respecto a una recta en el plano del círculo que es la distancia $R>r$ desde el centro del círculo. Encuentre el volumen del toroide.

El círculo tiene área $A=\pi r^{2}$, por simetría su centroide es su centro, por tanto, la distancia recorrida por el centroide durante una rotación está dada como $d=2\pi R$.

Por el teorema de Pappus (volumen), el volumen del toroide es:

$$V=Ad=(\pi r^{2})(2\pi R)=2\pi ^{2}r^{2}R$$

  • Calcule el área de la superficie del toro del ejercicio anterior.

Del segundo teorema de Pappus (Área) tenemos que:

$$A=2\pi L d=2 \pi (r)(2\pi R)=4\pi ^{2} rR$$

  • Calcula el área de la superficie generada por una circunferencia cuyo radio es de $3m$, girando $2\pi$ alrededor de una recta tangente.

Tenemos que la longitud es $L=2 \pi (3)=6 \pi$

Por el segundo teorema de Pappus calculamos el área de la superficie como:

$$A=2 \pi L d=2 \pi (6 \pi) (3)=36 \pi ^{2}$$

  • Calcula el centroide de un alambre semicircular de radio $R$, que gira alrededor del eje $x$.

Para calcular el centroide podemos utilizar cualquiera de los dos teoremas de Pappus, en este caso, es fácil calcular el centroide por el teorema de Pappus de áreas, veamos:

Sabemos que el área generada es:

$$A=4 \pi R^{2}$$

Y la longitud es:

$$L=\pi R$$

Por el teorema de Pappus (áreas), tenemos que:

$$4 \pi R^{2}=2 \pi \bar{y} (\pi R) \Rightarrow \bar{y}=\frac{2R}{\pi}$$

  • Calcule el volumen del sólido generado por un cuadrado de lado $a=3$ que gira alrededor del eje $y$.

Sabemos que el área lo calculamos como:

$$A=a^{2}=3^{2}=9$$

Sabemos que el centroide de un cuadrado está justo en el centro, o a la mitad de cada cara, por lo que:

$$\bar{y}=1.5$$

Así, calculando el volumen por el teorema de Pappus para volúmenes, tenemos que:

$$V=2\pi A \bar{y}=2\pi (9)(1.5)=27 \pi$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Hallar el volumen y el área de la superficie de un solido de una esfera de radio r.
  2. Hallar el volumen de un solido de un cono con altura h y radio r.
  3. Calcule el volumen del solido obtenido al hacer girar el triangulo con vértices $(2, 3)$, $(2, 5)$ y $(5, 4)$ respecto al eje x.
  4. La región cuadrada con vértices $(0, 2)$, $(2, 0)$, $(4, 2)$ y $(2, 4)$ se hace girar alrededor del eje $x$ para generar un solido. Determine el volumen y el área de la superficie del sólido.
  5. Localice el centroide de una región semicircular entre la semicircunferencia $y=\sqrt{a^{2}-x^{2}}$ y el eje x.

Más adelante…

Vimos en esta sección el teorema de Pappus con el que se puede calcular el volumen, centroide y el área de un solio de revolución, en la siguiente sección veremos una aplicación más de la integral, en este caso, en el área de la física, que es cálculo de momentos y centros de masa.

Entradas relacionadas

Geometría Moderna I: Cuadrángulo ortocéntrico

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada veremos que los cuatro triángulos que se forman con los vértices de un cuadrángulo ortocéntrico, tienen la misma circunferencia de los nueve puntos y derivaremos algunas otras propiedades.

Cuadrángulo ortocéntrico

Definición. Un cuadrángulo ortocéntrico es el conjunto de puntos formado por los vértices de un triángulo y su ortocentro.

Nos referiremos a los cuatro triángulos que se pueden formar con los cuatro puntos de un cuadrángulo ortocéntrico como grupo ortocéntrico de triángulos.

Teorema 1. Cualquier punto de un cuadrángulo ortocéntrico es el ortocentro del triángulo formado por los otros tres puntos y los triángulos de este grupo ortocéntrico tienen el mismo triangulo órtico.

Demostración. Sea $\triangle ABC$ y $H$ su ortocentro.

Figura 1

Notemos que el ortocentro de $\triangle BHC$ es $A$ pues $AB \perp HC$, $AH \perp BC$ y $AC \perp HB$.

De manera análoga podemos ver que $B$ es el ortocentro de $\triangle AHC$ y $C$ es el ortocentro de $\triangle AHB$.

Por otro lado, los pares de rectas perpendiculares $AH$, $BC$; $BH$, $AC$ y $CH$, $AB$, se intersecan en $D$, $E$ y $F$, respectivamente.

Por lo tanto, estos tres puntos son fijos, así el triángulo órtico es el mismo para los cuatro triángulos $\triangle ABC$, $\triangle HAB$, $\triangle HAC$ y $\triangle HBC$.

$\blacksquare$

Corolario 1. Las circunferencias de los nueve puntos de un grupo ortocéntrico de triángulos coinciden y sus circunradios son iguales.

Demostración. Como el circuncírculo del triángulo órtico de un triángulo dado es la circunferencia de los nueve puntos, por el teorema 1, los triángulos de un grupo ortocéntrico tienen la misma circunferencia de los nueve puntos.

En la entrada anterior vimos que el radio de la circunferencia de los nueve puntos es igual a la mitad del circunradio de su triángulo de referencia.

Por lo tanto, $\triangle ABC$, $\triangle HAB$, $\triangle HAC$ y $\triangle HBC$ tienen el mismo circunradio (figura 1).

$\blacksquare$

Circuncentros

Teorema 2. Los circuncentros de un grupo ortocéntrico de triángulos forman un cuadrángulo ortocéntrico.

Demostración. Por el teorema 2 de la entrada anterior, sabemos que el circuncentro de un triángulo es la reflexión de su ortocentro respecto de $N$, el centro de los nueve puntos.

Como los triángulos de un grupo ortocéntrico tienen el mismo centro de los nueve puntos, los circuncentros $O_a$, $O_b$, $O_c$ y $O$ de $\triangle HBC$, $\triangle HAC$, $\triangle HAB$ y $\triangle ABC$ son las reflexiones de $A$, $B$, $C$ y $H$ respectivamente respecto a $N$.

Figura 2

Dado que una reflexión es una homotecia de razón $-1$ entonces las figuras $ABCH$ y $O_aO_bO_cO$ son congruentes y por lo tanto $O_aO_bO_cO$ es un cuadrángulo ortocéntrico.

$\blacksquare$

Corolario 2. Un grupo ortocéntrico de triángulos y el grupo ortocéntrico de triángulos formado por sus circuncentros tienen la misma circunferencia de los nueve puntos.

Demostración. Como las figuras $ABCH$ y $O_aO_bO_cO$ son simétricas respecto a $N$ entonces también sus circunferencias de los nueve puntos son simétricas respecto a $N$.

Como $N$ es el centro de una de estas circunferencias, entonces coinciden.

Observación. Notemos que como $O_aO_bO_cO$ es un grupo ortocéntrico de triángulos, entonces la reflexión de sus ortocentros respecto al centro de los nueve puntos $N$ será el conjunto de sus circuncentros.

Entonces $A$, $B$, $C$ y $H$ son los circuncentros de $\triangle O_bO_cO$, $\triangle O_aO_cO$, $\triangle O_aO_bO$ y $\triangle O_aO_bO_c$ respectivamente.

$\blacksquare$

Problema. Construye un triángulo $\triangle ABC$ dados el centro de los nueve puntos $N$ y los circuncentros $O_b$ y $O_c$ de los triángulos $\triangle CAH$ y $\triangle ABH$ respectivamente donde $H$ es el ortocentro de $\triangle ABC$.

Solución. $O_b$ y $O_c$ son los ortocentros de $\triangle O_aO_cO$ y $\triangle O_aO_bO$ respectivamente y si los reflejamos respecto a $N$ obtendremos a los circuncentros de sus respectivos triángulos, estos son los vértices $B$ y $C$ del triángulo requerido.

Ahora tenemos dos vértices y el centro de los nueve puntos, este problema lo resolvimos en la entrada anterior.

$\blacksquare$

Centroices

Teorema 3. Los cuatro centroides de un grupo ortocéntrico de triángulos forman un cuadrángulo ortocéntrico.

Demostración. Sea $\triangle ABC$ y $H$ su ortocentro.

Sabemos que el centro de los nueve puntos $N$ de $\triangle ABC$ divide internamente al segmento $HG$ en razón $3:1$, donde $G$ es el centroide de $\triangle ABC$.

Figura 3

Como el grupo ortocéntrico de triángulos $\triangle ABC$, $\triangle HBC$, $\triangle HAC$, $\triangle HAB$ tienen el mismo centro de los nueve puntos $N$, entonces sus respectivos centroides $G$, $G_a$, $G_b$, $G_c$ están en homotecia con $H$, $A$, $B$, $C$ respectivamente desde $N$ y la razón de homotecia es $-3$.

Como dos figuras homotéticas son semejantes, entonces $GG_aG_bG_c$ es un cuadrángulo ortocéntrico.

$\blacksquare$

Corolario 3. La circunferencia de los nueve puntos de un grupo ortocéntrico de triángulos y la circunferencia de los nueve puntos del grupo ortocéntrico formado por sus centroides son concéntricas.

Demostración. Como las figuras $HABC$ y $GG_aG_bG_c$ están en homotecia desde el centro de los nueve puntos $N$ de $\triangle ABC$ entonces sus respetivas circunferencias de los nueve puntos también están en homotecia desde $N$.

Como $N$ es el centro de una de ellas, entonces son concéntricas.

$\blacksquare$

Corolario 4. Dado un cuadrángulo ortocéntrico, el cuadrángulo ortocéntrico formado por sus circuncentros y el cuadrángulo ortocéntrico formado por sus centroides tienen el mismo centro de los nueve puntos y además existe una homotecia entre ellos con centro en este punto.

Demostración. Por los corolarios 2 y 3, $OO_aO_bO_c$ y $GG_aG_bG_c$ tienen el mismo centro de los nueve puntos que $HABC$ y son homotéticos con este último precisamente desde $N$ en razón $-1$ y $-3$ respectivamente.

Figura 4

Por lo tanto, existe una homotecia con centro en $N$ y razón $3$ que lleva a $GG_aG_bG_c$ en $OO_aO_bO_c$.

$\blacksquare$

Incentro y excentros

Teorema 4. El incentro y los excentros de un triángulo dado forman un cuadrángulo ortocéntrico y el circuncírculo del triángulo dado es la circunferencia de los nueve puntos de este grupo ortocéntrico de triángulos.

Demostración. Como las bisectrices interna y externa de los ángulos de un triángulo $\triangle ABC$ son perpendiculares entre si entonces el incentro $I$ es el ortocentro del triángulo formado por los excentros $\triangle I_aI_bI_c$ y el triángulo $\triangle ABC$ es el triángulo órtico de $\triangle I_aI_bI_c$.

Figura 5

Entonces, por el teorema 1 y corolario 1, $I_aI_bI_cI$ es un grupo ortocéntrico de puntos y su circunferencia de los nueve puntos es el circuncírculo de $\triangle ABC$.

$\blacksquare$

Proposición. El segmento que une el ortocentro de un triángulo dado con el circuncentro del triángulo formado por los excentros del triángulo dado es bisecado por el incentro del triángulo medial del triángulo dado.

Demostración. Sea $\triangle ABC$ un triángulo, $I$, $I_a$, $I_b$, $I_c$, el incentro y sus respectivos excentros, $O$ y $O_e$ los circuncentros de $\triangle ABC$ y $\triangle I_aI_bI_c$ respectivamente.

Figura 6

Por el teorema anterior, $I$ y $O$ son el ortocentro y el centro de los nueve puntos respectivamente de $\triangle I_aI_bI_c$, por lo tanto, $O$ es el punto medio de $IO_e$.

Sean $H$ y $G$ el ortocentro y el centroide respectivamente de $\triangle ABC$, como $H$, $G$ y $O$ son colineales y $G$ triseca el segmento $OH$, entonces, $G$ es el centroide de $\triangle IO_eH$.

Por lo tanto, $IG$ biseca a $O_eH$ en $I’$ y $\dfrac{IG}{2} = GI’$.

Por otro lado, sabemos que existe una homotecia con centro en $G$ y razón $\dfrac{-1}{2}$, que lleva a $\triangle ABC$, a su triangulo medial $\triangle A’B’C’$, por lo que sus respectivos incentros $I$ y $I_m$ son puntos homólogos de esta homotecia, es decir $I$, $G$ y $I_m$ son colineales y $G$ triseca al segmento $II_m$.

Como $I’$ cumple con estas características entonces $I’ = I_m$.

$\blacksquare$

Más adelante…

En la próxima entrada estudiaremos otra recta notable del triángulo, la recta de Simson, veremos que la intersección de dos rectas de Simson se intersecan en la circunferencia de los nueve puntos y que cierto conjunto de rectas de Simson forman un cuadrángulo ortocéntrico.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que las rectas de Euler de los cuatro triángulos de un grupo ortocéntrico son concurrentes.
  2. Demuestra que el simétrico del circuncentro de un triángulo con respecto a uno de los lados del triángulo coincide con el simétrico del vértice opuesto al lado considerado respecto al centro de los nueve puntos del triángulo.
  3. Muestra que los vértices de un grupo ortocéntrico de triángulos pueden ser considerados como los centroides de otro grupo ortocéntrico de triángulos.
  4. Sea $\triangle ABC$ un triángulo rectángulo con $\angle A = \dfrac{\pi}{2}$, $D$ el pie de la altura por $A$, las bisectrices de $\angle BAD$ y $\angle DAC$ intersecan a $BC$ en $P$ y $P’$ respectivamente. Las bisectrices de $\angle DBA$ y $\angle ACD$ intersecan a $AD$ en $Q$ y $Q’$ respectivamente.
    $i)$ Muestra que $PP’QQ’$ es un cuadrángulo ortocéntrico,
    $ii)$ si $I$, $J$ y $K$ son los incentros de $\triangle ABC$, $\triangle ABD$ y $\triangle ADC$, muestra que $AIJK$ es un cuadrángulo ortocéntrico.
  5. Prueba que la suma de los cuadrados de dos segmentos no adyacentes que unen vértices de un cuadrángulo ortocéntrico es igual al cuadrado del circundiámetro de los triángulos de este grupo ortocéntrico.
  6.  Construye un triángulo $\triangle ABC$ dados su circuncentro $O$, y los circuncentros de los triángulos $\triangle II_bI_c$ y $\triangle II_aI_c$, donde $I$, $I_a$, $I_b$ y $I_c$ es el incentro y los excentros de $\triangle ABC$.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 109-115.
  • Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 165-167.
  • Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 58.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Triángulo medial y recta de Euler

Por Rubén Alexander Ocampo Arellano

2 respuestas

Introducción

Continuando con el estudio de las propiedades del centroide, en esta entrada veremos que es colineal con el ortocentro y el circuncentro, y que además triseca al segmento que une dichos puntos. Para establecer estos resultados, veremos primero algunos resultados del triángulo medial de un triángulo dado.

Triángulo medial

Definición 1. Al triángulo que tiene como vértices los puntos medios de un triángulo dado se le conoce como triángulo medial o triángulo complementario del triángulo dado.

Teorema 1. Un triángulo y su triángulo medial son homotéticos además comparten el mismo centroide.

Demostración. Sean $\triangle ABC$, $A’$, $B’$ y $C’$ los puntos medios de $BC$, $AC$ y $AB$ respectivamente.

Por el teorema del segmento medio, los lados del triángulo medial $\triangle A’B’C’$ son paralelos a los lados de $\triangle ABC$ y por lo tanto son homotéticos.

Ya que las rectas determinadas por dos puntos homólogos, $AA’$, $BB’$ y $CC’$ son las medianas de $\triangle ABC$, entonces el centroide $G$ es el centro de homotecia y sabemos que $AG = 2GA’$, por lo que la razón de homotecia es $\dfrac{-1}{2}$, donde el signo menos indica que dos puntos homólogos de esta homotecia se encuentran en lados opuestos respecto del centro de homotecia.

Figura 1

Como $BC$ y $B’C’$ son rectas homotéticas, entonces el punto homólogo de $A’ \in BC$ es $E = A’G \cap B’C’$, y como $A’$ es el punto medio de $BC$ entonces $E$ es el punto medio de $B’C’$, pues la homotecia preserva las proporciones.

Por lo tanto, $A’G$ es mediana de $\triangle A’B’C’$, de manera similar podemos ver que $B’G$ y $C’G$ son medianas de $\triangle A’B’C’$, por lo tanto, $G$ es el centroide de $\triangle A’B’C’$.

$\blacksquare$

Proposición 1. El circuncentro de un triángulo es el ortocentro de su triángulo medial.

Demostración. Se sigue del hecho de que las mediatrices de un triángulo son las alturas de su triángulo medial, esto es así porque los vértices del triángulo medial son, por definición, los puntos medios de un triángulo dado y los lados del triángulo medial son paralelos a los lados del triángulo dado.

$\blacksquare$

Figura 2

Triángulo anticomplementario

Definición 2. Dado un triángulo, al triángulo formado por las rectas paralelas a los lados del triángulo dado a través de los respectivos vértices opuestos, se le conoce como triángulo anticomplementario del triángulo dado.

Proposición 2. Un triángulo y su triángulo anticomplementario son homotéticos y tienen el mismo centroide.

Demostración. Consideremos $\triangle ABC$ y $\triangle A’’B’’C’’$ su triángulo anticomplementario.

Figura 3

Como $\square C’’BCA$ y $\square ABCB’’$ son paralelogramos entonces $C’’A = BC = AB’’$, por lo tanto, $A$ es el punto medio de $B’’C’’$. De manera análoga vemos que $B$ y $C$ son puntos medio de $A’’C’’$ y $A’’B’’$ respectivamente,

Por lo tanto, $\triangle ABC$ es el triángulo medial de $\triangle A’’B’’C’’$ y por el teorema 1 se tiene el resultado.

$\blacksquare$

Circunferencia de Droz Farny

Proposición 3. El producto de los segmentos en que el ortocentro divide a la altura de un triángulo es igual para las tres alturas del triángulo.

Demostración. Sean $\triangle ABC$ y $D$, $E$ y $F$ los pies de las alturas por $A$, $B$ y $C$ respectivamente y $H$ el ortocentro.

Figura 4

Notemos que $\triangle AFH \sim \triangle CDH$ y $\triangle AEH \sim \triangle BDH$ (son semejantes) pues son triángulos rectángulos y comparten un ángulo opuesto por el vértice, por lo tanto
$\dfrac{AH}{CH} = \dfrac{FH}{DH}$ $\Rightarrow AH \times DH = CH \times HF$,
$\dfrac{AH}{BH} = \dfrac{EH}{DH}$ $\Rightarrow AH \times DH = BH \times HE$.

De esto se sigue que
$CH \times HF = AH \times DH = BH \times HE$.

$\blacksquare$

Teorema 2. Si tomamos los vértices de un triángulo como centros de circunferencias del mismo radio, estas cortaran a los respectivos lados de su triángulo medial en tres pares de puntos que son equidistantes del ortocentro del triángulo.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo medial, tracemos tres circunferencias del mismo radio $(A, r)$, $(B, r)$ y $(C, r)$ las cuales intersecan a $B’C’$, $A’C’$ y $A’B’$ en $P$, $P’$; $Q$, $Q’$ y $R$, $R’$, respectivamente.

Sean $D \in BC$ el pie de la altura por $A$, y $M = AD \cap B’C’$, por el teorema de Pitágoras en $\triangle AMP$ y $\triangle HMP$ tenemos
$AP^2 – AM^2 = MP^2 = HP^2 – HM^2$
$\Rightarrow AP^2 – HP^2 = AM^2 – HM^2 = (AM + HM)(AM – HM)$.

Figura 5

Como $\triangle AC’B’ \cong \triangle C’BA’$ son congruentes por criterio LLL entonces sus alturas desde $A$ y $C’$, respectivamente, son iguales , por lo tanto $AM = MD$,
$\Rightarrow AP^2 – HP^2 = (MD + HM)AH = HD \times AH$.

Por otra parte, $\triangle PAP’$ es isósceles y como $AM$ es altura entonces $AM$ es mediatriz de $PP’$, por lo tanto $HP = HP’$$\Rightarrow$
$\begin{equation} HP’^2 = HP^2 = AP^2 – AH \times HD. \end{equation}$.

Si consideramos $E$ y $F$ los pies de las alturas por $B$ y $C$ respectivamente podemos encontrar fórmulas análogas
$\begin{equation} HQ’^2 = HQ^2 = BQ^2 – BH \times HE, \end{equation} $
$\begin{equation} HR’^2 = HR^2 = CR^2 – CH \times HF. \end{equation} $.

Como $(A, r)$, $(B, r)$ y $(C, r)$ tienen el mismo radio, entonces $AP = BQ = CR$ y por la proposición 3, $AH \times DH = BH \times HE = CH \times HF$.

Tomando lo anterior en cuenta y a las ecuaciones $(1)$, $(2)$ y $(3)$ se sigue que
$HP = HP’ = HQ = HQ’ = HR = HR’$.

$\blacksquare$

Recta de Euler

Teorema 3. El circuncentro, el centroide y el ortocentro de todo triangulo son colineales, con el centroide siempre en medio, a la recta determinada por estos tres puntos se le conoce como recta de Euler del triángulo, además $HG = 2GO$.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo medial, por el teorema 1, $\triangle ABC$ y $\triangle A’B’C’$ están en homotecia desde $G$, el centroide, que es el mismo para ambos triángulos, y la razón de homotecia es $\dfrac{-1}{2}$.

Consideremos la altura $AD$ de $\triangle ABC$, la homotecia de $AD$ es una recta paralela a ella y que pasa por el punto homólogo de $A$, $A’$, es decir la homotecia de una altura de $\triangle ABC$ es una altura de $\triangle A’B’C’$.

Figura 6

Como el ortocentro $H$ de $\triangle ABC$ es la intersección de sus alturas, entonces su punto homologo bajo la homotecia estará en la intersección de las alturas de $\triangle A’B’C’$, esto es, el ortocentro de $\triangle A’B’C’$, $H’$.

Con esto tenemos que el ortocentro de $\triangle A’B’C’$ es colineal con $G$ el centroide y el ortocentro de $\triangle ABC$ respectivamente, además, debido a la razón de homotecia, $HG = 2GH’$.

Por la proposición 1, el ortocentro del triángulo medial $\triangle A’B’C’$ es el circuncentro $O$ de $\triangle ABC$.

Así, $O$, $G$ y $H$ son colineales y $HG = 2GO$.

$\blacksquare$

Observación. Notemos que si el triángulo es equilátero el ortocentro, el centroide y el circuncentro son el mismo punto y por lo tanto la recta de Euler degenera en un punto.

Problema. Construye un triángulo $\triangle ABC$ dados el vértice $A$, el circuncentro $O$ y las distancias de $A$ al ortocentro $AH$, y al centroide $AG$.

Solución. El centroide $G$ se encuentra en la circunferencia con centro en $A$ y radio $AG$, $(A, AG)$, el ortocentro $H$ se encuentra en la circunferencia con centro en $A$ y radio $H$, $(A, AH)$.

Por el teorema 3 sabemos que $H$, $G$ y $O$ son colineales y que $HO = 3GO$, por lo que $H$ y $G$ se encuentran en homotecia desde $O$.

Entonces, a $(A, AH)$ le aplicamos una homotecia con centro en $O $ y razón $\dfrac{1}{3}$, esto será una circunferencia $\Gamma$ y $G$ resultara de la intersección de $\Gamma$ con $(A, AG)$.

Figura 7

Teniendo a $G$ construido, como tenemos el circuncírculo $(O, OA)$ y un vértice del triángulo, el problema se reduce a la solución del problema 2 de la entrada anterior.

$\blacksquare$

Distancia entre puntos notables

Teorema 4. Para un triángulo con lados $a$, $b$, $c$, ortocentro $H$, centroide $G$, y circuncírculo $(O, R)$ tenemos:
$OH^2 = 9R^2 – (a^2 + b^2 + c^2)$,
$HG^2 = 4R^2 – \dfrac{4}{9}( a^2 – b^2 + c^2)$.

Demostración. Por el teorema 3 sabemos que $OH = 3OG$ y $HG = 2GO$, además en la entrada anterior calculamos
$OG^2 = R^2 – (\dfrac{a^2 + b^2 + c^2}{9})$.

Por lo tanto,
$OH^2 = 9OG^2 = 9R^2 – (a^2 + b^2 + c^2)$,
$HG^2 = 4OG^2 = 4R^2 – \dfrac{4}{9}(a^2 + b^2 + c^2)$.

$\blacksquare$

Corolario. Podemos calcular la suma de los cuadrados de las distancias del ortocentro a los vértices del triángulo en función del circunradio y los lados del triángulo con la siguiente fórmula.
$HA^2 + HB^2 + HC^2 = 12R^2 + (a^2 + b^2 + c^2)$.

Demostración. Por el teorema 4, y usando las fórmulas encontradas en la entrada anterior
$HA^2 + HB^2 + HC^2 = GA^2 + GB^2 + GC^2 + 3HG^2$,
$GA^2 + GB^2 + GC^2 = \dfrac{a^2 + b^2 + c^2}{3}$ .

Esto implica que,
$HA^2 + HB^2 + HC^2 = \dfrac{a^2 + b^2 + c^2}{3} + 12R^2 – \dfrac{4}{3}(a^2 + b^2 + c^2)$
$= 12R^2 – (a^2 + b^2 + c^2)$.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos otro triángulo asociado a un triángulo dado, aquel cuyos vértices son los pies de las alturas del triángulo dado.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que el triángulo complementario y el triángulo anticomplementario de un triángulo dado son homotéticos, encuentra el centro y la razón de homotecia.
  2. Sea $\triangle ABC$ y $P$ un punto en el plano, considera $A’$, $B’$ y $C’$ los pies de las perpendiculares dese $P$ a $BC$, $AC$ y $AB$ respectivamente. Desde los puntos medios de $A’B’$, $A’C’$ y $B’C’$ traza perpendiculares a los lados de $AB$, $AC$ y $BC$ respectivamente, muestra que este último conjunto de perpendiculares son concurrentes.
  3. Sean $D$, $D’ \in BC$ de un triangulo $\triangle ABC$, tal que el punto medio de $BC$ es el punto medio de $DD’$, sea $E = AD \cap B’C’$, donde $B’$ y $C’$ son los puntos medios de $AC$ y $AB$ respectivamente, muestra que $ED’$ pasa por el centroide de $\triangle ABC$.
  4. Muestra que la recta de Euler de un triángulo pasa por uno de los vértices del triángulo si y solo si el triángulo es isósceles o rectángulo.
  5. Prueba que la recta que une el centroide de un triangulo con un punto $P$ en su circuncírculo biseca al segmento que une el punto diametralmente opuesto a $P$ con el ortocentro.
  6. Sean $H$, $G$, $(O, R)$ y $(I, r)$, el ortocentro, el centroide, el circuncírculo y el incírculo de un triángulo, muestra que:
    $i)$ $HI^2 + 2OI^2 = 3(IG^2 + 2OG^2)$,
    $ii)$ $3(IG^2 + \dfrac{HG^2}{2}) – IH^2 = 2R(R – 2r)$.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 68-69, 94-96, 101-102.
  • Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 18-19.
  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 65-68.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»