Introducción

En esta ocasión veremos que nueve puntos notables del triángulo son concíclicos, a saber, los puntos medios de los lados, los pies de las alturas y los puntos medios de los segmentos que unen al ortocentro con los vértices del triángulo. A esta circunferencia se le conoce como circunferencia de los nueve puntos y su centro se encuentra en la recta de Euler del triángulo considerado.

Triángulo de Euler

Definición 1. A los puntos medios de los segmentos que unen los vértices de un triángulo dado con su ortocentro se les conoce como puntos de Euler, y el triángulo que tiene como vértices los puntos de Euler es el triángulo de Euler del triángulo dado.

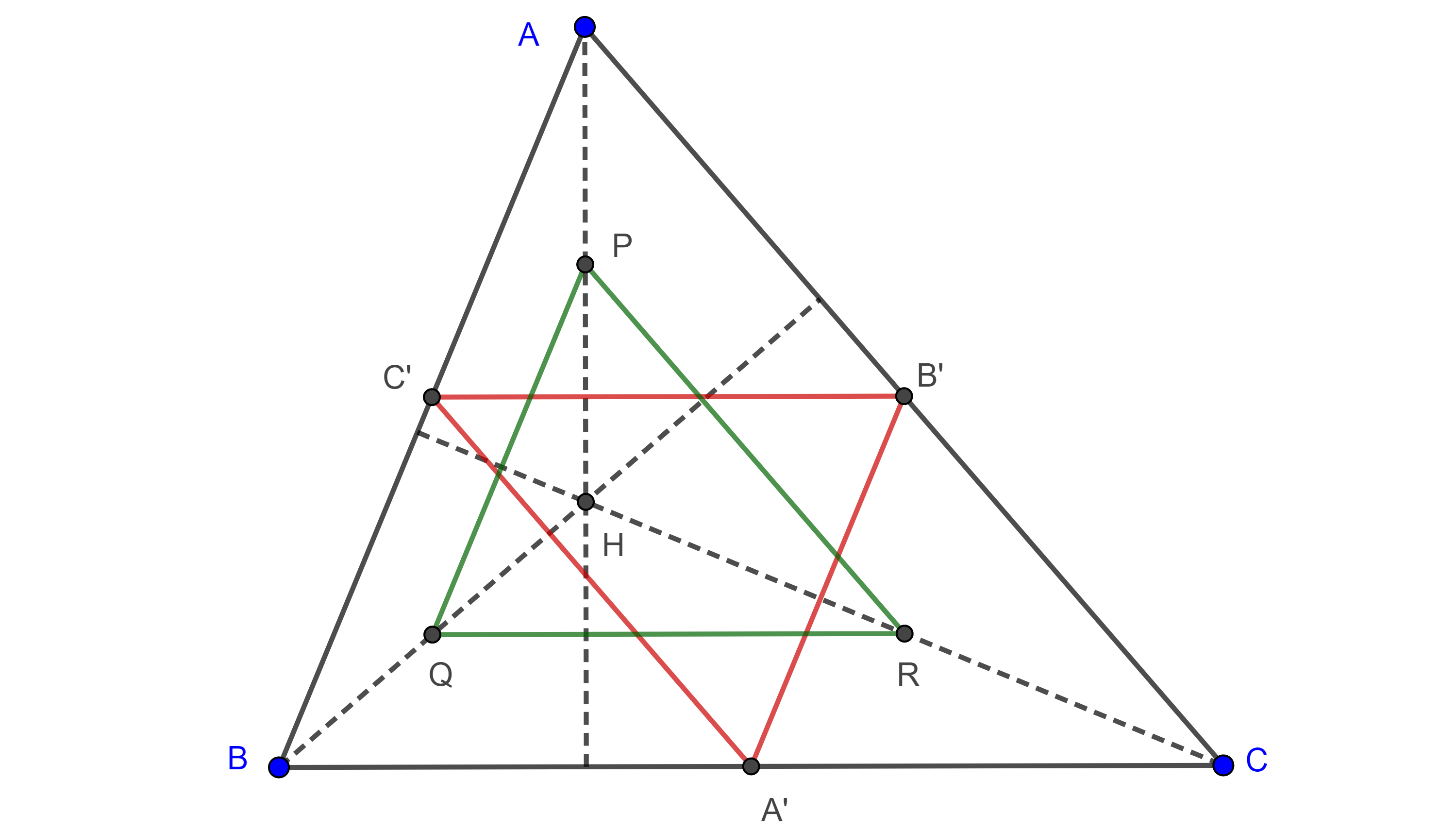
Observación. Por la definición anterior, un triángulo y su triángulo de Euler son homotéticos (figura 1), con centro de homotecia en el ortocentro y razón de homotecia ${\displaystyle \frac{1}{2}}$.

Proposición 1. El triángulo de Euler y el triángulo medial de todo triángulo son congruentes y sus respectivos lados son paralelos.

Demostración. Sean $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ el triángulo medial y $\mathrm{△}PQR$ el triángulo de Euler de $\mathrm{△}ABC$, (figura 1).

$C^{\prime }$ y $B^{\prime }$ son puntos medios de $AB$ y $AC$ respectivamente, así que $C^{\prime }{B}^{\prime }$ es un segmento medio de $\mathrm{△}ABC$, de igual manera $QR$ es un segmento medio de $\mathrm{△}HBC$, donde $H$ es el ortocentro de $\mathrm{△}ABC$.

Por lo tanto, $C^{\prime }{B}^{\prime }\parallel BC\parallel QR$, y $2C^{\prime }{B}^{\prime }=BC=2QR$.

De manera análoga podemos ver que $A^{\prime }{C}^{\prime }=RP$ y $A^{\prime }{B}^{\prime }=QP$, por criterio de congruencia LLL, $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }\cong \mathrm{△}PQR$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Circunferencia de los nueve puntos

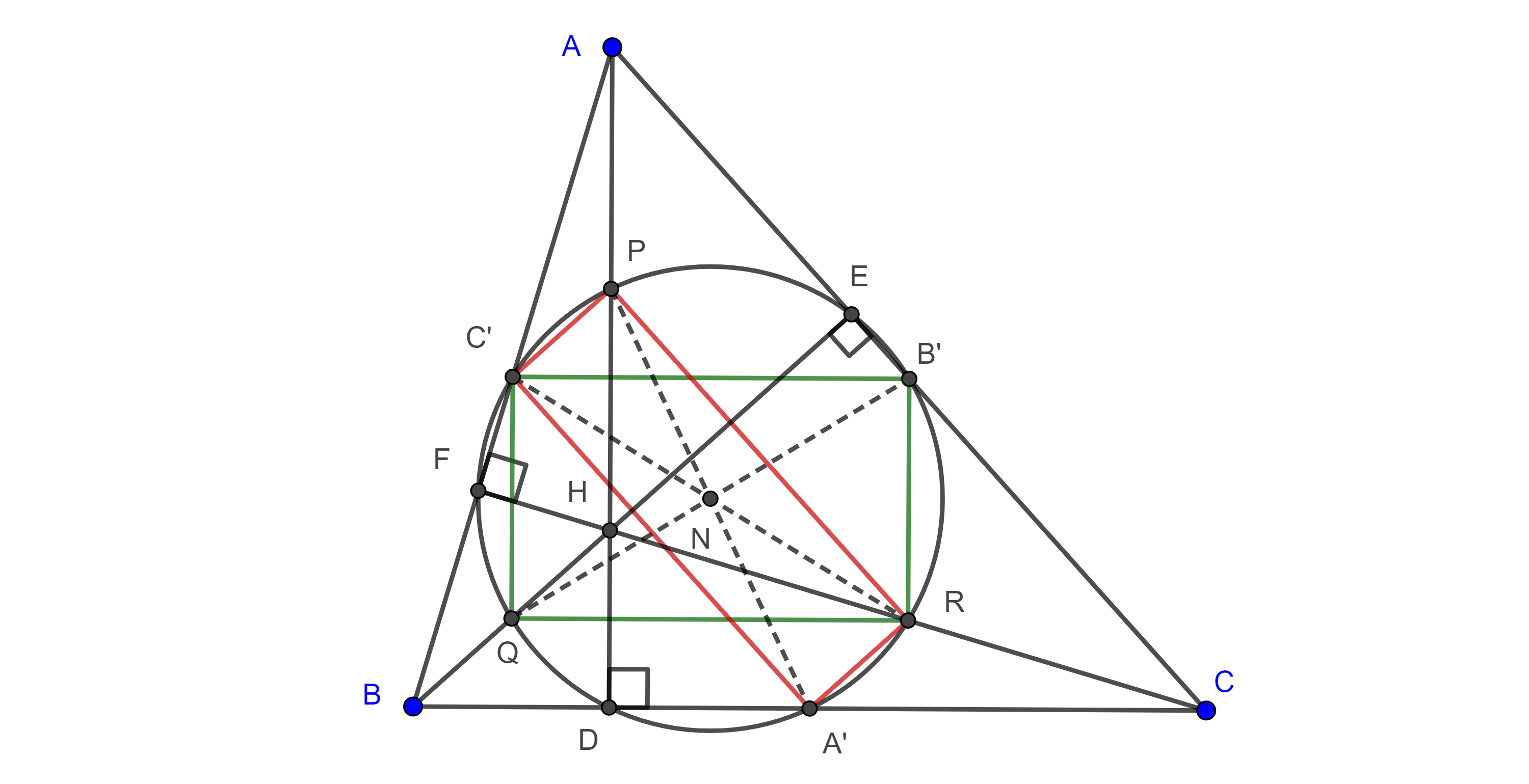
Teorema 1. El triángulo de Euler, el triángulo medial y el triángulo órtico de todo triángulo tienen el mismo circuncírculo.

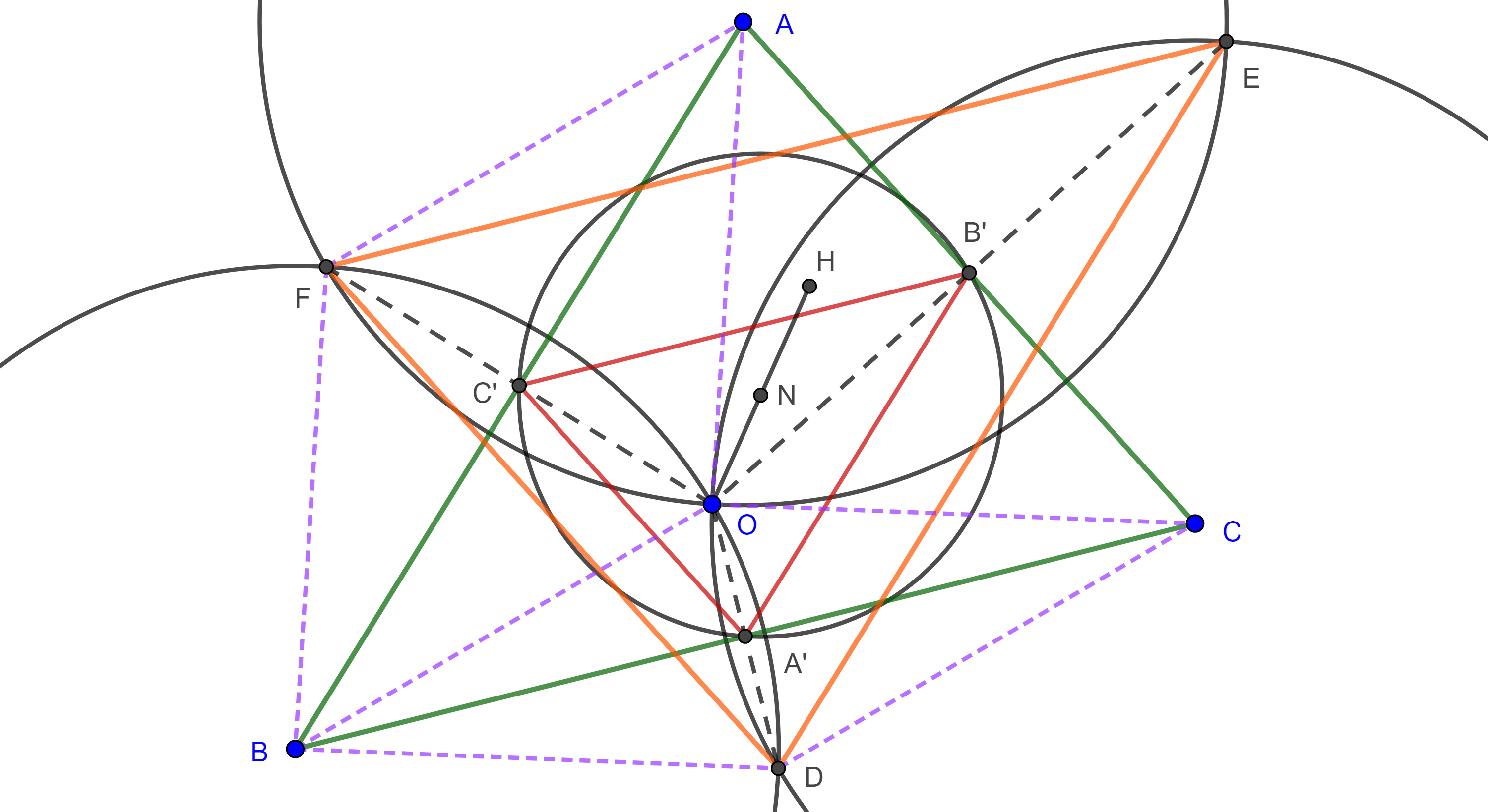
Demostración. Por la proposición 1 y empleando la misma notación de esta, sabemos que $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}{C}^{\prime }QR{B}^{\prime }$ es un paralelogramo (figura 2).

$C^{\prime }Q$ es un segmento medio de $\mathrm{△}BAH$, así que $C^{\prime }Q\parallel AH$ $\Rightarrow C^{\prime }Q\perp BC$.

Y como $QR\parallel BC$, entonces, $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}{C}^{\prime }QR{B}^{\prime }$ es un rectángulo, lo que significa que las diagonales $C^{\prime }R$ y $Q{B}^{\prime }$ tienen la misma longitud y se cortan en su punto medio, $N$.

De manera análoga podemos probar que $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}P{C}^{\prime }{A}^{\prime }R$ es un rectángulo y que $P{A}^{\prime }$ y $C^{\prime }R$ tienen la misma longitud y se cortan en su punto medio.

Como el punto medio de $C^{\prime }R$ es $N$, entonces, los puntos $A^{\prime }$, $B^{\prime }$, $C^{\prime }$, $P$, $Q$ y $R$ son equidistantes a $N$.

Sean $D$, $E$ y $F$ los pies de las alturas por $A$, $B$ y $C$ respectivamente.

Como $A^{\prime }P$, $B^{\prime }Q$ y $C^{\prime }R$ son diámetros de esta circunferencia y además $\mathrm{\angle }{A}^{\prime }DP=\mathrm{\angle }QE{B}^{\prime }=\mathrm{\angle }RF{C}^{\prime }={\displaystyle \frac{\pi }{2}}$, es decir estos diámetros subtienden ángulos rectos en los puntos $D$, $E$ y $F$ respectivamente, entonces $D$, $E$ y $F$ se encuentran en la misma circunferencia.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Definición 2. Nos referiremos al centro de la circunferencia de los nueve puntos de un triángulo como el centro de los nueve puntos y los denotaremos como $N$.

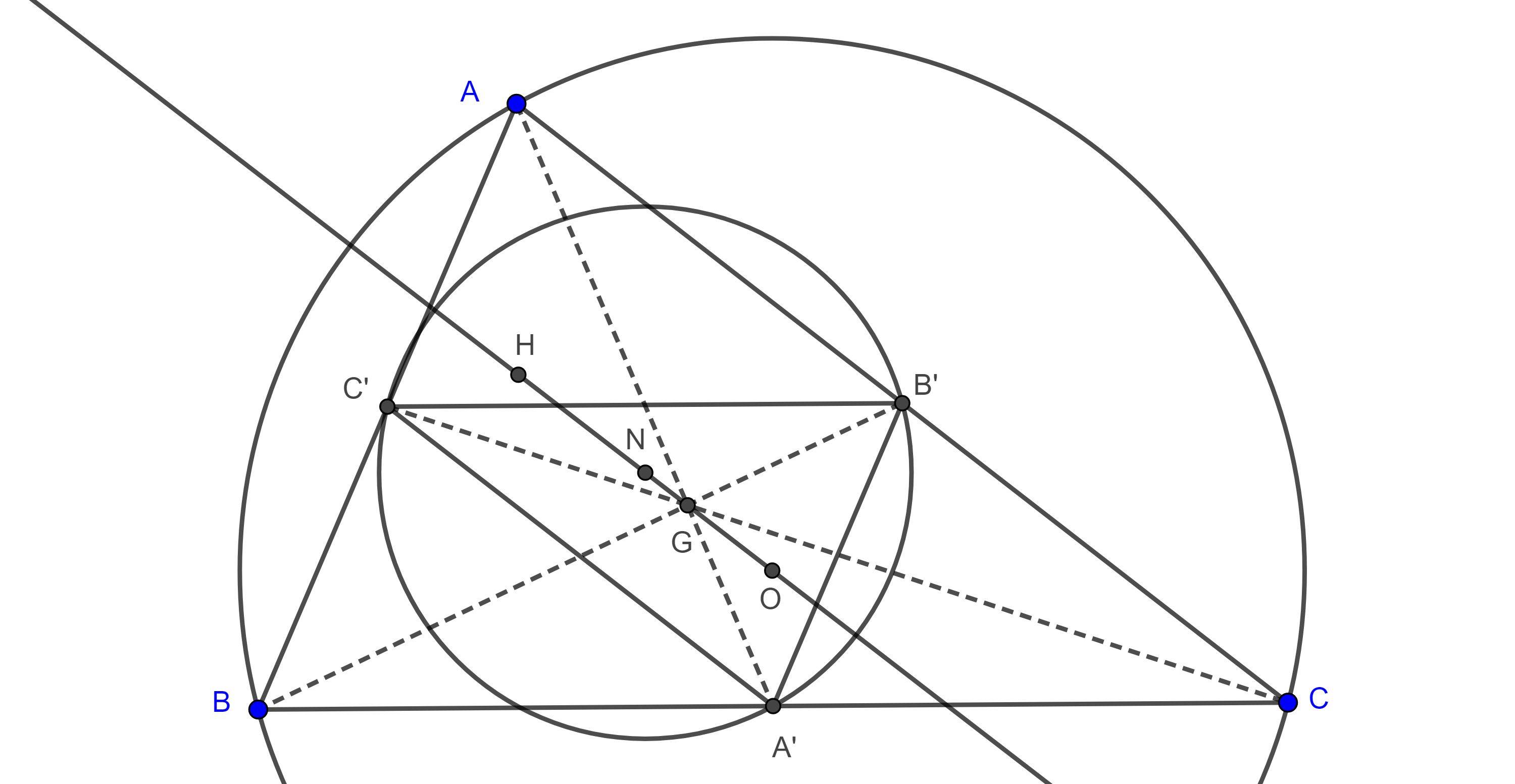
Teorema 2. El radio de la circunferencia de los nueve puntos de un triángulo es igual a la mitad del circunradio y el centro de los nueve puntos biseca al segmento que une al circuncentro con el ortocentro.

Demostración. Recordemos que todo triángulo está en homotecia con su triángulo medial, esto implica que son semejantes, con razón ${\displaystyle \frac{-1}{2}}$ y centro de homotecia en el centroide $G$ del triángulo.

Por lo tanto, el radio de la circunferencia de los nueve puntos de un triángulo es la mitad del circunradio de este.

De la relación de homotecia también tenemos que $G$ triseca el segmento $ON$ de los circuncentros $O$ y $N$ de $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$, su triángulo medial, esto es, $OG=2GN$.

Y sabemos que $2OG=GH$, donde $H$ es el ortocentro.

Por lo tanto, $HN=ON$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Triángulo tangencial

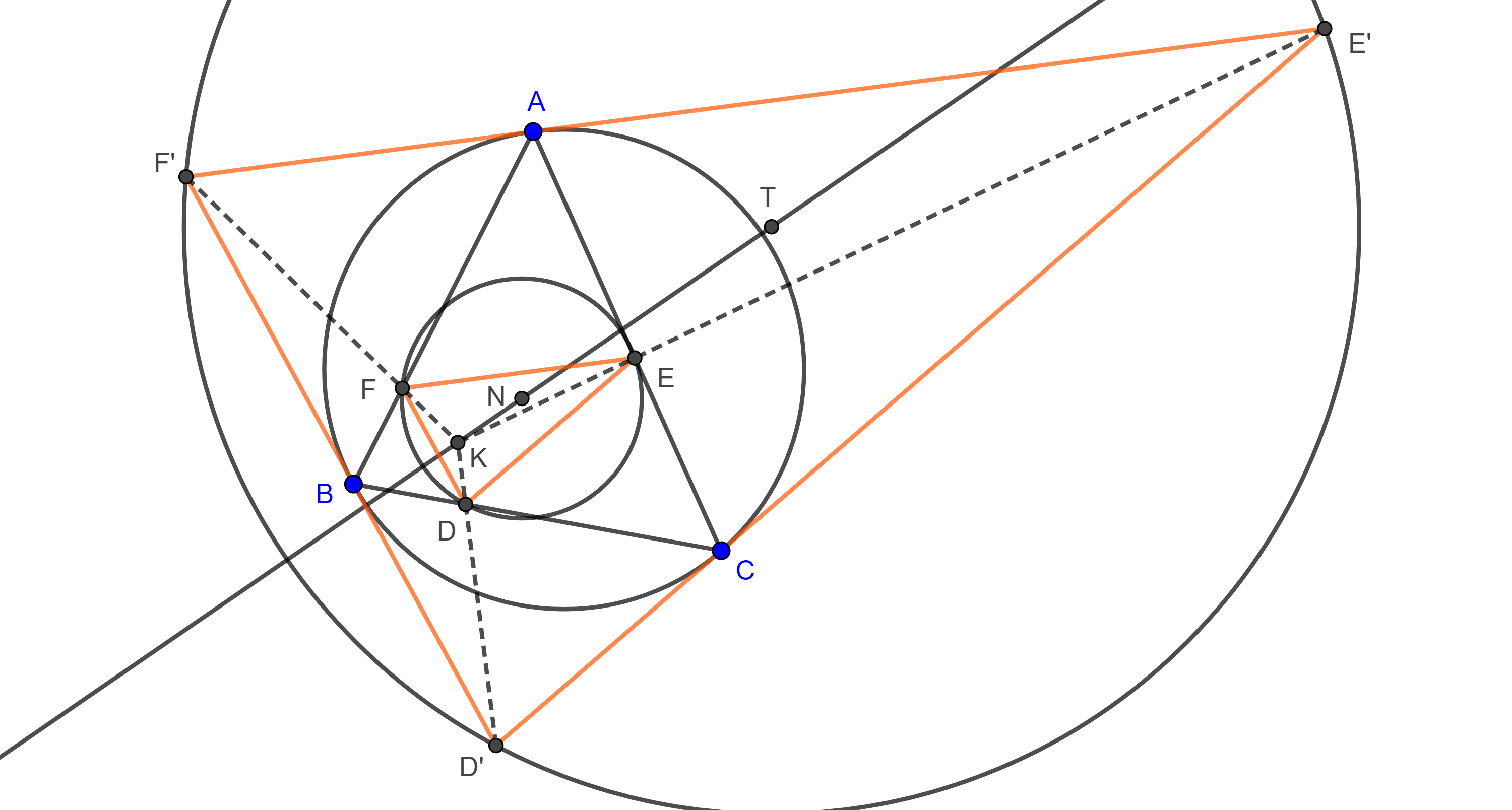
Teorema 3. El circuncentro del triángulo tangencial de un triángulo dado se encuentra en la recta de Euler del triángulo dado.

Demostración. Recordemos que el triángulo tangencial $\mathrm{△}{D}^{\prime }{E}^{\prime }{F}^{\prime }$ y el triángulo órtico $\mathrm{△}DEF$ de un triángulo $\mathrm{△}ABC$ están en homotecia desde un punto $K$ que se encuentra en la recta de Euler de $\mathrm{△}ABC$.

Ahora, como los circuncentros de los triángulos tangencial y el triángulo órtico, $T$ y $N$, respectivamente, son puntos correspondientes de esta homotecia, entonces $T$ es colineal con $N$ y $K$.

Por el teorema 2, $N$ esta en la recta de Euler de $\mathrm{△}ABC$, por lo tanto, $T$ está en la recta de Euler de $\mathrm{△}ABC$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Corolario 1. El circuncentro de un triángulo dado se encuentra en la recta de Euler del triángulo formado por los puntos de tangencia del incírculo con los lados del triángulo dado.

Demostración. Notemos que todo triángulo es el triángulo tangencial del triángulo formado por los puntos de tangencia de su incírculo con sus lados.

El resultado se sigue al aplicar el teorema 3.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Corolario 2. El cuadrado del circunradio de un triángulo es dos veces el producto del inradio de su triángulo órtico por el circunradio de su triángulo tangencial.

Demostración. Sean $R$, $p$ y $q$ los circunradios de $\mathrm{△}ABC$, de su triángulo tangencial $\mathrm{△}{D}^{\prime }{E}^{\prime }{C}^{\prime }$ y el inradio de su triángulo órtico $\mathrm{△}DEF$, respectivamente.

Como $\mathrm{△}{D}^{\prime }{E}^{\prime }{F}^{\prime }$ y $\mathrm{△}DEF$ son homotéticos entonces la razón entre sus inradios y la razón entre sus circunradios son iguales a su razón de homotecia y por lo tanto son iguales entre si, además por el teorema 2, $R$ es dos veces el circunradio de $\mathrm{△}DEF$.

${\displaystyle \frac{R}{q}}={\displaystyle \frac{p}{{\displaystyle \frac{R}{2}}}}$
$\Rightarrow R^2=2pq$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplos

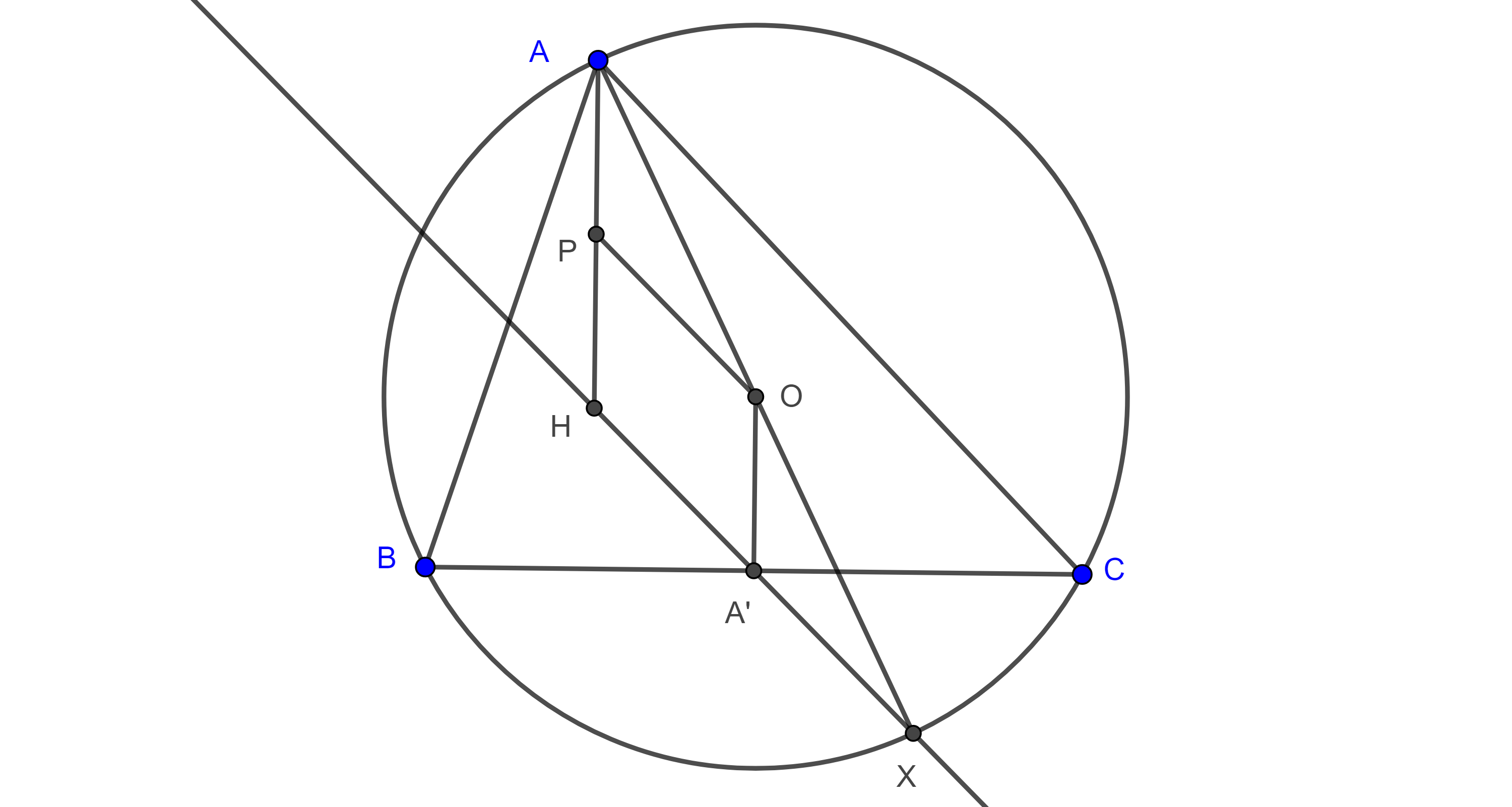
Proposición 2. La recta determinada por el ortocentro de un triángulo y el punto medio de uno de sus lados pasa por el punto diametralmente opuesto, en su circuncírculo, al vértice opuesto del lado considerado.

Demostración. Sean $\mathrm{△}ABC$, $(O,R)$ su circuncírculo, $X$ el punto diametralmente opuesto a $A$, $H$ el ortocentro, $A^{\prime }$ el punto medio de $BC$ y $P$ el punto de Euler entre $A$ y $H$.

$PO$ es un segmento medio de $\mathrm{△}AHX$, por lo tanto, $HX\parallel PO$.

Por la proposición 6 de la entrada anterior tenemos que $PH=O{A}^{\prime }$ y ambos son perpendiculares a $BC$, por lo tanto, $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}PH{A}^{\prime }O$ es un paralelogramo, es decir, $H{A}^{\prime }\parallel PO$.

Como la paralela a una recta por un punto exterior a ella es única, entonces $H$, $A^{\prime }$ y $X$ son colineales.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 3. Sean $A$, $B$ y $C$ los centros de tres circunferencias distintas, con el mismo radio y que tienen un punto $O$ en común.

Consideremos los otros puntos en común, $D=(B,r)\cap (C,r)$, $E=(A,r)\cap (C,r)$ y $F=(A,r)\cap (B,r)$, entonces el circunradio de $\mathrm{△}DEF$ es igual al de las tres circunferencias dadas y su circuncentro es el ortocentro de $\mathrm{△}ABC$.

Demostración. Notemos primero que $OA=OB=OC=r$, por lo tanto, el circuncentro de $\mathrm{△}ABC$ es $O$ y su circunradio es $r$.

Como $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}AFBO$ y $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}OBDC$ son rombos entonces $AF=BO=CD$ y $AF\parallel BO\parallel CD$.

Por tanto, $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}AFDC$ es paralelogramo y así $\Rightarrow AC=DF$ y $AC\parallel DF$.

De manera análoga podemos ver que $AB=DE$, $AB\parallel DE$ y $BC=EF$ y $BC\parallel EF$

Por lo tanto, $\mathrm{△}ABC$ y $\mathrm{△}DEF$ son congruentes por criterio LLL y sus respectivos lados son paralelos.

Como $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}OBDC$ es un rombo entonces, $OD\perp BC$ además $OD$ y $BC$ se intersecan en su punto medio, $A^{\prime }$.

De manera análoga podemos ver $AB\perp OF$, se bisecan en $C^{\prime }$ y $AC\perp OE$, se bisecan en $B^{\prime }$.

De lo anterior se sigue que $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ es el triángulo medial de $\mathrm{△}ABC$, que $DO$, $EO$ y $FO$ son las alturas de $\mathrm{△}DEF$.

Por lo tanto $O$ es el ortocentro de $\mathrm{△}DEF$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ es el triángulo de Euler de $\mathrm{△}DEF$.

En consecuencia, la circunferencia de los nueve puntos es la misma para $\mathrm{△}ABC$ y $\mathrm{△}DEF$, por el teorema 2, se sigue que sus circunradios son iguales, por lo tanto, el circunradio de $\mathrm{△}DEF$ es $r$.

También por el teorema 2, sabemos que el centro de los nueve puntos biseca al segmento que une ortocentro con el circuncentro.

Como el centro de los nueve puntos es el mismo para $\mathrm{△}ABC$ y $\mathrm{△}DEF$, y ya que el circuncentro de $\mathrm{△}ABC$ coincide con el ortocentro de $\mathrm{△}DEF$ entonces el circuncentro de $\mathrm{△}ABC$ coincide con el ortocentro de $\mathrm{△}DEF$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

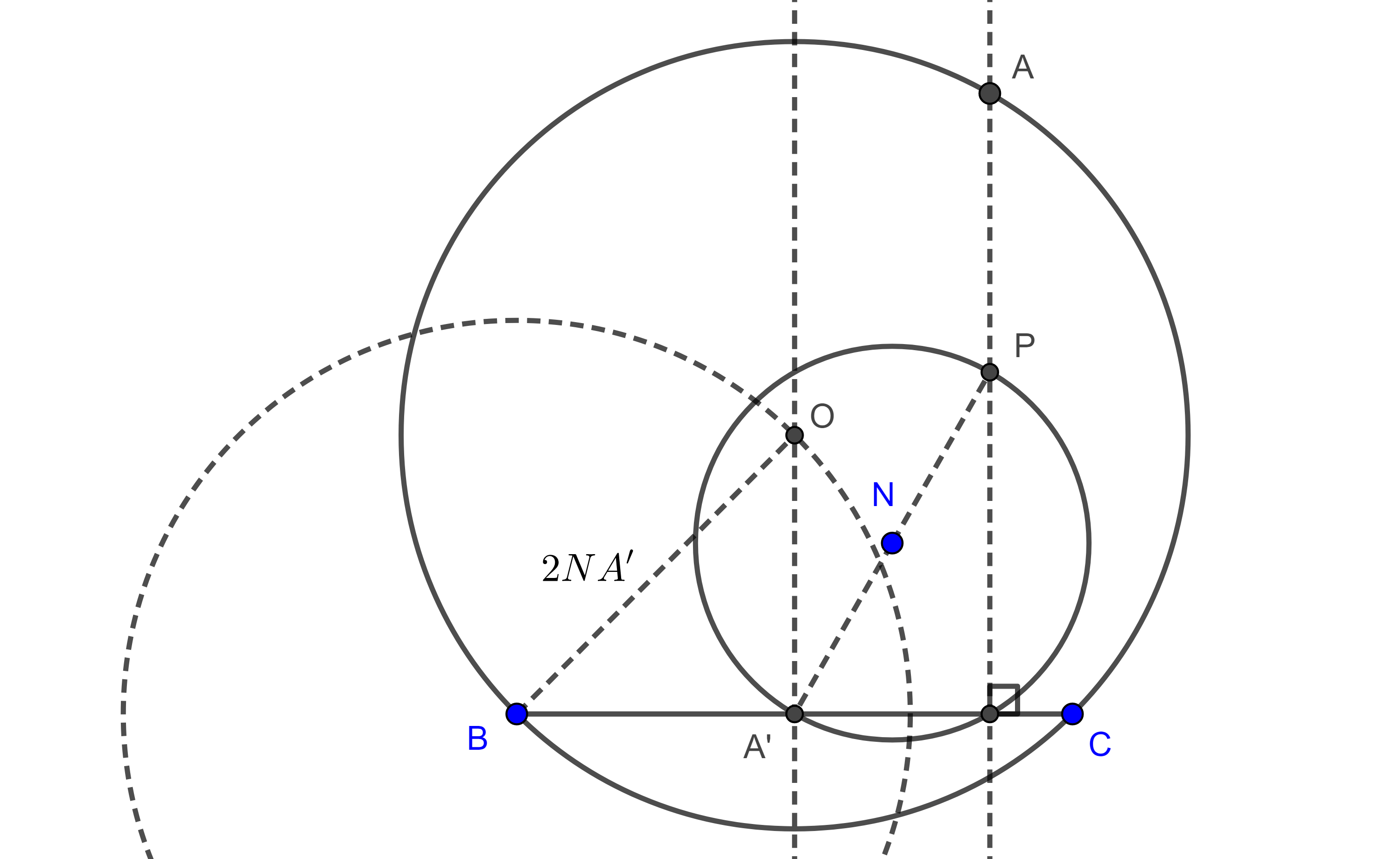
Problema. Construir un triángulo $\mathrm{△}ABC$ dados dos vértices $B$, $C$ y el centro de los nueve puntos, $N$.

Solución. Trazamos $BC$ y su punto medio $A^{\prime }$,

Con el radio $N{A}^{\prime }$ de la circunferencia de los nueve puntos, obtenemos el circunradio de $\mathrm{△}ABC$, $2N{A}^{\prime }$.

Ahora podemos encontrar al circuncentro de $\mathrm{△}ABC$ que se encuentra en la mediatriz de $BC$, trazando una circunferencia con centro en $B$ o en $C$ y radio $2N{A}^{\prime }$.

El simétrico de $A^{\prime }$ respecto a $N$ será $P$, el punto de Euler que se encuentra entre $N$ y el vértice buscado. Como la perpendicular a $BC$ por $P$ es la altura por $A$, entonces su intersección con el circuncírculo $(O,2N{A}^{\prime })$ de $\mathrm{△}ABC$, es el vértice faltante.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Más adelante…

En la próxima entrada veremos como cierto conjunto de triángulos al que llamaremos grupo ortocéntrico de triángulos tienen la misma circunferencia de los nueve puntos y otros resultados relacionados.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Muestra que el triángulo de Euler $\mathrm{△}PQR$ y el triangulo $\mathrm{△}{C}^{\prime }{B}^{\prime }D$ son congruentes, (figura 2).
2. Por los puntos medios de un triángulo dado traza paralelas a las bisectrices externas de los correspondientes ángulos opuestos. Prueba que el triángulo formado por estas paralelas y el triángulo dado tienen la misma circunferencia de los nueve puntos.
3. Muestra que las paralelas a las bisectrices internas de un triángulo dado trazadas por los respectivos puntos de Euler del triángulo dado son concurrentes, también prueba que la recta que pasa por el punto de concurrencia y el centro de los nueve puntos del triángulo dado es paralela con la recta que pasa por el circuncentro y el incentro del triángulo dado.
4. Demuestra que la circunferencia de los nueve puntos biseca cualquier segmento que une al ortocentro con un punto en el circuncírculo.
5.  Construye un triángulo dados un vértice, el ortocentro y el centro de los nueve puntos.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Triángulo órtico.
• Siguiente entrada del curso: Cuadrángulo ortocéntrico.
• Otros cursos.

Fuentes

• Altshiller, N., College Geometry. New York: Dover, 2007, pp 103-105.
• Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 20-22.
• Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 69-70.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»