Introducción

Continuando con el estudio de triángulos asociados a un triangulo dado, en esta entrada veremos algunas propiedades del triángulo órtico de un triangulo dado.

Mostraremos solo las proposiciones referentes a triángulos acutángulos, por ser muy parecidas las correspondientes versiones para triángulos obtusángulos, quedaran como ejercicio.

Preliminares

Proposición 1. El vértice de un triángulo es el punto medio del arco formado por las intersecciones de su circuncírculo con las alturas del triángulo que no pasan por el vértice considerado.

Demostración. Sean $\mathrm{△}ABC$ y $D$, $E$, $F$ los pies de las alturas por $A$, $B$, $C$, respectivamente (figura 1).

Los triángulos rectángulos $\mathrm{△}BEA$ y $\mathrm{△}CFA$ son semejantes pues $\mathrm{\angle }A$ es un ángulo en común, por lo tanto, $\mathrm{\angle }EBA=\mathrm{\angle }ACF$.

Por otro lado, consideremos $D^{\prime }=AD\cap (O,R)$, $E^{\prime }=BE\cap (O,R)$ y $F^{\prime }=CF\cap (O,R)$, las intersecciones de las alturas con el circuncírculo de $\mathrm{△}ABC$, entonces $\mathrm{\angle }{E}^{\prime }BA=\mathrm{\angle }EBA=\mathrm{\angle }ACF=\mathrm{\angle }AC{F}^{\prime }$.

Esto implica que los respectivos ángulos centrales son iguales $\mathrm{\angle }{E}^{\prime }OA=\mathrm{\angle }AO{F}^{\prime }$, por lo tanto, la longitud de arco es la misma $\stackrel{⌢}{E^{\prime }A}=\stackrel{⌢}{A{F}^{\prime }}$ y así $A$ es el punto medio de $\stackrel{⌢}{E^{\prime }{F}^{\prime }}$.

De manera análoga vemos que $B$ y $C$ bisecan a los arcos $\stackrel{⌢}{F^{\prime }{D}^{\prime }}$, $\stackrel{⌢}{D^{\prime }{E}^{\prime }}$ respectivamente.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 2. El pie de la altura de un triángulo acutángulo es el punto medio del segmento que une el ortocentro y la intersección de la altura considerada con el circuncentro.

Demostración. Por la proposición 1, $B$ es el punto medio del arco $\stackrel{⌢}{F^{\prime }{D}^{\prime }}$, por lo tanto $\mathrm{\angle }{F}^{\prime }OB=\mathrm{\angle }BO{D}^{\prime }$ y así $\mathrm{\angle }{F}^{\prime }CB=\mathrm{\angle }BC{D}^{\prime }$.

De esto se sigue que los triángulos rectángulos $\mathrm{△}HCD$, $\mathrm{△}{D}^{\prime }CD$ son congruentes por criterio ALA, por lo tanto, $HD=D{D}^{\prime }$.

Por lo tanto, $D$ es el punto medio de $H{D}^{\prime }$, de manera análoga podemos ver que $E$ y $F$ son los puntos medio de $H{E}^{\prime }$ y $H{F}^{\prime }$ respetivamente.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Triángulo órtico

Definición 1. Al triángulo cuyos vértices son los pies de las alturas de un triángulo dado se le conoce como triangulo órtico del triángulo dado.

Proposición 3. El triángulo órtico de un triángulo y el triángulo cuyos vértices son las intersecciones de su circuncírculo con las alturas del triángulo son homotéticos.

Demostración. Por la proposición 2, $E$ y $F$ son puntos media de $H{E}^{\prime }$ y $H{F}^{\prime }$ respectivamente (figura 1), por tanto, $EF$ es un segmento medio del triángulo $\mathrm{△}H{E}^{\prime }{F}^{\prime }$, entonces $EF\parallel E^{\prime }{F}^{\prime }$ y $2EF=E^{\prime }{F}^{\prime }$.

De manera análoga podemos ver que $FD\parallel F^{\prime }{D}^{\prime }$, $2FD=F^{\prime }{D}^{\prime }$ y $DE\parallel D^{\prime }{E}^{\prime }$, $2DE=D^{\prime }{E}^{\prime }$.

De lo anterior concluimos que $\mathrm{△}DEF$ está en homotecia con $\mathrm{△}{D}^{\prime }{E}^{\prime }{F}^{\prime }$ con centro en $H$ y razón ${\displaystyle \frac{1}{2}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Teorema 1. El ortocentro y los vértices de un triángulo acutángulo son en incentro y los excentros respectivamente de su triangulo órtico.

Demostración. Por la proposición 1, $A$ es el punto medio del arco $\stackrel{⌢}{E^{\prime }{F}^{\prime }}$ (figura 1), por lo tanto, $\mathrm{\angle }{E}^{\prime }{D}^{\prime }A=\mathrm{\angle }A{D}^{\prime }{F}^{\prime }$.

Por la proposición 3, los lados de $\mathrm{△}DEF$ son paralelos a los lados de $\mathrm{△}{D}^{\prime }{E}^{\prime }{F}^{\prime }$, por lo tanto $\mathrm{\angle }EDA=\mathrm{\angle }{E}^{\prime }{D}^{\prime }A=\mathrm{\angle }A{D}^{\prime }{F}^{\prime }=\mathrm{\angle }ADF$.

Entonces $AD$ es bisectriz de $\mathrm{\angle }EDF$, así podemos ver que las otras alturas de $\mathrm{△}ABC$ son las bisectrices de su triangulo órtico, con lo que $H$ es el incentro de $\mathrm{△}DEF$.

Como los lados del triángulo son perpendiculares a las alturas entonces son las respectivas bisectrices exteriores de su triangulo órtico, de esto se sigue el resultado.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Triángulo tangencial

Definición 2. Al triangulo cuyos lados son las rectas tangentes al circuncírculo de un triángulo dado a través de sus vértices, se le conoce como triángulo tangencial del triángulo dado.

Proposición 4. Los radios del circuncírculo de un triángulo que pasan por los vértices del triángulo son perpendiculares a los respetivos lados de su triangulo órtico.

Demostración. $\mathrm{△}{E}^{\prime }O{F}^{\prime }$ es isósceles (figura 2), pues $O{E}^{\prime }$ y $O{F}^{\prime }$ son radios del circuncírculo de $\mathrm{△}ABC$.

Por la proposición 1, $A$ es el punto medio del arco $\stackrel{⌢}{E^{\prime }{F}^{\prime }}$, por lo que $OA$ es bisectriz de $\mathrm{\angle }{E}^{\prime }O{F}^{\prime }$, por lo tanto, $OA$ es mediatriz de $E^{\prime }{F}^{\prime }$.

Por la proposición 3, $E^{\prime }{F}^{\prime }\parallel EF$ $\Rightarrow OA\perp EF$.

De manera análoga se ve que $OB\perp FD$ y $OC\perp DE$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

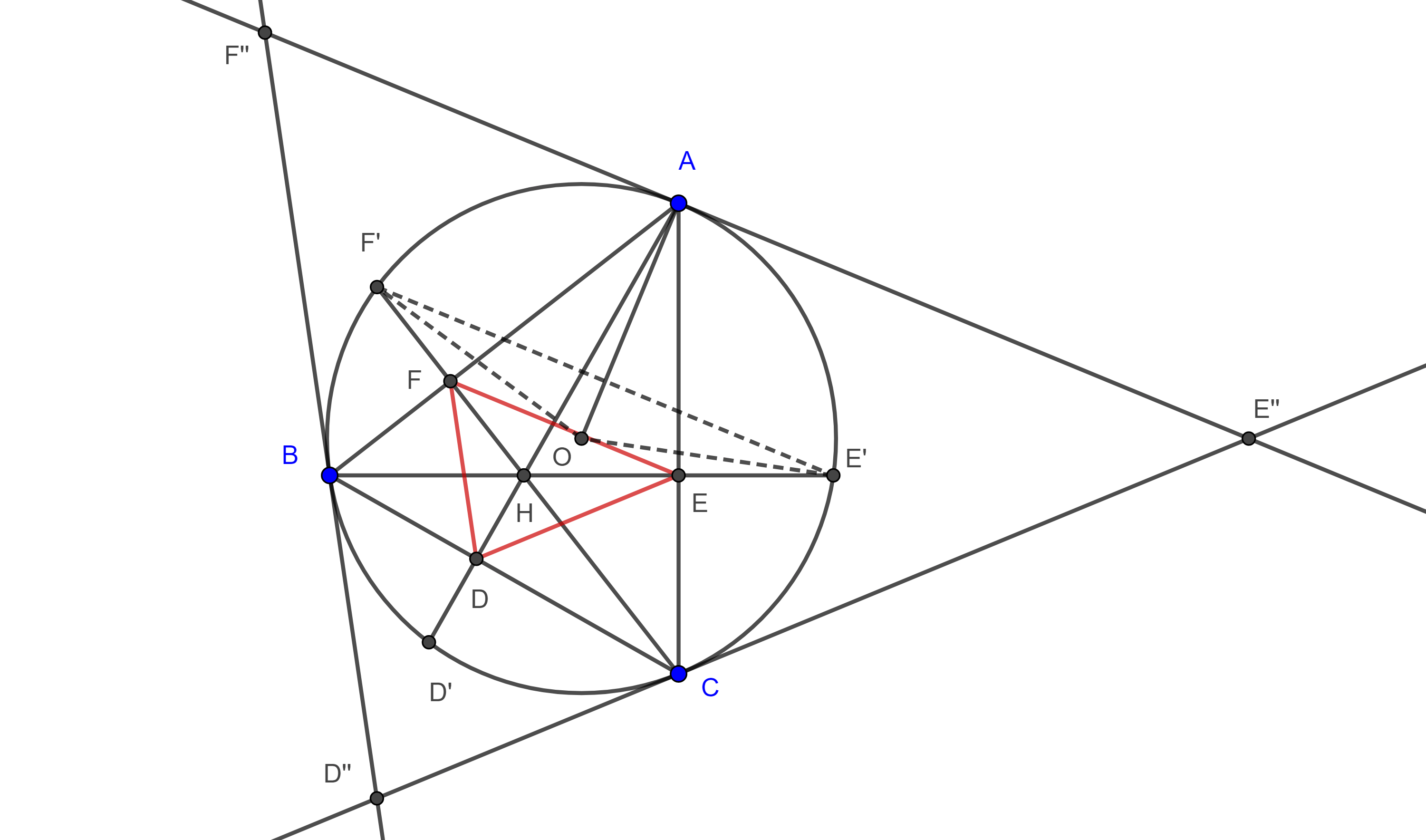
Teorema 2. El triángulo órtico y el triángulo tangencial de un triángulo dado son homotéticos y el centro de homotecia se encuentra en la recta de Euler del triángulo dado.

Demostración.  Sean $\mathrm{△}DEF$ y $\mathrm{△}{D}^{″}{E}^{″}{F}^{″}$ el triángulo órtico y tangencial respectivamente de $\mathrm{△}ABC$ (figura 2).

Como los lados del triángulo tangencial son perpendiculares a los radios que pasan por los vértices del triángulo dado, por la proposición 4, los lados del triángulo órtico son paralelos a los lados del triángulo tangencial y esto implica que los triángulos son homotéticos.

Como $\mathrm{△}DEF$ y $\mathrm{△}{D}^{″}{E}^{″}{F}^{″}$ son homotéticos entonces sus respectivos incentros son puntos homólogos.

Por el teorema 1, el incentro de $\mathrm{△}DEF$ es el ortocentro de $\mathrm{△}ABC$ y por construcción el incentro de $\mathrm{△}{D}^{″}{E}^{″}{F}^{″}$ es el circuncentro de $\mathrm{△}ABC$.

Como el centro de homotecia se encuentra en la recta que pasa por cualquier par de puntos homólogos, entonces el centro de homotecia de $\mathrm{△}DEF$ y $\mathrm{△}{D}^{″}{E}^{″}{F}^{″}$ se encuentra en la recta determinada por $H$ y $O$, es decir, la recta de Euler de $\mathrm{△}ABC$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Perímetro del triángulo órtico

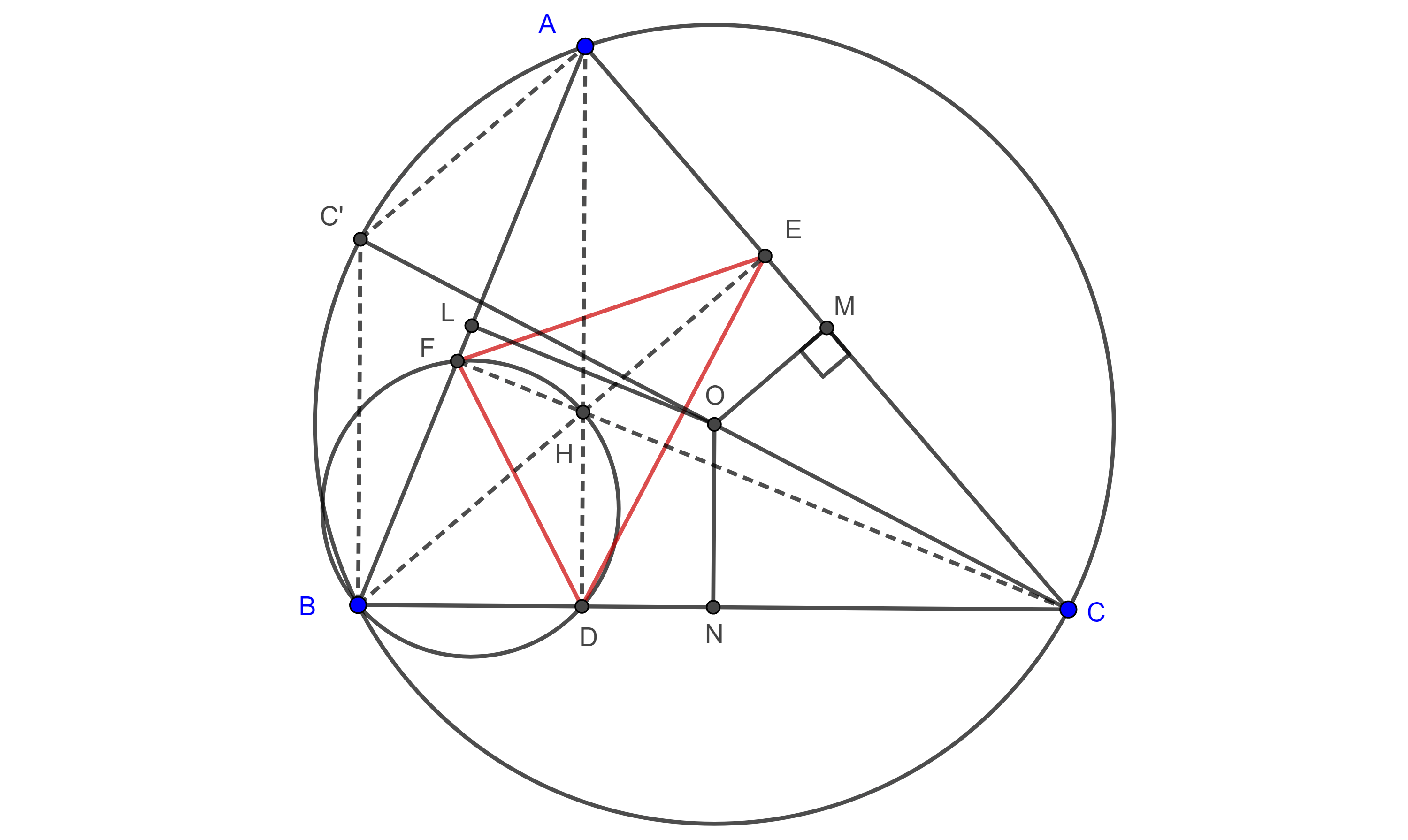
Proposición 5. Los lados del triángulo órtico de un triángulo acutángulo dividen al triángulo acutángulo en tres triángulos semejantes al triángulo dado.

Demostración. Sean $D$, $E$ y $F$ los pies de las alturas de un triangulo $\mathrm{△}ABC$ y $H$ su ortocentro, (figura 3).

Como la suma de los ángulos internos de todo cuadrilátero convexo es $2\pi$, en $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}HDCE$ tenemos $\mathrm{\angle }D+\mathrm{\angle }E=\pi$
$\Rightarrow \mathrm{\angle }C+\mathrm{\angle }H=\pi$
$\Rightarrow \mathrm{\angle }DHE=\mathrm{\angle }A+\mathrm{\angle }B$

Como $\mathrm{\angle }BHD+\mathrm{\angle }DHE=\mathrm{\angle }BHE=\pi$
$\Rightarrow \mathrm{\angle }BHD=\mathrm{\angle }C$.

Por otro lado, $\mathrm{△}FBH$ y $\mathrm{△}DBH$ son triángulos rectángulos que tienen la misma hipotenusa, por lo tanto $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}FBDH$ es cíclico.

Entonces $\mathrm{\angle }BHD=\mathrm{\angle }BFD$, pues abarcan el mismo arco
$\Rightarrow \mathrm{\angle }BFD=\mathrm{\angle }C$.

Por criterio de semejanza AA, $\mathrm{△}DBF\sim \mathrm{△}ABC$.

Podemos hacer un procedimiento similar para los demás triángulos.

Por lo tanto, $\mathrm{△}ABC\sim \mathrm{△}DBF\sim \mathrm{△}DEC\sim \mathrm{△}AEF$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 6. En un triángulo la distancia de uno de sus lados al circuncentro es igual a la mitad de la distancia del vértice opuesto al ortocentro del triángulo.

Demostración. Sea $(O,R)$ el circuncírculo de $\mathrm{△}ABC$, consideremos $C^{\prime }$ el punto diametralmente opuesto a $C$ y $M$ el pie de la perpendicular a $AC$ desde $O$, (figura 3).

Notemos que $M$ es el punto medio de $AC$ pues $O$ está en la mediatriz de $AC$.

Como $O$ es el punto medio de $C{C}^{\prime }$ entonces $OM$ es un segmento medio de $\mathrm{△}CA{C}^{\prime }$, así $2OM=C^{\prime }A$.

$\mathrm{\angle }{C}^{\prime }AC=\mathrm{\angle }CB{C}^{\prime }={\displaystyle \frac{\pi }{2}}$, pues $C{C}^{\prime }$ es diámetro

Por lo tanto, $AH$ y $C^{\prime }B$ son perpendiculares a $BC$
$\Rightarrow AH\parallel C^{\prime }B$.

Y $C^{\prime }A$ y $BH$ son perpendiculares a $AC$,
$\Rightarrow C^{\prime }A\parallel BH$.

Entonces $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}A{C}^{\prime }BH$ es un paralelogramo, por lo tanto, $BH=C^{\prime }A=2OM$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 7. La razón entre un lado de un triángulo acutángulo y el lado correspondiente a su triangulo órtico es igual a la razón entre el circunradio y la distancia del lado considerado al circuncentro.

Demostración. En la proposición 5 vimos que $\mathrm{△}ABC\sim \mathrm{△}DBF$ y que $A$, $F$, $H$ y $E$ están inscritos en una misma circunferencia cuyo diámetro es $BH$, (figura 3).

Por lo tanto, la razón entre sus circundiametros guarda la razón de semejanza, es decir,
${\displaystyle \frac{AC}{DF}}={\displaystyle \frac{2R}{BH}}={\displaystyle \frac{2R}{2OM}}={\displaystyle \frac{R}{OM}}$.

Donde $R$ es el circunradio y la segunda igualdad se debe a la proposición 6.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

 Teorema 3. El perímetro del triángulo órtico de un triángulo acutángulo es igual a dos veces el área del triángulo acutángulo dividido por el circunradio (figura 3).

Demostración. Consideremos $N$, $M$ y $L$ los pies de las perpendiculares a $BC$, $AC$ y $AB$ desde $O$ respectivamente.

Por la proposición 7 tenemos que
$DE+EF+FD={\displaystyle \frac{OL\times AB+ON\times BC+OM\times AC}{R}}$.

Y notemos que
$(\mathrm{△}ABC)=(\mathrm{△}BOC)+(\mathrm{△}COA)+(\mathrm{△}AOB)$
$={\displaystyle \frac{ON\times BC+OM\times AC+OL\times AB}{2}}$.

Por lo tanto, $DE+EF+FD={\displaystyle \frac{2(\mathrm{△}ABC)}{R}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Problema de Fagnano

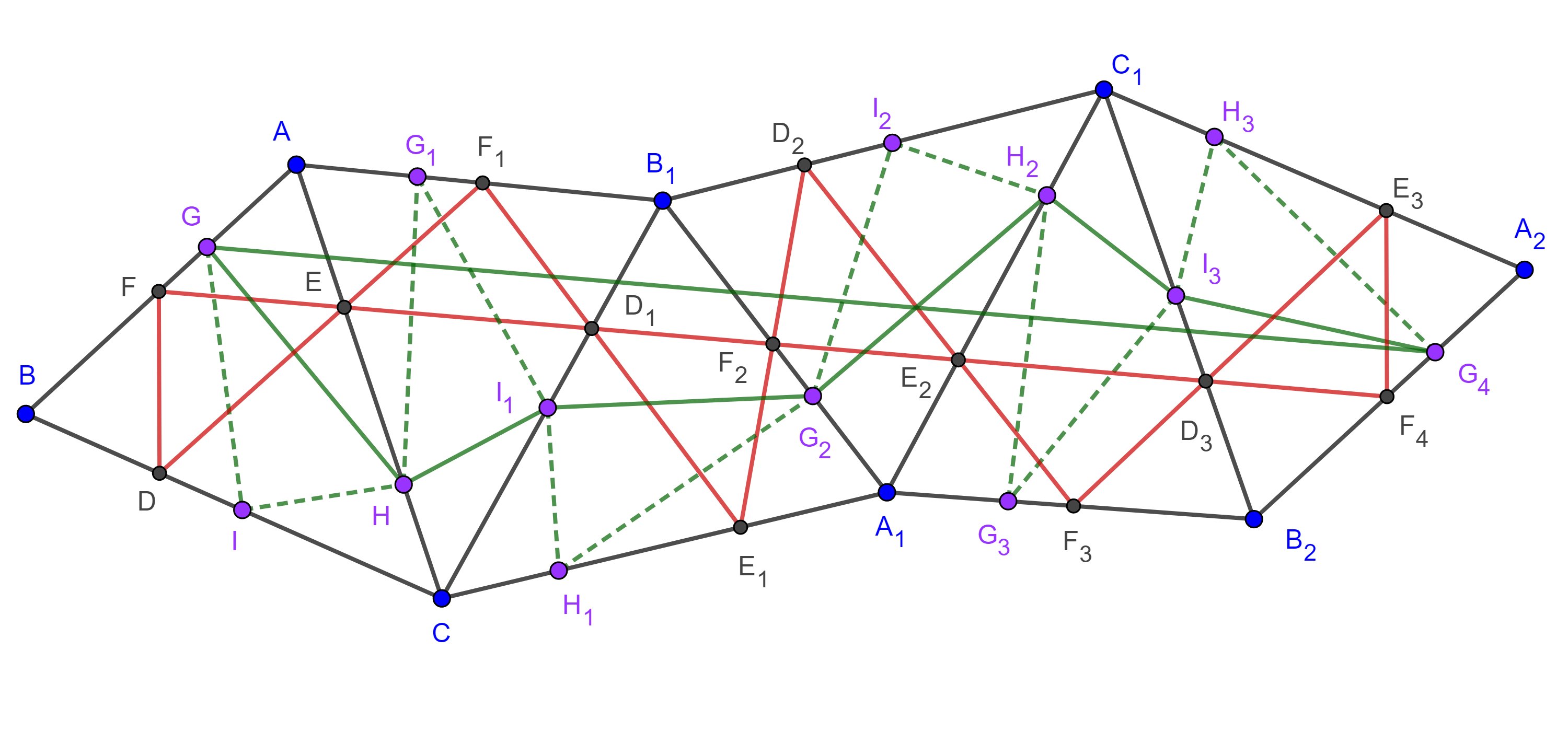
Teorema 4. De entre todos los triángulos inscritos en un triángulo acutángulo, su triángulo órtico es el de menor perímetro.

Demostración. Sean $\mathrm{△}ABC$ un triángulo acutángulo, $\mathrm{△}DEF$ su triangulo órtico y $\mathrm{△}GHI$ cualquier otro triangulo inscrito en $\mathrm{△}ABC$.

Hacemos una sucesión de reflexiones del triángulo $\mathrm{△}ABC$ a través de uno de sus lados, empezando por $AC$, luego $B_{1}C$, $B_1{A}_1$, $A_1{C}_1$ y finalmente $B_2{C}_1$ (figura 4).

El camino que sigue el segmento $AB$ es el siguiente, primerio una rotación $2\mathrm{\angle }A$ alrededor de $A$ en sentido antihorario, después una rotación $2\mathrm{\angle }B$ alrededor de $B_1$ en sentido antihorario, a continuación, una rotación $2\mathrm{\angle }A$ alrededor de $A_1$ en sentido horario y finalmente una rotación $2\mathrm{\angle }B$ alrededor de $B_2$ en sentido horario.

Por lo tanto, $AB$ y $A_2{B}_2$ son paralelas, se sigue que $F$, $G\in AB$ y sus respectivas imágenes $F_4$, $G_4\in A_2{B}_2$ forman un paralelogramo por lo que $F{F}_4=G{G}_4$.

Por otro lado, la simetría de $D$ y $D_1$ nos garantiza que $\mathrm{\angle }DEC=\mathrm{\angle }CE{D}_1$, además, por el teorema 1, $BE$ es bisectriz de $\mathrm{\angle }FED$, por lo tanto, $\mathrm{\angle }AEF=\mathrm{\angle }DEC$.

Entonces, $\mathrm{\angle }FE{D}_1=\mathrm{\angle }FED+\mathrm{\angle }DEC+\mathrm{\angle }CE{D}_1=\mathrm{\angle }FED+\mathrm{\angle }2DEC=\pi$, por lo tanto, $F$, $E$ y $D_1$ son colineales.

Por lo anterior podemos afirmar que $FE{D}_1{F}_2{E}_2{D}_3{F}_4$ es una recta, coincide con $F{F}_4$ y es igual a dos veces el perímetro del triángulo órtico.

Como no podemos hacer las mismas afirmaciones para $\mathrm{△}GHI$, tenemos que el camino $GH{I}_1{G}_2{H}_2{I}_3{G}_4$ es igual a dos veces el perímetro de $\mathrm{△}GHI$ y es claramente mayor o igual que el segmento $G{G}_4$ que equivale a dos veces el perímetro de $\mathrm{△}DEF$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Más adelante…

En la siguiente entrada veremos como los circuncírculos del triángulo medial y del triángulo órtico, coinciden para cualquier triangulo dado.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Verifica que las proposiciones $1$, $2$, $3$, $4$, y los teoremas $1$ y $2$ se cumplen también para triángulos con un ángulo obtuso.
2. Construye un triángulo dados los puntos de intersección de las alturas con el circuncírculo del triángulo.
3. Si $P$ y $Q$ son los pies de las perpendiculares desde los vértices $B$ y $C$ de un triangulo $\mathrm{△}ABC$, a los lados $DF$ y $DE$ respectivamente de su triangulo órtico, muestra que $EQ=FP$.

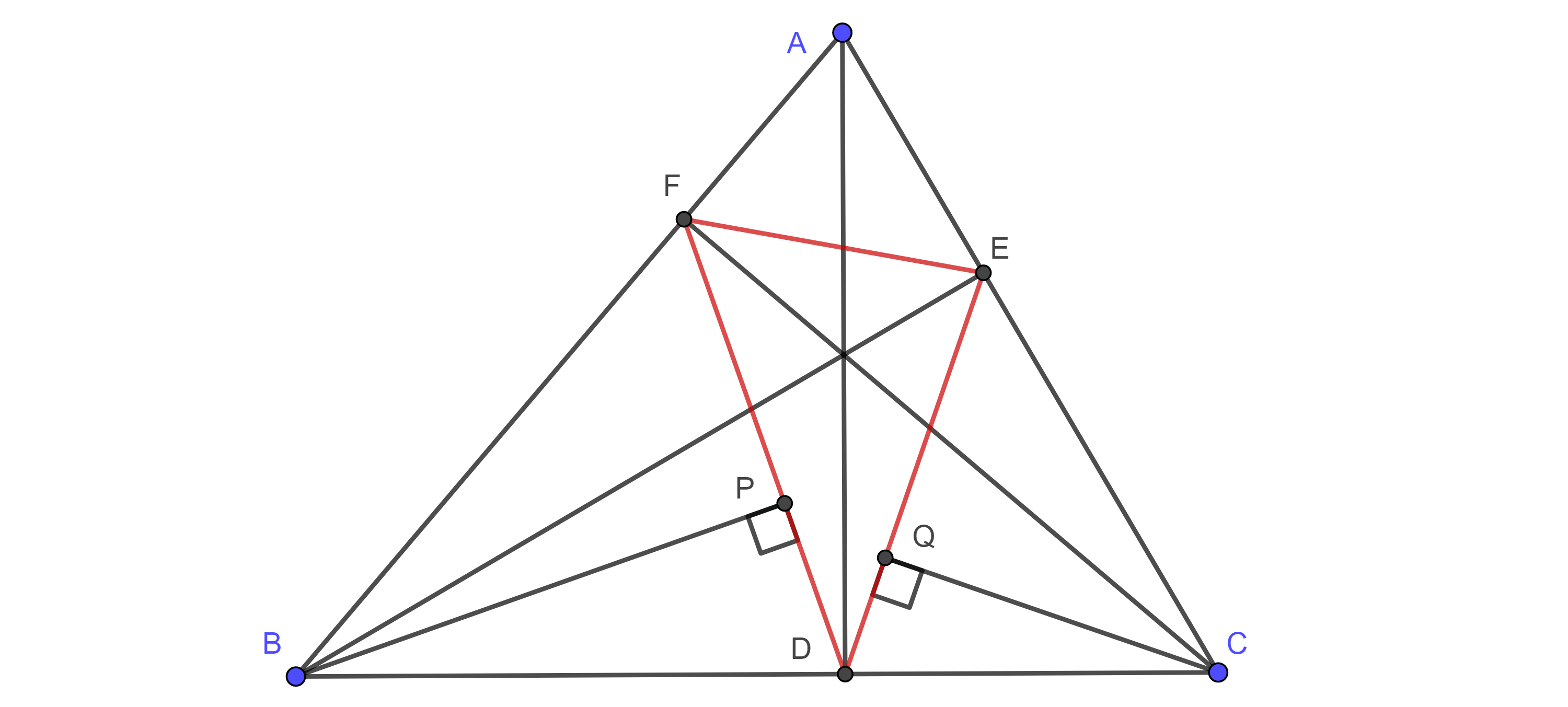
4. Muestra que los pies de las perpendiculares trazadas desde el pie de una altura en un lado de un triángulo a los otros lados y las otras alturas del triángulo son colineales.

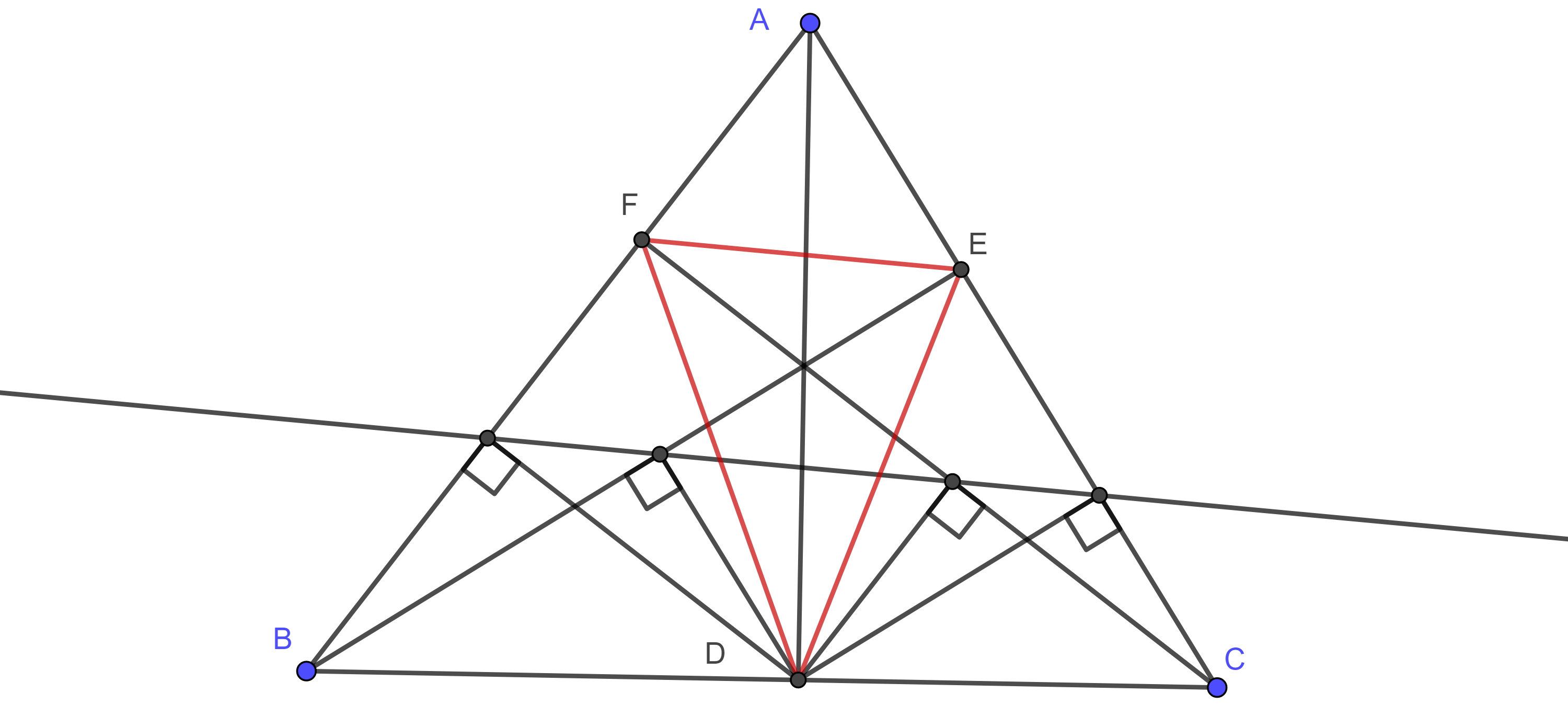
5. Demuestra que el perímetro del triángulo órtico de un triángulo acutángulo es menor o igual que dos veces cualquiera de las alturas del triángulo acutángulo.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Triángulo medial y recta de Euler.
• Siguiente entrada del curso: Circunferencia de los nueve puntos.
• Otros cursos.

Fuentes

• Altshiller, N., College Geometry. New York: Dover, 2007, pp 97-102.
• Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 16-18, 88-89.
• Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 84-85.
• Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 168-169.
• Honsberger, R., Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington: The Mathematical Association of America, 1995, pp 17-26.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»