Introducción
En esta ocasión veremos algunas proposiciones sobre concurrencia de rectas, principalmente el teorema de Ceva y su forma trigonométrica, a partir de los cuales mostraremos otros resultados.
Teorema de Ceva
Definición 1. Si una recta pasa por el vértice de un triángulo, el segmento comprendido entre el vértice y la intersección con el lado opuesto, se llama ceviana.
Teorema 1, de Ceva. Sean $\triangle ABC$ y $AX$, $BY$, $CZ$ cevianas, entonces $AX$, $BY$, $CZ$ son concurrentes si y solo si
$\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = 1$.
Demostración. Supongamos que $AX$, $BY$ y $CZ$ concurren en $S$.
Aplicamos el teorema de Menelao a $\triangle ABX$ y la trasversal $ZSC$
$\dfrac{AZ}{ZB} \dfrac{BC}{CX} \dfrac{XS}{SA} = – 1$.
Nuevamente, usamos el teorema de Menelao, ahora en $\triangle AXC$ y la transversal $BYS$
$\dfrac{AS}{SX} \dfrac{XB}{BC} \dfrac{CY}{YA} = – 1$.
Multiplicamos estas dos igualdades y reordenamos
$\dfrac{AZ}{ZB} \dfrac{XB}{CX} \dfrac{CY}{YA} \dfrac{XS}{SA} \dfrac{AS}{SX} \dfrac{BC}{BC} = 1$.
Simplificamos empleando segmentos dirigidos
$\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = 1$.
$\blacksquare$
Conversamente, supongamos que para las tres cevianas $AX$, $BY$ y $CZ$, se cumple la igualdad $\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = 1$, sea $S = BY \cap CZ$, queremos ver que $AX$ pasa por $S$.
Sea $X’ = AS \cap BC$, entonces las cevianas $AX’$, $BY$ y $CZ$ son concurrentes por lo tanto
$\dfrac{AZ}{ZB} \dfrac{BX’}{X’C} \dfrac{CY}{YA} = 1$.
Como resultado de esta igualdad y nuestra hipótesis obtenemos
$\dfrac{BX}{XC} = \dfrac{BX’}{X’C}$.
Es decir, $X$ y $X’$ dividen a $BC$ en la misma razón, por lo tanto, $X = X’$.
$\blacksquare$
Forma trigonométrica del teorema de Ceva
Forma trigonométrica del teorema de Ceva. Sean $AZ$, $BY$ y $CZ$ cevianas de un triángulo $\triangle ABC$, entonces $AX$, $BY$, $CZ$ son concurrentes si y solo si
$\dfrac{\sin \angle ACZ}{\sin \angle ZCB} \dfrac{\sin \angle BAX}{\sin \angle XAC} \dfrac{\sin \angle CBY}{\sin \angle YBA} = 1$.
Demostración. Aplicamos el lema de la razón a los puntos $X$, $Y$, $Z$ (figura 1)
$\dfrac{BX}{XC} = \dfrac{BA}{AC} \dfrac{\sin \angle BAX}{\sin \angle XAC}$,
$\dfrac{CY}{YA} = \dfrac{CB}{BA} \dfrac{\sin \angle CBY}{\sin \angle YBA}$,
$\dfrac{AZ}{ZB} = \dfrac{AC}{CB} \dfrac{\sin \angle ACZ}{\sin \angle ZCB}$.
Multiplicamos las tres igualdades
$\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} $
$= \dfrac{\sin \angle ACZ}{\sin \angle ZCB} \dfrac{\sin \angle BAX}{\sin \angle XAC} \dfrac{\sin \angle CBY}{\sin \angle YBA}$.
Por el teorema de Ceva, $\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = 1$
si y solo si $AX$, $BY$, $CZ$ son concurrentes.
Por lo tanto,
$\dfrac{\sin \angle ACZ}{\sin \angle ZCB} \dfrac{\sin \angle BAX}{\sin \angle XAC} \dfrac{\sin \angle CBY}{\sin \angle YBA} = 1$
si y solo si $AX$, $BY$, $CZ$ son concurrentes.
$\blacksquare$
Conjugados isotómicos
Proposición 1. Sea $\triangle ABC$ y $P$ un punto en el plano, sean $X = AP \cap BC$, $Y = BP \cap CA$, $Z = CP \cap AB$, considera los puntos isotómicos $X’$, $Y’$, $Z’$ de $X$, $Y$, $Z$ respectivamente, entonces las cevianas $AX’$, $BY’$, $CZ’$ son concurrentes, al punto de concurrencia se le conoce como conjugado isotómico de $P$ respecto a $\triangle ABC$.
Demostración. Como $AX$, $BY$, $CZ$ son concurrentes, por el teorema de Ceva $\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = 1$.
Ya que $X’$, $Y’$, $Z’$ son las reflexiones de $X$, $Y$, $Z$, respectivamente, respecto de los puntos medios de $BC$, $CA$ y $AB$ respectivamente entonces
$\dfrac{AZ’}{Z’B} \dfrac{BX’}{X’C} \dfrac{CY’}{Y’A}$
$= \dfrac{ZB}{AZ} \dfrac{XC}{BX} \dfrac{YA}{CY}$
$= (\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA})^{- 1} = 1$.
Por lo tanto, por el teorema de Ceva, $AX’$, $BY’$, $CZ’$ son concurrentes.
$\blacksquare$
Teorema de Blanchet
Definición 2. Si tres cevianas $AX$, $BY$, $CZ$ de un triángulo $\triangle ABC$ concurren en un punto $P$, a $\triangle XYZ$ se le conoce como triángulo de Ceva de $P$ respecto de $\triangle ABC$.
Teorema 2, de Blanchet. Sea $\triangle ABC$ y $X$ el pie de la altura por $A$, sea $P$ cualquier punto en $AX$, $\triangle XYZ$ el triángulo de Ceva de $P$ respecto de $\triangle ABC$, entonces $AX$ es la bisectriz de $\angle ZXY$.
Demostración. Sean $l$ la paralela a $BC$ por $A$, $D = XZ \cap l$, $E = XY \cap l$, entonces tenemos las siguientes semejanzas $\triangle YCX \sim \triangle YAE$, $\triangle ZAD \sim \triangle ZBX$, esto es,
$\dfrac{YC}{YA} = \dfrac{CX}{AE}$ y $\dfrac{ZA}{ZB} = \dfrac{AD}{BX}$.
Como las cevianas $AX$, $BY$, $CZ$ son concurrentes, por el teorema de Ceva tenemos
$\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = 1$.
Sustituimos las ecuaciones derivadas de la semejanza
$\dfrac{DA}{BX} \dfrac{BX}{XC} \dfrac{XC}{AE} = 1$.
Esto implica que $DA = AE$.
Como $\angle EAX = \angle XAD = \dfrac{\pi}{2}$, por criterio de congruencia LAL, $\triangle XAE \cong \triangle XAD$.
Por lo tanto, $\angle DXA = \angle AXE$.
$\blacksquare$
Teorema del nido de Ceva
Teorema 3. Sean $AD$, $BE$, $CF$ tres cevianas de un triángulo $\triangle ABC$; $DX$, $EY$, $FZ$, tres cevianas de $\triangle DEF$, si dos de las tercias $(AD, BE, CF)$; $(DX, EY, FZ)$; $(AX, BY, CZ)$, entonces la tercera también es concurrente.
Demostración. Supongamos que $(AD, BE, CF)$ y $(DX, EY, FZ)$ son concurrentes, la prueba para otros casos es análoga.
Aplicamos el lema de la razón a los triángulos $\triangle AEF$, $\triangle BFD$, $\triangle CDE$ y los respectivos puntos $X$, $Y$, $Z$,
$\dfrac{EX}{XF} = \dfrac{EA}{AF} \dfrac{\sin \angle EAX}{\sin \angle XAF}$,
$\dfrac{FY}{YD} = \dfrac{FB}{BD} \dfrac{\sin \angle FBY}{\sin \angle DBY}$,
$\dfrac{DZ}{ZE} = \dfrac{DC}{CE} \dfrac{\sin \angle DCZ}{\sin \angle ECZ}$.
Sean $X’ = AX \cap BC$, $Y’ = BY \cap CA$, $Z’ = CZ \cap AB$, recordemos que si dos ángulos son suplementarios su seno es igual, ahora multiplicamos las tres ecuaciones y reacomodamos
$\dfrac{DZ}{ZE} \dfrac{EX}{XF} \dfrac{FY}{YD}$
$= (\dfrac{AF}{FB} \dfrac{BD}{DC} \dfrac{CE}{EA})^{- 1} \dfrac{\sin \angle X’AC}{\sin \angle X’AB} \dfrac{\sin \angle Y’BA}{\sin \angle CBY’} \dfrac{\sin \angle Z’CB}{\sin \angle ACZ’}$.
Por otra parte, como $(AD, BE, CF)$ y $(DX, EY, FZ)$ son concurrentes, por el teorema de Ceva
$\dfrac{AF}{FB} \dfrac{BD}{DC} \dfrac{CE}{EA} = 1$,
$\dfrac{DZ}{ZE} \dfrac{EX}{XF} \dfrac{FY}{YD} = 1$.
Por lo tanto,
$\dfrac{\sin \angle ACZ’}{\sin \angle Z’CB} \dfrac{\sin \angle X’AB}{\sin \angle X’AC} \dfrac{\sin \angle CBY’}{\sin \angle Y’BA} = 1$.
Por la forma trigonométrica del teorema de Ceva, $AX’ = AX$, $BY’ = BY$, $CZ’ = CZ$, son concurrentes.
$\blacksquare$
Teorema de Jacobi
Teorema 4, de Jacobi. Sean $\triangle ABC$, $X$, $Y$, $Z$ puntos tales que $\angle XBC = \angle ABZ = \beta_1$, $\angle BCX = \angle YCA = \gamma_1$, $\angle CAY = \angle ZAB = \alpha_1$, entonces las rectas $AX$, $BY$, $CZ$ son concurrentes, al punto de concurrencia se le conoce como punto de Jacobi.
Demostración. Sean $\angle BAC = \alpha_0$, $\angle CBA = \beta_0$, $\angle ACB = \gamma_0$, $Q = BX \cap CA$, $R = CX \cap AB$.
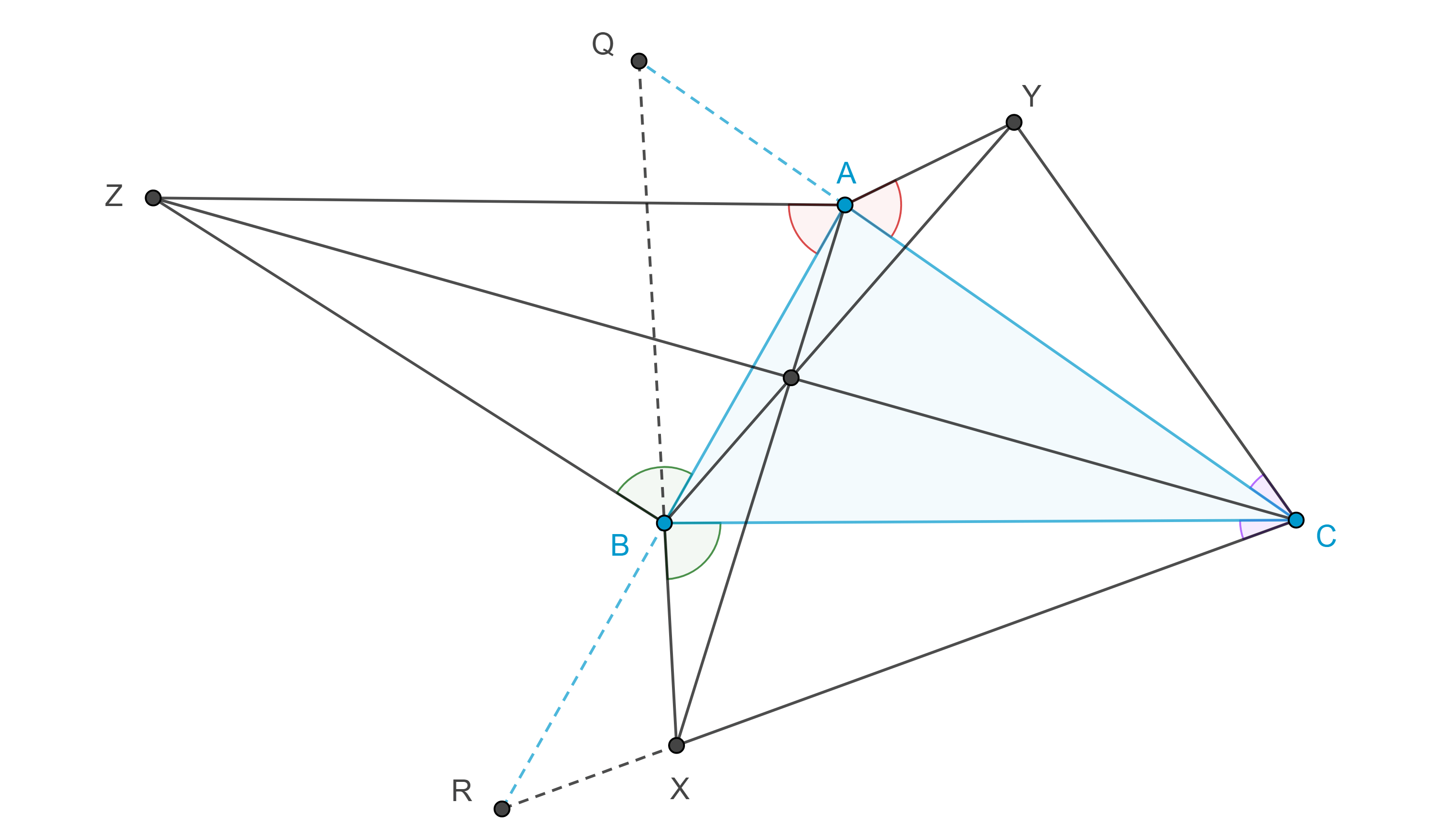
Como $AX$, $BQ$, $CR$ concurren en $X$, por el teorema de Ceva trigonométrico,
$\dfrac{\sin \angle ACR}{\sin \angle RCB} \dfrac{\sin \angle BAX}{\sin \angle XAC} \dfrac{\sin \angle CBQ}{\sin \angle QBA} = 1$.
Por lo tanto,
$1 = \dfrac{\sin \angle BAX}{\sin \angle XAC} \dfrac{\sin \gamma_0 + \gamma_1}{\sin \gamma_1} \dfrac{\sin \pi – \beta_1}{\sin \pi – (\beta_0 + \beta_1)}$
$= \dfrac{\sin \angle BAX}{\sin \angle XAC} \dfrac{\sin \gamma_0 + \gamma_1}{\sin \gamma_1} \dfrac{\sin \beta_1}{\sin \beta_0 + \beta_1}$.
Igualmente podemos encontrar
$\dfrac{\sin \angle ACZ}{\sin \angle ZCB} \dfrac{\sin \beta_0 + \beta_1}{\sin \beta_1} \dfrac{\sin \alpha_1}{\sin \alpha_0 + \alpha_1} = 1$,
$\dfrac{\sin \angle CBY}{\sin \angle YBA} \dfrac{\sin \alpha _0 + \alpha _1}{\sin \alpha _1} \dfrac{\sin \gamma _1}{\sin \gamma _0 + \gamma _1} = 1$.
Multiplicando estas tres ecuaciones y obtenemos
$\dfrac{\sin \angle ACZ}{\sin \angle ZCB} \dfrac{\sin \angle BAX}{\sin \angle XAC}\dfrac{\sin \angle CBY}{\sin \angle YBA} = 1$.
Lo que significa, por la forma trigonométrica del teorema de Ceva que $AX$, $BY$, $CZ$ son concurrentes.
Observación. Notemos que el punto de Jacobi es una generalización de los puntos de Fermat que vimos en la unidad 2.
$\blacksquare$
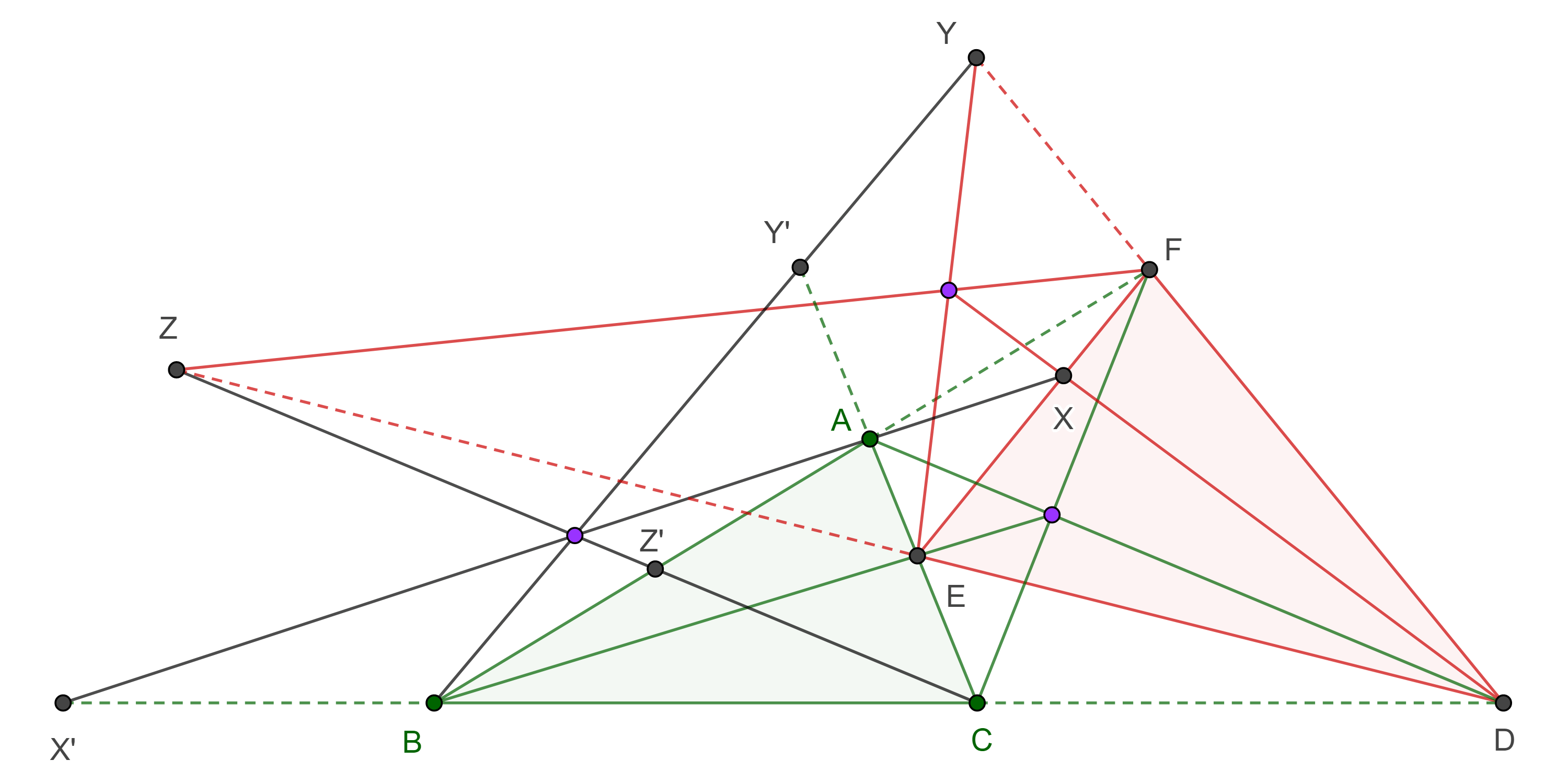
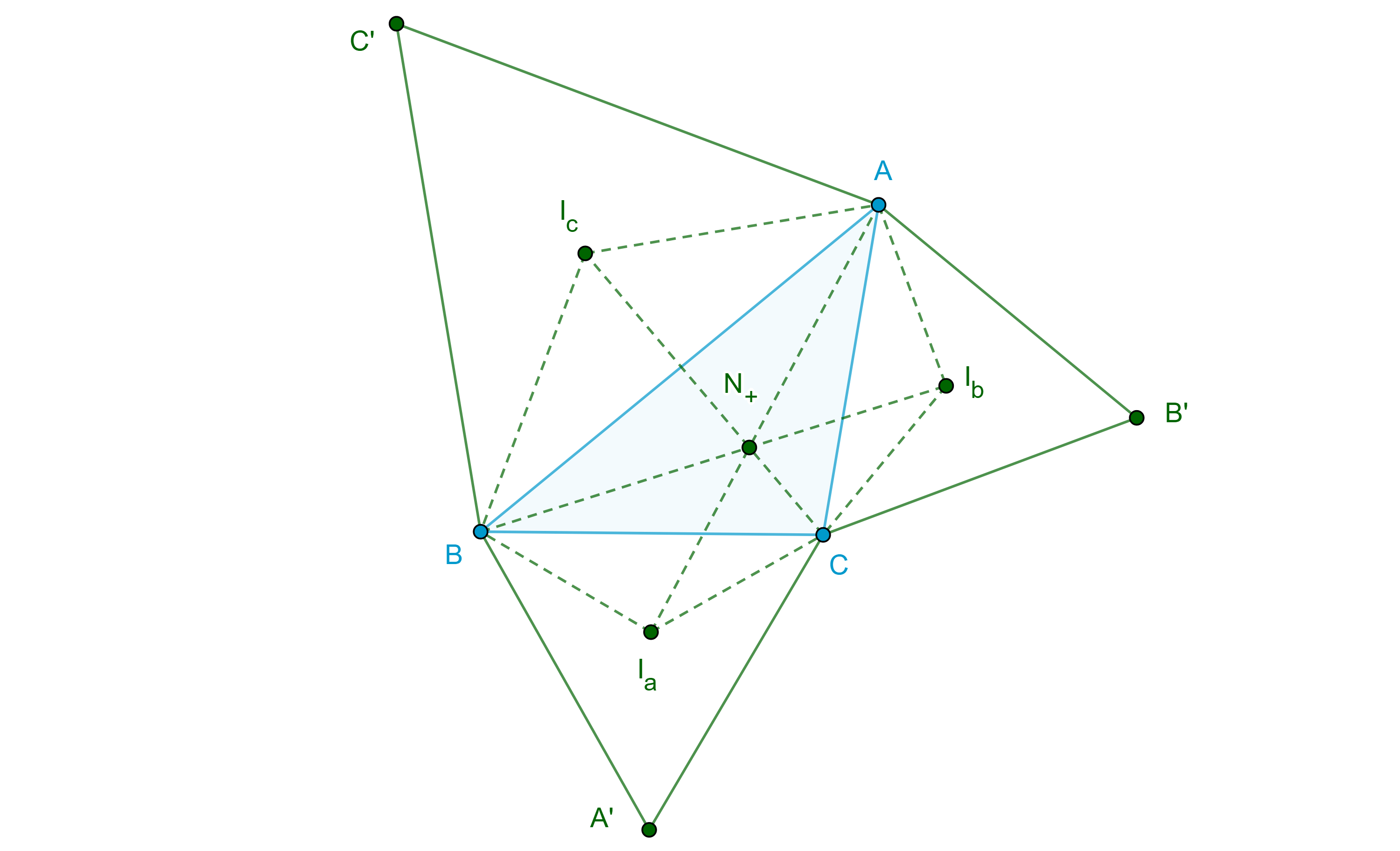
Puntos de Napoleón
Corolario. Sea $ABCA’B’C’$ una configuración externa (interna) de Napoleón, sean $I_a$, $I_b$, $I_c$, los incentros de $\triangle A’BC$, $\angle AB’C$, $\angle ABC’$ respectivamente, entonces $AI_a$, $BI_b$, $CI_c$ son concurrentes, al punto de concurrencia $N_+$ ($N_-$) se le conoce como primer (segundo) punto de Napoleón.
Demostración. Como $\triangle A’BC$, $\triangle AB’C$, $\triangle ABC’$ son equiláteros y están construidos externamente (internamente) sobre los lados de $\triangle ABC$ entonces $\angle I_aBC = \angle ABI_c = \angle BCI_a = \angle I_bCA = \angle CAI_b = \angle I_cAB = \dfrac{\pi}{6}$.
Por el teorema de Jacobi, $AI_a$, $BI_b$, $CI_c$ son concurrentes.
$\blacksquare$
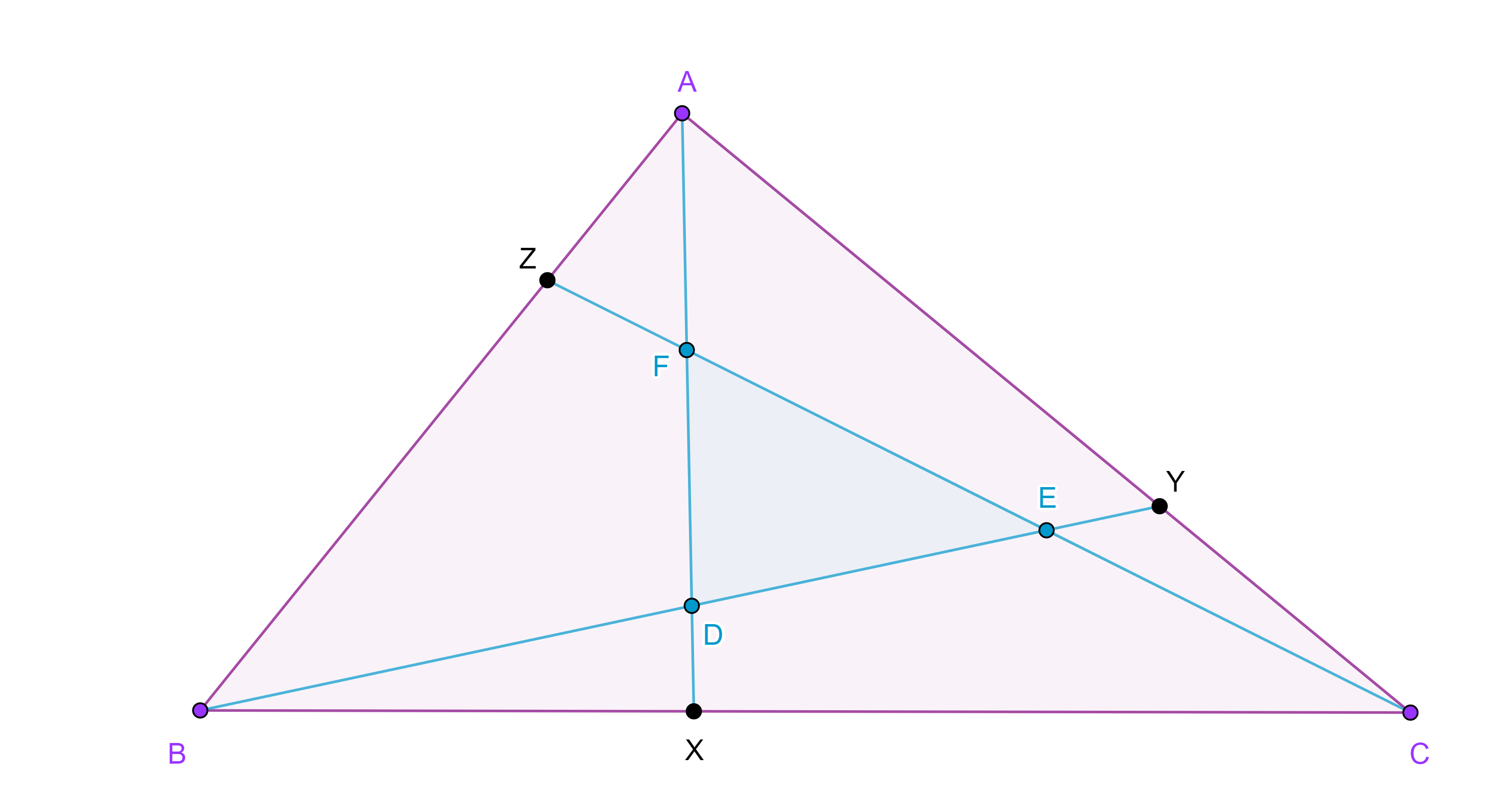
Teorema de Routh
Teorema 5, de Routh. Sean $AX$, $BY$, $CZ$ cevianas de un triángulo $\triangle ABC$ y considera $D = BY \cap AX$, $E = BY \cap CZ$, $F = AX \cap CZ$, $z = \dfrac{AZ}{ZB}$, $x = \dfrac{BX}{XC}$, $y = \dfrac{CY}{YB}$ entonces el área de $\triangle DEF$ se puede calcular mediante la siguiente formula:
$(\triangle DEF) = \dfrac{(1 – xyz)^2}{(xy + y + 1)(yz + z + 1)(zx + x + 1)}(\triangle ABC)$.
Demostración. Como $\triangle AFC$ y $\triangle AXC$ tienen la misma altura desde $C$ entonces.
$\dfrac{(\triangle AFC)}{(\triangle AXC)} = \dfrac{AF}{AX} = \dfrac{AF}{AF + FX} = \dfrac{1}{1 + \dfrac{FX}{AF}}$.
Aplicando el teorema de Menelao en $\triangle ABX$ y la transversal $ZFC$
$\dfrac{AZ}{ZB} \dfrac{BC}{CX} \dfrac{XF}{FA} = – 1$
$\Leftrightarrow \dfrac{XF}{FA} = \dfrac{ZB}{AZ} \dfrac{XC}{BC} = \dfrac{1}{z} \times \dfrac{XC}{BX + XC} = \dfrac{1}{z(x + 1)}$.
Como resultado,
$(\triangle AFC) = \dfrac{1}{1 + \dfrac{1}{z(x + 1)}}(\triangle AXC) = \dfrac{z(x + 1)}{zx + z + 1} (\triangle AXC)$
Por otro lado,
$\dfrac{(\triangle AXC)}{(\triangle ABC)} = \dfrac{XC}{BC} = \dfrac{XC}{BX + XC} = \dfrac{1}{x + 1}$.
Por lo tanto,
$(\triangle AFC) = \dfrac{z(x + 1)}{zx + z + 1} \times \dfrac{1}{1 + x} (\triangle ABC) = \dfrac{z}{zx + z + 1}(\triangle ABC)$.
Igualmente podemos encontrar
$(\triangle BDA) = \dfrac{x}{xy + x + 1}(\triangle ABC)$,
$(\triangle CEB) = \dfrac{y}{yz + y + 1}(\triangle ABC)$.
Finalmente
$(\triangle DEF) = (\triangle ABC) – (\triangle AFC) – (\triangle BDA) – (\triangle CEB)$
$= (\triangle ABC)(1 – \dfrac{z}{zx + z + 1} – \dfrac{x}{xy + x + 1} – \dfrac{y}{yz + y + 1})$
$= \dfrac{(1 – xyz)^2}{(xy + y + 1)(yz + z + 1)(zx + x + 1)} (\triangle ABC)$.
Los cálculos de la última ecuación quedan para el lector.
$\blacksquare$
Observación. Notemos que este resultado generaliza el teorema de Ceva pues si $AX$, $BY$, $CZ$ son concurrentes entonces $(\triangle DEF) = 0$, lo que implica que $\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = xyz = 1$.
Por el contrario, si $xyz = 1$, entonces $(\triangle DEF) = 0$, es decir $AX$, $BY$, $CZ$ son concurrentes.
Más adelante…
En la siguiente entrada hablaremos sobre el punto de Nagel, un punto notable del triángulo con varias propiedades interesantes, la existencia de los conjugados isotómicos nos permitirá presentar este punto.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Empleando el teorema de Menelao, muestra que las medianas, las alturas y las bisectrices internas de todo triángulo son concurrentes.
- Sea $\triangle ABC$ y $X$, $X’ \in BC$; $Y$, $Y’ \in CA$; $Z$, $Z’ \in AB$, los puntos en que una circunferencia interseca a los lados de $\triangle ABC$, prueba que si $AX$, $BY$, $CZ$ son concurrentes, entonces $AX’$, $BY’$, $CZ’$ son concurrentes.
- In un triangulo $\triangle ABC$, $D$, $E$, $F$ son los pies de las alturas desde $A$, $B$, $C$, muestra que las perpendiculares desde $A$, $B$, y $C$ a $EF$, $DF$ y $DE$, respectivamente son concurrentes.
- Si las diagonales de un cuadrilátero convexo $\square ABCD$ se intersecan en $P$ muestra que
$\dfrac{\sin \angle PAD}{\sin \angle PAB}\dfrac{\sin \angle PBA}{\sin \angle PBC}\dfrac{\sin \angle PCB}{\sin \angle PCD}\dfrac{\sin \angle PDC}{\sin \angle PDA} = 1$. - Teorema de Kariya. Sea $\Gamma(I)$ el incírculo de un triángulo $\triangle ABC$, sean $D$, $E$, $F$ los puntos de tangencia de $\Gamma(I)$ con $BC$, $CA$ y $AB$ respectivamente, sean $(I, r)$ una circunferencia con centro en $I$ y radio $r$, $X = (I, r) \cap ID$, $Y = (I, r) \cap IE$, $Z = (I, r) \cap IF$, demuestra que $AX$, $BY$, $CZ$ son concurrentes.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Triángulos en perspectiva.
- Siguiente entrada del curso: Punto de Nagel.
- Otros cursos.
Fuentes
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 37-53, 85-93.
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 158-160.
- Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 36-42.
- Wikipedia
- The University of Georgia
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»