Introducción

Continuando con el estudio de las propiedades del centroide, en esta entrada veremos que es colineal con el ortocentro y el circuncentro, y que además triseca al segmento que une dichos puntos. Para establecer estos resultados, veremos primero algunos resultados del triángulo medial de un triángulo dado.

Triángulo medial

Definición 1. Al triángulo que tiene como vértices los puntos medios de un triángulo dado se le conoce como triángulo medial o triángulo complementario del triángulo dado.

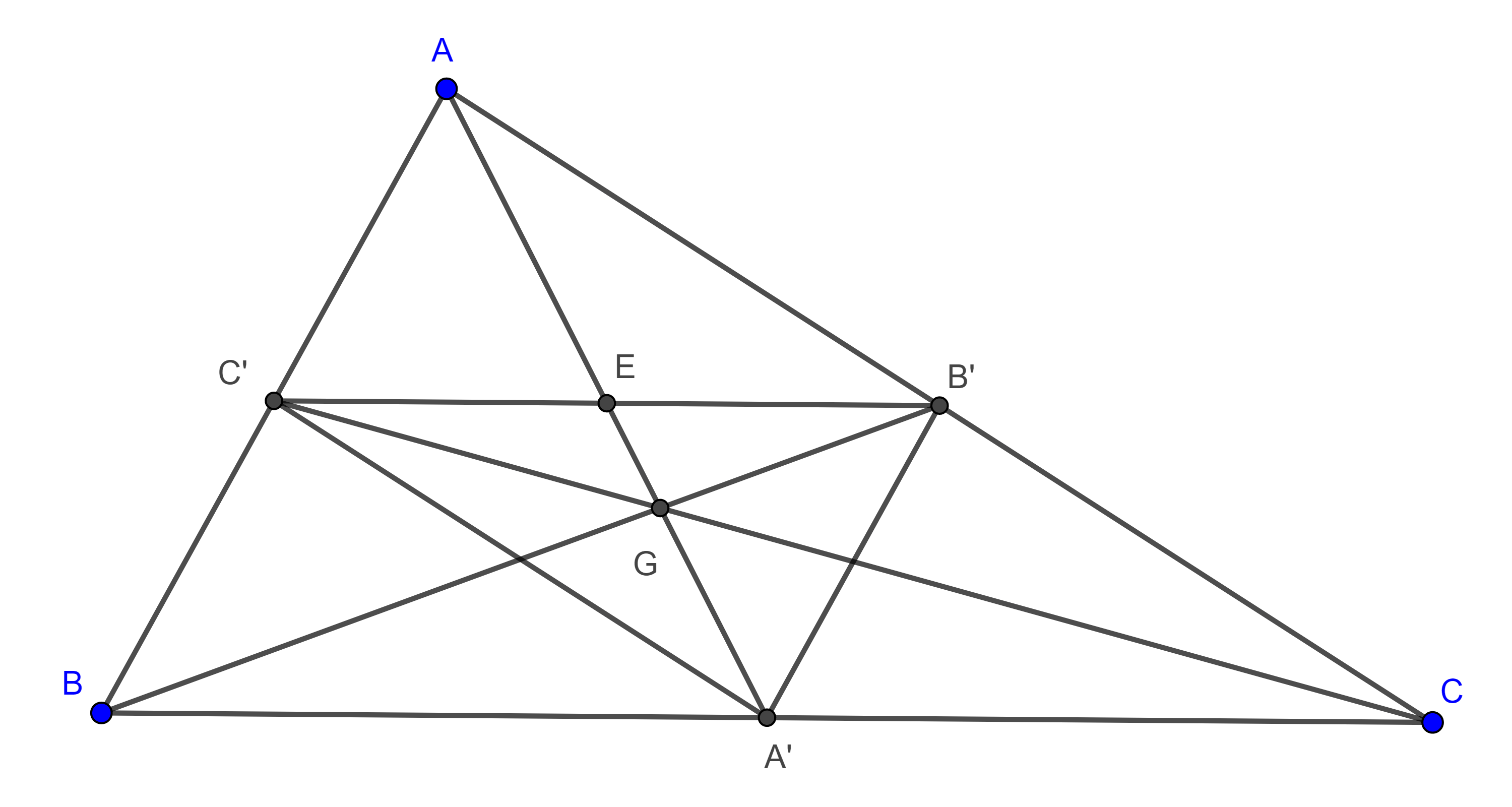
Teorema 1. Un triángulo y su triángulo medial son homotéticos además comparten el mismo centroide.

Demostración. Sean $\triangle ABC$, $A’$, $B’$ y $C’$ los puntos medios de $BC$, $AC$ y $AB$ respectivamente.

Por el teorema del segmento medio, los lados del triángulo medial $\triangle A’B’C’$ son paralelos a los lados de $\triangle ABC$ y por lo tanto son homotéticos.

Ya que las rectas determinadas por dos puntos homólogos, $AA’$, $BB’$ y $CC’$ son las medianas de $\triangle ABC$, entonces el centroide $G$ es el centro de homotecia y sabemos que $AG = 2GA’$, por lo que la razón de homotecia es $\dfrac{-1}{2}$, donde el signo menos indica que dos puntos homólogos de esta homotecia se encuentran en lados opuestos respecto del centro de homotecia.

Como $BC$ y $B’C’$ son rectas homotéticas, entonces el punto homólogo de $A’ \in BC$ es $E = A’G \cap B’C’$, y como $A’$ es el punto medio de $BC$ entonces $E$ es el punto medio de $B’C’$, pues la homotecia preserva las proporciones.

Por lo tanto, $A’G$ es mediana de $\triangle A’B’C’$, de manera similar podemos ver que $B’G$ y $C’G$ son medianas de $\triangle A’B’C’$, por lo tanto, $G$ es el centroide de $\triangle A’B’C’$.

$\blacksquare$

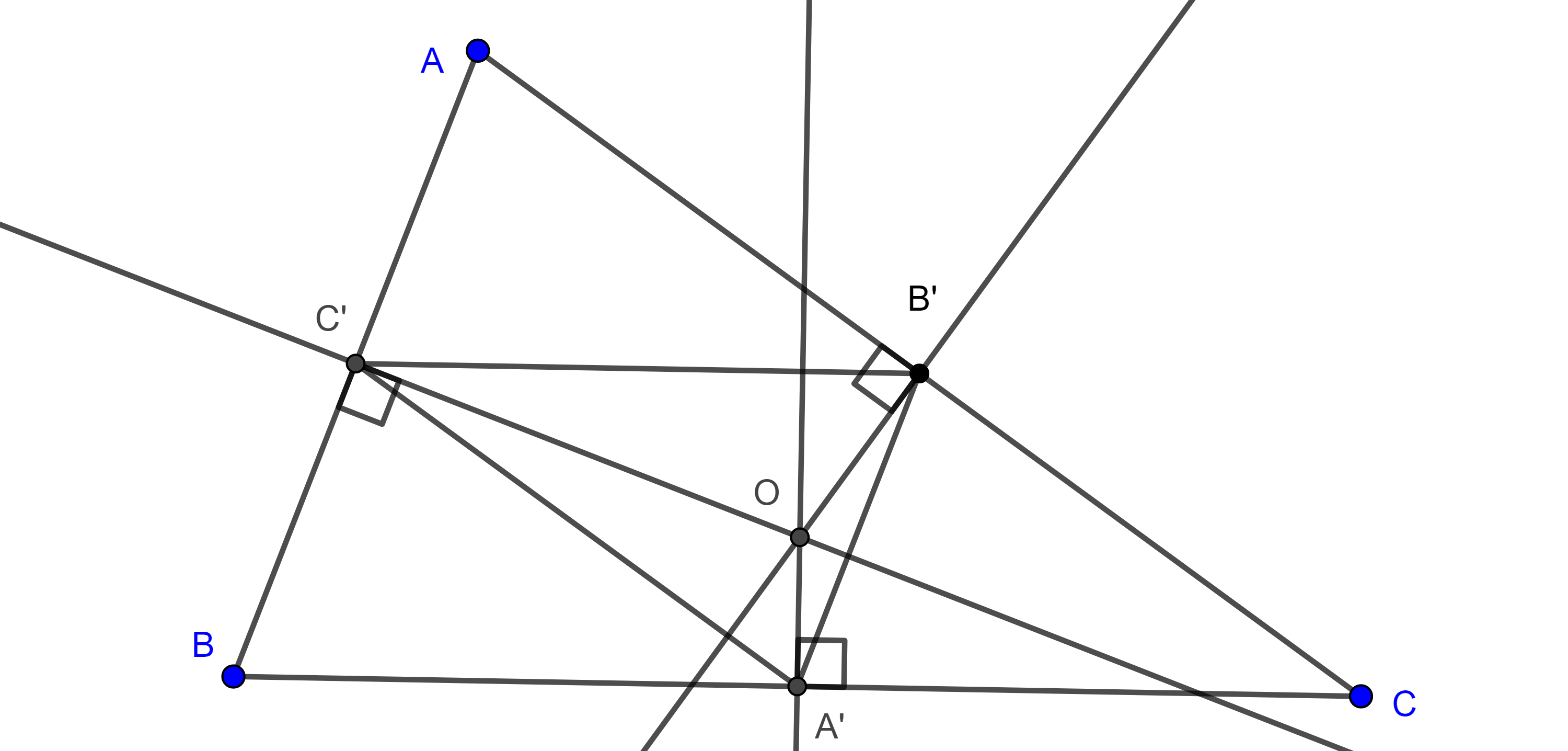
Proposición 1. El circuncentro de un triángulo es el ortocentro de su triángulo medial.

Demostración. Se sigue del hecho de que las mediatrices de un triángulo son las alturas de su triángulo medial, esto es así porque los vértices del triángulo medial son, por definición, los puntos medios de un triángulo dado y los lados del triángulo medial son paralelos a los lados del triángulo dado.

$\blacksquare$

Triángulo anticomplementario

Definición 2. Dado un triángulo, al triángulo formado por las rectas paralelas a los lados del triángulo dado a través de los respectivos vértices opuestos, se le conoce como triángulo anticomplementario del triángulo dado.

Proposición 2. Un triángulo y su triángulo anticomplementario son homotéticos y tienen el mismo centroide.

Demostración. Consideremos $\triangle ABC$ y $\triangle A’’B’’C’’$ su triángulo anticomplementario.

Como $\square C’’BCA$ y $\square ABCB’’$ son paralelogramos entonces $C’’A = BC = AB’’$, por lo tanto, $A$ es el punto medio de $B’’C’’$. De manera análoga vemos que $B$ y $C$ son puntos medio de $A’’C’’$ y $A’’B’’$ respectivamente,

Por lo tanto, $\triangle ABC$ es el triángulo medial de $\triangle A’’B’’C’’$ y por el teorema 1 se tiene el resultado.

$\blacksquare$

Circunferencia de Droz Farny

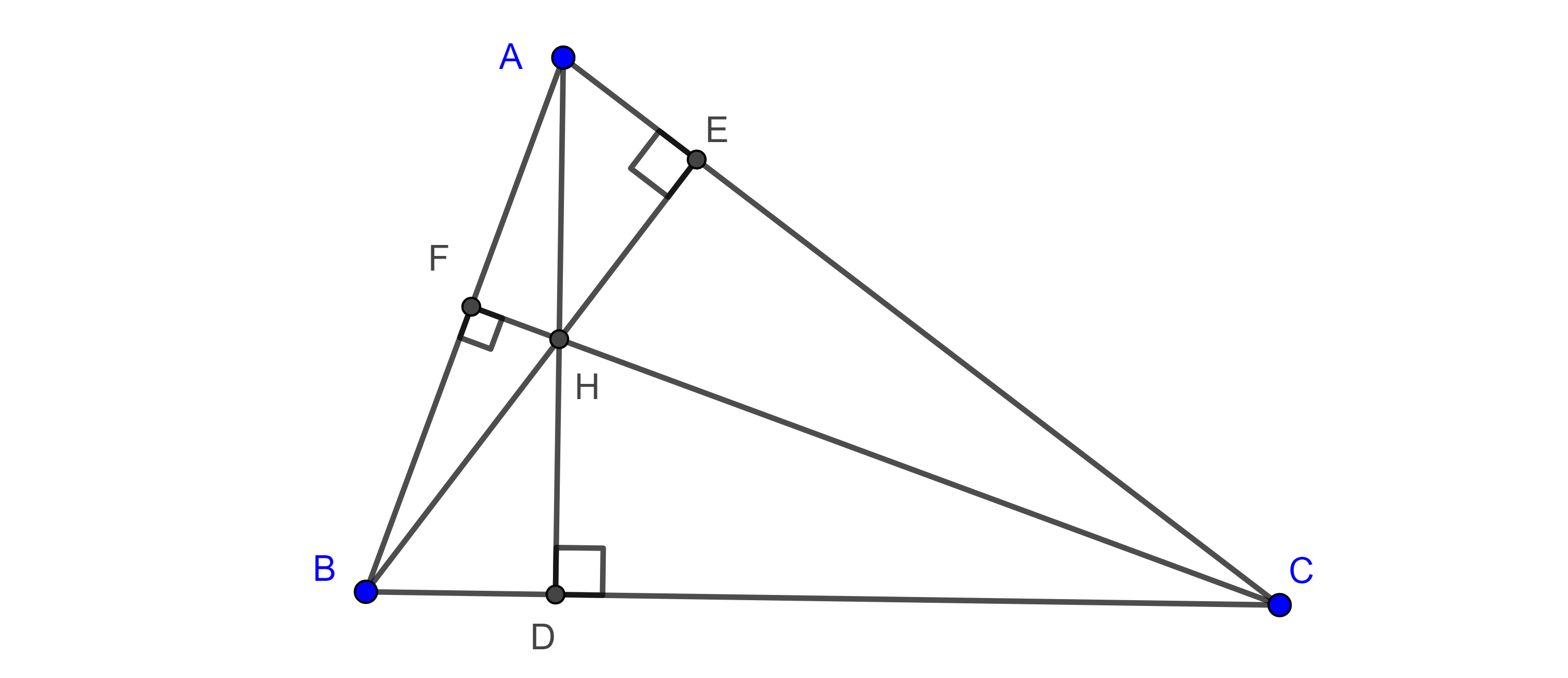
Proposición 3. El producto de los segmentos en que el ortocentro divide a la altura de un triángulo es igual para las tres alturas del triángulo.

Demostración. Sean $\triangle ABC$ y $D$, $E$ y $F$ los pies de las alturas por $A$, $B$ y $C$ respectivamente y $H$ el ortocentro.

Notemos que $\triangle AFH \sim \triangle CDH$ y $\triangle AEH \sim \triangle BDH$ (son semejantes) pues son triángulos rectángulos y comparten un ángulo opuesto por el vértice, por lo tanto
$\dfrac{AH}{CH} = \dfrac{FH}{DH}$ $\Rightarrow AH \times DH = CH \times HF$,
$\dfrac{AH}{BH} = \dfrac{EH}{DH}$ $\Rightarrow AH \times DH = BH \times HE$.

De esto se sigue que
$CH \times HF = AH \times DH = BH \times HE$.

$\blacksquare$

Teorema 2. Si tomamos los vértices de un triángulo como centros de circunferencias del mismo radio, estas cortaran a los respectivos lados de su triángulo medial en tres pares de puntos que son equidistantes del ortocentro del triángulo.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo medial, tracemos tres circunferencias del mismo radio $(A, r)$, $(B, r)$ y $(C, r)$ las cuales intersecan a $B’C’$, $A’C’$ y $A’B’$ en $P$, $P’$; $Q$, $Q’$ y $R$, $R’$, respectivamente.

Sean $D \in BC$ el pie de la altura por $A$, y $M = AD \cap B’C’$, por el teorema de Pitágoras en $\triangle AMP$ y $\triangle HMP$ tenemos
$AP^2 – AM^2 = MP^2 = HP^2 – HM^2$
$\Rightarrow AP^2 – HP^2 = AM^2 – HM^2 = (AM + HM)(AM – HM)$.

Como $\triangle AC’B’ \cong \triangle C’BA’$ son congruentes por criterio LLL entonces sus alturas desde $A$ y $C’$, respectivamente, son iguales , por lo tanto $AM = MD$,
$\Rightarrow AP^2 – HP^2 = (MD + HM)AH = HD \times AH$.

Por otra parte, $\triangle PAP’$ es isósceles y como $AM$ es altura entonces $AM$ es mediatriz de $PP’$, por lo tanto $HP = HP’$$\Rightarrow$
$\begin{equation} HP’^2 = HP^2 = AP^2 – AH \times HD. \end{equation}$.

Si consideramos $E$ y $F$ los pies de las alturas por $B$ y $C$ respectivamente podemos encontrar fórmulas análogas
$\begin{equation} HQ’^2 = HQ^2 = BQ^2 – BH \times HE, \end{equation} $
$\begin{equation} HR’^2 = HR^2 = CR^2 – CH \times HF. \end{equation} $.

Como $(A, r)$, $(B, r)$ y $(C, r)$ tienen el mismo radio, entonces $AP = BQ = CR$ y por la proposición 3, $AH \times DH = BH \times HE = CH \times HF$.

Tomando lo anterior en cuenta y a las ecuaciones $(1)$, $(2)$ y $(3)$ se sigue que
$HP = HP’ = HQ = HQ’ = HR = HR’$.

$\blacksquare$

Recta de Euler

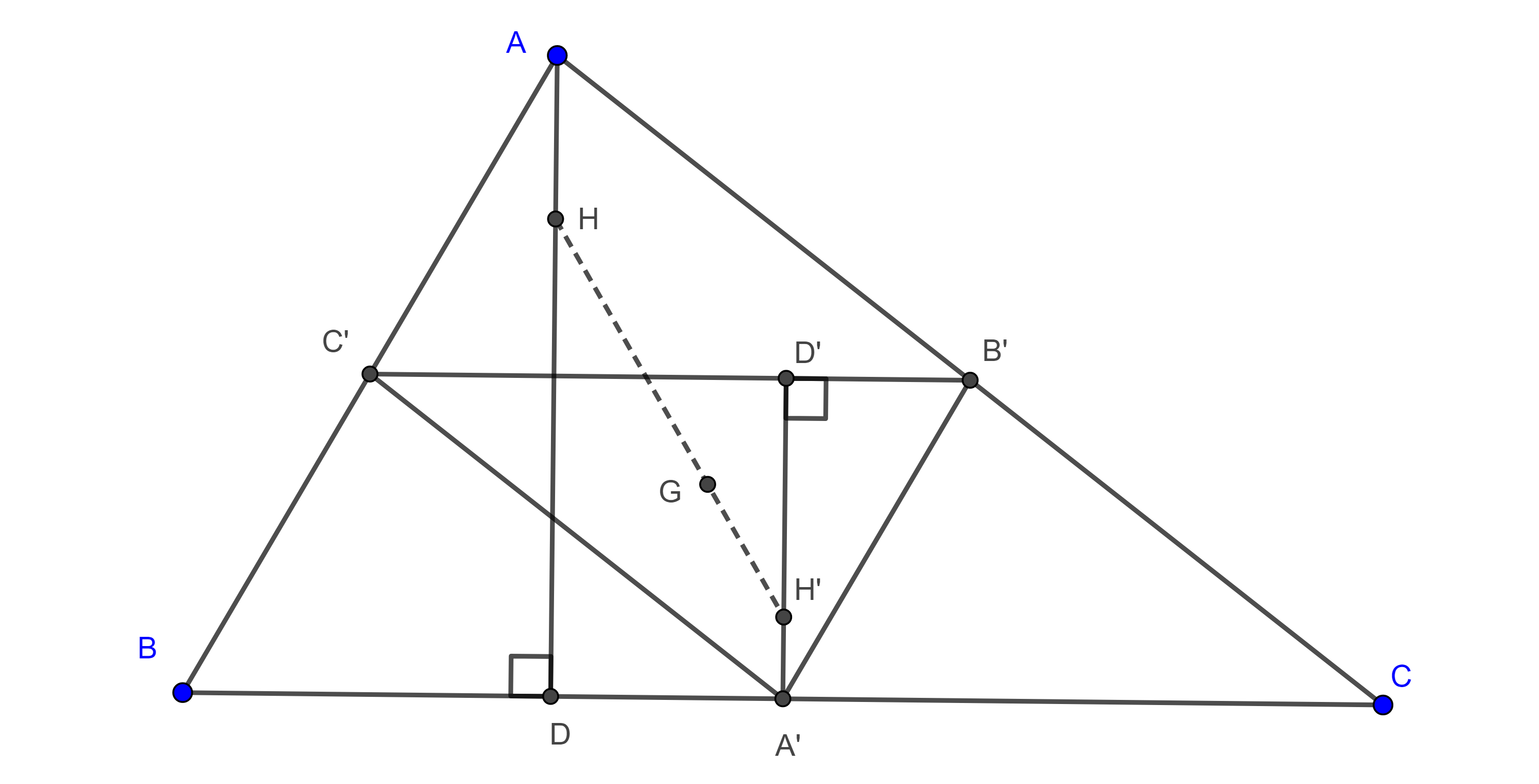
Teorema 3. El circuncentro, el centroide y el ortocentro de todo triangulo son colineales, con el centroide siempre en medio, a la recta determinada por estos tres puntos se le conoce como recta de Euler del triángulo, además $HG = 2GO$.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo medial, por el teorema 1, $\triangle ABC$ y $\triangle A’B’C’$ están en homotecia desde $G$, el centroide, que es el mismo para ambos triángulos, y la razón de homotecia es $\dfrac{-1}{2}$.

Consideremos la altura $AD$ de $\triangle ABC$, la homotecia de $AD$ es una recta paralela a ella y que pasa por el punto homólogo de $A$, $A’$, es decir la homotecia de una altura de $\triangle ABC$ es una altura de $\triangle A’B’C’$.

Como el ortocentro $H$ de $\triangle ABC$ es la intersección de sus alturas, entonces su punto homologo bajo la homotecia estará en la intersección de las alturas de $\triangle A’B’C’$, esto es, el ortocentro de $\triangle A’B’C’$, $H’$.

Con esto tenemos que el ortocentro de $\triangle A’B’C’$ es colineal con $G$ el centroide y el ortocentro de $\triangle ABC$ respectivamente, además, debido a la razón de homotecia, $HG = 2GH’$.

Por la proposición 1, el ortocentro del triángulo medial $\triangle A’B’C’$ es el circuncentro $O$ de $\triangle ABC$.

Así, $O$, $G$ y $H$ son colineales y $HG = 2GO$.

$\blacksquare$

Observación. Notemos que si el triángulo es equilátero el ortocentro, el centroide y el circuncentro son el mismo punto y por lo tanto la recta de Euler degenera en un punto.

Problema. Construye un triángulo $\triangle ABC$ dados el vértice $A$, el circuncentro $O$ y las distancias de $A$ al ortocentro $AH$, y al centroide $AG$.

Solución. El centroide $G$ se encuentra en la circunferencia con centro en $A$ y radio $AG$, $(A, AG)$, el ortocentro $H$ se encuentra en la circunferencia con centro en $A$ y radio $H$, $(A, AH)$.

Por el teorema 3 sabemos que $H$, $G$ y $O$ son colineales y que $HO = 3GO$, por lo que $H$ y $G$ se encuentran en homotecia desde $O$.

Entonces, a $(A, AH)$ le aplicamos una homotecia con centro en $O $ y razón $\dfrac{1}{3}$, esto será una circunferencia $\Gamma$ y $G$ resultara de la intersección de $\Gamma$ con $(A, AG)$.

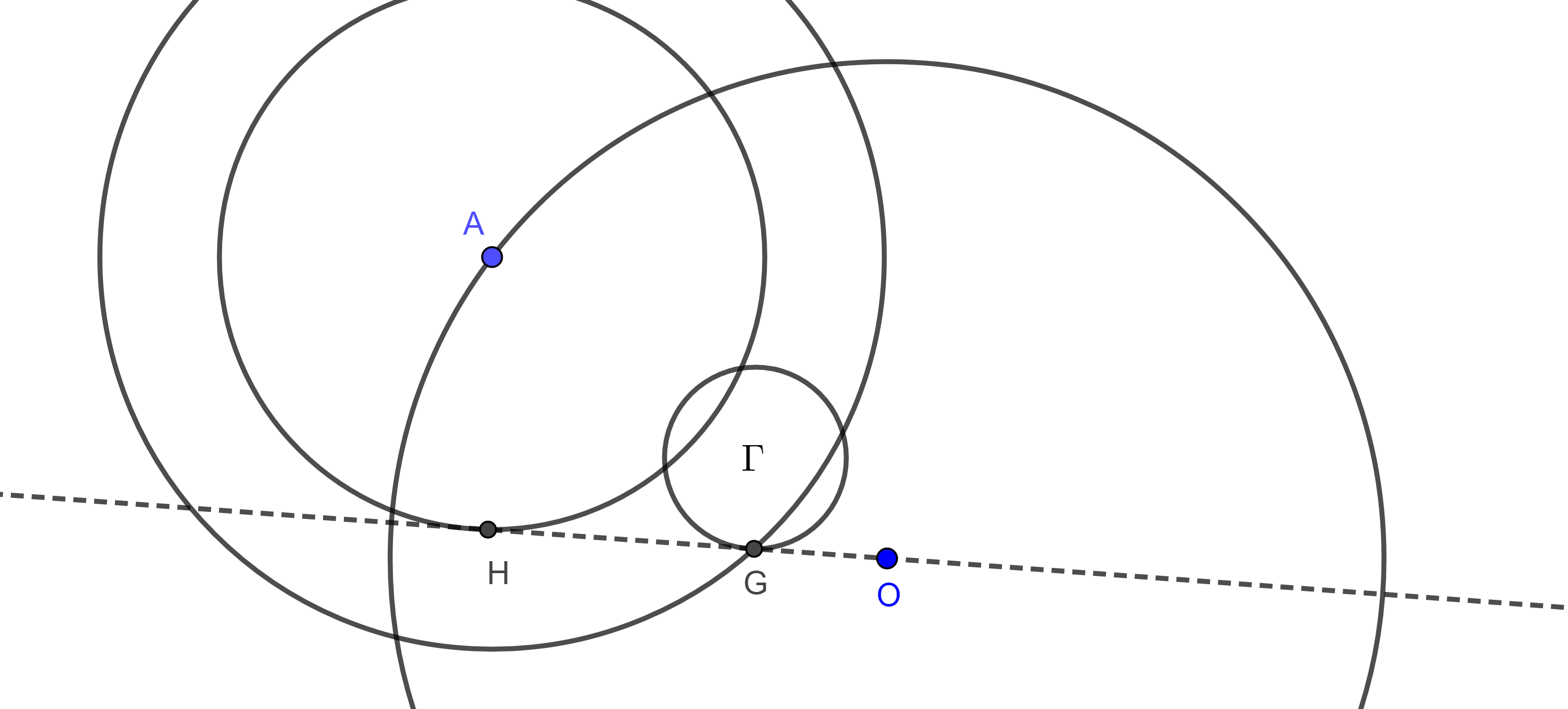
Teniendo a $G$ construido, como tenemos el circuncírculo $(O, OA)$ y un vértice del triángulo, el problema se reduce a la solución del problema 2 de la entrada anterior.

$\blacksquare$

Distancia entre puntos notables

Teorema 4. Para un triángulo con lados $a$, $b$, $c$, ortocentro $H$, centroide $G$, y circuncírculo $(O, R)$ tenemos:
$OH^2 = 9R^2 – (a^2 + b^2 + c^2)$,
$HG^2 = 4R^2 – \dfrac{4}{9}( a^2 – b^2 + c^2)$.

Demostración. Por el teorema 3 sabemos que $OH = 3OG$ y $HG = 2GO$, además en la entrada anterior calculamos
$OG^2 = R^2 – (\dfrac{a^2 + b^2 + c^2}{9})$.

Por lo tanto,
$OH^2 = 9OG^2 = 9R^2 – (a^2 + b^2 + c^2)$,
$HG^2 = 4OG^2 = 4R^2 – \dfrac{4}{9}(a^2 + b^2 + c^2)$.

$\blacksquare$

Corolario. Podemos calcular la suma de los cuadrados de las distancias del ortocentro a los vértices del triángulo en función del circunradio y los lados del triángulo con la siguiente fórmula.
$HA^2 + HB^2 + HC^2 = 12R^2 + (a^2 + b^2 + c^2)$.

Demostración. Por el teorema 4, y usando las fórmulas encontradas en la entrada anterior
$HA^2 + HB^2 + HC^2 = GA^2 + GB^2 + GC^2 + 3HG^2$,
$GA^2 + GB^2 + GC^2 = \dfrac{a^2 + b^2 + c^2}{3}$ .

Esto implica que,
$HA^2 + HB^2 + HC^2 = \dfrac{a^2 + b^2 + c^2}{3} + 12R^2 – \dfrac{4}{3}(a^2 + b^2 + c^2)$
$= 12R^2 – (a^2 + b^2 + c^2)$.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos otro triángulo asociado a un triángulo dado, aquel cuyos vértices son los pies de las alturas del triángulo dado.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Muestra que el triángulo complementario y el triángulo anticomplementario de un triángulo dado son homotéticos, encuentra el centro y la razón de homotecia.
2. Sea $\triangle ABC$ y $P$ un punto en el plano, considera $A’$, $B’$ y $C’$ los pies de las perpendiculares dese $P$ a $BC$, $AC$ y $AB$ respectivamente. Desde los puntos medios de $A’B’$, $A’C’$ y $B’C’$ traza perpendiculares a los lados de $AB$, $AC$ y $BC$ respectivamente, muestra que este último conjunto de perpendiculares son concurrentes.
3. Sean $D$, $D’ \in BC$ de un triangulo $\triangle ABC$, tal que el punto medio de $BC$ es el punto medio de $DD’$, sea $E = AD \cap B’C’$, donde $B’$ y $C’$ son los puntos medios de $AC$ y $AB$ respectivamente, muestra que $ED’$ pasa por el centroide de $\triangle ABC$.
4. Muestra que la recta de Euler de un triángulo pasa por uno de los vértices del triángulo si y solo si el triángulo es isósceles o rectángulo.
5. Prueba que la recta que une el centroide de un triangulo con un punto $P$ en su circuncírculo biseca al segmento que une el punto diametralmente opuesto a $P$ con el ortocentro.
6. Sean $H$, $G$, $(O, R)$ y $(I, r)$, el ortocentro, el centroide, el circuncírculo y el incírculo de un triángulo, muestra que:
   $i)$ $HI^2 + 2OI^2 = 3(IG^2 + 2OG^2)$,
   $ii)$ $3(IG^2 + \dfrac{HG^2}{2}) – IH^2 = 2R(R – 2r)$.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Medianas y centroide.
• Siguiente entrada del curso: Triángulo órtico.
• Otros cursos.

Fuentes

• Altshiller, N., College Geometry. New York: Dover, 2007, pp 68-69, 94-96, 101-102.
• Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 18-19.
• Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 65-68.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»